Background

Detecting inclusions such as acid slags in steel mill products without causing damage is important for guaranteeing their quality and performance. Ultrasonic waves are widely used to detect inclusions, and the size and location of the inclusions can be evaluated from the flight time and amplitude of the scattered wave (Sachse 1975; Bifulco & Sachse 1975). In general, an ultrasonic signal is affected by changes in size and shape as well as the elastic properties of the inclusions. Over the past few decades, many studies on material characterization using ultrasonic waves have been reported. A technique to determine the grain size and homogeneity of materials using backscattered ultrasonic waves was proposed by Willems and Goebbels (Willems & Goebbels 1981). Castagnède et al. showed the decision method to determine the elastic constants in solid using frequency shift information and the velocity of an ultrasonic wave (Castagnède et al. 1990). Luo and Bungey used surface waves to determine the Young modulus and Poisson ratio of concrete materials (Luo & Bungey 1996), and Rogers utilized the phase velocity of Lamb waves for the estimation of the elastic constants in plates (Rogers 1995).

A state-space approach (Gandossi & Simola 2006; Khan & Ramuhalli 2008; Kaipio & Somersalo 2005) based on Bayesian theory has been applied for the identification of defect properties. The Kalman filter (Kalman 1960) is a Bayesian filtering method that can estimate the state variables in a linear dynamic system. The Kalman filter was also extended for solving various linear problems (Fahrmeir 1992; Julier & Uhlmann 1997). Meanwhile, filtering algorithms such as the Monte Carlo filter (Kitagawa 1996) and the Bayesian bootstrap filter (Gordon et al. 1993) were proposed for problems with a nonlinear system. The Monte Carlo and Bootstrap filter methods express the state variables using random data sampling and associated weights. These methods are often referred to as particle filters (Kaipio & Somersalo 2005).

In this paper, a particle filter (PF) is applied for the identification of the elastic properties, wave velocity, and density of an inclusion in a steel mill component. The PF can numerically solve these identification problems to modify the state variable using available observation data. The PF is used in conjunction with a reliable numerical simulation model that describes ultrasonic wave transmission and reception in ultrasonic testing (UT). Here, ultrasonic signals are calculated with a finite integration technique (FIT) (Fellinger et al. 1995; Schubert 2004). We verify the effectiveness of the PF for UT through the demonstrations of the elastic parameters identification. In this paper, shear horizontal (SH) ultrasonic waves are used for the identification of wave velocity and density of an inclusion.

Method

Particle filter (PF)

The PF aims to estimate the state variables x t for time t while incorporating measured variable data y t . Generally, the state variables x t are hidden in the measured data. The relationship between the state variable vector x t and measured data y t is represented by the measurement model as

$$ {\boldsymbol{y}}_t = {h}_t\left({{\boldsymbol{x}}_{t\Big|t-1}}^{\left(\mathrm{i}\right)}\right)+{{\boldsymbol{w}}_{\boldsymbol{t}}}^{\left(\mathrm{i}\right)}\begin{array}{cc}\hfill, \hfill & \hfill {\boldsymbol{w}}_{\boldsymbol{t}}\hfill \end{array}\sim N\left(\kappa, {\sigma}^2\right) $$
(1)

where w t denotes the measurement noise which is distributed with a mean of κ and a variance of σ 2. The system model which describes the next state vector x t|t-1 is written by using the previous state vector x t-1 as

$$ {{\boldsymbol{x}}_{t\Big|t-1}}^{\left(\mathrm{i}\right)} = {f}_t\left({{\boldsymbol{x}}_{t-1}}^{\left(\mathrm{i}\right)}\right)+{{\boldsymbol{v}}_t}^{\left(\mathrm{i}\right)}\begin{array}{cc}\hfill, \hfill & \hfill {\boldsymbol{v}}_t\hfill \end{array}\sim N\left(\kappa, {\sigma}^2\right) $$
(2)

where v t represents the system noise. The functions h and f in Eqs. (1) and (2) are known. In the PF, a total of N samples (particles) are used to show the probabilistic density of x t , and the particles are labeled with superscripts as x t (1), x t (2), . . ., x t (N). At every step, the importance likelihood λ t of each particle is calculated as

$$ {\lambda_t}^{(i)}=\frac{ \exp \left[-\frac{1}{2}{\left({\boldsymbol{y}}_t-{h}_t\left({{\boldsymbol{x}}_{t\Big|t-1}}^{(i)}\right)\right)}^T{{\boldsymbol{R}}_t}^{-1}\left({\boldsymbol{y}}_t-{h}_t\left({{\boldsymbol{x}}_{t\Big|t-1}}^{(i)}\right)\right)\right]}{\sqrt{{\left(2\pi \right)}^m\left|{\boldsymbol{R}}_t\right|}} $$
(3)

where m indicates the number of dimensions of the vector x t , and R represents the variance-covariance matrix. The flow of calculation on the PF process in this paper is as follows:

  1. A.

    x o (i) : Initial particles are randomly generated.

  2. B.

    For t = 1, . . ., T, steps (a), (b), and (c) described below are carried out.

    1. (a)

      For each particle i, perform the following sequence:

      1. 1.

        Generate the system noise randomly : v t (i)

      2. 2.

        Predict the next state variable : x t|t-1 (i)  = f t (x t-1 (i)) + v t (i)

      3. 3.

        Calculate the likelihood of the particle : λ t (i)

    2. (b)

      Compute the summation of the likelihood as

      $$ S={\displaystyle \sum_{j=1}^N{\lambda_t}^{(j)}} $$
      (4)
    3. (c)

      Sample N times with replacement from the set of particles x t (i) according to the following normalized importance likelihood

$$ {\beta}^{(i)}=\frac{{\lambda_t}^{(i)}}{S} $$
(5)

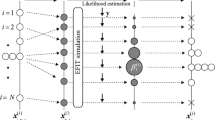
The state vectors are modified each time and updated. As shown in Fig. 1, the particles with low likelihoods are eliminated. On the other hand, those with high likelihood remain and then split for the generation of new particles. This procedure is referred to as sequential importance resampling (SIR). In the SIR, the expected sampling value of each particle is expressed as Nβ (i). Therefore, the ratio of the eliminated particle to the predicted particles \( {\left\{{{\boldsymbol{x}}_{t\Big|t-1}}^{(i)}\right\}}_{i=1}^N \) can be expressed as \( \sqrt{\beta^{(i)}\left(1-{\beta}^{(i)}\right)/N} \). It should be noted that a small sample number N may cause a large variance of the particle.

Fig. 1
figure 1

Flowchart of the prediction and resampling process in the particle filter

Full size image

The selection of the number N of particles is a key factor for the efficient and accurate identification in the PF. The computational load and the convergence of the filter depend on this number. Most applications select a fixed number of particles in advance, using ad hoc criteria or statistical methods (Boers 1999).

Finite integration technique (FIT)

A numerical tool to calculate the ultrasonic signal is introduced in the PF. Here, we utilize a FIT for modeling SH wave transmission and reception (Nakahata & Kimoto 2012). In this section, we briefly summarize the formulation of the FIT. Cartesian coordinates (x 1, x 2, x 3) are considered, and the anti-plane direction is set to the x 3-axis. The particle velocity is indicated as u 3, and the shear stresses are τ 31 and τ 32. The equation of motion and the constitutive law in the integral form are expressed as

$$ \frac{\partial }{\partial t}{\displaystyle {\int}_V\rho \left(\boldsymbol{x}\right){v}_3\left(\boldsymbol{x},t\right)dV\left(\boldsymbol{x}\right)={\displaystyle {\int}_{\partial V}{\tau}_{31}\left(\boldsymbol{x},t\right)}{n}_1}\left(\boldsymbol{x}\right)+{\tau}_{32}\left(\boldsymbol{x},t\right){n}_2\left(\boldsymbol{x}\right) dc\left(\boldsymbol{x}\right) $$
(6)
$$ \frac{\partial }{\partial t}{\displaystyle {\int}_V\frac{\tau_{3\alpha}\left(\boldsymbol{x},t\right)}{\mu \left(\boldsymbol{x}\right)}dV\left(\boldsymbol{x}\right)\kern0.5em =\kern0.5em {\displaystyle {\int}_{\partial V}{v}_3\left(\boldsymbol{x},t\right)}{n}_{\alpha }}\left(\boldsymbol{x}\right) dc\left(\boldsymbol{x}\right)\begin{array}{cc}\hfill \hfill & \hfill \left(\alpha =1,2\right)\hfill \end{array} $$
(7)

where ρ denotes the mass density, μ represents the shear modulus, and n denotes the outward normal. The shear wave velocity in a solid is expressed using the mass density and shear modulus as

$$ {c}_T=\sqrt{\frac{\mu }{\rho }} $$
(8)

Equations (6) and (7) are discretized with integration cells of small squares as shown in Fig. 2. The stress components τ 31 and τ 32 are allocated at half-time steps, while the velocity v 3 is allocated at full-time steps. The discretization in the time domain is based on a leap-frog time-marching scheme. Let V3, T31, and T32 be computational arrays to store the solutions of v 3, τ 31 and τ 32, respectively. The updating process in Eqs. (6) and (7) can be expressed as

Fig. 2
figure 2

Spatial grid arrangement of V3, T31, and T32 in the FIT for an SH wave field

Full size image
$$ {V}_3\left(i+\frac{1}{2},j+\frac{1}{2}\right)\Leftarrow {V}_3\left(i+\frac{1}{2},j+\frac{1}{2}\right)+\delta \left[{T}_{31}\left(i+1,j+\frac{1}{2}\right)-{T}_{31}\left(i,j+\frac{1}{2}\right)+{T}_{32}\left(i+\frac{1}{2},j+1\right)-{T}_{32}\left(i+\frac{1}{2},j\right)\right] $$
(9)
$$ \begin{array}{l}{T}_{31}\left(i,j+\frac{1}{2}\right)\Leftarrow {T}_{31}\left(i,j+\frac{1}{2}\right)+{\varepsilon}_1\left[{V}_3\left(i+\frac{1}{2},j+\frac{1}{2}\right)-{V}_3\left(i-\frac{1}{2},j+\frac{1}{2}\right)\right]\\ {}{T}_{32}\left(i+\frac{1}{2},j\right)\Leftarrow {T}_{32}\left(i+\frac{1}{2},j\right)+{\varepsilon}_2\left[{V}_3\left(i+\frac{1}{2},j+\frac{1}{2}\right)-{V}_3\left(i+\frac{1}{2},j-\frac{1}{2}\right)\right]\end{array} $$
(10)

where δ and ε are defined as

$$ \begin{array}{l}\delta =\frac{\varDelta t}{\rho \left(\mathrm{i}+1/2,\mathrm{j}+1/2\right)\varDelta x}\begin{array}{cc}\hfill, \hfill & \hfill {\varepsilon}_1=\hfill \end{array}\frac{1}{2}\left(\frac{1}{\mu \left(\mathrm{i}+1/2,\mathrm{j}+1/2\right)}+\frac{1}{\mu \left(\mathrm{i}\hbox{-} 1/2,\mathrm{j}+1/2\right)}\right)\frac{\varDelta t}{\varDelta x}\\ {}{\varepsilon}_2=\frac{1}{2}\left(\frac{1}{\mu \left(\mathrm{i}+1/2,\mathrm{j}+1/2\right)}+\frac{1}{\mu \left(\mathrm{i}+1/2,\mathrm{j}-1/2\right)}\right)\frac{\varDelta t}{\varDelta x}\end{array} $$
(11)

Therefore, Eqs. (9) and (10) are executed by incrementing the time step Δt in sequence. Various boundary conditions were explained by Schubert (Schubert 2004).

Since the FIT uses a unified grid size, an image-based model can be applied. In image-based modeling, a numerical model can be constructed from digital images and then pixel data can be directly fed into the FIT (Nakahata et al. 2014). In the PF, a number of simulations have to be performed to model the functional h in Eq. (1). Since a parallel calculation with graphics processing units (GPUs) showed good speed efficiency in our previous paper (Nakahata & Kimoto 2012), we use the same calculation method in this study and accelerate the FIT simulation.

Simulation of identification of elastic parameters

Consider two-dimensional (2D) problems of the identification of the SH wave velocity c T and the density ρ of an inclusion in a steel material. The state variables for this problem are expressed as

$$ \boldsymbol{x}={\left[{c}_T,\rho \right]}^{\mathrm{T}} $$
(12)

In this paper, these two variables are independent of the time. Therefore, the system model can be expressed using the prior state and system noise as

$$ {{\boldsymbol{x}}_{t\Big|t-1}}^{\left(\mathrm{i}\right)}={{\boldsymbol{x}}_{t-1}}^{\left(\mathrm{i}\right)}+{{\boldsymbol{v}}_{\boldsymbol{t}}}^{\left(\mathrm{i}\right)} $$
(13)

As shown in Fig. 3, we consider an inclusion with a diameter of 10 mm, which is embedded in steel (c T  = 3100 m/s, ρ = 7850 kg/m3). An ultrasonic SH wave with a center frequency of 1.0 MHz is transmitted into the steel material from a transducer with a diameter of 10 mm and located on the top surface. The frequency spectrum of the reflected wave from the inclusion is used in the PF identification.

Fig. 3
figure 3

The inclusion embedded in the steel material and the transducer with 1.0 MHz center frequency that is located on top of the material

Full size image

Results and discussion

In Fig. 4, a numerical example of SH wave propagation calculated with the FIT is shown. This figure illustrates the magnitude of displacement u 3(=∫v 3 dt) at certain time steps. First, the incident wave is emitted from the transducer (Fig. 4a) and then scatters at the upper interface between the steel and the inclusion. The scattered wave is recorded at the same transducer as the first reflection echo (Fig. 4c). Meanwhile, a part of the incident wave propagates through the inside of the inclusion and then scatters at the lower interface between the inclusion and the steel. The scattered wave from the lower interface is recorded as the second reflected wave (Fig. 4e).

Fig. 4
figure 4

Visualization results of ultrasonic propagation calculated with the FIT. The colors indicate the magnitude of u 3

Full size image

In this study, the Fourier spectrum of the reflected echo is used for the evaluation of the likelihood in Eq. (3). The PF uses a large number (normally more than 1000) of particles. In this research, however, ten particles (N = 10) are used due to the simplicity of the problem. As shown in Fig. 3, we assumed that the true values of c T and ρ of the inclusion were 2400 m/s and 7000 kg/m3, respectively. Although the measured signals were supposed to be used in the identification process, we substituted the artificial signal obtained via numerical calculations for the measured one. Figure 5 shows the transition of the ten particles whose initial positions were located at regular intervals. Initially, c T and ρ were distributed between 1000 and 2800 m/s, and 1000 and 10000 kg/m3, respectively. From Fig. 5, it can be seen that most particles gathered around the true value after several time steps. The convergent point can indicate the true values of c T and ρ of the inclusion.

Fig. 5
figure 5

Identification result by the PF. The initial allocation of the particles was at regular intervals with respect to c T and ρ

Full size image

Figure 6 shows another result of the PF that commenced with a different initial particle distribution. In this case, we aligned initial particles at a regular interval with respect to only c T . At first, c T and ρ were distributed between 1000 and 3000 m/s, and 4000 and 8500 kg/m3, respectively. The calculation of the PF was terminated after thirty calculation steps. Although good convergence at early steps was not seen, the particles converged on the true value eventually.

Fig. 6
figure 6

Identification result by the PF. The initial allocation of the particles was at regular intervals with respect to only c T

Full size image

Conclusions

In this paper, we proposed an identification method for determining the elastic parameters of an inclusion in a steel material as an UT tool. A PF was applied to identify the wave velocity and density in an inclusion. The PF is a data assimilation technique based on a Bayesian approach. In the PF, a FIT was used to assist the description of the measurement model in UT. In the simulation, the estimated value of the wave velocity and density showed good convergence to the true value.

In the future, we aim to validate our approach using experimentally measured signals and apply it for the identification of multivariable parameters with a large number of particles. Furthermore, we will apply our method to 3D problems using a GPU-accelerated 3D FIT simulation.