Spatio-temporal characteristics of frictional properties on the subducting Pacific Plate off the east of Tohoku district, Japan estimated from stress drops of small earthquakes

Abstract

The east coast of the Tohoku district, Japan has a high seismicity, including aftershocks of the 2011 M9 Tohoku earthquake. We analyzed 1142 earthquakes with $4.4 \le M_{W} \le 5.0$ that occurred in 2003 through 2018 and obtained spatio-temporal pattern of stress drop on the Pacific Plate that subducts beneath the Okhotsk Plate. Here we show that small earthquakes at edges of a region with a large slip during the 2011 Tohoku earthquake had high values of stress drop, indicating that the areas had a high frictional strength and suppressed the coseismic slip of the 2011 Tohoku earthquake. In addition, stress drops of small earthquakes in some of the areas likely decreased after the 2011 Tohoku earthquake. This indicates that the frictional strength decreased at the areas due to the following aftershocks of the 2011 Tohoku earthquake, consistent with a high aftershock activity. This also supports that the frictional properties on a subducting plate interface can be monitored by stress drops of small earthquakes, as pointed out by some previous studies.

Background

Tectonics and characteristics of earthquakes off the east coast of the Tohoku district, Japan

Numerous large earthquakes as well as the huge 2011 Tohoku earthquake with $M_{W}$ 9.0 have been observed off the east coast of the Tohoku district, Japan, associated with the subduction of the Pacific Plate beneath the Okhotsk Plate at a rate of 80–100 mm/year (DeMets et al. 1990). Some previous studies have suggested the spatial heterogeneity of the frictional properties on the plate interface in this region.

Yamanaka and Kikuchi (2004) analyzed source processes of large interplate earthquakes that occurred off the east coast of the Tohoku district, Japan and found that areas with a large coseismic displacement, where they refer to as asperities, distributed as stepping stones. They also pointed out that the typical size of individual asperities in northeastern Japan was M7 class and that an M8 class earthquake could be caused when several asperities were synchronized. Uchide et al. (2014) investigated spatial pattern of stress drop before the 2011 Tohoku earthquake in the same region by a method different from that of our present study. They reported a lateral variation along the strike direction of the 2011 Tohoku earthquake and pointed out that a high stress drop zone was located just south of the large slip area of the earthquake, which possibly acted as a barrier to further rupture propagation during the 2011 Tohoku earthquake. They also found a strong increase in stress drop with depth between 30 km and 60 km, and that earthquakes in shallower and deeper depths had nearly constant stress drop. Nishikawa et al. (2019) analyzed waveforms of slow earthquakes observed by the new S-net ocean-bottom seismic network and investigated their spatial distribution along the Japan Trench. They found that the area that ruptured during the 2011 Tohoku earthquake was bounded by areas that have large numbers of slow earthquakes. They reported that a segmentation likely caused to cease the coseismic rupture of the 2011 Tohoku earthquake, which provides important information for a risk assessment from future major earthquakes. Baba et al. (2020) detected very low frequency earthquakes (VLFEs) off the Hokkaido and Tohoku Pacific coasts by a matched-filter technique. They pointed out that their spatial distribution is consistent with the afterslip of the 2003 Tokachi-Oki earthquake ($M_{W}$ 8.0). They also found that the VLFE activity inside a large coseismic slip area of the 2011 Tohoku earthquake was low thereafter, whereas outside the area, VLFE activity increased after the 2011 Tohoku earthquake. These results suggest that there is significant spatial heterogeneity of the frictional properties on the plate interface in this region.

As a lot of small earthquakes have been occuring on the subducting Pacific Plate off the east coast of the Tohoku district, they provide an excellent opportunity for studying the pattern of their stress drops in both space and time and its implication with respect to the frictional properties on the plate interface. We investigated stress drops of these small earthquakes in this study following the method of Yamada et al. (2010, 2015, 2017) and discussed the correlation of their spatial pattern with the coseismic slip distribution of the 2011 Tohoku earthquake and other large historical earthquakes, as well as their temporal change. In the next subsection, we summarize the significance of stress drop analysis.

Significance of analysis on stress drop

Stress drop is a fundamental and crucial source parameter which indicates the difference between the initial and residual stress levels associated with an earthquake. Let us consider what kind of information we can retrieve from values of stress drop.

First, we will consider the effect of the initial stress. As the stress drop is the difference between the initial and final stresses, it would be affected by the heterogeneity of the initial stress. Here we have to note that a point with an extremely low initial stress will not be included inside the fault plane during an earthquake, because the dynamic stress concentration during the earthquake will not be enough to rupture the point. The heterogeneity of the initial stress will of course affect values of stress drop, but extreme heterogeneity of the initial stress will not be included in the stress drop estimates, because the value of stress drop will be estimated for each earthquake and will thus reflect the average characteristics over the fault plane. We will move on to the discussion of the effect of the dynamic stress level. Di Toro et al. (2011) showed that the dynamic frictional coefficient for regular earthquakes, whose slip rate will be around 1 m/s, will become less than 0.4. As the confining pressure would be around 200 MPa at a depth of 60 km, earthquakes with a depth of 60 km would have a value of dynamic stress level lower than 80 MPa. Because the huge heterogeneity of the initial stress will not be included in values of stress drop as we discussed earlier, this implies stress drops of these earthquakes may have the ambiguity of 80 MPa at most as an indicator of the difference between the shear strength and the dynamic stress level. This suggests that the spatial pattern of stress drop with the heterogeneity larger than the broad range of values of the dynamic stress level can be treated as the qualitative indicator of the spatial distribution of the shear strength. As a result, we would be able to treat values of stress drop as important physical proxies associated with the fault strength.

Stress drops have been vigorously investigated and have almost confirmed that the earthquake rupture is mostly self-similar (Kanamori and Anderson 1975; Abercrombie 1995; Prieto et al. 2004; Yamada et al. 2005, 2007; Kwiatek et al. 2011; Yoshimitsu et al. 2014). This self-similarity supports the fact that we can investigate the difference between the shear strength and the dynamic stress level by the stress drop analysis, independent of the earthquake size. We have to note here that the self-similarity of earthquakes for a broad range of magnitude remains a matter of debate and is not fully confirmed. Some studies have pointed out that earthquakes might have a weak dissimilarity (Malagnini et al. 2008). However, small earthquakes with a narrow range of magnitude, as investigated in this study, do not indicate a strong dissimilarity and their stress drops provide important information on frictional properties.

Heterogeneity of stress drop in space and time has been investigated, especially for the last fifteen years. Allman and Shearer (2007) estimated stress drops of small earthquakes and discussed their variations in space and time around the source region of the 2004 Parkfield, California, earthquake. They pointed out that earthquakes around the coseismic rupture area of the 2004 Parkfield earthquake had relatively higher values of stress drop. For even finer scale, Yamada et al. (2010) calculated stress drops of small earthquakes which took place on the fault plane of the 2006 Kīholo Bay earthquake with $M_{W}$ 6.7 in Hawaii and discussed the spatial characteristics of stress drop compared to the coseismic slip distribution of the earthquake. They reported that small earthquakes around patches with a large displacement during the main shock had larger values of stress drop and concluded that the spatial pattern of the stress drop reflects coherent variations in the difference of strength and the residual stress level. Urano et al. (2015) carried out a similar analysis for the 2007 Noto Hanto earthquake and pointed out that static stress drops of aftershocks in the area with a large coseismic slip during the mainshock are higher than those in a small slip area. Their result also suggests that in-situ frictional properties can be estimated from stress drops of small earthquakes, supporting the conclusion of Yamada et al. (2010). Oth (2013) pointed out that stress drops have a strong correlation to the spatial pattern of heat flow in Japan. Yamada et al. (2015) investigated an activity of swarm-like earthquakes in the Tanzawa Mountains region, Japan and found that it showed the hypocenter migration and consisted of earthquakes with a small stress drop. They concluded that the activity would be triggered by the increase of pore pressure due to fluid, that is, the decrease of the shear strength. Yamada et al. (2017) found that the spatial pattern in stress drops has a good correlation with spatial characteristics of coseismic displacements during individual historical large earthquakes off the Pacific coast of Hokkaido, Japan by the stress drop analysis of small earthquakes. Moyer et al. (2018) estimated stress drops of small earthquakes ($2.3 \le M_{W}\le 4.0$) on Gofar transform fault at the East Pacific Rise and found an inverse correlation between stress drop and the reduction of P wave velocity, which they interpreted as the effect of damage around the fault zone. They also pointed out that earthquakes following the mainshock ($M_{W} 6.0$) had lower values of stress drop, consistent with increased damage and decreased fault strength after a large earthquake. Although estimation of stress drop in general includes some assumptions such as circular faults explained in the next section, these previous studies strongly suggest that the results of stress drop indicate actual physical characteristics on fault planes of earthquakes.

Some studies, on the other hand, raised questions if the values of estimated stress drop reflect frictional properties. Hardebeck (2020) compiled stress drop catalogs of small earthquakes ($1.8 \le M \le 3.1$) in Southern California, including results of Shearer et al. (2006) and Hardebeck and Aron (2009), and investigated their spatial correlation to stress drops of moderate-to-large earthquakes, as well as the correlation among catalogs. She confirmed that stress drops of larger earthquakes would be predictable from values of stress drop for nearby smaller earthquakes. However, she also pointed out that the spatial correlation was weak between stress drops of moderate-to-large earthquakes and those of small earthquakes, suggesting that the spatial pattern of stress drop derived from the analysis of small earthquakes might be less useful for the prediction on rupture characteristics of future large earthquakes. As results of stress drop can be compared to coseismic displacements of several large earthquakes off the east coast of Tohoku district, Japan, our study will provide an example whether or not stress drops estimated from seismograms can contribute to the investigation of frictional properties on earthquake faults.

Fig. 1

a Seismicity around the study region from 2003 to 2018. Hypocenters with M equal to or greater than 3.0, as determined by JMA, are plotted. The size and color of the symbols show the magnitude and depth of earthquakes, respectively. It is clearly described that most earthquakes take place on the subduction interface of the Pacific Plate. b Epicenters of analyzed earthquakes and locations of seismic stations used in this study. The red circles show hypocenters, and the blue squares represent seismic stations, including stations of Hi-net (NIED), JMA, Hokkaido University, Hirosaki University, and Tohoku University. The depth of the upper surface of the subducting Pacific Plate is indicated by orange lines with an interval of 20 km (Kita et al. 2010; Nakajima and Hasegawa 2006; Nakajima et al. 2009). Waveforms observed at the stations N.TROH and N.IWEH are displayed in Figs. 2, 10, 11, and 12

Methods

Following the method of Yamada et al. (2010, 2015, 2017), we investigated stress drops of 1142 small earthquakes ($4.4 \le M \le 5.0$) off the east coast of Tohoku district, Japan, that occurred in 2003 through 2018 (Fig.1). Both earthquakes before and after the 2011 M9 Tohoku earthquake are included in the analysis. Note that M indicates the magnitude of an earthquake as determined by the Japan Meteorological Agency (JMA) in this paper. The hypocenters of the 1142 earthquakes were located 35.0$^\circ$ N through 41.5$^\circ$ N and 140.5$^\circ$ E through 145.0$^\circ$ E in latitude and longitude directions, respectively, with a depth of ± 15 km from the interface of the Pacific Plate, which had been derived by Nakajima and Hasegawa (2006). Because of the poor azimuthal coverage of seismic stations, the distance of 15 km in depth direction is within the range of uncertainty in the hypocenter estimation in the study area. We analyzed waveforms recorded at stations, which have been maintained by National Research Institute for Earth Science and Disaster Resilience, Japan (NIED), Hokkaido University, Hirosaki University, Tohoku University, and JMA.

A recorded seismogram as a function of time W(t) consists of the effects of the source S(t), the path from a hypocenter to a seismic station P(t), site amplification effects A(t), and the instrumental responce of a seismometer I(t), that is:

$$\begin{aligned} W(t) = S(t) * P(t) * A(t) * I(t), \end{aligned}$$

(1)

where the operator $*$ indicates convolution. Because the convolution is expressed as a scalar product in the frequency domain, the following equation holds:

$$\begin{aligned} W(f) = S(f) \cdot P(f) \cdot A(f) \cdot I(f), \end{aligned}$$

(2)

where W(f), S(f), P(f), A(f), and I(f) are expressions of W(t), S(t), P(t), A(t), and I(t) in the frequency domain, respectively. If we know the functions of P(f), A(f), and I(f), we can then obtain the Green’s function and extract the source term from the observed seismogram. As it is difficult in actual to estimate the Green’s function precisely, we adopted the method of empirical Green’s function (EGF) (Hartzell 1978).

The observed seismograms of two earthquakes at a receiver can be expressed as follows:

$$W_{1} \;(f)\; = \;S_{1} \;(f) \cdot P_{1} (f) \cdot A_{1} (f) \cdot I(f),$$

(3)

$$W_{2} (f) = \;S_{2} (f) \cdot P_{2} (f) \cdot A_{2} (f) \cdot I(f).$$

(4)

If the two earthquakes are colocated in space, the soil beneath the seismic station acts linearly independent of the amplitude of the incoming waveforms, and no velocity change takes place during the two earthquakes, then the path and site effects in Eqs. (3, 4) are exactly the same, which shows

$$\begin{aligned} P_{1}(f) = P_{2}(f), \end{aligned}$$

(5)

and

$$\begin{aligned} A_{1}(f) = A_{2}(f). \end{aligned}$$

(6)

In this case, we can derive the ratio of source effects on two earthquakes by calculating the ratio of the observed seismograms in the frequency domain,

$$\begin{aligned} \frac{W_{1}(f)}{W_{2}(f)} = \frac{S_{1}(f) \cdot P_{1}(f) \cdot A_{1}(f) \cdot I(f)}{S_{2}(f) \cdot P_{2}(f) \cdot A_{2}(f) \cdot I(f)} = \frac{S_{1}(f)}{S_{2}(f)}. \end{aligned}$$

(7)

Equation (7) gives the spectral ratio for each pair of recorded waveforms. It is assumed in this study that source spectrum of an earthquake $S^{C}(f)$ can be expressed by the omega-squared model of Boatwright (1978), which is formulated as follows:

$$\begin{aligned} S^{C}(f) = R^{C}(f) \cdot M_{0}^{C}(f) \cdot \left\{ \frac{1}{1+\left( f/f_{0}^{C} \right) ^{4}} \right\} ^{1/2}, \end{aligned}$$

(8)

where R, $M_{0}$, and $f_{0}$ are the coefficient of the radiation pattern, the seismic moment, and the corner frequency of the earthquake, respectively. C indicates the wave type, which corresponds to either P or S. This assumption suggests that we approximated the fault as a circular plane. On the spectral amplitude as a function of frequency, the source model of Boatwright (1978) has shaper bend around the corner frequency than the model of Brune (1970), which is also widely used as an omega-squared model. This characteristic of the Boatwright source model reduces the ambiguity in estimating the corner frequency, resulting in the smaller error in the stress drop analysis. This is why we adopted the Boatwright source model as an omega-squared model. Further discussion will be made in the section “Discussion”.

The deconvolved spectra of velocity $| {\dot{u}}_{r}^{C}(f) |$ can then be expressed by the following equation:

$$\begin{aligned} \left| {\dot{u}_{r}^{C} (f)} \right|\; = & \;\left| {\frac{{S_{A}^{C} (f)}}{{S_{E}^{C} (f)}}} \right| = \frac{{R_{A}^{C} \cdot M_{{0A}} }}{{R_{E}^{C} \cdot M_{{0E}} }} \cdot \left\{ {\frac{{1 + \left( {f/f_{{0E}}^{C} } \right)^{4} }}{{1 + \left( {f/f_{{0A}}^{C} } \right)^{4} }}} \right\}^{{1/2}} \\ = & \;R_{r}^{C} M_{{0r}} \cdot \left\{ {\frac{{1 + \left( {f/f_{{0E}}^{C} } \right)^{4} }}{{1 + \left( {f/f_{{0A}}^{C} } \right)^{4} }}} \right\}^{{1/2}} , \\ \end{aligned}$$

(9)

where subscripts A and E correspond to analyzed and EGF earthquakes, respectively. Moreover, $R_{r}^{C}$ and $M_{0r}$ indicate the relative values of $R_{A}^{C}/R_{E}^{C}$ and $M_{0A}/M_{0E}$, respectively. The value of $R_{r}^{C}$ is equal to 1 if the analyzed and EGF earthquakes are colocated and have exactly the same focal mechanisms. Please note that the similarity of focal mechanisms for analyzed and EGF earthquakes is not necessarily required in our analysis, because the product $P(f) \cdot A(f) \cdot I(f)$ in Eqs. (2, 3, 4, 5, 6, 7) is independent of the focal mechanism. Also, the discrepancy of focal mechanisms is considered by estimating values of $R_{r}^C M_{0r}$ in Eq. (9) for individual earthquake pairs. The sampling frequency of waveforms analyzed in this study was 100 Hz. We used waveforms of earthquakes with M3.5 in 2012 through 2018 (after the 2011 Tohoku earthquake) which were closest to the hypocenters of the analyzed earthquakes as the EGFs. A list of analyzed and EGF earthquakes in this study is available as an additional file (refer to Additional file 1).

We adopted M3.5 earthquakes as EGFs and analyzed corner frequencies of earthquakes in a relatively narrow magnitude range ($4.4 \le M \le 5.0$) because of the following considerations. In order to ensure a good signal-to-noise ratio of EGFs, especially for spectra of lower frequencies, we used waveforms of earthquakes with M3.5 as EGFs. The lower limit (M4.4) of the analyzed earthquakes was set for keeping a difference in magnitude of about 1 compared to the EGFs and ensuring quality in estimating the corner frequencies. As stress drops are calculated for individual earthquakes, the values for large earthquakes would represent the average characteristics of individual large fault planes. This is not good condition because the values of stress drop for large earthquakes might not reflect local frictional characteristics. We can avoid this problem by adopting an upper limit of magnitude for analyzing stress drops of earthquakes. We then fixed the maximum size of earthquake in the analysis to M5.0, whose source dimension is a couple of kilometers in general.

Ideally, source areas of analyzed and EGF earthquakes should be overlapped so that we can retrieve the ratio of the source effect from Eqs. (7, 8, 9). Referring to the Additional file 1, the maximum distance between the analyzed and EGF earthquakes was 53.6 km. Although this absolute value implies that the two earthquakes were not close very much for this pair, it is acceptable in taking the ambiguity in the hypocenter determination for earthquakes far off the coast as well as the distance between the hypocenter and a seismic station into account. In addition, the file Additional file 1 shows that 95% of the earthquake pairs analyzed in this study have the distance between hypocenters less than 20 km. Compared to the distance between hypocenters of analyzed earthquakes and seismic stations, which is a few hundred kilometers, the distance between hypocenters of analyzed and EGF earthquakes (less than 20 km) suggests that the EGF earthquakes are valid and the results in this study are reliable.

We estimated the spectral ratios of P and S waves for individual pairs of an earthquake and an EGF. The spectral ratios were analyzed for three time windows with a length of 1024 data points, or 10.23 s. The begining of the first time window were set to be 0.50 s prior to the arrival times of either the P or S waves. The elapsed times of the two successive time windows were set to be 1.28 and 2.56 s, respectively. The spectral ratio can be approximated as following equations by taking the logarithm of Eq. (9):

$$\begin{aligned} \ln \left| {\dot{u}}_{r}^{C}(f) \right|\approx & {} g \left( f; f_{0A}^{C}; f_{0E}^{C} \right) , \end{aligned}$$

(10)

$$\begin{aligned} g \left( f; f_{0A}^{C}; f_{0E}^{C} \right)= & {} \ln \left( R_{r}^{C}M_{0r} \right) - \frac{1}{2}\ln \left\{ 1+\left( f/f_{0A}^{C} \right) ^{4} \right\} \nonumber \\&+ \frac{1}{2} \ln \left\{ 1+\left( f/f_{0E}^{C} \right) ^{4} \right\} . \end{aligned}$$

(11)

Before fitting individual analyzed spectral ratios with the theoretical function expressed by Eqs. (10, 11), we resampled the data points so that the interval in frequency was equal to 0.05 on a $\log _{10}$ scale. As a result, we had 20 data points (frequency bands) for each order of frequency. This procedure allowed us to treat high- and low-frequency data equivalently. We also estimated the standard deviation of the spectral ratio for each frequency band and used the value as a weight in fitting data, as explained below.

We investigated the values of $R_{r}^{C}M_{0r}$, $f_{0A}^{C}$, and $f_{0E}^{C}$ in Eq. (11) for each station by a grid search that gave the minimum residual for the spectral ratios of three time windows, which is a similar procedure as in Imanishi and Ellsworth (2006). Here values of residual R can be defined by the following equation,

$$\begin{aligned} R = \Sigma _{i} \frac{ \left\{ \ln {\dot{u}}_{r}^{C}(f_{i}) - g\left( f_{i}; f_{0A}^{C}; f_{0E}^{C} \right) \right\} ^{2} }{\sigma _{i}^{2}} \end{aligned}$$

(12)

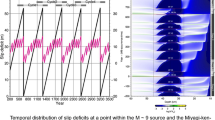
where $\sigma _{i}$ is the standard deviation for each frequency band calculated in resampling the spectral ratio. All of the earthquakes analyzed in this study have four or more stations available for calculation of the corner frequency. We used data within the frequency range of 0.7 Hz through 20 Hz for calculating the residual in Eq. (12) and investigated corner frequencies by grid search from 0.3 to 20 Hz. This frequency range and the length of the time window (10.23 s, or 1024 data points) were adopted so that corner frequencies of earthquakes with $4.4 \le M \le 5.0$ could be estimated correctly, which would be around 1–3 Hz as expected by the self-similarity of earthquakes. Figure 2 shows an example of the corner frequency analysis, including S-wave velocity seismograms, their spectra, deconvolved spectra after the resampling, and the obtained curves of spectral ratio that were used for investigating a corner frequency. Another example is provided as a supplemental figure Fig. 10, which shows the analysis for the P wave for the same earthquake and the same station as shown in Fig. 2. Examples for another earthquake are also provided as supplemental figures (Figs. 11 and 12). We confirm that waveforms have a good signal-to-noise ratio larger than a factor of five even for low frequencies between 0.7 and 2 Hz for EGF earthquakes.

Fig. 2

a Example of an analyzed waveform of an earthquake with M4.8. The horizontal color bars show three time windows used in obtaining spectra, which were (S0) – 0.50 to 9.73 s, (S1) 0.78 to 11.01 s, and (S2) 2.06 to 12.29 s after the arrival time of S wave. The gray line indicates a time window from 12.00 to 1.77 s before the P arrival, which was used to calculate the noise spectrum in (b). Individual time windows include 1,024 data points. b Waveform spectra for the four time windows marked in (a). c Example of a waveform of an M3.5 earthquake that was used for an EGF. Note that the vertical scale is different from that in (a). d Waveform spectra for the four time windows marked in (c). e Deconvolved spectra with the best-fit omega-squared model. The color lines show deconvolved source spectra, that is, (b) divided by (d), for three individual time windows with a resampling of frequency bands. The black broken line indicates the best-fit omega-squared model with corner frequencies of 1.0 and 2.5 Hz for the analyzed and EGF earthquakes, respectively

Finally, we estimated the values of stress drop following Madariaga (1976):

$$\begin{aligned} \Delta \sigma ^{C} = \frac{7}{16} M_{0A} \left( \frac{f_{0A}^{C}}{kV_{S}} \right) ^{3}, \end{aligned}$$

(13)

where $V_{S}$ is the shear wave velocity, which we set 4.5 km/s refering to Matsubara and Obara (2011), and C corresponds to the wave type (P or S). As Eq. (11) gave values of corner frequency $f_{0A}^{C}$ for individual stations, we calculated stress drop for each earthquake as the log average of values derived from Eq. (13) for individual stations. The seismic moment $M_{0}$ in newton meters (Nm) can be calculated from $M_{W}$ using the following equation Hanks and Kanamori (1979): $\log _{10} M_{0} = 1.5 M_{W} + 9.1$. We fixed the value k as 0.32 and 0.21 for P and S waves, respectively, assuming that the rupture of earthquakes expanded with a speed of $0.9V_{S}$ (Madariaga 1976). It is assumed in this study that M is equivalent to the moment magnitude $M_{W}$ in calculating stress drops. The effect of the value k on our analysis, as well as the validity of the assumption of $M = M_{W}$ will be discussed in the section “Discussion.”

Fig. 3

a Stress drops for individual earthquakes estimated from P waves. The color and scale of circles express values of stress drop and earthquake magnitudes, respectively. The thick lines show the depth of the upper surface of the subducting Pacific Plate (Kita et al. 2010; Nakajima and Hasegawa 2006; Nakajima et al. 2009). Thin contours indicate the coseismic displacement of the 2011 Tohoku earthquake with $M_W$9.0 (Iinuma et al. 2012) at an interval of 2 m. b Spatially smoothed pattern of stress drop, which was derived from (a) at grid points at intervals of 0.1 degrees in latitude and longitude. Value at individual grid points were calculated as the average of stress drops of earthquakes within 20 km of the epicentral distance from the grid points. No values were assigned at grid points with less than four earthquakes within 20 km of the epicentral distance. c Values of stress drop obtained from S waves. d Spatially smoothed pattern of stress drop derived from (c). e Spatial pattern of the stress drop ratio derived from P and S waves. f The ratio of stress drops derived from P and S waves as a function of the values estimated from S waves

Fig. 4

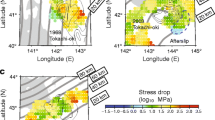
Spatially smoothed stress drop derived from (a) P-wave and (b) S-wave analyses, the same as Fig. 3. Thin contours show coseismic displacements of the following M7-8 large earthquakes for the 1968 Tokachi-oki, the 1978 Miyagi-oki, the 1981 Miyagi-oki, the 1989 Sanriku-oki, and the 2003 Miyagi-oki at an interval of 0.5 m (Nagai et al. 2001; Yamanaka and Kikuchi 2004). Areas A and B, corresponding to areas where repeating earthquakes have been observed (Uchida et al. 2007; Okuda and Ide 2018), have higher values of stress drop. Refer to the text in detail

Results

Spatial pattern of stress drop

Figures 3, 4 show the spatial distribution of stress drop estimated from P and S waves, which are superposed on the coseismic slip distribution of large earthquakes, including the 2011 Tohoku earthquake. The results of individual earthquakes in Fig. 3a, c are available as Additional files 2, 3. Both of the results derived from P and S waves indicate the quite similar pattern of spatial heterogeneity on stress drop (Fig. 3e, f), suggesting that the frictional properties on the Pacific plate are heterogeneous in space. Please note that though we carried out the grid search of the corner frequency for the frequency range between 0.3 and 20 Hz, estimated corner frequencies are roughly in the range of 1 to 7 Hz. This suggests that the results are within the range of resolvable corner frequency and do not deviate from the corner frequency fitting criterion of Abercrombie et al. (2017) and Ruhl et al. (2017).

We found that areas with a large coseismic displacement during the 1968 Tokachi-oki earthquake have higher values of stress drop. This is consistent with the result of Yamada et al. (2017) and suggests that these areas have higher shear strength. Similarly, an area with a large stress drop can be recognized at the south-east tip of the coseismic displacement during the 1978 Miyagi-oki earthquake. It is likely that the area acted as a barrier because of a higher shear strength in 1978, whereas it had been included inside the source area in 1936. In addition, the areas marked as A and B in Fig. 4 have a higher value of stress drop. Both of the areas coincide with the regions where moderate-sized earthquakes regularly take place every several years (Uchida et al. 2007; Okuda and Ide 2018). These results can also be reasonably explained that there is significant spatial heterogeneity in frictional properties and these areas have a higher shear strength.

However, we have to note that slip distributions obtained by the waveform inversion may include large uncertainty (Mai et al. 2016). The significance of the results, as well as the discrepancy between the absolute values of stress drop derived from P and S waves will be discussed in the section “Discussion.”

Fig. 5

a Spatial distribution of smoothed stress drop estimated by S-wave analyses from 2003 to 2010, which is before the 2011 Tohoku earthquake. Thin contours show the coseismic displacement of the 2011 Tohoku earthquake at an interval of 2 m, the same as Fig. 3 (Iinuma et al. 2012). Please note that values were not assigned at grid points with less than four earthquakes within 20 km of the epicentral distance. b Stress drops from 2012 to 2018. Clear temporal changes are observed associated with the 2011 Tohoku earthquake in areas C and D, corresponding to edges of the coseismic slip. c Stress drops for all the analyzed period of 2003 through 2018

Temporal change of stress drop: Effects of the 2011 Tohoku earthquake

We would also like to point out the temporal change in stress drop associated with the 2011 Tohoku earthquake. Figure 5 shows spatial patterns of stress drop before and after the 2011 Tohoku earthquake, as well as that estimated from all the earthquakes analyzed in this study (2003 through 2018). Areas marked as C and D, which correspond to western tips of the large coseismic displacement during the 2011 Tohoku earthquake, have higher values of stress drop before the earthquake (Fig. 5a). After the 2011 Tohoku earthquakes, values of stress drop in these areas decreased to the value around the average all over the study area as shown in Fig. 5b. Figure 6 shows stress drops of analyzed earthquakes as a function of depth and seismic moment, as well as the temporal changes. Stress drops of earthquakes show no clear dependency on depth, seismic moment, and time. Therefore, the temporal changes in Figs. 5a, b and 6d, e suggest the changes of frictional properties in time and are not artifacts nor apparent changes.

Fig. 6

a Values of stress drop estimated from S waves as a function of focal depth. The red circles show average values for each depth band for every 10 km. Vertical bars express standard errors for individual earthquakes, as obtained from results at individual seismic stations and components. b Values of stress drop estimated from S waves as a function of magnitude. The red circles indicate average values for individual magnitude ranges. Vertical bars show standard errors (same as (a)). c Stress drops as a function of time for all the analyzed earthquakes. d Temporal characteristics of stress drop in the area C. e Temporal features of stress drop in the area D

It was reported that the interplate seismicity became lower just after the 2011 Tohoku earthquake (Hawegawa et al. 2011). This might cause an apparent temporal change as if stress drops increased after the 2011 Tohoku earthquake if we could hardly distinguish intraplate and interplate earthquakes, because intraplate earthquakes have in general higher values of stress drop than those for interplate ones. We have checked depths and focal mechanisms of earthquakes in areas C and D on NIED F-net website (https://www.fnet.bosai.go.jp/event/joho.php?LANG=en), and confirmed the temporal changes in these areas are not apparent ones associated with the temporal change of seismicity on interplate earthquakes.

We discuss these results from physical point of view in the next section.

Discussion

Interpretation of our results from the physical viewpoint of earthquake rupture

We found that earthquakes at edges of a large coseismic slip with a large gradient in displacement during the 2011 Tohoku earthquake show a high value of stress drop. As mentioned in the subsection 1.2, stress drop is an indicator of the difference between the shear strength and the dynamic stress level. Therefore, the spatial pattern obtained in this study likely to reflect the spatial heterogeneity in frictional properties on the plate interface between the Pacific and Okhotsk plates.

In addition, stress drops of earthquakes at the above area seem to decrease after the 2011 Tohoku earthquake. This would indicate a gradual weakening of the shear strength due to the stress concentration associated with the coseismic slip during the 2011 Tohoku earthquake (Ohnaka and Shen 1999). Another possibility would be an effect of fluid (Yamada et al. 2015). As fluid confined in a crack on the plate interface can reduce the normal stress, the increase of fluid pressure can decrease the shear strength, resulting in a smaller stress drop.

It is true that a smaller stress drop would be observed if the dynamic stress level increased for some reason. However, it would be hard to be the case. As we commented in the subsection “Significance of analysis on stress drop”, Di Toro et al. (2011) pointed out that the frictional coefficient depends on the slip velocity; a slower slip velocity gives a higher frictional coefficient. Their results suggest that an earthquake with a slower slip velocity would have a higher dynamic stress level. If the decrease of stress drop were caused by a slow-down of the slip velocity, all the events after the 2011 Tohoku earthquake had to have a slower slip velocity. If this were the case, observed waveforms would have shown some notable change of their characteristics, which we did not observe at all. Therefore, we conclude that the observed temporal change in stress drop would be caused not by the increase of the dynamic stress level, but the decrease of the shear strength due to the stress concentration associated with the coseismic slip of the 2011 Tohoku earthquake.

Difference of stress drops from P and S waves

The value of stress drop for an earthquake calculated from P wave should be the same as that derived from S wave, because each earthquake has one value of stress drop. However, our results in Figs. 3,  4 indicate that the absolute values of stress drop deduced from P waves are much lower than the values derived from S waves. One possibility is that corner frequencies for P waves were underestimated because of the limited bandwidth of frequencies. If this is the case, difference of stress drops derived from P and S waves should become larger for smaller earthquakes, which in general have higher corner frequencies. Another possibility is that this discrepancy originates from the value of k in Eq. (13), that is, the rupture speed assumed in the analysis. The proportionality of stress drops estimated from P and S waves, which is clearly shown in Fig. 3e, f, supports that the latter possibility is the main reason in our analysis. As a result, the discrepancy provides an insight into the rupture characteristics of analyzed small earthquakes (Yamada et al. 2017). We briefly explain the significance of the discrepancy here.

The model of Madariaga (1976), which is used in this study and is commonly adopted in stress drop estimation, assumes that the rupture initiates from the center of a circular fault plane and propagates with a certain rupture speed that is slower than the P-wave velocity. The values of 0.32 and 0.21 for constant k in Eq. (13) depend on the assumed rupture speed, which we fixed to be $90\%$ of the shear wave velocity $V_{S}$. These factors become smaller for a slower rupture propagation, and the value k for P wave is much more sensitive to the rupture speed than that for S wave (Madariaga 1976). Because the results of stress drop from P waves in our study are smaller than those from S waves, slower rupture speeds let the values of stress drop to be closer. Thus, results in this study suggest that the actual rupture speed of the analyzed earthquakes would be slower than 0.9$V_{S}$. This is consistent with many studies of source process that reported the rupture on a fault plane propagates with a speed of $70-80\%$ of $V_{S}$, independent of earthquake size (Wald and Heaton 1994; Yamada et al. 2005), with a couple of exceptions, including Ji et al. (2002) and Walker and Shearer (2009).

Stress drops derived from P and S waves in Figs. 3, 4 show exactly the same spatial pattern. This strongly indicates that values of stress drop in this study are stably estimated and that their lateral characteristics suggest the spatial heterogeneity of the frictional properties on the interface of the subdcting Pacific Plate in the study area.

Fig. 7

Relationship between the JMA magnitude and the apparent magnitude derived as the sum of the magnitude of EGF earthquakes (3.5) and values of $\left( 2/3\right) \log \left( R_{r}^{C} M_{0r}\right)$ in Eq. (9). Results in (a, b) show those derived from P and S waves, respectively. Red circles indicate average values of apparent magnitudes for individual JMA magnitude bins

Validity associated with the assumption on earthquake magnitude

We estimated values of stress drop under the assumption that the moment magnitude $M_{W}$ is equivalent to the value of M determined by JMA. Here we investigate the validity of this assumption because it might throw an artifact in our results. Fig. 7 shows the relationship between M and values of $3.5 + \left( 2/3\right) \log _{10} \left( R^{C}_{r} M_{0r} \right)$ in Eq. (9) for individual earthquakes, which correspond to values of moment magnitude for analyzed earthquakes if individual pairs of analyzed and EGF earthquakes have identical focal mechanisms ($R^{C}_{r} =1$) and if the values of $M_{W}$ for EGF earthquakes are 3.5 (M3.5 $= M_{W}$ 3.5). We herein refer to the value of $3.5 + \left( 2/3\right) \log _{10} \left( R^{C}_{r} M_{0r} \right)$ as apparent magnitude. As we adopted earthquakes with M3.5 as EGFs, Fig. 7 suggests that the actual values of $M_{W}$ would be slightly smaller than M values, which is consistent with Uchide and Imanishi (2018). This result implies that the absolute values of stress drop derived in this study might be overestimated. However, Fig. 7 shows a clear linear correlation between the two parameters with a slope of 1. This fact strongly supports that the spatial pattern in stress drop obtained in this study is stable and reliable.

Comparison to previous studies

Uchide et al. (2014) investigated spatial pattern of stress drop before the 2011 Tohoku earthquake in the same region by a method different from that of this paper. The spatial distribution of stress drop before the 2011 Tohoku earthquake in our results is very much consistent with that shown in Uchide et al. (2014), suggesting the robustness of our analysis. However, there is a discrepancy between the two results. Although Uchide et al. (2014) insisted that they found a strong increase in stress drop with depth between 30 km and 60 km, such an increase cannot be seen in our result (Fig. 6). We are not sure of the reason, but one possibility would be the difference of waveforms used as empirical Green’s functions. We used waveforms of earthquakes (M3.5) in the vicinity of individual analyzed earthquakes with a good signal-to-noise ratio for all over the frequency band used in the analysis (Figs. 2, 10, 11 and 12) as local empirical Green’s functions so that fine-scale heterogeneity can be detected.

Cocco et al. (2016) complied stress drops calculated based on several source models, such as Brune (1970) and Madariaga (1976). Comparing to results of other studies complied in Cocco et al. (2016), results of this study have a wider variety of stress drops, including extremely high values for several earthquakes. One reason is that the rupture model of Madariaga (1976) is assumed in this study. Another reason would be that we used the model of Boatwright (1978) as an omega-squared model in estimating corner frequencies from spectral ratios. Further discussion will be made in the following two subsections.

Accumulation of the in-situ seismic data, including ones observed by S-net (Kubota et al. 2020), would provide good opportunity for investigating source characteristics, such as stress drop, of earthquakes with higher precision in the region analyzed in this paper in the near future.

Source models proposed by Brune (1970) and Boatwright (1978): effects in estimation of corner frequencies

We used the source model of Boatwright (1978) in this study, which has an omega-squared spectrum. Another source model of Brune (1970) is also widely used as an omega-squared model, which shows the broader change in spectral amplitude around the corner frequency. Here we overview the difference of the two models and discuss effects on estimating corner frequencies. Spectral ratio of the model of Brune (1970) is expressed by the following equation,

$$\begin{aligned} \left| {\dot{u}}_{r}^{C}(f) \right| = R_{r}^{C}M_{0r} \cdot \frac{1+ \left( f/f_{0E}^{C} \right) ^{2}}{1+ \left( f/f_{0A}^{C} \right) ^{2}}, \end{aligned}$$

(14)

which is similar to Eq. (9) for the model of Boatwright (1978). Fig. 8 shows synthetic spectral ratios for two pairs of waveforms in the frequency domain, following Eqs. (9) and (14). Blue and red lines indicate the ratios associated with models of Brune (1970) and Boatwright (1978), respectively. Functions in Fig. 8a, b have different corner frequencies as shown by black arrows; (a) 2.0 and 6.0 Hz, and (b) 2.0 and 30.0 Hz for larger (analyzed) and smaller (EGF) earthquakes. The factor $R_{r}^{C}M_{0r}$ in Eqs. (9) and (14) is set to 10.0. We can clearly see that the slope in proportion to $f^{-2}$ between the two corner frequencies $f_{0A}^{C}$ and $f_{0E}^{C}$ is unclear for the model of Brune (1970). This suggests that the model of Brune (1970) may include larger ambiguity in estimating the corner frequencies and the value of $R_{r}^{C}M_{0r}$ for spectral ratios with a clear proportionality to $f^{-2}$ between the two corner frequencies, such as examples shown in Figs. 2 and 10 in this study. This is a reason why we adopted the model of Boatwright (1978) in this study as an omega-squared source model.

Fig. 8

Spectral ratios for source models of Brune (1970) (blue) and Boatwright (1978) (red) as a function of frequency. Two panels have different corner frequencies of analyzed and EGF earthquakes ($f_{0A}^{C}$ and $f_{0E}^{C}$); (a) 2.0 and 6.0 Hz and (b) 2.0 and 30.0 Hz, respectively, which are shown by black arrows. The factor $R_{r}^{C}M_{0r}$ in Eqs. (9) and (14) is set to 10.0. We can clearly see that spectral ratios get asymptotically close to values of $R_{r}^{C}M_{0r}$ and $R_{r}^{C}M_{0r} \cdot \left( f_{0A}^{C}/f_{0E}^{C}\right) ^{2}$ for $f \rightarrow 0$ and $f \rightarrow +\infty$, respectively

Fig. 9

Two examples of spectral ratios with different corner frequencies. Blue and red lines indicate spectral ratios for the source model of Brune (1970) with corner frequencies of 1.6 and 40.0 Hz, and that of Boatwright (1978) with corner frequencies of 2.0 and 30.0 Hz, respectively. These corner frequencies are shown by blue and red arrows. Values of $R_{r}^{C}M_{0r}$ for models of Brune (1970) and Boatwright (1978) are equal to 10.0 and 7.0, respectively. These two functions give similar spectral ratios for the frequency range from 0.7 to 20.0 Hz, which we used in estimating corner frequencies

We have to note another point associated with estimated values of corner frequencies, or stress drops. Fig. 9 shows two examples of spectral ratios with different corner frequencies. Blue and red lines indicate spectral ratios for the source model of Brune (1970) with corner frequencies of 1.6 and 40.0 Hz, and that of Boatwright (1978) with corner frequencies of 2.0 and 30.0 Hz, respectively. Values of $R_{r}^{C}M_{0r}$ for models of Brune (1970) and Boatwright (1978) are equal to 10.0 and 7.0, respectively. These two functions give similar spectral ratios for the frequency range from 0.7 to 20.0 Hz, which we used in estimating corner frequencies. This suggests the possibility that corner frequencies of analyzed earthquakes estimated from the model of Boatwright (1978) might be higher than those derived from the model of Brune (1970). This difference of corner frequency can result in significant discrepancy in stress drop estimates by the two source models, because the value of stress drop is proportional to the value of corner frequency to the third. This may be one reason why our results include extremely high values of stress drop for several earthquakes, compared to results of Cocco et al. (2016). Please note that this does not cause any problem in discussing relative characteristics of stress drop values in space and time.

Rupture models and their effects in estimating stress drops

A model proposed by Brune (1970) is widely used for stress drop analyses. The model assumes the rupture on a circular fault happens instantly, that is, the rupture speed is infinity. It is an excellent and simple model, but it neglects a fundamental concept of the continuum mechanics that the rupture speed does not exceed the P-wave velocity. This is why we used a model of Madariaga (1976) in estimating stress drops.

Please note that the absolute values of stress drop derived from the model of Madariaga (1976) become 5.6 times larger than the values estimated by the model of Brune (1970). This is why values of stress drop in the present study are 5–10 times higher than those in other studies on stress drop.

Conclusion

We summarize our conclusion as follows.

• 1. Areas with a high stress drop are located at edges of a large coseismic slip with a high gradient in displacement during the 2011 Tohoku earthquake.

• 2. The areas with a high stress drop showed temporal change on values of stress drop after the 2011 Tohoku earthquake.

• 3. The fact (2) may indicate a gradual weakening of the shear strength due to the stress concentration associated with the coseismic slip during the 2011 Tohoku earthquake (Ohnaka and Shen 1999).

• 4. Temporal change in stress drop likely to reflect the change in the shear strength. As the dynamic stress level depends on the slip velocity (Di Toro et al. 2011), our results can hardly be explained as the change in the dynamic stress level.

Our results suggest that the frictional properties on a subducting plate interface can be monitored by stress drops of small earthquakes, as pointed out by some previous studies including Yamada et al. (2017), which provides important information for strong motion estimation due to future large earthquakes.

Appendix A. Other examples of the corner frequency analyses

In addition to Fig. 2, we will show three examples of deconvolved spectra as well as waveforms in time and frequency domains (Figs. 10, 11, 12). We can see waveforms analyzed have good signal-to-noise ratios and confirm that deconvolved spectra are well fitted by the omega-squared model.

Fig. 10

a Waveform of the UD component at the station N.TROH for the same earthquake as shown in Fig. 2a. The horizontal color bars show three time windows used in obtaining spectra, which were (P0) – 0.50 to 9.73 s, (P1) 0.78 to 11.01 s, and (P2) 2.06 to 12.29 s after the arrival time of P wave. Please refer to the figure caption of Fig. 2 for the gray line. b Waveform spectra for the four time windows shown in (a). c Waveform of the UD component at the station N.TROH for the same earthquake as shown in Fig. 2c. d Waveform spectra for the four time windows shown in (c). e Deconvolved spectra with the best-fit omega-squared model. The color lines show deconvolved source spectra, that is, ( b) divided by ( d), for three individual time windows with a resampling of frequency bands. The black broken line indicates the best-fit omega-squared model with corner frequencies of 1.0 and 3.2 Hz for the analyzed and EGF earthquakes, respectively

Fig. 11

a Example of an analyzed waveform of an earthquake with M4.4, which was recorded by the UD component at the station N.IWEH. b Waveform spectra for the four time windows shown in (a). c Example of a waveform of an M3.5 earthquake that was used for an EGF. Note that the vertical scale is different from that in (a). d Waveform spectra for the four time windows shown in (c). e Deconvolved spectra with the best-fit omega-squared model. The color lines show deconvolved source spectra, that is, (b) divided by (d), for three individual time windows with a resampling of frequency bands. The black broken line indicates the best-fit omega-squared model with corner frequencies of 10.0 and 15.8 Hz for the analyzed and EGF earthquakes, respectively

Fig. 12

a Waveform of the NS component at the station N.IWEH for the same earthquake as in Fig. 11. b Waveform spectra for the four time windows shown in (a). c Example of a waveform of an M3.5 earthquake that was used for an EGF. Note that the vertical scale is different from that in (a). d Waveform spectra for the four time windows shown in (c). e Deconvolved spectra with the best-fit omega-squared model. The color lines show deconvolved source spectra, that is, (b) divided by (d), for three individual time windows with a resampling of frequency bands. The black broken line indicates the best-fit omega-squared model with corner frequencies of 6.3 and 12.6 Hz for the analyzed and EGF earthquakes, respectively