Abstract
The deep borehole heat exchanger (DBHE) shows great potential in seasonal thermal energy storage and its high performance efficiency with smaller land occupancy attracts increasing attention as a promising geothermal energy exploitation technique. With respect to a vertical BHE with extremely long length pipes buried underground, thermal analysis of the unsteady heat transfer process of the system is quite complicated. Due to the high temperature underground, the deeper part of BHE can extract more heat from the rock, which leads to a higher heat extraction rate. The heterogeneous distribution of heat flux density and geothermal gradient cannot be described properly by the existing analytical models. Although a full 3D numerical solution can reflect these features, it always requires high computational resources and presents numerical instabilities. In this paper, we propose a hybrid modeling method with high efficiency to simulate the temperature evolution inside the DBHE, and the heat propagation front in the surrounding rock mass. The temperature evolution inside the DBHE is solved by finite difference schemes, while the heat propagation in the surrounding rock is determined by an analytical formulation of thermal impacted radius. The coupling is achieved via source/sink term by incorporating the heat flux between the DBHE and the surrounding rock. Furthermore, an innovative analytical formulation describing the heat flux density is also presented, which accounts for the key parameters affecting the thermal performance of the DBHE system. Our proposed model is further verified against results with full 3D numerical solution under the same configurations. It is demonstrated that the proposed model can capture the key physical process of the heat transfer problem, while maintaining the calculation accuracy required by the engineering application. Regarding the calculation speed, the model results are around 30 times faster when compared to the full 3D numerical solution.
Similar content being viewed by others
Introduction
Clean and renewable energy resources are drawing increasing attention due to their advantages compared to fossil fuels which have a considerable impact on global warming and environmental pollution. As one of the primary choices to replace conventional energy sources, geothermal energy is becoming more and more attractive with wide availability, low operational cost and low CO2 emissions. It has been rapidly developed for space heating and cooling in the recent decades (Diao and Fang 2006; Yang et al. 2010). Borehole heat exchangers (BHE) are the most common application in the ground source heat pump (GSHP) system for shallow geothermal energy exploitation. There are two ways of upscaling BHE installations, either by increasing the number or by extending the depth of the boreholes (Holmberg et al. 2015). Although the first alternative stands for the majority of the installations today, it requires substantial land plots to install the ground loops, which poses a great challenge for its wider applications especially in densely populated cities and towns with scarcity of area (Fang et al. 2018; Wang et al. 2017; Kristian et al. 2015; Schulte et al. 2016; Welsch et al. 2016). Ideally, deep borehole heat exchangers (DBHE) extracts geothermal energy at a depth which significantly exceeds the typical BHE length of 100 m and gets down to a depth up to 1000-3000 m below the ground surface where the temperature may reach 40–80 °C (Schulte et al. 2016; Henrik and Erling 2015; Sapinska-Sliwa et al. 2016).
With the advantages of much less land demand, potentially higher temperature available, particularly for high geothermal gradient areas, and higher efficiency of heat pump units, DBHEs can be constructed almost everywhere due to the fact that neither naturally occurring thermal aquifer systems nor special geological structures are needed (Le Lous et al. 2015; Hellström and Sanner 1994; Jia et al. 2017; Deng et al. 2019). They can be made space effective with a small or negligible visual footprint (Welsch et al. 2017) and provide a desirable complementary heat source especially for applications in cold-climate regions with a negatively balanced thermal load where more thermal energy is extracted than recharged. Therefore, they are a viable option to the traditional shallow BHEs of ground source heat pump systems. To fully benefit from the temperature increasing along a vertical deep BHE, coaxial borehole heat exchangers (CBHE) have been found to be an efficient option compared to traditional configurations such as U-tube or double-U BHEs. A deep borehole with a coaxial tube is schematically shown in Fig. 1.
Schematic of heat transfer process for deep borehole heat exchanger: inverse loop (left) and forward loop (right). Reproduced with permission from Elsevier from Bär et al. (2015); this work is licensed under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/)
Over the past few decades, notable theoretical development for modeling BHE systems includes analytical, numerical, and semi-numerical models which have been reported in the literatures (Sidiropoulos et al. 1983; Zarrella et al. 2017; Mingzhi et al. 2016; Fossa et al. 2011; Li et al. 2014; Li and Lai 2013, 2015; Zhang et al. 2015, 2016; Kim et al. 2014; Rees and He 2013; Seama and Rosen 2013; Wang et al. 2013; Zanchini and Lazzari 2014; Kolditz et al. 2012). In general, BHE modelers have paid more attention to the development of analytical solutions (Mingzhi et al. 2016; Fossa et al. 2011; Li et al. 2014; Li and Lai 2013, 2015; Zhang et al. 2016; Kim et al. 2014; Li and Lai 2012). Analytical models such as infinite line source method (IFLS) (Molina et al. 2011; Erol and Bertrand 2018), finite line source method (FLS) (Abdelaziz et al. 2014; Bandos et al. 2009), and finite cylinder source method (FCS) (Diao and Fang 2006; Eskilson 1987; Hellström 1991) have contributed greatly to the applications of vertical shallow BHEs. On the contrary, the analytical and mathematical modeling of DBHE remain poorly studied. Until recently, the analytical models for DBHEs are gaining more and more attention. Beier et al. (2011) provided analytical models for the vertical temperature profile within a DBHE with a known geothermal gradient, but did not provide the corresponding near-field modeling capabilities. Beier et al. (2014) further developed the model to account for the temperature distribution near the borehole, but simplified the far-field temperatures into a single value. However, the analytical solutions remain limited to cases that the geothermal gradient is often not taken into account. Obviously, it is not valid for DBHEs where the temperature gradient cannot be ignored from the surface to a depth of 2000–3000 m below the surface. Since heat flux at a given depth along the BHE depends on the thermal properties of each geological layer and temperature gradient, it does not necessarily distribute uniformly along the depth profile of a BHE in real scenario. Moreover, predefined uniform heat flux density distribution may lead to overestimation for lower thermal conductivity or underestimation for higher thermal conductivity of the rock (Koohi-Fayegh and Rosen 2012; Rivera et al. 2015).
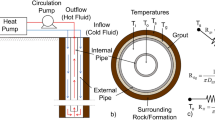
The numerical models of DBHE systems appear to be practical complements to account for the complexity of the geological settings and geothermal gradient. Diersch (2014) presented a finite element tool for the modeling of borehole heat exchangers, which demonstrated great potential to DBHE modeling. Chen et al. (2019) implemented a FEM numerical model using the open source software OpenGeoSys for the performance analysis of the DBHE. Ma et al. (2020) proposed a heat transfer analytical model for downhole coaxial heat exchangers and the piecewise calculation method was adopted both on the time scale and in the depth dimension. It was concluded that the DBHE modeling could be improved by increasing the Reynolds number, but its increments gradually decreased. Fang and Dia (2018) developed a computationally efficient method for thermal analysis by finite difference method and the numerical algorithm was validated by the reference data from simulation results by finite element method. However, in their model the dynamic far-field boundary location evolving with operation time in the radial direction was not analyzed physically, and the performance of DBHE due to a combined influence of the operation parameters (inlet water temperature and flow rate, among others) of GSHP system (see Fig. 2) coupled with temperature field underground has not been properly modeled. The thermal response is simulated through the given annual load profile, and the heat flux density distribution law along the borehole in depth was not clarified. Although the numerical models capture the features, it requires high cost in computational resources and presents flaws in numerical instabilities.
Semi-analytical models make a good compromise between the computational efficiency and the complexities of the geological settings. Eskilson (1987) developed a semi-analytical model for heat flow in a borehole heat exchanger, constituting two fluid channels and a borehole wall embedded in an axial symmetric soil mass. The governing heat equations of the two fluid channels are solved using the Laplace transform and that for the soil mass using the finite difference method. Seama and Rosen (2013) introduced a semi-analytical model for heat flow subjected to multiple infinite line heat sources with time-varying heat fluxes. The proposed model used flux-based analytical models to account for the heat flow transport, while the heat flux interacted between the involved heat sources is solved using an numerical iterative algorithm. Bnilam and Al-Khoury (2017) presented a semi-analytical model for simulating transient conductive–convective heat flow in a three-dimensional shallow BHE system consisting of multiple borehole heat exchangers embedded in a multilayer soil.
Existing semi-analytical approaches of BHE mainly focused on the temperature evolution outside the borehole (Rees and He 2013; Seama and Rosen 2013; Zhang et al. 2015; Wang et al. 2013; Zanchini and Lazzari 2014; Xiao et al. 2015; Liu et al. 2010; Claesson and Hellström 2011) under the given heat extraction rate, and heat flux density over the depth is usually assumed as uniformly distributed. It is a traditional assumption of the line/cylinder source model limited to the vertical shallow BHE that has been used for decades. It is crucial to develop an adequate and convenient method integrating various operational and geological parameters for overall thermal analysis. It is noted that the analytical solution holds under the assumption that borehole and pipe diameters together with the pipe material keep constant along the depth. This assumption is valid for typical cases for shallow BHEs, but not valid for DBHEs, considering that borehole and pipe diameters usually vary with depth. Therefore, a numerical solution is necessary.
The objective of this paper is to present a general and efficient algorithm for the deep coaxial BHE system which integrates the numerical and analytical approaches. The heat transport equation inside DBHE is solved by a finite difference method while that for the surrounding soil and rock mass uses an analytical model. The approach is achieved by the interacted heat flux between BHE and soil (rock) represented by Neumann boundary conditions (or a source term). The algorithm can manage the initial geothermal gradient and can handle a temperature distribution which varies in time and depth. To account for the heat flux density changes in time also with depth, the transient thermal impacted radius is properly formulated, which depicts the temporal heat propagation front (evolution with operational time). A precise analytical expression of the heat flux density is further established, which indicates the key parameters influencing the thermal performance of the DBHE system.
This paper is organized as follows. First of all, in the “Method” section, we will introduce the integrated analytical and numerical model to be used in the new approach. In the “Numerical models” section, we will highlight the establishment of the analytical expression of the thermal impacted radius and extracted heat flux density distribution along depth. This section ends with a flow-chart of the proposed algorithm. Secondly, we will present a concrete DBHE model for study with the simulation settings summarized in detail, followed by the “Result and discussion” section where the numerical verifications are performed to assess and validate the approach proposed in this paper. Specifically, the key parameters including heat flux density distribution along the depth, thermal impacted radius, total heat extraction output and outflow temperature are simulated to evaluate the thermal performance of DBHE. A further discussion of the results also follows in this section. The “Conclusions” section makes a summary with some potential applications of the proposed algorithm.
Methods
A deep BHE system consists basically of two thermally interacting domains: the borehole heat exchanger and the surrounding soil and rock, while the two areas are bounded by the borehole wall. The simulation of DBHE operation comprises the calculation of the temperature distribution in the two branch pipes inside the borehole and the thermal interaction of DBHE with the surrounding soil or rock.
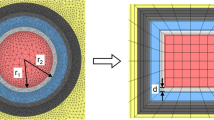
Three-dimensional unsteady heat conduction in soil or rock coupled with quasi-steady heat conduction in the backfill zone and turbulent flow convection in the circulating fluid evolves both in the horizontal and vertical direction under complex boundary conditions. Because of all the complications of this problem and its long-time scale, analytical methods treat the BHE as either a line source or a cylinder source in semi-infinite medium with predefined initial temperature distribution. The heat transfer process may usually be analyzed in two separated regions (as shown in Fig. 3a) (Diao and Fang 2006; Yang et al. 2010; Carslaw and Jaeger 1947). One is the solid soil/rock outside the borehole, where the heat conduction must be treated as a transient process. Another sector often segregated for analysis is the region inside the borehole, including the cement, the pipes and the circulating fluid inside the pipes (Diao and Fang 2006; Hellström 1991). The main objective of this analysis is to determine the inlet and outlet temperatures of the circulating fluid according to the borehole wall temperature and the heat exchange rate of the BHE. Detailed analyses on single U-tube (Li and Lai 2013), double-U-tube (Zanchini and Lazzari 2014) and coaxial tube (Saadi and Gomri 2017) boreholes have been available. The two separate regions must be linked on the borehole wall where a uniform temperature distribution is usually assumed. A new analytical model of coaxial borehole heat exchangers was presented by Beier et al. (2014), which considered the vertical temperature profile on the borehole wall, but still assumed a uniform initial temperature distribution.
In this section, we present an efficient model for heat transfer outside the borehole where thermal analysis inside the borehole under the condition of heat extraction is based on the classical quasi-steady-state model. In view of calculation, a hybrid approach of analytical solution (outside the borehole) coupled with numerical calculation (inside the borehole) is employed.
Modeling assumptions
Considering the larger amount of heat extraction output of a single DBHE compared to the shallow one, thermal interference among the deep boreholes can be negligible due to the large enough spacing among them. Therefore, this study focuses on heat transfer in a single deep borehole with coaxial tubes. The following assumptions were taken into considerations for the heat transfer model to facilitate the proposed algorithm (Fang et al. 2018; Wang et al. 2017):
-
1.
The soil and rock surrounding the DBHE is regarded as a few horizontal layers of homogeneous media to account for the multiple geological layers, whose thermal properties do not change with temperature.
-
2.
The domain studied is considered as semi-infinite for numerical simulation. The temperature fluctuation of air on the top layer of the rock is ignored, and far-field boundary condition for temperature is considered at the bottom of the domain.
-
3.
Groundwater advection is neglected and the heat transfer between the heat exchanger and the rock–soil is considered as pure heat conduction.
-
4.
The backfill materials and the outer pipe of the borehole wall are fully contacted and there is no resistance between them.
-
5.
Radial conduction is the dominant mechanism for heat transfer in rock and cement, however convection overweighs conduction for the circulating fluid in pipes along the axial direction within the borehole. Besides, the temperature and velocity distribution of the fluid in pipes at any cross section are uniform, and turbulence influence on heat transfer is incorporated into the convection coefficient by lumped parameter method.
Dynamic description of transient heat transfer outside the borehole
Rocks outside the borehole are discretized into several micro-cylindrical columns from the borehole along the radial direction of the thermal impacted circle (horizontal plane of the simulation zone concerned) which spreads gradually with operation time. Considering heat conduction of single DBHE, rock temperature distribution is assumed to be homogeneous circumferentially and varies in the direction of drilling depth, i.e., \( T_{s} = T_{s} \left( {r,z} \right) \). Given that the borehole boundary is \( r = r_{b} \), the radius of the far-field (radius of the thermal impacted circle) is \( r = r_{\infty } \), therefore, heat flow flux extracted from the rock mass into the borehole at a certain rate \( q \) satisfies the second type of boundary condition as (Eskilson 1987; Hellström 1991; Carslaw and Jaeger 1947):
Also, rock temperature field is assumed to be fully developed at the thermal impacted circle (heat propagation front), and no heat flux flows in, satisfying:
On the other hand, evolution of the rock temperature underground could be approximated as ideal heat conduction in cylindrical coordinate which is described by:
Here, \( a_{s} = {{\lambda_{s} } \mathord{\left/ {\vphantom {{\lambda_{s} } {\rho_{s} c_{s} }}} \right. \kern-0pt} {\rho_{s} c_{s} }} \) is the thermal diffusivity of rock.
The initial temperature distribution according to geothermal gradient is close to be linear along depth, and heat flux contribution in the radial direction dominates over the vertical in general. So, the vertical heat conduction term can be neglected, and Eq. 3 could be further simplified as:
Solution of Eq. 4 is first given by Carslaw and Jaeger through the Laplace transformation method (Carslaw and Jaeger 1947) as following:
where \( \alpha_{n} \) is the positive root of Eq. 6:
and \( J_{0} \), \( J_{1} \), \( Y_{0} \), \( Y_{1} \) and are the first and second Bessel equations, respectively.
Solution 5 can be divided into the following three parts:
-
1.
The first part is the item that is linearly related to time:
$$ T_{s,1} \left( \tau \right) = \frac{q}{{\pi \lambda_{s} }}\frac{{a_{s} \tau }}{{r_{\infty }^{2} - r_{b}^{2} }}. $$(7) -
2.
The second part is time-independent:
$$ T_{s,2} \left( r \right) = \frac{q}{{2\pi \lambda_{s} }}\frac{{r_{\infty }^{2} }}{{\left( {r_{\infty }^{2} - r_{b}^{2} } \right)}}\left( {\ln \left( {\frac{{r_{\infty } }}{r}} \right) - \frac{3}{4} + \frac{1}{2}\left( {\frac{r}{{r_{\infty } }}} \right)^{2} - \frac{1}{4}\left( {\frac{{r_{b} }}{{r_{\infty } }}} \right)^{2} + \frac{{r_{b}^{2} }}{{r_{\infty }^{2} - r_{b}^{2} }}\ln \left( {\frac{{r_{\infty } }}{{r_{b} }}} \right)} \right), $$(8)where \( r_{\infty } \) (radius of the thermal impacted circle) correlates to operation time, and \( T_{s,2} \left( r \right) \) depicts the temperature distribution profile within the radius of thermal impacted circle at a given time.
-
3.
The third part is the series that describes the transient change of rock temperature and quickly converges to zero over time:
$$ T_{s,3} \left( {r,\tau } \right) = - \frac{q}{{2\lambda_{s} }}\frac{{r_{\infty }^{{}} }}{{r_{\infty }^{2} - r_{b}^{2} }}\sum\limits_{n = 1}^{\infty } {\frac{{e^{{ - a_{s} \alpha_{n}^{2} \tau }} J_{1} \left( {\alpha_{n} r_{b} } \right)J_{1} \left( {\alpha_{n} R} \right)\left[ {Y_{1} \left( {\alpha_{n} r_{\infty }^{{}} } \right)J_{0} \left( {\alpha_{n} r} \right) - Y_{0} \left( {\alpha_{n} r} \right)J_{1} \left( {\alpha_{n} r_{\infty }^{{}} } \right)} \right]}}{{\alpha_{n} \left[ {J_{1} \left( {\alpha_{n} r_{\infty }^{{}} } \right)^{2} - J_{1} \left( {\alpha_{n} r_{b} } \right)^{2} } \right]}}} $$(9)
Table 1 gives the distribution of the minimum positive root \( \alpha_{1} \) (the first root) of Eq. 6 at different radii of thermal impacted circle (in the form of \( \alpha_{1} r_{\infty } \)). The series term \( T_{s,3} \left( {r,\tau } \right) \) is exponentially decaying, and the exponent of the first term \( a_{s} \alpha_{1}^{2} \tau \) can be used to measure the time scale of the transient attenuation of the temperature field. When \( a_{s} \alpha_{1}^{2} \tau = 3 \), the first term of the exponential decaying series is approximately attenuated to 5% of the initial value. For the other parts of the series term, the attenuation speed is much faster than the first term due to the corresponding root \( \alpha_{n}^{{}} > \alpha_{1}^{{}} \), so the temperature change converges to the steady-state solution after a certain time \( \tau_{\text{conv}} \) as (Carslaw and Jaeger 1947):
To derive the radius \( r_{\infty } \) of thermal impacted circle (Fig. 3b), we combine the time-dependent term in the first and third parts of the solution \( T_{s} \left( {r,\tau } \right) \) with consideration that rock temperature should keep constant as undisturbed at the boundary of the thermal impacted circle \( r = r_{\infty } \), therefore, the temperature distribution in the radial direction of the thermal impacted circle could be determined as:
According to the definition of average temperature of rock within thermal impacted circle after heat extraction, we have:
On the other hand, due to the conservation law that heat flow flux extracted from the rock mass contributes to the temperature decline in the thermal impacted circle, it yields:
Combining Eqs. 11–13, the following formula holds:
In order to analyze the distribution profile of rock temperature \( T_{s} \left( {r,\tau } \right) \) in the thermal impacted circle given by Eq. 11 and evolution characteristics of thermal impacted circle \( r_{\infty } \) with operation time from Eq. 14, we consider the functions \( g\left( t \right) \) and \( f\left( t \right) \), respectively (as depicted in Fig. 4):
Herein, analytical function \( g\left( t \right) \) shows the temperature distribution profile in the thermal impacted circle (Fig. 4a): temperature varies sharply in the vicinity of DBHE, getting flat soon along the radial direction and gradually spreads almost constantly towards the heat propagation front. Heat flux \( q \) indicates whether the temperature change in the thermal impacted circle is a process of heating or cooling. In case of \( q < 0 \), DBHE extracts heat from the rock and rock temperature drops (as depicted in Fig. 4a, where \( g\left( t \right) < 0 \)), so \( T_{s} \left( {r,\tau } \right) \) in the thermal impacted circle is always less than the initial temperature of the rock \( T_{\text{init}} \), which is consistent with the actual physical process. Moreover, from function \( f\left( t \right) \) illustrated in Fig. 4b, it can be seen that the radius of the thermal impacted circle spreads nonlinearly with time, and the longer the running time \( \tau \), the slower the evolving rate. This observation indicates that thermal equilibrium soon builds and stays nearly steady state, which right uncovers the physical mechanism for the evolution characteristics of thermal impacted radius of DBHE.
Given the evolution of thermal impacted radius with operation time by Eq. 14, the radial heat flux density distribution \( {\text{flux}}_{\text{radi}} \left( {z,\tau } \right) \) along the depth of DBHE could be consistently evaluated as (see Appendix A for detail):
where \( R_{b} \) is the thermal resistance in the borehole, \( {\text{Flux}}\left( z \right) \) and \( T_{f1} \left( z \right) \) denote cumulative heat flux extraction after a period of operation and the fluid temperature in the outer pipe along DBHE depth, respectively.
TRCM model for thermal resistances within the borehole
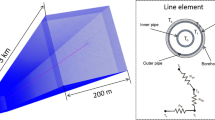
Thermal resistances within the borehole can be implemented into the numerical model (presented thereafter) by applying the methods in analogy to the electric networks. A geometrical simplification is made such that the different parts of the borehole are represented by single nodes (as depicted in Fig. 5).
Numerical models based on this methodology have earlier been referred to as thermal resistance and capacity model (TRCM); TRCM model for coaxial BHEs have been published by Refs. (Bauer et al. 2011; De Carli et al. 2010; Claesson and Hellström 2011; Beier et al. 2011, 2014). A thermal circuit would be used to describe the local heat flow between the flow pipes and the borehole wall and heat flow as functions of the temperature difference, and derive the corresponding thermal resistances of outer pipe to the borehole wall \( R_{11} \) (also \( R_{b} \)) and inner pipe to the outer pipe \( R_{12} \):
where \( h_{f} \) is the convection coefficient calculated by:
where \( {\text{Re}} \) and \( Pr \) are the Reynolds number and Prandtl number of the circulating flow, respectively.
Quasi-steady-state modeling inside the borehole of DBHE
In the quasi-steady-state model, the fluid temperature and borehole wall vary in the axial direction, and the inlet and outlet temperature of the circulating fluid changes with time due to the heat flux distribution along the borehole wall determined by the temperature difference and thermal resistance. The model is able to evaluate the influence of short-circulating among the branch pipes (Diao and Fang 2006; Yang et al. 2010).
During heat extraction of DBHE, return water from the heat pump units flows into the outer pipe (annular domain) and circulates out from the inner pipe (circular domain). On the basis of the heat flux distribution along depth in Eq. 17 aforementioned, the energy equilibrium equations for upward and downward flow of the circulating fluid in DBHE shown in Fig. 6 are formulated to model the dynamic heat transfer process. According to the quasi-steady-state heat transfer analysis inside the borehole, the temperature of the fluid flowing downward in the outer tube (named as pipe 1) and upward in the inner tube (named as pipe 2) varies along the depth as:
where, \( q_{1 - 2} \) and \( q_{l} \) are the local heat flow between the flow pipes and the borehole wall, respectively.
In light of the TRCM model, the local heat flow between the flow pipes and the borehole wall in the quasi-steady-state model of DBHE inside the borehole could consistently be formulated as:
Therefore, we can obtain the quasi-steady-state heat transfer equation for fluid flow inside the borehole:
The boundary conditions for the heat transfer in Eq. 22 are:
where \( t_{\text{in}} \) is the inlet temperature of the circulating fluid, and \( H \) denotes the borehole depth.
Introducing the variables: \( R_{12}^{*} = \dot{m}c_{p} R_{12} ,R_{11}^{*} = \dot{m}c_{p} R_{11} \), then numerical solution of Eq. 22 could be carried out by finite difference scheme as:
where the subscript \( n \) denotes the \( n \)th DBHE discrete element.
To solve the discretized Eq. 24, an iterative algorithm is adopted assuming the outlet temperature \( t_{\text{out}} \) and temperature distribution along the branch pipes 1 and 2 under the given inlet temperature \( t_{\text{in}} \) and flow rate \( \dot{m} \). The iteration stops until the total heat extraction calculated as \( Q_{1} = \sum {{\text{flux}}_{\text{radi}} \left( {z,\tau } \right)\Delta z} \) is balanced with \( Q_{2} = c_{p} \dot{m}\left( {t_{\text{out}} - t_{\text{in}} } \right) \) due to the circulating water temperature change after a cycling loop.
Flow-chart of the whole calculation procedure for DBHE is illustrated in Fig. 7 that is promising to generalize to thermal analysis of any vertical closed loops including single or double-U pipe and coaxial pipe applied in shallow BHEs.
Numerical models
Model setup
In order to study the operation characteristics of DBHE for further optimization of the structure design and optimal operation control of the deep borehole ground-coupled system, we carry out a comprehensive simulation on the basis of the proposed method for the dynamic heat transfer problem. Geological settings for the DBHE in study are depicted in Fig. 8. It should be noted that the DBHE in study comes from a pilot demonstration project in Qingdao, located in Shandong Province, China. The coaxial tube DBHE was installed in a deep borehole with the overall depth of 2600 m and drilling diameter of 216 mm. The DBHE wall is made of steel and has an outer diameter of 178 mm and a thickness of 9.5 mm, the inner pipe is made of high-temperature resistant material applied in oil collection engineering with a lower thermal conductivity of 0.01 W/m/K, whose diameter is valued at 90 mm with a thickness of 10 mm. In situ field tests for the project will be introduced in our future work. This paper focuses on the simulation results of its thermal performance.
Establishment of the heat transfer model for DBHE includes three aspects in general:
-
1.
(1). Input variations:
The input variations of the simulator could be classified into four groups:
-
i.
Geological data.
All the related geological parameters for geothermal temperature and groundwater condition as well as rock/soil multi-layers properties are shown in Tables 2 and 3.
Table 2 Geological parameters of deep borehole Table 3 Properties of the rock/soil layers -
ii
DBHE structural parameters.
Borehole section and geometry settings of DBHE are listed in Table 4.
Table 4 Construction parameters of DBHE -
iii
Operating condition parameters.
Parameters settings for operation condition during the heating season include inlet flow temperature, flow rate, operation hours, etc. (see Table 5).
Table 5 Operation parameters of DBHE in the heating season -
iv
Material parameters.
The properties of the circulating water, inner pipe and backfill materials used in the model are summarized in Table 6.
Table 6 Thermal parameters of the fluid, backfill material, inner pipe and outer pipe in the model
-
i.
-
2.
Output parameters:
The outflow temperature, total heat extraction amount and the heat flux density distribution along the borehole depth are given as outputs of the system to analyze the effect of the primary input parameters on the heat transfer performance of DBHE.
-
3.
Boundary conditions:
For the section inside borehole, real-time flow rate and inlet temperature are taken as the inlet boundary condition of the coaxial heat exchanger (see Table 5). With respect to the rock zone, initial geothermal temperature distribution is set as the far-field boundary in the radial direction along the depth, and isothermal boundary is considered at the bottom of DBHE. In the shallow layer of the rock, zero heat flux boundary is set below the constant temperature layer without consideration of the variable temperature zone due to atmosphere influence for simplicity of simulation.
-
4.
Model discretization:
In the scenario studied, the DBHE model with a depth of 2600 m is discretized into 1500 segments vertically and uniform grids with a scale of 0.5 m are applied in the radial direction from the location of DBHE to the dynamic thermal impacted radius, in order to calculate temporal temperature distribution in the rock zone.
Model validation
In this section, analysis of DBHE performance during heating season is carried out in detail. In order to validate the proposed efficient model, a cross check is performed using the detailed heat transfer solution (or full 3D numerical solution, see Appendix B for the numerical schemes) of the problem.
Figure 9 depicts the overall dynamic evolution process of heat extraction rate and outlet temperature with time during the heating season. A fast decrease in outflow temperature and heat extraction exists ranging approximately from 20 to 60 days at the start-up of DBHE, after the unsteady stage outflow temperature and the heat extraction output of DBHE vary so small as to be neglected safely. Moreover, excepting the relatively larger difference at the initial stage between the proposed efficient simulation results and the detailed solution for the case (analyzed thereafter in this part), it could be seen that the temperature difference from 60 days until the end of heating season at 120 days (during the stable stage) is not more than 0.2 °C. Besides, the average relative error of heat extraction rate is 1.07% during the overall simulation (402.05 kW for the efficient modeling and 397.78 kW for the detailed solution, respectively), which is within the reasonable range for engineering application. Therefore, the simulation data obtained from the proposed method in the paper agree well with the detailed numerical solution and is reliable enough to predict the thermal performance of DBHE in the long run. The slight difference was caused by the computational errors and modeling simplification.
As a summary of the operation characteristics for DBHE, the overall operation process could be divided into three typical stages: descend stage, transition stage and stable stage. At the initial or start-up stage, fast decline would occur in the outflow temperature and heat extraction output. Soon after a transition stage with gradual decline speed from unsteady state to steady state, DBHE would run stable and all the thermal performance parameters variation trend remain basically unchanged. This observation validates our modeling for the heat propagation front in the rock evolution (thermal impacted circle) in a previous section as depicted in Fig. 4b.
Results and discussion
Thermal performance analysis of DBHE
Figures 10, 11 and 12 show the comparison of simulation results for the key thermal performance parameters of DBHE including borehole temperature, extracted heat flux density distribution along depth, as well as circulating flow temperature profiles in the annulus and the inner pipe along depth. It should be noted that, at the descend stage of DBHE, efficient modeling method gives a higher estimation of them over those predicted from the detailed solution during the heating season. As a matter of fact, the overestimation originates from the underestimation of thermal impacted radius at the descend stage in essence. Clearly, it could be seen that there exists a fast decline in heat extraction output of DBHE during the initial operation days, so accumulated heat extraction density \( {\text{Flux}}\left( z \right) \) at depth \( z \) along borehole was underestimated by Eq. 13:
And the effective operation time should be modified as:
With respect to the decline trend of heat extraction with operation time as mentioned above, it could be easily concluded that:
It could be seen that the effective operation time \( \tau_{\text{eff}} \) proves to be longer than real operation hours \( \tau \). On the other hand, from Eq. 14 we can see that longer operation time corresponds to smaller thermal impacted radius, and smaller thermal impacted radius leads to higher heat flux density extracted from rock as indicated by Eq. 17. Therefore, the relatively larger deviation at the descend stage for the simulation results of the key thermal performance parameters on the basis of efficient modeling could be justified (see simulation results at 5 days in Figs. 10, 11 and 12). Actually, nominal capacity of DBHE during the stable stage is more helpful for engineers in preliminary design and practical analysis (Fang et al. 2018) which proves accurate enough according to the proposed efficient simulation results. To facilitate modeling and programming of DBHE, further improvement for accuracy at the initial stage is not presented in this paper, which would be introduced in the future work.
Moreover, another important observation from the simulation results in Fig. 10 indicates that the borehole temperature is almost proportional to depth underground while the geothermal gradient (28 °C/km) is taken into consideration. In view of the initial temperature of rock determined by geothermal gradient which is linearly distributed along depth, it is understandable that the temperature difference between circulating water in the annulus and borehole surface is almost linearly increasing which is responsible for the linear heat flux density distribution as depicted in Fig. 11. This observation proves that geothermal gradient could never be neglected and heat flux density over the depth could not be assumed as uniformly distributed (as is the case for shallow BHE) to study the transient thermal performance characteristics of DBHE. Also, heat extraction rate of DBHE is dynamically evolving with time which may be not balanced with the given terminal load for simulation and should be determined under the given operating condition as well as geological settings, therefore it is not proper to assume DBHE operating under a given load to perform simulation of rock temperature response outside borehole especially in the descend stage.
Figure 12 depicts the temperature profile of circulating fluid. It can be seen that the cold water enters the outlet annulus to utilize the borehole wall as heat exchanger surface at full length and reaches its peak temperature at the borehole bottom, and then returns back to the surface through the insulated central pipe. Once DBHE runs stable, outflow temperature and circulating flow temperature profiles along depth would stay at a relatively steady state, with minor fluctuations. While slight differences of outflow temperature between the proposed efficient modeling calculation result and detailed solution exist, the temperature difference approximately stabilizes at 0.1 °C for the simulation scenario, which could be safely neglected for prediction of DBHE thermal performance.
Figure 13 describes the heat flux loss between annulus and inside inner pipe due to thermal short-circuiting with depth. We can see that maximum short-circuiting heat flux occurs at the outlet of DBHE where maximum temperature difference of circulating water exists. In addition, short-circuiting heat flux reaches its peak at the start-up stage and soon converges to a steady state. Owing to the good thermal insulation material of inner pipe, thermal short-circuiting effect is not so severe and heat loss per meter due to thermal short-circuiting is reduced to be only 2 W/m. Therefore, circulating water flows upward inside the inner pipe almost without any temperature loss (see flow temperature profile in the inside inner pipe in Fig. 12).
Furthermore, distribution of the thermal impacted radius and comparison of radial far-field rock temperature with initial rock temperature along depth during the heating season are also investigated. Thermal impacted radius during the heating season is almost uniformly distributed along depth as illustrated in Fig. 14. This is because that heat extraction occurs at full length of DBHE due to the low inlet temperature at 5 °C. In view of the relatively uniform rock thermal parameters distribution along depth, it is understandable that the heat propagation front in the surrounding rock spreads almost at the same speed along depth, thus creating a uniform thermal impacted radius profile. It could be clearly seen that the heat propagation front spreads fast at the initial unsteady and transition stage for 5–60 days, and would stabilize approximately at 25 m (because the DBHE would run stable after 60 days according to Fig. 9a), thus, the borehole space should be at least 50 m to avoid any thermal interaction between borehole clusters (if more DBHEs are needed in practical design). Finally, good agreement between radial far-field rock temperature and initial rock temperature along depth validates again the physical modeling for thermal impacted radius evolution and rock temperature distribution in the thermal impacted scope (Eqs. 11 and 14).
Variation of thermal impacted radius and rock temperature near the boundary of thermal impacted radius (radial far field temperature of rock) on the basis of efficient modeling along depth with time during the heating season. a 5 days, b 20 days, c 40 days, d 60 days. The black and black dotted line denoting rock temperature refer to the left y-axis, while the red line denoting thermal impacted radius refers to the right y-axis
Distributions of rock temperature field underground during the heating season are shown in Fig. 15. Generally speaking, simulation results from the two approaches agree well. Isothermal contour presents as a V profile, and more temperature decrease occurs in the rock mass located at the bottom section of DBHE than at the top section on account of the linearly increasing heat flux extraction density along depth. What should be noted is that a local coldness accumulation near the borehole at the shallow layer of rock mass reaching the depth of 100 m could be seen noticeably, and the scope on the basis of proposed efficient modeling is comparatively larger than that from detailed solution at the descend stage (20 days and 40 days) as marked by the red circle. This is due to the fact that rock temperature distribution in the thermal impacted scope is determined by the analytical solution where great temperature gradient exists near the borehole. When DBHE runs more stable at 60 days, the difference is diminishing gradually indicating that the analytical solution for rock temperature distribution in the thermal impacted scope is quite precise and reasonable. In addition, on account of the large temperature difference between rock and circulating water, small time step is necessary to depict the rock temperature evolution based on the detailed solution to solve the three-dimensional unsteady state heat conduction problem, and negative temperature would easily appear especially near the borehole where local sharp temperature gradient exists. Owing to the analytical solution for thermal impacted radius evolution and rock temperature distribution, simulation results for rock temperature on the basis of the proposed efficient modeling are very smooth and robust without any fluctuation or negative value encountered.
Rock temperature distribution underground during the heating season. A, B, C, D depict the simulation results at 5, 20, 40, and 60 days from the proposed efficient modeling in the paper, respectively. a, b, c, d show the corresponding results from the detailed simulation. Rock temperature unit is °C in the color bar
Simulation efficiency and precision validation
Thanks to the high efficiency of calculation in the proposed method, the update time step could be large enough without oscillation of the calculation results, which could be set comparable to the running hours for the operation condition. According to our simulation, computation task of the case in study with a running time of 3 years took only around 1.5 h on a common computer with a CPU of 2.9 GHz and RAM of 16 GB. Calculation cost for 3 years simulation of DBHE operation characteristics based on our efficient simulation method versus traditional detailed solution solving the unsteady state heat conduction problem, is shown in Table 7. It can be seen that compared to traditional numerical method, the proposed efficient simulation approach for DBHE is highly efficient with an acceleration ratio of calculation at almost 30 times. The high efficiency of calculation by the proposed method is based on that analytical solutions for heat flux distribution along the borehole and dynamic thermal impacted radius have been properly formulated for the operation condition.
Since larger deviations exist at the initial stage of DBHE from the efficient modeling method, as pointed out before, average outflow temperature and heat extraction rate during the initial 60 days (initial stage) of heating season for the case are specifically compared between detailed solution and our efficient simulation in Table 7. It shows that under the default operation condition with the average inlet temperature at 5 °C and flow rate 50 m3/h, the average outlet temperature and heat extraction rate of the coaxial DBHE from efficient simulation are 12.52 °C and 438.5 kW, respectively. The simulated values of the average outlet water temperature and heat extraction rate are 12.29 °C and 425.1 kW according to detailed solution. The simulated results are in good agreement with the detailed solution (with a relative error of 3.15%) indicating that our efficient simulation approach adopted to analyze the heat transfer characteristics of DBHE is both efficient and reasonable for engineering application. Moreover, the proposed efficient modeling approach for thermal analysis of DBHE in this paper is also promising to be generalized to heat transfer modeling of various closed borehole heat exchanger configurations, including single U-type, double-U-type and coaxial pipe applied in shallow geothermal energy exploitation scenarios, as well as thermal analysis for large U-shaped or L-type geothermal well for medium and deep hot dry rock energy utilization. Simulation of DBHE with other configurations based on the method would be introduced in our future work as a complement of deep coaxial BHE in study.
Conclusions
The results from this study can be potentially used as a reference to guide the design and optimization of coaxial DBHE system and promote the utilization of medium deep geothermal energy. Main findings can be summarized as follows:
-
1.
An efficient hybrid model for DBHE combining analytical and numerical solutions is set up for the modeling of operational conditions through quantifying the heat propagation front outside the borehole. Several important thermal performance parameters of DBHE were analyzed and the analytical expressions for them were derived.
-
2.
Compared with the detailed heat transfer solution of DBHE by numerical calculations that involve a large number of complex grids generation and adaptive distribution in the simulation zone, the efficient hybrid approach developed in this paper improved the calculation speed by one order of magnitude. This was possible by combining analytical solutions for the temperature evolution outside the borehole and heat flux density distribution along depth, with the numerical solution for fluid temperature distribution of the branch pipes employing the iterative algorithm.
-
3.
The simulated results for key thermal performance parameters of DBHE on the basis of the proposed model are in good agreement with the numerical solution in reference. Therefore, it is both efficient and reliable for engineering applications.
-
4.
The unsteady heat conduction process of DBHE evolves into steady state soon in the initial stage. The overall operation process could be divided into three stages: descend stage, transition stage and stable stage. At the initial or start-up stage, fast decline would occur in the outflow temperature and heat extraction output, and relatively larger deviation exists for the new modeling method. Soon after a transition stage with gradual decline speed from unsteady state to steady state, DBHE would run stably and all the thermal performance parameters remain basically unchanged with relatively minor fluctuation that could be neglected.
Availability of data and materials
The DBHE model in study presented in the paper oriented from a pioneering demonstration project in Qingdao, Shandong province. All the geological settings and operation condition parameters were collected from in situ field test. Interested readers might obtain the information of the project as well as the source code by contacting the correspondence author.
Change history
25 February 2021
A Correction to this paper has been published: https://doi.org/10.1186/s40517-021-00191-2
Abbreviations
- \( T_{f2} (z) \) :
-
Fluid temperature in the inner pipe along depth, °C
- BHE:
-
Borehole heat exchanger
- DBHE:
-
Deep borehole heat exchanger
- TRCM:
-
Thermal resistance and capacity model
- c p :
-
Specific heat capacity of the fluid, kJ/kg/K
- c s :
-
Specific heat capacity of the rock, kJ/kg/K
- ρ s :
-
Density of the rock, kg/m3
- λ s :
-
Thermal conductivity of the rock, W/m/K
- λ b :
-
Thermal conductivity of the backfills, W/m/K
- λ p :
-
Thermal conductivity of DBHE annulus or inner pipe, W/m/K
- h f :
-
Heat convection coefficient, W/m2/K
- \( \dot{m} \) :
-
Fluid flow rate, m3/h
- T init :
-
Initial temperature of rock, °C
- T decay :
-
Average temperature of rock within thermal impacted circle after heat extraction, °C
- T s :
-
Rock temperature distribution, °C
- J 0, J 1 :
-
The first kind of Bessel function
- r ∞ :
-
Radius of the thermal impacted circle, m
- r b :
-
Radius of the borehole, m
- Y 0, Y 1 :
-
The second kind of Bessel function
- R 11 :
-
Thermal resistances of the outer pipe to borehole wall, K*m/W
- R 12 :
-
Thermal resistance between inner and outer pipes, K*m/W
- \( T_{f1} (z) \) :
-
The fluid temperature in the outer pipe along depth, °C
- z :
-
Depth, m
- H :
-
Borehole depth, m
- q l :
-
Line heat source intensity, W/m
- r o :
-
Radius of the outer pipe, m
- r i :
-
Radius of the inner pipe, m
- t in :
-
Inlet temperature of the circulating fluid, °C
- t out :
-
Outlet temperature of the circulating fluid, °C
- \( {\text{flux}}_{\text{radii}} (z,\tau ) \) :
-
Radial heat flux density along depth, W/m
- Flux (z) :
-
Cumulative heat flux extraction after a period of operation, J/m
- \(\tau\) :
-
Operation time, s
- α n :
-
Positive root of Bessel equation
- 0:
-
The order of Bessel function
- 1/i:
-
The order of Bessel function or outer pipe
- 2/o:
-
Inner pipe
- n:
-
Sequence serial number
- b:
-
Borehole
- f:
-
Fluid
- s:
-
Rock
- in:
-
Inlet
- out:
-
Outlet
References
Abdelaziz SL, Ozudogru TY, Olgun CG, Martin II JR. Multilayer finite line source model for vertical heat exchangers. Geothermics. 2014;51:406–16.
Bandos TV, Montero A, Fernández E, Santander JLG, Isidro JM, Pérez J, et al. Finite line-source model for borehole heat exchangers: effect of vertical temperature variations. Geothermics. 2009;38(2):263–70.
Bär K, Rühaak W, Welsch B, Schulte D, Homuth S, Sass I. Seasonal high temperature heat storage with medium deep borehole heat exchangers. Energy Proc. 2015;76:351–60.
Bauer D, Heidemann W, Müller-Steinhagen H, Diersch HJG. Thermal resistance and capacity models for borehole heat exchangers. Int J Energy Res. 2011;35(4):312–20.
Beier RA, Smith MD, Spitler JD. Reference data sets for vertical borehole ground heat exchanger models and thermal response test analysis. Geothermics. 2011;40(1):79–85.
Beier RA, Acuña J, Mogensen P, Palm B. Transient heat transfer in a coaxial borehole heat exchanger. Geothermics. 2014;51:470–82.
Bnilam N, Al-Khoury R. A spectral element model for nonhomogeneous heat flow in shallow geothermal systems. Int J Heat Mass Transf. 2017;104:703–17.
Carslaw HS, Jaeger JC. Conduction of heat in solids. Oxford: Claremore Press; 1947. p. 257–65.
Chen C, Shao H, Naumov D, Kong Y, Tu K, Kolditz O. Numerical investigation on the performance, sustainability, and efficiency of the deep borehole heat exchanger system for building heating. Geothermal Energy. 2019;7(1):1–26.
Claesson J, Hellström G. Multipole method to calculate borehole thermal resistances in a borehole heat exchanger. HVAC&R Res. 2011;17(6):895–911.
Claesson J, Javed S. An analytical method to calculate borehole fluid temperatures for time-scales from minutes to decades. ASHARE Conference. 2011.
De Carli MD, Tonon M, Zarrella A, Zecchin R. A computational capacity resistance model (CaRM) for vertical ground-coupled heat exchangers. Renew Energy. 2010;35(7):1537–50.
Deng J, Wei Q, Liang M, He S, Zhang H. Field test on energy performance of medium-depth geothermal heat pump systems (MD-GHPs). Energy Build. 2019;184:289–99.
Diao NR, Fang ZH. Ground-coupled heat pump technology. Beijing: Higher Education Press; 2006. p. 47–68.
Diersch HJG. FEFLOW: finite element modeling of flow, mass and heat transport in porous and fractured media. Berlin: Springer; 2014.
Erol S, Bertrand F. Multilayer analytical model for vertical ground heat exchanger with groundwater flow. Geothermics. 2018;71:294–305.
Eskilson P. Thermal analysis of heat extraction boreholes. Doctoral Thesis, Department of Mathematical Physics, University of Lund, Sweden. 1987.
Fang L, Diao NR. Thermal analysis model of deep borehole heat exchanger. IGSHPA Research Track. 2018.
Fang L, Diao N, Shao Z, Zhu K, Fang Z. A computationally efficient numerical model for heat transfer simulation of deep borehole heat exchangers. Energy Build. 2018;167:79–88.
Fossa M. A fast method for evaluating the performance of complex arrangements of borehole heat exchangers. HVAC R Res. 2011;17(6):948–58.
Hellström G. Ground heat storage Thermal analysis of duct storage systems. Doctoral Thesis, Department of Mathematical Physics, University of Lund, Sweden. 1991.
Hellström G, Sanner B. Earth energy designer: software for dimensioning of deep boreholes for heat extraction. Lund: Lund University; 1994. p. 185–92.
Henrik H, Erling N. Deep borehole heat exchangers. Proceed World Geothermal Congress: Application to Ground Source Heat Pump Systems; 2015.
Holmberg H, Acuña J, Næss E, Sønju OK. Deep borehole heat exchangers, application to ground source heat pump systems. In: Proceed World Geothermal Congress. 2015.
Jia G, Chai JC, Zhou C, Zhao M, Tao Z, Zhang L. Heat transfer performance of buried extremely long ground coupled heat exchangers with concentric pipes. Energy Proc. 2017;143:106–11.
Kim EJ, Bernier M, Cauret O, Roux JJ. A hybrid reduced model for borehole heat exchangers over different time-scales and regions. Energy. 2014;77:318–26.
Kolditz O, Bauer S, Bilke L, Böttcher N, Delfs JO, Fischer T, et al. OpenGeoSys: an open-source initiative for numerical simulation of thermo-hydro-mechanical/chemical (THM/C) processes in porous media. Environ Earth Sci. 2012;67(2):589–99.
Koohi-Fayegh S, Rosen MA. On thermally interacting multiple boreholes with variable heating strength: comparison between analytical and numerical approaches. Sustainability. 2012;4(8):1848–66.
Le Lous M, Larroque F, Dupuy A, Moignard A. Thermal performance of a deep borehole heat exchanger: insights from a synthetic coupled heat and flow model. Geothermics. 2015;57:157–72.
Li M, Lai ACK. Heat-source solution to heat conduction in anisotropic media with application to pile and borehole ground heat exchangers. Appl Energy. 2012;96:451–8.
Li M, Lai ACK. Analytical model for short-time responses of ground heat exchangers with U-shaped tubes: model development and validation. Appl Energy. 2013;104:510–6.
Li M, Lai ACK. Review of analytical models for heat transfer by vertical ground heat exchangers (GHEs): a perspective of time and space scales. Appl Energy. 2015;151:178–91.
Li M, Li P, Chan V, Lai ACK. Full-scale temperature response function (G-function) for heat transfer by borehole ground heat exchangers (GHEs) from sub-hour to decades. Appl Energy. 2014;136:197–205.
Li XX, Hu XM, Zhang ZW. Calculation method of thermal response radius for vertical borehole heat exchangers. Transact Chin Soc Agric Eng; 2015.
Liu J. Discussion on several basic problems of underground heat transfer process of ground source heat pump system. Doctoral Thesis, Tongji University, China. 2010.
Ma L, Zhao YZ, Yin HM, Zhao J. A coupled heat transfer model of medium-depth downhole coaxial heat exchanger based on the piecewise analytical solution. Energy Convers Manag. 2020. https://doi.org/10.1016/j.enconman.2019.112308.
Mingzhi Y, Tenteng M, Kai Z, Ping C, Aijuan H, Zhaohong F. Simplified heat transfer analysis method for large-scale boreholes ground heat exchangers. Energy Build. 2016;116:593–601.
Molina GN, Blum P, Zhu K, Bayer P, Fang Z. A moving finite line source model to simulate borehole heat exchangers with groundwater advection. Int J Therm Sci. 2011;50(12):2506–13.
Rees SJ, He M. A three-dimensional numerical model of borehole heat exchanger heat transfer and fluid flow. Geothermics. 2013;46:1–13.
Rivera JA, Blum P, Bayer P. Ground energy balance for borehole heat exchangers: vertical fluxes, groundwater and storage. Renew Energy. 2015;83:1341–51.
Saadi MS, Gomri R. Investigation of dynamic heat transfer process through coaxial heat exchangers in the ground. Int J Hydrog Energy. 2017;42(28):1–17.
Sapinska-Sliwa A, Rosen MA, Gonet A, Sliwa T. Deep borehole heat exchangers—a conceptual and comparative review. Int J Air Condition Refrig. 2016;24(1):1630001–15.
Schulte DO. Simulation and optimization of medium deep borehole thermal energy storage systems. Doctoral Thesis, Technische Universitat, Darmstadt. 2016.
Schulte DO, Rühaak W, Oladyshkin S, Welsch B, Sass I. Optimization of medium-deep borehole thermal energy storage systems. Energy Tech. 2016;4(1):104–13.
Seama KF, Rosen MA. Review of the modeling of thermally interacting multiple boreholes. Sustainability. 2013;5(6):2519–36.
Sidiropoulos E, Tzimopoulos C. Sensitivity analysis of a coupled heat and mass transfer model in unsaturated porous media. J. Hydrol. 1983;64(4):298.
Wang J, Long E, Qin W. Numerical simulation of ground heat exchangers based on dynamic thermal boundary conditions in solid zone. Appl Therm Eng. 2013;59(1–2):106–15.
Wang ZH, Wang FH, Liu J, Ma ZJ, Han ES, Song MJ. Field test and numerical investigation on the heat transfer characteristics and optimal design of the heat exchangers of a deep borehole ground source heat pump system. Energy Convers Manag. 2017;153:603–15.
Welsch B, Schulte DO, Rühaak W, Bär K, Sass I. Thermal impact of medium deep borehole thermal energy storage on the shallow subsurface. EGU General Assembly Conference Abstracts. 2017.
Welsch B, Rühaak W, Schulte DO, Bär K, Sass I. Characteristics of medium deep borehole thermal energy storage. Int J Energy Res. 2016;40:1855–68.
Yang H, Cui P, Fang Z. Vertical-borehole ground-coupled heat pumps: a review of models and systems. Appl Energy. 2010;87(1):16–27.
Zanchini E, Lazzari S. New g-functions for the hourly simulation of double-U-tube borehole heat exchanger fields. Energy. 2014;70:444–55.
Zarrella A, Emmi G, De Carli MD. A simulation-based analysis of variable flow pumping in ground source heat pump systems with different types of borehole heat exchangers: a case study. Energy Convers Manag. 2017;131:135–50.
Zhang C, Chen P, Liu Y, Sun S, Peng D. An improved evaluation method for thermal performance of borehole heat exchanger. Renew. Energy. 2015;77:142–51.
Zhang L, Zhang Q, Huang G. A transient quasi-3D entire time scale line source model for the fluid and ground temperature prediction of vertical ground heat exchangers (GHEs). Appl Energy. 2016;170:65–75.
Acknowledgements
This work has been financially supported by the “Transformation Technologies for Clean Energy and Demonstration”, Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDA 21020202). The authors gratefully acknowledge the editorial members and specialists in the field of geothermal energy utilization for their helpful suggestions and corrections on the manuscript of our paper.
Author information
Authors and Affiliations
Contributions
This study is part of the PhD work of ZY supervised by PZ. ZY formulated the modeling of DBHE and programmed the algorithm. PZ was in charge of the project funding acquisition as well as design and conceptualization of the study. HY provided some suggestions on the model calibration. MZ contributed treatment of the thermal physical parameters of rock layers and operational parameters of the DBHE model. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised: Several references were incorrect and credit line in figure 1 caption was missed out in the original article. The references and figure 1 caption was updated.
Appendix
Appendix
A. Distribution of heat flux density along the depth of DBHE
After a period of operation, from Eq. 11 the temperature gradient at the boundary of backfill zone can be determined as:
And we have the heat flow flux at borehole wall:
Therefore, rock temperature distribution \( T_{s} \left( {r,\tau } \right) \) satisfies:
Consider the rock temperature at borehole interface:
Herein, \( R_{b} \) is the thermal resistance in the borehole as mentioned above in Eq. 17.
Meanwhile, temperature continuous condition (the first type of boundary condition) is satisfied at the boundary of the backfill hole, combining Eqs. 30 and 31, heat flux density \( {\text{flux}}_{\text{radi}} \left( {z,\tau } \right) \) along the depth of DBHE is determined as:
It can be seen from Eq. 32 that the heat flux density distribution according to this solution is only related to the total operation time, geothermal property parameters and inlet water temperature in the current state, but the operation history has not yet been properly modeled. In order to include the operation history of DBHE in the heat flux density distribution, we perform the quasi-steady-state treatment of the temperature distribution solution near the backfill zone as follows.
The heat flow flux and temperature near the backfill zone approximately satisfy the following quasi-steady-state solution:
Therefore, temperature distribution of the rock near the backfill hole \( T_{s} \left( {r,\tau } \right)\left| {_{{r \to r_{b} }} } \right. \) can be approximated by Eq. 33 as:
That is:
where \( A \) is a coefficient to be determined.
Substituting Eq. 36 into Eq. 12, \( A \) is determined as:
It should be pointed out that Eq. 37 approximately holds, because Eq. 35 is valid in the region near the backfill hole, not for the holistic thermal impacted circle. However, the temperature distribution characteristics in the thermal impacted circle from Fig. 4 show that the temperature change almost completes near the backfill hole (close to 80%), while the change is small near the boundary of thermal impacted circle, so Eq. 37 is an approximation with good precision.
From Eq. 37, we can get:
Thereby, heat flux density \( {\text{flux}}_{\text{radi}} \left( {z,\tau } \right) \) along the depth of DBHE can be obtained as:
In addition, according to the conservation law, heat extracted by the DBHE causes the temperature change of rock to meet the following equation:
On the other hand, cumulative heat flux extraction \( {\text{Flux}}\left( z \right) \) along the depth of DBHE is recorded through \( {\text{flux}}_{\text{radi}} \left( {z,\tau } \right) \) as:
where \( \tau \) denotes the total operation time.
Combining Eqs. 40 and 41, temperature change of rock and heat flux density \( {\text{flux}}_{\text{radi}} \left( {z,\tau } \right) \) could be related by:
As a matter of fact, the total heat flow flux contributing to the change of rock temperature in the thermal impacted circle can be divided into two parts: radial heat flow \( {\text{flux}}_{\text{radi}} \) and heat flow in the vertical direction \( {\text{flux}}_{\text{vert}} \). So the total heat amount in history extracted from the rock \( {\text{Flux}} \) in Eq. 41 should be corrected as:
where \( \Delta \tau_{i} \) is the operation time step.
The heat flow flux extracted in the vertical direction \( {\text{flux}}_{\text{vert}} \left( {z,\tau } \right) \) is:
where \( T_{{s,z + {\text{d}}z}} \), \( T_{{s,z - {\text{d}}z}} \), \( \lambda_{{s,z + {\text{d}}z}} \), \( \lambda_{{s,z - {\text{d}}z}} \) are temperature and thermal conductivity of the segments right above and right below the segment at depth \( z \), respectively.
Further, the radial heat flux density distribution \( {\text{flux}}_{\text{radi}} \left( {z,\tau } \right) \) along the depth of BHE could be determined from Eqs. 39 and 49 as:
B. Detailed heat transfer solution of the problem
Theoretically, temperature evolution of DBHE in the three zones: inner pipe, outer pipe and rock, are all unsteady state heat transfer problems, whose governing equations could be summarized as following:
For the inner pipe:
For the outer pipe:
where \( R_{f1} \) and \( R_{f2} \) are heat conduction resistance in the vertical direction of water in the outer pipe and inner pipe of DBHE, respectively, which could be determined as:
Here, \( \lambda_{f} \) is the thermal conductivity of water.
For the temperature distribution outside borehole in the rock, it is assumed to be homogeneous circumferentially, so we have:
where, \( R_{l,s} \) and \( R_{r,s} \) are the heat conduction resistance from the left side and right side of a given rock segment in the radial direction, respectively. \( R_{v,s} \) is the heat conduction resistance in the vertical direction.
Numerical schemes for Eqs. 46, 47 and 49 could be reformulated as 50–52, respectively, by introducing the variables as following:\( \begin{aligned} & R_{12,2}^{*} = \rho c_{p} \pi r_{i}^{2} R_{12} ,R_{12,1}^{*} = \rho c_{p} \pi \left( {r_{o}^{2} - r_{i}^{2} } \right)R_{12} ,R_{11}^{*} = \rho c_{p} \pi \left( {r_{o}^{2} - r_{i}^{2} } \right)R_{11} ,R_{f2}^{*} = \rho c_{p} \Delta zR_{f2} , \\ & R_{f1}^{*} = \rho c_{p} \Delta zR_{f1} ,R_{v,s}^{*} = \rho c_{p} \Delta zR_{v,s} ,R_{l,s}^{*} = \rho c_{p} \pi \left( {r_{j + 1}^{2} - r_{j}^{2} } \right)R_{l,s} ,R_{r,s}^{*} = \rho c_{p} \pi \left( {r_{j + 1}^{2} - r_{j}^{2} } \right)R_{r,s} \\ \end{aligned} \):
where the subscript \( j \) denotes time step, \( n \) and \( m \) denote segment order of the discrete elements in the vertical and radial direction, respectively.
Solving the complex unsteady state heat transfer equations within the borehole coupled with rock outside the borehole based on the full discretization numerical schemes 50–52 requires a huge computational effort. Here, we carried out detailed simulation at refined time step and spatial resolution for the dynamic process, where the simulation results could be taken as a benchmark for the verification of the proposed efficient method.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhao, Y., Pang, Z., Huang, Y. et al. An efficient hybrid model for thermal analysis of deep borehole heat exchangers. Geotherm Energy 8, 18 (2020). https://doi.org/10.1186/s40517-020-00170-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40517-020-00170-z