New algorithms for approximating zeros of inverse strongly monotone maps and J-fixed points

Abstract

Let E be a real Banach space with dual space $E^{*}$. A new class of relatively weakJ-nonexpansive maps, $T:E\rightarrow E^{*}$, is introduced and studied. An algorithm to approximate a common element of J-fixed points for a countable family of relatively weak J-nonexpansive maps and zeros of a countable family of inverse strongly monotone maps in a 2-uniformly convex and uniformly smooth real Banach space is constructed. Furthermore, assuming existence, the sequence of the algorithm is proved to converge strongly. Finally, a numerical example is given to illustrate the convergence of the sequence generated by the algorithm.

1 Introduction

Let E be a real Banach space with dual space $E^{*}$. A mapping $J:E\rightarrow2^{E^{*}}$ defined by $J(x):= \{x^{*}\in E^{*}: \langle x,x^{*} \rangle=\Vert x \Vert^{2}, \Vert x^{*} \Vert=\Vert x\Vert, \forall x\in E \}$, is called the normalized duality map on E, where $\langle\cdot,\cdot \rangle$ denotes the duality pairing between the elements of E and $E^{*}$. A mapping $A: E\to E$ is said to be accretive if for each $x,y\in E$, there exists $j(x-y)\in J(x-y)$ such that the following inequality holds: $\langle Ax-Ay,j(x-y)\rangle\geq0$. A mapping $A:E\rightarrow E^{*}$ is said to be monotone if for each $x,y\in E$, the following inequality holds: $\langle x- y,Ax - Ay \rangle\geq0$. In a real Hilbert space, accretive operators are called monotone.

It is known that many physically significant problems can be modeled in the form of the following evolution equation: $\frac{du}{dt} + Au = 0$, where $A: E\to E$ is an accretive-type map. This equation describes any system that generates energy over time. Observe that at equilibrium, u is independent of time so that the equation reduces to

$$\begin{aligned} Au=0, \end{aligned}$$

(1.1)

whose solutions correspond to the equilibrium state of the system described by equation $\frac{du}{dt} + Au = 0$.

Approximation of solutions of Eq. (1.1) has been studied extensively by various authors (see, e.g., Aoyama et al. [4], Blum and Oettli [6], Censor, Gibali, Reich and Sabach [12], Censor, Gibali and Reich [9–11], Chidume [14], Chidume et al. [15, 16, 18, 23, 25, 26], Gibali, Reich and Zalas [27], Iiduka and Takahashi [29], Iiduka et al. [31], Kassay, Reich and Sabach [33], Kinderlehrer and Stampacchia [34], Lions and Stampacchia [36], Liu [37], Liu and Nashed [38], Ofoedu and Malonza [43], Osilike et al. [44], Reich and Sabach [48], Reich [46], Rockafellar [49], Su and Xu [51], Zegeye et al. [58], Zegeye and Shahzad [57], and the references therein).

For approximating a solution of Eq. (1.1) in a real Hilbert space H, where $A:H\rightarrow H$ is monotone, assuming existence, Browder [7] introduced an operator $T:=I-A$, where I is the identity map on H. He called such an operator a pseudocontraction. It is trivial to observe that zeros of A correspond to fixed points of T. Interest in pseudocontractive-type map stems mainly from this firm connection with the accretive-type maps. Hence, approximating fixed points of pseudocontractive maps has become a flourishing area of interest to researchers in nonlinear operator theory (see, e.g., the monographs of Alber [1], Berinde [5], Chidume [14], Goebel and Reich [28], and the references therein).

Let a function $f: E\to \mathbb{ R}\cup\{\infty\}$ be convex and proper. The subdifferential of f, $\partial f:E \to2^{E^{*}}$, is defined for each $x\in E$ by

$$\partial f(x):=\bigl\{ x^{*}\in E^{*}: f(y)-f(x)\geq\bigl\langle y-x,x^{*}\bigr\rangle , \forall y\in E\bigr\} . $$

It is known that ∂f is a monotone map on E, and $0\in \partial f(v)$ if and only if v is a minimizer of f. In general, if $A:=\partial f:E\rightarrow2^{E^{*}}$ is a monotone-type map defined on an appropriate real normed space E, solutions of equation

$$\begin{aligned} 0 \in Au, \end{aligned}$$

(1.2)

in this case whereAis of monotone type, correspond to minimizers of some convex functional defined onE. This is one of the motivations for studying the equation $Au=0$, where $A:E \to E^{*}$ is monotone.

Clearly, Browder’s fixed point technique for the equation $Au=0$, where $A:E \to E$is of accretive-type, is not applicable to the equation $Au=0$, where $A:E \to E^{*}$ is monotone, for an arbitrary real normed space E more general than Hilbert spaces.

As has been rightly observed by Hazewinkle, a Series Editor of Kluwer Academic Publishers,

“…many, and probably most, mathematical objects and models do not naturally live in Hilbert space.”

They live generally in real Banach spaces more general than Hilbert spaces.

Let E be a smooth real normed space, and let $T:E\rightarrow E^{*}$ be a map. If $J:E\rightarrow{E^{*}}$ is the normalized duality map, then $x\in E$ is called a J-fixed point of T if $Tx=Jx$ (see, e.g., Chidume et al. [23–25] and Chidume and Idu [20]). This concept was introduced by Zegeye [55] in 2008, who called such a fixed point a semi-fixed point. The concept was later, in 2012, called duality fixed point by Cheng et al. [13], Liu [37], and Su and Xu [51]. The notion of J-fixed point has been found to have numerous applications, and provides for monotone maps $T:E\rightarrow E^{*}$ the analog of Browder’s pseudocontractive maps for accretive maps, $T:E\rightarrow E$. For more on J-fixed points, the reader may consult any of the following references: Chidume and Monday [21, 22].

A map $A:E\to E^{*}$ is called inverse strongly monotone if there exists $\alpha>0$ such that

$$ \langle x-y,Ax-Ay \rangle\geq\alpha \Vert Ax-Ay \Vert ^{2}, \quad\mbox{for all } x,y\in E. $$

Chidume et al. [23] called a map $T:E\rightarrow E^{*}$strictlyJ-pseudocontractive if for every $x,y\in E$, there exists $\alpha>0$ such that the following inequality holds:

$$\begin{aligned} \langle Tx-Ty,x-y\rangle\leq\langle Jx-Jy,x-y\rangle- \alpha \bigl\Vert (Jx-Tx)-(Jy-Ty) \bigr\Vert ^{2}. \end{aligned}$$

(1.3)

Remark 1

Liu [37] called this concept α-strongly duality.

By setting $A:=J-T:E\rightarrow E^{*}$, where E is a real normed space with dual space $E^{*}$ and T is a strictly J-pseudocontractive map, we list some properties of A and T (Chidume et al. [23]):

• (i) $x\in E$ is a J-fixed point of T if and only if x is a zero of A,

• (ii) A is inverse strongly monotone if and only if T is strictly J-pseudocontractive.

We recall the following definitions.

Definition 1.1

Let C be a nonempty closed and convex subset of E; let $T:C\to E$ be a map. A point $x^{*} \in C$ is called a fixed point of T if $Tx^{*} = x^{*}$. The set of fixed points of T is denoted by $F(T)$. We say that $(I-T)$ is demiclosed at zero whenever a sequence $\{x_{n}\}$ in C converges weakly to x and $\{ x_{n} - Tx_{n}\}$ converges strongly to 0, then $x \in F(T)$. A point $p\in C$ is said to be an asymptotic fixed point of T if C contains a sequence $\{x_{n}\}_{n=1}^{\infty}$ which converges weakly to p and $\lim_{n\rightarrow\infty}\Vert Tx_{n} - x_{n}\Vert= 0$. The set of asymptotic fixed points of T is denoted by $\widehat{F}(T)$.

Definition 1.2

(Chidume and Idu [20])

Let E be a smooth real normed space with dual space $E^{*}$. Let $T:E\rightarrow E^{*}$ be any map. A point $x\in E$ is called a J-fixed point of T if $Tx=Jx$.

The set of J-fixed point of a map T is denoted by $F_{J}(T)=\{ x\in E: Tx=Jx \}$. We now give some examples of J-fixed points.

Example 1

Let H be a real Hilbert space; let $T:H\to H$ be any map with $F(T):=\{x \in H:Tx=x\} \neq\emptyset$. Then, $F(T)=F_{J}(T)$.

Example 2

(Chidume and Idu [20])

It is known that in $l_{p}$ spaces, $1< p<\infty$,

$$Jx= \Vert x \Vert _{l_{p}}^{2-p}\bigl( \vert x_{1} \vert ^{p-2}x_{1}, \vert x_{2} \vert ^{p-2}x_{2},\ldots\bigr), $$

for any $x=(x_{1},x_{2},\ldots)\in l_{p}$ (see, e.g., Alber [3], p. 36). For $1< q< p$, we set $\gamma_{p}:=(1+\frac{1}{2^{p}})^{\frac{2-p}{p}}$ and define $T:l_{p}\to l_{q}$ ($\subset l_{p}$) by

$$T(x_{1},x_{2},x_{3},\ldots)=\biggl( \gamma_{p}x_{1},\frac{\gamma _{p}}{2^{p-1}}x_{2},0,0,\ldots \biggr). $$

For any $\lambda\in \mathbb{ R}$, let $x_{\lambda}=(\lambda,\frac{\lambda }{2},0,0,\ldots)$. Then, $x_{\lambda}\in F_{J}(T)$.

Let E be a smooth real Banach space with dual space $E^{*}$. A function $\phi:E\times E\to\mathbb{R}$, defined by

$$\begin{aligned} \phi(x,y)= \Vert x \Vert ^{2}-2\langle x,Jy\rangle+ \Vert y \Vert ^{2}, \quad\forall x,y\in E, \end{aligned}$$

(1.4)

where J is the normalized duality mapping from E into $E^{*}$ will play a central role in what follows. It was introduced by Alber and has been studied by Alber and Ryazantseva [3], Alber and Guerre-Delabriere [2], Chidume et al. [16, 17, 23], Chidume and Idu [20], Kamimura and Takahashi [32], Reich [47], Takahashi and Zembayashi [53, 54], Zegeye [55], and a host of other authors.

If $E=H$, a real Hilbert space, Eq. (1.4) reduces to $\phi(x,y)=\Vert x-y\Vert^{2}$, $\forall x,y\in H$.

Definition 1.3

A map $T:C\rightarrow E$ is said to be relatively nonexpansive if the following conditions hold (see, e.g., Matsushita and Takahashi [40] and Reich [45]):

• (1) $F(T)\neq\emptyset$,

• (2) $\phi(p, Tx) \leq\phi(p, x)$, $\forall x\in C$ and $p\in F(T)$,

• (3) $\widehat{F}(T) = F(T)$.

Definition 1.4

A point $p\in C$ is said to be a strong asymptotic fixed point of T if C contains a sequence $\{x_{n}\}_{n=1}^{\infty}$ which converges strongly to p and $\lim_{n\rightarrow\infty}\Vert Tx_{n} - x_{n}\Vert= 0$ (see, e.g., Reich [45]). The set of strongly asymptotic fixed points of T is denoted by $\widetilde{F}(T)$.

Definition 1.5

A map $T:C\rightarrow E$ is said to be relatively weak nonexpansive if the following conditions hold (see, e.g., Liu [39] and Zegeye and Shahzad [56]):

• (1) $F(T)\neq\emptyset$,

• (2) $\phi(p, Tx) \leq\phi(p, x)$, $\forall x\in C$ and $p\in F(T)$,

• (3) $\widetilde{F}(T) = F(T)$.

If E is a strictly convex and reflexive real Banach space and $A: E\rightarrow E^{*}$ is a continuous monotone map with $A^{-1}(0) \neq\varnothing$, it is known that $J_{r} := (J + rA)^{-1}J$, for $r>0$, is relatively weak nonexpansive (see, e.g., Kohasaka [35]). Clearly, every relatively nonexpansive map is relatively weak nonexpansive. Let $T:C\rightarrow E$ be a map; we have that $F(T)\subset\widetilde{F}(T) \subset\widehat{F}(T)$. It follows that $F(T)= \widetilde {F}(T) = \widehat{F}(T)$ for any relatively nonexpansive map.

An example of a relatively weak nonexpansive map which is not a relatively nonexpansive map is given in Zhang et al. [59]. In the following definitions, we assume that the space E is reflexive, strictly convex, and smooth real Banach space with dual space $E^{*}$.

Definition 1.6

(Chidume et al. [15])

Let $T:E\to E^{*}$ be a map. A point $x^{*}\in E$ is called an asymptoticJ-fixed point ofT if there exists a sequence $\{x_{n}\}\subset E$ such that $x_{n}\rightharpoonup x^{*}$ and $\|Jx_{n}-Tx_{n}\| \to0$ as $n \to\infty$. We shall denote the set of asymptotic J-fixed points of T by $\widehat{F}_{J}(T)$.

Definition 1.7

(Chidume et al. [15])

A map $T:E\to E^{*}$ is said to be relativelyJ-nonexpansive if

• (i) $\widehat{F}_{J}(T)=F_{J}(T) \neq\emptyset$,

• (ii) $\phi(p,J^{-1}Tx)\leq\phi(p,x)$, $\forall x\in E$, $p\in F_{J}(T)$.

In 2008, Iiduka and Takahashi [30] introduced an iterative algorithm for finding a zero of an inverse strongly monotone map A in a 2-uniformly convex and uniformly smooth real Banach space. They proved a strong convergence theorem to some element of $A^{-1}(0)$.

For appropriating zeros of inverse strongly monotone maps and fixed points of relatively weak nonexpansive maps, Zegeye and Shahzad [56] in 2009 introduced a generalized projection algorithm and proved that the sequence generated by their algorithm converges strongly to a common element of the sets of zeros for inverse strongly monotone maps and fixed points of relatively weak nonexpansive maps

For finding an element in the set of solutions of zeros for an inverse strongly monotone map and fixed points for a countable family of relatively weak nonexpansive maps in a 2-uniformly convex and uniformly smooth real Banach space, Chidume et al. [19] proved the following theorem.

Theorem 1.8

LetEbe a 2-uniformly convex and uniformly smooth real Banach space with dual space $E^{*}$. Let $A:E\to E^{*}$be anα-inverse strongly monotone map, and let $T_{i}:E\rightarrow E$, $i=1,2,\dots$, be a countable family of relatively weak nonexpansive maps. Assume that $W:= \bigcap_{i=1}^{\infty }F(T_{i})\cap A^{-1}0\neq\emptyset$, where $A^{-1}0=\{u \in E: Au=0\}\neq\emptyset$. For arbitrary $x_{1} \in E$, let the sequence $\{x_{n}\}_{n=1}^{\infty}$be iteratively defined by

$$\begin{aligned} \textstyle\begin{cases} x_{1}\in E:=C_{1},\\ u_{n}= J^{-1}(Jx_{n}-\lambda Ax_{n}), \\ y_{n}=J^{-1} ( \sum_{i=1}^{\infty}\alpha_{i} JT_{i}u_{n} ),\\ C_{n+1}=\{v\in C_{n}:\phi(v,y_{n})\leq\phi(v,x_{n})\},\\ x_{n+1}=\varPi_{C_{n+1}}x_{1}, \quad\forall n\ge1, \end{cases}\displaystyle \end{aligned}$$

(1.5)

where $J: E \rightarrow E^{*}$is the normalized duality map, $\lambda \in (0,\frac{\alpha}{2L} )$, $L>0$denotes the Lipschitz constant of $J^{-1}$, and $\{\alpha_{i}\} _{i=1}^{\infty}$is a sequence in $(0,1)$such that $\sum_{i=1}^{\infty}\alpha_{i}=1$. Then, the sequences $\{x_{n}\}_{n=1}^{\infty}$and $\{u_{n}\}_{n=1}^{\infty}$converge strongly to some $x^{*}\in W:= \bigcap_{i=1}^{\infty}F(T_{i})\cap A^{-1}0$.

Remark 2

This theorem is a significant improvement on the result of Zegeye and Shahzad [56]. We observe that the relatively weak nonexpansive maps studied in Zegeye and Shahzad [56] and Chidume et al. [19] are maps from a real normed space to itself.

It is our purpose in this paper to introduce a new class of maps called relatively weak J-nonexpansive maps from a real normed spaceEto its dual space $E^{*}$. We first give some properties of this class of maps, and we then construct an algorithm to approximate a common element of J-fixed points for a countable family of relatively weak J-nonexpansive maps and zeros of a countable family of inverse strongly monotone maps in a 2-uniformly convex and uniformly smooth real Banach space. We prove a strong convergence theorem. Finally, we give a numerical example to illustrate the convergence of the sequence generated by the algorithm.

2 Preliminaries

It is obvious from the definition of the function ϕ that

$$\begin{aligned} \bigl( \Vert x \Vert - \Vert y \Vert \bigr)^{2} \leq\phi(x,y)\leq\bigl( \Vert x \Vert + \Vert y \Vert \bigr)^{2}, \quad\forall x,y\in E. \end{aligned}$$

(2.1)

Remark 3

It is known that if E is a reflexive, strictly convex and smooth real Banach space, then, for all $x,y\in E$, $\phi(x,y)=0$ if and only if $x=y$ (see, e.g., Zhou et al. [60]).

Define a map $V:E\times E^{*}\to\mathbb{R}$ by $V(x,x^{*})=\Vert x\Vert^{2}-2\langle x,x^{*}\rangle+\Vert x^{*}\Vert^{2}$. Then, it is easy to see that $V(x,x^{*})=\phi(x,J^{-1}(x^{*}))$, $\forall x\in E$, $x^{*}\in E^{*}$. Let C be a nonempty closed and convex subset of a smooth, strictly convex, and reflexive real Banach space E. The generalized projection map introduced by Alber [1], is a map $\varPi_{C}:E\rightarrow C$ such that, for any $x\in E$, there corresponds a unique element $x_{0}:=\varPi_{C} (x) \in C$ such that $\phi(x_{0},x)= \min_{y\in C}\phi(y,x)$. We note that the existence and uniqueness of the generalized projection map $\varPi_{C}$ follows from the strict monotonicity and properties of the Lyapunov functional ϕ (see, e.g., Takahashi [52], Alber [1], and Alber and Ryazantseva [3]). If E is a real Hilbert space, we remark that the generalized projection $\varPi_{C}$ coincides with the metric projection from E onto C.

The following lemmas are needed in the sequel.

Lemma 2.1

(Matsushita and Takahashi [41])

LetEbe a strictly convex and smooth Banach space; letCbe a closed convex subset ofE, and letTbe a relatively nonexpansive mapping fromCinto itself. Then, $F(T )$is a closed convex subset ofC.

Lemma 2.2

(Schu [50])

LetEbe a uniformly convex Banach space andCbe a nonempty closed convex subset ofE. LetTbe a nonexpansive mapping ofCinto itself. Then, $(I-T)$is demiclosed at zero.

Lemma 2.3

(Chidume et al. [19])

LetCbe a closed convex subset of a uniformly convex and uniformly smooth real Banach spaceE, and let $T_{i}:C\rightarrow E$, $i=1,2,\dots$, be a countable family of relatively weak nonexpansive maps. Assume that $\bigcap_{i=1}^{\infty}F(T_{i})\neq\emptyset$and $\{\alpha_{i}\} _{i=1}^{\infty}$is a sequence in $(0,1)$such that $\sum_{i=1}^{\infty}\alpha_{i}=1$. Let the map $T:C\rightarrow E$be defined by $Tx=J^{-1} ( \sum_{i=1}^{\infty}\alpha_{i} JT_{i}x )$for each $x\in C$. Then, Tis relatively weak nonexpansive and $F(T)= \bigcap_{i=1}^{\infty}F(T_{i})$.

Lemma 2.4

(Bruck [8])

SupposeEis strictly convex and $\{T_{n}\}$is a sequence of nonexpansive mappings $T_{n}:C\rightarrow E$. Then there exists a nonexpansive mapping $T:C\rightarrow E$such that $F(T)= \bigcap_{i=1}^{\infty}F(T_{i})$.

Remark 4

It was proved in Bruck [8] that the map $T:C\rightarrow E$ defined by $Tx= \sum_{i=1}^{\infty}\alpha_{i} T_{i}x$, for each $x\in C$, where $\{\alpha_{i}\}_{i=1}^{\infty}$ is a sequence in $(0,1)$ such that $\sum_{i=1}^{\infty}\alpha_{i}=1$, is nonexpansive.

3 Main results

Definition 3.1

Let E be a reflexive, strictly convex, and smooth real Banach space with dual space $E^{*}$. Let $T:E\to E^{*}$ be a map. A point $p\in E$ will be called a strong asymptoticJ-fixed point of T if E contains a sequence $\{x_{n}\}_{n=1}^{\infty}$ which converges strongly to p and $\lim_{n\rightarrow \infty}\Vert Tx_{n} - Jx_{n}\Vert= 0$. The set of strongly asymptotic J-fixed points of T will be denoted by $\widetilde{F_{J}}(T)$.

Definition 3.2

Let E be a reflexive, strictly convex, and smooth real Banach space with dual space $E^{*}$. A map $T:E\rightarrow E^{*}$ will be called relatively weakJ-nonexpansive if the following conditions hold:

• (1) $F_{J}(T)\neq\emptyset$,

• (2) $\phi(p, J^{-1}Tx) \leq\phi(p, x)$, $\forall x\in E$ and $p\in F_{J}(T)$,

• (3) $\widetilde{F_{J}}(T) = F_{J}(T)$.

An example of a relatively weakJ-nonexpansive map that is not relatively J-nonexpansive (see Zhang et al. [59]). In addition, we provide the following example.

Example 3

Let $\ell_{p}(\mathbb{R})$ be the sequence space, for $1< p<\infty$. Let the sequence $\{x_{n}\}_{n=1}^{\infty}\in\ell_{p}(\mathbb{R})$ be defined by $x_{0} = (1,0,0,0,\ldots)$, $x_{1} = (1,1,0,0,0,\ldots)$, $x_{2} = (1,0,1,0,0,0,\ldots)$, $x_{3} = (1,0,0,1,0,0,0,\ldots)$, …, $x_{n} = (\zeta_{n,1},\zeta_{n,2},\zeta_{n,3},\ldots,\zeta _{n,k+1},0, \ldots)$, …, where

$$\begin{aligned} \zeta_{n,k}= \textstyle\begin{cases} 1, & \text{if } k=1,n+1; \\ 0, & \text{if } k \neq1, k \neq n+1. \end{cases}\displaystyle \end{aligned}$$

Let $T:\ell_{p}(\mathbb{R})\rightarrow\ell_{q}(\mathbb{R})$ be a map defined as follows:

$$\begin{aligned} T(x)= \textstyle\begin{cases} \frac{n}{n+1}Jx_{n}, & \text{if } x=x_{n}, \\ -Jx, & \text{if } x \neq x_{n}, \end{cases}\displaystyle \end{aligned}$$

(3.1)

where $J:\ell_{p}(\mathbb{R})\rightarrow\ell_{q}(\mathbb{R})$ is the single valued normalized duality map and $\frac{1}{p} + \frac{1}{q}=1$. It is easy to see that the sequence $\{x_{n}\}_{n=1}^{\infty}$ converges weakly to $x_{0}$.

Let $f=(\alpha_{1},\alpha_{2},\ldots,\alpha_{n+1},\ldots)\in\ell _{q}(\mathbb{R})$, for $1< q<\infty$; we have that $f(x_{n}-x_{0})=\langle f,x_{n}-x_{0}\rangle=\alpha_{n+1} \rightarrow0$ as $n \rightarrow\infty$. Therefore, $\{x_{n}\}_{n=1}^{\infty}$ converges weakly to $x_{0}$. Clearly, $\{x_{n}\}_{n=1}^{\infty}$ is not Cauchy since $\Vert x_{n} - x_{m}\Vert=\sqrt{2}$, for $n\neq m$, and the J-fixed point of T is zero, i.e., $F_{J}(T)=\{0\}$. Since $\{x_{n}\}_{n=1}^{\infty}$ converges weakly to $x_{0}$ and

$$\Vert Tx_{n} - Jx_{n} \Vert = \biggl\Vert \frac{n}{n+1}Jx_{n} - Jx_{n} \biggr\Vert = \frac{1}{n+1} \Vert Jx_{n} \Vert \rightarrow0, $$

we see that $\widehat{F_{J}}(T)=\{x_{0}\}$, i.e., $x_{0}$ is an asymptotic J-fixed point of T. Hence, $\widehat{F_{J}}(T)\neq {F_{J}}(T)$, i.e., T is not a relatively J-nonexpansive map.

We now show that zero is a unique strong asymptotic J-fixed point of T. Let $\{y_{n}\}_{n=1}^{\infty }\in\ell_{p}(\mathbb{R})$ such that $y_{n} \rightarrow y^{*}$ and $\Vert Ty_{n} - Jy_{n}\Vert\rightarrow0$ as $n \rightarrow\infty$. Since $\{x_{n}\}_{n=1}^{\infty}$ is not Cauchy, there exists sufficiently large N such that $y_{n}\neq x_{m}$, for $n, m >N$. Now, $Ty_{n}= - Jy_{n}$, for $n>N$; this implies that $Ty_{n}-Jy_{n}= - 2Jy_{n}$, for $n>N$. It follows that $\Vert Ty_{n} - Jy_{n}\Vert=2\Vert Jy_{n} \Vert\rightarrow0$, and thus, $y_{n} \rightarrow y^{*}=0$. Consequently, $\widetilde{F_{J}}(T) = F_{J}(T)$.

We now show that T is a relatively weak J-nonexpansive map. Based on the definition of T, we obtain

$$\phi\bigl(0, J^{-1}Tx\bigr)= \Vert Tx \Vert ^{2}\leq \Vert x \Vert ^{2} = \Vert 0 \Vert ^{2} +\langle0,Jx \rangle+ \Vert x \Vert ^{2} =\phi(0, x),\quad \forall x\in \ell_{p}(\mathbb{R}). $$

It follows that T is a relatively weak J-nonexpansive map. Hence, the map T is an example of a relatively weak J-nonexpansive map, which is not a relatively J-nonexpansive map.

Lemma 3.3

LetEbe a reflexive, strictly convex, and smooth real Banach space with dual space $E^{*}$. Let $T:E\to E^{*}$be a map. Then, $F_{J}(T)\subset\widetilde{F_{J}}(T) \subset\widehat{F_{J}}(T)$.

Proof

Let $p\in F_{J}(T)$. Then, $T(p)=Jp$. Set $x_{n}=p$, $\forall n\geq1$, so $Tx_{n}=Tp=Jp$. Therefore, $F_{J}(T)\subset\widetilde{F_{J}}(T)$. Clearly, $\widetilde {F_{J}}(T) \subset\widehat{F_{J}}(T)$. Hence, $F_{J}(T)\subset\widetilde{F_{J}}(T) \subset\widehat{F_{J}}(T)$. □

Theorem 3.4

LetEbe a reflexive, strictly convex, and smooth real Banach space with dual space $E^{*}$. Let $T:E\to E^{*}$be a relativelyJ-nonexpansive map. Then, Tis relatively weakJ-nonexpansive.

Proof

Since T is a relatively J-nonexpansive map, we get that

• (1) $\widehat{F_{J}}(T) = F_{J}(T)\neq\emptyset$,

• (2) $\phi(p, J^{-1}Tx) \leq\phi(p, x)$, $\forall x\in E$ and $p\in F_{J}(T)$.

Using Lemma 3.3 and the fact that $\widehat{F_{J}}(T) = F_{J}(T)$, we see that $F_{J}(T)\subset\widetilde{F_{J}}(T) \subset\widehat{F_{J}}(T) = F_{J}(T)$. This implies that $F_{J}(T)=\widetilde{F_{J}}(T)=\widehat{F_{J}}(T)$. Therefore, T is relatively weak J-nonexpansive. □

Theorem 3.5

LetEbe a reflexive, strictly convex, and smooth real Banach space with dual space $E^{*}$. Let $T:E\to E^{*}$be a relatively weakJ-nonexpansive map. Then, theJ-fixed point set ofT, $F_{J}(T)$, is closed and convex.

Proof

We first show that $F_{J}(T)$ is closed. Let $\{x_{n}\}_{n=1}^{\infty}$ be any sequence in $F_{J}(T)$ such that $x_{n} \rightarrow x \in E$ as $n\rightarrow\infty$. Using the fact that T is relatively weak J-nonexpansive and definition of ϕ, we see that $\phi(x_{n}, J^{-1}Tx) \leq\phi(x_{n}, x)\rightarrow0$ as $n\rightarrow\infty$. Thus, $\phi(x_{n}, J^{-1}Tx)\rightarrow0$. We observe that $\phi(x_{n}, J^{-1}Tx)=\Vert x_{n} \Vert^{2}-2\langle x_{n},J(J^{-1}Tx)\rangle+\Vert JJ^{-1}Tx \Vert^{2}$, and so $\lim_{n\rightarrow\infty}\phi(x_{n}, J^{-1}Tx) = \phi(x, J^{-1}Tx)=0$. From Remark 3, this implies that $J^{-1}Tx=x$, so $Tx=Jx$. Therefore, $x\in F_{J}(T)$. It follows that $F_{J}(T)$ is closed.

We now show that the set $F_{J}(T)$ is convex. Let $x_{1}, x_{2} \in F_{J}(T)$, $t\in(0,1)$, and set $x_{3}=tx_{1}+(1-t)x_{2}$; we show that $x_{3} \in F_{J}(T)$. From the definition of ϕ and the fact that T is relatively weak J-nonexpansive, we see that

$$\begin{aligned} \phi\bigl(x_{3},J^{-1}Tx_{3}\bigr) =& \Vert x_{3} \Vert ^{2}-2\langle x_{3},Tx_{3} \rangle + \bigl\Vert JJ^{-1}Tx_{3} \bigr\Vert ^{2} \\ =& \Vert x_{3} \Vert ^{2}-2\bigl\langle tx_{1}+(1-t)x_{2},Tx_{3}\bigr\rangle + \bigl\Vert JJ^{-1}Tx_{3} \bigr\Vert ^{2} \\ =& \Vert x_{3} \Vert ^{2}-2t\langle x_{1},Tx_{3}\rangle-2(1-t)\langle x_{2},Tx_{3} \rangle+ \bigl\Vert JJ^{-1}Tx_{3} \bigr\Vert ^{2} \\ =& \Vert x_{3} \Vert ^{2}+t\phi\bigl(x_{1},J^{-1}Tx_{3} \bigr)+(1-t)\phi \bigl(x_{2},J^{-1}Tx_{3}\bigr)-t \Vert x_{1} \Vert ^{2} \\ &{}-(1-t) \Vert x_{2} \Vert ^{2} \\ \leq& \Vert x_{3} \Vert ^{2}+t\phi(x_{1},x_{3})+(1-t) \phi(x_{2},x_{3})-t \Vert x_{1} \Vert ^{2}-(1-t) \Vert x_{2} \Vert ^{2} \\ =& \Vert x_{3} \Vert ^{2}-2\langle x_{3},Jx_{3}\rangle+ \Vert x_{3} \Vert ^{2}=0, \end{aligned}$$

so $\phi(x_{3},J^{-1}Tx_{3})=0$. Therefore, we see that $J^{-1}Tx_{3}=x_{3}$ from Remark 3, and this implies that $Tx_{3}=Jx_{3}$, i.e., $x_{3} \in F_{J}(T)$. Therefore, $F_{J}(T)$ is convex. Hence, the J-fixed point set of T, $F_{J}(T)$, is closed and convex. □

Lemma 3.6

LetEbe a uniformly smooth and uniformly convex real Banach space with dual space $E^{*}$. Then, the map $T:E\to E^{*}$is relatively weakJ-nonexpansive map if and only if the map $J^{-1}T:E\to E$is relatively weak nonexpansive map. Moreover, $F_{J}(T)=F(J^{-1}T)$and $\widetilde{F}(J^{-1}T)=\widetilde{F}_{J}(T)$.

Proof

We first show that $F_{J}(T)=F(J^{-1}T)$. $y^{*}\in F_{J}(T)$ iff $Ty^{*}=Jy^{*}$ iff $J^{-1}Ty^{*}=y^{*}$ iff $y^{*}\in F(J^{-1}T)$. Therefore, $F_{J}(T)=F(J^{-1}T)$. We now show that $\widetilde {F}(J^{-1}T)=\widetilde{F}_{J}(T)$. $p\in\widetilde{F}_{J}(T)$ if and only if there exists a sequence $\{ x_{n}\}_{n=1}^{\infty}\subseteq E$ which converges strongly to p and $\lim_{n\rightarrow\infty}\Vert Tx_{n} - Jx_{n}\Vert= 0$ if and only if there exists a sequence $\{x_{n}\}_{n=1}^{\infty}\subseteq E$ which converges strongly to p and $\lim_{n\rightarrow\infty}\Vert J^{-1}Tx_{n} - x_{n}\Vert= 0$ if and only if $p\in\widetilde{F}(J^{-1}T)$.

Therefore, $\widetilde{F}(J^{-1}T)=\widetilde{F}_{J}(T)$.

Now, T is a relatively weak J-nonexpansive map if

• (1) $\widetilde{F}_{J}(T) = F_{J}(T)\neq\emptyset$,

• (2) $\phi(p, J^{-1}Tx) \leq\phi(p, x)$, $\forall x\in E$ and $p\in F_{J}(T)$.

In addition, $J^{-1}T$ is a relatively weak nonexpansive map if

• (1) $\widetilde{F}(J^{-1}T) = F(J^{-1}T)\neq\emptyset$,

• (2) $\phi(p, J^{-1}Tx) \leq\phi(p, x)$, $\forall x\in E$ and $p\in F(J^{-1}T)$.

To show that $T:E\to E^{*}$ is relatively weak J-nonexpansive map if and only if the map $J^{-1}T:E\to E$ is relatively weak nonexpansive map, it suffices to show from the definitions above that $F_{J}(T)=F(J^{-1}T)$ and $\widetilde{F}(J^{-1}T)=\widetilde{F}_{J}(T)$. Moreover, we have already shown that $F_{J}(T)=F(J^{-1}T)$ and $\widetilde{F}(J^{-1}T)=\widetilde{F}_{J}(T)$. Hence, $T:E\to E^{*}$ is a relatively weak J-nonexpansive map if and only if the map $J^{-1}T:E\to E$ is relatively weak nonexpansive. □

We now prove the following lemma.

Lemma 3.7

LetEbe a uniformly smooth and 2-uniformly convex real Banach space with dual space $E^{*}$. Let $A:E\to E^{*}$be anα-inverse strongly monotone map, and let $T:E\rightarrow E^{*}$be a relatively weakJ-nonexpansive map. Assume that $W:=F_{J}(T)\cap A^{-1}0\neq\emptyset$. For arbitrary $x_{1} \in C_{1}$, let the sequence $\{x_{n}\}_{n=1}^{\infty}$be iteratively defined by

$$\begin{aligned} \textstyle\begin{cases} x_{1}\in E:=C_{1},\\ u_{n}= J^{-1}(Jx_{n}-\lambda Ax_{n}), \\ y_{n}=J^{-1}Tu_{n},\\ C_{n+1}=\{v\in C_{n}:\phi(v,y_{n})\leq\phi(v,x_{n})\},\\ x_{n+1}=\varPi_{C_{n+1}}x_{1},\quad\forall n\ge1, \end{cases}\displaystyle \end{aligned}$$

(3.2)

where $J: E \rightarrow E^{*}$is the normalized duality map, $\lambda \in (0,\frac{\alpha}{ 2L} )$and $L>0$denotes a Lipschitz constant of $J^{-1}$. Then, the sequences $\{x_{n}\}_{n=1}^{\infty}$and $\{u_{n}\}_{n=1}^{\infty}$converge strongly to some $x^{*}\in W$.

Proof

Since T is a relatively weak J-nonexpansive map, it follows from Lemma 3.6 that $J^{-1}T$ is relatively weak nonexpansive and $F_{J}(T)=F(J^{-1}T)$. Using Theorem 1.8, we have that the sequences $\{x_{n}\}_{n=1}^{\infty}$ and $\{u_{n}\}_{n=1}^{\infty}$ converge strongly to some $x^{*}\in W$. □

4 Strong convergence theorems for countable families of maps

Lemma 4.1

LetEbe a uniformly smooth and uniformly convex real Banach space with dual space $E^{*}$. Let $T_{i}:E\rightarrow E^{*}$, for each $i=1,2,\dots$, be a countable family of relatively weakJ-nonexpansive maps such that $\bigcap_{i=1}^{\infty}F_{J}(T_{i})\neq\emptyset$. Let a map $T:E\rightarrow E^{*}$be defined by $Tx= \sum_{i=1}^{\infty}\delta_{i} T_{i}x$, for each $x\in E$, where $\{ \delta_{i}\}_{i=1}^{\infty}$is a sequence in $(0,1)$such that $\sum_{i=1}^{\infty}\delta_{i}=1$. Then, Tis relatively weakJ-nonexpansive and $F_{J}(T)= \bigcap_{i=1}^{\infty}F_{J}(T_{i})$.

Proof

Given that the map T is defined by $Tx= \sum_{i=1}^{\infty}\delta _{i} T_{i}x$, for each $x\in E$. This implies that $J^{-1}Tx=J^{-1} ( \sum_{i=1}^{\infty}\delta_{i} J(J^{-1}T_{i})x )$. Using the fact that $T_{i}$ is relatively weak J-nonexpansive for each i, it follows from Lemma 3.6 that $J^{-1}T_{i}$, for each i, is relatively weak nonexpansive and $F_{J}(T_{i})=F(J^{-1}T_{i})$. By applying Lemma 2.3, we obtain that $J^{-1}T$ is relatively weak nonexpansive and $F(J^{-1}T)= \bigcap_{i=1}^{\infty }F(J^{-1}T_{i})$. It follows from Lemma 3.6 that T is relatively weak J-nonexpansive, and $F_{J}(T)=F(J^{-1}T)= \bigcap_{i=1}^{\infty}F(J^{-1}T_{i})= \bigcap_{i=1}^{\infty}F_{J}(T_{i})$. □

Lemma 4.2

LetEbe a uniformly convex and uniformly smooth real Banach space with dual space $E^{*}$. Let $A_{i}:E\to E^{*}$, for each $i=1,2,\dots$, be a countable family of $\alpha_{i}$-inverse strongly monotone maps such that $\alpha:= \inf_{i\geq1}\alpha_{i}>0$and $\bigcap_{i=1}^{\infty }A_{i}^{-1}(0)\neq\emptyset$. Let a map $A:E\rightarrow E^{*}$be defined by $Ax= \sum_{i=1}^{\infty}\beta_{i} A_{i}x$, for each $x\in E$, where $\{\beta_{i}\}_{i=1}^{\infty}$is a sequence in $(0,1)$such that $\sum_{i=1}^{\infty}\beta_{i}=1$. Then, (i) Ais well defined, (ii) Aisα-inverse strongly monotone, (iii) $A^{-1}(0)= \bigcap_{i=1}^{\infty}A_{i}^{-1}(0)$.

Proof

(i) Let $x\in E$ and $x^{*}\in\bigcap_{i=1}^{\infty}A_{i}^{-1}(0)$. Since $A_{i}$, for each $i=1,2,\dots$, is Lipschitz, we obtain $\Vert\beta_{i} A_{i}x \Vert=\Vert\beta_{i}(A_{i}x-A_{i}x^{*}) \Vert\leq \frac{1}{\alpha}\Vert x-x^{*} \Vert$. Hence, for each $x\in E$, the series $\sum_{i=1}^{\infty}\beta_{i} A_{i}x$ converges absolutely. This shows that the map A is well defined.

(ii) Let $x,y\in E$. Then, using the fact that $A_{i}$, for each $i=1,2,\dots$, is $\alpha_{i}$-inverse strongly monotone and a result of Nilsrakoo and Saejung [42], we have that

$$\begin{aligned} \langle x-y, Ax-Ay\rangle =& \sum_{i=1}^{\infty} \beta_{i} \langle x-y, A_{i}x-A_{i}y\rangle \\ \geq& \sum_{i=1}^{\infty}\beta_{i} \alpha_{i} \Vert A_{i}x-A_{i}y \Vert ^{2} \\ \geq& \alpha \Biggl\Vert \sum_{i=1}^{\infty} \beta_{i}A_{i}x- \sum_{i=1}^{\infty} \beta_{i}A_{i}y \Biggr\Vert ^{2} \\ =&\alpha \Vert Ax-Ay \Vert ^{2}. \end{aligned}$$

This yields that A is α-inverse strongly monotone.

(iii) It is obvious that $\bigcap_{i=1}^{\infty}A_{i}^{-1}(0)\subseteq A^{-1}(0)$. We now show that $A^{-1}(0)\subseteq\bigcap_{i=1}^{\infty}A_{i}^{-1}(0)$. Let $x\in A^{-1}(0)$. We show that $x\in\bigcap_{i=1}^{\infty}A_{i}^{-1}(0)$. Let $y_{0}\in\bigcap_{i=1}^{\infty}A_{i}^{-1}(0)$. This implies that $y_{0}\in A^{-1}(0)$. From the definition of A, we get

$$\begin{aligned} 0=\langle x-y_{0}, Ax-Ay_{0}\rangle=\sum _{i=1}^{\infty}\beta_{i} \langle x-y_{0}, A_{i}x-A_{i}y_{0}\rangle. \end{aligned}$$

(4.1)

By applying the fact that $A_{i}$, for each $i=1,2,\dots$, is monotone and $\sum_{i=1}^{\infty}\beta_{i}=1$, it follows from Eq. (4.1) that

$$\begin{aligned} \langle x-y_{0}, A_{i}x-A_{i}y_{0} \rangle=0, \quad\text{for each } i=1,2,\ldots. \end{aligned}$$

(4.2)

Using the fact that $A_{i}$, for each $i=1,2,\dots$, is $\alpha _{i}$-inverse strongly monotone and $y_{0}\in\bigcap_{i=1}^{\infty}A_{i}^{-1}(0)$, we obtain

$$0= \langle x-y_{0}, A_{i}x-A_{i}y_{0} \rangle\geq\alpha_{i} \Vert A_{i}x-A_{i}y_{0} \Vert ^{2}\geq\alpha \Vert A_{i}x \Vert ^{2}. $$

This implies that $A_{i}x=0$, for each $i=1,2,\dots$, so $x\in\bigcap_{i=1}^{\infty}A_{i}^{-1}(0)$. Thus, $A^{-1}(0)\subseteq\bigcap_{i=1}^{\infty}A_{i}^{-1}(0)$. Hence, $A^{-1}(0)= \bigcap_{i=1}^{\infty}A_{i}^{-1}(0)$. This completes the proof. □

We now prove the following theorem.

Theorem 4.3

LetEbe a uniformly smooth and 2-uniformly convex real Banach space with dual space $E^{*}$. Let $A_{i}:E\to E^{*}$, for each $i=1,2,\dots$, be a countable family of $\alpha_{i}$-inverse strongly monotone maps such that $\alpha:= \inf_{i\geq1}\alpha_{i}>0$and $\bigcap_{i=1}^{\infty }A_{i}^{-1}(0)\neq\emptyset$. Let $T_{i}:E\rightarrow E^{*}$, for each $i=1,2,\dots$, be a countable family of relatively weakJ-nonexpansive maps such that $\bigcap_{i=1}^{\infty}F_{J}(T_{i})\neq\emptyset$. Let $\{\beta_{i}\}_{i=1}^{\infty}$and $\{\delta_{i}\}_{i=1}^{\infty}$be sequences in $(0,1)$such that $\sum_{i=1}^{\infty}\beta_{i}=1$, $\sum_{i=1}^{\infty}\delta_{i}=1$, and $W:=F_{J} ( \sum_{i=1}^{\infty}\delta_{i} T_{i} )\cap ( \sum_{i=1}^{\infty}\beta_{i} A_{i} )^{-1}0\neq\emptyset$. For arbitrary $x_{1} \in C_{1}$, let the sequence $\{x_{n}\}_{n=1}^{\infty}$be iteratively defined by

$$\begin{aligned} \textstyle\begin{cases} x_{1}\in E:=C_{1},\\ u_{n}= J^{-1}(Jx_{n}-\lambda ( \sum_{i=1}^{\infty}\beta_{i} A_{i} )x_{n}), \\ y_{n}=J^{-1} ( \sum_{i=1}^{\infty}\delta_{i} T_{i} )u_{n},\\ C_{n+1}=\{v\in C_{n}:\phi(v,y_{n})\leq\phi(v,x_{n})\},\\ x_{n+1}=\varPi_{C_{n+1}}x_{1}, \quad\forall n\ge1, \end{cases}\displaystyle \end{aligned}$$

(4.3)

where $J: E \rightarrow E^{*}$is the normalized duality map, $\lambda \in (0,\frac{\alpha}{ 2L} )$, and $L>0$denotes a Lipschitz constant of $J^{-1}$. Then, the sequences $\{x_{n}\}_{n=1}^{\infty}$and $\{u_{n}\}_{n=1}^{\infty}$converge strongly to some $x^{*}\in W$.

Proof

We observe from Lemma 4.1 that the map $T:E\rightarrow E^{*}$ defined by $Tx:= \sum_{i=1}^{\infty}\delta_{i} T_{i}x$, for each $x\in E$, where $\{\delta_{i}\}_{i=1}^{\infty}$ is a sequence in $(0,1)$ such that $\sum_{i=1}^{\infty}\delta_{i}=1$, is relatively weak J-nonexpansive and $F_{J}(T)= \bigcap_{i=1}^{\infty}F_{J}(T_{i})$. Also, consider the map $A:E\rightarrow E^{*}$ defined by $Ax= \sum_{i=1}^{\infty}\beta _{i} A_{i}x$, for each $x\in E$ where $\{\beta_{i}\}_{i=1}^{\infty}$ is a sequence in $(0,1)$ such that $\sum_{i=1}^{\infty}\beta_{i}=1$. Then, we have the following by Lemma 4.2: (i) A is well defined, (ii) A is α-inverse strongly monotone, (iii) $A^{-1}(0)= \bigcap_{i=1}^{\infty}A_{i}^{-1}(0)$. It follows by Lemma 3.7 that the sequences $\{x_{n}\}_{n=1}^{\infty}$ and $\{u_{n}\}_{n=1}^{\infty}$ converge strongly to some $x^{*}\in W:=F_{J} ( \sum_{i=1}^{\infty}\delta_{i} T_{i} )\cap ( \sum_{i=1}^{\infty}\beta_{i} A_{i} )^{-1}0\neq\emptyset$. □

Corollary 4.4

Let $E=L_{p}, \ell_{p}, \textit{ and } W_{m}^{p}$, $1< p\leq2$. Let $A_{i}:E\to E^{*}$, for each $i=1,2,\dots$, be a countable family of $\alpha_{i}$-inverse strongly monotone maps such that $\alpha:= \inf_{i\geq1}\alpha_{i}>0$and $\bigcap_{i=1}^{\infty }A_{i}^{-1}(0)\neq\emptyset$. Let $T_{i}:E\rightarrow E^{*}$, for each $i=1,2,\dots$, be a countable family of relatively weakJ-nonexpansive maps such that $\bigcap_{i=1}^{\infty}F_{J}(T_{i})\neq\emptyset$. Let $\{\beta_{i}\}_{i=1}^{\infty}$and $\{\delta_{i}\}_{i=1}^{\infty}$be sequences in $(0,1)$such that $\sum_{i=1}^{\infty}\beta_{i}=1$, $\sum_{i=1}^{\infty}\delta_{i}=1$, and $W:=F_{J} ( \sum_{i=1}^{\infty}\delta_{i} T_{i} )\cap ( \sum_{i=1}^{\infty}\beta_{i} A_{i} )^{-1}0\neq\emptyset$. For arbitrary $x_{1} \in C_{1}$, let the sequence $\{x_{n}\}_{n=1}^{\infty}$be iteratively defined by

$$\begin{aligned} \textstyle\begin{cases} x_{1}\in E:=C_{1},\\ u_{n}= J^{-1}(Jx_{n}-\lambda ( \sum_{i=1}^{\infty}\beta_{i} A_{i} )x_{n}), \\ y_{n}=J^{-1} ( \sum_{i=1}^{\infty}\delta_{i} T_{i} )u_{n},\\ C_{n+1}=\{v\in C_{n}:\phi(v,y_{n})\leq\phi(v,x_{n})\},\\ x_{n+1}=\varPi_{C_{n+1}}x_{1}, \quad\forall n\ge1, \end{cases}\displaystyle \end{aligned}$$

(4.4)

where $J: E \rightarrow E^{*}$is the normalized duality map, $\lambda\in (0,\frac{\alpha}{ 2L} )$, and $L>0$denotes a Lipschitz constant of $J^{-1}$. Then, the sequences $\{x_{n}\}_{n=1}^{\infty}$and $\{u_{n}\}_{n=1}^{\infty}$converge strongly to some $x^{*}\in W$.

Proof

We observe that E is a 2-uniformly convex and uniformly smooth real Banach space. It follows from Theorem 4.3 that the sequences $\{x_{n}\}_{n=1}^{\infty}$ and $\{u_{n}\}_{n=1}^{\infty}$ converge strongly to some $x^{*}\in W:=F_{J} ( \sum_{i=1}^{\infty}\delta_{i} T_{i} )\cap ( \sum_{i=1}^{\infty}\beta_{i} A_{i} )^{-1}0\neq\emptyset$. □

Corollary 4.5

Let $E=H$be a real Hilbert space. Let $A_{i}:H\to H$, for each $i=1,2,\dots$, be a countable family of $\alpha_{i}$-inverse strongly monotone maps such that $\alpha:= \inf_{i\geq1}\alpha_{i}>0$and $\bigcap_{i=1}^{\infty }A_{i}^{-1}(0)\neq\emptyset$. Let $T_{i}:H\rightarrow H$, for each $i=1,2,\dots$, be a countable family of nonexpansive maps such that $\bigcap_{i=1}^{\infty}F(T_{i})\neq\emptyset$. Let $\{\beta_{i}\}_{i=1}^{\infty}$and $\{\delta_{i}\}_{i=1}^{\infty}$be sequences in $(0,1)$such that $\sum_{i=1}^{\infty}\beta_{i}=1$, $\sum_{i=1}^{\infty}\delta_{i}=1$, and $W:=F_{J} ( \sum_{i=1}^{\infty}\delta_{i} T_{i} )\cap ( \sum_{i=1}^{\infty}\beta_{i} A_{i} )^{-1}0\neq\emptyset$. For arbitrary $x_{1} \in C_{1}$, let the sequence $\{x_{n}\}_{n=1}^{\infty}$be iteratively defined by

$$\begin{aligned} \textstyle\begin{cases} x_{1}\in H:=C_{1},\\ u_{n}= x_{n}-\lambda ( \sum_{i=1}^{\infty}\beta_{i} A_{i} )x_{n}, \\ y_{n}= ( \sum_{i=1}^{\infty}\delta_{i} T_{i} )u_{n},\\ C_{n+1}=\{v\in C_{n}: \Vert v-y_{n} \Vert \leq \Vert v-x_{n} \Vert \},\\ x_{n+1}=P_{C_{n+1}}x_{1}, \quad\forall n\ge1, \end{cases}\displaystyle \end{aligned}$$

(4.5)

where $\lambda\in (0,\frac{\alpha}{ 2} )$and $P_{C_{n+1}}$denotes the projection map fromHonto $C_{n+1}$. Then, the sequences $\{x_{n}\}_{n=1}^{\infty}$and $\{u_{n}\} _{n=1}^{\infty}$converge strongly to some $x^{*}\in W$.

Proof

The map $T:H\rightarrow H$ defined by $Tx= \sum_{i=1}^{\infty}\delta _{i} T_{i}x$, for each $x\in H$, where $\{\delta_{i}\}_{i=1}^{\infty}$ is a sequence in $(0,1)$ such that $\sum_{i=1}^{\infty}\delta_{i}=1$, is nonexpansive by Remark 4. It suffices to show that if T is nonexpansive in a Hilbert space, then T is relatively weak J-nonexpansive. We only need to show that $\widehat{F}(T)\subset F(T)$ since for any map, T, $F(T)\subset\widetilde{F}(T) \subset\widehat{F}(T)$. Let $p\in \widehat{F}(T)$. Then, E contains a sequence $\{x_{n}\}_{n=1}^{\infty}$ which converges weakly to p and $\lim_{n\rightarrow\infty}\Vert Tx_{n} - x_{n}\Vert= 0$. The fact that T is nonexpansive map gives by Lemma 2.2 that $(I-T)$ is demiclosed at zero. Thus, we obtain $Tp=p$, i.e., $p\in F(T)$. Thus, $\widehat{F}(T)\subset F(T)$. Since H is a real Hilbert space and the map T is nonexpansive, it follows that $\phi(Tx,Ty)\leq\phi(x,y)$, for all $x,y \in H$. Hence, T is a relatively nonexpansive map, so T is a relatively weak nonexpansive map. This implies that T is relatively weak J-nonexpansive. It follows by Theorem 4.3 that the sequences $\{x_{n}\}_{n=1}^{\infty}$ and $\{ u_{n}\}_{n=1}^{\infty}$ converge strongly to some $x^{*}\in W$. □

5 Numerical illustration

We now present a numerical example to illustrate the convergence of the sequence generated by our algorithm in Theorem 4.3.

Example 4

Let $E=\mathbb{R}$ and $C=[a,b]$, for $a,b \in\mathbb{R}$. Let $A_{i}:\mathbb {R} \rightarrow\mathbb{R}$, for each $i=1,2,\dots$, be defined by $A_{i}x=2x$. Let a map $A:\mathbb{R}\rightarrow\mathbb {R}$ be defined by $Ax= \sum_{i=1}^{\infty}\beta_{i} A_{i}x=2x$, for each $x\in\mathbb {R}$, where $\beta_{i}=\frac{1}{2^{i}}$ is a sequence in $(0,1)$ and $\sum_{i=1}^{\infty}\beta_{i}=1$. Let $T_{i}:\mathbb{R} \rightarrow\mathbb{R}$, for each $i=1,2,\dots$, be defined by $T_{i}x=\frac{4}{7}x$. Let a map $T:\mathbb{R}\rightarrow \mathbb{R}$ be defined by $Tx= \sum_{i=1}^{\infty}\delta_{i} T_{i}x=\frac{4}{7}x$, for each $x\in \mathbb{R}$, where $\delta_{i}=\frac{1}{2^{i}}$ is a sequence in $(0,1)$ and $\sum_{i=1}^{\infty}\delta_{i}=1$. It is clear that A is $\frac{1}{2}$-inverse strongly monotone map and T is nonexpansive map with zero as its unique fixed point, so T is relatively nonexpansive map. We observe that the intersection of the set of zeros of A and the fixed points of T is zero. We consider two different initial values $x_{1}=1.8$ and $x_{1}=-1.8$ with $\lambda=\frac{1}{8}$ and define a map

$$P_{C}x= \textstyle\begin{cases} a,& \text{if }x< a,\\ x, & \text{if }x\in C,\\ b, & \text{if }x>b, \end{cases} $$

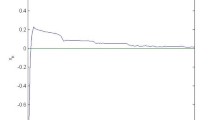
where $P_{C}$ denotes the projection map from H onto C. It follows by Theorem 4.3 that the sequence generated by algorithm (3.2) converges to zero. The sketch of the numerical example is given in Figs. 1 and 2, where the y-axis represents the value of $x_{n}-0$, while the x-axis represents the number of iterations n.

Figure 1

Convergence of the sequence $\{x_{n}\}$ with two different initial values $x_{1}=1.8,-1.8$

Figure 2

Convergence of the sequence $\{x_{n}\}$ with two different initial values $x_{1}=1.8, -1.8$

Conclusion. It is obvious that our algorithm (3.2) can be implemented from Figs. 1 and 2 and that the sequence $\{x_{n}\}$ converges to the solution we desire.

5.1 Analytical representations of duality maps in $L_{p}$, $l_{p}$, and $W^{p}_{m}$ spaces, $1< p<\infty$

The analytical representations of duality maps are known in a number of Banach spaces. In particular, they are known in $L_{p}$, $l_{p}$, and $W^{p}_{m}$, $1< p<\infty$, (see, e.g., Alber and Ryazantseva [3], page 36).

6 Conclusion

In this paper, we introduced and studied a new class of maps called relatively weak J-nonexpansive maps from a real normed spaceEto its dual space $E^{*}$. An algorithm was constructed to approximate a common element of J-fixed points for a countable family of relatively weak J-nonexpansive maps and zeros of a countable family of inverse strongly monotone maps in a 2-uniformly convex and uniformly smooth real Banach space. We proved a strong convergence theorem and gave a numerical example to illustrate the convergence of the sequence generated by the algorithm.