On approximation of Bernstein–Chlodowsky–Gadjiev type operators that fix $e^{-2x}$

Abstract

that fix the function $e^{-2x}$ for $x\geq 0$. Then, we provide the approximation properties of these newly defined operators for different types of function spaces. In addition, we focus on the rate of convergence utilizing appropriate moduli of continuity. Then, we provide the Voronovskaya-type theorem for these new operators. Finally, in order to validate our theoretical results, we provide some numerical experiments that are produced by a MATLAB complier.

1 Introduction

In approximation theory, the main target is to obtain the representation of an arbitrary function in terms of simpler and more useful functions. In 1912, Bernstein [12] gave the following definition, which was referred to by his name, for the proof of the Weierstrass approximation theorem. In more detail, Bernstein polynomials are defined as

$$ B_{n}(f;x)=\sum_{k=0}^{n} f \biggl( \frac{k}{n} \biggr)\binom{n}{k}x^{k}(1-x)^{n-k} , $$

for every bounded function on $[0,1]$, $n\geq 1$ and $x\in [0,1]$. Bernstein polynomials have been an active study subject for more than a century with their useful structure and applications in many disciplines (physics, engineering sciences, computer technologies, etc.). In addition to these, a number of generalizations and modifications of Bernstein polynomials have been studied in the literature. Some of the main objectives in these generalizations and modifications can be said to move Bernstein polynomials over unbounded intervals, which allow us to approximate continuous functions on compact intervals, and to expand the class to which the desired function belongs. For example, Chlodowsky [16] moved polynomials from $[0,1]$ to $[0,p_{n}]$ $(p_{n}\rightarrow \infty , \frac{p_{n}}{n}\rightarrow 0)$ by obtaining a new modification of Bernstein polynomials. In detail, for $n\geq 1$ and $x\geq 0$, Chlodowsky introduced the following Berstein-type operators

$$ B_{n,p_{n}}(f;x)=\sum_{k=0}^{n}f \biggl( p_{n}\frac{k}{n} \biggr) \binom{n}{k} \biggl( \frac{x}{p_{n}} \biggr)^{k} \biggl(1- \frac{x}{p_{n}} \biggr)^{n-k}, $$

where $(p_{n})_{n\geq 1}$ is a sequence of strictly positive real numbers such that

$$ \lim_{n\rightarrow \infty }p_{n}=\infty \quad \text{and}\quad \lim _{n \rightarrow \infty } \frac{p_{n}}{n}= 0 . $$

As can be seen, the operator given above is not a positive operator. For this reason, the following operators, called Berstein–Chlodowsky operators, are defined as

$$B_{n,p_n}^{\ast }(f;x)=\{\begin{array}{cc}{\sum }_{k=0}^{n}f(p_n\frac{k}{n})\left(\begin{array}{c}n\\ k\end{array}\right){(\frac{x}{p_n})}^k{(1-\frac{x}{p_n})}^{n-k},\hfill & \text{if }0\le x\le p_n,\hfill \\ f(x),\hfill & \text{if }x\ge p_n,\hfill \end{array}$$

and were studied in [7, 11] in detail.

Another aim of the ongoing studies on Bernstein polynomials is to increase the speed of approximation and to decrease the number of errors that are the natural result of the approximation process. One of these studies was done by Gadjiev and Ghorbanalizadeh [17] in 2010. In this study, the authors defined the following operators

$$ B_{n}^{\alpha , \beta }(f;x) = \textstyle\begin{cases} (\frac{n+\beta _{2}}{n} )^{n}\sum_{k=0}^{n}f ( \frac{k+\alpha _{1}}{n+\beta _{1}} ) \binom{n}{k} \\ \quad {}\times (x-\frac{\alpha _{2}}{n+\beta _{2}} )^{k} ( \frac{n+\alpha _{2}}{n+\beta _{2}}-x )^{n-k} ,&\text{if } \frac{\alpha _{2}}{n+\beta _{2}}\leq x\leq \frac{n+\alpha _{2}}{n+\beta _{2}}, \\ f(x),&\text{if } x \in [0, \frac{\alpha _{2}}{n+\beta _{2}} ] \cup [\frac{n+\alpha _{2}}{n+\beta _{2}},1 ], \end{cases} $$

where $\alpha _{1},\beta _{1}, \alpha _{2},\beta _{2}\in \mathbb{R}$ and $0\leq \alpha _{2} \leq \alpha _{1}\leq \beta _{2}\leq \beta _{1}$. In this study, the authors focused on the convergence properties of these operators in a moving interval as it enlarges to $[0,1]$. Motivating by this study, Aral and Acar [8] introduced a new interpretation of Bernstein–Chlodowsky–Gadjiev-type linear positive operators as follows

$$ B_{n,p_{n}}^{\alpha , \beta }(f;x) = \textstyle\begin{cases} (\frac{n+\beta _{2}}{n} )^{n}\sum_{k=0}^{n}f ( \alpha _{3} x+p_{n}\frac{k+\alpha _{1}}{n+\beta _{1}}\beta _{3} ) \binom{n}{k} (\frac{x}{p_{n}}- \frac{\alpha _{2}}{n+\beta _{2}} )^{k} ( \frac{n+\alpha _{2}}{n+\beta _{2}}-\frac{x}{p_{n}} )^{n-k} , \\ \hphantom{f(x),}\quad \text{if } p_{n}\frac{\alpha _{2}}{n+\beta _{2}}\leq x\leq p_{n} \frac{n+\alpha _{2}}{n+\beta _{2}}, \\ f(x),\quad \text{if } x \in [0, p_{n}\frac{\alpha _{2}}{n+\beta _{2}} ] \cup [p_{n}\frac{n+\alpha _{2}}{n+\beta _{2}},\infty ], \end{cases} $$

(1.1)

where $\alpha _{1},\beta _{1}, \alpha _{2},\beta _{2}\in \mathbb{R}$ and $0\leq \alpha _{2} \leq \alpha _{1}\leq \beta _{2}\leq \beta _{1}$, $\alpha _{3}+\beta _{3}=1$ and $p_{n}$ are defined as above. Aral and Acar first studied the weighted approximation properties of these newly defined operators and showed their superior properties. Secondly, they focused on the derivative of these new operators and gave a weighted approximation theorem in Lipchits space.

On the other hand, King’s inspiration [25] made a tremendous impact on approximation theory and has been successfully applied to a number of well-known sequences of operators. The main motivation of King was fixing the function $x^{2}$ instead of function x for the classical Bernstein operators that approximate better compared to previous ones. Regarding King’s brilliant idea, the innovative papers presented by Acar et al. [1, 2], who introduced modified Szasz–Mirakyan operators preserving constants and $e^{2ax}$, $a>0$. This idea has been the source of inspiration of a number of qualified papers in approximation theory and was successfully applied to several well-known sequences of operators too. In more detail, in [13, 27], constant and $e^{ax}$ for $a>0$, in [9, 10, 26], $e^{ax}$ and $e^{2ax}$ for $a>0$ have been preserved with modified version of some positive linear operators. Soon after, in [19, 20, 22], constant and $e^{-x}$, in [5, 19, 21], constant and $e^{-2x}$ were fixed in a similar manner. Regarding a similar motivation, the most recent paper is due to Acar et al. [4], who obtained a general class of linear positive approximation processes defined on bounded and unbounded intervals designed using an appropriate function and Voronovskaya-type theorems.

This paper aims to introduce a modified version of Bernstein–Chlodowsky–Gadjiev-Type operators that preserve constant and $e^{-2x}$ for $\alpha _{3}=0$ and $\beta _{3}=1$. In the meantime, we present the approximation properties of these newly defined operators for both in spaces of continuous functions and in some weighted functions spaces. In addition to these, we provide a Voronoskaya-type theorem for the newly defined Bernstein–Chlodowsky–Gadjiev-Type operator.

The overall structure of the paper takes the form of six sections including this section. The remainder of this work is organized as follows: In Sect. 2, the main facts and definitions are reviewed, while the new type Bernstein–Chlodowsky–Gadjiev-Type operators that fix the constant and $e^{-2x}$ are introduced in Sect. 3. In Sect. 4, the approximation properties of the newly define operators are provided. In Sect. 5, a Voronovskaya-type theorem is given, while numerical experiments are given in Sect. 6. Some conclusions and further directions of research are discussed in Sect. 7.

2 Preliminaries

Throughout this and the next sections, we shall denote by $\mathcal{S}$ the set of $[0,\infty )$. We will use the notation $C(\mathcal{S})$ for the space of all continuous real-valued functions on $\mathcal{S}$. In this manner, we shall use $C_{b}(\mathcal{S})$ for the space consisting of all bounded functions in $C(\mathcal{S})$. Additionally, let $C_{*}(\mathcal{S})$ and $C_{0}(\mathcal{S})$ be the Banach sublattices of all real-valued bounded continuous functions on $\mathcal{S}$, ($C_{b}(\mathcal{S})$), endowed with the natural order and the supremum norm $\Vert \cdot \Vert _{\infty }$, which are

$$ C_{*}(\mathcal{S})=\Bigl\lbrace f\in C(\mathcal{S}) : \exists \lim _{x\to \infty }f(x)\in \mathbb{R} \Bigr\rbrace , $$

and

$$ C_{0}(\mathcal{S})=\Bigl\lbrace f\in C_{*}(\mathcal{S}) : \lim_{x\to \infty }f(x)=0 \Bigr\rbrace , $$

respectively.

Now, let us consider the weighted space

$$ \Omega _{k}:=\Bigl\lbrace f\in C(\mathcal{S}):\sup _{x\geq 0} \varpi _{k}(x) \bigl\vert f(x) \bigr\vert \in \mathbb{R} \Bigr\rbrace , $$

where $\varpi _{k}(x)=\frac{1}{1+x^{k}}$ is the weight function for $k\geq 1$ and $x\geq 0$. It is clear that this weighted space is endowed with the norm

$$ \Vert f \Vert _{k}= \sup_{x\geq 0} \varpi _{k}(x) \bigl\vert f(x) \bigr\vert , $$

where $f\in \Omega _{k}$ and its natural subspaces

$$ \Omega _{k}^{*}= \Bigl\lbrace f\in \Omega _{k}: \exists \lim_{x\to \infty } \varpi _{k}(x) f(x)\in \mathbb{R} \Bigr\rbrace , $$

and

$$ \Omega _{k}^{0}= \Bigl\lbrace f\in \Omega _{k}: \lim_{x\to \infty } \varpi _{k}(x) f(x)=0 \Bigr\rbrace . $$

It must be noted that $C_{0}(\mathcal{S})$ is dense in $\Omega _{k}^{0}$ as a consequence of the Stone–Weierstrass theorem.

In addition, throughout this and the next sections, we consider a fixed real parameter $\mu >0$ and consider the exponential function $f_{\mu }$ as

$$ f_{\mu }(t)=e^{-\mu t}. $$

(2.1)

Additionally, as usual, we denote by $e_{i}$ the polynomial functions defined by $e_{i}(t)=t^{i}$ ($t\geq 0$, $i\in \mathbb{N}$).

Now, for convenience, to obtain the new operator for $\alpha _{3}=0$ and $\beta _{3}=1$, we need to deduce $G^{\alpha ,\beta }_{n}(f_{\mu };x)$ for every $n\geq 1$ and $x\leq p_{n}$, that is,

$$\begin{aligned}& B_{n,p_{n}}^{\alpha , \beta }(f_{\mu }) (x) \\& \quad = \biggl[ 1+ \frac{\alpha _{2}}{n} \bigl( 1-e^{-\mu p_{n} /(n+\beta _{1}) } \bigr)-x \biggl(\frac{n+\beta _{2}}{np_{n}} \bigl(1- e^{-\mu p_{n} /(n+ \beta _{1}) } \bigr) \biggr) \biggr]^{n} e^{-\mu p_{n} \alpha _{1}/(n+ \beta _{1}) }, \end{aligned}$$

(2.2)

where $\alpha _{1},\beta _{1},\alpha _{2},\beta _{2}\in \mathbb{R}$ and $0\leq \alpha _{2}\leq \alpha _{1} \leq \beta _{2}\leq \beta _{1}$. Hence, it can be easily deduced that for each $f\in C_{*}(\mathcal{S})$,

$$ \lim_{n\rightarrow \infty } B_{n,p_{n}}^{\alpha , \beta }(f)=f $$

uniformly on $\mathcal{S}$, under the given hypothesis,

$$ \lim_{n\rightarrow \infty }\frac{p_{n}}{n}=0 \quad \text{and}\quad \lim _{n\rightarrow \infty }p_{n}=\infty . $$

(2.3)

3 Bernstein–Chlodowsky–Gadjiev-type operators that fix $e^{-2x}$

Now, we can introduce a general version of Bernstein–Chlodowsky–Gadjiev-Type operators that preserve the function $f_{2}$. For that, first, we need to introduce a sequence $(s_{n})_{n\geq 1}$ of real functions such that the operators,

$$ \mathcal{G}^{\alpha ,\beta }_{n}:=G^{\alpha ,\beta }_{n} \circ s_{n}, $$

(3.1)

preserve the function $f_{2}(x)$. Now, in order to construct a new operator that preserves $f_{2}(x)$, we need to compute the $s_{n}(x)$ with the help of (2.2), that is,

$$ \biggl[ 1+\frac{\alpha _{2}}{n} \bigl( 1-e^{-2 p_{n} /(n+\beta _{1}) } \bigr)-s_{n}(x) \biggl(\frac{n+\beta _{2}}{np_{n}} \bigl(1- e^{-2 p_{n} /n+\beta _{1} } \bigr) \biggr) \biggr]^{n} e^{-2 p_{n} \alpha _{1}/n+ \beta _{1} }=f_{2}, $$

where $\alpha _{1},\beta _{1},\alpha _{2},\beta _{2}\in \mathbb{R}$ and $0\leq \alpha _{2}\leq \alpha _{1} \leq \beta _{2}\leq \beta _{1}$, which yields,

$$ s_{n}(x)=\frac{p_{n}}{n+\beta _{2}} \biggl( \alpha _{2}+n \frac{1-e^{2p_{n} \alpha _{1}/n(n+\beta _{1})-2x/n}}{1-e^{-2p_{n}/(n+\beta _{1})}} \biggr) $$

for $s_{n}(x) \leq p_{n}$. The point to be considered here is

$$ \lim_{n\rightarrow \infty }s_{n}(x)=x. $$

Additionally, thanks to the fact that $1-e^{-x}\leq x$ for $x\geq \frac{p_{n}\alpha _{1}}{n+\beta _{1}}$, we can easily deduce that

$$ s_{n} \biggl(\frac{p_{n}\alpha _{1}}{n+\beta _{1}} \biggr)= \frac{p_{n}\alpha _{2}}{n+\beta _{2}} $$

and

$$ \frac{p_{n} \alpha _{2}}{n+\beta _{2}}\leq s_{n}(x) \leq \frac{p_{n} \alpha _{2}}{n+\beta _{2}}+ N_{n} x, $$

(3.2)

where

$$ N_{n}:=\frac{2 p_{n}}{(n+\beta _{2})(1-e^{-2p_{n}/(n+\beta _{1})})} $$

for $n\geq 1$. In addition, with the help of (2.3), one can deduce that

$$ \lim_{n\rightarrow \infty }N_{n}=1. $$

Considering all of these, for each $n\geq 1$, $x\geq 0$ and $f\in C_{*}(\mathcal{S})$, the new Bernstein–Chlodowsky–Gadjiev-Type Operators $(\mathcal{G}_{n}^{\alpha _{1},\beta _{1}})_{n\geq 1}$ can be defined as,

$$ \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(f;x) = \textstyle\begin{cases} \sum_{k=0}^{n} f (p_{n} \frac{k+\alpha _{1}}{n+\beta _{1}} ) \binom{n}{k} ( \frac{1-e^{2p_{n} \alpha _{1}/n(n+\beta _{1})-2x/n}}{1-e^{-2p_{n}/(n+\beta _{1})}} )^{k} \\ \quad {}\times (1- \frac{1-e^{2p_{n} \alpha _{1}/n(n+\beta _{1})-2x/n}}{1-e^{-2p_{n}/(n+\beta _{1})}} )^{n-k} ,&\text{if } x\in \mathcal{I}_{n}, \\ f(x),&\text{if }x\in \mathcal{S}/\mathcal{I}_{n}, \end{cases} $$

(3.3)

where $\mathcal{I}_{n}= [p_{n}\frac{\alpha _{1}}{n+\beta _{1}},p_{n} \frac{n+\alpha _{1}}{n+\beta _{1}} ]$, $\alpha _{1},\beta _{1}\in \mathbb{R}$ and $0\leq \alpha _{1} \leq \beta _{1}$. The relation between the proposed operator and its classical counterpart is now observed as

$$ \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}f(x)=B_{n,p_{n}}^{\alpha , \beta } f \bigl(s_{n}(x) \bigr). $$

(3.4)

Now, we can obtain the moments of the newly defined operators utilizing the above-mentioned equalities.

Lemma 1

For each $x\in I_{n}$ and $n\in \mathbb{N}$, then the following identities hold:

• (i) $\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(e_{0};x)=1$,

• (ii) $\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(e_{1};x)= \frac{p_{n}}{n+\beta _{1}} ( \alpha _{1}-\alpha _{2}+s_{n}(x) \frac{n+\beta _{2}}{p_{n}} )=\frac{p_{n}}{n+\beta _{1}} (\alpha _{1}+n \frac{1-e^{2p_{n} \alpha _{1}/n(n+\beta _{1})-2x/n}}{1-e^{-2p_{n}/(n+\beta _{1})}} )$,

• (iii)
  $$\begin{aligned} \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(e_{2};x)={}& \biggl[2p_{n} \frac{\alpha _{1}}{n+\beta _{1}}+\frac{n-1}{n} \biggl( \frac{n+\beta _{2}}{n+\beta _{1}} \biggr) \biggl(s_{n}(x)-p_{n} \frac{\alpha _{2}}{n+\beta _{2}} \biggr)+p_{n}\frac{1}{n+\beta _{1}} \biggr] \\ &{}\times \biggl( \frac{n+\beta _{2}}{n+\beta _{1}} \biggr) \biggl(s_{n}(x)-p_{n} \frac{\alpha _{2}}{n+\beta _{2}} \biggr) \\ &{}+ \biggl(p_{n}\frac{\alpha _{1}}{n+\beta _{1}} \biggr)^{2}, \end{aligned}$$

where $\alpha _{1},\beta _{1}\in \mathbb{R}$ and $0\leq \alpha _{1} \leq \beta _{1}$.

It can be easily seen that the results in (ii) and (iii) convergence to $e_{1}(x)$ and $e_{2}(x)$ in the limit case ($n\rightarrow \infty$), which shows that the new operators introduced in (3.3) preserve the Korovkin test functions.

All the results given so far and hereinafter were computed by MAPLE software that is a Computer Algebra System on attitudes towards mathematics. In addition, these results also show that the newly defined operator protects Korovkin test functions in the limit case.

In particular, if one considers the function described for each $x\geq 0$, as

$$ E_{t}^{m}=\bigl(e_{1}(t)-xe_{0}(t) \bigr)^{m} $$

we have the following lemma.

Lemma 2

For each $x\in I_{n}$ and $n\in \mathbb{N}$, then the following identities hold:

• (i) $\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(E_{t}^{0};x)=0$,

• (ii) $\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(E_{t}^{1};x)= \frac{p_{n}}{n+\beta _{1}} (\alpha _{1}+n \frac{1-e^{2p_{n} \alpha _{1}/n(n+\beta _{1})-2x/n}}{1-e^{-2p_{n}/(n+\beta _{1})}} )-x$,

• (iii)
  $$\begin{aligned} \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}\bigl(E_{t}^{2};x \bigr)={}& \biggl(2p_{n} \frac{\alpha _{1}}{n+\beta _{1}}+\frac{n-1}{n} \biggl( \frac{n+\beta _{2}}{n+\beta _{1}} \biggr) \biggl(s_{n}(x)-p_{n} \frac{\alpha _{2}}{n+\beta _{2}} \biggr)+p_{n}\frac{1}{n+\beta _{1}} \biggr) \\ &{}\times \biggl(\frac{n+\beta _{2}}{n+\beta _{1}} \biggr) \biggl(s_{n}(x)-p_{n} \frac{\alpha _{2}}{n+\beta _{2}} \biggr)+ \biggl(p_{n} \frac{\alpha _{1}}{n+\beta _{1}} \biggr)^{2} \\ &{}-2x \frac{p_{n}}{n+\beta _{1}} \biggl( \alpha _{1}-\alpha _{2}+s_{n}(x) \frac{n+\beta _{2}}{p_{n}} \biggr)+x^{2}, \end{aligned}$$

where $\alpha _{1},\beta _{1}\in \mathbb{R}$ and $0\leq \alpha _{1} \leq \beta _{1}$.

In conclusion, one can easily deduce the following equality for the exponential function given in (2.1),

$$\begin{aligned} \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(f_{\mu };x) =&e^{-\mu p_{n} \alpha _{1}/(n+\beta _{1})} \biggl[ 1- \bigl(1-e^{-\mu p_{n}/(n+\beta _{1})} \bigr) \biggl( s_{n}(x) \frac{n+\beta _{2}}{np_{n}}- \frac{\alpha _{2}}{n} \biggr) \biggr]^{n}, \\ =&e^{-\mu p_{n} \alpha _{1}/(n+\beta _{1})} \biggl[ 1- \bigl(1-e^{- \mu p_{n}/(n+\beta _{1})} \bigr) \biggl( \frac{1-e^{2p_{n} \alpha _{1}/n(n+\beta _{1})-2x/n}}{1-e^{-2p_{n}/(n+\beta _{1})}} \biggr) \biggr]^{n} . \end{aligned}$$

(3.5)

It is clear that $\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(f_{\mu };x)\rightarrow f_{ \mu }$ as $n\rightarrow \infty$. As a result, $(\mathcal{G}_{n}^{\alpha _{1},\beta _{1}})_{n\geq 1}$ is an approximation process in $C(\mathcal{S})$; i.e., for every $f\in C(\mathcal{S})$,

$$ \lim_{n\rightarrow \infty }\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(f)=f, $$

uniformly on $\mathcal{S}$.

In particular, if one considers the function described for each $x\geq 0$, as

$$ F_{t}^{m}=\bigl(e^{-t}-e^{-x} \bigr)^{m} $$

then we can easily deduce the following lemma.

Lemma 3

For each $x\in \mathcal{S}$ and $n\in \mathbb{N}$, then the following identities hold:

• (i) $\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(F_{t}^{0};x)=1$,

• (ii) $\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(F_{t}^{1};x)=e^{-p_{n} \alpha _{1}/(n+\beta _{1})} [ 1- ( \frac{1-e^{2p_{n} \alpha _{1}/n(n+\beta _{1})-2x/n}}{1+e^{-p_{n}/(n+\beta _{1})}} ) ]^{n}-e^{-x}$,

• (iii) $\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(F_{t}^{2};x)=2e^{-2x}-2e^{-x}e^{-p_{n} \alpha _{1}/(n+\beta _{1})} [ 1- ( \frac{1-e^{2p_{n} \alpha _{1}/n(n+\beta _{1})-2x/n}}{1+e^{-p_{n}/(n+\beta _{1})}} ) ]^{n}$,

where $\alpha _{1},\beta _{1}\in \mathbb{R}$ and $0\leq \alpha _{1} \leq \beta _{1}$.

Now, let us focus on the properties of the function $s_{n}(x)$.

Proposition 1

For each $n\geq 1$ and any $x\in \mathcal{S}$, we have

$$ s_{n}(x)\geq \biggl( \frac{n+\beta _{1}}{n+\beta _{2}} \biggr)x-p_{n} \frac{\alpha _{1}-\alpha _{2}}{n+\beta _{2}}, $$

(3.6)

where $\alpha _{1},\beta _{1},\alpha _{2},\beta _{2}\in \mathbb{R}$ and $0\leq \alpha _{2}\leq \alpha _{1} \leq \beta _{2}\leq \beta _{1}$.

Proof

To begin with, for $n\geq 1$ we know that $s_{n}$ is a convex down increasing function in $\mathcal{I}_{n}$ since it is a function of $-f_{2/n}(x)$. In addition, since $s_{n} ( p_{n}\frac{\alpha _{1}}{n+\beta _{1}} )=p_{n} \frac{\alpha _{2}}{n+\beta _{2}}$ and $s_{n} ( p_{n}\frac{n+\alpha _{1}}{n+\beta _{1}} )=p_{n} \frac{n+\alpha _{2}}{n+\beta _{2}}$, we can easily deduce that $s_{n}(x)\geq ( \frac{n+\beta _{1}}{n+\beta _{2}} )x-p_{n} \frac{\alpha _{1}-\alpha _{2}}{n+\beta _{2}}$ for $x\in \mathcal{I}_{n}$, thus the proof is completed. □

Proposition 2

For $\alpha _{1},\beta _{1},\alpha _{2},\beta _{2}\in \mathbb{R}$ and $0\leq \alpha _{2}\leq \alpha _{1} \leq \beta _{2}\leq \beta _{1}$,

$$ \lim_{n \to \infty } s_{n} =e_{1}(x) $$

uniformly on compact subintervals of $\mathcal{S}$.

Proof

It is clear that, $\lim_{n \to \infty } s_{n} =e_{1}(x)$ pointwise on $\mathcal{S}$. Additionally, each $s_{n}(x)$ is concave and the convergence is indeed uniform on every compact interval of $\mathcal{S}$. □

4 Approximation properties of $(\mathcal{G}_{n}^{\alpha _{1},\beta _{1}})_{n\geq 1}$

Previously, we have provided the properties of the newly defined Bernstein–Chlodowsky–Gadjiev-Type operators that fix the function $e^{-2x}$. Now, we can introduce some approximation properties of these new operators for the different spaces of continuous functions. Additionally, we provide the rate of convergence of $\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}$.

Theorem 1

Let $x>0$ be fixed and $\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}$, $n\geq 1$, be the operator defined in (3.3). Then, $\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}$ is a linear positive operator from $C_{*}(\mathcal{S})$ into itself. In addition, $\Vert \mathcal{G}_{n}^{\alpha _{1},\beta _{1}} \Vert _{ C_{*}( \mathcal{S})} =1$.

Proof

It can be easily shown that for each $n\in \mathbb{N}$, $s_{n}(x)$ is an increasing and convex real continuous function satisfying

$$ s_{n} \biggl( p_{n}\frac{\alpha _{1}}{n+\beta _{1}} \biggr)=p_{n} \frac{\alpha _{2}}{n+\beta _{2}}\quad \text{and}\quad s_{n} \biggl( p_{n} \frac{n+\alpha _{1}}{n+\beta _{1}} \biggr)=p_{n} \frac{n+\alpha _{2}}{n+\beta _{2}}. $$

As an explicit consequence of equations (3.1) and (3.2), one can conclude that $\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}$ is a positive operator. Additionally, if $f\in C_{*}(\mathcal{S})$, one can say that $B_{n,p_{n}}^{\alpha , \beta }(f)\in C_{*}(\mathcal{S})$ resulting from (1.1), which yields $B_{n,p_{n}}^{\alpha , \beta }(f)\in C(\mathcal{S})$. Then, it can be easily seen that $\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(f)\in C(\mathcal{S})$ since $s_{n}(x)$ satisfy the above properties and the relation (3.4). Moreover, it is obvious that $\lim_{x\to \infty }\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(f)(x)= \lim_{x\to \infty }(f)(x)\in \mathbb{R}$. As a consequence, $\Vert \mathcal{G}_{n}^{\alpha _{1},\beta _{1}} \Vert _{C_{*}( \mathcal{S})}=\Vert \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(e_{0}) \Vert _{\infty }=1$ due to the positivity of each $\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}$. □

Theorem 2

For the same assumptions of Theorem 1, the following expression

$$ \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}\bigl(C_{0}(\mathcal{S}) \bigr)\subset C_{0}( \mathcal{S}) $$

holds.

Proof

From the direct consequence of Theorem 1 and $\lim_{x\to \infty }\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(f)(x)= \lim_{x\to \infty }(f)(x)=0$ whenever $f\in C_{0}(\mathcal{S})$, one can easily show the proof of the theorem. □

Theorem 3

For the fixed $n \geq 1$, consider the operators $\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}$ defined by (3.3). Then,

$$ \lim_{n\rightarrow \infty }\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(f)=f\quad \textit{uniformly on } \mathcal{S} $$

if $f\in C_{*}(\mathcal{S})$.

Proof

In an attempt to prove the theorem we need to show that

$$ \lim_{n\to \infty }\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(f_{\mu })=f_{ \mu }\quad \text{uniformly on } \mathcal{S}, $$

(4.1)

for every $\mu >0$. In line with this objective, for every $z>0$, we use the following useful inequality given in [23, Lemma 3.1]

$$ e^{-z\vartheta _{n}}-e^{-z}< \frac{z_{n}}{2e},\quad n\geq 1 , $$

(4.2)

where $\vartheta _{n}=\frac{1-e^{-z_{n}}}{z_{n}}$ and $(z_{n})_{n\geq 1}$ is a sequence of strictly positive real numbers. Then, by following the similar steps of the proof of [23, Corollary 3.4], we can obtain that

$$\begin{aligned}& \bigl\vert \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(f_{\mu }) (x)-(f_{\mu }) (x) \bigr\vert \\& \quad \leq e^{-\mu p_{n} \alpha _{1}/(n+\beta _{1})} \biggl[ 1- \bigl(1-e^{-\mu p_{n}/(n+\beta _{1})} \bigr) \biggl( s_{n}(x) \frac{n+\beta _{2}}{np_{n}}- \frac{\alpha _{2}}{n} \biggr) \biggr]-e^{- \mu x}, \\& \quad = e^{-\mu p_{n} \alpha _{1}/(n+\beta _{1})} e^{n\ln [ 1- (1-e^{- \mu p_{n}/(n+\beta _{1})} ) ( s_{n}(x) \frac{n+\beta _{2}}{np_{n}}-\frac{\alpha _{2}}{n} ) ]}-e^{-\mu x}, \\& \quad \leq e^{-\mu p_{n} \alpha _{1}/(n+\beta _{1})}e^{-ns_{n}(x)[(n+ \beta _{2})/np_{n}][1-e^{-\mu p_{n}/(n+\beta _{1})}] }e^{\alpha _{2}[1-e^{- \mu p_{n}/(n+\beta _{1})}] }-e^{-\mu x}, \\& \quad = e^{-\mu p_{n} \alpha _{1}/(n+\beta _{1})}e^{[\alpha _{2} \mu p_{n}/(n+ \beta _{1})] \frac{[1-e^{-\mu p_{n}/(n+\beta _{1})}]}{\mu p_{n}/(n+\beta _{1})} }e^{-ns_{n}(x)[(n+ \beta _{2})/np_{n}][\mu p_{n}/(n+\beta _{1})] \frac{[1-e^{-\mu p_{n}/(n+\beta _{1})}]}{\mu p_{n}/(n+\beta _{1})} } \\& \qquad {} -e^{-\mu x}, \\& \quad \leq e^{-\mu p_{n} (\alpha _{1}-\alpha _{2})/(n+\beta _{1})} \bigl( e^{-\mu s_{n}(x)[(n+\beta _{2})/(n+\beta _{1})] \frac{[1-e^{-\mu p_{n}/(n+\beta _{1})}]}{\mu p_{n}/(n+\beta _{1})} }- e^{- \mu s_{n}(x)[(n+\beta _{2})/(n+\beta _{1})]} \bigr) \end{aligned}$$

since $\ln x\leq x-1$, $\frac{[1-e^{-\mu p_{n}/(n+\beta _{1})}]}{\mu p_{n}/(n+\beta _{1})} \leq 1$ for (2.3) and the inequality (3.6) holds. Then, using (4.2) for

$$ z=-\mu s_{n}(x)\frac{(n+\beta _{2})}{(n+\beta _{1})} \quad \text{and}\quad z_{n}= \frac{\mu p_{n}}{(n+\beta _{1})}, $$

we deduce that

$$ \bigl\vert \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(f_{\mu }) (x)-f_{\mu }(x) \bigr\vert \leq e^{-\mu p_{n} (\alpha _{1}-\alpha _{2})/(n+\beta _{1})} \frac{\mu p_{n}}{2e(n+\beta _{1})} $$

and

$$ \bigl\Vert \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(f_{\mu })-f_{\mu } \bigr\Vert _{ \infty } \leq e^{-\mu p_{n} (\alpha _{1}-\alpha _{2})/(n+\beta _{1})} \frac{\mu p_{n}}{2e(n+\beta _{1})} $$

(4.3)

for $x\in \mathcal{S}$ and the proof of (4.1) is completed. Then, relying on the direct result of (4.1) and [14], we can prove the theorem. □

Theorem 4

For the same assumptions of Theorem 3, then

$$ \lim_{n\rightarrow \infty }\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(f)=f \quad \textit{uniformly on compact subsets of } \mathcal{S} $$

if $f\in C_{b}(\mathcal{S})$.

Proof

From the the results provided above, we note that

$$\begin{aligned}& \vert \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(e_{0}) (x)-e_{0}(x) =0, \\& \bigl\vert \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(e_{1}) (x)-e_{1}(x) \bigr\vert \leq p_{n}\frac{\alpha _{1}-\alpha _{2}}{n+\beta _{2}}+p_{n} \frac{\alpha _{2}}{n+\beta _{1}}+x \biggl( N_{n} \frac{n+\beta _{2}}{n+\beta _{1}}-1 \biggr), \end{aligned}$$

and

$$\begin{aligned}& \bigl\vert \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(e_{2}) (x)-e_{2}(x) \bigr\vert \\& \quad \leq x^{2} \biggl( \frac{n-1}{n} \biggl( \frac{n+\beta _{2}}{n+\beta _{1}} \biggr)^{2}N_{n}^{2}-1 \biggr)+p_{n} \frac{(2\alpha _{1}+1)(n+\beta _{2})}{(n+\beta _{1})^{2}}N_{n} x+ \biggl( p_{n}\frac{\alpha _{1}}{n+\beta _{1}} \biggr)^{2}, \end{aligned}$$

thereby, $\lim_{n\to \infty }\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(\lbrace e_{0},e_{1},e_{2} \rbrace )=\lbrace e_{0},e_{1},e_{2} \rbrace$ uniformly on compact subsets of $\mathcal{S}$, due to the fact that $\lim_{n \rightarrow \infty }N_{n}=1$. As a result, as $\lbrace e_{0},e_{1},e_{2} \rbrace \subset \Omega _{2}^{*}$, the consequence follows from [6, Theorem 3.5]. □

In order to estimate the rate of convergence of $(\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(f))$ for $n\geq 1$ to f in Theorem 3, we need to increase our knowledge about the modulus of continuity. In this estimation, we will take advantage of the following definition of the modulus of continuity introduced in [23]:

Definition 1

Let $f\in C_{*}(\mathcal{S})$. Then, the modulus of continuity of a function, $\omega ^{*} ( f,\delta )$, is defined for $\delta \geq 0$ by

$$ \omega ^{*} ( f,\delta )=\sup_{ \substack{x,t\geq 0\\ \vert e^{-x}-e^{-t} \vert \leq \delta }} \bigl\vert f(x)-f(t) \bigr\vert . $$

(4.4)

In other words, this modulus of continuity can be stated concerning the standard modulus of continuity by

$$ \omega ^{*} ( f,\delta )=\omega ( \mathbf{f}, \delta ), $$

where $\mathbf{f}:C_{*}(\mathcal{S}) \rightarrow C(\mathcal{S})$ is the continuous function defined by

$$ \mathbf{f}(\theta )= \textstyle\begin{cases} f(-\ln \theta ), & \text{if }\theta \in (0,1], \\ 1, & \text{if }\theta =0 . \end{cases} $$

Then, the following theorem would be helpful in order to express the next theorems.

Theorem 5

([23])

If $Q_{n}: C_{*}(\mathcal{S}) \rightarrow C_{*}(\mathcal{S})$ is a sequence of positive linear operators for $n \geq 1$ with

$$\begin{aligned} \rho _{n} =& \bigl\Vert Q_{n}(e_{0})-e_{0} \bigr\Vert _{\infty }, \\ \xi _{n} =& \bigl\Vert Q_{n}(f_{1})-f_{1} \bigr\Vert _{\infty }, \\ \kappa _{n} =& \bigl\Vert Q_{n}(f_{2})-f_{2} \bigr\Vert _{\infty }, \end{aligned}$$

where $\rho _{n}, \xi _{n}, \kappa _{n} \rightarrow 0$ as $n\rightarrow \infty$, then,

$$ \bigl\Vert Q_{n}(f)-f \bigr\Vert _{\infty }\leq \Vert f \Vert _{\infty }\rho _{n}+(2+ \rho _{n})\omega ^{*} ( f,\sqrt{\rho _{n}+2\xi _{n}+\kappa _{n}} ), $$

for $f\in C_{*}(\mathcal{S})$.

In this regard, it is clear that there is a close relation between $\omega ^{*} ( f,\delta )$ and the particular Korovkin subset chosen for the space $C_{*}(\mathcal{S})$, (see [23]). Then, we can state the following theorem with the help of the above.

Theorem 6

For every $f\in C_{*}(\mathcal{S})$ and $n\geq 1$,

$$ \bigl\Vert \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}(f)-f \bigr\Vert _{\infty } \leq 2\omega ^{*} \biggl( f,\sqrt{e^{-p_{n}(\alpha _{1}-\alpha _{2})/(n+ \beta _{1})} \frac{p_{n}}{ e(n+\beta _{1})}} \biggr), $$

under the same assumptions of Theorem 3.

Proof

It is obvious that, $\rho _{n}$ and $\kappa _{n}$ equal zero due to their definitions. On the other hand, it is easy to show that

$$ \xi _{n}=e^{-p_{n}(\alpha _{1}-\alpha _{2})/(n+\beta _{1})} \frac{p_{n}}{2 e(n+\beta _{1})}, $$

from (4.3) with $\lambda =1$ for every $n\geq 1$. Hence, the proof is completed. □

5 Voronovksya type theorem

In this section, the pointwise convergence of the Bernstein–Chlodowsky–Gadjiev-Type operators that fix $e^{-2x}$ is provided. To present the convergence we present Voronovskaja-type theorem in quantitative mean that allows us to find both the degree of aimed convergence and the upper bound for the error of approximation.

The quantitative Voronovskaja-type theorem for the Bernstein–Chlodowsky–Gadjiev-Type operators acting on bounded intervals and unbounded intervals can be found in the papers [3, 15, 18, 24], respectively. Here, we consider the modulus of continuity given in (4.4). Now, we can present the theorem of this section.

Theorem 7

Let $f,f^{\prime \prime }\in C_{*}(\mathcal{S})$. Then, the inequality

$$\begin{aligned}& \biggl\vert \frac{n}{p_{n}} \bigl[ \mathcal{G}_{n}^{\alpha _{1}, \beta _{1}} ( f;x ) -f ( x ) \bigr]-xf'(x)- \frac{1}{2}x f''(x) \biggr\vert \\& \quad \leq \bigl\vert f^{\prime }(x) \bigr\vert \bigl\vert \mathcal{A}_{n}(x) \bigr\vert + \bigl\vert f^{ \prime \prime } ( x ) \bigr\vert \bigl\vert \mathcal{B}_{n}(x) \bigr\vert + 2 \bigl\vert 2 \mathcal{B}_{n}(x)+x \bigr\vert +2\mathcal{C}_{n}(x) \omega ^{\ast } \biggl(f'',\frac{1}{\sqrt{n}} \biggr), \end{aligned}$$

holds for any $x\in \mathcal{S}$, $\alpha _{1},\beta _{1}\in \mathbb{R}$ and $0\leq \alpha _{1} \leq \beta _{1}$, where

$$\begin{aligned} \mathcal{A}_{n}(x) =& \frac{n}{p_{n}}\mathcal{G}_{n}^{\alpha _{1}, \beta _{1}} \bigl(E_{t}^{1};x\bigr)-x, \\ \mathcal{B}_{n}(x) =&\frac{1}{2}\frac{n}{p_{n}} \mathcal{G}_{n}^{ \alpha _{1},\beta _{1}}\bigl(E_{t}^{2};x \bigr)-x, \\ \mathcal{C}_{n} ( x ) =& \frac{n^{2}}{p_{n}}\sqrt{ \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}\bigl( E_{t}^{4};x \bigr)}\sqrt{ \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}\bigl( F_{t}^{4};x\bigr).} \end{aligned}$$

Proof

With the help of a Taylor expansion of f at the point $x\in \mathcal{S}$, one can easily deduce that

$$ f ( t ) =f ( x ) + f^{\prime } ( x ) ( t-x ) +\frac{f^{\prime \prime } ( x ) }{2} ( t-x ) ^{2}+\Delta ( t,x ) ( t-x ) ^{2}, $$

(5.1)

where

$$ \Delta ( t,x ) := \frac{f^{\prime \prime } ( \epsilon ) -f^{\prime \prime } ( x ) }{2} $$

and ϵ is a number between x and t. Then, by applying the Bernstein–Chlodowsky–Gadjiev-Type operators $\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}$ to both sides of equality (5.1) and utilizing $\mathcal{G}_{n}^{\alpha _{1},\beta _{1}} ( e_{0} ) =e_{0}$, we immediately deduce that

$$ \biggl\vert \mathcal{G}_{n}^{\alpha _{1},\beta _{1}} ( f;x )-f ( x ) - f^{\prime }(x)\mathcal{G}_{n}^{\alpha _{1}, \beta _{1}}\bigl(E_{t}^{1};x \bigr) -\frac{1 }{2}f^{\prime \prime } ( x )\mathcal{G}_{n}^{\alpha _{1},\beta _{1}} \bigl(E_{t}^{2};x\bigr) \biggr\vert \leq \bigl\vert \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}\bigl( \Delta E_{t}^{2};x \bigr) \bigr\vert . $$

Then, by rearranging the above inequality, one easily obtains that

$$\begin{aligned}& \biggl\vert \frac{n}{p_{n}} \bigl[ \mathcal{G}_{n}^{\alpha _{1}, \beta _{1}} ( f;x ) -f ( x ) \bigr]-xf'(x)- \frac{1}{2}x f''(x) \biggr\vert \\& \quad \leq \bigl\vert f^{\prime }(x) \bigr\vert \biggl\vert \frac{n}{p_{n}} \mathcal{G}_{n}^{\alpha _{1}, \beta _{1}}\bigl(E_{t}^{1};x \bigr)-x \biggr\vert +\frac{1 }{2} \bigl\vert f^{ \prime \prime } ( x ) \bigr\vert \biggl\vert \frac{n}{p_{n}}\mathcal{G}_{n}^{\alpha _{1},\beta _{1}} \bigl(E_{t}^{2};x\bigr)-x \biggr\vert \\& \qquad {} + \biggl\vert \frac{n}{p_{n}}\mathcal{G}_{n}^{\alpha _{1},\beta _{1}} \bigl( \Delta E_{t}^{2};x\bigr) \biggr\vert . \end{aligned}$$

For the sake of convenience, we shall denote by

$$\begin{aligned} \mathcal{A}_{n}(x) =& \frac{n}{p_{n}}\mathcal{G}_{n}^{\alpha _{1}, \beta _{1}} \bigl(E_{t}^{1};x\bigr)-x, \end{aligned}$$

and

$$\begin{aligned} \mathcal{B}_{n}(x) =& \frac{1}{2}\frac{n}{p_{n}} \mathcal{G}_{n}^{ \alpha _{1},\beta _{1}}\bigl(E_{t}^{2};x \bigr)-x. \end{aligned}$$

From the consequences of Lemma 2, it is clear that $\mathcal{A}_{n} \rightarrow 0$ and $\mathcal{B}_{n}(x)\rightarrow 0$ as $n\rightarrow \infty$ at any point $x\in \mathcal{S}$. Hence, we have that

$$\begin{aligned}& \biggl\vert \frac{n}{p_{n}} \bigl[ \mathcal{G}_{n}^{\alpha _{1}, \beta _{1}} ( f;x ) -f ( x ) \bigr]-xf'(x)- \frac{1}{2}x f''(x) \biggr\vert \\& \quad \leq \bigl\vert f^{\prime }(x) \bigr\vert \bigl\vert \mathcal{A}_{n}(x) \bigr\vert + \bigl\vert f^{ \prime \prime } ( x ) \bigr\vert \bigl\vert \mathcal{B}_{n}(x) \bigr\vert + \biggl\vert \frac{n}{p_{n}} \mathcal{G}_{n}^{\alpha _{1}, \beta _{1}}\bigl(\Delta E_{t}^{2};x \bigr) \biggr\vert . \end{aligned}$$

As a last step to finalize the proof of the theorem, we must estimate the last term $\vert \frac{n}{p_{n}}\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}( \Delta E_{t}^{2};x) \vert$. With the help of the inequality in Holhos’s paper [23], we obtain that

$$ \bigl\vert \Delta ( t,x ) \bigr\vert \leq \biggl( 1+ \frac{ ( e^{-x}-e^{-t} ) ^{2}}{\delta ^{2}} \biggr) \omega ^{\ast } \bigl( f^{\prime \prime };\delta \bigr) $$

and

$$ \textstyle\begin{cases} \vert \Delta ( t,x ) \vert \leq 2\omega ^{ \ast } ( f^{\prime \prime };\delta ) & \text{if } \vert e^{-x}-e^{-t} \vert \leq \delta , \\ \vert \Delta ( t,x ) \vert \leq 2 \frac{ ( e^{-x}-e^{-t} ) ^{2}}{\delta ^{2}}\omega ^{\ast } ( f^{ \prime \prime };\delta ) & \text{if } \vert e^{-x}-e^{-t} \vert >\delta .\end{cases}$$

As a consequence, we have $\vert \Delta ( t,x ) \vert \leq 2 ( 1+ \frac{ ( e^{-x}-e^{-t} ) ^{2}}{\delta ^{2}} ) \omega ^{\ast } ( f^{\prime \prime };\delta )$. With the help of this, we can easily obtain that

$$\begin{aligned} \biggl\vert \frac{n}{p_{n}}\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}\bigl( \Delta E_{t}^{2};x\bigr) \biggr\vert \leq & \frac{2n}{p_{n}}\omega ^{ \ast } \bigl( f^{\prime \prime };\delta \bigr) \mathcal{G}_{n}^{ \alpha _{1},\beta _{1}}\bigl( E_{t}^{2};x \bigr) +\frac{2n}{\delta ^{2}p_{n}}\omega ^{\ast } \bigl( f^{\prime \prime }; \delta \bigr) \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}\bigl( E_{t}^{2}F_{t}^{2};x\bigr), \end{aligned}$$

and applying the long-familiar Cauchy–Schwarz inequality, we obtain

$$\begin{aligned} \frac{n}{p_{n}}\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}\bigl( \bigl\vert \Delta E_{t}^{2} \bigr\vert ;x\bigr) \leq & \frac{2n}{p_{n}}\omega ^{\ast } \bigl( f^{\prime \prime };\delta \bigr) \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}\bigl( E_{t}^{2};x \bigr) \\ &{}+ \frac{2n}{\delta ^{2}p_{n}}\omega ^{\ast } \bigl( f^{\prime \prime }; \delta \bigr) \sqrt{\mathcal{G}_{n}^{\alpha _{1},\beta _{1}}\bigl( E_{t}^{4};x\bigr)} \sqrt{\mathcal{G}_{n}^{\alpha _{1},\beta _{1}} \bigl( F_{t}^{4};x\bigr)}. \end{aligned}$$

By choosing $\delta =\frac{1}{\sqrt{n}}$ and denoting by $\mathcal{C} _{n} ( x ) =\frac{n^{2}}{p_{n}}\sqrt{ \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}( E_{t}^{4};x)}\sqrt{ \mathcal{G}_{n}^{\alpha _{1},\beta _{1}}( F_{t}^{4};x)}$, we deduce that

$$\begin{aligned}& \biggl\vert \frac{n}{p_{n}} \bigl[ \mathcal{G}_{n}^{\alpha _{1}, \beta _{1}} ( f;x ) -f ( x ) \bigr]-xf'(x)- \frac{1}{2}x f''(x) \biggr\vert \\& \quad \leq \bigl\vert f^{\prime }(x) \bigr\vert \bigl\vert \mathcal{A}_{n}(x) \bigr\vert + \bigl\vert f^{ \prime \prime } ( x ) \bigr\vert \bigl\vert \mathcal{B}_{n}(x) \bigr\vert \\& \qquad {} + 2 \bigl\vert 2 \mathcal{B}_{n}(x)+x \bigr\vert +2 \mathcal{C}_{n}(x)\omega ^{ \ast } \biggl(f'', \frac{1}{\sqrt{n}} \biggr), \end{aligned}$$

thus the proof is completed. □

Corollary 1

Let $f,f^{\prime \prime }\in C_{*}(\mathcal{S})$. Then, the inequality

$$ \lim_{n\rightarrow \infty }\frac{n}{p_{n}} \bigl[ \mathcal{G}_{n}^{ \alpha _{1},\beta _{1}} ( f;x ) -f ( x ) \bigr]=xf'(x)+\frac{1}{2}xf''(x), $$

holds for any $x\in \mathcal{S}$.

6 Numerical examples

In this part of the paper, we provide a series of numerical experiments for the newly defined operators. For this purpose, we present the graphical presentations for a classical Bernstein–Chlodowsky operator, a Bernstein–Chlodowsky–Gadjiev operator and our operators introduced above. In these experiments, we have used three different test functions and different parameters. All the implementations of the newly defined operators are performed in MATLAB.

Example 1

We shall now illustrate the convergence of the new type Bernstein–Chlodowsky–Gadjiev operator based on its classical counterparts. The new construction of the Bernstein–Chlodowsky–Gadjiev operator and its standard version algorithm is applied to the test function $f(x):[0,1]\rightarrow \mathbb{R}$, where $p_{n}=n^{1/2}$ and $n=10 0$ with

$$ f(x)=e^{-2x} , $$

such that $\alpha _{2}=1$, $\alpha _{1}=2$, $\alpha _{3}=0$, $\beta _{1}=3$, $\beta _{2}=4$ and $\beta _{3}=1$.

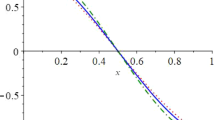
In Fig. 1 we draw the results of standard Bernstein–Chlodowsky operators, a Bernstein–Chlodowsky–Gadjiev operator, the new construction of Bernstein–Chlodowsky–Gadjiev operators and a test function. Clearly, the proposed operator shows better convergence behavior than its classic counterparts.

Figure 1

$f(x)=e^{-2x}$, the classical Bernstein–Chlodowsky operator, the Bernstein–Chlodowsky–Gadjiev operator and the newly defined Bernstein–Chlodowsky–Gadjiev-Type operator versus x with $c_{n}=n^{1/2}$, $\alpha _{2}=1$, $\alpha _{1}=2$, $\alpha _{3}=0$, $\beta _{1}=3$, $\beta _{2}=4$ and $\beta _{3}=1$: Exact function (Red), classical Bernstein–Chlodowsky operator (Green – Diamond), Bernstein–Chlodowsky–Gadjiev operator (Blue – Circle) and newly defined Bernstein–Chlodowsky–Gadjiev operator (Magenta – Star) on an equally spaced evaluation grid

Example 2

Secondly, we will show the convergence of the new type Bernstein–Chlodowsky–Gadjiev operator based on its classical counterparts. The new construction of the Bernstein–Chlodowsky–Gadjiev operator and its standard version algorithm is applied to the test function $f(x):[0.1,2]\rightarrow \mathbb{R}$, where $p_{n}=n^{1/2}$ and $n=100$ with

$$ f(x)=\frac{1}{1+25x^{2}} , $$

such that $\alpha _{2}=1$, $\alpha _{1}=2$, $\alpha _{3}=0$, $\beta _{1}=3$, $\beta _{2}=4$ and $\beta _{3}=1$.

Similarly, in Fig. 2, we draw the results of standard Bernstein–Chlodowsky operators, a Bernstein–Chlodowsky–Gadjiev operator, the new construction of Bernstein–Chlodowsky–Gadjiev operators and a test function. Clearly, the proposed operator shows better convergence behavior than its classic counterparts to the test function.

Figure 2

$f(x)=\frac{1}{1+25x^{2}}$, the classical Bernstein–Chlodowsky operator, the Bernstein–Chlodowsky–Gadjiev operator and the newly defined Bernstein–Chlodowsky–Gadjiev-Type operator versus x with $c_{n}=n^{1/2}$, $\alpha _{2}=1$, $\alpha _{1}=2$, $\alpha _{3}=0$, $\beta _{1}=3$, $\beta _{2}=4$ and $\beta _{3}=1$: Exact function (Red), classical Bernstein–Chlodowsky operator (Green – Diamond), Bernstein–Chlodowsky–Gadjiev operator (Blue – Circle) and newly defined Bernstein–Chlodowsky–Gadjiev operator (Magenta – Star) on an equally spaced evaluation grid

7 Concluding remarks

In this paper, we introduced a generalization of Bernstein–Chlodowsky–Gadjiev-Type operators that preserve constant and $e^{-2x}$ for $x\geq 0$. In order to show the approximation properties of these newly defined operators, we used several different function spaces. Additionally, we provide the rate and convergence and a Voronovksya-type theorem for Bernstein–Chlodowsky–Gadjiev-Type operators.