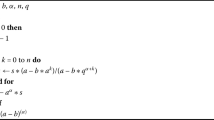1 Introduction

It is clear to everyone that fractional calculus has been one of the most important and popular topics for researchers in the last decade [1–5]. Perhaps the reason for this popularity can be traced to the high efficiency of this type of calculations in modeling of various natural phenomena, engineering, and biological mathematics [6–12]. During the research on this subject, various types of fractional derivative operators such as Riemann–Liouville, Caputo, Caputo–Fabrizio, Caputo–Hadamard have been introduced and studied by some researchers [13–27]. On the other hand, in 1910, with the research work of Frank Hilton Jackson, the exciting world of quantum computing emerged [28, 29]. Quantum calculus is a generalization of the ordinary calculus in which the limit is omitted. Two types of quantum calculus have been developed more than the others, namely q-calculus and h-calculus. It did not take long for a combination of advances in these two important areas to do much in the fields of physics, thermodynamics, and differential equations. In recent years, many researchers have addressed differential inclusion as a tool with high potential for modeling [19, 30–49].

In 2014, Ghorbanian et al. investigated the existence of solution for the fractional inclusion problem

$$ ^{c}\mathcal{D}^{\pounds }l(t) \in \mathcal{F} \bigl(t,l(t),l'(t),l''(t)\bigr) $$

with considering the boundary conditions that follow.

$$ \textstyle\begin{cases} l(0)+l(\nu )+l(1)=\int _{0}^{1}g_{0}(s,l(s))\,ds, \\ ^{c}\mathcal{D}^{\lambda }l(0)+^{c}\mathcal{D}^{\lambda }l(\nu )+^{c} \mathcal{D}^{\lambda }l(1)=\int _{0}^{1}g_{1}(s,l(s))\,ds, \\ ^{c}\mathcal{D}^{\jmath }l(0)+^{c}\mathcal{D}^{\jmath }l(\nu )+^{c} \mathcal{D}^{\jmath }l(1)=\int _{0}^{1}g_{2}(s,l(s))\,ds, \end{cases} $$

where \(t \in J=[0,1]\), \(\pounds \in (2,3)\), \(\lambda ,\nu \in (0,1)\), \(\jmath \in (1,2)\), and \(\mathcal{F}:J \times \mathbb{R} \times \mathbb{R} \times \mathbb{R} \to \mathcal{P}_{cp}(\mathbb{R})\) is a multifunction, \(g_{1},g_{2},g_{3}\in C(J \times \mathbb{R},\mathbb{R})\), \(^{c}\mathcal{D}^{\pounds }\) represents the fractional Caputo derivative, and \(\mathcal{P}_{cp}(\mathbb{R})\) is the set of all compact subsets of \(\mathbb{R}\) [50]. After that in 2017, Rezapour et al. perused the existence of solution for the fractional inclusion problem for convex and nonconvex compact multifunction

$$ ^{c}\mathcal{D}^{\pounds }l(t) \in \mathcal{F} \bigl(t,l(t),^{c}\mathcal{D}^{ \jmath }l(t),l'(t) \bigr) $$

for almost all \(t \in J=[0,1]\), with the following conditions:

$$ \textstyle\begin{cases} l(0)+l'(0)+^{c}\mathcal{D}^{\jmath }l(t)=\int _{0}^{\nu }l(s)\,ds, \\ l(1)+l'(1)+^{c}\mathcal{D}^{\jmath }l(t)=\int _{0}^{\lambda }l(s)\,ds, \end{cases} $$

where \(\mathcal{F}:J \times \mathbb{R} \times \mathbb{R} \times \mathbb{R} \to 2^{\mathbb{R}}\) is a compact-valued multifunction [51].

By combining the ideas mentioned above, we now intend to examine the following q-inclusion:

$$ ^{c}\mathcal{D}_{q}^{\pounds }l(t) \in \mathcal{F}\bigl(t,l(t),l'(t),l''(t),^{c} \mathcal{D}_{q}^{\hbar _{1}}l(t),^{c} \mathcal{D}_{q}^{\hbar _{2}}l(t)\bigr) $$
(1)

with introducing new integral boundary conditions:

$$ \textstyle\begin{cases} l(0)+{\boldsymbol{S}}l'(0)=0, \\ al(\eth )+b\int _{0}^{1}l(t)\,dt =0, \\ {\boldsymbol{P}}l''(1)+c\int _{0}^{1}l(t)\,dt =0, \end{cases} $$
(2)

for all \(t \in \mathfrak{J}=[0,1]\), and \(\eth \in (0,1)\), \({\boldsymbol{S}}=\sum_{j=0}^{j=k}u_{j}\), \({\boldsymbol{P}}=\prod_{j=0}^{j=k}w_{j}\) with \(u_{j}, w_{j} \in \mathbb{R}\), and \(^{c}\mathcal{D}_{q}^{\pounds }\) denotes Caputo quantum fractional derivative of order \(\pounds \in (2,3]\), also \(\hbar _{1}, \hbar _{2} \in (1,2]\), where \(\mathcal{F}:\mathfrak{J} \times \mathbb{R}^{5}\to \mathcal{P}( \mathbb{R})\) is a compact-valued multifunction such that \(\mathcal{P}(\mathbb{R})\) is a set of all subsets of \(\mathbb{R}\).

2 Preliminaries

In this section, we summarize what we need from quantum calculus to examine the subject of this research. Throughout this work we always apply quantum calculations to the time scale \(\mathcal{T}_{t_{0}}=\{t_{0},t_{0}q,t_{0}q^{2}, \ldots\}\cup \{0\}\) such that \(t_{0} \in \mathbb{R}\) and \(0< q<1\) [28].

Definition 2.1

([28])

For every real number y, we define the q-analogue of y as

$$ [y]_{q}=\frac{1-q^{y}}{1-q}=1 + q + \cdots + q^{y -1}. $$

Also, for the power function \((w - s)_{q}^{n}\), its q-analogue for \(n\in \mathbb{N}_{0}\) is expressed as

$$ {\textstyle\begin{cases} (w-s)_{q}^{(n)} = \prod_{i=0}^{ n-1}(w - s q^{i}) \quad \text{for } n \ge 1, \\ (w-s)_{q}^{(0)}=1, \end{cases}\displaystyle } $$
(3)

such that \(w,s \in \mathbb{R}\) and \(\mathbb{N}_{0}=\mathbb{N} \cup \{0\}\). The (3) can be expressed for any real number β as follows:

$$ (w-s)_{q}^{(\beta )}= w^{\beta } \prod _{n=0}^{\infty } \frac{1 - (\frac{s}{w})q^{n}}{1- (\frac{s}{w}) q^{\beta + n}}, \quad w \ne 0. $$

If \(s=0\), it is clear that \(w^{(\beta )}=w^{\beta }\) [52].

Definition 2.2

([29])

The q-gamma function for \(w \in \mathbb{R}-\{0,-1,-2, \dots \}\) is calculated using the following equation:

$$ \Gamma _{q}(w) = \frac{ (1-q)^{ (w -1)}}{ (1-q)^{w - 1}}, $$
(4)

it is worth noting that \(\Gamma _{q}(w +1)=[w]_{q} \Gamma _{q} (w)\) is valid.

Here we present Algorithm 1 for calculating different values of the q-gamma function; also in Table 1 some numerical results for \(q=\frac{1}{5}\), \(q=\frac{1}{2}\), \(q=\frac{8}{9}\) are provided.

Algorithm 1
figure a

The proposed procedure to calculate \(\Gamma _{q} (w)\)

Full size image
Table 1 Numerical result for \(\Gamma _{q}(w)\)
Full size table

Definition 2.3

([53])

Suppose that \(\hbar (w)\) is a continuous function, then the q-derivative of this function is defined as

$$ ( \mathcal{D}_{q} \hbar ) (w)= \frac{\hbar (w) - \hbar (qw)}{ (1-q)w}, $$

as well as, \((\mathcal{D}_{q} \hbar )(0) = \lim_{w\to 0}(\mathcal{D}_{q} \hbar )(w)\). Moreover, we can extend the q-derivative of this function to any arbitrary order by means of \((\mathcal{D}_{q}^{n} \hbar )(w)= \mathcal{D}_{q} (\mathcal{D}_{q}^{n -1} \hbar )(w)\), such that \(n \in \mathbb{N}\), and \((\mathcal{D}_{q}^{n} \hbar )(w)=\hbar (w)\).

Definition 2.4

([53])

Let ħ be a continuous map defined on \([0,\mathfrak{b}]\), then the q-antiderivative of ħ is called the Jackson integral of ħ and is illustrated as follows:

$$ \mathcal{I}_{q}\hbar (w)= \int _{0}^{w}\hbar (s)\,d_{q}s=w(1-q) \sum_{j=0}^{ \infty }q^{j}\hbar \bigl(q^{j}w\bigr), \quad \bigl(w \in [0,\mathfrak{b}]\bigr) $$

that the right-hand side absolutely converges. The q-antiderivative of ħ can be extended to any arbitrary order by means of \(\mathcal{I}^{n}_{q}\hbar (w)=\mathcal{I}(\mathcal{I}^{n-1}_{q} \hbar (w))\).

Remark 2.1

([53])

Let the function ħ be continuous at \(w=0\), then we have

$$ \textstyle\begin{cases} \mathcal{I}_{q}(\mathcal{D}_{q}\hbar (w))=\hbar (w)-\hbar (0), \\ \mathcal{D}_{q}(\mathcal{I}_{q}\hbar (w))=\hbar (w) \quad \text{for all } w. \end{cases} $$

Remark 2.2

([53])

According to the following relations, we can replace the order of double q-integral:

$$ \int _{0}^{w} \int _{0}^{u}\hbar (s)\,d_{q}s\,d_{q}u= \int _{0}^{w} \int _{qs}^{w} \hbar (u)\,d_{q}u\,d_{q}s $$

since

$$\begin{aligned} \int _{0}^{w} \int _{qs}^{w}\hbar (u)\,d_{q}u\,d_{q}s &= \int _{0}^{w}(w-qs)^{ \kappa -1}\hbar (s)\,d_{q}s \\ &=w(1-q)\sum_{j=0}^{\infty }q^{j} \hbar \bigl(q^{j}w\bigr) \bigl(w-q^{j+1}w\bigr) \\ &=w^{2}(1-q)^{2}\sum_{j=0}^{\infty }q^{j} \hbar \bigl(q^{j}w\bigr)\Biggl[\sum_{j=0}^{ \infty }q^{j} \Biggr]. \end{aligned}$$

Moreover, it can be written for the left

$$\begin{aligned} \int _{0}^{w} \int _{0}^{u}\hbar (s)\,d_{q}s\,d_{q}u &= w(1-q)\sum_{j=0}^{ \infty }q^{j} \int _{0}^{wq^{j}}\hbar (u)\,d_{q}u \\ &= w^{2}(1-q)^{2}\sum_{j=0}^{\infty } \sum_{k=0}^{\infty }q^{j+2k} \hbar \bigl(q^{j+k}w\bigr). \end{aligned}$$

Definition 2.5

([54])

The fractional Riemann–Liouville quantum integral of order £ for a continuous function \(l(w):[0,\infty ]\to \mathbb{R}\) is defined by

$$ \mathcal{I}^{\pounds }_{q}l(w)= \frac{1}{\Gamma _{q}(\pounds )} \int _{0}^{w}(w-qs)^{ \pounds -1}l(s)\,d_{q}s. $$
(5)

Definition 2.6

([54])

The fractional Caputo quantum derivative of order £ for a continuous function \(l(w):[0,\infty ]\to \mathbb{R}\) is defined by

$$ ^{c}\mathcal{D}^{\pounds }l(w)= \frac{1}{\Gamma _{q}(n-\pounds )} \int _{0}^{w}(w-qs)^{n- \pounds -1} \mathcal{D}_{q}^{n}l(s)\,d_{q}s, \quad n=[ \pounds ]+1. $$
(6)

Lemma 2.7

([55])

Let \(n=[\pounds ]+1\), then

$$ \bigl({}^{C}\mathcal{I}_{q}^{\pounds }\, {}^{C}\mathcal{D}_{q}^{\pounds }l\bigr) (w)= l(w) - \sum_{k=0}^{n-1} \frac{w^{k}}{\Gamma _{q} ( k + 1 ) } \bigl( \mathcal{D}_{q}^{k} l\bigr) (0). $$

Indeed, the general solution for \({}^{C}\mathcal{D}_{q}^{ \pounds }l(w) =0\) is \(l(w) = \mathfrak{y}_{0} + \mathfrak{y}_{1} w + \mathfrak{y}_{2} w^{2} + \cdots + \mathfrak{y}_{n-1} w^{n-1}\) such that \(\mathfrak{y}_{0}, \dots , \mathfrak{y}_{n-1}\in \mathbb{R}\).

Here, to help visualize fractional calculations, we present graphs of two functions in Figs. 1 and 2.

Figure 1
figure 1

The graph of \(\mathcal{I}^{\pounds }e^{x^{2}}\), where \(\mathcal{I}^{\pounds }\) is the Riemann–Liouville fractional integral

Full size image
Figure 2
figure 2

The graph of \(\mathcal{D}^{\alpha }\sin (x)\), where \(\mathcal{D}^{\alpha }\) is the Riemann–Liouville fractional derivative

Full size image

Notation 2.8

Assume that \((\mathcal{K},\mathfrak{d})\) is a metric space. We denote the set of all subsets of \(\mathcal{K}\) and the set of all nonempty subsets of \(\mathcal{K}\) by \(\mathcal{P}(\mathcal{K})\) and \(2^{\mathcal{K}}\), respectively. Also assume that the symbols \(\mathcal{P}_{{b}d}(\mathcal{K})\), \(\mathcal{P}_{cl}(\mathcal{K})\), \(\mathcal{P}_{cp}(\mathcal{K})\), and \(\mathcal{P}_{cv}(\mathcal{K})\) represent the class of all bounded, closed, compact, and convex subsets of \(\mathcal{K}\), respectively.

Definition 2.9

([56])

Let \(\mathcal{F}:\mathcal{K} \to 2^{\mathcal{K}}\) be a mapping. It is called a multifunction on \(\mathcal{K}\), also an element \(p \in \mathcal{K}\) is a fixed point of \(\mathcal{F}\) whenever \(p \in \mathcal{F}(p)\). Moreover, for multifunction \(\mathcal{F}\), an element \(p \in \mathcal{K}\) is called an endpoint of \(\mathcal{F}\) whenever \(\mathcal{F}(p)=\{p\}\). Also, we say that \(\mathcal{F}\) has an approximate property whenever \(\inf_{p \in \mathcal{K}}\sup_{r\in \mathcal{F}(p)}\mathfrak{d}(p,r)=0\).

Suppose that \(\mathcal{F}:\mathcal{K} \to \mathcal{P}_{cl}(\mathcal{K})\) is a multifunction and A is an open set in \(\mathcal{K}\), then we say that \(\mathcal{F}\) is lower semi-continuous(lsm) if the set \(\mathcal{F}^{-1}(A):=\{r \in \mathcal{K}:\mathcal{F}(r)\cap A \ne \phi \}\) is open [57]. Also it is called upper semi-continuous(usm) if the set \(\{r \in \mathcal{K}:\mathcal{F}(r) \subset A \}\) is open. A multifunction \(\mathcal{F}:\mathcal{K} \to \mathcal{P}_{cp}(\mathcal{K})\) is called compact if \(\overline{\mathcal{F}(B)}\) is a compact set of \(\mathcal{K}\) for any bounded subset B of \(\mathcal{K}\). Let \(\mathcal{I}=[0,1]\), and the multifunction \(\mathcal{F}:\mathcal{I} \to \mathcal{P}_{cl}(\mathbb{R})\) is called measurable if the function \(f \mapsto \mathfrak{d}(r,\mathcal{F}(f))=\inf \{\vert r-y\vert : y \in \mathcal{F}(f)\}\) is measurable for all \(r \in \mathbb{R}\) [57].

Definition 2.10

([57])

Let \((\mathcal{K},\mathfrak{d})\) be a metric space, we define the well-known Pompeiu–Hausdorff metric \(\mathcal{H}_{\mathfrak{d}}:2^{\mathcal{K}}\times 2^{\mathcal{K}}\to [0, \infty ]\) by

$$ \mathcal{H}_{\mathfrak{d}}(U,V)=\Bigl\{ \sup_{u\in U} \mathfrak{d}(u,V),\sup_{v \in V}\mathfrak{d}(U,v)\Bigr\} , $$

where \(\mathfrak{d}(U,v)=\inf_{u\in U}\mathfrak{d}(u,v)\). Then \((\mathcal{P}_{bd,cl}(\mathcal{K}),\mathcal{H}_{\mathfrak{d}})\) is a metric space and \((\mathcal{P}_{cl}(\mathcal{K}),\mathcal{H}_{\mathfrak{d}})\) is a generalized metric space.

A multifunction \(\mathcal{F}:\mathcal{K} \to \mathcal{P}_{cl}(\mathcal{K})\) is called an α-contraction if \(\exists \alpha \in (0,1)\) whenever \(\mathcal{H}_{\mathfrak{d}}(\mathcal{F}(p_{1}),\mathcal{F}(p_{2})) \le \alpha \mathfrak{d}(p_{1},p_{2})\) for all \(p_{1},p_{2} \in \mathcal{K}\). Nadler’s fixed point theorem states that: if \(\mathcal{F}\) is a closed-valued contractive set-valued map on a complete metric space, then \(\mathcal{F}\) has a fixed point [58].

Definition 2.11

Let \(\mathfrak{A}=C(\mathfrak{J},\mathbb{R})\), we define the following spaces:

$$ \mathcal{Z}_{i}=\bigl\{ l(t):l(t),l'(t),l''(t),^{c} \mathcal{D}_{q}^{\hbar _{i}}l(t) \in \mathfrak{A} \bigr\} $$

endowed with the norm

$$ \Vert l \Vert _{i}=\sup_{t \in \mathfrak{J}} \bigl\vert l(t) \bigr\vert +\sup_{t \in \mathfrak{J}} \bigl\vert l'(t) \bigr\vert +\sup_{t \in \mathfrak{J}} \bigl\vert l''(t) \bigr\vert +\sup_{t \in \mathfrak{J}} \bigl\vert ^{c}\mathcal{D}_{q}^{\hbar _{i}}l(t) \bigr\vert . $$

Now, regard the space \(\mathcal{K}=\mathcal{Z}_{1}\times \mathcal{Z}_{2}\) endowed with the norm \(\Vert (l_{1},l_{2})\Vert =\Vert l_{1}\Vert +\Vert l_{2}\Vert \), then \((\mathcal{K},\Vert . \Vert )\) is a Banach space [58].

Definition 2.12

For \(l=(l_{1},l_{2}) \in \mathcal{K}\), we define

$$ \mathcal{S}^{*}_{\mathcal{F},l}=\bigl\{ \mathfrak{f} \in L^{1}(\mathfrak{J}): \mathfrak{f}(t) \in \mathcal{F} \bigl(t,l(t),l'(t),l''(t),^{c} \mathcal{D}_{q}^{ \hbar _{1}}l(t),^{c} \mathcal{D}_{q}^{\hbar _{2}}l(t)\bigr) \text{ for all } t \in \mathfrak{J} \bigr\} $$

that is called the set of selection of \(\mathcal{S}^{*}\). If \(\operatorname{dim} \mathcal{K}< \infty \), then \(\mathcal{S}^{*}_{\mathcal{F},l}\ne \phi \) for all \(l\in \mathcal{K}\) [58].

To prove our main result, we use the endpoint technique presented in 2010 by Amini-Harandi [56].

Lemma 2.13

([56])

Let \((\mathcal{K},\mathfrak{d})\) be a complete metric space, and regard:

  1. 1

    A map \(\psi : [0, \infty ) \to [0, \infty )\) that is (usm) where \(\psi (w) < w\) and \(\liminf_{\substack{w\to \infty }}(w - \psi (w))>0\) for all \(w>0\);

  2. 2

    A multifunction map \(\mathcal{F}:\mathcal{K}\to \mathcal{P}_{cl,bd}(\mathcal{K})\) with \(\mathcal{H}_{\mathfrak{d}}(\mathcal{F}(p),\mathcal{F}(r))\le \psi ( \mathfrak{d}(p,r))\) for any \(p,r \in \mathcal{K}\).

Then \(\mathcal{F}\) has a unique endpoint iff \(\mathcal{F}\) has an approximate endpoint property.

3 Main results

Now, after stating the above preparations, we can get our main results. First we start with a lemma.

Lemma 3.1

Let \(\pounds \in (2,3]\) and \(v(t) \in \mathfrak{A}\). Then the quantum fractional problem \(^{c}\mathcal{D}_{q}^{\pounds }l(t)=v(t)\) with boundary condition (2) has a unique solution which is obtained by

$$ l(t)=\mathcal{I}^{\pounds }_{q}v(t)+\theta \mathfrak{B}_{1}(t) \mathcal{I}^{\pounds }_{q}v(\eth )+\theta \mathfrak{B}_{2}(t) \mathcal{I}^{\pounds }_{q} \bigl[\mathfrak{I}^{\pounds }_{q}v(r)\bigr](1)+\theta \mathfrak{B}_{3}(t)\mathcal{I}^{\pounds -2}_{q}v(1){} $$
(7)

such that

$$ \theta = \biggl[\biggl(2{\boldsymbol{P}}+\frac{c}{3}\biggr) \biggl(a \eth +\frac{b}{2}-{\boldsymbol{S}}(a+b)\biggr)-c\biggl(a\eth ^{2}+ \frac{b}{3}\biggr) \biggl(\frac{1}{2}-{ \boldsymbol{S}}\biggr)\biggr]^{-1}\ne 0 $$
(8)

and

$$\begin{aligned}& \mathfrak{B}_{1}(t)=a\biggl(2{\boldsymbol{P}}+\frac{c}{3} \biggr) ({ \boldsymbol{S}}-t)+ac\biggl(\frac{1}{2}-{\boldsymbol{S}} \biggr)t^{2}, \\& \begin{aligned} \mathfrak{B}_{2}(t)={}& \biggl[c\biggl(a\eth ^{2}+ \frac{b}{3}\biggr)-(a+b) \biggl(2{ \boldsymbol{P}}+\frac{c}{3} \biggr)\biggr](t-{\boldsymbol{S}})\\ &{}+c\biggl[b\biggl({ \boldsymbol{S}}+ \frac{1}{2}\biggr)+{\boldsymbol{S}}(a+b)-a \eth -\frac{b}{2} \biggr]t^{2}, \end{aligned} \\& \mathfrak{B}_{3}(t)={\boldsymbol{P}}\biggl(a\eth ^{2}+ \frac{b}{3}\biggr) (t-{\boldsymbol{S}})+{\boldsymbol{P}}\biggl({ \boldsymbol{S}}(a+b)-a\eth -\frac{b}{2}\biggr)t^{2}. \end{aligned}$$

Proof

With regard to Lemma 2.7 the solution of \(^{c}\mathcal{D}_{q}^{\pounds }l(t)=v(t)\) is

$$ l(t)=\mathcal{I}^{\pounds }_{q}v(t)+ \mathfrak{y}_{0} + \mathfrak{y}_{1} t + \mathfrak{y}_{2} t^{2} $$
(9)

such that \(\mathfrak{y}_{0}, \mathfrak{y}_{1} \text{and} \mathfrak{y}_{2} \in \mathbb{R}\). Now, by taking derivative from \(l(t)\), we have

$$ \textstyle\begin{cases} l'(t)=\mathfrak{y}_{1}+2\mathfrak{y}_{2} t+\mathcal{I}^{\pounds -1}_{q}v(t), \\ l''(t)=2\mathfrak{y}_{2}+ \mathcal{I}^{\pounds -2}_{q}v(t), \end{cases} $$
(10)

and by exerting the boundary conditions (2) to (10) we have

$$ \textstyle\begin{cases} \mathfrak{y}_{0}+{\boldsymbol{S}}\mathfrak{y}_{1}=0, \\ (a+b)\mathfrak{y}_{0}+(a\eth +\frac{b}{2})\mathfrak{y}_{1} +(a\eth ^{2}+ \frac{b}{3})\mathfrak{y}_{2}=-a\mathcal{I}^{\pounds }_{q}v(\eth )-b \mathcal{I}^{\pounds }_{q}[\mathfrak{I}^{\pounds }_{q}v(r)]_{ (1)}, \\ c\mathfrak{y}_{0}+\frac{c}{2}\mathfrak{y}_{1}+({\boldsymbol{P}}+\frac{c}{3})\mathfrak{y}_{2}=-{\boldsymbol{P}}\mathcal{I}^{\pounds -2}_{q}v(1)-c\mathcal{I}^{\pounds }_{q}[ \mathfrak{I}^{\pounds }_{q}v(r)]_{(1)}. \end{cases} $$

Now we can compute \(\mathfrak{y}_{0}\), \(\mathfrak{y}_{1}\), \(\mathfrak{y}_{2}\) as follows:

$$ \textstyle\begin{cases} \mathfrak{y}_{0}={\boldsymbol{S}}\theta [a(2{ \boldsymbol{P}}+\frac{c}{3})\mathcal{I}^{\pounds }_{q}v( \eth )- [c(a\eth ^{2}+\frac{b}{3}) \\ \hphantom{\mathfrak{y}_{0}=}{}-(a+b)(2{\boldsymbol{P}}+\frac{c}{3}) ]\mathcal{I}^{ \pounds }_{q}[\mathfrak{I}^{\pounds }_{q}v(r)]_{(1)}-{ \boldsymbol{P}}(a\eth ^{2}+\frac{b}{3})\mathcal{I}^{ \pounds -2}_{q}v(1) ], \\ \mathfrak{y}_{1}=\theta [ [c(a\eth ^{2}+\frac{b}{3})-(a+b)(2{ \boldsymbol{P}}+\frac{c}{3}) ]\mathcal{I}^{\pounds }_{q}[ \mathfrak{I}^{\pounds }_{q}v(r)]_{(1)} \\ \hphantom{\mathfrak{y}_{1}=}{}-a(2{\boldsymbol{P}}+\frac{c}{3})\mathcal{I}^{\pounds }_{q}v( \eth )+{\boldsymbol{P}}(a\eth ^{2}+\frac{b}{3})\mathcal{I}^{ \pounds -2}_{q}v(1) ], \\ \mathfrak{y}_{2}=\theta [ac(\frac{1}{2}-{\boldsymbol{S}})\mathcal{I}^{\pounds }_{q}v(\eth )+ [c (b({ \boldsymbol{S}}+\frac{1}{2})+{\boldsymbol{S}}(a+b)-a \eth -\frac{b}{2} ) ]\mathcal{I}^{\pounds }_{q}[\mathfrak{I}^{ \pounds }_{q}v(r)]_{(1)} \\ \hphantom{\mathfrak{y}_{2}=}{} +{\boldsymbol{P}}({\boldsymbol{S}}(a+b)-a \eth -\frac{b}{2})\mathcal{I}^{\pounds -2}_{q}v(1) ]. \end{cases} $$

Now, by replacing \(\mathfrak{y}_{0}\), \(\mathfrak{y}_{1}\), \(\mathfrak{y}_{2}\) in (9), we obtain (7). □

Notation 3.2

To continue the work and for ease of understanding of the calculations performed, we introduce some symbols here. According to the definition of \(\mathfrak{B}_{1}(t)\), \(\mathfrak{B}_{2}(t)\), \(\mathfrak{B}_{3}(t)\), we have

$$\begin{aligned}& \bigl\vert \mathfrak{B}_{1}(t) \bigr\vert \le \vert a \vert \biggl(2 \vert { \boldsymbol{P}} \vert +\frac{ \vert c \vert }{3} \biggr) \vert { \boldsymbol{S}}+1 \vert + \vert c \vert \biggl\vert \frac{1}{2}+ \biggr\vert {\boldsymbol{S}} \vert \vert := \mathfrak{B}^{*}_{1}, \\& \begin{aligned} \bigl\vert \mathfrak{B}_{2}(t) \bigr\vert \le{}& \vert c \vert \biggl( \vert a \vert \eth ^{2}+\frac{ \vert b \vert }{3} \biggr)+ \vert a+b \vert \biggl(2 \vert { \boldsymbol{P}} \vert + \frac{ \vert c \vert }{3} \biggr) \bigl(1+ \vert { \boldsymbol{S}} \vert \bigr)\\ &{}+ \vert c \vert \biggl( \vert b \vert \biggl( \vert {\boldsymbol{S}} \vert +\frac{1}{2}\biggr)+ \vert {\boldsymbol{S}} \vert \vert a+b \vert + \vert a \vert \eth + \frac{ \vert b \vert }{2} \biggr):= \mathfrak{B}^{*}_{2}, \end{aligned} \\& \bigl\vert \mathfrak{B}_{3}(t) \bigr\vert \le \vert { \boldsymbol{P}} \vert \biggl( \vert a \vert \eth ^{2}+ \frac{ \vert b \vert }{3} \biggr) \bigl(1+ \vert { \boldsymbol{S}} \vert \bigr)+ \vert {\boldsymbol{P}} \vert \biggl( \vert {\boldsymbol{S}} \vert \vert a+b \vert + \vert a \vert \eth +\frac{ \vert b \vert }{2} \biggr):= \mathfrak{B}^{*}_{3}; \end{aligned}$$

moreover

$$\begin{aligned}& \bigl\vert \mathfrak{B}'_{1}(t) \bigr\vert \le \vert a \vert \biggl(2 \vert { \boldsymbol{P}} \vert + \frac{ \vert c \vert }{3} \biggr)+ \vert a \vert \vert c \vert \biggl\vert \frac{1}{2}+ \biggr\vert {\boldsymbol{S}} \vert \vert := \mathfrak{B}^{*'}_{1}, \\& \begin{aligned} \bigl\vert \mathfrak{B}'_{2}(t) \bigr\vert \le{}& \vert c \vert \biggl( \vert a \vert \eth ^{2}+ \frac{ \vert b \vert }{3} \biggr)+ \vert a+b \vert \biggl(2 \vert { \boldsymbol{P}} \vert +\frac{ \vert c \vert }{3} \biggr)\\ &{}+2 \vert c \vert \biggl( \vert b \vert \biggl( \vert {\boldsymbol{S}} \vert + \frac{1}{2}\biggr)+ \vert {\boldsymbol{S}} \vert \vert a+b \vert + \vert a \vert \eth +\frac{ \vert b \vert }{2} \biggr):=\mathfrak{B}^{*'}_{2}, \end{aligned} \\& \bigl\vert \mathfrak{B}'_{3}(t) \bigr\vert \le \vert {\boldsymbol{P}} \vert \biggl( \vert a \vert \eth ^{2}+ \frac{ \vert b \vert }{3} \biggr)+2 \vert { \boldsymbol{P}} \vert \biggl( \vert {\boldsymbol{S}} \vert \vert a+b \vert + \vert a \vert \eth + \frac{ \vert b \vert }{2} \biggr):= \mathfrak{B}^{*'}_{3}, \end{aligned}$$

also

$$\begin{aligned}& \bigl\vert \mathfrak{B}''_{1}(t) \bigr\vert \le \vert a \vert \vert c \vert \biggl\vert \frac{1}{2}+ \biggr\vert {\boldsymbol{S}} \vert \vert := \mathfrak{B}^{*''}_{1}, \\& \bigl\vert \mathfrak{B}''_{2}(t) \bigr\vert \le 2 \vert c \vert \biggl( \vert b \vert \biggl( \vert { \boldsymbol{S}} \vert +\frac{1}{2}\biggr)+ \vert {\boldsymbol{S}} \vert \vert a+b \vert + \vert a \vert \eth + \frac{ \vert b \vert }{2} \biggr):=\mathfrak{B}^{*''}_{2}, \\& \bigl\vert \mathfrak{B}''_{3}(t) \bigr\vert \le 2 \vert {\boldsymbol{P}} \vert \biggl( \vert { \boldsymbol{S}} \vert \vert a+b \vert + \vert a \vert \eth + \frac{ \vert b \vert }{2} \biggr):=\mathfrak{B}^{*''}_{3}{ .} \end{aligned}$$

Now, by applying quantum Caputo fractional derivative from order \(\hslash _{i} \in (1,2]\), \(i=1, 2\) on \(\mathfrak{B}_{1}(t)\), \(\mathfrak{B}_{2}(t)\), \(\mathfrak{B}_{3}(t)\), we get

$$\begin{aligned}& ^{c}\mathcal{D}_{q}^{\hbar _{i}} \mathfrak{B}_{1}(t)=a\biggl(2{\boldsymbol{P}}+\frac{c}{3} \biggr) \biggl[- \frac{1}{\Gamma _{q}(2-\hslash _{i})}t^{(1-\hslash _{i})} \biggr]+ac\biggl( \frac{1}{2}-{\boldsymbol{S}}\biggr) \biggl[ \frac{2}{\Gamma _{q}(3-\hslash _{i})}t^{(2-\hslash _{i})} \biggr]{ ,} \\& \begin{aligned} ^{c}\mathcal{D}_{q}^{\hbar _{i}} \mathfrak{B}_{2}(t) ={}& \biggl(c\biggl(a\eth ^{2}+ \frac{b}{3}\biggr)-(a+b) \biggl(2{\boldsymbol{P}}+\frac{c}{3} \biggr) \biggr) \biggl[\frac{1}{\Gamma _{q}(2-\hslash _{i})}t^{(1-\hslash _{i})} \biggr] \\ &{}+ c \biggl(b\biggl({\boldsymbol{S}}+\frac{1}{2}\biggr)+{ \boldsymbol{S}}(a+b)-a\eth -\frac{b}{2} \biggr) \biggl[ \frac{2}{\Gamma _{q}(3-\hslash _{i})}t^{(2-\hslash _{i})} \biggr]{ ,} \end{aligned} \\& \begin{aligned} ^{c}\mathcal{D}_{q}^{\hbar _{i}} \mathfrak{B}_{3}(t)={}&{\boldsymbol{P}}\biggl(a\eth ^{2}+ \frac{b}{3}\biggr) \biggl[ \frac{1}{\Gamma _{q}(2-\hslash _{i})}t^{(1-\hslash _{i})} \biggr]\\ &{}+{ \boldsymbol{P}} \biggl({\boldsymbol{S}}(a+b)-a \eth - \frac{b}{2} \biggr) \biggl[\frac{2}{\Gamma _{q}(3-\hslash _{i})}t^{(2- \hslash _{i})} \biggr], \end{aligned} \end{aligned}$$

from which it can be concluded

$$\begin{aligned}& \bigl\vert ^{c}\mathcal{D}_{q}^{\hbar _{i}} \mathfrak{B}_{1}(t) \bigr\vert \le \vert a \vert \biggl(2 \vert {\boldsymbol{P}} \vert + \frac{ \vert c \vert }{3} \biggr) \biggl[ \frac{1}{\Gamma _{q}(2-\hslash _{i})} \biggr]+ \vert a \vert \vert c \vert \biggl\vert \frac{1}{2}+ \biggr\vert {\boldsymbol{S}} \vert \vert \biggl[ \frac{2}{\Gamma _{q}(3-\hslash _{i})} \biggr]:=\mathfrak{B}^{**}_{1}{ ,} \\& \begin{aligned} \bigl\vert ^{c} \mathcal{D}_{q}^{\hbar _{i}}\mathfrak{B}_{2}(t) \bigr\vert \le{}& \vert c \vert \biggl( \vert a \vert \eth ^{2}+ \frac{ \vert b \vert }{3} \biggr)+ \vert a+b \vert \biggl(2 \vert { \boldsymbol{P}} \vert + \frac{ \vert c \vert }{3} \biggr) \biggl[ \frac{1}{\Gamma _{q}(2-\hslash _{i})} \biggr] \\ &{}+ \vert c \vert \biggl( \vert b \vert \biggl( \vert { \boldsymbol{S}} \vert +\frac{1}{2}\biggr)+ \vert {\boldsymbol{S}} \vert \vert a+b \vert + \vert a \vert \eth +\frac{ \vert b \vert }{2} \biggr) \biggl[ \frac{2}{\Gamma _{q}(3-\hslash _{i})} \biggr]:=\mathfrak{B}^{**}_{2}{ ,} \end{aligned} \\& \begin{aligned} \bigl\vert ^{c}\mathcal{D}_{q}^{\hbar _{i}} \mathfrak{B}_{3}(t) \bigr\vert \le {}&\vert {\boldsymbol{P}} \vert \biggl( \vert a \vert \eth ^{2}+ \frac{ \vert b \vert }{3} \biggr) \biggl[ \frac{1}{\Gamma _{q}(2-\hslash _{i})} \biggr]\\ &{}+ \vert {\boldsymbol{P}} \vert \biggl( \vert {\boldsymbol{S}} \vert \vert a+b \vert + \vert a \vert \eth + \frac{ \vert b \vert }{2} \biggr) \biggl[ \frac{2}{\Gamma _{q}(3-\hslash _{i})} \biggr]:= \mathfrak{B}^{**}_{3}. \end{aligned} \end{aligned}$$

The following conditions must be met to prove our main theorem.

(\(\mathfrak{C}_{1}\)) Given the multivalued map \(\mathcal{F}:\mathfrak{J}\times \mathbb{R}^{5}\to \mathcal{P}_{cp}( \mathbb{R})\) is integrable bounded, so that \(\mathcal{F}(\cdot,v,u,x,y,z):[0. 1]\to \mathcal{P}_{cp}(\mathbb{R})\) is measurable.

(\(\mathfrak{C}_{2}\)) For the nondecreasing (usc) map \(\psi :[0,\infty )\to [0,\infty )\), we have \(\liminf_{w \to \infty }(w - \psi (w))>0\) and \(\psi (w) < w\) for any \(w>0\).

(\(\mathfrak{C}_{3}\)) There exists \(\mho \in C(\mathfrak{J},[0,\infty ))\) such that

$$ \begin{aligned} &\mathcal{H}_{\mathfrak{d}} \bigl(\mathcal{F}(t,u_{1},u_{2},u_{3},u_{4},u_{5}), \mathcal{F}(t,v_{1},v_{2},v_{3},v_{4},v_{5}) \bigr)\\ &\quad \le \frac{1}{\boldsymbol{\Im _{1}}+\boldsymbol{\Im _{2}}+\boldsymbol{\Im _{3}}+\boldsymbol{\Im _{4_{1}}}+\boldsymbol{\Im _{4_{2}}}} \mho (t)\psi \Biggl(\sum _{i=1}^{5} \vert u_{k}-v_{k} \vert \Biggr) \end{aligned} $$

for all \(t\in \mathfrak{J}\) and \(u_{k},v_{k} \in \mathbb{R}\), \(k=1, \dots ,5\), where

$$\begin{aligned}& \boldsymbol{\Im _{1}}= \Vert \mho \Vert \biggl[ \frac{1}{\Gamma _{q}(\pounds +1)}+ \frac{ \vert \theta \vert \mathfrak{B}^{*}_{1}}{\Gamma _{q}(\pounds +1)} \eth ^{\pounds }+ \frac{ \vert \theta \vert \mathfrak{B}^{*}_{2}}{\Gamma _{q}(\pounds +2)}+ \frac{ \vert \theta \vert \mathfrak{B}^{*}_{3}}{\Gamma _{q}(\pounds -1)} \biggr], \\& \boldsymbol{\Im _{2}}= \Vert \mho \Vert \biggl[ \frac{1}{\Gamma _{q}(\pounds -1)}+ \frac{ \vert \theta \vert \mathfrak{B}^{*'}_{1}}{\Gamma _{q}(\pounds +1)} \eth ^{\pounds }+ \frac{ \vert \theta \vert \mathfrak{B}^{*'}_{2}}{\Gamma _{q}(\pounds +2)}+ \frac{ \vert \theta \vert \mathfrak{B}^{*'}_{3}}{\Gamma _{q}(\pounds -1)} \biggr], \\& \boldsymbol{\Im _{3}}= \Vert \mho \Vert \biggl[ \frac{1}{\Gamma _{q}(\pounds -2)}+ \frac{ \vert \theta \vert \mathfrak{B}^{*''}_{1}}{\Gamma _{q}(\pounds +1)} \eth ^{\pounds }+ \frac{ \vert \theta \vert \mathfrak{B}^{*''}_{2}}{\Gamma _{q}(\pounds +2)}+ \frac{ \vert \theta \vert \mathfrak{B}^{*''}_{3}}{\Gamma _{q}(\pounds -1)} \biggr], \end{aligned}$$

and for \(i=1,2\),

$$ \boldsymbol{\Im _{4_{i}}}= \Vert \mho \Vert \biggl[ \frac{1}{\Gamma _{q}(\pounds -\hslash _{i}+1)}+ \frac{ \vert \theta \vert \mathfrak{B}^{**}_{1}}{\Gamma _{q}(\pounds +1)} \eth ^{\pounds }+ \frac{ \vert \theta \vert \mathfrak{B}^{**}_{2}}{\Gamma _{q}(\pounds +2)}+ \frac{ \vert \theta \vert \mathfrak{B}^{**}_{3}}{\Gamma _{q}(\pounds -1)} \biggr]. $$

(\(\mathfrak{C}_{4}\)) Let \(\boldsymbol{\mathfrak{M}}:\mathcal{K}\to 2^{\mathcal{K}}\) be given as follows:

$$ \boldsymbol{\mathfrak{M}}(\boldsymbol{k})=\bigl\{ \mathfrak{p} \in \mathcal{K}: \boldsymbol{\exists } \mathfrak{f}\in \mathcal{S}^{*}_{ \mathcal{F},l} \mathfrak{p}(t)=\ell (t), \forall t \in \mathfrak{J} \bigr\} $$

such that

$$ \ell (t)=\mathcal{I}^{\pounds }_{q}\mathfrak{f}(t)+\theta \mathfrak{B}_{1}(t) \mathcal{I}^{\pounds }_{q} \mathfrak{f}(\eth )+\theta \mathfrak{B}_{2}(t) \mathcal{I}^{\pounds }_{q} \bigl[\mathfrak{I}^{\pounds }_{q}\mathfrak{f}(r)\bigr](1)+ \theta \mathfrak{B}_{3}(t)\mathcal{I}^{\pounds -2}_{q} \mathfrak{f}(1). $$

Theorem 3.3

Suppose that conditions (\(\mathfrak{C}_{1})-(\mathfrak{C}_{4}\)) are satisfied. If \(\boldsymbol{\mathfrak{M}}:\mathcal{K}\to 2^{\mathcal{K}}\) has the approximate endpoint property, then quantum problem (1)–(2) has a solution.

Proof

We prove that the endpoint of \(\boldsymbol{\mathfrak{M}}:\mathcal{K}\to 2^{\mathcal{K}}\) is the solution to inclusion (1)–(2). For this, we first show that \(\boldsymbol{\mathfrak{M}}(\boldsymbol{k})\) is a closed subset of \(\mathcal{K}\) for all \(\boldsymbol{k} \in \mathcal{K}\).

For \(\forall \boldsymbol{k} \in \mathcal{K}\), the map \(t \mapsto \mathcal{F}(t,l(t),l'(t),l''(t),^{c}\mathcal{D}_{q}^{ \hbar _{1}}l(t),^{c}\mathcal{D}_{q}^{\hbar _{2}}l(t))\) is measurable and closed value. So, it has measurable selection, and hence \(\mathfrak{f}\in \mathcal{S}^{*}_{\mathcal{F},l}\ne \phi \) for all \(l \in \mathcal{K}\).

Let \(\boldsymbol{k} \in \mathcal{K}\), and \(\{\mathfrak{x}_{n} \}_{n\ge 1}\) be a sequence in \(\boldsymbol{\mathfrak{M}}( \boldsymbol{k})\) such that \(\mathfrak{x}_{n} \to \mathfrak{x}\). \(\forall n \in \mathbb{N}\), choose \(\mathfrak{f}_{n} \in \mathcal{S}^{*}_{\mathcal{F},l}\), where

$$ \mathfrak{x}_{n}=\mathcal{I}^{\pounds }_{q} \mathfrak{f}_{n}(t)+\theta \mathfrak{B}_{1}(t) \mathcal{I}^{\pounds }_{q}\mathfrak{f}_{n}(\eth )+ \theta \mathfrak{B}_{2}(t)\mathcal{I}^{\pounds }_{q} \bigl[\mathfrak{I}^{ \pounds }_{q}\mathfrak{f}_{n}(r) \bigr](1)+\theta \mathfrak{B}_{3}(t) \mathcal{I}^{\pounds -2}_{q} \mathfrak{f}_{n}(1){} $$

for all \(t\in \mathfrak{J}\).

As we know, \(\mathcal{F}\) has compact values, then the sequence \(\mathfrak{f}_{n}\) has a subsequence that converges to some \(\mathfrak{f} \in L^{1}[0,1]\). We show this again with \(\mathfrak{f}_{n}\).

It is easy to check that \(\mathfrak{f} \in \mathcal{S}^{*}_{\mathcal{F},l}\) and

$$ \mathfrak{x}_{n}(t) \to \mathfrak{x}(t)=\mathcal{I}^{\pounds }_{q} \mathfrak{f}(t)+\theta \mathfrak{B}_{1}(t)\mathcal{I}^{\pounds }_{q} \mathfrak{f}(\eth )+\theta \mathfrak{B}_{2}(t)\mathcal{I}^{\pounds }_{q} \bigl[ \mathfrak{I}^{\pounds }_{q}\mathfrak{f}(r)\bigr](1)+ \theta \mathfrak{B}_{3}(t) \mathcal{I}^{\pounds -2}_{q} \mathfrak{f}(1) $$

for all \(t\in \mathfrak{J}\). Indeed, this gives that \(\mathfrak{x} \in \boldsymbol{\mathfrak{M}}(\boldsymbol{k})\), therefore \(\mathcal{K}\) has closed values. Moreover, since \(\mathcal{F}\) has compact values, then \(\boldsymbol{\mathfrak{M}}(\boldsymbol{k})\) for all \(\boldsymbol{k} \in \mathcal{K}\) is a bounded set.

Finally, we shall show that \(\mathcal{H}_{\mathfrak{d}} (\boldsymbol{\mathfrak{M}}(u), \boldsymbol{\mathfrak{M}}(v) )\le \psi (\Vert u-v\Vert )\). Let \(u,v \in \mathcal{K}\) and \(\mathfrak{p}_{1} \in \boldsymbol{\mathfrak{M}}(v)\). Choose \(\mathfrak{f}_{1}\in \mathcal{S}^{*}_{\mathcal{F},l}\) such that

$$ \mathfrak{p}_{1}(t)=\mathcal{I}^{\pounds }_{q} \mathfrak{f}_{1}(t)+ \theta \mathfrak{B}_{1}(t) \mathcal{I}^{\pounds }_{q}\mathfrak{f}_{1}( \eth )+ \theta \mathfrak{B}_{2}(t)\mathcal{I}^{\pounds }_{q} \bigl[ \mathfrak{I}^{\pounds }_{q}\mathfrak{f}_{1}(r) \bigr](1)+\theta \mathfrak{B}_{3}(t) \mathcal{I}^{\pounds -2}_{q} \mathfrak{f}_{1}(1){} $$

for almost all \(t\in \mathfrak{J}\).

But since

$$\begin{aligned}& \mathcal{H}_{\mathfrak{d}} \bigl(\mathcal{F}(t,u_{1},u_{2},u_{3},u_{4},u_{5}), \mathcal{F}(t,v_{1},v_{2},v_{3},v_{4},v_{5}) \bigr)\\& \quad \le \frac{1}{\boldsymbol{\Im _{1}}+\boldsymbol{\Im _{2}}+\boldsymbol{\Im _{3}}+\boldsymbol{\Im _{4_{1}}}+\boldsymbol{\Im _{4_{2}}}} \mho (t)\psi \Biggl(\sum _{i=1}^{5} \vert u_{k}-v_{k} \vert \Biggr){ ,} \end{aligned}$$

thus \(\exists w \in \mathcal{F}(t,l(t),l'(t),l''(t),^{c}\mathcal{D}_{q}^{ \hbar _{1}}l(t),^{c}\mathcal{D}_{q}^{\hbar _{2}}l(t))\) such that \(\forall t\in \mathfrak{J}\):

$$ \bigl\vert \mathfrak{f}_{1}(t)-w \bigr\vert \le \frac{1}{\boldsymbol{\Im _{1}}+\boldsymbol{\Im _{2}}+\boldsymbol{\Im _{3}}+\boldsymbol{\Im _{4_{1}}}+\boldsymbol{\Im _{4_{2}}}} \mho (t)\psi \Biggl(\sum_{i=1}^{5} \vert u_{k}-v_{k} \vert \Biggr). $$

Regard the set-valued map \(\boldsymbol{\mathfrak{N}}:\mathfrak{J}\to \mathcal{P}(\mathbb{R})\) by

$$ \boldsymbol{\mathfrak{N}}(t)=\Biggl\{ w\in \mathbb{R}: \bigl\vert \mathfrak{f}_{1}(t)-w \bigr\vert \le \frac{1}{\boldsymbol{\Im _{1}}+\boldsymbol{\Im _{2}}+\boldsymbol{\Im _{3}}+\boldsymbol{\Im _{4_{1}}}+\boldsymbol{\Im _{4_{2}}}} \mho (t) \psi \Biggl(\sum_{i=1}^{5} \vert u_{k}-v_{k} \vert \Biggr)\Biggr\} . $$

Since \(\frac{1}{\boldsymbol{\Im _{1}}+\boldsymbol{\Im _{2}}+\boldsymbol{\Im _{3}}+\boldsymbol{\Im _{4_{1}}}+\boldsymbol{\Im _{4_{2}}}} \mho (t)\psi (\sum_{i=1}^{5}\vert u_{k}-v_{k}\vert )\) and \(\mathfrak{f}_{1}\) are measurable, hence the set-valued map \(\boldsymbol{\mathfrak{N}}(\cdot)\cap \mathcal{F}(\cdot,l(\cdot),l'(\cdot),l''(\cdot),^{c} \mathcal{D}_{q}^{\hbar _{1}}l(\cdot),^{c}\mathcal{D}_{q}^{\hbar _{2}}l(\cdot))\) is measurable.

Choose \(\mathfrak{f}_{2}(t) \in \mathcal{F}(t,l(t),l'(t),l''(t),^{c} \mathcal{D}_{q}^{\hbar _{1}}l(t),^{c}\mathcal{D}_{q}^{\hbar _{2}}l(t))\) such that \(\forall t\in \mathfrak{J}\)

$$ \bigl\vert \mathfrak{f}_{1}(t)-\mathfrak{f}_{2}(t) \bigr\vert \le \frac{1}{\boldsymbol{\Im _{1}}+\boldsymbol{\Im _{2}}+\boldsymbol{\Im _{3}}+\boldsymbol{\Im _{4_{1}}}+\boldsymbol{\Im _{4_{2}}}} \mho (t)\psi \Biggl(\sum _{i=1}^{5} \vert u_{k}-v_{k} \vert \Biggr). $$

Now, for all \(t\in \mathfrak{J}\), let \(\mathfrak{p}_{2}\in \boldsymbol{\mathfrak{M}}(\boldsymbol{k})\) by

$$ \mathfrak{p}_{2}=\mathcal{I}^{\pounds }_{q} \mathfrak{f}_{2}(t)+\theta \mathfrak{B}_{1}(t) \mathcal{I}^{\pounds }_{q}\mathfrak{f}_{2}(\eth )+ \theta \mathfrak{B}_{2}(t)\mathcal{I}^{\pounds }_{q} \bigl[\mathfrak{I}^{ \pounds }_{q}\mathfrak{f}_{2}(r) \bigr](1)+\theta \mathfrak{B}_{3}(t) \mathcal{I}^{\pounds -2}_{q} \mathfrak{f}_{2}(1). $$

Afterwards, let \(\sup_{t \in \mathfrak{J}}\vert \mho (t)\vert =\Vert \mho \Vert \), so

$$\begin{aligned} \bigl\vert \mathfrak{p}_{1}(t)-\mathfrak{p}_{2}(t) \bigr\vert \le{} & \mathcal{I}^{ \pounds }_{q}[ \mathfrak{f}_{1}-\mathfrak{f}_{2}](t)+\theta \mathfrak{B}_{1}(t)\mathcal{I}^{\pounds }_{q}[ \mathfrak{f}_{1}- \mathfrak{f}_{2}](\eth ) \\ &{}+\theta \mathfrak{B}_{2}(t)\mathcal{I}^{\pounds }_{q} \bigl[\mathfrak{I}^{ \pounds }_{q}[\mathfrak{f}_{1}- \mathfrak{f}_{2}](r)\bigr](1) + \theta \mathfrak{B}_{3}(t) \mathcal{I}^{\pounds -2}_{q}[\mathfrak{f}_{1}- \mathfrak{f}_{2}](1) \\ \le{}& \frac{1}{\boldsymbol{\Im _{1}}+\boldsymbol{\Im _{2}}+\boldsymbol{\Im _{3}}+\boldsymbol{\Im _{4_{1}}}+\boldsymbol{\Im _{4_{2}}}} \Vert \mho \Vert \psi \bigl( \Vert u-v \Vert \bigr) \biggl[ \frac{1}{\Gamma _{q}(\pounds +1)}+ \frac{ \vert \theta \vert \mathfrak{B}^{*}_{1}}{\Gamma _{q}(\pounds +1)} \eth ^{\pounds } \\ &{}+ \frac{ \vert \theta \vert \mathfrak{B}^{*}_{2}}{\Gamma _{q}(\pounds +2)}+ \frac{ \vert \theta \vert \mathfrak{B}^{*}_{3}}{\Gamma _{q}(\pounds -1)} \biggr]= \frac{\boldsymbol{\Im _{1}}}{\boldsymbol{\Im _{1}}+\boldsymbol{\Im _{2}}+\boldsymbol{\Im _{3}}+\boldsymbol{\Im _{4_{1}}}+\boldsymbol{\Im _{4_{2}}}} \psi \bigl( \Vert u-v \Vert \bigr). \end{aligned}$$

Also,

$$\begin{aligned} \bigl\vert \mathfrak{p'}_{1}(t)- \mathfrak{p'}_{2}(t) \bigr\vert \le{}& \frac{1}{\boldsymbol{\Im _{1}}+\boldsymbol{\Im _{2}}+\boldsymbol{\Im _{3}}+\boldsymbol{\Im _{4_{1}}}+\boldsymbol{\Im _{4_{2}}}} \Vert \mho \Vert \psi \bigl( \Vert u-v \Vert \bigr) \biggl[ \frac{1}{\Gamma _{q}(\pounds -1)}+ \frac{ \vert \theta \vert \mathfrak{B}^{*'}_{1}}{\Gamma _{q}(\pounds +1)} \eth ^{\pounds } \\ &{}+ \frac{ \vert \theta \vert \mathfrak{B}^{*'}_{2}}{\Gamma _{q}(\pounds +2)}+ \frac{ \vert \theta \vert \mathfrak{B}^{*'}_{3}}{\Gamma _{q}(\pounds -1)} \biggr]= \frac{\boldsymbol{\Im _{2}}}{\boldsymbol{\Im _{1}}+\boldsymbol{\Im _{2}}+\boldsymbol{\Im _{3}}+\boldsymbol{\Im _{4_{1}}}+\boldsymbol{\Im _{4_{2}}}} \psi \bigl( \Vert u-v \Vert \bigr), \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \bigl\vert \mathfrak{p''}_{1}(t)- \mathfrak{p''}_{2}(t) \bigr\vert \le{}& \frac{1}{\boldsymbol{\Im _{1}}+\boldsymbol{\Im _{2}}+\boldsymbol{\Im _{3}}+\boldsymbol{\Im _{4_{1}}}+\boldsymbol{\Im _{4_{2}}}} \Vert \mho \Vert \psi \bigl( \Vert u-v \Vert \bigr) \biggl[ \frac{1}{\Gamma _{q}(\pounds -2)}+ \frac{ \vert \theta \vert \mathfrak{B}^{*''}_{1}}{\Gamma _{q}(\pounds +1)} \eth ^{\pounds } \\ &{}+ \frac{ \vert \theta \vert \mathfrak{B}^{*''}_{2}}{\Gamma _{q}(\pounds +2)}+ \frac{ \vert \theta \vert \mathfrak{B}^{*''}_{3}}{\Gamma _{q}(\pounds -1)} \biggr]= \frac{\boldsymbol{\Im _{3}}}{\boldsymbol{\Im _{1}}+\boldsymbol{\Im _{2}}+\boldsymbol{\Im _{3}}+\boldsymbol{\Im _{4_{1}}}+\boldsymbol{\Im _{4_{2}}}} \psi \bigl( \Vert u-v \Vert \bigr){.} \end{aligned} \end{aligned}$$

Moreover, for \(i=1,2\), we have

$$\begin{aligned} &\bigl\vert ^{c}\mathcal{D}_{q}^{\hbar _{i}} \mathfrak{f}_{1}(t)-^{c} \mathcal{D}_{q}^{\hbar _{i}} \mathfrak{f}_{2}(t) \bigr\vert \\ &\quad \le \frac{1}{\boldsymbol{\Im _{1}}+\boldsymbol{\Im _{2}}+\boldsymbol{\Im _{3}}+\boldsymbol{\Im _{4_{1}}}+\boldsymbol{\Im _{4_{2}}}} \Vert \mho \Vert \psi \bigl( \Vert u-v \Vert \bigr) \biggl[ \frac{1}{\Gamma _{q}(\pounds -\hslash _{i}+1)}+ \frac{ \vert \theta \vert \mathfrak{B}^{**}_{1}}{\Gamma _{q}(\pounds +1)} \eth ^{\pounds } \\ &\qquad {}+ \frac{ \vert \theta \vert \mathfrak{B}^{**}_{2}}{\Gamma _{q}(\pounds +2)}+ \frac{ \vert \theta \vert \mathfrak{B}^{**}_{3}}{\Gamma _{q}(\pounds -1)} \biggr]= \frac{\boldsymbol{\Im _{4_{i}}}}{\boldsymbol{\Im _{1}}+\boldsymbol{\Im _{2}}+\boldsymbol{\Im _{3}}+\boldsymbol{\Im _{4_{1}}}+\boldsymbol{\Im _{4_{2}}}} \psi \bigl( \Vert u-v \Vert \bigr). \end{aligned}$$

Finally, according to the above relations, it can be concluded that

$$\begin{aligned} \Vert \mathfrak{p}_{1}-\mathfrak{p}_{2} \Vert ={}& \sup_{t \in \mathfrak{J}} \bigl\vert \mathfrak{p}_{1}(t)- \mathfrak{p}_{2}(t) \bigr\vert + \sup_{t \in \mathfrak{J}} \bigl\vert \mathfrak{p'}_{1}(t)-\mathfrak{p'}_{2}(t) \bigr\vert +\sup_{t \in \mathfrak{J}} \bigl\vert \mathfrak{p''}_{1}(t)- \mathfrak{p''}_{2}(t) \bigr\vert \\ &{}+ \sup_{t \in \mathfrak{J}} \bigl\vert ^{c} \mathcal{D}_{q}^{\hbar _{1}} \mathfrak{f}_{1}(t)-^{c} \mathcal{D}_{q}^{\hbar _{1}}\mathfrak{f}_{2}(t) \bigr\vert +\sup_{t \in \mathfrak{J}} \bigl\vert ^{c} \mathcal{D}_{q}^{\hbar _{2}} \mathfrak{f}_{1}(t)-^{c} \mathcal{D}_{q}^{\hbar _{2}}\mathfrak{f}_{2}(t) \bigr\vert \\ \le{}& \frac{1}{\boldsymbol{\Im _{1}}+\boldsymbol{\Im _{2}}+\boldsymbol{\Im _{3}}+\boldsymbol{\Im _{4_{1}}}+\boldsymbol{\Im _{4_{2}}}} \psi \bigl( \Vert u-v \Vert \bigr) (\boldsymbol{ \Im _{1}}+\boldsymbol{\Im _{2}}+ \boldsymbol{\Im _{3}}+\boldsymbol{\Im _{4_{1}}}+ \boldsymbol{\Im _{4_{2}}})\\ ={}&\psi \bigl( \Vert u-v \Vert \bigr), \end{aligned}$$

so \(\mathcal{H}_{\mathfrak{d}} (\boldsymbol{\mathfrak{M}}(u), \boldsymbol{\mathfrak{M}}(v) )\le \psi (\Vert u-v\Vert )\) for all \(u,v \in \mathcal{K}\).

Using Lemma 2.13 and the endpoint property of \(\boldsymbol{\mathfrak{M}}\), there exists \(u^{*} \in \mathcal{K}\) such that \(\boldsymbol{\mathfrak{M}}(u^{*})=\{u^{*}\}\). Thereupon, \(u^{*}\) is a solution for quantum inclusion problem (1)–(2). □

4 Illustrative examples

To better understand our main result, we give an example in this section.

Example 4.1

Consider the nonlinear second order differential equation:

$$ \textstyle\begin{cases} ^{c}\mathcal{D}_{q}^{\frac{5}{2}}l(t) \in \mathcal{F} [0, \frac{3t^{2}}{50(1+t^{2})}\sin l(t)+\frac{3}{50}\cos l'(t)+ \frac{3}{50}\frac{ \vert l''(t) \vert }{1+ \vert l''(t) \vert }+ \frac{3}{50} \frac{e^{ \vert ^{c}\mathcal{D}_{q}^{\frac{3}{2}}l(t) \vert }}{1+e^{ \vert ^{c}\mathcal{D}_{q}^{\frac{3}{2}}l(t) \vert }} ], \\ l(0)+2l'(0)=0, \\ \frac{11}{100}l(\frac{3}{50})+\frac{22}{100}\int _{0}^{1}l(t)\,dt =0, \\ \frac{1}{16}l''(1)+\frac{33}{100}\int _{0}^{1}l(t)\,dt =0, \end{cases} $$
(11)

such that \(t\in \mathfrak{J}=[0,1]\). Regard the multifunction \(\mathcal{F}:\mathfrak{J}\times \mathbb{R}^{4}\to \mathcal{P}_{cp}( \mathbb{R})\) as follows:

$$\begin{aligned}& \mathcal{F}(t,u_{1},u_{2},u_{3},u_{4})\\& \quad = \biggl[0, \frac{3t^{2}}{50(1+t^{2})}\sin u_{1}(t)+\frac{3}{50} \cos u_{2}(t)+ \frac{3}{50}\frac{ \vert u_{3}(t) \vert }{1+ \vert u_{3}(t) \vert }+ \frac{3}{50} \frac{e^{ \vert u_{4}(t) \vert }}{1+e^{ \vert u_{4}(t) \vert }} \biggr]. \end{aligned}$$

In this case it is clear that we set: \(\pounds =\frac{5}{2}\), \(\hslash _{1}=\frac{3}{2}\), \(a=\frac{11}{100}\), \(b=\frac{22}{100}\), \(c=\frac{33}{100}\), \(\eth =\frac{3}{50}\), \({\boldsymbol{S}}=\sum_{j=0}^{4}u_{j}=2\) by \(u_{j}=\frac{1}{2}\), \({\boldsymbol{P}}=\prod_{j=0}^{j=k}w_{j}=\frac{1}{16}\) by \(w_{j}=\frac{1}{2}\), and about functions ℧, ψ, we have \(\mho :[0,1]\to [0,\infty )\) with \(\mho (t)=\frac{5}{70}t\), \(\Vert \mho \Vert =\frac{5}{70}\), and \(\psi (t)=\frac{t}{8}\). It is obvious that ψ is nondecreasing (usc) on \(\mathfrak{J}\). Hence, we have

$$\begin{aligned} \theta ={}& \biggl[\biggl(2{\boldsymbol{P}}+\frac{c}{3}\biggr) \biggl(a \eth + \frac{b}{2}-{\boldsymbol{S}}(a+b) \biggr)-c\biggl(a\eth ^{2}+ \frac{b}{3}\biggr) \biggl(\frac{1}{2}-{ \boldsymbol{S}}\biggr) \biggr]^{-1} \\ ={}& \biggl[\biggl(2\frac{1}{16}+\frac{11}{100}\biggr) \biggl( \frac{11}{100}\frac{3}{50}+ \frac{11}{100}-2\biggl( \frac{11}{100}+\frac{22}{100}\biggr) \biggr)\\ &{}-\frac{33}{100} \biggl( \frac{11}{100}\biggl(\frac{3}{50}\biggr)^{2}+ \frac{22}{300}\biggr) \biggl(\frac{1}{2}-2\biggr) \biggr]^{-1} \\ ={}& 4.21. \end{aligned}$$

In the same way, we can write

$$\begin{aligned} \mathfrak{B}^{*}_{1} &= \vert a \vert \biggl(2 \vert {\boldsymbol{P}} \vert +\frac{ \vert c \vert }{3} \biggr) \vert { \boldsymbol{S}}+1 \vert + \vert c \vert \biggl\vert \frac{1}{2}+ \vert { \boldsymbol{S}} \vert \biggr\vert \\ &= \frac{11}{100} \biggl(2\frac{1}{16}+\frac{11}{100} \biggr) (3)+ \frac{33}{100}\frac{5}{2}=0.9025. \end{aligned}$$

Also,

$$ \textstyle\begin{cases} \mathfrak{B}^{*}_{1}=0.9025,\qquad \mathfrak{B}^{*}_{2}=0.6947,\qquad \mathfrak{B}^{*}_{3}=0.0623, \\ \mathfrak{B}^{*'}_{1}=0.0968,\qquad \mathfrak{B}^{*'}_{2}=0.9774,\qquad \mathfrak{B}^{*'}_{3}=0.1016, \\ \mathfrak{B}^{*''}_{1}=0.9075, \qquad \mathfrak{B}^{*''}_{2}=0.8755,\qquad \mathfrak{B}^{*''}_{3}=0.0970. \end{cases} $$

By using Algorithm 1 and Table 1 for \(q=\frac{1}{5}\), we have

$$ \textstyle\begin{cases} \mathfrak{B}^{**}_{1}=0.0060 [\frac{1}{\Gamma _{q}(\frac{1}{2})} ]+0.1815 [\frac{1}{\Gamma _{q}(\frac{3}{2})} ]=0.2828, \\ \mathfrak{B}^{**}_{2}=0.1018 [\frac{1}{\Gamma _{q}(\frac{1}{2})} ]+0.8755 [\frac{1}{\Gamma _{q}(\frac{3}{2})} ]=0.7830, \\ \mathfrak{B}^{**}_{3}=0.0046 [\frac{1}{\Gamma _{q}(\frac{1}{2})} ]+0.0970 [\frac{1}{\Gamma _{q}(\frac{3}{2})} ]=0.0918. \end{cases} $$

In the same way, one can compute for \(q=\frac{1}{5}\) and get \(\boldsymbol{\Im _{1}}=0.1957\), \(\boldsymbol{\Im _{2}}=0.2678\), \(\boldsymbol{\Im _{3}}=0.2643\), \(\boldsymbol{\Im _{4}}=0.2377\). Then it is easy to review that

$$ \mathcal{H}_{\mathfrak{d}} \bigl(\mathcal{F}(t,u_{1},u_{2},u_{3},u_{4}), \mathcal{F}(t,v_{1},v_{2},v_{3},v_{4}) \bigr)\le \frac{1}{\boldsymbol{\Im _{1}}+\boldsymbol{\Im _{2}}+\boldsymbol{\Im _{3}}+\boldsymbol{\Im _{4}}} \mho (t)\psi \Biggl(\sum _{i=1}^{4} \vert u_{k}-v_{k} \vert \Biggr){ ,} $$

and \(\inf_{u\in \mathcal{K}} (\sup_{v \in \mathfrak{M}(u)}\Vert u-v \Vert )=0\). Hence, by the endpoint property and using Theorem 3.3, inclusion problem (11) has a solution. In Figs. 3 and 4 some of the functions in Example 4.1 are illustrated.

Figure 3
figure 3

The graph of \(\mathcal{F}(t,l(t))\)

Full size image
Figure 4
figure 4

The graph of \(\mathcal{F}(l'(t),l''(t))\)

Full size image

5 Conclusion

Understanding and interpreting physical phenomena have always been one of the topics of interest to researchers. Attempts to provide a better explanation of these phenomena have led to progress in various scientific fields and the connection between them. Quantum calculus, as an interdisciplinary subject in mathematics and physics, is one of the tools of modeling and approximation. In this paper, we investigated a quantum differential inclusion problem using the endpoint property technique with the new boundary conditions. One illustrative example and some numerical results have been provided to validate our results and to show their importance.