1 Introduction

Fractional-order systems are dynamical systems that can be modeled by a fractional differential equation carried with a non-integer derivative. Recently, much research work was focused on such a concept, for example [1–3]. Indeed, the authors in [1] have presented the problem of the existence and uniqueness of solutions of boundary value problems (BVPs) for a nonlinear fractional differential equation of order \(2<\alpha <3\). In addition, the work in [2] has concentrated on solution of fractional differential equations via coupled fixed point. Furthermore, Badr Alqahtani et al. in [3] have suggested a solution for Volterra fractional integral equations by hybrid contractions.

Since the middle of the last century, the control theory has been subject to a revolution and a very huge amount of research work in the literature. A great majority of work, established until now, has focused on the classical integer-order systems, modeled with differential equations where an integer-order derivative is used. Meanwhile, with the development of science and applied mathematics, it has been discovered that several physical systems are really described with differential fractional-order equations, where a fractional derivative order is used. Consequently, such systems cannot be effectively modeled using the classical differential integer-order equations. As a result to this fact, a growing interest is being given by researchers in the last few decades, to investigate fractional-order systems and various problems inside the control theory, such as state estimation, control, finite-time stability and fault diagnosis, are being tackled. Note that, compared to the integer-order case, the fractional-order framework represents a fertile field of research, since it has been “recently” addressed by researchers and several specific questions are still to investigate for fractional-order systems.

In the literature, many researchers have been studied the stability of the solution for fractional-order system (see [10–12] and [17–19]). In some cases, however, it is advantageous that a dynamical system has the finite-time stability (FTS) property which plays an essential issue in the analysis of the transient behavior of systems. The FTS can be divided into two types. The stability of a system on a finite-time interval is studied; see [4, 5, 7, 9, 13] and [15] and [20–23]. The other work can be described as the trajectories of the system converges on a finite-time interval to the equilibrium point; see [16].

The main contribution of this research work is to deal with the FTS of a class of linear stochastic fractional-order systems with time delay for \(\alpha \in (\frac{1}{2},1)\) using the generalized Gronwall inequality and the classical techniques of the stochastic analysis.

The structure of the paper is organized as follows. In Sect. 2, we introduce some hypotheses and classical notions. In Sect. 3, by applying the generalized Gronwall inequality, the FTS of linear stochastic fractional-order systems with time delay is studied. In Sect. 4, we give two illustrative examples to show our theory.

2 Preliminaries and definitions

In this section, we introduce some basic notions and definitions which are useful for our results. For more details see [6] and [14].

Let \(\{X,\mathcal{F}, (\mathcal{F}_{t})_{t\geq 0},\mathbb{P}\}\) be a complete probability space with a filtration fulfilling the usual conditions. \(W(t)\) is a 1-dimensional Brownian motion defined on the probability space.

Let \(C([-\tau , 0];\mathbb{R}^{n})\) be the space of the continuous functions \(\overline{\varphi }:[-\tau , 0]\rightarrow \mathbb{R}^{n}\) with the norm \(\|\overline{\varphi }\|= \sup_{-\tau \leq s\leq 0}\| \overline{\varphi }(s)\|\) where \(\|\lambda \|=\sqrt{\lambda ^{T}\lambda }\) for any \(\lambda \in \mathbb{R}^{n}\). Consider the linear stochastic fractional-order time delay systems of the form

$$ {}^{C}D_{0,t}^{\alpha } y(t)=Ay(t)\,dt+By(t-\nu )\,dt + Cy(t-\nu )\,dW(t), $$
(2.1)

where the initial condition is \(\{x(t), -\nu \leq t\leq 0\}=\overline{\varphi }(t)\in \mathbb{R}^{n}\).

\({}^{C}D_{0,t}^{\alpha }\) denotes the operator of the Caputo fractional derivative (CFD) of order \(\frac{1}{2}<\alpha <1\); \(A;B;C\in \mathbb{R}^{n\times n}\).

Definition 2.1

Given \(0<\eta <1\). The CFD is defined as

$$ {}^{C}D_{0,s}^{\eta } x(s)= \frac{1}{\Gamma (1-\eta )} \frac{d}{ds} \int _{0}^{s} (s-\zeta )^{-\eta } \bigl(x(\zeta )-x(0) \bigr)\,d\zeta . $$
(2.2)

Definition 2.2

The Mittag-Leffler function (MLF) in two parameters is defined by

$$ E_{\beta ,\mu }(z)= \sum_{m\geq 0} \frac{z^{m}}{\Gamma (m \beta +\mu )}, $$
(2.3)

where \(\beta >0\), \(\mu >0\) \(z\in \mathbb{C}\).

Remark 2.1

For \(\mu =1\), \(E_{\beta ,1}=E_{\beta }\) and \(E_{1,1}(z)=\exp (z)\).

Definition 2.3

System (2.1) is finite-time stochastically stable (FTSS) w.r.t. \(\{\delta , \varepsilon , T\}\), \(\delta < \varepsilon \), if

$$ {\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}< \delta } $$

implying

$$ \mathbb{E} \bigl\Vert y(t) \bigr\Vert ^{2}< \varepsilon , \quad \forall t\in [0,T]. $$

3 Main results

Let \(T>\nu \) and \(m\in \mathbb{N}\) with \((m+1)\nu < T\leq (m+2)\nu \).

Theorem 3.1

System (2.1) is FTSS with respect to \((\delta ,\varepsilon ,T)\), if the following condition is fulfilled:

$$ l_{T}(\nu )\leq \frac{\varepsilon }{\delta }, $$
(3.1)

with

$$\begin{aligned}& l_{T}(\nu )= \biggl[4+\frac{M_{1}}{2}\bigl(1-e^{-2T} \bigr)l_{m+1}(\nu )+M_{2} \frac{T^{2\alpha -1}}{2\alpha -1}l_{m+1}( \nu ) \biggr]e^{(M_{3}+2)T}, \\& l_{k+1}(\nu )= \biggl[4+\frac{M_{1}}{2}\bigl(1-e^{-2(k+1)\nu } \bigr)l_{k}(\nu )+M_{2} \frac{((k+1)\nu )^{2\alpha -1}}{2\alpha -1}l_{k}( \nu ) \biggr]e^{(M_{3}+2)(k+1) \nu }, \end{aligned}$$

for \(k\in [0,m]\), \({l_{0}(\nu )=1}\), \({M_{1}= \frac{8\Gamma (2\alpha -1)}{4^{\alpha }\Gamma ^{2}(\alpha )}\|B\|^{2}}\), \({M_{2}=\frac{4}{\Gamma ^{2}(\alpha )}\|C\|^{2}}\) and \(M_{3}={ \frac{8\Gamma (2\alpha -1)}{4^{\alpha }\Gamma ^{2}(\alpha )}\|A\|^{2}}\).

Proof

The solution of the system (2.1) satisfies the following equation:

$$\begin{aligned} y(t) =&y(0)+\frac{1}{\Gamma (\alpha )} \int _{0}^{t}(t-s)^{\alpha -1}Ay(s)\,ds+ \frac{1}{\Gamma (\alpha )} \int _{0}^{t}(t-s)^{\alpha -1}By(s-\nu )\,ds \\ &{}+\frac{1}{\Gamma (\alpha )} \int _{0}^{t}(t-s)^{\alpha -1}Cy(s-\nu )\,dW(s). \end{aligned}$$
(3.2)

Using the Cauchy–Schwartz inequality, we get

$$\begin{aligned} \bigl\Vert y(t) \bigr\Vert ^{2} \leq &4 \Vert \overline{\varphi } \Vert ^{2}+ \frac{4}{\Gamma ^{2}(\alpha )} \biggl[ \biggl( \int _{0}^{t}(t-s)^{ \alpha -1} \Vert A \Vert \bigl\Vert y(s) \bigr\Vert \,ds \biggr)^{2} \\ &{}+ \biggl( \int _{0}^{t}(t-s)^{ \alpha -1} \Vert B \Vert \bigl\Vert y(s-\nu ) \bigr\Vert \,ds \biggr)^{2} \biggr] \\ &{}+\frac{4}{\Gamma ^{2}(\alpha )} \biggl\Vert \int _{0}^{t}(t-s)^{\alpha -1}Cy(s- \nu )\,dW(s) \biggr\Vert ^{2} \\ \leq &4 \Vert \overline{\varphi } \Vert ^{2}+\frac{4}{\Gamma ^{2}(\alpha )} \biggl( \int _{0}^{t}e^{2s}(t-s)^{2\alpha -2}\,ds \biggr) \biggl[ \int _{0}^{t}e^{-2s} \Vert A \Vert ^{2} \bigl\Vert y(s) \bigr\Vert ^{2}\,ds \\ &{}+ \int _{0}^{t}e^{-2s} \Vert B \Vert ^{2} \bigl\Vert y(s-\nu ) \bigr\Vert ^{2}\,ds \biggr] \\ &{}+\frac{4}{\Gamma ^{2}(\alpha )} \biggl\Vert \int _{0}^{t}(t-s)^{\alpha -1}Cy(s- \nu )\,dW(s) \biggr\Vert ^{2}. \end{aligned}$$

Taking the expectation on the two sides, one has

$$\begin{aligned} \mathbb{E} \bigl\Vert y(t) \bigr\Vert ^{2} \leq &4\mathbb{E} \Vert \overline{\varphi } \Vert ^{2} \\ &{}+ \frac{8\Gamma (2\alpha -1)}{\Gamma ^{2}(\alpha )4^{\alpha }}e^{2t} \biggl[ \int _{0}^{t}e^{-2s} \Vert A \Vert ^{2}\mathbb{E} \bigl\Vert y(s) \bigr\Vert ^{2}\,ds+ \int _{0}^{t}e^{-2s} \Vert B \Vert ^{2}\mathbb{E} \bigl\Vert y(s-\nu ) \bigr\Vert ^{2}\,ds \biggr] \\ &{}+\frac{4}{\Gamma ^{2}(\alpha )} \int _{0}^{t}(t-s)^{2\alpha -2} \Vert C \Vert ^{2} \mathbb{E} \bigl\Vert y(s-\nu ) \bigr\Vert ^{2}\,ds. \end{aligned}$$

Then

$$\begin{aligned} \mathbb{E} \bigl\Vert y(t) \bigr\Vert ^{2} \leq& 4\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+M_{1}e^{2t} \int _{0}^{t}e^{-2s}\mathbb{E} \bigl\Vert y(s-\nu ) \bigr\Vert ^{2}\,ds \\ &{}+M_{2} \int _{0}^{t}(t-s)^{2 \alpha -2}\mathbb{E} \bigl\Vert y(s-\nu ) \bigr\Vert ^{2}\,ds \\ &{}+M_{3}e^{2t} \int _{0}^{t}e^{-2s}\mathbb{E} \bigl\Vert y(s) \bigr\Vert ^{2}\,ds, \end{aligned}$$
(3.3)

where \({M_{1}= \frac{8\Gamma (2\alpha -1)}{4^{\alpha }\Gamma ^{2}(\alpha )}\|B\|^{2}}\), \({M_{2}=\frac{4}{\Gamma ^{2}(\alpha )}\|C\|^{2}}\) and \(M_{3}={ \frac{8\Gamma (2\alpha -1)}{4^{\alpha }\Gamma ^{2}(\alpha )}\|A\|^{2}}\).

Thus,

$$\begin{aligned} e^{-2t}\mathbb{E} \bigl\Vert y(t) \bigr\Vert ^{2} \leq& 4 \mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+M_{1} \int _{0}^{t}e^{-2s}\mathbb{E} \bigl\Vert y(s-\nu ) \bigr\Vert ^{2}\,ds \\ &{}+M_{2} \int _{0}^{t}(t-s)^{2 \alpha -2}\mathbb{E} \bigl\Vert y(s-\nu ) \bigr\Vert ^{2}\,ds \\ &{}+M_{3} \int _{0}^{t}e^{-2s}\mathbb{E} \bigl\Vert y(s) \bigr\Vert ^{2}\,ds, \end{aligned}$$
(3.4)

For \(t\in [0,\nu ]\), we obtain

$$\begin{aligned} e^{-2t}\mathbb{E} \bigl\Vert y(t) \bigr\Vert ^{2} \leq &4\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+M_{1} \int _{0}^{t}e^{-2s}\mathbb{E} \bigl\Vert y(s-\nu ) \bigr\Vert ^{2}\,ds \\ &{}+M_{2} \int _{0}^{t}(t-s)^{2\alpha -2}\mathbb{E} \bigl\Vert y(s-\nu ) \bigr\Vert ^{2}\,ds \\ &{}+M_{3} \int _{0}^{t}e^{-2s}\mathbb{E} \bigl\Vert y(s) \bigr\Vert ^{2}\,ds \\ \leq &4\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+ \frac{M_{1}}{2}\bigl(1-e^{-2t}\bigr) \mathbb{E} \Vert \overline{ \varphi } \Vert ^{2}+ \frac{M_{2}t^{2\alpha -1}}{2\alpha -1}\mathbb{E} \Vert \overline{ \varphi } \Vert ^{2} \\ &{}+M_{3} \int _{0}^{t}e^{-2s}\mathbb{E} \bigl\Vert y(s) \bigr\Vert ^{2}\,ds \\ \leq & \biggl(4+\frac{M_{1}}{2}\bigl(1-e^{-2\nu }\bigr)+ \frac{M_{2}\nu ^{2\alpha -1}}{2\alpha -1} \biggr)\mathbb{E} \Vert \overline{\varphi } \Vert ^{2} \\ &{}+M_{3} \int _{0}^{t}e^{-2s}\mathbb{E} \bigl\Vert y(s) \bigr\Vert ^{2}\,ds. \end{aligned}$$

By the Gronwall inequality, we have

$$ e^{-2t}\mathbb{E} \bigl\Vert y(t) \bigr\Vert ^{2}\leq \biggl(4+\frac{M_{1}}{2}\bigl(1-e^{-2 \nu }\bigr)+\frac{M_{2}\nu ^{2\alpha -1}}{2\alpha -1} \biggr)e^{M_{3}t} \mathbb{E} \Vert \overline{\varphi } \Vert ^{2}. $$
(3.5)

Therefore, we obtain

$$\begin{aligned} \mathbb{E} \bigl\Vert y(t) \bigr\Vert ^{2} \leq & \biggl(4+ \frac{M_{1}}{2}\bigl(1-e^{-2\nu }\bigr)+ \frac{M_{2}\nu ^{2\alpha -1}}{2\alpha -1} \biggr)e^{(M_{3}+2)\nu } \mathbb{E} \Vert \overline{\varphi } \Vert ^{2} \\ \leq &l_{1}(\nu )\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}, \quad \forall t\in [0,\nu ], \end{aligned}$$

where \({l_{1}(\nu )= (4+\frac{M_{1}}{2}(1-e^{-2\nu })+ \frac{M_{2}\nu ^{2\alpha -1}}{2\alpha -1} )e^{(M_{3}+2)\nu }}\).

For \(t\in [\nu ,2\nu ]\), we have

$$\begin{aligned} e^{-2t}\mathbb{E} \bigl\Vert y(t) \bigr\Vert ^{2} \leq &4\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+ \frac{M_{1}}{2}\bigl(1-e^{-2t}\bigr)l_{1}(\nu )\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+\frac{M_{2}t^{2\alpha -1}}{2\alpha -1}l_{1}( \nu )\mathbb{E} \Vert \overline{\varphi } \Vert ^{2} \\ &{}+M_{3} \int _{0}^{t}e^{-2s}\mathbb{E} \bigl\Vert y(s) \bigr\Vert ^{2}\,ds \\ \leq & \biggl(4+\frac{M_{1}}{2}\bigl(1-e^{-2(2\nu )}\bigr)l_{1}( \nu )+ \frac{M_{2}(2\nu )^{2\alpha -1}}{2\alpha -1}l_{1}(\nu ) \biggr) \mathbb{E} \Vert \overline{\varphi } \Vert ^{2} \\ &{}+M_{3} \int _{0}^{t}e^{-2s}\mathbb{E} \bigl\Vert y(s) \bigr\Vert ^{2}\,ds. \end{aligned}$$

Using the Gronwall inequality, we get

$$ \mathbb{E} \bigl\Vert y(t) \bigr\Vert ^{2} e^{-2t} \leq \biggl(\frac{M_{1}}{2}\bigl(1-e^{-2(2 \nu )}\bigr)l_{1}(\nu )+4+ \frac{M_{2}(2\nu )^{2\alpha -1}}{2\alpha -1}l_{1}( \nu ) \biggr)\mathbb{E} \Vert \overline{ \varphi } \Vert ^{2}e^{M_{3}t}. $$
(3.6)

Therefore, we obtain

$$\begin{aligned} \mathbb{E} \bigl\Vert y(t) \bigr\Vert ^{2} \leq & \biggl(4+ \frac{M_{1}}{2}\bigl(1-e^{-2(2\nu )}\bigr)l_{1}( \nu )+ \frac{M_{2}(2\nu )^{2\alpha -1}}{2\alpha -1}l_{1}(\nu ) \biggr)e^{(M_{3}+2)(2 \nu )}\mathbb{E} \Vert \overline{\varphi } \Vert ^{2} \\ \leq &l_{2}(\nu )\mathbb{E} \Vert \overline{\varphi } \Vert ^{2},\quad \forall t\in [0,\nu ], \end{aligned}$$

where \({l_{2}(\nu )= (4+\frac{M_{1}}{2}(1-e^{-2(2\nu )})l_{1}( \nu )+\frac{M_{2}(2\nu )^{2\alpha -1}}{2\alpha -1}l_{1}(\nu ) )e^{(M_{3}+2)(2 \nu )}}\).

For \(t\in [0,(k+1)\nu ]\), \(k\in [0,m]\), we have

$$\begin{aligned} e^{-2t}\mathbb{E} \bigl\Vert y(t) \bigr\Vert ^{2} \leq &4\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+ \frac{M_{1}}{2}\bigl(1-e^{-2t}\bigr)l_{k}(\nu )\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+\frac{M_{2}t^{2\alpha -1}}{2\alpha -1}l_{k}( \nu )\mathbb{E} \Vert \overline{\varphi } \Vert ^{2} \\ &{}+M_{3} \int _{0}^{t}e^{-2s}\mathbb{E} \bigl\Vert y(s) \bigr\Vert ^{2}\,ds \\ \leq & \biggl(4+\frac{M_{1}}{2}\bigl(1-e^{-2(k+1)\nu }\bigr)l_{k}( \nu )+ \frac{M_{2}((k+1)\nu )^{2\alpha -1}}{2\alpha -1}l_{k}(\nu ) \biggr) \mathbb{E} \Vert \overline{\varphi } \Vert ^{2} \\ &{}+M_{3} \int _{0}^{t}e^{-2s}\mathbb{E} \bigl\Vert y(s) \bigr\Vert ^{2}\,ds. \end{aligned}$$

Using the Gronwall inequality, we have

$$\begin{aligned}& e^{-2t}\mathbb{E} \bigl\Vert y(t) \bigr\Vert ^{2} \\& \quad \leq \biggl(4+\frac{M_{1}}{2}\bigl(1-e^{-2(k+1) \nu }\bigr)l_{k}(\nu )+ \frac{M_{2}((k+1)\nu )^{2\alpha -1}}{2\alpha -1}l_{k}( \nu ) \biggr)\mathbb{E} \Vert \overline{ \varphi } \Vert ^{2}e^{M_{3}t}. \end{aligned}$$
(3.7)

Therefore, we obtain

$$\begin{aligned} \mathbb{E} \bigl\Vert y(t) \bigr\Vert ^{2} \leq & \biggl(4+ \frac{M_{1}}{2}\bigl(1-e^{-2(1+k) \nu }\bigr)l_{k}(\nu )+ \frac{M_{2}((1+k)\nu )^{2\alpha -1}}{2\alpha -1}l_{k}( \nu ) \biggr)e^{(M_{3}+2)(1+k)\nu }\mathbb{E} \Vert \overline{\varphi } \Vert ^{2} \\ \leq &l_{k+1}(\nu )\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}, \quad \forall t\in \bigl[0,(1+k)\nu \bigr], \end{aligned}$$

where \({l_{k+1}(\nu )= (4+\frac{M_{1}}{2}(1-e^{-2(1+k)\nu })l_{k}( \nu )+\frac{M_{2}((1+k)\nu )^{2\alpha -1}}{2\alpha -1}l_{k}(\nu ) )e^{(M_{3}+2)(1+k)\nu }}\).

For all \(t\in [0,T]\), we get

$$ \mathbb{E} \bigl\Vert y(t) \bigr\Vert ^{2}\leq \biggl(4+ \frac{M_{1}}{2}\bigl(1-e^{-2T}\bigr)l_{m+1}( \nu )+M_{2}\frac{T^{2\alpha -1}}{2\alpha -1}l_{m+1}(\nu ) \biggr)e^{(M_{3}+2)T} \mathbb{E} \Vert \overline{\varphi } \Vert ^{2}, $$
(3.8)

which completes the proof. □

Remark 3.2

It is clear that \(l_{0}(\nu )\leq l_{1}(\nu )\leq \cdots \leq l_{T}(\nu )\).

Remark 3.3

In the case when \(0< T\leq \nu \), we obtain the FTS for the system (2.1) if we have the following condition:

$$ l_{T}(\nu )= \biggl[4+\frac{M_{1}}{2}\bigl(1-e^{-2T} \bigr)+M_{2} \frac{T^{2\alpha -1}}{2\alpha -1} \biggr]e^{(M_{3}+2)T}\leq \frac{\varepsilon }{\delta }. $$

Theorem 3.4

System (2.1) is FTSS with respect to \((\delta ,\varepsilon ,I)\), if the following condition \(\mathcal{A}\) is fulfilled:

$$ \max \bigl(e^{2\nu },4 \bigr)\exp \biggl[ \biggl( \frac{{M}_{1}+{M}_{3}}{2\alpha -1}+2 \biggr)T \biggr]E_{2\alpha -1} \bigl({M}_{2} \Gamma (2\alpha -1)T^{2\alpha -1} \bigr)\leq \frac{\varepsilon }{\delta }, $$
(3.9)

where \({M_{1}= \frac{8\Gamma (2\alpha -1)}{4^{\alpha }\Gamma ^{2}(\alpha )}\|B\|^{2}}\), \({M_{2}=\frac{4}{\Gamma ^{2}(\alpha )}\|C\|^{2}}\) and \(M_{3}={ \frac{8\Gamma (2\alpha -1)}{4^{\alpha }\Gamma ^{2}(\alpha )}\|A\|^{2}}\).

Proof

By inequality (3.3), we get the following estimation:

$$\begin{aligned} \mathbb{E} \bigl\Vert y(t) \bigr\Vert ^{2} \leq& 4\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+M_{1}e^{2t} \int _{0}^{t}e^{-2s}\mathbb{E} \bigl\Vert y(s-\nu ) \bigr\Vert ^{2}\,ds \\ &{}+M_{2} \int _{0}^{t}(t-s)^{2 \alpha -2}\mathbb{E} \bigl\Vert y(s-\nu ) \bigr\Vert ^{2}\,ds \\ &{}+M_{3}e^{2t} \int _{0}^{t}e^{-2s}\mathbb{E} \bigl\Vert y(s) \bigr\Vert ^{2}\,ds. \end{aligned}$$
(3.10)

Thus,

$$\begin{aligned} e^{-2t}\mathbb{E} \bigl\Vert y(t) \bigr\Vert ^{2} \leq &4\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+M_{1} \int _{0}^{t}e^{-2s}\mathbb{E} \bigl\Vert y(s-\nu ) \bigr\Vert ^{2}\,ds \\ &{}+M_{2}e^{-2t} \int _{0}^{t}(t-s)^{2\alpha -2}\mathbb{E} \bigl\Vert y(s-\nu ) \bigr\Vert ^{2}\,ds \\ &{}+M_{3} \int _{0}^{t}e^{-2s}\mathbb{E} \bigl\Vert y(s) \bigr\Vert ^{2}\,ds \\ \leq &4\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+M_{1} \int _{0}^{t}e^{-2s} \mathbb{E} \bigl\Vert y(s-\nu ) \bigr\Vert ^{2}\,ds \\ &{}+M_{2} \int _{0}^{t}(t-s)^{2\alpha -2}e^{-2s} \mathbb{E} \bigl\Vert y(s-\nu ) \bigr\Vert ^{2}\,ds \\ &{}+M_{3} \int _{0}^{t}e^{-2s}\mathbb{E} \bigl\Vert y(s) \bigr\Vert ^{2}\,ds. \end{aligned}$$

Let \({h(t)=e^{-2t}\mathbb{E}\|y(t)\|^{2}}\), then we obtain, \(\forall t\in [0,T]\),

$$\begin{aligned} h(t) \leq &4\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+M_{1}e^{-2\nu } \int _{0}^{t}h(s- \nu )\,ds+M_{2}e^{-2\nu } \int _{0}^{t}(t-s)^{2\alpha -2}h(s-\nu )\,ds \\ &{}+M_{3} \int _{0}^{t}h(s)\,ds \\ \leq &4\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+M_{1} \int _{0}^{t}h(s- \nu )\,ds+M_{2} \int _{0}^{t}(t-s)^{2\alpha -2}h(s-\nu )\,ds \\ &{}+M_{3} \int _{0}^{t}h(s)\,ds. \end{aligned}$$

Let \({g(t)=\sup_{\theta \in [-\nu ,t]}h(\theta )}\), for all \(t\in [0,T]\).

We have, \(\forall s\in [0,T]\), \({h(s)\leq g(s)}\) and \({h(s-\nu )\leq g(s)}\).

Thus, for all \(t\in [0,T]\), we obtain

$$ h(t)\leq 4\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+ (M_{1}+M_{3} ) \int _{0}^{t}g(s)\,ds+M_{2} \int _{0}^{t}(t-s)^{2\alpha -2}g(s)\,ds. $$

Therefore, using a change of variable \(v=t-s\), we have \(\forall \theta \in [0,t]\)

$$ h(\theta )\leq 4\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+ (M_{1}+M_{3} ) \int _{0}^{\theta }g(s)\,ds+M_{2} \int _{0}^{\theta }s^{2\alpha -2}g( \theta -s)\,ds. $$
(3.11)

\({\theta \mapsto \int _{0}^{\theta }s^{2\alpha -2}g( \theta -s)\,ds}\) and \({\theta \mapsto \int _{0}^{\theta }g(s)\,ds}\) are two increasing functions because g is non-negative and increasing. Thus, we have \(\forall \theta \in [0,t]\)

$$ h(\theta )\leq 4\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+ (M_{1}+M_{3} ) \int _{0}^{t}g(s)\,ds+M_{2} \int _{0}^{t}s^{2\alpha -2}g(t-s)\,ds. $$
(3.12)

Thus, we get \(\forall t\in [0,T]\)

$$\begin{aligned} g(t) \leq &\max \Bigl\{ \sup_{\theta \in [-\nu ,0]}h(\theta ),\sup _{ \theta \in [0,t]}h(\theta )\Bigr\} \\ \leq &\max \bigl\{ e^{2\nu },4\bigr\} \mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+ (M_{1}+M_{3} ) \int _{0}^{t}g(s)\,ds+M_{2} \int _{0}^{t}s^{2 \alpha -2}g(t-s)\,ds \\ \leq &\max \bigl\{ e^{2\nu },4\bigr\} \mathbb{E} \Vert \overline{\varphi } \Vert ^{2}+ (M_{1}+M_{3} ) \int _{0}^{t}g(s)\,ds+M_{2} \int _{0}^{t}(t-s)^{2 \alpha -2}g(s)\,ds. \end{aligned}$$

Using the generalized Gronwall inequality (Corollary 2.3 in [8]), for \(t\in [0,T]\), we get

$$ g(t)\leq \max \bigl(e^{2\nu },4 \bigr)\mathbb{E} \Vert \overline{ \varphi } \Vert ^{2}\exp \biggl[ ({M}_{1}+{M}_{3} ) \frac{t}{2\alpha -1} \biggr]E_{2\alpha -1} \bigl({M}_{2}\Gamma (2 \alpha -1)t^{2\alpha -1} \bigr). $$
(3.13)

Then, for all \(t\in [0,T]\), we obtain

$$ h(t)\leq \max \bigl(e^{2\nu },4 \bigr)\mathbb{E} \Vert \overline{ \varphi } \Vert ^{2}\exp \biggl[ ({M}_{1}+{M}_{3} ) \frac{t}{2\alpha -1} \biggr]E_{2\alpha -1} \bigl({M}_{2}\Gamma (2 \alpha -1)t^{2\alpha -1} \bigr). $$
(3.14)

Therefore, for all \(t\in [0,T]\), we have

$$\begin{aligned} \mathbb{E} \bigl\Vert y(t) \bigr\Vert ^{2} \leq &\max \bigl(e^{2\nu },4 \bigr)\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}\exp \biggl[ \biggl( \frac{{M}_{1}+{M}_{3}}{2\alpha -1}+2 \biggr)t \biggr]E_{2\alpha -1} \bigl({M}_{2}\Gamma (2\alpha -1)t^{2\alpha -1} \bigr) \\ \leq &\max \bigl(e^{2\nu },4 \bigr)\mathbb{E} \Vert \overline{\varphi } \Vert ^{2}\exp \biggl[ \biggl(\frac{{M}_{1}+{M}_{3}}{2\alpha -1}+2 \biggr)T \biggr]E_{2\alpha -1} \bigl({M}_{2}\Gamma (2\alpha -1)T^{2\alpha -1} \bigr). \end{aligned}$$

Then, if \({\mathbb{E}\|\overline{\varphi }\|^{2}<\delta }\) and condition \(\mathcal{A}\) hold, we have \({\mathbb{E}\|y(t)\|^{2}<\varepsilon , \forall t\in [0,T]}\).

The proof is therefore complete. □

4 Illustrative examples

Two illustrative examples, in this section, show the usefulness and interest of the main results.

Example 4.1

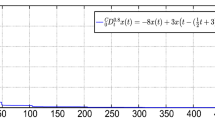
Consider the following system:

D 0 , t α C x ( t ) = ( 0.2 0 0 0.1 ) ( x 1 ( t ) x 2 ( t ) ) d t + ( 0.5 0 0 0.4 ) ( x 1 ( t − ν ) x 2 ( t − ν ) ) d t + ( 0.5 0 0 1 ) ( x 1 ( t − ν ) x 2 ( t − ν ) ) d W ( t ) ,
(4.1)

where the initial condition is

$$ x(t)=\varphi (t),\quad -\nu \leq t \leq 0. $$

It is easily to verify that \(\|A\| =0.2\), \(\|B\| = 0.5\), and \(\|C\| = 1\).

Let \(\delta =0.1\), \(\varepsilon =10\) and \(\nu =0.1\).

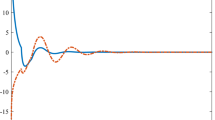
Based on the inequality (3.1) in Theorem 3.1 with \(\alpha = 0.9\), the calculated estimated time T of the system (4.2) is equal to \(T=0.3\), however, using Theorem 3.4, the computed estimated time T in inequality (3.9) is equal to \(T=0.23\).

Example 4.2

Consider the following system:

D 0 , t α C x ( t ) = ( 1 0 0 0.8 ) ( x 1 ( t ) x 2 ( t ) ) d t + ( 0.1 0 0 0.05 ) ( x 1 ( t − ν ) x 2 ( t − ν ) ) d t + ( 0.08 0 0 0.1 ) ( x 1 ( t − ν ) x 2 ( t − ν ) ) d W ( t ) ,
(4.2)

where the initial condition is

$$ x(t)=\varphi (t),\quad -\nu \leq t \leq 0. $$

It is easily to verify that \(\|A\| =1\), \(\|B\| = 0.1\), and \(\|C\| = 0.1\).

Let \(\delta =0.1\), \(\varepsilon =10\) and \(\nu =0.1\).

Based on the inequality (3.9) in Theorem 3.4 with \(\alpha = 0.6\), the calculated estimated time T of the system (4.1) is equal to \(T=1.27\), however, using Theorem 3.1, the computed estimated time T in inequality (3.1) is equal to \(T = 0.295\).

5 Conclusion

In this paper, finite-time stability of linear stochastic fractional-order systems with time delay has been investigated. Both the Gronwall lemma and stochastic calculus techniques have been used to study the finite-time stability. We have analyzed two illustrative examples to show the interest of our results. Note that the oldest two fractional derivatives in the literature are the Caputo derivative and the Riemann–Liouville fractional derivative. The choice of the Caputo derivative is addressed in our work because it is better for the stability analysis than the one defined by Riemann–Liouville. As a perspective of this work, an extension to other types of fractional derivative can be an interesting future research.