Approximation of linear one dimensional partial differential equations including fractional derivative with non-singular kernel

Abstract

In this article we propose a hybrid method based on a local meshless method and the Laplace transform for approximating the solution of linear one dimensional partial differential equations in the sense of the Caputo–Fabrizio fractional derivative. In our numerical scheme the Laplace transform is used to avoid the time stepping procedure, and the local meshless method is used to produce sparse differentiation matrices and avoid the ill conditioning issues resulting in global meshless methods. Our numerical method comprises three steps. In the first step we transform the given equation to an equivalent time independent equation. Secondly the reduced equation is solved via a local meshless method. Finally, the solution of the original equation is obtained via the inverse Laplace transform by representing it as a contour integral in the complex left half plane. The contour integral is then approximated using the trapezoidal rule. The stability and convergence of the method are discussed. The efficiency, efficacy, and accuracy of the proposed method are assessed using four different problems. Numerical approximations of these problems are obtained and validated against exact solutions. The obtained results show that the proposed method can solve such types of problems efficiently.

1 Introduction

The integer order derivatives are local in nature, i.e., using these derivatives changes in a neighborhood of a point can be described, but using the arbitrary order derivatives we can describe changes in an interval. Namely, fractional derivatives are nonlocal in nature. That is why arbitrary order derivatives are suitable to model more physical phenomena such as electrodynamics, earthquake vibrations, diffusion process, polymers, fluid flow, elasticity, hydrology, and signal and image processing [1–7]. Fractional order derivative of a function is in fact its definite integral. A geometrically fractional derivative accumulates the function. The corresponding accumulation includes the integer order derivative as a special case. In the literature a large number of arbitrary order derivatives are available such as the Marchaud, Grünwald–Letnikov, Riemann–Liouville, and Caputo derivatives [8–15]. However, these derivatives have certain disadvantages, these derivatives contain kernels with singularities. It is reported in the literature that these derivatives face problems when someone tries to model nonlocal phenomenon [1, 16]. Therefore, to model the non-local phenomenon accurately, recently a new fractional derivative has been defined, called the Caputo–Fabrizio (CF) derivative [17].

The research community took great interest in the CF derivative due to its non-singular kernel. The CF derivative has a large number of applications, and researchers have applied it successfully to many phenomena like signal processing [18], ground water pollution [19], groundwater flow in a confined aquifer [1, 20], the mass–spring damper system [21], non-Darcian flow and solute transport [22].

In many real world problems as regards their modeling, we need to obtain their exact solution which is some times quite difficult specially for nonlinear problems. Therefore, we need some sophisticated tools to deal with such problems. The researchers increasingly have used numerical and analytical techniques to handle the problems for corresponding numerical and analytical solutions. For example a homotopy analysis method based on the Laplace transform is proposed for solving linear problems including the CF derivative in [2, 23]. In [1] the authors solved the model of groundwater flow with the CF derivative using the Sumudu transform. In [24] a fractional order Fisher diffusion equation with the CF derivative is solved via some iterative method. The Crank–Nicholson scheme in [25] is applied for approximating the solution of the Allen Cahn model with CF derivative. A numerical approximation of the solution of groundwater pollution model with space–time fractional CF derivative in [19] is obtained via the Crank–Nicholson scheme. The Laplace and Fourier transforms are utilized in [26] for obtaining the fundamental solution of advection–diffusion equation with the CF derivative. In [27] the authors applied the CF derivative to the analysis of a rock fracture process. Many other numerical and analytical techniques for the solutions of different fractional order models can be found in [28–39] and the references therein. In this work our aim is to approximate linear PDEs with the CF derivative via the Laplace transform (LT) and local meshless method. The Laplace transform is coupled with a local meshless method for avoiding the time stepping procedure. The Laplace transform will help us in obtaining the solution in less computation time and without time instability. The paper is organized as follows: In Sect. 2 some basic definitions are given; In Sect. 3 the Laplace transform and contour integration methods are discussed; Sect. 3.1 shows how to construct the differentiation matrices via a local meshless method; Sect. 4 discusses the convergence of the method; Sect. 5 discusses the stability of the method; Sect. 6 contains the numerical tests, where theory and experiment are compared.

2 Preliminaries

Definition 2.1

The LT of a piecewise continuous function $f(t)$, $t>0$ is defined as

$$ \mathscr{L}\bigl[f(t)\bigr]=\hat{f}(s)= \int ^{\infty }_{0} e^{-st}f(t)\,dt. $$

(1)

Definition 2.2

The CF derivative of fractional order α is defined as [17]

$$ {}^{CF}_{0}D^{\alpha }_{t}f(t)= \frac{(2-\alpha )B(\alpha )}{2(1-\alpha )} \int ^{t}_{0} \exp \biggl( \frac{-\alpha (t-s)}{1-\alpha } \biggr) \frac{d^{n}f(s)}{ds^{n}}\,ds,\quad \alpha \in (n-1,n), $$

(2)

where $B(\alpha )$ denotes the normalization function, satisfying $B(0)=B(1)=1$.

Definition 2.3

If $n \in \mathbb{N}$, and $0\leq \alpha \leq 1$ then the LT of the CF fractional derivative is defined as [2, 24]

$$ \mathscr{L}\bigl[{}^{CF}_{0}D^{\alpha +n}_{t}f(t) \bigr](s)= \frac{s^{n+1}\hat{f}(s)-s^{n}f(0)-s^{n-1}f'(0)-\cdots-f^{n}(0)}{s+\alpha (1-s)}, $$

(3)

using $n=0$ we get

$$ \mathscr{L}\bigl[{}^{CF}_{0}D^{\alpha }_{t}f(t) \bigr](s)= \frac{s\hat{f}(s)-f(0)}{s+\alpha (1-s)}, $$

(4)

and for $n=1$ we have

$$ \mathscr{L}\bigl[{}^{CF}_{0}D^{\alpha +1}_{t}f(t) \bigr](s)= \frac{s^{2}\hat{f}(s)-sf(0)-f'(0)}{s+\alpha (1-s)}. $$

(5)

3 Numerical scheme

In order to validate our method let us consider a linear one dimensional partial differential equation with the CF derivative for $q-1<\alpha +n\leq q$:

$$ {{}^{CF}_{0}}D^{\alpha }_{t}u(x,t)+ \mathcal{L}u(x,t)=h(x,t), \quad x\in \Omega , \text{and } 0 \leq t \leq T, $$

(6)

the boundary and initial conditions are

$$ \partial ^{l}_{t}u(x,0)=u_{l}(x),\quad l=0,1,2, \ldots,q-1, $$

and

$$ \mathcal{B}u(x,t)=g(x,t),\quad x\in \partial \Omega , $$

(7)

where $\mathcal{L}$ is the linear differential operator and $\mathcal{B}$ is the boundary operator. Applying the LT to Eq. (6) and Eq. (7), we have

$$ \mathscr{L} \bigl[{}^{CF}_{0}D^{\alpha +n}_{t}u(x,t)+ \mathcal{L}u(x,t) \bigr]= \mathscr{L} \bigl[h(x,t) \bigr] $$

(8)

and

$$ \mathcal{B}\hat{u}(x,s)=\hat{g}(x,s). $$

(9)

From Eq. (8), we have

$$ \frac{s^{n+1}\hat{u}(x,s)-s^{n}u(x,0)-s^{n-1}u'(x,0)-\cdots-u^{n}(x,0)}{s+\alpha (1-s)}+ \mathcal{L}\hat{u}(x,s)=\hat{g}(x,s), $$

(10)

on simplification we get

$$\begin{aligned}& \biggl[ \biggl(\frac{s^{n+1}}{s(1-\alpha )+\alpha } \biggr)I+ \mathcal{L} \biggr] \hat{u}(x,s)= \hat{\mathcal{G}}(x,s), \end{aligned}$$

(11)

$$\begin{aligned}& \mathcal{B}\hat{u}(x,s)=\hat{g}(x,s), \end{aligned}$$

(12)

where $\hat{\mathcal{G}}(x,s)$ is

$$ \hat{\mathcal{G}}(x,s)= \frac{s^{n}u(x,0)+s^{n-1}u'(x,0)+\cdots+u^{n}(x,0)}{s(1-\alpha )+\alpha }+ \hat{g}(x,s). $$

We obtain the solution $u(x,t)$ of (6)–(7) by representing it as an integral along a smooth curve as

$$ u(x,t)=\frac{1}{2 \pi i} \int ^{\sigma +\iota \infty }_{\sigma -\iota \infty } e^{st}\hat{u}(x,s)\,ds= \frac{1}{2 \pi i} \int _{\Gamma } e^{st} \hat{u}(x,s)\,ds,\quad \sigma >\sigma _{0}, $$

(13)

where $\sigma _{0} \in \mathbb{R}$ is the convergence abscissa, it is large enough and the contour Γ is a suitably selected line $\Gamma _{0}$ perpendicular to x axis connecting $\sigma -\iota \infty$ and $\sigma +\iota \infty$. Then in Eq. (13), $u(x,t)$ is the inverse Laplace of $\hat{u}(x,s)$, with the condition that the $\Gamma _{0}$ lie to the right of all the singularities of the transform $\hat{u}(x,s)$. For our purposes, however, we assume that $\hat{u}(x,s)$ may be continued analytically in an appropriate way. We shall want to take for $\Gamma _{0}$ a deformed contour Γ in the set $\Sigma ^{\delta }_{\phi }= \{0\}\cup \{s \neq 0:|\arg s|< \phi \}$. The deformed contour will show asymptotic behavior like the couple of lines in the left half complex plane with $\operatorname{Im} s \rightarrow \pm \infty$ and $\operatorname{Re} s\rightarrow -\infty$, forcing the factor $e^{s t}$ to decay in the direction of both ends of the contour Γ. In this work we select Γ with the parametric representation of the form [40]

$$ s(\boldsymbol{\mu })=\delta +\xi -\xi \sin (\theta -\iota \boldsymbol{\mu })),\quad \boldsymbol{\mu }\in \mathbb{R}, $$

(14)

where

$$ 0< \theta < \phi -\frac{\pi }{2}, \quad \xi >0,\quad \text{and}\quad \delta >0 . $$

(15)

Letting $s=x+\iota y$, we notice that Eq. (14) serves as the left part of the hyperbola defined by

$$ \biggl(\frac{x-\delta -\xi }{\xi \sin \theta } \biggr)^{2}- \biggl( \frac{y}{\xi \cos \theta } \biggr)^{2}=1, $$

(16)

where for Eq. (16) the asymptotes are $y=\pm (x-\delta -\xi )\cot \theta$, and its x-intercept is $s=\delta +\xi (1-\sin \theta )$. Equation (15) ensures that the contour Γ lies in $\Sigma ^{\delta }_{\phi }=\delta +\Sigma _{\phi }\subset \Sigma _{\phi }$, and extends towards the left half complex plane. Using Eq. (14) in Eq. (13) we have

$$ u(x,t)=\frac{1}{2 \pi \iota } \int ^{\infty }_{-\infty }e^{s(\boldsymbol{\mu })t} \hat{u}\bigl(x,s(\boldsymbol{ \mu })\bigr)s'(\boldsymbol{\mu })\,d\boldsymbol{\mu }. $$

(17)

The approximation of Eq. (17) can be obtained by employing the trapezoidal rule as

$$ u_{k}(x,t)=\frac{k}{2 \pi \iota }\sum ^{M}_{j=-M} e^{s_{j} t}\hat{u}(x,s_{j})s'_{j},\quad \boldsymbol{\mu }_{j}=jk, s_{j}= s(\boldsymbol{\mu }_{j}), s'_{j}=s'(\boldsymbol{\mu }_{j}). $$

(18)

The solution $u_{k}(x,t)$, can be obtained by solving the system of equations in (11)–(12) in parallel for the nodes $s_{j}$. In order to do this we employ the meshless method in local setting for discretization of the operators $\mathcal{L}$ and $\mathcal{B}$.

3.1 Local meshless scheme

For data points $\{x_{i}\}^{N}_{i=1}$ in $\mathbb{R}^{d}$, $d\geq 1$ the local meshless approximation of $\hat{u}(x)$ is given by

$$ \hat{u}(x_{i})=\sum_{x_{j}\in \Omega _{i}} \lambda ^{i}_{j}\phi \bigl( \bigl\Vert x_{i}-x^{i}_{j} \bigr\Vert \bigr), $$

(19)

where the vector ${\boldsymbol{\lambda }}^{i}=\{\lambda ^{i}_{j}\}^{n}_{j=1}$ represents the expansion coefficients, $\phi (r)$ is kernel function and $r=\|x_{i}-x_{j}\|$ is the distance between $x_{i}$ and $x_{j}$. $\Omega _{i}$ and Ω are local and global domains, respectively. The local domain $\Omega _{i}$ includes the center $x_{i}$ and its n neighboring centers around it. Hence we have N $n \times n$ linear systems as

$$\begin{array}{rl}& \left(\begin{array}{c}\hat{u}(x_1^i)\\ \hat{u}(x_2^i)\\ ⋮\\ \hat{u}(x_n^i)\end{array}\right)=\left(\begin{array}{cccc}\varphi (\parallel x_1^i-x_1^i\parallel )& \varphi (\parallel x_1^i-x_2^i\parallel )& \cdots & \varphi (\parallel x_1^i-x_n^i\parallel )\\ \varphi (\parallel x_2^i-x_1^i\parallel )& \varphi (\parallel x_2^i-x_2^i\parallel )& \cdots & \varphi (\parallel x_2^i-x_n^i\parallel )\\ ⋮& ⋮& ⋮& ⋮\\ \varphi (\parallel x_n^i-x_1^i\parallel )& \varphi (\parallel x_n^i-x_2^i\parallel )& \cdots & \varphi (\parallel x_n^i-x_n^i\parallel )\end{array}\right)\left(\begin{array}{c}{\lambda }_1^i\\ {\lambda }_2^i\\ ⋮\\ {\lambda }_n^i\end{array}\right),\\ & i=1,2,\dots ,N,\end{array}$$

(20)

which can be written as

$$ \hat{\boldsymbol{u}}^{i}=\Phi ^{i}{\boldsymbol{\lambda }}^{i},\quad 1 \leq i \leq N, $$

(21)

where $\Phi ^{i}$ is called the system matrix having entries of the form $b^{i}_{kj}=\phi (\|x^{i}_{k}-x^{i}_{j}\|)$, where $x^{i}_{k},x^{i}_{j} \in \Omega _{i}$. Solving the N systems in Eq. (21) we obtain the unknowns ${\boldsymbol{\lambda }}^{i}=\{\lambda ^{i}_{j}\}^{n}_{j=1}$. The differential operator $\mathcal{L}$ can be approximated as

$$ \mathcal{L}\hat{u}(x_{i})=\sum _{x_{j}\in \Omega _{i}}{\boldsymbol{\lambda }}^{i}_{j} \mathcal{L} \phi \bigl( \bigl\Vert x_{i}-x^{i}_{j} \bigr\Vert \bigr), $$

(22)

Equation (22) can be written as

$$ \mathcal{L}\hat{u}(x_{i})={\boldsymbol{\lambda }}^{i}\cdot {\boldsymbol{\nu }}^{i}, $$

(23)

where the vectors ${\boldsymbol{\nu }}^{i}$ and ${\boldsymbol{\lambda }}^{i}$ have orders $1 \times n$ and $n \times 1$, respectively. The entries of ${\boldsymbol{\nu }}^{i}$ are of the form

$$ {\boldsymbol{\nu }}^{i}=\mathcal{L}\phi \bigl( \bigl\Vert x_{i}-x^{i}_{j} \bigr\Vert \bigr),\quad x^{i}_{j} \in \Omega _{i}, $$

(24)

solving Eq. (21) and Eq. (23) for ${\boldsymbol{\lambda }}^{i}$, we have

$$ \mathcal{L}\hat{u}(x_{i})={\boldsymbol{\nu }}^{i} \bigl(\Phi ^{i}\bigr)^{-1}\hat{\boldsymbol{u}}^{i}= \boldsymbol{\varpi }^{i}\hat{\boldsymbol{u}}^{i}, $$

(25)

where

$$ \boldsymbol{\varpi }^{i}={\boldsymbol{\nu }}^{i}\bigl( \Phi ^{i}\bigr)^{-1}, $$

(26)

hence at each center $x_{i}$ the operator $\mathcal{L}$ can be approximated via a local meshless method as

$$ \mathcal{L}\hat{u}\equiv \textbf{D}\hat{\boldsymbol{u}}, $$

(27)

where $D_{N \times N}$ is a sparse system matrix obtained via meshless method in local setting approximating $\mathcal{L}$. We can approximate the operator $\mathcal{B}$ in a similar way.

4 Accuracy and convergence

The process of approximating the solution of the problem defined in Eq. (1)–Eq. (3) involves the transformation of the given equation by employing the Laplace transform, no error occurs in this process. Then we employ the meshless method in a local setting for solving the transformed problem. The error estimate is $O(\gamma ^{\frac{1}{\epsilon h}})$, $0<\gamma <1$ (where h is the fill distance and ϵ is the shape parameter) for the meshless method in the local setting. Finally, we obtain the solution of the problem via the inverse Laplace transform by representing it as a Bromwhich integral (17). The integral is then approximated to high accuracy via the trapezoidal rule. While approximating the integral (17) the convergence rate is dependent on Γ. Also in this process the convergence orders are dependent on the step k and on the chosen temporal domain $[t_{0}, T]$. For optimal results and best convergence we choose an optimal temporal domain. A proof of the error is given in the next theorem.

Theorem 1

([40], Theorem 2.1)

Let (6) have solution $u(x,t)$ with $\hat{u}(x,s)$ analytic in $\Sigma ^{\delta }_{\phi }$. Let $\Gamma \subset \Omega _{r}\subset \Sigma ^{\delta }_{\phi }$, and define for $b>0$, $\cosh (b)= (\eta \tau \sin (\theta ) )^{-1}$, where $0<\tau _{0}<T$, $\tau =\frac{t_{0}}{T}$, $0<\eta < 1.0$ and let $\xi = \frac{\eta \overline{r}M}{bT}$. Then with $k=\frac{b}{M}\leq \frac{\overline{r}}{\log 2}$, for Eq. (18), we have $|u(x,t)-u_{k}(x,t)|\leq CQe^{\delta \tau }l (\|u_{0}\|+\| \widehat{\mathcal{H}}\|_{\Sigma ^{\delta }_{\phi }} )(\rho _{r}M)e^{- \mu M}$, for $\mu =\frac{\overline{r}(1-\eta )}{b}$, $\rho _{r}= \frac{\eta \overline{r} \tau \sin (\theta -r)}{b}$, $\overline{r}=2\pi r$, $r>0$, $\tau _{0}\leq t \leq T$, $l(x)= \max (1,\log (\frac{1}{x}))$, and $C=C_{\delta ,r,\phi }$. Hence we have

$$ error_{\mathit{est}}= \bigl\vert u_{k}(x,t)-u(x,t) \bigr\vert =O \bigl(e^{-\mu M}\bigr). $$

5 Stability of the method

For the stability of the system defined in Eq. (11)–Eq. (12), we write the system in matrix form given as

$$ \boldsymbol{Q}\hat{\boldsymbol{u}}= \mathfrak{R}, $$

(28)

where $\boldsymbol{Q}_{N \times N}$ is obtained via a local meshless method. The constant of stability for the system Eq. (28) is defined as

$$ S_{c}=\sup_{\hat{\boldsymbol{u}}\neq 0} \frac{ \Vert \hat{\boldsymbol{u}} \Vert }{ \Vert \boldsymbol{Q}\hat{\boldsymbol{u}} \Vert }, $$

(29)

for any discrete norm $\|\cdot\|$ defined on $R^{N}$ the constant $S_{c}$ is finite. From Eq. (29) we may write

$$ \Vert \boldsymbol{Q} \Vert ^{-1} \leq \frac{ \Vert \hat{\boldsymbol{u}} \Vert }{ \Vert \boldsymbol{Q}\hat{\boldsymbol{u}} \Vert } \leq S_{c}, $$

(30)

also for the pseudoinverse $\boldsymbol{Q}^{\dagger }$ of Q, we have

$$ \bigl\Vert \boldsymbol{Q}^{\dagger } \bigr\Vert = \sup _{\boldsymbol{B} \neq 0} \frac{ \Vert \boldsymbol{Q}^{\dagger } \boldsymbol{B} \Vert }{ \Vert \boldsymbol{B} \Vert }. $$

(31)

Thus, we have

$$ \bigl\Vert \boldsymbol{Q}^{\dagger } \bigr\Vert \geq \sup _{\boldsymbol{B}=\boldsymbol{Q}\hat{\boldsymbol{B}}\neq 0} \frac{ \Vert \boldsymbol{Q}^{\dagger }\boldsymbol{Q}\hat{\boldsymbol{u}} \Vert }{ \Vert \boldsymbol{Q}\hat{\boldsymbol{u}} \Vert }=\sup_{\hat{\boldsymbol{u}} \neq 0} \frac{ \Vert \hat{\boldsymbol{u}} \Vert }{ \Vert \boldsymbol{Q}\hat{\boldsymbol{u}} \Vert }=S_{c}. $$

(32)

From Eq. (30) and Eq. (32) we observe that the constant $S_{c}$ is bounded. Calculation of the pseudoinverse for the system (28) may be computationally expensive, but it confirms the stability. For square matrices we can use the MATLAB’s function condest for estimating $\|\boldsymbol{Q}^{-1}\|_{\infty }$, hence we have

$$ S_{c}=\frac{\operatorname{condest}(\boldsymbol{Q}')}{ \Vert \boldsymbol{Q} \Vert _{\infty }} $$

(33)

For our sparse matrix Q this works well in a very short time of computation (Fig.1).

Figure 1

(a) The plot of the stability constant $S_{c}$ for Example 2, with $N=35$, $n=9$, $M=70$, and $\alpha =0.3321$ at $t=1$. We see that $1.3008 \leq S_{c} \leq 1.3504$. It is observed that the upper and lower bounds for the stability constant are very small numbers, which guarantees that the proposed localized meshless scheme is stable. (b) The contour of integration

6 Numerical experiments

Here we employ our proposed numerical scheme for the approximations different one dimensional linear PDEs. For optimization of the shape parameter we have utilized the uncertainty principle due to [41]. In our numerical experiments for generating the quadrature nodes the command $\boldsymbol{\mu }=-M:k:M$ is used, also the multiquadrics (MQ) kernel is used in all experiments. Other optimal parameters involved for the contour of integration are $\theta =0.15410$, $r=0.13870$, $\eta =0.10$, $\tau =\frac{t0}{T}$, $\delta =2.0$, $t \in [t_{0},T]=[0.5,5]$. The accuracy of the method is measured via the $L_{\infty }$ error given by

$$ L_{\infty }= \bigl\Vert u(x,t)-u_{k}(x,t) \bigr\Vert _{\infty }= \max_{1 \leq j \leq N}\bigl( \bigl\vert u(x,t)-u_{k}(x,t) \bigr\vert \bigr). $$

Here $u(x,t)_{k}$ and $u(x,t)$ are the numerical and exact solutions respectively.

Example 1

Here we consider a 1-D linear differential equation with the CF derivative [2]

$$ {}^{CF}_{0}D^{\alpha +1}_{t} u(x,t)- \frac{1}{2}x^{2} D_{x x} u(x,t)=0,\quad x, t, \alpha \in (0,1) \text{ where } D_{x x}= \frac{\partial ^{2}}{\partial x^{2}}. $$

(34)

the initial conditions are

$$ u(x,0)=x,\qquad D_{t} u(x,0)=x^{2}. $$

(35)

The boundary conditions are extracted from the exact solution

$$ u(x,t)=x+x^{2} \biggl(\frac{e^{t}-e^{-\alpha t}}{1+\alpha } \biggr). $$

(36)

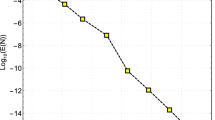
The results obtained for different centers n in local domain $\Omega _{i}$ and N in global domain Ω are given in Table 1 for fractional order $\alpha =0.22211$ and various quadrature points. The condition number κ, $L_{\infty }$ errors, shape parameter ε, and the error estimates are also given in Table 1. From Table 1 it is clear that the proposed method gives an acceptable accuracy. The approximate and exact solutions are plotted in Fig. 2(a) and Fig. 2(b), respectively, which clearly shows good agreement between them. The contour plot of absolute error is shown in Fig. 3(a), which shows a high accuracy. The plot of actual error vs error estimate is shown in Fig. 3(b), which shows good agreement between them. From the results we conclude that the proposed method is effective.

Figure 2

(a) Approximate solution for $\alpha =0.22211$. (b) Exact solution for $\alpha =0.22211$

Figure 3

(a) The contour plot of absolute error. (b) The actual error vs error estimate

Table 1 The results are obtained for $\alpha =0.22111$, $x \in [0,1]$, and $t=1$

Example 2

Here we consider a non-homogeneous linear differential equation with the CF derivative [2]:

$$ {}^{CF}_{0}D^{\alpha }_{t} u(x,t)+x D_{x} u(x,t)+ D_{x x} u(x,t)=2\bigl(t^{2}+x^{2}+1 \bigr),\quad x, t, \alpha \in (0,1). $$

(37)

the initial condition being

$$ u(x,0)=x^{2}, $$

(38)

the boundary conditions can be obtained from the exact solution

$$ u(x,t)=x^{2}+\frac{2t^{\alpha }(1+(t-\alpha )\alpha )}{1+\alpha }. $$

(39)

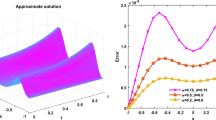
The results obtained for different centers n in local domain $\Omega _{i}$ and N in global domain Ω are shown in Table 2 with fractional order $\alpha =0.22211$ and various quadrature nodes. From the observations on this table also we conclude that the results obtained using the proposed numerical scheme are acceptable. The plots of exact and approximate solutions are given in Fig. 4(a), and Fig. 4(b), respectively. The error functions for different values of α are shown in Fig. 5(a), we observe that the error decreases as we increase α. In Fig. 5(b) the actual error and error estimates are shown, which shows good agreement between them.

Figure 4

(a) Numerical solution for $\alpha =0.3321$. (b) Exact solution for $\alpha =0.3321$

Figure 5

In (a) absolute errors for different α, the error decreases as we increase α. In (b) the actual error and error estimate are shown and good agreement is observed

Table 2 The results are obtained for $\alpha =0.3321$, $x \in [0,1]$, and $t=1$

Example 3

Next the 1-D non-homogeneous diffusion equation with the CF derivative is considered:

$$ {}^{CF}_{0}D^{\alpha }_{t} u(x,t)+ D_{x x} u(x,t)=h(x,t),\quad -1< x< 1, 0< t< 1 0< \alpha \leq 1. $$

(40)

with the forcing term

$$\begin{aligned} h(x,t)={}&\frac{1}{1-\alpha }\sin (2 \pi x) \biggl( \frac{3 t^{2}}{\boldsymbol{P}}- \frac{6 t}{\boldsymbol{P}^{2}}+\frac{6}{\boldsymbol{P}^{3}}\bigl(1-e^{-\boldsymbol{P}t}\bigr) \biggr) \\ &{}+4 \pi ^{2}\bigl(t^{3}+1\bigr) \sin (2 \pi x),\quad \text{where } \boldsymbol{P}=\frac{\alpha }{1-\alpha }. \end{aligned}$$

(41)

The problem has the following exact solution:

$$ u(x,t)=\sin (2 \pi x) \bigl(t^{3}+1\bigr). $$

(42)

The initial and boundary conditions are extracted from the exact solution. The results obtained for different nodes $n \in \Omega _{i}$, $N \in \Omega$ and different quadrature nodes with $\alpha =0.3$, $\alpha =0.7$ are shown Table 3 and Table 4. A clear improvement is observed in the accuracy as we increase the spatial and quadrature nodes. The plots of exact and numerical solutions are given in Fig. 6(a) and in Fig. 6(b). In Fig. 7(a) the contour plot of the absolute error is given, which shows a high accuracy of the proposed numerical scheme. In Fig. 7(b) the plot of the actual error and error estimate is shown, which shows good agreement between them. The results ensure the convergence, stability, and efficiency of our method.

Figure 6

(a) Numerical solution. (b) Exact solution

Figure 7

(a) The contour plot of absolute error. (b) The actual error vs error estimate

Table 3 The results are obtained for $\alpha =0.3$, $x \in [-1,1]$, and $t=1$

Table 4 The results are obtained for $\alpha =0.7$, $x \in [-1,1]$, and $t=1$

Example 4

The next test problem is the 1-D non-homogeneous diffusion equation with the CF derivative:

$$ {}^{CF}_{0}D^{\alpha }_{t} u(x,t)+ D_{x x} u(x,t)=h(x,t),\quad \chi , \tau ,\alpha \in (0,1). $$

(43)

The initial condition is

$$ u(x,0)=x^{2}\bigl(1-x^{2}\bigr), $$

(44)

with the forcing term

$$\begin{aligned} h(x,t)={}&\frac{1}{1-\alpha }x^{2}(1-x)^{2} \biggl( \frac{3 t^{2}}{\boldsymbol{P}}-\frac{6t}{\boldsymbol{P}^{2}}+\frac{6}{\boldsymbol{P}^{3}}\bigl(1-e^{- \boldsymbol{P}t} \bigr) \biggr) \\ &{}-\bigl(t^{3}+1\bigr) \bigl(12x^{2}-12x+2 \bigr), \quad \text{where } \boldsymbol{P}= \frac{\alpha }{1-\alpha }. \end{aligned}$$

(45)

The exact solution is

$$ u(x,t)=\bigl(t^{3}+1\bigr) x^{2}(1- x)^{2}. $$

(46)

The initial and boundary conditions are extracted from the exact solution. The results obtained for different nodes $n \in \Omega _{i}$, $N \in \Omega$ and different quadrature nodes with $\alpha =0.7$ are given Table 5. The plots of exact and numerical solutions are given in Fig. 8(a) and in Fig. 8(b). In Fig. 9(a) the contour plot of absolute error is shown, and in Fig. 9(b) the plot of actual error vs error estimate is shown, which shows good agreement between them. For this problem also the method produced accurate and stable results.

Figure 8

(a) Numerical solution. (b) Exact solution

Figure 9

(a) The contour plot of absolute error. (b) The actual error vs error estimate

Table 5 The results are obtained for $\alpha =0.7$, $x \in [0,1]$, and $t=1$

7 Conclusion

In this work, we have coupled the Laplace transform and a meshless method in a local setting successfully for the approximation of linear one dimensional partial differential equations with the CF derivative. The Laplace transform reduced the problem to a time independent problem and in this way the classical time stepping procedure and hence the time instability issues were avoided. The local meshless method produced sparse differentiation matrices and the issues of ill conditioning and shape parameter sensitivity were resolved. We discussed the convergence and stability of the method. Some numerical experiments were performed on one dimensional problems with a CF derivative for different fractional orders. Numerical results confirmed the stability and high accuracy of the proposed method. The obtained results ensured the efficiency and applicability of the method for such problems.