1 Introduction

In this manuscript, we agree that a, b, and \(T ^{*}\) are real numbers such that \(a < b\) and \(T^{*}>0\). We fix the spatial domain \(B = (a , b)\) and the space-time domain \(\Omega = B \times (0 , T^{*})\). The notation Ω̅ is used to denote the closure of the set Ω in the usual topology of \(\mathbb{R} ^{2}\), and we use ∂B to represent the boundary of the set B. In this work, we assume that the functions \(T,U,V :\overline{\Omega } \rightarrow \mathbb{R}\) are sufficiently smooth. Meanwhile, the constants β, d, k, δ, γ, c, and N represent nonnegative numbers. Also, we define the functions \(\phi _{T},\phi _{U},\phi _{V}:\overline{B} \rightarrow \mathbb{R}\) and \(\psi _{T},\psi _{U},\psi _{V}:\partial B\times [0,T] \rightarrow \mathbb{R}\). Assume additionally that \(\phi _{W}(x)=\psi _{W}(x,0)\) holds for each \(x\in \partial B\) and \(W \in \{T,U,V\}\).

Under these conventions and nomenclature, the model of type-1 human immunodeficiency virus (HIV-1) infection of CD4+T cells with diffusion is described by the one-dimensional problem with initial-boundary conditions:

$$ \begin{aligned} &\frac{\partial T}{\partial t} = \beta -\kappa V T-dT+\gamma U+ \frac{\partial ^{2} T}{\partial x^{2}}, \quad \forall (x , t) \in \Omega , \\ &\frac{\partial U}{\partial t} = \kappa VT-(\gamma +\delta )U+ \frac{\partial ^{2} U}{\partial x^{2}}, \quad \forall (x , t) \in \Omega , \\ &\frac{\partial V}{\partial t} = N\delta U-cV+ \frac{\partial ^{2} V}{\partial x^{2}} , \quad \forall (x , t) \in \Omega , \\ &\quad \text{such that } \textstyle\begin{cases} T(x,0)= \phi _{T} (x), & \forall x \in B, \\ U(x,0)=\phi _{U} (x), & \forall x \in B, \\ V(x,0)=\phi _{V} (x), & \forall x \in B, \\ T = \psi _{T} ,\qquad U=\psi _{U} , \qquad V=\psi _{V}, & \forall (x,t) \in \partial B\times [0,T]. \end{cases}\displaystyle \end{aligned} $$
(1)

This model is a system with diffusion. The functions \(T(x,t)\), \(U(x,t)\), and \(V(x,t)\) represent the normalized densities of the uninfected CD4+T cells, infected CD4+T cells, and the free HIV-1 infection particles in the blood, respectively. The physical meanings of the parameters β, d, κ, δ, γ, c, and N are given in Table 1.

Table 1 Physical meaning of the parameters in the continuous model (1)
Full size table

In order to express system (1) in an equivalent form, we suppose that T, U, and V are positive solutions of system (1), and let \(\lambda \in \mathbb{R}^{+}\) be a free constant. Dividing both sides of each equation of the population system by \(T(x,t)+\lambda \), \(U(x,t)+\lambda \), and \(V(x,t)+\lambda \), respectively, and using the chain rule at the left-hand side of each equation, we obtain the following equivalent system:

$$ \begin{aligned} &\frac{\partial }{\partial t} \ln (T+\lambda ) = \frac{1}{T+\lambda } \biggl[\beta -\kappa V T-dT+\gamma U+ \frac{\partial ^{2} T}{\partial x^{2}} \biggr] , \quad \forall (x , t) \in \Omega , \\ &\frac{\partial }{\partial t} \ln (U+\lambda ) = \frac{1}{U+\lambda } \biggl[ \kappa VT-(\gamma +\delta )U+ \frac{\partial ^{2} U}{\partial x^{2}} \biggr] , \quad \forall (x , t) \in \Omega , \\ &\frac{\partial }{\partial t} \ln (V+\lambda ) = \frac{1}{V+\lambda } \biggl[ N\delta U-cV+\frac{\partial ^{2} V}{\partial x^{2}} \biggr] ,\quad \forall (x , t) \in \Omega , \\ &\quad \text{such that } \textstyle\begin{cases} T(x,0)= \phi _{T} (x), & \forall x \in B, \\ U(x,0)=\phi _{U} (x), & \forall x \in B, \\ V(x,0)=\phi _{V} (x), & \forall x \in B, \\ T = \psi _{T} ,\qquad U=\psi _{U} ,\qquad V=\psi _{V}, & \forall (x,t) \in \partial B\times [0,T]. \end{cases}\displaystyle \end{aligned} $$
(2)

This equivalent form is employed to propose an exponential-type discretization of the continuous problem under investigation. In particular, we provide a Bhattacharya-type discrete scheme to solve the mathematical model (2). The reason to follow this approach obeys the need to preserve some important features of the relevant solutions of this system and to provide an unconditionally stable and explicit numerical solution for our differential model.

It is worth pointing out that the mathematical investigation of the human immunodeficiency virus HIV-1 is an interesting avenue of research. In fact, some works investigate mathematical models to estimate HIV-1 virological failure and establish rigorously the role of lymph node drug penetration [1], the global analysis of the dynamics of predictive systems for intermittent HIV-1 treatment [2], mathematical models of cell-wise spread of HIV-1 which include temporal delays [3], models for patterns of the sexual behavior and their relation with the spread of HIV-1 [4], and the long-term dynamics in mathematical models of HIV-1 with temporal delay in various variants of the drug therapy [5]. Some of these models are based on ordinary differential equations, and their analytical study is followed by simulation experiments which assess the validity of the qualitative results. To that end, various numerical methodologies have been designed and analyzed, like some algorithms for simulating the HIV-1 dynamics at a cellular level [6], stem cells therapy of HIV-1 infections [7], fractional optimal control problems on HIV-1 infection of CD4+T cells using Legendre spectral collocation [8], HIV-1 cure models with fractional derivatives which possess a nonsingular kernel [9], stochastic HIV-1/AIDS epidemic models in two-sex populations [10], among other reports [5, 11–13].

Notice that system (2) is an integer-order diffusive extension of some HIV-1 propagation models available in the literature [9, 14]. The use of such a system is due to the current information available of the mechanisms of CD4+T cells and free HIV-1 infection particles in the blood. In our investigation, we propose a two-level finite difference discretization of (2). Our approach hinges on an exponential-type discretization of the mathematical model, and we prove that the numerical model has various numerical and analytical properties which make it a useful research tool in the study of the propagation of HIV-1. For instance, we prove that the scheme is capable of preserving the positivity and boundedness of solutions. This feature is of the utmost importance in view that the variables under investigation are densities [15]. The properties of consistency, stability, and convergence are thoroughly established in this work. In particular, we show that the scheme is unconditionally stable, and that it has first order of convergence in time and second order in space. We provide some simulations to assess the validity of the theoretical results. Moreover, the computer implementation of the scheme used to obtain the simulations is provided in the Appendix at the end of this work.

Before we begin our study, we must mention that the system under investigation (1) has attracted the attention of these authors due to many important reasons. As we pointed out before, the mathematical model is motivated by various particular models available in the literature which do not consider the presence of diffusion. Those systems are described by ordinary differential equations, whence the investigation of their diffusive generalizations is an important topic of research. Indeed, the consideration of a nonconstant diffusion gives rise to a more realistic and complex scenario. Physically and mathematically, the study of (1) would yield more interesting results. From the numerical perspective, it becomes necessary to possess a reliable tool to investigate the solutions of the mathematical model. After the theoretical and computational investigation of the scheme, researchers in the area would possess a means to obtain trustworthy results to propose predictions on the propagation of HIV-1 in the human body.

2 Numerical model

In this stage, we introduce discrete operators to provide a discrete model to approximate the analytical solutions of continuous problem (2). Our approach employs finite differences, and the method to solve the continuous problem is introduced herein. The main structural features of the proposed scheme is rigorously established in the second half of this section.

Let us define the sets \(I_{q}={1,2,\ldots ,q}\) and \(\overline{I} _{q}=\{0\}\cup I_{q}\) for each \(q \in \mathbb{N}\). Let M and K be natural numbers. We define the set \(\partial J=\overline{I}_{M}\cap \partial B\) and consider discrete partitions corresponding to the intervals \([a,b]\) and \([0,T^{*}]\) as

$$\begin{aligned}& a=x_{0}< x_{1}< x_{2}< \cdots < x_{m}< \cdots < x_{M-1}< x_{M} =b, \quad \forall m \in \bar{I}_{M}, \end{aligned}$$
(3)
$$\begin{aligned}& 0=t_{0}< t_{1}< t_{2}< \cdots < t_{k}< \cdots < t_{K-1}< t_{K} =T^{*},\quad \forall k \in \bar{I}_{K}, \end{aligned}$$
(4)

respectively. In the first partition, the value \(x_{m}\) is given by \(x_{m}=x_{0}+mh\), where \(h=(b-a)/M\) for each \(m\in \bar{I}_{M}\). In the second partition, the value of \(t_{k}\) is given by \(t_{k}=k\tau \), where \(\tau =T^{*}/K\) for each \(k\in \bar{I}_{K}\). We use the nomenclatures \(T_{m}^{k}\), \(U_{m}^{k}\), and \(V_{m}^{k}\) to denote numerical approximations to the exact solutions T, U, and V, respectively, at the point \(x_{m}\) and time \(t_{k}\) for each \(m\in \bar{I}_{M}\) and \(k \in \bar{I}_{K}\).

Let W be any of T, U, or V. We introduce the following discrete quantities for each \(m\in I_{M-1}\) and each \(k \in I _{K-1}\):

$$\begin{aligned}& \delta _{t} W_{m}^{k} = \frac{W_{m}^{k+1}-W_{m}^{k}}{\tau }, \end{aligned}$$
(5)
$$\begin{aligned}& \delta _{x}^{2} W_{m}^{k} = \frac{W_{m+1}^{k}-2W_{m}^{k}+W_{m-1}^{k}}{h^{2}}. \end{aligned}$$
(6)

It is well known that the first operator yields a first-order estimate for the partial derivative of W with respect to t at the point \((x_{m},t_{k})\), while the second operator yields a second-order estimate of the second partial derivative of W with respect to x at the point \((x_{m},t_{k})\). Substituting these discrete operators at the time \(t _{k}\) into model (2), we reach the next finite-difference scheme to estimate the solutions of (2) at \((m , k) \in I_{M-1} \times \bar{I}_{K-1}\):

$$\begin{aligned}& \delta _{t} \ln \bigl(T_{m}^{k}+\lambda \bigr) = \frac{1}{T_{m}^{k}+\lambda } \bigl[\beta -\kappa V_{m}^{k} T_{m}^{k}-dT_{m}^{k}+\gamma U_{m}^{k}+ \delta _{x}^{2} T_{m}^{k} \bigr] , \\& \delta _{t} \ln \bigl(U_{m}^{k}+\lambda \bigr) = \frac{1}{U_{m}^{k}+\lambda } \bigl[ \kappa V_{m}^{k}T_{m}^{k}-( \gamma +\delta )U_{m}^{k}+\delta _{x}^{2} U_{m}^{k} \bigr] , \\& \delta _{t} \ln \bigl(V_{m}^{k}+\lambda \bigr) = \frac{1}{V_{m}^{k}+\lambda } \bigl[ N\delta U_{m}^{k}-cV_{m}^{k}+ \delta _{x}^{2} V_{m}^{k} \bigr] , \\& \quad \text{such that } \textstyle\begin{cases} T_{m}^{0}= \phi _{T} (x_{m}), & \forall m \in \overline{I}_{M}, \\ U_{m}^{0}=\phi _{U} (x_{m}), & \forall m \in \overline{I}_{M}, \\ V_{m}^{0}=\phi _{V} (x_{m}), & \forall m \in \overline{I}_{M}, \\ T_{m}^{k} = \psi _{T} (x_{m},t_{k}), & \forall (m,k) \in \partial J \times \overline{I}_{K}, \\ U_{m}^{k}=\psi _{U} (x_{m},t_{k}), & \forall (m,k) \in \partial J \times \overline{I}_{K}, \\ V_{m}^{k}=\psi _{V} (x_{m},t_{k}), & \forall (m,k) \in \partial J \times \overline{I}_{K}. \end{cases}\displaystyle \end{aligned}$$
(7)

It is clear that this numerical model is a two-step exponential discretization of the continuous problem (2). Indeed, using the discrete operators, it is an easy algebraic task to check that (7) can be equivalently rewritten as follows:

$$ \begin{aligned} &T_{m}^{k+1} =\bigl(T_{m}^{k}+\lambda \bigr)\exp \biggl[ \frac{\tau (\beta - ( \kappa V_{m}^{k}+d+\frac{2}{h^{2}} )T_{m}^{k} + \gamma U_{m}^{k} + a_{T,m}^{k} + e_{T,m}^{k} )}{T_{m}^{k}+\lambda } \biggr] - \lambda , \\ &U_{m}^{k+1} =\bigl(U_{m}^{k}+ \lambda \bigr) \exp \biggl[ \frac{\tau ( \kappa V_{m}^{k} T_{m}^{k}- ( \gamma +\delta +\frac{2}{h^{2}} )U_{m}^{k} + a_{U,m}^{k}+e_{U,m}^{k} )}{U_{m}^{k}+\lambda } \biggr] - \lambda , \\ &V_{m}^{k+1} = \bigl(V_{m}^{k}+ \lambda \bigr) \exp \biggl[ \frac{\tau ( N\delta U_{m}^{k}- ( c+\frac{2}{h^{2}} )V_{m}^{k} + a_{V,m}^{k} + e_{V,m}^{k} )}{V_{m}^{k}+\lambda } \biggr]-\lambda , \\ &\quad \text{such that } \textstyle\begin{cases} T_{m}^{0}= \phi _{T} (x_{m}), & \forall m \in \overline{I}_{M}, \\ U_{m}^{0}=\phi _{U} (x_{m}), & \forall m \in \overline{I}_{M}, \\ V_{m}^{0}=\phi _{V} (x_{m}), & \forall m \in \overline{I}_{M}, \\ T_{m}^{k} = \psi _{T} (x_{m},t_{k}), & \forall (m,k) \in \partial J \times \overline{I}_{K}, \\ U_{m}^{k}=\psi _{U} (x_{m},t_{k}), & \forall (m,k) \in \partial J \times \overline{I}_{K}, \\ V_{m}^{k}=\psi _{V} (x_{m},t_{k}), & \forall (m,k) \in \partial J\times \overline{I}_{K}, \end{cases}\displaystyle \end{aligned} $$
(8)

where \(a_{W,m}^{k}=h^{- 2}W_{m+1}^{k}\) and \(e_{W,m}^{k}=h^{- 2}W_{m-1}^{k}\) for each \(m \in I_{M-1}\), each \(k \in \bar{I}_{K-1}\), and \(W \in \{T,U,V\}\). Notice that each of the three equations in (8) can be expressed as \(T_{m}^{k+1}=F_{T}(T_{m}^{k})\), \(U_{m}^{k+1}=F_{U}(U_{m}^{k})\), and \(V_{m}^{k+1}=F_{V}(V_{m}^{k})\), respectively. Here, the expressions of the functions \(F_{T}\), \(F_{U}\), and \(F_{V}\) are as follows:

$$ \textstyle\begin{cases} F_{T}(w) =g_{T}(w)\exp (\varphi _{T}(w) )-\lambda , \\ F_{U}(w) =g_{U}(w)\exp (\varphi _{U}(w) )-\lambda , \\ F_{V}(w) =g_{V}(w)\exp (\varphi _{V}(w) )-\lambda . \end{cases} $$
(9)

In turn, each function \(g_{T}\), \(g_{U}\), and \(g_{V}\) is given by \(g_{W}(w)=w+\lambda \) with \(W\in \{T,U,V\}\), and \(\varphi _{T}\), \(\varphi _{U}\), \(\varphi _{V}\) are

$$\begin{aligned}& \varphi _{T}(w) =\frac{\tau }{w+\lambda } \biggl(\beta - \biggl( \kappa V_{m}^{k}+d+\frac{2}{h^{2}} \biggr)w + \gamma U_{m}^{k} + a_{T,m}^{k} + e_{T,m}^{k} \biggr), \end{aligned}$$
(10)
$$\begin{aligned}& \varphi _{U}(w) = \frac{\tau }{w+\lambda } \biggl( \kappa V_{m}^{k} T_{m}^{k}- \biggl( \gamma +\delta +\frac{2}{h^{2}} \biggr)w + a_{U,m}^{k}+e_{U,m}^{k} \biggr), \end{aligned}$$
(11)
$$\begin{aligned}& \varphi _{V}(w) = \frac{\tau }{w+\lambda } \biggl( N\delta U_{m}^{k}- \biggl( c+\frac{2}{h^{2}} \biggr)w + a_{V,m}^{k} + e_{V,m}^{k} \biggr). \end{aligned}$$
(12)

For convenience, we define the \((M + 1)\)-dimensional real vectors

$$\begin{aligned}& T^{k} = \bigl(T_{0}^{k},T_{1}^{k}, \ldots ,T_{m}^{k},\ldots ,T_{M-1}^{k},T_{M}^{k} \bigr), \end{aligned}$$
(13)
$$\begin{aligned}& U^{k} = \bigl(U_{0}^{k},U_{1}^{k}, \ldots ,U_{m}^{k},\ldots ,U_{M-1}^{k},U_{M}^{k} \bigr), \end{aligned}$$
(14)
$$\begin{aligned}& V^{k} = \bigl(V_{0}^{k},V_{1}^{k}, \ldots ,V_{m}^{k},\ldots ,V_{M-1}^{k},V_{M}^{k} \bigr), \end{aligned}$$
(15)

for each \(k \in \bar{I}_{K}\). In general, we say that a vector \(W \in \mathbb{R}\) is positive if all the components are positive. In such a case, we use the notation \(W > 0\). We say that W is bounded from above by \(s \in \mathbb{R}\) if all the components of W are less that s, in which case we employ the notation \(W < s\). Finally, if s is a positive number, then we use \(0 < W < s\) to represent that \(W > 0\) and \(W < s\).

The following results show the existence and uniqueness of the solutions of (8) along with the preservation of the constant solutions.

Theorem 1

(Existence and uniqueness)

Let \(k \in \bar{I}_{K-1}\). If \(T^{k}>0\), \(U^{k}>0\), \(V^{k}>0\), and \(\lambda >0\), then the discrete model (8) has a unique solution \(T^{k+1}\), \(U^{k+1}\), and \(V^{k+1}\).

Proof

The numbers \(T_{m}^{k}+\lambda \), \(U_{m}^{k}+\lambda \), and \(V_{m}^{k}+\lambda \) are greater than zero. As a consequence, the real numbers \(T_{m}^{k+1}=F_{T}(T_{m}^{k})\), \(U_{m}^{k+1}=F_{U}(U_{m}^{k})\), and \(V_{m}^{k+1}=F_{V}(V_{m}^{k})\) are defined uniquely, whence the existence and uniqueness readily follow. □

Theorem 2

(Constant solutions)

For each \(k \in \overline{I} _{K}\), let \(T ^{k}\), \(U ^{k}\), and \(V ^{k}\) be the zero vectors of dimension \(M + 1\). Then the sequences \((T^{k})_{k=0}^{K}\), \((U^{k})_{k=0}^{K}\), and \((V^{k})_{k=0}^{K}\) form a solution of model (8) if \(\phi _{T},\phi _{U},\phi _{V},\psi _{T},\psi _{U},\psi _{V} \equiv 0\) and \(\beta =0\).

Proof

By the hypothesis, the vectors \(T^{0}=U^{0}=V^{0}=0\) satisfy the initial-boundary conditions. Now, if \(T^{k}=U^{k}=V^{k}=0\) for some \(k \in \bar{I}_{K-1}\), it is easy to verify that \(\varphi _{T}(0)=\varphi _{U}(0)=\varphi _{V}(0)=0\). This implies in particular that \(T_{m}^{k+1}=F_{T}(0)=0\), \(U_{m}^{k+1}=F_{U}(0)=0\), and \(V_{m}^{k+1}=F_{V}(0)=0\) for each \(m \in I_{M-1}\). The conclusion follows using induction. □

The next lemma is an important tool to show the positivity and boundedness of the solutions of the discrete system. The proposition is a result from real analysis, and its proof is established through the mean value theorem.

Lemma 3

Let \(F,g,\varphi :[0,1] \rightarrow \mathbb{R}\) be such that \(F(w)=g(w)\exp (\varphi (w) )-\lambda \) for each \(w \in [0,1]\) and some \(\lambda \in \mathbb{R}\). Suppose that g and φ are differential and that, for each \(w \in [0,1]\), the inequality

$$ g^{\prime }(w)+g(w)\varphi ^{\prime }(w)>0 $$
(16)

holds. Then F is an increasing function in \([0,1]\).

Lemma 4

Let \(\lambda >0\) and \(k \in \bar{I}_{K-1}\). Define the following positive constants:

$$\begin{aligned}& B_{T}^{0} =\beta +\gamma + \biggl(\kappa +d+ \frac{2}{h^{2}} \biggr) \lambda +\frac{2}{h^{2}}, \end{aligned}$$
(17)
$$\begin{aligned}& B_{U}^{0} = \biggl(\gamma +\delta + \frac{2}{h^{2}} \biggr)\lambda + \kappa +\frac{2}{h^{2}}, \end{aligned}$$
(18)
$$\begin{aligned}& B_{V}^{0} = \biggl(c+\frac{2}{h^{2}} \biggr) \lambda + N\delta + \frac{2}{h^{2}}, \end{aligned}$$
(19)

and assume that \(0< T^{k}<1\), \(0< U^{k}<1\), and \(0< V^{k}<1\). If the inequalities \(\tau B_{T}^{0}<\lambda \), \(\tau B_{U}^{0}<\lambda \), and \(\tau B_{V}^{0}<\lambda \) hold, then \(F_{T}(T_{m}^{k})\), \(F_{U}(U_{m}^{k})\), and \(F_{V}(V_{m}^{k})\) are increasing functions for each \(m\in I_{M-1}\) and each \(k\in \bar{I}_{K-1}\).

Proof

Define \(H_{W}(w)=g_{W}^{\prime }(w)+g_{W}(w)\varphi _{W}^{\prime }(w)\) for each \(W\in \{T,U,V\}\) and each \(w \in [0,1]\). After some algebra, it is possible to see that

$$\begin{aligned}& H_{T}(w) =\frac{G_{T}(w)}{w+\lambda }, \quad \forall w \in [0 , 1], \end{aligned}$$
(20)
$$\begin{aligned}& H_{U}(w) =\frac{G_{U}(w)}{w+\lambda }, \quad \forall w \in [0 , 1], \end{aligned}$$
(21)
$$\begin{aligned}& H_{V}(w) =\frac{G_{V}(w)}{w+\lambda }, \quad \forall w \in [0 , 1], \end{aligned}$$
(22)

where

$$\begin{aligned}& G_{T}(w) =w+\lambda +\tau \biggl[\gamma U_{m}^{k}+a_{T,m}^{k}+e_{T,m}^{k}- \kappa \lambda V_{m}^{k}-d\lambda -\frac{2\lambda }{h^{2}}- \beta \biggr], \end{aligned}$$
(23)
$$\begin{aligned}& G_{U}(w) =w+\lambda -\tau \biggl[\gamma \lambda +\delta \lambda + \frac{2\lambda }{h^{2}} + \kappa V_{m}^{k} T_{m}^{k}+a_{U,m}^{k}+e_{U,m}^{k} \biggr], \end{aligned}$$
(24)
$$\begin{aligned}& G_{V}(w) =w+\lambda -\tau \biggl[c\lambda + \frac{2\lambda }{h^{2}}+N \delta U_{m}^{k}+a_{V,m}^{k}+e_{V,m}^{k} \biggr], \end{aligned}$$
(25)

for each \(w \in [0 , 1]\). Using Lemma 3, we want to prove that the functions \(F_{T}\), \(F_{U}\), and \(F_{V}\) are increasing in \([0,1]\). To that effect, we need to show that the functions \(H_{T}\), \(H_{U}\), and \(H_{V}\) are positive on \([0,1]\) or, equivalently, that the functions \(G_{T}\), \(G_{U}\), and \(G_{V}\) are positive. Using the hypotheses, note

$$\begin{aligned}& \bigl\vert a_{W,m}^{k} \bigr\vert \leq \frac{1}{h^{2}},\quad \forall W \in \{T,U,V\}, \end{aligned}$$
(26)
$$\begin{aligned}& \bigl\vert e_{W,m}^{k} \bigr\vert \leq \frac{1}{h^{2}},\quad \forall W \in \{T,U,V\}. \end{aligned}$$
(27)

As a consequence, observe that \(G_{W}(w)\geq \lambda -\tau B_{W}^{0}>0\) for each \(W\in \{T,U,V\}\) and \(w\in [0,1]\). In this way, the functions \(G_{T}\), \(G_{U}\), and \(G_{V}\) are positive on \([0,1]\). Using Lemma 3, we conclude that the functions \(F_{T}\), \(F_{U}\), and \(F_{V}\) are increasing in the interval \([0,1]\). □

Let \(W\in \{T,U,V\}\). In the following, \(\mathcal{R}_{\phi _{W}}\) and \(\mathcal{R}_{\psi _{W}}\) represent the ranges of the functions \(\phi _{W}\) and \(\psi _{W}\), respectively, over the interval \([0,1]\).

Theorem 5

(Positivity and boundedness)

Let \(\lambda >0\), and suppose that the following inequalities are satisfied:

$$ \textstyle\begin{cases} \beta +\gamma < d, \\ \kappa +\delta < \gamma , \\ N\delta < c. \end{cases} $$
(28)

Let \(B_{T}^{0}\), \(B_{U}^{0}\), and \(B_{V}^{0}\) be as in Lemma 4, and suppose that \(\mathcal{R}_{\phi _{W}}, \mathcal{R}_{\psi _{W}} \subseteq (0,1)\). If the inequalities \(\tau B_{T}^{0}<\lambda \), \(\tau B_{U}^{0}<\lambda \), and \(\tau B_{V}^{0}<\lambda \) hold, then there are unique sequences of vectors \((T^{k})_{k=0}^{K}\), \((U^{k})_{k=0}^{K}\), and \((V^{k})_{k=0}^{K}\) that satisfy \(0< T^{k}<1\), \(0< U^{k}<1\), and \(0< V^{k}<1\) for each \(k \in \overline{I} _{K}\).

Proof

We use induction to reach the conclusion. By hypothesis, the conclusion of this theorem is satisfied for \(k=0\), so let us assume that it holds also for some \(k \in \bar{I}_{K-1}\). Lemma 3 assures that the functions \(F_{T}\), \(F_{U}\), and \(F_{V}\) are increasing on \([0,1]\). Let \(m \in I_{K-1}\). If \(\beta =0\) and \(T_{m}^{k}=U_{m}^{k}=V_{m}^{k}=0\), then it follows that

$$\begin{aligned}& F_{T}(0) =\lambda \exp \biggl(\frac{\tau }{\lambda } \bigl(\beta + \gamma U_{m}^{k} \bigr) \biggr)-\lambda =0, \end{aligned}$$
(29)
$$\begin{aligned}& F_{U}(0) =\lambda \exp \biggl(\frac{\tau }{\lambda } \bigl(\kappa V_{m}^{k} T_{m}^{k} \bigr) \biggr)-\lambda =0, \end{aligned}$$
(30)
$$\begin{aligned}& F_{V}(0) =\lambda \exp \biggl(\frac{\tau }{\lambda } \bigl(N\delta U_{m}^{k} \bigr) \biggr)-\lambda =0. \end{aligned}$$
(31)

On the other hand, the hypothesis establishes that

$$\begin{aligned}& \varphi _{T}(1) < \frac{\tau }{1+\lambda }(\beta -d+\gamma )< 0, \end{aligned}$$
(32)
$$\begin{aligned}& \varphi _{U}(1) < \frac{\tau }{1+\lambda }(\kappa -\gamma +\delta )< 0, \end{aligned}$$
(33)
$$\begin{aligned}& \varphi _{V}(1) < \frac{\tau }{1+\lambda }(N\delta -c)< 0. \end{aligned}$$
(34)

This and (9) show that \(F_{T}(1)<1\), \(F_{U}(1)<1\), and \(F_{V}(1)<1\). Notice that the functions \(F_{T},F_{U},F_{V}:[0,1]\rightarrow \mathbb{R}\) are increasing and that \(0< F_{W}(0)< F_{W}(1)<1\) for each \(W \in \{T,U,V\} \). The inequalities \(0< W^{k}<1\) for \(W = T , U , V\) imply that \(T_{m}^{k+1}=F_{T}(T_{m}^{k})\), \(U_{m}^{k+1}=F_{U}(U_{m}^{k})\), and \(V_{m}^{k+1}=F_{V}(V_{m}^{k})\) all are numbers in the set \((0,1)\) for each \(m \in I_{M-1}\). Using the data at the boundary, we reach \(0< T_{m}^{k+1}<1\), \(0< U_{m}^{k+1}<1\), and \(0< V_{m}^{k+1}<1\). The conclusion follows using induction. □

As a conclusion of this section, the numerical methodology is a structure-preserving scheme to approximate the solutions of (2). In this manuscript, the concept of ‘structure preservation’ or ‘dynamical consistency’ refers not only to the capacity of discrete models to keep discrete versions of some physical features. In this context, these notions refer also to the capability of a numerical method to be able to conserve some mathematical characteristics of the solutions of interest of continuous paradigms, like positivity [16], boundedness [17, 18], monotonicity [19], and convexity of approximations [20], among other physically relevant features [21].

3 Numerical properties

In this stage, we present the main numerical features of the finite-differences scheme (8). More precisely, we are interested in proving consistency, unconditional stability, and convergence. To show the consistency of the numerical scheme, we require the following continuous operators:

$$\begin{aligned}& \mathcal{L}_{T} T =( T+\lambda ) \frac{\partial }{\partial t} \ln (T+ \lambda ) - \beta +\kappa V T+dT-\gamma U- \frac{\partial ^{2} T}{\partial x^{2}} , \end{aligned}$$
(35)
$$\begin{aligned}& \mathcal{L}_{U} U =(U+\lambda )\frac{\partial }{\partial t} \ln (U+ \lambda ) - \kappa VT+(\gamma +\delta )U- \frac{\partial ^{2} U}{\partial x^{2}} , \end{aligned}$$
(36)
$$\begin{aligned}& \mathcal{L}_{V} V =(V+\lambda )\frac{\partial }{\partial t} \ln (V+ \lambda ) - N\delta U+cV-\frac{\partial ^{2} V}{\partial x^{2}} \end{aligned}$$
(37)

for each \((x , t) \in \Omega \). Also, we define the difference operators

$$\begin{aligned}& L_{T} T(x_{m},t_{k}) = \bigl(T_{m}^{k}+\lambda \bigr)\delta _{t} \ln \bigl(T_{m}^{k}+ \lambda \bigr) -\beta + \bigl(\kappa V_{m}^{k} + d - \delta _{x} ^{2} \bigr) T_{m}^{k}- \gamma U_{m}^{k} , \end{aligned}$$
(38)
$$\begin{aligned}& L_{U} U(x_{m},t_{k}) = \bigl(U_{m}^{k}+\lambda \bigr)\delta _{t} \ln \bigl(U_{m}^{k}+ \lambda \bigr) - \kappa V_{m}^{k}T_{m}^{k}+(\gamma + \delta )U_{m}^{k}- \delta _{x}^{2} U_{m}^{k} , \end{aligned}$$
(39)
$$\begin{aligned}& L_{V} V(x_{m},t_{k}) = \bigl(V_{m}^{k}+\lambda \bigr)\delta _{t} \ln \bigl(V_{m}^{k}+ \lambda \bigr) - N\delta U_{m}^{k}+cV_{m}^{k}- \delta _{x}^{2} V_{m}^{k} \end{aligned}$$
(40)

for each \(m\in I_{M-1}\) and \(k \in \bar{I}_{K-1}\). For the remainder, the symbols \(\Vert \cdot \Vert _{2} \) and \(\Vert \cdot \Vert _{\infty }\) are used to denote the Euclidean and the maximum norms in \(\mathbb{R}^{M + 1}\), respectively.

Theorem 6

(Consistency)

If \(T , U , V \in \mathcal{C}^{4,3}_{x,t}(\overline{\Omega })\) and \(\lambda >0\), then there exist positive constants \(C _{T}\), \(C _{U}\), and \(C _{V}\), which are independent of τ and h, such that

$$ \bigl\vert \mathcal{L}_{W} W(x,t) - L_{W} W(x_{m},t_{k}) \bigr\vert \leq C _{W} \bigl(\tau +h^{2} \bigr) $$
(41)

for each \(m\in I_{M-1}\), \(k \in \bar{I}_{K-1}\), and \(W \in \{T,U,V\}\).

Proof

We prove the consistency only for \(W = T\), the consistencies for \(W = U\) and \(W = V\) are proved in a similar fashion. To that end, we employ the usual arguments based on Taylor polynomials. As a consequence of the hypotheses on the regularity of T, there exist positive constants \(C_{T,1}\) and \(C_{T,2}\) independent of τ and h such that, for each \((m , k) \in I _{M - 1} \times \overline{I} _{K - 1}\),

$$\begin{aligned}& \biggl\vert \bigl( T _{m} ^{k}+\lambda \bigr) \frac{\partial }{\partial t} \ln \bigl(T _{m} ^{k}+\lambda \bigr) - \bigl(T_{m}^{k}+\lambda \bigr)\delta _{t} \ln \bigl(T_{m}^{k}+ \lambda \bigr) \biggr\vert \leq C_{T,1} \tau , \end{aligned}$$
(42)
$$\begin{aligned}& \biggl\vert \frac{\partial ^{2} T}{\partial x^{2}}(x_{m},t_{k}) - \delta _{x}^{2} T_{m}^{k} \biggr\vert \leq C_{T,2} h^{2}. \end{aligned}$$
(43)

On the other hand, observe that

$$\begin{aligned}& \bigl\vert \kappa V(x_{m},t_{k}) T(x_{m},t_{k})+dT(x_{m},t_{k}) - \kappa V_{m}^{k} T_{m}^{k}-dT_{m}^{k} \bigr\vert = 0, \end{aligned}$$
(44)
$$\begin{aligned}& \bigl\vert \gamma U(x_{m},t_{k}) - \gamma U_{m}^{k} \bigr\vert = 0. \end{aligned}$$
(45)

Finally, the conclusion follows now from the triangle inequality after we define the positive constant \(C_{T}=\max \{C_{T,1}, C_{T,2}\}\), which is independent of τ and h. Similarly, we may show the inequalities corresponding to \(W = U\) and \(W = V\). □

Under the assumptions of this theorem, there is a positive constant C which is independent of τ and h with the property that, for each \(m\in I_{M-1}\), \(k \in \bar{I}_{K-1}\), and \(W \in \{T,U,V\}\),

$$ \bigl\vert \mathcal{L}_{W} W(x,t) - L_{W} W(x_{m},t_{k}) \bigr\vert \leq C \bigl(\tau +h^{2} \bigr). $$
(46)

Indeed, observe that \(C = C _{T} \vee C _{U} \vee C _{V}\) is a constant which satisfies this inequality. This fact will be employed when we prove the convergence of scheme (7). In our next step, we show the stability of the proposed scheme. To that end, we fix two systems of initial-boundary data which are labeled \(\Phi = (\phi _{T} , \phi _{U} , \phi _{V} , \psi _{T} , \psi _{U} , \psi _{V})\) and \(\widetilde{\Phi } = (\widetilde{\phi } _{T} , \widetilde{\phi } _{U} , \widetilde{\phi } _{V} , \widetilde{\psi } _{T} , \widetilde{\psi } _{U} , \widetilde{\psi } _{V})\). The corresponding solutions of (7) are represented respectively by \((T , U , V)\) and \((\widetilde{T} , \widetilde{U} , \widetilde{V})\). In particular, notice that the following result proves that the scheme is unconditionally stable.

Theorem 7

(Stability)

Let Φ and Φ̃ be two sets of initial-boundary conditions for problem (7), and let \(\lambda > 0\). Suppose that the hypotheses of Theorem 5are satisfied for both triplets \((T , U , V)\) and \((\widetilde{T} , \widetilde{U} , \widetilde{V})\). There is a constant C, which is independent of the initial data such that

$$ \bigl\Vert W^{k}-\widetilde{W}^{k} \bigr\Vert _{\infty } \leq C \bigl\Vert W^{0} - \widetilde{W}^{0} \bigr\Vert _{\infty },\quad \forall k \in \bar{I}_{K}, \forall W \in \{ T , U , V \}. $$
(47)

Proof

Beforehand, notice that Theorem 5 guarantees that \((T , U , V)\) and \((\widetilde{T} , \widetilde{U} , \widetilde{V})\) exist and that they are bounded. On the other hand, let \(W=T\) and introduce the function \(\Phi _{m}^{k}:[0,1]^{(M+1)} \rightarrow \mathbb{R}\) for each \(m\in I_{M-1}\) and \(\bar{I}_{K-1}\) by

$$ \Phi _{m}^{k}(T)= \bigl(T_{m}^{k}+ \lambda \bigr)\exp \biggl( \frac{\tau \Psi (T)}{T_{m}^{k}+\lambda } \biggr)-\lambda ,\quad \forall T\in [0,1]^{(M+1)}. $$
(48)

Here, the function \(\Psi (T)\) is defined by

$$ \Psi (T)=\beta - \biggl( \kappa V_{m}^{k}+d+ \frac{2}{h^{2}} \biggr)T_{m}^{k} + \gamma U_{m}^{k} + a_{T,m}^{k} + e_{T,m}^{k}. $$
(49)

It is readily checked that the function \(\Phi _{m}^{k}\) is of class \(\mathcal{C}^{1} ([0,1]^{(M+1)} )\) for each \(k \in \overline{I} _{K}\). As a consequence of this, the number \(C_{m,k}=\max_{[0,1]^{(M+1)}} \Vert \nabla \Phi _{m}^{k} \Vert _{2} \) exists. For each \(T, \widetilde{T} \in [0,1]^{(M+1)}\), there exists some \(\xi \in [0,1]^{(M+1)}\) with the property that

$$ \bigl\vert \Phi _{m}^{k}(T)- \Phi _{m}^{k}(\widetilde{T}) \bigr\vert \leq \bigl\Vert \nabla \Phi _{m}^{k}(\xi ) \bigr\Vert _{2} \Vert T-\widetilde{T} \Vert _{2} \leq C_{m,k} \sqrt{(M+1)} \Vert T-\widetilde{T} \Vert _{ \infty }. $$
(50)

As consequence, note that, for each \(m\in I_{M-1}\),

$$ \bigl\vert T_{m}^{k} - \widetilde{T}_{m}^{k} \bigr\vert = \bigl\vert \Phi _{m}^{k}(T)- \Phi _{m}^{k}( \widetilde{T}) \bigr\vert \leq C_{k} \bigl\Vert T^{k} - \widetilde{T}^{k} \bigr\Vert _{\infty }, $$
(51)

where

$$ C_{k}=1 \vee \max \bigl\lbrace C_{m,k} \sqrt{(M+1)}: 1 \leq m \leq M-1 \bigr\rbrace . $$
(52)

Using (51), it is clear that \(\Vert T^{k+1} - \widetilde{T}^{k+1} \Vert _{\infty } \leq C_{k} \Vert T^{k} - \widetilde{T}^{k} \Vert _{\infty } \) for each \(k \in \bar{I}_{K+1}\). Finally, recursion shows now that the inequality \(\Vert T^{k} - \widetilde{T}^{k} \Vert _{\infty } \leq C _{T} \Vert T^{0} - \widetilde{T}^{0} \Vert _{\infty }\) is satisfied for each \(k \in \bar{I}_{K}\), where

$$ C _{T} =(M+1)^{K/2} \prod_{k=0}^{K-1} C_{k}. $$
(53)

Similarly, we can prove that there exist positive constants \(C _{U}\) and \(C _{W}\), with the property that \(\Vert U^{k} - \widetilde{U}^{k} \Vert _{\infty } \leq C _{U} \Vert U^{0} - \widetilde{U}^{0} \Vert _{\infty }\) and \(\Vert V^{k} - \widetilde{V}^{k} \Vert _{\infty } \leq C _{V} \Vert V^{0} - \widetilde{V}^{0} \Vert _{\infty }\). The conclusion is reached now if we define \(C = C _{T} \vee C _{U} \vee C _{V}\). □

Finally, we study the convergence of the numerical scheme (8). In the next result, we let \((T , U , V)\) be a solution of differential problem (2) associated with the set of initial-boundary data \(\Phi = (\phi _{T} , \phi _{U} , \phi _{V} , \psi _{T} , \psi _{U} , \psi _{V})\). Meanwhile, the numerical solution obtained through the discrete model (8) is denoted by \((\widetilde{T} , \widetilde{U} , \widetilde{V})\).

Theorem 8

(Convergence)

Let Φ be a set of initial-boundary data which are bounded in \((0 , 1)\), and let \(\lambda > 0\). Assume that problem (2) has a unique solution bounded in \((0 , 1)\) such that \(T , U , V \in \mathcal{C} _{x , t} ^{4 , 3} (\overline{\Omega })\). Suppose that the conditions of Theorem 5hold, and let

$$ \exp (\tau / \lambda )-1\leq 2\tau / \lambda . $$
(54)

For each \(W = T , U , V\), there is a constant \(C_{W}\) independent of τ and h such that, for each \(k \in \bar{I}_{K}\),

$$ \bigl\Vert W^{k} - \widetilde{W}^{k} \bigr\Vert _{\infty } \leq C_{W} \bigl(\tau + h^{2} \bigr). $$
(55)

Proof

Beforehand, notice that Theorem 5 assures that positive and bounded solutions for discrete problem (7) exist. Without loss of generality, let \(W=T\) and define the difference \(e^{k}_{m}=T^{k}_{m}-\widetilde{T}^{k}_{m}\) for each \(m \in \bar{I}_{M}\) and \(k \in \bar{I}_{K}\). Notice that the exact solution T of problem (1) satisfies scheme (8) at the point \((x_{m},t_{k})\) having some local truncation error \(R_{m}^{k}\) for each \(m \in \bar{I}_{M-1}\) and \(k \in \bar{I}_{K-1}\). Also, for each \(m\in \bar{I}_{M-1}\) and \(k \in \bar{I}_{K-1}\), the analytical and discrete solutions satisfy, respectively,

$$\begin{aligned}& \bigl(W_{m}^{k} + \lambda \bigr)L_{T} T_{m}^{k} = R_{m}^{k}, \end{aligned}$$
(56)
$$\begin{aligned}& \bigl(\widetilde{T}_{m}^{k} +\lambda \bigr)L_{T} \widetilde{T}_{m}^{k} = 0 . \end{aligned}$$
(57)

By Theorem (6), there exists \(C_{0}>0\) such that \(\vert R_{m}^{k} \vert \leq C_{0} (\tau +h^{2}) \) for each \(m\in \bar{I}_{M-1}\) and \(k \in \bar{I}_{K-1}\). Using the definitions of the discrete operators in equations (56) and (57), we have that

$$\begin{aligned}& T_{m}^{k+1} = \bigl(T_{m}^{k}+ \lambda \bigr) \exp \biggl( \frac{\tau R_{m}^{k}}{T_{m}^{k} + \lambda } \biggr) \exp \bigl( \varphi _{T} \bigl(T_{m}^{k} \bigr) \bigr) - \lambda , \end{aligned}$$
(58)
$$\begin{aligned}& \widetilde{T}_{m}^{k+1} = \bigl(\widetilde{T}_{m}^{k}+ \lambda \bigr) \exp \bigl(\varphi _{T} \bigl(\widetilde{T}_{m}^{k} \bigr) \bigr)-\lambda \end{aligned}$$
(59)

for each \(m\in \bar{I}_{M-1}\) and \(k \in \bar{I}_{K-1}\). Subtracting \(\widetilde{T}_{m}^{k}\) of \(T_{m}^{k}\), we have

$$ \begin{aligned} \bigl\vert e_{m}^{k} \bigr\vert & \leq \bigl(T_{m}^{k}+\lambda \bigr) \exp \biggl[ \biggl(\frac{\tau R_{m}^{k}}{T_{m}^{k} + \lambda } \biggr) -1 \biggr] \exp \bigl( \varphi _{T} \bigl(T_{m}^{k} \bigr) \bigr) + \bigl\vert \Phi _{m}^{k}(T) - \Phi _{m}^{k}( \widetilde{T}) \bigr\vert \\ & \leq (1+\lambda ) D_{m}^{k} \bigl[\exp \bigl(\tau R_{m}^{k} / \lambda \bigr)-1 \bigr] + C_{m}^{k} \bigl\Vert T^{k}- \widetilde{T}^{k} \bigr\Vert _{\infty } \\ & \leq D \tau R_{m}^{k} + C \bigl\Vert e^{k} \bigr\Vert _{\infty } , \end{aligned} $$
(60)

where

$$\begin{aligned}& e^{k} = \bigl(e_{0}^{k}, e_{1}^{k}, e_{2}^{k}, \ldots , e_{M-1}^{k}, e_{M}^{k} \bigr), \end{aligned}$$
(61)
$$\begin{aligned}& D_{m}^{k} = \max \bigl\lbrace \exp \bigl( \varphi _{T} \bigl(T_{m}^{k} \bigr) \bigr) : T \in [0,1]^{M+1} \bigr\rbrace \end{aligned}$$
(62)

for each \(m\in \bar{I}_{M-1}\) and \(k \in \bar{I}_{K-1}\). In addition, we let

$$\begin{aligned}& C = \max \bigl\lbrace C_{m}^{k} \sqrt{M+1} : m=1, \ldots ,M-1; k=1, \ldots , K-1 \bigr\rbrace , \end{aligned}$$
(63)
$$\begin{aligned}& D = \max \biggl\lbrace \frac{2(1+\lambda )D_{m}^{k}}{\lambda } : m=1, \ldots ,M-1; k=1,\ldots ,K-1 \biggr\rbrace . \end{aligned}$$
(64)

The constants \(\Phi _{m}^{k}\) and \(C_{m}^{k}\) are as in the proof of Theorem 7. Moreover, all the constants \(C_{m}^{k}\) are in the interval \([0,1]\), therefore C is an element of the interval \([0,1]\). Theorem 6 implies now that, for each \(k\in \bar{I}_{K-1}\),

$$ \bigl\Vert e^{k+1} \bigr\Vert _{\infty }- \bigl\Vert e^{k} \bigr\Vert _{\infty } \leq \bigl\Vert e^{k+1} \bigr\Vert _{\infty } - C \bigl\Vert e^{k} \bigr\Vert _{\infty } \leq C_{0} D \tau \bigl( \tau +h^{2} \bigr). $$
(65)

Taking the sum on both ends of the previous inequality and using the initial data, we have

$$ \bigl\Vert e^{l+1} \bigr\Vert _{\infty } = \bigl\Vert e^{l+1} \bigr\Vert _{\infty } - \bigl\Vert e^{0} \bigr\Vert _{\infty } \leq C_{0} DT^{*} \bigl(\tau + h^{2} \bigr) = C _{T} \bigl( \tau + h^{2} \bigr), $$
(66)

where \(l\in \bar{I}_{K-1}\) and \(C _{T} =C_{0}DT^{*}\). The conclusion of this result has been reached now when \(W = T\). Analogously, we may easily prove the inequality of the conclusion when \(W = U\) and \(W = V\). □

4 Application

In this section, we show some computer simulations obtained using the finite-difference scheme (8). Beforehand, notice that the discrete model is an explicit scheme. To describe its computational implementation, for each \(k\in \bar{I}_{K+1}\), we redefine the real vectors \(T^{k}\), \(U^{k}\), and \(V^{k}\) as follows:

$$\begin{aligned}& T^{k} = \bigl(T^{k}_{1},T^{k}_{2}, \ldots , T^{k}_{M-2},T^{k}_{M-1} \bigr), \end{aligned}$$
(67)
$$\begin{aligned}& U^{k} = \bigl(U^{k}_{1},U^{k}_{2}, \ldots , U^{k}_{M-2},U^{k}_{M-1} \bigr), \end{aligned}$$
(68)
$$\begin{aligned}& V^{k} = \bigl(V^{k}_{1},V^{k}_{2}, \ldots , V^{k}_{M-2},V^{k}_{M-1} \bigr). \end{aligned}$$
(69)

These vectors belong to the set \(\mathbb{R}_{+}^{M+1}\), where \(\mathbb{R}_{+}\) is the system of positive numbers. Also, we define the vectors of initial conditions \(\boldsymbol{\phi} _{\mathbf{T}}, \boldsymbol{\phi} _{\mathbf{U}}, \boldsymbol{\phi} _{\mathbf{V}} \in \mathbb{R}_{+}^{M-1} \) as follows:

$$\begin{aligned}& \boldsymbol{\phi} _{\mathbf{T}} = \bigl(\phi _{T}(x_{1}), \phi _{T}(x_{2}),\ldots , \phi _{T}(x_{M-2}), \phi _{T}(x_{M-1}) \bigr), \end{aligned}$$
(70)
$$\begin{aligned}& \boldsymbol{\phi} _{\mathbf{U}} = \bigl(\phi _{U}(x_{1}), \phi _{U}(x_{2}),\ldots , \phi _{U}(x_{M-2}), \phi _{U}(x_{M-1}) \bigr), \end{aligned}$$
(71)
$$\begin{aligned}& \boldsymbol{\phi} _{\mathbf{V}} = \bigl(\phi _{V}(x_{1}), \phi _{V}(x_{2}),\ldots , \phi _{V}(x_{M-2}), \phi _{V}(x_{M-1}) \bigr). \end{aligned}$$
(72)

Meanwhile, for each \(k \in \bar{I}_{K}\), we define the vectors \(\boldsymbol{\psi} _{\mathbf{T}}^{k}, \boldsymbol{\psi} _{\mathbf{U}}^{k}, \boldsymbol{\psi} _{\mathbf{V}}^{k} \in \mathbb{R}_{+}^{M+1}\) of the boundary conditions through

$$\begin{aligned}& \boldsymbol{\psi} _{\mathbf{T}}^{k} = \bigl(\psi _{T}(x_{0},t_{k}),0,\ldots ,0,\psi _{T}(x_{M},t_{k}) \bigr), \end{aligned}$$
(73)
$$\begin{aligned}& \boldsymbol{\psi} _{\mathbf{U}}^{k} = \bigl(\psi _{U}(x_{0},t_{k}),0,\ldots ,0,\psi _{U}(x_{M},t_{k}) \bigr), \end{aligned}$$
(74)
$$\begin{aligned}& \boldsymbol{\psi} _{\mathbf{V}}^{k} = \bigl(\psi _{V}(x_{0},t_{k}),0,\ldots ,0,\psi _{V}(x_{M},t_{k}) \bigr). \end{aligned}$$
(75)

With the previous definitions and for each \(k\in \bar{I}_{K}\), we express the discrete model (8) in vector form as follows:

$$ \begin{aligned} &T^{k+1} = \bigl(T^{k}+\lambda \bigr)\exp \biggl[ \frac{\tau (\beta - ( \kappa V^{k}+d+\frac{2}{h^{2}} )T^{k} + \gamma U^{k} + a_{T}^{k} + e_{T}^{k} )}{T^{k}+\lambda } \biggr] - \lambda , \\ &U^{k+1} =\bigl(U^{k}+\lambda \bigr) \exp \biggl[ \frac{\tau ( \kappa V^{k} T^{k}- ( \gamma +\delta +\frac{2}{h^{2}} )U^{k} + a_{U}^{k}+e_{U}^{k} )}{U^{k}+\lambda } \biggr] - \lambda , \\ &V^{k+1} = \bigl(V^{k}+\lambda \bigr) \exp \biggl[ \frac{\tau ( N\delta U^{k}- ( c+\frac{2}{h^{2}} )V^{k} + a_{V}^{k} + e_{V}^{k} )}{V^{k}+\lambda } \biggr]-\lambda \\ &\quad \text{such that } \textstyle\begin{cases} T^{0} = \boldsymbol{\phi} _{\mathbf{T}}, \\ U^{0} = \boldsymbol{\phi} _{\mathbf{U}}, \\ V^{0} = \boldsymbol{\phi} _{\mathbf{V}} . \end{cases}\displaystyle \end{aligned} $$
(76)

For each \(k \in \bar{I}_{K}\) and \(W\in \{T,U,V\}\), the vectors \(a_{W}^{k}\) and \(e_{W}^{k}\) are defined as follows:

$$\begin{aligned}& a_{W}^{k} =\frac{1}{h^{2}} \bigl(W_{2}^{k},W_{3}^{k}, \ldots ,W_{M-1}^{k},W_{M}^{k} \bigr), \end{aligned}$$
(77)
$$\begin{aligned}& e_{W}^{k} =\frac{1}{h^{2}} \bigl(W_{0}^{k},W_{1}^{k}, \ldots ,W_{M-3}^{k},W_{M-2}^{k} \bigr). \end{aligned}$$
(78)

Using the boundary conditions, we readily have that \(W_{M}^{k}=\psi _{W}(x_{M},t_{k})\) and \(W_{0}^{k}=\psi _{W}(x_{0},t_{k})\) for each \(k\in \bar{I}_{K+1}\) and \(W\in \{T,U,V\}\). So, for all \(k \in \bar{I}_{K}\), the vector form of the finite-difference scheme (8) is defined as follows:

$$\begin{aligned}& \mathbf{T}^{k} = \bigl(\psi _{T}(x_{0},t_{k}),T^{k}_{1},T^{k}_{2}, \ldots , T^{k}_{M-2},T^{k}_{M-1}, \psi _{T}(x_{M},t_{k}) \bigr), \end{aligned}$$
(79)
$$\begin{aligned}& \mathbf{U}^{k} = \bigl(\psi _{U}(x_{0},t_{k}),U^{k}_{1},T^{k}_{2}, \ldots , U^{k}_{M-2},U^{k}_{M-1}, \psi _{U}(x_{M},t_{k}) \bigr), \end{aligned}$$
(80)
$$\begin{aligned}& \mathbf{V}^{k} = \bigl(\psi _{V}(x_{0},t_{k}),V^{k}_{1},T^{k}_{2}, \ldots , V^{k}_{M-2},V^{k}_{M-1}, \psi _{V}(x_{M},t_{k}) \bigr). \end{aligned}$$
(81)

The next experiments employ variations of the computer code in the Appendix, which is a basic computational implementation of our finite-difference scheme. The parameter values and the type of initial conditions are motivated by data used in the literature for similar models but without diffusion [9, 14].

Example 9

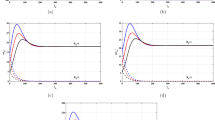
In this example, we let \(B=(0,100)\) and define the initial conditions \(\phi _{T}\), \(\phi _{U}\), and \(\phi _{V}\) as \(\phi _{T}(x)=x^{2}\), \(\phi _{U}(x)=0\), and \(\phi _{V}(x)=1\) for each \(x \in B\). These initial data describe an initial state in which no infected CD4+T cells are present, and the entire medium is formed from free HIV-1 infection particles. In turn, the normal density of the uninfected CD4+T cells increases in the linear medium considered herein. Let \(\lambda =0.1\), \(\beta =2\), \(d=5.05\), \(\kappa =0.03\), \(\delta =0.016\), \(\gamma =3.0\), \(c=20.4\), and \(N=1000\). Under this situation, Fig. 1 provides snapshots of the normalized solutions T, U, and V at the times \(t=0\), \(t=1\), \(t=3\), and \(t=5\). The graphs show that the solutions are positive and bounded in accordance with the results obtained in the previous sections. In our simulations, we used the following computational parameters \(\tau =0.00001\) and \(h=1\).

Figure 1
figure 1

Snapshots of the approximate solutions T, U, and V of (1) for each row at the time \(t=0\), \(t=1\), \(t=3\), and \(t=5\). The parameters employed are \(\lambda =0.1\), \(\beta =2\), \(d=5.05\), \(\kappa =0.03\), \(\delta =0.016\), \(\gamma =3.0\), \(c=20.4\), and \(N=1000\). We let \(\phi _{T} (x)\), \(\phi _{U} (x)\), and \(\phi _{V} (x)\) be as in Example 9. The approximations were calculated using our implementation of (76) in the Appendix, with \(\tau = 0.00001\) and \(h=1\)

Full size image

Example 10

Let \(B=(0,100)\) be as in the previous example, and use the initial conditions \(\phi _{T}(x)=-x^{2}+100x\), \(\phi _{U}(x)=0\), and \(\phi _{V}(x)=1\) for each \(x\in B\). Set the model and computational parameter values as before. Under these circumstances, Fig. 2 provides snapshots of the normalized solutions T, U, and V at the times \(t=0\), \(t=1\), \(t=3\), and \(t=5\). Once again, the results show that the numerical solutions are positive and bounded.

Figure 2
figure 2

Snapshots of the approximate solutions T, U, and V of (1) for each row at the time \(t=0\), \(t=1\), \(t=3\), and \(t=5\). The parameters employed are \(\lambda =0.1\), \(\beta =2\), \(d=5.05\), \(\kappa =0.03\), \(\delta =0.016\), \(\gamma =3.0\), \(c=20.4\), and \(N=1000\). We let \(\phi _{T} (x)\), \(\phi _{U} (x)\), and \(\phi _{V} (x)\) be as in Example 10. The approximations were calculated using our implementation of (76) in the Appendix, with \(\tau = 0.00001\) and \(h=1\)

Full size image

Before closing this section, we would like to point out the biological meaningfulness of the figures obtained in the previous examples. To start with, graphs (a), (d), (g), and (j) of Fig. 1 represent the evolution with respect to the time of the quantity of the uninfected CD4+T cells. Biologically, the quantity of these cells tends to decrease since there is a significant interaction of the HIV-1 infection with the CD4+T cells, resulting in an increment of them. The respective increments of the infected CD4+T cells with respect to the time are shown in graphs (b), (e), (h), and (k). Moreover, the quantity of the infected CD4+T cells could decrease since an infected cell could die or return to being an uninfected cell. Obviously, this phenomenon is biologically possible. In turn, graphs (c), (f), (i), and (l) represent the evolution of the HIV-1 infection. From these graphs, it is easy to see that the infection is decreasing with respect to the time due to the presence of an active death rate. The interpretation of the graphs in Fig. 2 is analogous.

5 Conclusions

In this manuscript, we numerically studied a coupled model consisting of three diffusive nonlinear partial differential equations. The system under investigation is a biological model which describes the interaction of the HIV-1 infection with the CD4+T cells. One of the equations of the model describes the rate of change of the density of the uninfected CD4+T cells, the second describes the rate of change of the infected CD4+T cells, and the third governs the rate of change of the free HIV-1 infection. The differential system was discretized using finite differences to estimate the analytical solutions. The technique that we used in this work is an exponential type that maintains the most important characteristics of the solutions of the continuous model. More concretely, the method was motivated by the well-known family of Bhattacharya exponential-type schemes [22–24]. Bhattacharya’s discretizations have been employed to derive computational techniques to solve various nonlinear partial differential equations [25–28]. As it is well known, the main advantage of this family of models is its computational efficiency.

The scheme presented in this work was analyzed to study its most important properties. The most important structural features proved in this work were related to the unique solvability of the discrete model. We also established that the scheme is able to preserve the nonnegativity and the boundedness of the estimations. These properties are highly relevant in light that the functions under investigation represent densities which are positive and bounded. From the numerical point of view, we proved the consistency of the scheme. Moreover, the method is stable, and it converges to the exact solutions with first order in the temporal variable and second order in the spatial. Finally, we provided some computational simulations to illustrate the capability of the scheme to preserve the positivity and the boundedness of the numerical solutions. A Matlab implementation of the method is provided in the Appendix for reproducibility purposes. It is worth pointing out that a study of the mathematical model (1) in two dimensions can be easily performed by extending the theoretical results of this work. Also, an implementation of our scheme in two dimensions is also easily feasible.

Before we close this work, there are various important comments that require to be thoroughly addressed. To start with, it is important to point out that there are some works in the literature where fractional-type models like (1) without diffusion have been investigated [9, 14]. Naturally, one would wonder which are the effects of considering a fractional diffusion in such HIV-1 systems. At this point, it is important to mention that one of the authors of the present manuscript has devoted part of his efforts to develop numerical methods for Riesz space-fractional partial differential equations [29, 30]. In that context, the differentiation order of the diffusion terms affect the speed of propagation of the spread of effects into the medium. Of course, it would be interesting to propose and analyze numerical models for fractional forms of the system under current investigation. However, the meaningfulness of the use of fractional derivatives in the realistic investigation of HIV-1 may be still questionable. Indeed, not many medical journals employ fractional operators to model the propagation of HIV-1, though the problem is mathematically interesting and challenging.