Positive solutions for some discrete semipositone problems via bifurcation theory

Abstract

Let $T > 1$ be an integer, and let $\mathbb{T}=\{1, 2,\ldots ,T\}$. We show the existence of positive solutions of the Dirichlet boundary value problem with second-order difference operator

$$ \textstyle\begin{cases} -\triangle ^{2} u(j-1)=\lambda f(j, u(j)), \quad j\in \mathbb{T},\\ u(0)=u(T + 1)=0, \end{cases} $$

where $\lambda >0$ is a parameter, and $f:\mathbb{T}\times \mathbb{R} ^{+}\to \mathbb{R}$ is a continuous function satisfying $f(j, 0)<0$ for all $j\in \mathbb{T}$. The proofs of the main results are based upon topological degree and global bifurcation techniques.

1 Introduction

In this paper, we deal with the existence of positive solutions of the discrete Dirichlet boundary value problems (BVP)

$$ \textstyle\begin{cases} -\triangle ^{2} u(j-1)=\lambda f(j, u(j)), & j\in \mathbb{T},\\ u(0)=u(T + 1)=0, \end{cases} $$

(1.1)

where $T > 1$ is an integer, $\mathbb{T}=\{1, 2,\ldots ,T\}$, △ is the forward difference operator defined by $\triangle u(j)=u(j+1)-u(j)$, $\triangle ^{2} u(j)=\triangle (\triangle u(j))$, $\lambda >0$ is a parameter, and $f:\mathbb{T}\times \mathbb{R}^{+} \to \mathbb{R}$ is a continuous function satisfying the condition

$(f_{1})$:

$f(j, 0)<0$, $\forall j\in \mathbb{T}$.

Problem (1.1) is referred as a semipositone problem, which is introduced by Castro and Shivaji [7] for Dirichlet problems of differential equations.

On the contrary, if

$$ f(j, 0)\geq 0, \quad \forall j\in \mathbb{T}, $$

then (1.1) is called a positone problem. It has been extensively studied by many authors by using different methods, such as those of topology degree theory, critical point theory, and the fixed point theorem in cones; see Agarwal, Perera, and O’Regan [2], Merdivenci [15], Bai and Xu [5], Henderson and Thompson [11, 12], Li, Niu, and Sun [13], Zhang and Ge [18], D’Aguìa, Mawhin, and Sciammetta [8], and the references therein.

Since 1989, the existence of positive solutions for semipositone problems of ordinary differential equations has also been extensively studied; we refer the reader to the celebrated works by Ambrosetti, Arcoya, and Buffoni [3] and Anuradha, Hai, and Shivaji [4].

However, relatively little is known about the existence of positive solutions for semipositone problems of difference equations; see Bai and Xu [6].

In particular, employing the fixed point theorem in cones due to Guo and Krasnoselskii, Bai and Xu [6] obtained the existence of at least one positive solution for the semipositone Sturm–Liouville-like BVP of the second-order difference equation

$$ \textstyle\begin{cases} -\triangle [p(j-1)\triangle u(j-1)]=\lambda f(j, u(j)), \quad j\in \mathbb{T},\\ \gamma _{1}u(0)-\gamma _{2}p(0)\triangle u(0)=0, \qquad \gamma _{3}u(T+1)+\gamma _{4}p(T)\triangle u(T)=0, \end{cases} $$

(1.2)

under the assumptions $\gamma _{i}\geq 0 \ (i=1,\ldots ,4)$, $\gamma _{1}\gamma _{3}+\gamma _{1}\gamma _{4}+\gamma _{2}\gamma _{3}>0$, and $p(j)>0$, $j\in \{0, 1,\ldots ,T\}$ and the superlinear condition

• (A1) there exist two positive integers α and β with $0<\alpha <\beta <T$ such that

  $$ \lim_{s\to \infty } \frac{f(j, s)}{s}=\infty $$

  uniformly for $j\in \{\alpha ,\ldots ,\beta \}$.

It is worth pointing out that in [6], only the existence of positive solutions of (1.2) for sufficiently small λ, the norm of solutions obtained is also small, and no information is provided about the global behavior of the set of positive solutions.

Motivated by [3, 6], in this paper, we address three points of interest regarding the discrete semipositone problem (1.1):

• (i) Does (1.1) have solutions of large norm?

• (ii) Does (1.1) have solutions for sufficiently large λ?

• (iii) Does the set of positive solutions of (1.1) have a connected component?

Particular significance in these points lie in the fact that when a continuous BVP is discretized, strange and interesting changes can occur in the solutions. For example, properties such as the existence, uniqueness, and multiplicity of solutions may not be shared between the continuous differential equation and related discrete difference equation [1, p. 520]. Thus new challenges are faced, and innovation is required. For instance, for $r\in (1, \infty )$, the problem

$$ \textstyle\begin{cases} -w''(x)= w^{r}(x), \quad x\in (0,1),\\ w(0)=w(1)=0 \end{cases} $$

has a unique positive solution $w_{0}$. However, for the corresponding discrete analogue

$$ \textstyle\begin{cases} -\triangle ^{2} w(j-1)=w^{r}(j), \quad j\in \mathbb{T},\\ w(0)=w(T + 1)=0, \end{cases} $$

the uniqueness of a positive solution is still open.

The rest of the paper is arranged as follows. In Sect. 2, we give some notations and preliminaries. In Sect. 3, we prove an existence result for asymptotically linear problems by topological theory. Section 4 is devoted to investigating sublinear problems, and a uniqueness result allows us to show that (1.1) possesses positive solutions for $\lambda \geq \lambda ^{\ast }$. Finally, in Sect. 5, we study superlinear problems, and some a priori estimates help us prove that (1.1) has positive solutions, provided that λ is small enough.

For recent developments of nonlinear discrete BVP by using critical point theory and bifurcation theory, we refer the reader to [14, 16, 19, 20] and the references therein.

2 Some notations and preliminaries

Recall that $\mathbb{T}=\{1, 2,\ldots ,T\}$. Let $\widehat{\mathbb{T}}=\{0, 1,\ldots ,T, T+1\}$. We will work in the space $X:=\{u:\widehat{\mathbb{T}}\to \mathbb{R}: u(0)=u(T+1)=0\}$; the norm of this space is defined by $\|u\|=\max_{j\in \widehat{\mathbb{T}}}|u(j)|$. Let

$$ \varSigma = \bigl\{ (\lambda ,u)\in \mathbb{R}^{+}\times X: u\neq 0, ( \lambda , u) \text{ satisfies (1.1)} \bigr\} . $$

Let $H:=\{u:\hat{\mathbb{T}}\to \mathbb{R}\}$ with the inner product

$$ (u,v)=\sum_{j=0}^{T+1}u(j)v(j), \quad u, v\in H, $$

and the norm

$$ \Vert u \Vert _{H}=\sqrt{(u,u)}= \Biggl(\sum _{j=0}^{T+1}u^{2}(j) \Biggr)^{1/2}. $$

We also set $\mathbb{R}^{+}=[0,+\infty )$.

Lemma 2.1

Let$u,v\in X$. Then

$$ \sum_{j=1}^{T}\triangle ^{2}u(j-1)v(j)=\sum_{j=1}^{T} \triangle ^{2}v(j-1)u(j). $$

Proof

Since $u(0)=u(T+1)=0$ and $v(0)=v(T+1)=0$, we have

$$\begin{aligned} &\sum_{j=1}^{T}\triangle ^{2}u(j-1)v(j) \\ &\quad =\sum_{j=1}^{T}v(j) \bigl( \triangle u(j)- \triangle u(j-1) \bigr) \\ &\quad =\sum_{j=1}^{T}\triangle u(j)v(j)-\sum_{j=1}^{T} \triangle u(j-1)v(j) \\ &\quad =\sum_{j=1}^{T}\triangle u(j)v(j)-\sum_{k=0} ^{T-1}\triangle u(k)v(k+1) \quad (\text{by setting } k=j-1) \\ &\quad = \Biggl[\triangle u(T)v(T)+\sum_{j=1}^{T-1} \triangle u(j)v(j) \Biggr]- \Biggl[\triangle u(0)v(1)+\sum _{k=1}^{T-1}\triangle u(k)v(k+1) \Biggr] \\ &\quad = \bigl[\triangle u(T)\triangle v(T)-\triangle u(0)\triangle v(0) \bigr]+ \Biggl[\sum_{j=1}^{T-1}\triangle u(j)v(j)- \sum_{j=1}^{T-1}\triangle u(j)v(j+1) \Biggr] \\ &\quad =\triangle u(T)\triangle v(T)-\triangle u(0)\triangle v(0)- \sum _{j=1}^{T-1}\triangle u(j)\triangle v(j). \end{aligned}$$

Similarly, we have

$$ \sum_{j=1}^{T}\triangle ^{2}v(j-1)u(j)=\triangle u(T)\triangle v(T)- \triangle u(0)\triangle v(0)-\sum_{j=1}^{T-1}\triangle u(j) \triangle v(j). $$

Accordingly,

$$ \sum_{j=1}^{T}\triangle ^{2}u(j-1)v(j)=\sum_{j=1}^{T} \triangle ^{2}v(j-1)u(j). $$

 □

Define the difference operator $L:X\to X$ by

$$ Lu(j) = \textstyle\begin{cases} -\triangle ^{2} u(j-1), &j\in \mathbb{T},\\ 0, &j=0,\\ 0, &j=T+1. \end{cases} $$

Then it is easy to see that $L: X\to X$ is an isomorphism.

Define $G: \widehat{\mathbb{T}}\times \widehat{\mathbb{T}}\to \mathbb{R}^{+}$ by

$$ G(j,s)=\frac{1}{T+1} \textstyle\begin{cases} (T+1-j)s, & 1\leq s\leq j\leq T+1,\\ (T+1-s)j, & 0\leq j\leq s\leq T. \end{cases} $$

Define

$$ E= \biggl\{ j\in \mathbb{N}:\frac{T}{4}\leq j\leq \frac{3T}{4} \biggr\} , \qquad \delta =\min \biggl\{ \frac{1}{T}\min E, T+1- \frac{1}{T}\max E \biggr\} . $$

From [10, 17] it follows that

$$\begin{aligned}& G(j,s)\leq G(s,s), \quad s\in \mathbb{T}, j\in \widehat{\mathbb{T}}, \end{aligned}$$

(2.1)

$$\begin{aligned}& G(j,s)\geq \delta G(s,s), \quad s\in \mathbb{T}, j\in E, \end{aligned}$$

(2.2)

and $K: X\to X$ defined by

$$ K\phi (j)=\sum_{s=1}^{T}G(j,s)f \bigl(s, \phi (s) \bigr) $$

is well defined and continuous.

According to the previous notations, $u\in X$ is a solution of (1.1) if and only if it is a solution of the problem

$$ u- \lambda Kf(u) = 0, \quad u\in X. $$

(2.3)

Hereafter we will use the same symbol to denote both the function and the associated Nemitski operator.

The first eigenvalue of

$$ \textstyle\begin{cases} -\triangle ^{2} u(j-1)=\lambda u(j), \quad j\in \mathbb{T},\\ u(0)=u(T + 1)=0 \end{cases} $$

is denoted by $\lambda _{1}$, and $\varphi _{1}$ is the corresponding eigenfunction such that $\varphi _{1} > 0$ in $\mathbb{T}$ and $\|\varphi _{1}\|=1$.

Let $X\subset H$. Further, we let $\mathcal{L}$ be the linear operator induced by L in H. It is well known that $\mathcal{L}$ has a principal eigenvalue $\lambda _{1}>0$, and the corresponding eigenspace is spanned by a function $\varphi _{1}\in X$. Hence the space H admits the topological direct decomposition

$$ H=H_{1}\oplus \{c\varphi _{1}\}, $$

where $H_{1}$ is the orthogonal complement (in H) of $\{c\varphi _{1}\}$. Note that $H_{1}$ and $\{c\varphi _{1}\}$ are invariant under $\mathcal{L}$. Since $\varphi _{1}\in X$ and $X\subset H$, the space X is also decomposed in

$$ X=X_{1}\oplus \{c\varphi _{1}\}, $$

(2.4)

where $X_{1}=H_{1}\cap X$. Clearly, the restriction $\mathcal{L}^{-1} |_{X}$ maps X into itself and is compact.

3 Asymptotically linear problems

In this section, we suppose that f satisfies $(f_{1})$ and

$(f_{2})$:

there exists $m>0$ such that

$$ \lim_{u\to +\infty } \frac{f(j, u)}{u}=m \quad \text{uniformly in } j \in \widehat{\mathbb{T}}. $$

We further suppose that

$(A_{1})$:

$a(j):=\liminf_{u\to +\infty } (f(j, u)-mu)>0$ for all $j\in \mathbb{T}$;

$(A_{2})$:

$A(j):=\limsup_{u\to +\infty } (f(j, u)-mu)<0$ for all $j\in \mathbb{T}$.

Let $\lambda _{\infty }=\frac{\lambda _{1}}{m}$. Our main result is the following:

Theorem 3.1

Assume that$(f_{1})$and$(f_{2})$. Then

• (i) if$(A_{1})$is satisfied, then exists$\varepsilon > 0$such that (1.1) has positive solutions for$\lambda \in [\lambda _{\infty }- \varepsilon , \lambda _{\infty })$;

• (ii) if$(A_{2})$is satisfied, then there exists$\varepsilon '> 0$such that (1.1) has positive solutions for$\lambda \in (\lambda _{ \infty }, \lambda _{\infty }+\varepsilon ']$.

We divide the proof of Theorem 3.1 into several steps. First, let us extend $f(j,\cdot )$ to $\mathbb{R}$ by setting

$$ F(j, u) = f \bigl(j, \vert u \vert \bigr). $$

For the remainder of the proof, we will omit the dependence with respect to j.

Let

$$ \varPhi (\lambda , u) = u-\lambda K F(u). $$

Clearly, any $u > 0$ such that $\varPhi (\lambda , u)=0$ is a positive solution of (1.1). For $R>0$, let $B_{R}=\{u\in X: \|u\| < R\}$. We also denote by $\operatorname{deg}(\varPhi (\lambda , \cdot ), B_{R}, 0)$ the degree of $\varPhi (\lambda , \cdot )$ on $B_{R}$ with respect to 0.

To prove Theorem 3.1, we need the following preliminary results.

Lemma 3.2

Let$\varLambda \subset \mathbb{R}^{+}$be a compact interval with$\lambda _{\infty }\notin \varLambda$. Then there exists a number$r>0$such that for all$u\in X$with$\|u\|\geq r$and$\lambda \in \varLambda$, $\varPhi (\lambda , u)\neq 0$. Moreover:

• (i) if$(A_{1})$holds, then we can take$\varLambda =[\lambda _{\infty }, \lambda ]$, where$\lambda >\lambda _{\infty }$;

• (ii) if$(A_{2})$holds, then we can take$\varLambda =[0,\lambda _{ \infty }]$.

Proof

Suppose on the contrary that there exist $u_{n}\in X$ with $\|u_{n}\|\to \infty$ and $\mu _{n}\in \varLambda$ such that

$$ u_{n}=\mu _{n}KF(u_{n}). $$

We may assume that $\mu _{n}\to \mu \in \varLambda$.

Let $w_{n}=\frac{u_{n}}{\|u_{n}\|}$. Then

$$ w_{n}=\mu _{n}K\frac{F(u_{n})}{ \Vert u_{n} \Vert }. $$

Since $\frac{F(u_{n})}{\|u_{n}\|}$ is bounded in X, $w_{n}$ is a relatively compact set in X by the compactness of K. Assumption $(f_{2})$ and the definition of F yield that, after taking a subsequence if necessary, $w_{n}\to w$ in X, where w is a solution of the problem

$$ \textstyle\begin{cases} -\triangle ^{2} w(j-1)=\mu m \vert w(j) \vert , \quad j\in \mathbb{T},\\ w(0)=w(T + 1)=0, \end{cases} $$

and satisfies $\|w\|=1$. From the maximum principle it follows that $w\geq 0$. Since $\|w\| = 1$, we deduce that $\mu m=\lambda _{1}$, that is, $\mu =\lambda _{\infty }\notin \varLambda$, which is a contradiction.

Next, we will only prove (i) of Lemma 3.2 since applying the same method, with obvious changes, we may obtain (ii).

Suppose now there exist sequences $u_{n}$ in X and $\mu _{n}$ in $\mathbb{R}^{+}$ with $\|u_{n}\|\to \infty$, $\mu _{n}\to \lambda _{\infty }$, and $\mu _{n}>\lambda _{\infty }$ such that

$$ \varPhi (\mu _{n},u_{n})=0. $$

(3.1)

Arguing as in the proof of the previous statement, we set $w_{n}=\frac{u _{n}}{\|u_{n}\|}$ and conclude that, possibly passing to a subsequence, $w_{n}\to w$ in X, $\|w\|=1$, and $w\geq 0$ satisfies

$$ \textstyle\begin{cases} -\triangle ^{2} w(j-1)=\lambda _{1}w(j), \quad j\in \mathbb{T},\\ w(0)=w(T + 1)=0. \end{cases} $$

Subsequently, there exists $\beta > 0$ such that $w = \beta \varphi _{1}$. Then we have $u_{n}=\|u_{n}\|w_{n}\to +\infty$ for all $j\in \mathbb{T}$ and $F(u_{n})=f(u_{n})$ for n large. By (3.1) and Lemma 2.1 we have

$$ \lambda _{1}\sum_{j=1}^{T}u_{n}(j) \varphi _{1}(j)=\mu _{n}\sum _{j=1}^{T} \bigl(f \bigl(u_{n}(j) \bigr)-mu_{n}(j) \bigr)\varphi _{1}(j)+ \mu _{n}m\sum_{j=1}^{T}u _{n}(j)\varphi _{1}(j). $$

From $\mu _{n}>\lambda _{\infty }$ and $\sum_{j=1}^{T} u_{n}(j)\varphi _{1}(j) > 0$ for n large, it follows that

$$ \sum_{j=1}^{T} \bigl(f \bigl(u_{n}(j) \bigr)-mu_{n}(j) \bigr)\varphi _{1}(j)< 0 $$

for n large, which, together with the Fatou lemma, yields

$$\begin{aligned} 0 &\geq \liminf_{n\to \infty } \sum_{j=1}^{T} \bigl(f \bigl(u_{n}(j) \bigr)-mu _{n}(j) \bigr)\varphi _{1}(j) \\ &\geq \sum_{j=1}^{T} \Bigl(\liminf _{n \to \infty } \bigl(f \bigl(u_{n}(j) \bigr)-mu_{n}(j) \bigr) \Bigr)\varphi _{1}(j) \\ &= \sum_{j=1}^{T} a(j)\varphi _{1}(j) \\ &> 0, \end{aligned}$$

which is impossible, since $a(j)>0$ for all $j\in \mathbb{T}$. □

We follow the standard pattern. Let $z=\frac{u}{\|u\|^{2}}$ ($u\neq 0$), and let

$$ \varPsi (\lambda ,z)=\frac{\varPhi (\lambda ,u)}{ \Vert u \Vert ^{2}}=z-\lambda \Vert z \Vert ^{2}KF \biggl(\frac{z}{ \Vert z \Vert ^{2}} \biggr). $$

Then $\lambda _{\infty }$ is a bifurcation from infinity for (2.3) if and only if it is a bifurcation from the trivial solution $z=0$ for $\varPsi =0$.

Lemma 3.3

For$\lambda \in (0,\lambda _{\infty })$, $\operatorname{deg}(\varPsi (\lambda , \cdot ), B_{1/r}, 0)=1$.

Proof

Lemma 3.2, applied to the interval $\varLambda =[0, \lambda ]$, guarantees the existence of $r>0$ such that

$$ u-t\lambda K F(u)\neq 0 $$

for all $u\in X$ with $\|u\|\geq r$ and $t\in [0,1]$. Thus, performing the transformation $z=\frac{u}{\|u\|^{2}}$ ($u\neq 0$), we get

$$ z-t\lambda \Vert z \Vert ^{2}KF \biggl(\frac{z}{ \Vert z \Vert ^{2}} \biggr)\neq 0, \quad \forall z\in X, 0< \Vert z \Vert \leq \frac{1}{r}, \forall t\in [0,1]. $$

Hence

$$\begin{aligned} \operatorname{deg} \bigl(\varPsi (\lambda , \cdot ), B_{1/r}, 0 \bigr) &=\operatorname{deg} \bigl(\varPsi (0, \cdot ), B_{1/r}, 0 \bigr) \\ &= \operatorname{deg}(I, B_{1/r}, 0) \\ &= 1. \end{aligned}$$

 □

Lemma 3.4

If$\lambda > \lambda _{\infty }$, then there exists$r>0$such that for all$u\in X$with$\|u\|\geq r$,

$$ \varPhi (\lambda ,u)\neq \tau \varphi _{1}\quad \textit{for all } \tau \geq 0. $$

Proof

Suppose on the contrary that there exist sequences $u_{n}\in X$ with $\|u_{n}\|\to \infty$ and $\tau _{n}\geq 0$ such that

$$ \varPhi (\lambda , u_{n})=\tau _{n}\varphi _{1}. $$

Then

$$ K^{-1}(u_{n})=\lambda F(u_{n})+\tau _{n}\lambda _{1}\varphi _{1}, $$

(3.2)

and since $\tau _{n}\lambda _{1}\varphi _{1}\geq 0$ in $\mathbb{T}$, it follows by the maximum principle that $u_{n}\geq 0$ in $\mathbb{T}$. Let $u_{n}=w_{n}+s_{n}\varphi _{1}$ be decomposed according to decomposition (2.4). Then $s_{n}=(u_{n}, \varphi _{1})\geq 0$ for every $n\in \mathbb{N}$.

We first prove that $s_{n}\to +\infty$ as $n\to \infty$.

Suppose that $s_{n}$ is bounded. Then $\|w_{n}\|\to \infty$. Let $v_{n}=\frac{w_{n}}{\|w_{n}\|}$. Let $P: X\to X$ be the continuous projection of X onto $X_{1}$ parallel to $\{c\varphi _{1}\}$. Applying P to (3.2), by $(f_{2})$ we obtain

$$ K^{-1}(v_{n})=\frac{\lambda PF(u_{n})}{ \Vert w_{n} \Vert }\simeq \frac{\lambda mP(u_{n})}{ \Vert w_{n} \Vert }=\lambda mv_{n}. $$

We infer as in the proof of Lemma 3.2 that $v_{n}\to v$ in X, $\|v\|=1$, and $(v, \varphi _{1})=0$. Thus v has to change sign in $\mathbb{T}$. On the other hand, $u_{n}\geq 0$ in $\mathbb{T}$ implies that $v_{n}\geq -s_{n}\frac{\varphi _{1}}{\|w_{n}\|}$, and this contradicts the fact $v\geq 0$.

Taking the inner product of (3.2) with $\varphi _{1}$, we get

$$\begin{aligned} s_{n}\lambda _{1} &= \bigl(K^{-1}(u_{n}), \varphi _{1} \bigr) \\ &= (\lambda mu_{n}, \varphi _{1})+ \bigl(\lambda \bigl(F(u_{n})-mu_{n} \bigr), \varphi _{1} \bigr)+(\tau _{n}\lambda _{1}\varphi _{1}, \varphi _{1}) \\ &\geq \lambda ms_{n}+ \bigl(\lambda \bigl(F(u _{n})-mu_{n} \bigr), \varphi _{1} \bigr). \end{aligned}$$

Hence

$$ \lambda _{1}\geq \lambda m+\frac{(\lambda (F(u_{n})-mu_{n}), \varphi _{1})}{s_{n}}\to \lambda m \quad (n\to \infty ), $$

a contradiction to the assumption $\lambda >\lambda _{\infty }$. □

Lemma 3.5

For$\lambda >\lambda _{\infty }$, $\operatorname{deg}( \varPsi (\lambda , \cdot ), B_{1/r}, 0)=0$.

Proof

By Lemma 3.4 there exists $r>0$ such that $\varPhi ( \lambda ,u)\neq t\|u\|^{2}\varphi _{1}$ for $u\in X$ with $\|u\|\geq r$ and $t\in [0,1]$. Then

$$ \varPsi (\lambda ,z)\neq t\varphi _{1}, \quad \forall z\in X, 0< \Vert z \Vert \leq \frac{1}{r}, \forall t\in [0,1]. $$

We conclude that

$$ \operatorname{deg} \bigl(\varPsi (\lambda , \cdot ), B_{1/r}, 0 \bigr)= \operatorname{deg} \bigl(\varPsi ( \lambda , \cdot )-\varphi _{1}, B_{1/r}, 0 \bigr)=0. $$

 □

From the Lemma 3.3 and Lemma 3.5 we deduce the following:

Proposition 3.6

There exists an unbounded connected component$\varSigma _{\infty }\subset \varSigma$that meets$(\lambda _{\infty }, \infty )$. Moreover, if$(A_{1})$holds, then$\varSigma _{\infty }$bifurcates to the left, whereas if$(A_{2})$holds, then$\varSigma _{ \infty }$bifurcates to the right.

Proof of Theorem 3.1

Suppose there exists sequence $(\mu _{n}, u_{n})\subset \varSigma _{\infty }$ with $\|u_{n}\|\to \infty$ and $\mu _{n}\to \lambda _{\infty }$. We only to show that $u_{n}>0$ in $\mathbb{T}$ for n large. Arguing as in the proof of Lemma 3.2, let $w_{n}=\frac{u_{n}}{\|u_{n}\|}$. We find that, up to a subsequence, $w_{n}\to w$ in X, where $\|w\|=1$, $w>0$, and $w=\beta \varphi _{1}$, $\beta >0$. Hence we have $u_{n}>0$ in $\mathbb{T}$ for n large. □

Remark 3.7

In fact, solutions on $\varSigma _{\infty }$ can change sign, and the behavior $\varSigma _{\infty }$ depends on the definition of f for $u<0$. However, independently of such a definition, there exists a connected component $\varSigma _{0}\subset \varSigma$ bifurcating from $(0, 0)\in \mathbb{R}^{+}\times X$, consisting of negative solutions of (1.1), and such that $\varSigma _{\infty }\cap \varSigma _{0}=\emptyset$.

Remark 3.8

Suppose that there exists $\beta >0$ such that $f(\beta )=0$, $f(s)<0$ for $0< s<\beta$, and $f(s)>0$ for $s>\beta$. It is well known that if u is a positive solution of (1.1), then $\|u\|>\beta$. From the proof of Theorem 3.1 we have that the solutions on $\varSigma _{\infty }$ are positive as $\lambda \to \lambda _{\infty }$, and hence by the continuity argument we deduce that $\|u\|>\beta$ for all $(\lambda , u)\in \varSigma _{\infty }$.

4 Sublinear problems

In this section, we suppose that f satisfies $(f_{1})$ and

$(f_{3})$:

there exists $b\in X$ with $b>0$ such that for some $0\leq q<1$,

$$ \lim_{u\to +\infty } \frac{f(j, u)}{u^{q}}=b \quad \text{uniformly in } j\in \widehat{\mathbb{T}}. $$

Our main result is stated as follows.

Theorem 4.1

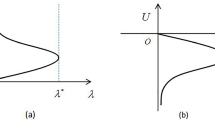
If$(f_{1})$and$(f_{3})$hold, then there exists$\lambda ^{\ast }>0$such that (1.1) has positive solutions for all$\lambda \geq \lambda ^{\ast }$. More precisely, there exists an unbounded connected component of positive solutions of (1.1) bifurcating from infinity at$\lambda _{\infty }=+\infty$.

Let us define the cone

$$ P= \bigl\{ u\in X: u(j)\geq 0 \text{ for } j\in \widehat{\mathbb{T}} \bigr\} . $$

Before we prove the main result, we first give the following:

Lemma 4.2

Let$0< q<1$, and letbbe as in$(f_{3})$. Then the nonlinear problem

$$ \textstyle\begin{cases} -\triangle ^{2} w(j-1)=b(j)w^{q}(j), \quad j\in \mathbb{T},\\ w(0)=w(T + 1)=0 \end{cases} $$

(4.1)

has a unique positive solution.

Proof

It is easy to verify that problem (4.1) has at least one positive solution by the fixed point theorem in cones; see [9, 15].

Suppose that $u_{1}$, $u_{2}$ are positive solutions of (4.1), that is,

$$\begin{aligned}& -\triangle ^{2} u_{1}(j-1)=b(j)u_{1}^{q}(j), \quad j\in \mathbb{T}, \\& -\triangle ^{2} u_{2}(j-1)=b(j)u_{2}^{q}(j), \quad j\in \mathbb{T}, \end{aligned}$$

and

$$ u_{1}(0)=u_{2}(0)=u_{1}(T + 1)=u_{2}(T + 1)=0. $$

Then $u_{1}$ and $u_{2}$ are concave down in $\widehat{\mathbb{T}}$.

We will show that $u_{1}\geq u_{2}$ and $u_{2}\geq u_{1}$ in $\widehat{\mathbb{T}}$.

Suppose on the contrary that $u_{1}\ngeq u_{2}$. We consider the element $\phi _{r}(j)$ of the form

$$ \phi _{r}(j)=u_{1}(j)-ru_{2}(j), \quad j\in \widehat{\mathbb{T}}. $$

We denote by $r_{0}$ the value of r such that $\phi _{r_{0}}\in P$ and $\phi _{r}\notin P$ for $r>r_{0}$. The number $r_{0}$ is positive since $u_{1}\geq 0$ and $\phi _{r}\in P$ for sufficiently small positive r.

From the definition of $r_{0}$ it follows that there exists $\tau _{0}\in (0,1)$ such that

$$ \phi _{r_{0}}(\tau _{0})=u_{1}(\tau _{0})-r_{0}u_{2}(\tau _{0})=0. $$

(4.2)

On the other hand,

$$\begin{aligned} -\triangle ^{2}\phi _{r_{0}}(j-1) &=-\triangle ^{2}u_{1}(j-1)+r_{0} \triangle ^{2}u_{2}(j-1) \\ &=b(j)u_{1}^{q}(j)-r_{0}b(j)u_{2}^{q}(j) \\ &=b(j) \bigl[u_{1}^{q}(j)-r_{0}u_{2}^{q}(j) \bigr] \\ &\geq b(j) \bigl[r_{0}^{q}u _{2}^{q}(j)-r_{0}u_{2}^{q}(j) \bigr] \\ &= b(j)u_{2}^{q}(j) \bigl(r_{0}^{q}-r _{0} \bigr) \\ &>0, \end{aligned}$$

and

$$ \phi _{r_{0}}(0)=\phi _{r_{0}}(T+1)=0. $$

Then

$$ \phi _{r_{0}}(j)>0, \quad j\in \mathbb{T}. $$

However, this contradicts (4.2).

Therefore we have $u_{1}\geq u_{2}$ in $\widehat{\mathbb{T}}$. By the same method we may prove that $u_{2}\geq u_{1}$ in $\widehat{\mathbb{T}}$. □

Proof of Theorem 4.1

As before, we extend f to $\mathbb{R}$ by setting

$$ F(u)=f \bigl( \vert u \vert \bigr). $$

Let

$$ G(u)=F(u)-b \vert u \vert ^{q}. $$

Then, from $(f_{3})$, it follows that $\lim_{u\to +\infty }G(u)=0$. Let

$$ w=\gamma u, \qquad \lambda =\gamma ^{q-1}, \quad \gamma >0. $$

It is easy to check that $(\lambda , u)$, $\lambda >0$, is a solution of

$$ \varPhi (\lambda , u)=0 $$

(4.3)

if and only if $(\gamma ,w)$ is a solution of

$$ w-K\hat{F}(\gamma , w)=0, $$

(4.4)

where

$$ \hat{F}(\gamma , w)= b \vert w \vert ^{q}+\gamma ^{q}G \biggl(\frac{w}{\gamma } \biggr), \quad \gamma >0. $$

We can define F̂ in $\mathbb{R}^{+}\times X$ by setting

$$ \hat{F}(0, w)=b \vert w \vert ^{q}. $$

From $(f_{3})$ it follows that $\hat{F}(\cdot ,w)$ is continuous in $\mathbb{R}^{+}$.

Let

$$ \mathcal{S}(\gamma ,w)=w-K\hat{F}(\gamma , w),\quad \gamma \in \mathbb{R} ^{+}. $$

Then $\mathcal{S}(\gamma ,\cdot )=I-\hat{\mathcal{K}}(\gamma ,\cdot )$, $\hat{\mathcal{K}}(\gamma ,\cdot )=K\hat{F}(\gamma ,\cdot )$, and $\hat{\mathcal{K}}$ is compact.

From Lemma 4.2 it follows that the problem

$$ \textstyle\begin{cases} -\triangle ^{2} w(j-1)=b(j)w^{q}(j), \quad j\in \mathbb{T},\\ w(0)=w(T + 1)=0 \end{cases} $$

(4.5)

has a unique positive solution $w_{0}$.

Let

$$ \varOmega _{\delta }= \bigl\{ w\in X: \Vert w-w_{0} \Vert \leq \delta \bigr\} , $$

and let $\lambda _{1}[bw_{0}^{q-1}]$ denote the first eigenvalue of the linearized problem

$$ \textstyle\begin{cases} -\triangle ^{2} v(j-1)=\lambda bw_{0}^{q-1}v(j), \quad j\in \mathbb{T},\\ v(0)=v(T + 1)=0. \end{cases} $$

Then (4.5) yields that $v=w_{0}$ is the eigenfunction associated with

$$ \lambda _{1} \bigl[bw_{0}^{q-1} \bigr]=1. $$

(4.6)

Note that $\mathcal{S}_{0}(w)=w-K\hat{F}_{0}(w)$. For $h\in X$, from $0< q<1$ and the fact

$$ (y_{0}+h)^{q}-y_{0}^{q}=qy_{0}^{q-1}h+ \circ \bigl( \Vert h \Vert \bigr) $$

it follows that

$$\begin{aligned} &\mathcal{S}_{0}(w_{0}+h) (j)-\mathcal{S}_{0}(w_{0}) (j) \\ &\quad = \bigl[(w _{0}+h)-Kb \vert w_{0}+h \vert ^{q} \bigr](j)- \bigl[w_{0}-Kb \vert w_{0} \vert ^{q} \bigr](j) \\ &\quad =h(j)-Kb \bigl[ \vert w_{0}+h \vert ^{q}(j)- \vert w_{0} \vert ^{q}(j) \bigr] \\ &\quad =h(j)-Kbqw_{0}^{q-1}(j)h(j)+ \circ \bigl( \Vert h \Vert \bigr). \end{aligned}$$

Hence the Fréchet derivative of $\mathcal{S}_{0}$ is given by

$$ \mathcal{S}'_{0}(w_{0})v= \textstyle\begin{cases} v-K[qbw_{0}^{q-1}]v, &0< q< 1, \\ v, &q=0. \end{cases} $$

It follows from $0< q<1$ and (4.6) that all the characteristic values of $I-\mathcal{S}'_{0}(w_{0})$ are greater than 1. Hence we deduce that

$$ \operatorname{deg} \bigl(\mathcal{S}_{0}(\cdot ), \varOmega _{\delta }, 0 \bigr)=1, \quad 0\leq q< 1. $$

By continuation we deduce that there exists a connected component $\mathcal{C}$ of solutions of $\mathcal{S}(\gamma ,w)=0$, $\gamma >0$, such that $(0, w_{0})\in \mathcal{C}$. Moreover, there exists $\gamma _{0}>0$ such that these solutions are positive, provided that $0<\gamma \leq \gamma _{0}$.

Notice that, by $w=\gamma u$ and $\lambda =\gamma ^{q-1}$, $\mathcal{C}$ can be transformed into a connected component $\varSigma _{\infty }$ of solutions of (1.1). These solutions are indeed positive for all $\lambda >\lambda ^{\ast }:=\gamma _{0}^{q-1}$, and, together with the fact

$$ \lambda \to +\infty \quad \text{if and only if} \quad \gamma \to 0, $$

we have that $\varSigma _{\infty }$ bifurcates from infinity at $\lambda _{\infty }=+\infty$. □

5 Superlinear problems

In this section, we suppose that f satisfies $(f_{1})$ and

$(f_{4})$:

there exists $b\in X$ with $b>0$ such that

$$ \lim_{u\to +\infty } \frac{f(j, u)}{u^{p}}=b \quad \text{uniformly in } j \in \hat{\mathbb{T}}, $$

with $p>1$.

The main result of this section is the following:

Theorem 5.1

If$(f_{1})$and$(f_{4})$hold, then there exists$\lambda _{\ast }>0$such that (1.1) has positive solutions for all$\lambda \in (0, \lambda _{\ast }]$. More precisely, there exists an unbounded connected component of positive solutions of (1.1) bifurcating from infinity at$\lambda _{\infty }=0$.

We will show that in this case that there exists the connected component of positive solutions of (1.1) bifurcating from infinity at $\lambda _{\infty }=0$. Following the same procedure as for the sublinear case, we employ the rescaling $w=\gamma u$, $\lambda =\gamma ^{p-1}$ and use the same notation, with p instead of q. As before, $(\lambda , u)$ solves (4.3) if and only if $(\gamma , w)$ satisfies (4.4).

It is worth pointing out that, for $\gamma =0$, solutions of $\mathcal{S}_{0}(w):=\mathcal{S}(0, w)=0$ are solutions of

$$ \textstyle\begin{cases} -\triangle ^{2} w(j-1)=b \vert w \vert ^{p}, \quad j\in \mathbb{T},\\ w(0)=w(T + 1)=0. \end{cases} $$

(5.1)

We claim that there exist two constant $r, R: R>r>0$, such that

$$\begin{aligned}& \mathcal{S}_{0}(w)\neq 0, \quad \forall \Vert w \Vert \geq R; \end{aligned}$$

(5.2)

$$\begin{aligned}& \mathcal{S}_{0}(w)\neq 0, \quad \forall \Vert w \Vert \leq r; \end{aligned}$$

(5.3)

$$\begin{aligned}& \operatorname{deg} \bigl(\mathcal{S}_{0}(\cdot ), B_{R} \setminus \bar{B}_{r}, 0 \bigr)=-1. \end{aligned}$$

(5.4)

Assume on the contrary that (5.2) is not true. Then there exists a sequence $\{w_{n}\}$ of solutions of (5.1) satisfying

$$ \Vert w_{n} \Vert \to \infty , \quad n\to \infty . $$

In fact, from (5.1) we have that

$$ \textstyle\begin{cases} -\triangle ^{2} w_{n}(j-1)=(b \vert w_{n}(j) \vert ^{p-1})w_{n}(j), \quad j\in \mathbb{T},\\ w_{n}(0)=w_{n}(T + 1)=0. \end{cases} $$

Since

$$ \lim_{n\to \infty } b \bigl\vert w_{n}(j) \bigr\vert ^{p-1}=\infty \quad \text{uniformly in } j\in \mathbb{T}, $$

it follows that $w_{n}$ must change its sign in $\widehat{\mathbb{T}}$, a contradiction.

Assume on the contrary that (5.3) is not true. Then there exists a sequence $\{w_{n}\}$ of solutions of (5.1) satisfying

$$ \Vert w_{n} \Vert \to 0, \quad n\to \infty . $$

Let $v_{n}=\frac{w_{n}}{\|w_{n}\|}$. Arguing as in the proof of (5.2), we have

$$ \lim_{n\to \infty } b \bigl\vert w_{n}(j) \bigr\vert ^{p-1}=0 \quad \text{uniformly in } j\in \mathbb{T}. $$

From this fact, by the standard argument, after taking a subsequence and relabeling if necessary, it follows that there exists $v_{\ast } \in X$ with $\|v_{\ast }\|=1$ such that

$$ v_{n}\to v_{\ast }, \quad n\to \infty , $$

and

$$ \textstyle\begin{cases} -\triangle ^{2} v_{\ast }(j-1)=0, \quad j\in \mathbb{T},\\ v_{\ast }(0)=v_{\ast }(T + 1)=0, \end{cases} $$

which implies that $v_{\ast }=0$, a contradiction.

To show (5.4), let us define the cone

$$ \hat{P}= \Bigl\{ u\in X: u(j)\geq 0, \min_{j\in E} u(j)\geq \delta \Vert u \Vert \Bigr\} , $$

where E and δ are given as in Sect. 2. Denote

$$ \varOmega _{\rho }= \bigl\{ u\in \hat{P}: \Vert u \Vert \leq \rho \bigr\} . $$

By (2.1), (2.2), and a similar argument as in [15], we can deduce that

$$ i \bigl(K\hat{F}(0, \cdot ), \varOmega _{r}, \hat{P} \bigr)=1, \qquad i \bigl(K\hat{F}(0, \cdot ), \varOmega _{R}, \hat{P} \bigr)=0, $$

and, subsequently,

$$ i \bigl(K\hat{F}(0, \cdot ), \varOmega _{R}\setminus \mathring{ \varOmega } _{r}, \hat{P} \bigr)=-1. $$

Combining this together with the fact $\mathcal{S}_{0}:X\to \varOmega _{R}\setminus \mathring{\varOmega }_{r}$ and using (5.2) and (5.3), we deduce that

$$ \operatorname{deg} \bigl(\mathcal{S}_{0}(\cdot ), B_{R} \setminus \bar{B}_{r}, 0 \bigr)=-1. $$

Lemma 5.2

There exists $\gamma _{0}>0$ such that

• (i) $\operatorname{deg}(\mathcal{S}(\gamma , \cdot ), B_{R}\setminus \bar{B} _{r}, 0)=-1$for$0\leq \gamma \leq \gamma _{0}$;

• (ii) if$\mathcal{S}(\gamma , w)=0$for$\gamma \in [0, \gamma _{0}]$and$\|w\|\in [r, R]$, then$w>0$in$\mathbb{T}$.

Proof

(i) It suffices to show that $\mathcal{S}(\gamma , w) \neq 0$ for all $\gamma \in [0, \gamma _{0}]$ and $\|w\|\in \{r, R\}$. Suppose on the contrary that there exists $(\gamma _{n}, w_{n})$ with $\gamma _{n}\to 0$ and $\|w_{n}\|\in \{r, R\}$ such that $\mathcal{S}( \gamma _{n}, w_{n})=0$. By the compactness of K and by the standard argument, after taking a subsequence and relabeling if necessary, we obtain $w_{n}\to w$, $\mathcal{S}_{0}(w)=0$, and $\|w\|\in \{r, R\}$. However, this contradicts with (5.2) and (5.3).

(ii) We still suppose that there exists a sequence $w_{n}\in X$ with $\{j\in \mathbb{T}: w_{n}(j)\leq 0\}\neq \emptyset$ such that $w_{n}\to w$, $\|w\|\in [r, R]$, and $\mathcal{S}(\gamma , w)=0$ for $\gamma \in [0, \gamma _{0}]$. Since w solves (5.1), we can deduce that $w>0$ in $\mathbb{T}$. Hence $w_{n}>0$ in $\mathbb{T}$ for n large since $w_{n}\to w$ in X, a contradiction. □

Proof of Theorem 5.1

By Lemma 5.2, (4.4) has a positive solution w for any $\gamma \in [0, \gamma _{0}]$. As remarked before, $\gamma >0$ and $p>1$, and hence $\lambda =\gamma ^{p-1}$ and $u=\frac{w}{\gamma }$ give a solution of (1.1) for $0<\lambda < \lambda _{\ast }:=\gamma _{0}^{p-1}$. Moreover, $\|w\|\geq r$ for all $\gamma \in [0, \gamma _{0}]$ implies that $\|u\|=\frac{\|w\|}{\gamma }\to \infty$ as $\gamma \to 0$. We complete the proof. □