Stochastically exponential synchronization for Markov jump neural networks with time-varying delays via event-triggered control scheme

Abstract

This paper focuses on the stochastically exponential synchronization problem for one class of neural networks with time-varying delays (TDs) and Markov jump parameters (MJPs). To derive a tighter bound of reciprocally convex quadratic terms, we provide an improved reciprocally convex combination inequality (RCCI), which includes some existing ones as its particular cases. We construct an eligible stochastic Lyapunov–Krasovskii functional to capture more information about TDs, triggering signals, and MJPs. Based on a well-designed event-triggered control scheme, we derive several novel stability criteria for the underlying systems by employing the new RCCI and other analytical techniques. Finally, we present two numerical examples to show the validity of our methods.

1 Introduction

Neural Networks (NNs) have attracted great attention in recent decades owing to their extensive application in many different fields, such as optimization and signal processing [1–5], pattern recognition [6–10], parallel computing [11–15], and so forth. In the implementation of such applications, the phenomenon of time-varying delays (TDs) is inevitably encountered due to the inherent communication time among neurons, the finite switching speed of the amplifier [16–19], and other reasons. Furthermore, the structure and parameters of NNs are often subject to random abrupt variations caused by the external environment sudden change, the information latching [20], and so on. Markov jump neural networks (MJNNs) with TDs, as a special kind of hybrid systems, are very suitable to describe those complicated dynamic characteristics of NNs [21–24]. The stability is a well-known important property of systems, but the existence of TDs and random abrupt variations often lead to chaos, oscillation, and even instability [25]. In addition, fast convergence of the networks is essential for realtime computation, and the exponential convergence rate is generally used to determine the speed of neural computations [26]. Thus it is of great theoretical and practical importance to study the exponential stability for MJNNs with TDs, and many fruitful results have been reported in the literature [27–32].

On the other hand, after the pioneer work [33], the problems of chaos synchronization for NNs have gained considerable focus in recent decades [34–36], and many effective control methods are designed to achieve exponential synchronization criteria for MJNNs with TDs, such as adaptive feedback control [37–40], sampled-data control [41–44], quantized output control [45–47], pinning control [48], impulsive control [49–56], and so on. However, in these control methods, the data packets are transmitted periodically, which implies that so many “unnecessary” data are also frequently sent. As a result, network resources may not be effectively and reasonably utilized, which is undesirable in practice, especially when the networks resources are limited. To reduce the “unnecessary” waste of network resources, the event-triggered control scheme (ETCS) is proposed [57] and developed [58–61]. [58] focused on the issue of exponential synchronization for chaotic delayed NNs by a hybrid ETCS. [59] studied the synchronization problems of coupled switched delayed NNs with communication delays via a discrete ETCS. By using an ETCS with discontinuous sign terms, [60] obtained the global synchronization criteria for memristor NNs. [61] discussed the event-triggered synchronization problem for semi-Markov NNs with TDs by using a generalized free-weighting-matrix integral inequality. However, as far as the author knows, the issue about event-triggered exponential synchronization for MJNNs with TDs has not been fully investigated, and there still remains much room for improvement.

It is worth mentioning that in the literature [30–32, 34–36, 39, 40, 43, 44, 47, 48, 58–61], reciprocally convex quadratic terms (RCQTs), that is, ${\mathcal{G}}_{n} (\alpha _{i} ) =\frac{1}{\alpha _{i}} \zeta _{i}^{T}(t) \Xi _{i} \zeta _{i}(t)$, $\alpha _{i} \in (0,1)$, $i =1, 2, 3, \ldots , n$, are often encountered when processing integral quadratic terms, such as $- \int _{t-\tau (t)}^{t} {\dot{\xi }(s) \Phi \dot{\xi }(s)\,ds}$, $- \int _{t-\tau }^{t-\tau (t)} {\dot{\xi }(s) \Phi \dot{\xi }(s)\,ds}$, which play a crucial role in deriving less conservative stability criteria. The reciprocally convex combination inequality (RCCI), as a powerful tool to estimate the bound of RCQTs, has been widely applied into the stability analysis and control synthesize for various systems with TDs since it was introduced in [62]. Then the RCCI in [62] with the case $n =2$ was improved in [63–65]. However, as reported in [65], it is still challenging to derive such an RCCI in [63–65] if ${\mathcal{G}}_{n} (\alpha _{i} )$ includes more than three terms, that is, $n\ge 3$. Consequently, motivated by the above discussion, in this paper, we consider the event-triggered exponential synchronization problem for MJNNs with TDs. First, we provide a more general RCCI, which includes several existing ones as its particular cases. Then we construct an eligible stochastic Lyapunov–Krasovskii functional (LKF) to capture more information about TDs and MJPs. Third, based on a suitable LKF, with the help of a well-designed ETCS, we derive two novel exponential synchronization criteria for the underlying systems by using the new RCCI and other analytical techniques. Finally, we verify the effectiveness of our methods by two numerical examples.

Notations: Let $\mathbb{Z}_{+}$ denote the set of nonpositive integers, $\mathbb{R}$ the set of real numbers, $\mathbb{R}^{n}$ the n-dimensional real space equipped with the Euclidean norm $\Vert \cdot \Vert$, $\mathbb{R}^{m \times n}$ the set of all ${m \times n}$ real matrices, and $\mathbb{S}_{+}^{n}$ and $\mathbb{S}^{n}$ the sets of symmetric positive definite and symmetric matrices of $\mathbb{R}^{n \times n}$, respectively. The symbol “∗” in a block matrix signifies the symmetric terms; $col \{ \cdots \}$ and $diag \{ \cdots \}$ express a column vector and a diagonal matrix, respectively. For any matrix $X \in \mathbb{R}^{n \times n}$, $\mathbb{H} \{ X \}$ means $X+X^{T}$, and $\lambda _{\max }(X)$ and $\lambda _{\min }(X)$ stand for the maximum and minimum eigenvalues of X, respectively. The zero and identity matrices of appropriate dimensions are denoted by 0 and I, respectively; $\bar{e}_{i} = (0, \ldots , 0, \underbrace{I}_{i}, 0, \ldots , 0, )$, (${i} =1,\ldots ,n$).

2 Problem statement and preliminaries

Consider the following master–slave MJNNs with TDs:

$$\begin{aligned} & \textstyle\begin{cases} \dot{x} ( t )= -\mathcal{B}_{\sigma (t)} x( t) +\mathcal{A}_{ \sigma (t)} g( {x ( t )}) +\mathcal{D}_{\sigma (t)} g(x(t - { \delta }(t)), \\ \phi (\theta ) =x(t_{0}+\theta ),\quad \theta \in [-\max (\delta ,\eta ), 0], \end{cases}\displaystyle \end{aligned}$$

(1)

$$\begin{aligned} & \textstyle\begin{cases} \dot{y} ( t )= -\mathcal{B}_{\sigma (t)} y( t) +\mathcal{A}_{ \sigma (t)} g( {y ( t )}) +\mathcal{D}_{\sigma (t)} g( y(t - { \delta }(t)) +\mathcal{{U}}(t), \\ \psi (\theta ) =y(t_{0}+\theta ), \quad \theta \in [-\max (\delta ,\eta ), 0], \end{cases}\displaystyle \end{aligned}$$

(2)

where $x(t)=col\{x_{1}(t), \ldots , x_{n}(t)\} \in \mathbb{R} ^{n}$ and $y(t)=col\{y_{1}(t), \ldots , y_{n}(t)\} \in \mathbb{R} ^{n}$ are the neuron state vectors of master system (1) and slave system (2), respectively, $\phi (\theta )$ and $\psi (\theta )$ are the initial values of systems (1) and (2), respectively, and $g(\cdot ) = col \{g_{1}(\cdot ), \ldots , g_{n}(\cdot )\} \in \mathbb{R} ^{n}$ is the nonlinear neuron activation function satisfying

$$\begin{aligned} \lambda _{l}^{-} \le \frac{g_{l}({\varrho _{1}}) -g_{l}({\varrho _{2}})}{{\varrho _{1}}-{\varrho _{2}}} \le \lambda _{l}^{+},\quad {\varrho _{1}} \ne {\varrho _{2}}, l= 1,2, \ldots , n, \end{aligned}$$

(3)

where $\lambda _{l}^{-}$, $\lambda _{l}^{+}$ are known scalars, which can be positive, negative, and zero; $\mathcal{{U}}(t) \in {\mathbb{R}^{n}}$ is the control input of the slave system (2), $\mathcal{B}_{\sigma (t)}$ is a positive diagonal matrix, $\mathcal{A}_{\sigma (t)}$ and $\mathcal{D}_{\sigma (t)}$ are the coefficient matrices of the connection weighted matrix and the time-varying delay connection weight matrix, respectively, and $\{ \sigma (t), t \ge 0 \}$ is a continuous-time Markov process taking values in a finite space $\mathcal{N} = ( {1,2, \ldots , {N}} )$ and governed by

$$ \Pr \bigl\{ {\sigma (t + \Delta ) = j} \mid {\sigma (t) = i} \bigr\} = \textstyle\begin{cases} {{\pi _{ij}}\Delta + o( \Delta ),} & i \ne j, \\ {1 + {\pi _{ii}}\Delta + o( \Delta ),} & i = j, \end{cases} $$

(4)

where $\Delta \ge 0$, $\lim_{\Delta \to 0} {{o ( \Delta )} / \Delta } = 0$, ${\pi _{ij}} \ge 0$ for $i \ne j \in \mathcal{N}$ is the transition rate from mode i at time t to mode j at time $t + \Delta$, and ${\pi _{ii}} = - \sum_{j = 1, j \ne i}^{{N}} {{\pi _{ij}}}$; ${\delta }(t)$ represents the time-varying delay and satisfies

$$\begin{aligned} 0 \le {\delta } (t) \le {\delta } ,\qquad {{\dot{\delta }}} (t) \le {\mu }, \end{aligned}$$

(5)

where δ and μ are known constants. To simplify some notations, for each $\sigma (t) = {i} \in {\mathcal{N}}$, we denote $\mathcal{{B}}_{\sigma (t)} = \mathcal{{B}}_{i}$, $\mathcal{{A}}_{\sigma (t)}= { \mathcal{{A}}}_{i}$, and $\mathcal{{D}}_{\sigma (t)} = \mathcal{{D}}_{i}$. Let $r(t) = y(t) - x(t)$ be the error state. The error dynamics can be described by

$$\begin{aligned} \textstyle\begin{cases} \dot{r}(t) = -\mathcal{B}_{i} r(t) + \mathcal{A}_{i} f({r(t)}) + \mathcal{D}_{i} f(r( t - {\delta }(t))) + \mathcal{U}(t), \\ \varphi (\theta )=r(t_{0}+\theta ), \quad \theta \in [-\max (\delta , \eta ), 0], \end{cases}\displaystyle \end{aligned}$$

(6)

where $f({r(\cdot )})= g({y(\cdot )})- g({x(\cdot )})$ and $\varphi (\theta ) =\phi (\theta ) -\psi (\theta )$. From condition (3) we can readily obtain that the function $g_{i}(\cdot )$ satisfies

$$\begin{aligned} \lambda _{l}^{-} \le \frac{f_{i}({\varrho }))}{{\varrho }} \le \lambda _{l}^{+},\quad {\varrho } \ne 0, l= 1,2, \ldots , n. \end{aligned}$$

(7)

To mitigate unnecessary waste of network resources, in the following subsection, we will introduce a discrete ETCS. Assume that the system state is sampled periodically and that the sampling sequence is depicted by the set $\Pi _{s}= \{0, h, 2h, \ldots , kh\}$ with $k\in \mathbb{Z}_{+}$, where h is a constant sampling period, and the event-triggered sequence is described by the set $\Pi _{e} = \{0, b_{1} h, b_{2}h, \ldots , b_{k} h\} \subseteq \Pi _{s}$ with $b_{k}\in \mathbb{Z}_{+}$. To decide whether the current sampling state is sent out to the controller, we adopt the following event-triggered condition:

$$\begin{aligned} {b_{{k}+1}}h = {b_{k}}h + l_{m} h, \end{aligned}$$

(8)

where $l_{m} = {\min }\{{l} | e^{T}({b_{k}}h +{l}h) {\Omega }e({b_{k}}h +{l}h) \ge {\lambda } r^{T}({b_{k}}h ){\Omega } r({b_{k}}h )\}$ with $l \in \mathbb{Z}_{+}$, $\lambda \in [0, 1)$ is the threshold, $\Omega \in \mathbb{S}_{+}^{n}$ is an unknown weighting matrix, and $e({b_{k}}h +{l}h) = r({b_{k}}h +lh) - r({b_{k}}h )$ expresses the error between the two states at the latest transmitted instant and the current sampling one. We define the following event-triggered state-feedback controller:

$$\begin{aligned} {\mathcal{U}}(t)=\mathcal{K}_{i} r(b_{k} h),\quad \forall t \in {\mathbb{I}}_{k} =[{b}_{k}h, {b}_{k+1}h). \end{aligned}$$

(9)

Similarly with [66], to depict clearly the ETCS, the triggering interval ${\mathbb{I}}_{k}$ can be decomposed as $\bigcup_{l=0}^{l_{m}-1} [(b_{k} + l) h , (b_{k}+l+1)h )$. Define the function

$$\begin{aligned} \eta (t) = t-(b_{k}+l)h,\quad t \in [(b_{k} + l) h , (b_{k}+l+1)h ). \end{aligned}$$

(10)

It is easy to see that $\eta (t)$ is a linear piecewise function and satisfies $0 \le \eta (t) \le \eta$, $\dot{\eta }(t)=1$. By combining with (6), (9), and (10), for all $t \in {\mathbb{I}}_{k}$, we have

$$\begin{aligned} \textstyle\begin{cases} \dot{r}(t) =-\mathcal{B}_{i} r(t) + \mathcal{A}_{i} f({r(t)}) + \mathcal{D}_{i} f(r( t - {\delta }(t))) + \mathcal{K}_{i} [ r(t-\eta (t))- e(t-\eta (t ))], \\ \varphi (\theta )=r(t_{0}+\theta ),\quad \theta \in [-\max (\delta , \eta ), 0]. \end{cases}\displaystyle \end{aligned}$$

(11)

We recall the following definition and lemmas, which play a key role in obtaining our main results.

Definition 2.1

([43])

System (2) is said to be stochastically exponentially synchronized in the mean square sense with system (1) if system (11) is stochastically exponentially stable in the mean square sense with convergence rate $\alpha > 0$, that is, there exists $M >0$ such that for all $t \ge t_{0}$,

$$ \mathbb{E} \bigl\{ \bigl\Vert r(t) \bigr\Vert ^{2} \bigr\} \le M e^{-\alpha (t -t_{0})} \mathbb{E} \Bigl\{ \sup _{\theta \in [- \max \{ \delta , \eta \}, 0]} \bigl\{ \bigl\Vert \varphi (\theta ) \bigr\Vert ^{2}, \bigl\Vert \dot{\varphi }(\theta ) \bigr\Vert ^{2} \bigr\} \Bigr\} . $$

(12)

Lemma 2.1

([67])

For a matrix $\Xi \in \mathbb{S}_{+}^{n}$, scalars $a< b$, and a differentiable vector function $\varpi (s): [a,b] \to \mathbb{R}^{n}$, we have the following inequality:

$$ -(b-a) \int _{a}^{b}\varpi ^{T}(s)\Xi \varpi (s)\,ds \leq - \biggl( \int _{a}^{b} \varpi (s)\,ds \biggr)^{T} \Xi \biggl( \int _{a}^{b} \varpi (s)\,ds \biggr) -3\Upsilon ^{T} \Xi \Upsilon , $$

(13)

where $\Upsilon =\int _{a}^{b} {\varpi (s)\,ds } - \frac{2}{{b - a}}\int _{a}^{b} {\int _{\theta }^{b} {\varpi (s)\,ds \,d\theta } }$.

Lemma 2.2

([62])

For scalars $\alpha _{1}, \alpha _{2} \in (0,1)$ satisfying $\alpha _{1} + \alpha _{2} = 1$ and matrices $R_{1}, R_{2} \in \mathbb{S}_{+}^{n}$ and $Y \in \mathbb{R}^{n\times n}$, we have the following inequality:

$$diag\{\frac{1}{{\alpha }_1}{R}_1,\frac{1}{{\alpha }_2}{R}_2\}\ge \left(\begin{array}{cc}{R}_1& Y\\ \ast & R_2\end{array}\right)\mathit{\text{if }}\left(\begin{array}{cc}{R}_1& Y\\ \ast & R_2\end{array}\right)>0.$$

(14)

Lemma 2.3

For given matrices $\mathcal{W}_{i} \in \mathbb{S}_{+}^{n}$ and scales $\alpha _{i} \in (0,1)$ with $\sum_{i=1}^{n}\alpha _{i} =1$, if there exist matrices $\mathcal{Y}_{i} \in \mathbb{S}^{n}$ and $\mathcal{Y}_{ij} \in \mathbb{R}^{n \times n}$ ($i, j =1, 2, \ldots , n$, $i < j$) such that

$$\left(\begin{array}{cc}{\overline{\mathcal{W}}}_i& {\mathcal{Y}}_{ij}\\ \ast & {\mathcal{W}}_j\end{array}\right)\ge 0,\left(\begin{array}{cc}{\mathcal{W}}_i& {\mathcal{Y}}_{ij}\\ \ast & {\overline{\mathcal{W}}}_j\end{array}\right)\ge 0,\left(\begin{array}{cc}{\mathcal{W}}_i& {\mathcal{Y}}_{ij}\\ \ast & {\mathcal{W}}_j\end{array}\right)\ge 0,$$

(15)

then we have the following inequality for any vectors $\zeta _{i}(t) \in {\mathbb{R}}^{n}$:

$$\begin{aligned} \sum_{i=1}^{n} \frac{1}{\alpha _{i}}\zeta _{i}^{T}(t) { \mathcal{W}}_{i} \zeta _{i}(t) \ge \sum_{i=1}^{n} \zeta _{i}^{T}(t) \hat{\mathcal{W}}_{i} \zeta _{i}(t) +\sum_{j >i =1}^{n} \mathbb{H}\bigl\{ \zeta _{i}^{T}(t) {{\mathcal{Y}}_{ij}} \zeta _{j}(t)\bigr\} , \end{aligned}$$

(16)

where $\bar{\mathcal{W}}_{i}={\mathcal{W}}_{i} - 2{\mathcal{Y}}_{i}$, $\bar{\mathcal{W}}_{j} ={\mathcal{W}}_{j} - 2{\mathcal{Y}}_{j}$, and $\hat{\mathcal{W}}_{i} ={\mathcal{W}}_{i} +(1-{\alpha _{i}}){{ \mathcal{Y}}_{i}}$.

Proof

Let ${\mathcal{G}}_{n} (\alpha _{i} ) =\sum_{i=1}^{n} \frac{1}{\alpha _{i}}\zeta _{i}^{T}(t) {\mathcal{W}}_{i} \zeta _{i}(t)$. We can obtain

$$\begin{aligned} \mathcal{G}_{n} (\alpha _{i} ) =\sum _{i=1}^{n} { \zeta _{i}^{T}(t)} {\mathcal{W}}_{i}\zeta _{i}(t) +\sum _{j >i =1}^{n} \mathcal{G}_{w}, \end{aligned}$$

(17)

where $\mathcal{G}_{w} =\frac{{\alpha }_{j}}{{\alpha }_{i}} {\zeta _{i}^{T}(t)} \mathcal{W}_{i} \zeta _{i}(t) + \frac{{\alpha }_{i}}{{\alpha }_{j}} { \zeta _{j}^{T}(t)} \mathcal{W}_{j} \zeta _{j}(t)$.

For $\alpha _{i} \in (0,1)$, it follows from (15) that

$$\left(\begin{array}{cc}{\mathcal{W}}_i-2{\alpha }_i{\mathcal{Y}}_i& {\mathcal{Y}}_{ij}\\ \ast & {\mathcal{W}}_j\end{array}\right)\ge 0,\left(\begin{array}{cc}{\mathcal{W}}_i& {\mathcal{Y}}_{ij}\\ \ast & {\mathcal{W}}_j-2{\alpha }_j{\mathcal{Y}}_j\end{array}\right)\ge 0.$$

(18)

By employing the Schur complement to (18) we have

$$\begin{aligned} 0 &\le { } diag\bigl\{ \mathcal{W}_{i} - 2{ \alpha }_{i} \mathcal{Y}_{i} - \mathcal{Y}_{ij} \mathcal{W}_{j}^{-1} \mathcal{Y}_{ij}^{T}, \mathcal{W}_{j} - 2{\alpha }_{j} \mathcal{Y}_{j} - \mathcal{Y}_{ij}^{T} \mathcal{W}_{i}^{-1} \mathcal{Y}_{ij}\bigr\} \\ &={ } diag\{\mathcal{W}_{i} - 2{\alpha }_{i} \mathcal{Y}_{i}, \mathcal{W}_{j} - 2{\alpha }_{j} \mathcal{Y}_{j}\} -diag\bigl\{ \mathcal{Y}_{ij}, \mathcal{Y}_{ij}^{T} \bigr\} \\ &\quad {}\times diag\bigl\{ \mathcal{W}_{j}^{ - 1}, \mathcal{W}_{i}^{-1} \bigr\} \times diag\bigl\{ \mathcal{Y}_{ij}^{T}, \mathcal{Y}_{ij} \bigr\} . \end{aligned}$$

(19)

Using the Schur complement again, from (19) it follows that

$$\left(\begin{array}{cccc}{\mathcal{W}}_i-2{\alpha }_i{\mathcal{Y}}_i& 0& {\mathcal{Y}}_{ij}& 0\\ \ast & {\mathcal{W}}_j-2{\alpha }_j{\mathcal{Y}}_j& 0& {\mathcal{Y}}_{ij}^T\\ \ast & \ast & {\mathcal{W}}_j& 0\\ \ast & \ast & \ast & {\mathcal{W}}_i\end{array}\right)\ge 0.$$

(20)

Pre- and postmultiplying inequality (20) by $col \{\sqrt{{\alpha }_{j}/{\alpha }_{i}} \zeta _{i}(t), \sqrt{{\alpha }_{i}/{\alpha }_{j}} \zeta _{j}(t), - \sqrt{{\alpha }_{i}/{\alpha }_{j}} \zeta _{j}(t), - \sqrt{{\alpha }_{j}/{\alpha }_{i}} \zeta _{i}(t) \}$, we have

$${\mathcal{G}}_w\ge {\left(\begin{array}{c}{\zeta }_i(t)\\ {\zeta }_j(t)\end{array}\right)}^T\left(\begin{array}{cc}{\alpha }_j{\mathcal{Y}}_i& {\mathcal{Y}}_{ij}\\ \ast & {\alpha }_i{\mathcal{Y}}_j\end{array}\right)\left(\begin{array}{c}{\zeta }_i(t)\\ {\zeta }_j(t)\end{array}\right).$$

(21)

Combining (17)–(21), we can derive (16). The proof is completed. □

Remark 2.1

It is well known that the RCCI in [62] with $n =2$ has been improved by the one in [63–65], because the RCCI in [63–65] could derive much tighter upper bound of RCQTs ${\mathcal{G}}_{2} (\alpha _{i} )$. However, as reported in [65], it is still challenging to derive such an RCCI in [63–65] if ${\mathcal{G}}_{n} (\alpha _{i} )$ includes more than three terms, that is, $n\ge 3$. We clearly see that the RCCI in Lemma 2.3 is becoming degenerate into the one in [62] if ${\mathcal{Y}_{i}} =0$, $\mathcal{Y}_{ij} =X_{ij}$, which implies that the RCCI in [62] can be seen as a case of Lemma 2.3. In other words, Lemma 2.3 improves the RCCI in [62] to some extent. Furthermore, when $n =2$, Lemma 2.3 reduces to the RCCI in [63–65], which implies that Lemma 2.3 extends that in [63–65]. Thus we can say that an important issue mentioned in Remark 2.1 has been tackled. Moreover, by comparing (16) and the RCCI in [62] we can easily find that Lemma 2.3 has more flexibility than that in [62] due to the existence of the free matrices ${{Y}_{i}}$. Besides, we clearly see that the RCCI in Lemma 2.3 encompasses both merits of those in [62] and [63–65], simultaneously. Thus the RCCI in Lemma 2.3 can estimate the bound of RCQTs ${\mathcal{G}}_{n} (\alpha _{i} )$ much tighter than the those in [62] and [63–65].

3 Main result

Before describing the main results, for simplification, we define some vectors and matrices:

$$\begin{aligned} &\begin{aligned} \xi (t) &=col\biggl\{ r(t), f \bigl( {r(t)} \bigr), r\bigl(t - \delta (t)\bigr), f \bigl( {r\bigl(t - \delta (t)\bigr)} \bigr), r(t - \delta ), \\ &\quad r \bigl( {t - \eta (t)} \bigr), r ( {t - \eta } ), e\bigl(t - \eta (t) \bigr), \int _{t-\delta (t)}^{t}{\frac{x(s)}{\delta (t)}\,ds}, \\ &\quad \int _{t-\delta }^{t-\delta (t)}{ \frac{r(s)}{\delta -\delta (t)}\,ds}, \int _{t-\eta (t)}^{t}{ \frac{r(s)}{\eta (t)}\,ds}, \int _{t-\eta }^{t-\eta (t)}{ \frac{r(s)}{\eta -\eta (t)}\,ds}, \dot{r}(t) \biggr\} , \end{aligned} \\ &\zeta _{11}=col\{\bar{e}_{1} -\bar{e}_{3}, \bar{e}_{1} +\bar{e}_{3} - \bar{e}_{9}\},\qquad \zeta _{12}=col\{\bar{e}_{3} -\bar{e}_{5}, \bar{e}_{3} +\bar{e}_{5} -\bar{e}_{10}\}, \\ &\zeta _{21}=col\{\bar{e}_{1} -\bar{e}_{6}, \bar{e}_{1} +\bar{e}_{6} - \bar{e}_{11}\},\qquad \zeta _{22}=col\{\bar{e}_{6} -\bar{e}_{7}, \bar{e}_{6} +\bar{e}_{7} -\bar{e}_{12}\}. \end{aligned}$$

Theorem 3.1

For given positive scalars δ, μ, η, α, and ω, system (11) is said to be stochastically exponentially stable in the mean square sens, if there exist matrices $P_{i}$, $S_{i}$, $Q_{1}$, $Q_{2}$, $Q_{3}$, $Q_{4}$, $R_{\nu }\in \mathbb{S}_{+}^{n}$, $X_{\nu }$, $Y_{\nu }\in \mathbb{S}^{2n}$ ($\nu =1, 2$), $X_{12}$, $Y_{12} \in \mathbb{R}^{2n \times 2n}$, $J_{i}$, $G_{i} \in \mathbb{R}^{n \times n}$ and diagonal matrices $M_{1}$, $M_{2} \in \mathbb{S}_{+}^{n}$ such that

$$\left(\begin{array}{cc}{\mathcal{R}}_1-2X_1& X_{12}\\ \ast & {\mathcal{R}}_1\end{array}\right)\ge 0,\left(\begin{array}{cc}{\mathcal{R}}_1& X_{12}\\ \ast & {\mathcal{R}}_1-2X_2\end{array}\right)\ge 0,\left(\begin{array}{cc}{\mathcal{R}}_1& X_{12}\\ \ast & {\mathcal{R}}_1\end{array}\right)\ge 0,$$

(22)

$$\left(\begin{array}{cc}{\mathcal{R}}_2-2Y_1& Y_{12}\\ \ast & {\mathcal{R}}_2\end{array}\right)\ge 0,\left(\begin{array}{cc}{\mathcal{R}}_2& Y_{12}\\ \ast & {\mathcal{R}}_2-2Y_2\end{array}\right)\ge 0,\left(\begin{array}{cc}{\mathcal{R}}_2& Y_{12}\\ \ast & {\mathcal{R}}_2\end{array}\right)\ge 0,$$

(23)

$$\begin{aligned} & \Phi _{i} |_{\delta (t) \in [0,\delta ], \eta (t) \in [0, \eta ]} < 0, \end{aligned}$$

(24)

where $\Phi _{i} ={\Phi _{1 i}} +{\Phi _{2 i}} +{\Phi _{3 i}} +{\Phi _{4 i}} +{\Phi _{5 i}}$, and

$$\begin{array}{rl}& {\mathrm{\Phi }}_{1i}=\mathbb{H}\left\{{{\overline{e}}_1}^T{P}_i{\overline{e}}_{13}\right\}+{\overline{e}}_1^T(\alpha P_i+\mathrm{\Pi }(P_j)){\overline{e}}_1+{({\overline{e}}_6-{\overline{e}}_8)}^T(\alpha S_i+\mathrm{\Pi }(S_j))({\overline{e}}_6-{\overline{e}}_8),\\ & \begin{array}{rl}{\mathrm{\Phi }}_{2i}& ={\overline{e}}_1^T(Q_1+Q_3+Q_4){\overline{e}}_1+{\overline{e}}_2^T{Q}_2{\overline{e}}_2-e^{-\alpha \delta }(1-\mu ){\overline{e}}_3^T{Q}_1{\overline{e}}_3\\ & -e^{-\alpha \delta }(1-\mu ){\overline{e}}_4^T{Q}_2{\overline{e}}_4-e^{-\alpha \delta }{\overline{e}}_5^T{Q}_3{\overline{e}}_5-e^{-\alpha \eta }{\overline{e}}_7^T{Q}_4{\overline{e}}_7,\end{array}\\ & \begin{array}{rl}{\mathrm{\Phi }}_{3i}& ={\delta }^2{\overline{e}}_{13}^T{R}_1{\overline{e}}_{13}-e^{-\alpha \delta }{\left(\begin{array}{c}{\zeta }_{11}\\ {\zeta }_{12}\end{array}\right)}^T\left(\begin{array}{cc}{\mathcal{R}}_1+(1-{\beta }_1)Y_1& X_{12}\\ \ast & {\mathcal{R}}_1+(1-{\beta }_2)Y_2\end{array}\right)\left(\begin{array}{c}{\zeta }_{11}\\ {\zeta }_{12}\end{array}\right)\\ & +{\eta }^2{\overline{e}}_{13}^T{R}_2{\overline{e}}_{13}-e^{-\alpha \eta }{\left(\begin{array}{c}{\zeta }_{21}\\ {\zeta }_{22}\end{array}\right)}^T\left(\begin{array}{cc}{\mathcal{R}}_2+(1-{\gamma }_1)Y_1& Y_{12}\\ \ast & {\mathcal{R}}_2+(1-{\gamma }_2)Y_2\end{array}\right)\left(\begin{array}{c}{\zeta }_{21}\\ {\zeta }_{22}\end{array}\right),\end{array}\\ & \begin{array}{rl}{\mathrm{\Phi }}_{4i}& =\omega {({\overline{e}}_6-{\overline{e}}_8)}^T\mathrm{\Omega }({\overline{e}}_6-{\overline{e}}_8)-{\overline{e}}_8^T\mathrm{\Omega }{\overline{e}}_8+\mathbb{H}\{{({\overline{e}}_{13}+{\overline{e}}_1)}^T{G}_i({\overline{e}}_6-{\overline{e}}_8)\}\\ & +\mathbb{H}\{{({\overline{e}}_{13}+{\overline{e}}_1)}^T{J}_i(-{\overline{e}}_{13}-B_i{\overline{e}}_1+A_i{\overline{e}}_2+D_i{\overline{e}}_4)\},\end{array}\\ & {\mathrm{\Phi }}_{5i}=-\mathbb{H}\{{({\overline{e}}_2-{\mathrm{\Lambda }}_1{\overline{e}}_1)}^T{M}_1({\overline{e}}_2-{\mathrm{\Lambda }}_2{\overline{e}}_1)+{({\overline{e}}_4-{\mathrm{\Lambda }}_1{\overline{e}}_3)}^T{M}_2({\overline{e}}_4-{\mathrm{\Lambda }}_2{\overline{e}}_3)\},\\ & \mathrm{\Pi }(P_j)=\sum _{j=1}^{\mathcal{N}}{\pi }_{ij}{P}_j,\mathrm{\Pi }(S_j)=\sum _{j=1}^{\mathcal{N}}{\pi }_{ij}{S}_j,{\mathcal{R}}_{\nu }=diag\{R_{\nu },3R_{\nu }\}(\nu =1,2,3,4).\end{array}$$

In addition, the control gain is designed as $\mathcal{K}_{i} =J_{i}^{-1} G_{i}$, $i \in \mathcal{N}$.

Proof

Consider the following stochastic Lyapunov–Krasovskii functional (LKF):

$$\begin{aligned} V\bigl(r(t),\sigma (t)\bigr) = {V_{1}}\bigl(r(t), \sigma (t)\bigr) + {V_{2}}\bigl(r(t),\sigma (t)\bigr) + {V_{3}}\bigl(r(t),\sigma (t)\bigr), \end{aligned}$$

(25)

where

$$\begin{aligned} &{V_{1}}\bigl(r(t),\sigma (t)\bigr) = {r^{T}}(t)P\bigl(\sigma (t)\bigr)r(t) + {r^{T}}({b_{k} h})S\bigl(\sigma (t)\bigr)r({b_{k} h}), \end{aligned}$$

(26)

$$\begin{aligned} &\begin{aligned}[b] {V_{{2}}}\bigl(r(t),\sigma (t)\bigr) &= { } \int _{t - \delta (t)}^{t} {{e^{\alpha (s - t)}} \bigl[{r^{T}}(s){Q_{1}}r(s) +{f^{T}}\bigl(r(s) \bigr){Q_{2}}f\bigl(r(s)\bigr) \bigr]\,ds} \\ &\quad{}+ \int _{t - \delta }^{t} {{e^{\alpha (s - t)}} {r^{T}}(s){Q_{3}}r(s)\,ds} + \int _{t - \eta }^{t} {{e^{\alpha (s - t)}} {r^{T}}(s){Q_{4}}r(s)\,ds} , \end{aligned} \end{aligned}$$

(27)

$$\begin{aligned} &\begin{aligned}[b] {V_{{3}}}\bigl(r(t),\sigma (t)\bigr) &= \delta \int _{ - \delta }^{0} { \int _{t+u}^{t} {{e^{\alpha (s - t)}} {{ \dot{r}}^{T}}(s){R_{1}}\dot{r}(s)\,ds} \,du} \\ &\quad{}+ \eta \int _{ - \eta }^{0} { \int _{t+u}^{t} {{e^{\alpha (s - t)}} {{ \dot{x}}^{T}}(s){R_{2}}\dot{x}(s)\,ds} \,du}. \end{aligned} \end{aligned}$$

(28)

Let $\mathcal{L}$ be the week infinitesimal operator acting on LKF (25):

$$\begin{aligned} \mathcal{L}V\bigl(r(t),\sigma (t)\bigr) =\lim_{\Delta \to 0} \frac{{\mathbb{E} \{ {V(r(t + \Delta ),\sigma (t + \Delta )=j) \mid {{r(t)},{\sigma (t)}=i}} \} - V(r(t),i)}}{\Delta }. \end{aligned}$$

Then along with the solution of system (11), we have

$$\begin{aligned} & \begin{aligned}[b] \mathcal{L} {V_{1}}\bigl(r(t),i\bigr) &= 2\dot{x}^{T}(t) P_{i} x(t) + {x}^{T}(t)\Pi (P_{j}) x(t) + {x^{T}}({b_{k}}h) \Pi (S_{j})x({b_{k}}h) \\ & =\xi ^{T}(t) \Phi _{1i} \xi (t) -\alpha {V_{1}} \bigl(r(t),i\bigr), \end{aligned} \end{aligned}$$

(29)

$$\begin{aligned} &\begin{aligned}[b] \mathcal{L} {V_{{2}}}\bigl(r(t),i\bigr) &\le {r^{T}}(t) ({Q_{1}}+{Q_{3}}+{Q_{4}}) r(t) +{f^{T}}\bigl(r(t)\bigr){Q_{2}}f\bigl(r(t)\bigr) \\ &\quad {} -(1-\mu ){e^{- \alpha \delta }} {r^{T}}\bigl(t - \delta (t) \bigr){Q_{1}}r\bigl(t - \delta (t)\bigr) \\ &\quad {} -(1-\mu ){e^{- \alpha \delta }} {f^{T}}\bigl(r\bigl(t - \delta (t)\bigr)\bigr){Q_{2}}f\bigl(r\bigl(t - \delta (t)\bigr)\bigr) \\ &\quad {} -{e^{-\alpha \delta }} {r^{T}}(t - \delta ){Q_{3}}r(t - \delta ) \\ & \quad {} -{e^{-\alpha \eta }} {r^{T}}(t - \eta ){Q_{4}}r(t - \eta ) -\alpha {V_{{2}}}\bigl(r(t),i\bigr) \\ & =\xi ^{T}(t) \Phi _{2i} \xi (t) -\alpha {V_{2}} \bigl(r(t),i\bigr), \end{aligned} \end{aligned}$$

(30)

$$\begin{aligned} &\begin{aligned}[b] \mathcal{L} {V_{{3}}}\bigl(r(t),i\bigr) &\le \dot{r}^{T}(t)\bigl[\delta ^{2} R_{1} +\eta ^{2} R_{2} \bigr] \dot{r}(t) - \alpha {V_{{3}}}\bigl(r(t),i\bigr) \\ & \quad {} -\delta \int _{ t- \delta }^{t} {{e^{\alpha (s - t)}} {{ \dot{r}}^{T}}(s){R_{1}} {\dot{r}}(s)\,ds} \\ &\quad{}-\eta \int _{ t- \eta }^{t} {{e^{\alpha (s - t)}} {{ \dot{r}}^{T}}(s){R_{2}} {\dot{r}}(s)\,ds}. \end{aligned} \end{aligned}$$

(31)

For the last four integral quadratic terms, by utilizing Lemma 2.1, we obtain that

$$\begin{aligned} &{-}\delta \int _{ t- \delta }^{t} {{e^{\alpha (s - t)}} {{ \dot{r}}^{T}}(s){R_{1}} {\dot{r}}(s)\,ds} \le -\xi ^{T}(t) \biggl\{ \frac{{e^{-\alpha \delta }}}{\beta _{1}}\zeta _{11}^{T} \mathcal{R}_{1} \zeta _{11} +\frac{{e^{-\alpha \delta }}}{\beta _{2}}\zeta _{12}^{T} \mathcal{R}_{1} \zeta _{12} \biggr\} \xi (t), \end{aligned}$$

(32)

$$\begin{aligned} &{-}\eta \int _{ t- \eta }^{t} {{e^{\alpha (s - t)}} {{ \dot{r}}^{T}}(s){R_{2}} {\dot{r}}(s)\,ds} \le -\xi ^{T}(t) \biggl\{ \frac{{e^{-\alpha \eta }}}{\gamma _{1}}\zeta _{21}^{T} \mathcal{R}_{2} \zeta _{21} +\frac{{e^{-\alpha \eta }}}{\gamma _{2}}\zeta _{22}^{T} \mathcal{R}_{2} \zeta _{22} \biggr\} \xi (t), \end{aligned}$$

(33)

where $\beta _{1} =\frac{\delta (t)}{\delta }$, $\beta _{2} = \frac{\delta -\delta (t)}{\delta }$, $\gamma _{1} =\frac{\eta (t)}{\eta }$, and $\gamma _{2} =\frac{\eta -\eta (t)}{\eta }$.

Applying Lemma 2.3, from (32)–(33), together with (22)–(23), it follows that

$$\begin{array}{rl}& -\delta {\int }_{t-\delta }^t{e}^{\alpha (s-t)}{\dot{x}}^T(s)R_2\dot{x}(s)ds\\ & \le {\xi }^T(t)\{-e^{-\alpha \delta }{\left(\begin{array}{c}{\zeta }_{11}\\ {\zeta }_{12}\end{array}\right)}^T\left(\begin{array}{cc}{\mathcal{R}}_1+(1-{\beta }_1)X1& X_{12}\\ \ast & {\mathcal{R}}_1+(1-{\beta }_2)X2\end{array}\right)\left(\begin{array}{c}{\zeta }_{11}\\ {\zeta }_{12}\end{array}\right)\}\xi (t),\end{array}$$

(34)

$$\begin{array}{rl}& -\eta {\int }_{t-\eta }^t{e}^{\alpha (s-t)}{\dot{x}}^T(s)R_3\dot{x}(s)ds\\ & \le {\xi }^T(t)\{-e^{-\alpha \eta }{\left(\begin{array}{c}{\zeta }_{21}\\ {\zeta }_{22}\end{array}\right)}^T\left(\begin{array}{cc}{\mathcal{R}}_2+(1-{\gamma }_1)Y1& Y_{12}\\ \ast & {\mathcal{R}}_2+(1-{\gamma }_2)Y2\end{array}\right)\left(\begin{array}{c}{\zeta }_{21}\\ {\zeta }_{22}\end{array}\right)\}\xi (t).\end{array}$$

(35)

Combining (31)–(35), we have

$$\begin{aligned} \mathcal{L} {V_{{3}}}\bigl(x(t),i\bigr) \le \xi ^{T}(t) \Phi _{3i} \xi (t) - \alpha {V_{{3}}} \bigl(x(t),i\bigr). \end{aligned}$$

(36)

In addition, when the current data need not be sent out, from the ETCS (8) we easily get that

$$\begin{array}{rl}0& <{\left[\begin{array}{c}x(t-\eta (t))\\ e(t-\eta (t))\end{array}\right]}^T\left[\begin{array}{cc}\omega \mathrm{\Omega }& -\omega \mathrm{\Omega }\\ \ast & (\omega -1)\mathrm{\Omega }\end{array}\right]\left[\begin{array}{c}x(t-\eta (t))\\ e(t-\eta (t))\end{array}\right]\\ & ={\xi }^T(t)\{\omega {({\overline{e}}_6-{\overline{e}}_8)}^T\mathrm{\Omega }({\overline{e}}_6-{\overline{e}}_8)-{\overline{e}}_8^T\mathrm{\Omega }{\overline{e}}_8\}\xi (t).\end{array}$$

(37)

Furthermore, from (11), for any matrices $J_{i}, K_{i} \in \mathbb{R}^{n \times n}$, we have

$$\begin{aligned} 0&={ } 2\bigl[\dot{x}(t) +x(t)\bigr]^{T} J_{i} \bigl[-B_{i} x(t) +A_{i} f\bigl(x(t)\bigr) +D_{i} f\bigl(x\bigl(t-d(t)\bigr)\bigr)\bigr] \\ &{ }\quad {} +2\bigl[\dot{x}(t) +x(t)\bigr]^{T} G_{i} \bigl[x\bigl(t-\eta (t)\bigr) -e\bigl(t-\eta (t)\bigr)\bigr] \\ &={ } {\xi ^{T}}(t) \bigl\{ \mathbb{H} \bigl\{ {{{ ({ \bar{e}_{13} + { \bar{e}_{1}}} )}^{T}} {G_{i}} ( {{\bar{e}_{6}} - {\bar{e}_{8}}} )} \bigr\} \\ & \quad {}+\mathbb{H} \bigl\{ {{{ ( {{\bar{e}_{13}} + { \bar{e}_{1}}} )}^{T}} {J_{i}} ( { - { \bar{e}_{13}} - {B_{i}} {\bar{e}_{1}} + {A_{i}} {\bar{e}_{2}} + {D_{i}} { \bar{e}_{4}}} )} \bigr\} \bigr\} \xi (t). \end{aligned}$$

(38)

According to (7), there exist diagonal matrices $M_{1}, M_{2} \in \mathbb{S}_{+}^{n}$ such that

$$\begin{aligned} &\begin{aligned}[b] 0 &\le - 2{ \bigl[ {f\bigl(r(t)\bigr) - {\Lambda _{1}}r(t)} \bigr]^{T}} {M_{1}} \bigl[ {f \bigl(r(t)\bigr) - {\Lambda _{2}}r(t)} \bigr] \\ &= {\xi ^{T}}(t) \bigl\{ { - \mathbb{H} \bigl\{ {{{ ( {{ \bar{e}_{2}} - {\Lambda _{1}} {\bar{e}_{1}}} )}^{T}} {M_{1}} ( {{\bar{e}_{2}} - {\Lambda _{2}} {\bar{e}_{1}}} )} \bigr\} } \bigr\} \xi (t), \end{aligned} \end{aligned}$$

(39)

$$\begin{aligned} &\begin{aligned}[b] 0 &\le - 2{ \bigl[ {f\bigl(r\bigl(t - \delta (t) \bigr)\bigr) - {\Lambda _{1}}r\bigl(t - \delta (t)\bigr)} \bigr]^{T}} {M_{2}} \bigl[ {f\bigl(r\bigl(t - \delta (t) \bigr)\bigr) - {\Lambda _{2}}r\bigl(t - \delta (t)\bigr)} \bigr] \\ &= {\xi ^{T}}(t) \bigl\{ { - \mathbb{H} \bigl\{ {{{ ( {{ \bar{e}_{4}} - {\Lambda _{1}} {\bar{e}_{3}}} )}^{T}} {M_{2}} ( {{\bar{e}_{4}} - {\Lambda _{2}} {\bar{e}_{3}}} )} \bigr\} } \bigr\} \xi (t), \end{aligned} \end{aligned}$$

(40)

where $\Lambda _{ 1 } = { diag } \{ \lambda _{ 1 } ^{ - } , \ldots , \lambda _{ n } ^{ - } \}$ and $\Lambda _{ 2 } = { diag } \{ \lambda _{ 1 } ^{ + } , \ldots , \lambda _{ n } ^{ + } \}$.

Therefore, combining (29)–(40) and (24), we obtain

$$\begin{aligned} \mathbb{E} \bigl\{ \mathcal{L} {V}\bigl(r(t),i\bigr) \bigr\} \le \xi ^{T} (t) \Phi _{i} \xi (t)-\alpha \mathbb{E} \bigl\{ {V} \bigl(r(t),i\bigr) \bigr\} \le - \alpha \mathbb{E} \bigl\{ {V}\bigl(r(t),i\bigr) \bigr\} , \end{aligned}$$

(41)

which implies that

$$\begin{aligned} \mathbb{E} \bigl\{ {V}\bigl(r(t),i\bigr) \bigr\} \le e^{-\alpha (t-t_{0})} \mathbb{E} \bigl\{ {V}\bigl(r(t_{0}),\sigma _{0}\bigr) \bigr\} . \end{aligned}$$

(42)

From (25) we easily get that

$$\begin{aligned} &\mathbb{E} \bigl\{ {V}\bigl(r(t),i\bigr) \bigr\} \ge \lambda _{\min }(P_{i}) \mathbb{E} \bigl\{ \bigl\Vert r(t) \bigr\Vert ^{2} \bigr\} , \end{aligned}$$

(43)

$$\begin{aligned} &\mathbb{E} \bigl\{ {V}\bigl(r(t_{0}),\sigma _{0}\bigr) \bigr\} \le ( \Gamma _{ 1 } + \Gamma _{ 2 } + \Gamma _{ 3 } ) \sup \bigl\{ \bigl\Vert \varphi ( \theta ) \bigr\Vert ^{ 2 }, \bigl\Vert \dot{ \varphi } ( \theta ) \bigr\Vert ^{ 2 } \bigr\} , \end{aligned}$$

(44)

where

$$\begin{aligned} &\Gamma _{ 1 }=\lambda _{ \max } ( P _{ i } + S_{ i } ),\qquad \Lambda = { diag } \{ \lambda _{ 1 } , \ldots , \lambda _{ n } \} ,\\ &\lambda _{ \tilde{\nu } } = \max \bigl\{ \bigl\vert \lambda _{ \tilde{\nu }} ^{ - } \bigr\vert , \bigl\vert \lambda _{ \tilde{\nu } } ^{ + } \bigr\vert \bigr\} ,\quad \tilde{\nu } =1, 2, \ldots , n, \\ &\Gamma _{ 2 }= \frac{ 1 - e ^{ - \alpha \delta } }{ \alpha } \bigl[ \lambda _{ \max } ( Q _{ 1 } ) + \lambda _{ \max } ( Q _{ 2 } ) \Vert \Lambda \Vert ^{ 2 } + \lambda _{ \max } ( Q _{ 3 } ) \bigr] + \frac{ 1 - e ^{ - \alpha \eta } }{ \alpha } \bigl[\lambda _{ \max } ( Q _{ 4 } ) \bigr], \\ &\begin{aligned} \Gamma _{ 3 } &=\frac{ ( e ^{ - \alpha \delta } + \alpha \delta - 1 ) }{ \alpha ^{ 2 } } \bigl[\delta \lambda _{ \max } ( R _{ 1} ) +(\delta + \eta ) e ^{\alpha \delta } \lambda _{ \max } ( R _{3} ) \bigr] \\ &\quad{}+ \frac{ ( e ^{ - \alpha \eta } + \alpha \eta - 1 ) }{ \alpha ^{ 2 } } \bigl[\eta \lambda _{ \max } ( R _{2} ) +(\delta + \eta ) e ^{\alpha \eta } \lambda _{ \max } ( R _{4} ) \bigr]. \end{aligned} \end{aligned}$$

From (42)–(44) we have

$$\begin{aligned} \mathbb{E} \bigl\{ \bigl\Vert r(t) \bigr\Vert ^{2} \bigr\} \le M e^{- \alpha (t-t_{0})} \mathbb{E} \bigl\{ \sup \bigl\{ \bigl\Vert \phi ( \theta ) \bigr\Vert ^{ 2 }, \bigl\Vert \dot{ \phi } ( \theta ) \bigr\Vert ^{ 2 } \bigr\} \bigr\} , \end{aligned}$$

(45)

where $M = \frac{\Gamma _{ 1 } + \Gamma _{ 2 } + \Gamma _{ 3 }}{\lambda _{\min }(P_{i})}$.

Therefore, according to the Definition 2.1, system (11) is stochastically exponentially stable in the mean square sense with convergence rate $\alpha >0$. In addition, the control gain is designed as $\mathcal{K}_{i} =J_{i}^{-1} G_{i}$, $i \in \mathcal{N}$. This completes the proof. □

Remark 3.1

It is found that LMI (24) in Theorem 3.1 depends on the TDs $\delta (t)$ and $\eta (t)$, which cannot be solved directly by Matlab LMI toolbox. Note that $\Phi _{i}$ is an affine function of variables $\delta (t)$ and $\eta (t)$. We can deduce that condition (24) is satisfied for all $\delta (t)\in [0, \delta ]$ and $\eta (t)\in [0, \eta ]$ if $\Phi _{i} |_{\delta (t)=0, \eta (t)=0, } <0$, $\Phi _{i} |_{\delta (t)=0, \eta (t)=\eta , } <0$, $\Phi _{i} |_{\delta (t)=\delta , \eta (t)=0, } <0$, and $\Phi _{i} |_{\delta (t)=\delta , \eta (t)=\eta }<0$. On the other hand, the constructed LKF ${V}(x(t), i)$ plays a key role in deriving the event-triggered exponential synchronization result. Specifically, the triggering signal state related to Markov jump parameters is considered in $V_{1}(r(t),i)$, and the information about the TDs, neuron activation function, and the Virtual delay η are taken into account in $V_{2}(x(t),i)$ and $V_{3}(x(t),i)$, which is more general than those given in [39, 40, 43, 44, 47, 48, 58–61] and is helpful to obtain less conservative stability criterion. Besides, in the proof of Theorem 3.1, we utilize a new RCCI to estimate the bound of RCQTs, which was shown to be more tighter than those based on other RCCIs [62]. Meanwhile, the new RCCI contains more coupled information between $\delta (t) \in [0, \delta ]$ and $\eta (t) \in [0, \eta ]$, which is effective in reducing the conservatism.

In what follows, as a particular case, when Markov jump parameters are not considered, system (11) will be reduced to the following equation:

$$\begin{aligned} \textstyle\begin{cases} \dot{r}(t) =-\mathcal{B} r(t) + \mathcal{A} f({r(t)}) + \mathcal{D} f(r( t - { \delta }(t))) + \mathcal{K} [ r(t-\eta (t))- e(t-\eta (t ))], \\ \varphi (\theta )=r(t_{0}+\theta ), \quad \theta \in [-\max (\delta , \eta ), 0]. \end{cases}\displaystyle \end{aligned}$$

(46)

Based on Theorem 3.1, we can readily derive the following criterion.

Theorem 3.2

For given positive scalars δ, μ, η, α, and ω, system (46) is exponentially stable in the mean square sense if there exist matrices P, S, $Q_{1}$, $Q_{2}$, $Q_{3}$, $Q_{4}$, $R_{\nu }\in \mathbb{S}_{+}^{n}$, $X_{\nu }$, $Y_{\nu }\in \mathbb{S}^{2n}$ ($\nu =1, 2$), $X_{12}$, $Y_{12} \in \mathbb{R}^{2n \times 2n}$, J, $G \in \mathbb{R}^{n \times n}$ and diagonal matrices $M_{1}$, $M_{2} \in \mathbb{S}_{+}^{n}$ such that

$$\left(\begin{array}{cc}{\mathcal{R}}_1-2X_1& X_{12}\\ \ast & {\mathcal{R}}_1\end{array}\right)\ge 0,\left(\begin{array}{cc}{\mathcal{R}}_1& X_{12}\\ \ast & {\mathcal{R}}_1-2X_2\end{array}\right)\ge 0,\left(\begin{array}{cc}{\mathcal{R}}_1& X_{12}\\ \ast & {\mathcal{R}}_1\end{array}\right)\ge 0,$$

(47)

$$\left(\begin{array}{cc}{\mathcal{R}}_2-2Y_1& Y_{12}\\ \ast & {\mathcal{R}}_2\end{array}\right)\ge 0,\left(\begin{array}{cc}{\mathcal{R}}_2& Y_{12}\\ \ast & {\mathcal{R}}_2-2Y_2\end{array}\right)\ge 0,\left(\begin{array}{cc}{\mathcal{R}}_2& Y_{12}\\ \ast & {\mathcal{R}}_2\end{array}\right)\ge 0,$$

(48)

$$\begin{aligned} & \Phi |_{\delta (t) \in [0,\delta ], \eta (t) \in [0, \eta ]} < 0, \end{aligned}$$

(49)

where $\Phi ={\Phi _{1}} +{\Phi _{2}} +{\Phi _{3}} +{\Phi _{4}} +{\Phi _{5}}$, and

$$\begin{array}{rl}& {\mathrm{\Phi }}_1=\mathbb{H}\left\{{{\overline{e}}_1}^{T}P{\overline{e}}_{13}\right\}+{\overline{e}}_1^T(\alpha P){\overline{e}}_1+{({\overline{e}}_6-{\overline{e}}_8)}^T(\alpha S)({\overline{e}}_6-{\overline{e}}_8),\\ & \begin{array}{rl}{\mathrm{\Phi }}_2& ={\overline{e}}_1^T(Q_1+Q_3+Q_4){\overline{e}}_1+{\overline{e}}_2^T{Q}_2{\overline{e}}_2-e^{-\alpha \delta }(1-\mu ){\overline{e}}_3^T{Q}_1{\overline{e}}_3\\ & -e^{-\alpha \delta }(1-\mu ){\overline{e}}_4^T{Q}_2{\overline{e}}_4-e^{-\alpha \delta }{\overline{e}}_5^T{Q}_3{\overline{e}}_5-e^{-\alpha \eta }{\overline{e}}_7^T{Q}_4{\overline{e}}_7,\end{array}\\ & \begin{array}{rl}{\mathrm{\Phi }}_3& ={\delta }^2{\overline{e}}_{13}^T{R}_1{\overline{e}}_{13}-e^{-\alpha \delta }{\left(\begin{array}{c}{\zeta }_{11}\\ {\zeta }_{12}\end{array}\right)}^T\left(\begin{array}{cc}{\mathcal{R}}_1+(1-{\beta }_1)Y_1& X_{12}\\ \ast & {\mathcal{R}}_1+(1-{\beta }_2)Y_2\end{array}\right)\left(\begin{array}{c}{\zeta }_{11}\\ {\zeta }_{12}\end{array}\right)\\ & +{\eta }^2{\overline{e}}_{13}^T{R}_2{\overline{e}}_{13}-e^{-\alpha \eta }{\left(\begin{array}{c}{\zeta }_{21}\\ {\zeta }_{22}\end{array}\right)}^T\left(\begin{array}{cc}{\mathcal{R}}_2+(1-{\gamma }_1)Y_1& Y_{12}\\ \ast & {\mathcal{R}}_2+(1-{\gamma }_2)Y_2\end{array}\right)\left(\begin{array}{c}{\zeta }_{21}\\ {\zeta }_{22}\end{array}\right),\end{array}\\ & \begin{array}{rl}{\mathrm{\Phi }}_4& =\omega {({\overline{e}}_6-{\overline{e}}_8)}^T\mathrm{\Omega }({\overline{e}}_6-{\overline{e}}_8)-{\overline{e}}_8^T\mathrm{\Omega }{\overline{e}}_8+\mathbb{H}\{{({\overline{e}}_{13}+{\overline{e}}_1)}^{T}G({\overline{e}}_6-{\overline{e}}_8)\}\\ & +\mathbb{H}\{{({\overline{e}}_{13}+{\overline{e}}_1)}^{T}J(-{\overline{e}}_{13}-B{\overline{e}}_1+A{\overline{e}}_2+D{\overline{e}}_4)\},\end{array}\\ & {\mathrm{\Phi }}_{5i}=-\mathbb{H}\{{({\overline{e}}_2-{\mathrm{\Lambda }}_1{\overline{e}}_1)}^T{M}_1({\overline{e}}_2-{\mathrm{\Lambda }}_2{\overline{e}}_1)+{({\overline{e}}_4-{\mathrm{\Lambda }}_1{\overline{e}}_3)}^T{M}_2({\overline{e}}_4-{\mathrm{\Lambda }}_2{\overline{e}}_3)\}.\end{array}$$

In addition, the control gain is designed as $\mathcal{K} =J^{-1} G$.

4 Numerical examples

In this section, we give two examples to demonstrate the effectiveness of our proposed methods.

Example 4.1

Consider system (11) with the following parameters:

$${\mathcal{A}}_1=\left(\begin{array}{cc}2& -0.1\\ -5& 3\end{array}\right),{\mathcal{D}}_1=\left(\begin{array}{cc}-1.5& -0.1\\ -0.2& -2.5\end{array}\right),$$

(50)

$${\mathcal{A}}_2=\left(\begin{array}{cc}2& -0.11\\ -5& 3.2\end{array}\right),{\mathcal{D}}_2=\left(\begin{array}{cc}-1.6& -0.1\\ -0.18& -2.4\end{array}\right),$$

(51)

$$\begin{aligned} &{\mathcal{B}}_{1}=diag\{1, 1\}, \qquad \mathcal{B}_{2}=diag \{0.8, 1\}, \\ &\Lambda ^{-} =diag\{0, 0\},\qquad \Lambda ^{+} =diag\{0.5, 0.5\}, \\ &\delta =0.2,\qquad \mu =0.2,\qquad \eta =0.2,\qquad \omega =0.1,\qquad \alpha =0.15. \end{aligned}$$

(52)

In this example, the generator matrix is taken as $\mathrm{\Pi }=\left(\begin{array}{cc}-3& 3\\ 5& -5\end{array}\right)$. Under these parameters, by applying the LMI toolbox in MATLAB soft to solve LMIs (22)–(24) in Theorem 3.1, the weighted matrix in ETCS and the control gain matrices are derived as $\mathrm{\Omega }=1.0e+04\times \left(\begin{array}{cc}7.2775& -0.1589\\ -0.1589& 0.2102\end{array}\right)$, ${\mathcal{K}}_1=\left(\begin{array}{cc}-0.7997& 0.0642\\ 2.1540& -1.4280\end{array}\right)$, and ${\mathcal{K}}_2=\left(\begin{array}{cc}-0.7166& 0.0637\\ 2.1816& -1.3329\end{array}\right)$. Meanwhile, the feasible solution matrices in Theorem 3.1 can be obtained:

$$\begin{array}{rl}& P_1=1.0e+04\times \left(\begin{array}{cc}2.7340& 0.0260\\ 0.0260& 0.0556\end{array}\right),P_2=1.0e+04\times \left(\begin{array}{cc}2.9535& 0.0261\\ 0.0261& 0.0587\end{array}\right),\\ & S_1=1.0e+03\times \left(\begin{array}{cc}4.9634& 0.2343\\ 0.2343& 0.0426\end{array}\right),S_2=1.0e+03\times \left(\begin{array}{cc}4.4595& 0.2900\\ 0.2900& 0.0212\end{array}\right),\\ & R_1=1.0e+04\times \left(\begin{array}{cc}3.9397& -0.4725\\ -0.4725& 0.2396\end{array}\right),R_2=1.0e+04\times \left(\begin{array}{cc}3.7446& 0.2189\\ 0.2189& 0.0150\end{array}\right),\end{array}$$

to list a few. Clearly, the effectiveness of our method is illustrated here.

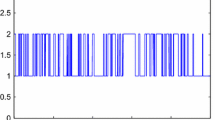
To reflect intuitively the feasibility and validity of the obtained result, when the neuron activation function $f_{i}(x) =0.5 (|x+1| -|x-1| )$ and the time-varying delay $\delta (t) =0.2 +0.2\sin (t)$, we present Figs. 1–3, which show the state response of systems (11) with parameters (50)–(51) under no any control and the well-designed ETCS (8), respectively. Clearly, ETCS (8) is effective. Furthermore, it is not hard to see from Fig. 2 that the frequency of control is reduced to large extent, which means that more network resources are saved by using the ETCS.

Figure 1

Curve of $x(t)$ without control for Example 4.1 under $r(0) = [-0.2;0.3]$

Figure 2

Release instants and intervals for Example 4.1 under $r(0) = [-0.2;0.3]$

Figure 3

Curve of $x(t)$ with ETCS for Example 4.1 under $r(0) = [-0.2;0.3]$

Example 4.2

Consider system (46) with the following parameters:

$$\mathcal{A}=\left(\begin{array}{cc}1& 0.5\\ 0.5& -1\end{array}\right),\mathcal{D}=\left(\begin{array}{cc}-0.5& -0.1\\ 0.6& 0.8\end{array}\right),$$

(53)

$$\begin{aligned} & {\mathcal{B}}= diag\{0.3, 0.3\},\qquad \Lambda ^{-} =diag \{0, 0\},\qquad \Lambda ^{+} =diag\{0.4, 0.8\}, \\ &\delta =0.6,\qquad \mu =0.2,\qquad \eta =0.5, \qquad \omega =0.2,\qquad \alpha =0.3. \end{aligned}$$

(54)

Under these parameters, by applying the LMI toolbox in MATLAB soft to solve LMIs (47)–(49) in Theorem 3.2 the weighted matrix in ETCS and the control gain matrix are derived as $\mathrm{\Omega }=\left(\begin{array}{cc}731.9461& 233.9629\\ 233.9629& 268.2341\end{array}\right)$ and $\mathcal{K}=\left(\begin{array}{cc}-0.6750& -0.1402\\ -0.0566& -0.3810\end{array}\right)$, respectively. Meanwhile, the feasible solution matrices in Theorem 3.2 are obtained:

$$\begin{array}{rl}& P=\left(\begin{array}{cc}443.1346& 103.5289\\ 103.5289& 255.6189\end{array}\right),S=\left(\begin{array}{cc}3.1639& 0.0759\\ 0.0759& 1.5234\end{array}\right),\\ & R_1=\left(\begin{array}{cc}802.7726& 256.7196\\ 256.7196& 311.9576\end{array}\right),R_2=\left(\begin{array}{cc}71.8761& 2.5943\\ 2.5943& 14.0628\end{array}\right),\end{array}$$

to list a few. Clearly, the effectiveness of our method provided in this paper is illustrated here.

To reflect intuitively the feasibility and validity of the obtained result in this paper, when the neuron activation function is $f_{i}(x) =0.5 (|x+1| -|x-1| )$ and the time-varying delay is $\delta (t) =0.4 +0.2\cos (t)$, we present Figs. 4–6, which show the state response of systems (46) with parameters (53)–(54) under no any control and the well-designed ETCS (8), respectively. Clearly, ETCS (8) is effective. Furthermore, it is not hard to see from Fig. 5 that the frequency of control is reduced to large extent, which means that more network resources are saved by using the ETCS.

Figure 4

Curve of $x(t)$ without control for Example 4.2 under $r(0) = [-0.2;0.3]$

Figure 5

Release instants and intervals for Example 4.2 under $r(0) = [-0.2;0.3]$

Figure 6

Curve of $x(t)$ with ETCS for Example 4.2 under $r(0) = [-0.2;0.3]$

5 Conclusions

In this paper, we studied an event-triggered exponential synchronization problem for a class of Markov jump neural networks with time-varying delay. To obtain a more tighter bound of reciprocally convex quadratic terms, we provided a general reciprocally convex combination inequality, which included several existing ones as its particular cases. Then we constructed a suitable Lyapunov–Krasovsikii functional by fully considering the information about time-varying delay, triggering signals, and Markov jump parameters. Based on a well-designed event-triggered control scheme, were presented two kinds of novel exponential synchronization criteria for the studied systems by employing the new reciprocally convex combination inequality and other analytical approaches. Finally, we gave two numerical examples to show the effectiveness of our results. By the way, we expect that the methods proposed in this paper can be used in the future to investigate other stability and control problems for various systems with mixed time-varying delays.