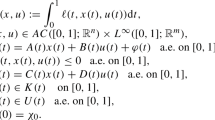Survey of duality between linear quadratic regulation and linear estimation problems for discrete-time systems

Abstract

The linear estimation (or optimal control) problem in the emerging area of time-delay systems, multiplicative noise systems, and Markov jump linear systems has been taken into consideration by the control engineers. The purpose of this survey is to provide a review of duality between linear estimation and optimal control in the above-mentioned area. The mentioned subjects are studied to indicate the essential connection between control and estimation problems and to investigate the major cause that the classical duality still holds (not holds) for the broader systems, such as time-delay systems, multiplicative noise systems, Markov jump linear systems, and the like.

1 Introduction

According to the duality principle, the linear quadratic regulation (LQR) problem for deterministic systems and the optimal estimation problem for additive noise including systems are dual [1]. According to this principle, the optimal estimation problem with the linear minimum mean square error (LMMSE) criterion could be converted to an optimal control problem with a quadratic performance index in the inverse time, and vice versa. The duality principle between control and estimate problems has been studied in the literature [2,3,4,5,6,7,8,9]. The duality principle between the LMMSE estimation problem for continuous systems containing multiple time delays appearing in a single observation channel and the LQR problem for continuous systems containing multiple input delays appearing in a single input channel has been established in [2]. Instead of using the information filter, a more general model of linear quadratic Gaussian duality has been established by using the Kalman–Bucy filter in [3]. Also, [5] discusses the duality between the LQR control with limited controller-system communication and the scalar Gauss Markov systems’ optimal schedule. Moreover, control and estimation problems have also generated considerable interest in the presence of constraints [6, 8]. The authors in [6] consider the constrained reference tracking’s control problem and show that there exists asymmetry in the estimation problem with that of the reference tracking problem. A natural question is: Does the classic duality between control and filtering of a linear system still hold for the Markov jump system, the multiplicative noise system, and the time-delay system? In the following we will give a survey of duality between the LQR and the linear estimation problem for discrete-time systems.

1.1 Duality for time-delay systems

Over the past few decades, the study of time delays has exerted great interest of plenty of scholars [10,11,12,13,14]. According to different kinds of time delay, many results have sprung up, such as communication delay [15, 16], control input delay [17,18,19,20], state-dependent delay [21,22,23,24], state-independent delay [25, 26], output delay [27, 28], distributed delay [29,30,31,32], time-varying delay [33, 34]. For example, communication links are usually imperfect and the limited bandwidth may result in delays. The system performance degradation or system instability could be arise from time delays. As for the estimation or control problems for the systems with time delay, there are several methods to settle such as the (partial difference) Riccati equation [35, 36], the game-theoretic approach [37], the linear matrix inequality (LMI) method [38, 39], and the convex optimization approach [40, 41].

The state augmentation method [42] and Kalman filter [43] have been employed to verify the LMMSE problem for discrete time-delay systems. Nevertheless, an augmentation approach may often result in high system dimension causing high computational demand. To save the computing cost in solving the estimation problem for measurement delay including systems, a reorganized innovation tool has been proposed [44]. According to the proposed tool, the optimal filter is obtained using two standard Riccati difference equations with dimension similar to the original state model. Moreover, we expand the results of [44] to the systems with multiplicative noise [45,46,47]. The signal coming from measurement [44, 45] can be divided two types: delayed and instantaneous measurements. Systems studied in [44, 45] could be considered as special cases of systems with single measurement channel and multiple measurement delays [48,49,50]. The LMMSE estimation problem for these systems is so complicated that could not be directly solved using the reorganized innovation tool. Recently, a partial difference Riccati equation approach has been employed to derive the optimal estimators containing predictor, filter, and smoother in the linear minimum variance sense for discrete-time packet dropping systems undergoing bounded random measurement delays [48]. The LMMSE estimation problem has been studied for systems containing constant state delay $d_{0}$, bounded random measurement delays, and packet dropping in [50].

In [51], smoothing estimation and duality concept have been employed to solve the LQR problem for linear time-invariant (LTI) systems with multiple input delays. Consequently, the authors in [35] established the duality between the LMMSE estimation problem for discrete systems containing multiple time delays appearing in a single observation channel and the LQR problem for discrete systems containing multiple input delays appearing in a single input channel. Unlike the works presented in [35, 51], in this study [36], a step-by-step optimization strategy has been proposed to deal with the control problem for universal time-delay systems. An associated dual backward stochastic system is defined to attain this goal. The optimal controller gains are calculated using a backward partial Riccati difference equation. After comparing the LMMSE estimator and the LQR controller results, we find that the duality between the LMMSE estimate problem for general time-delay discrete systems with additive noise and the LQR problem for general time-delay deterministic discrete systems with a quadratic criterion in the inverse time still holds, which extends the classic principle of duality. Both dual elements are clearly pointed out and the time inversion between the problems is indicated. A detailed discussion is carried out in Sect. 3.

1.2 Duality for systems with time-delay and multiplicative noise

Multiplicative noise is inevitable in fading or reflection of transmitted signals over an ionospheric channel [52, 53]. Such examples often occur in communication systems [54], image processing [55], fault detection [56, 57], and the like. State estimation problem in the presence of multiplicative noise is important when the state is not directly measurable [58,59,60]. It is obvious that the system state will be a process without Gaussian noise and the optimal estimator which produces minimum error variance will be in nonlinear form when the system involves multiplicative noise; thus, practically, it will be very difficult to achieve. From the practical point of viewpoint, the construction of high quality and easy-to-implement suboptimal filters becomes crucial. An important case of suboptimal filters is the linear one with minimum mean square error (MMSE), which has been widely used in the past decades [61,62,63].

By formulating the observation uncertainty via an independent and identically distributed (i.i.d) Bernoulli process, the estimator equations have been derived [64]. In [65], the convergence and the asymptotic stability of the LMMSE filter for a special case of linear systems with measurements including both multiplicative and additive noises have been investigated. In [66] a finite-horizon robust Kalman filter has been proposed for discrete-time systems including stochastic uncertainties. The author in [67] investigates the linear estimation problem of a remote signal generated from a discrete-time periodic system subject to multiplicative noise. In [68] the linear optimal estimator has been constructed by presenting a different model for describing random delays and packet dropping. The estimation problem for multiplicative noise systems with measurement delay is considered in [69], where the multichannel multiplicative noise is represented by a diagonal matrix, and a sufficient condition for the existence of the steady filter is presented.

On the other hand, the LQR controller design for systems undergoing multiplicative noise has been a hot topic over the past decades [70, 71] and is actively studied nowadays as well. There are several ways to solve the control problems for systems containing multiplicative noise, including the spectrum analysis [72], the generalized Riccati equation method [73, 74], and the linear matrix inequality method [75,76,77,78]. In [79], the state estimation and optimal control problems for stochastic systems containing multiplicative and addictive noises have been extended to the filtering case. The state estimator is based on availability of the feedback signal. The authors in [80] studied the stochastic optimal control for discrete-time linear systems undergoing Markovian jumps and multiplicative noises. The LQR problem has been investigated for discrete-time systems with multichannel multiplicative noise describing with a diagonal matrix [81]. Stabilization and observability concepts have been employed to solve the infinite horizon linear quadratic optimal control problem for discrete-time stochastic systems subject to state and control-dependent noise [82].

For the LMMSE estimation problem, the estimator gains can be calculated via forward Riccati and Lyapunov equations [65, 67, 69]. Meanwhile, for the LQR problem associated with multiplicative noise systems, the controller gains can be yielded via one backward generalized Riccati equation [73, 81]. Therefore, under unconstrained conditions, the classic duality principle is not necessarily true for multiplicative noise systems; that is to say, the LMMSE estimate is not dual to the LQR control. Some conditions should be satisfied to hold the duality concept for time-delay multiplicative noise systems. We have discussed the duality between the LMMSE estimation for time-delay systems containing multiplicative noise, and the LQR problem for deterministic time-delay systems subject to constraint condition has been studied [83].

1.3 Duality for Markov jump systems

Practically, some systems may undergo sudden changes in their structure and parameters and because of the environmental disturbance. These systems could be modeled as Markovian jump systems. Plenty of scholars have shown a great interest in studying the estimation problems for linear systems subject to Markovian jump. In these works, the LMI tool [84] and Riccati equation tool [85] are usually used to settle the estimation problems. The authors in [86] study a stationary LMMSE estimation problem for the linear systems with Markov jump, in which the jump parameters’ prior knowledge is unspecified. Apparently, it could be easily achieved, and the gain matrices could be calculated off-line. According to the discrete-time recursions [87], an estimator which is recursive and robust can be established for linear systems in addition to Markov jump with uncertain jump parameters. The model and the output measurement have been utilized to solve the state estimation problem for discrete-time Markov jump linear systems [88]. In [89], the finite-horizon LMMSE estimation problem for discrete-time linear systems which has measurement-delay and Markov jump is studied.

At the same time, the control problem for Markov jump systems has also been verified in the literature [90,91,92]. The book [93] introduces the discrete-time linear systems subject to Markov jump, including stochastic analysis and control theory. Solvability of the $\mathcal{H}_{2}$ control problem for discrete-time periodic systems including Markovian jumps and multiplicative noise is studied in [94]. A natural question is: Under what conditions the classical duality still holds for Markov jump systems? Fortunately, recently [95] demonstrated that if the jump parameters satisfy $\theta (t)=\eta (l-t)$, then the LMMSE estimation problem and the LQR problem are dual. The result beautifully extends the classic duality principle between filter and controller to the Markov jump systems. A detailed discussion will be presented in Sect. 5.

Notation: Throughout this paper, the superscripts “−1” and “T” represent the inverse and transpose of a matrix. $\mathcal{R} ^{n}$ denotes the n-dimensional Euclidean space. $\mathcal{R}^{n \times m}$ is the set of all $n\times m$ real matrices. $\delta _{ij}=0$ for $i\neq j$ and $\delta _{ii}=1$. The linear subspace spanning by the measuring samples $\{y(0), \ldots , y(k)\}$ is specified by $\mathcal{L} \{\{y(s)\}^{k}_{s=0} \}$. Moreover, the mathematical expectation operator is expressed with E. Furthermore, the matrix dimensions are assumed to be compatible such that algebraic operations could be written.

2 Classical duality between quadratic optimal control and linear estimation

Consider a discrete-time linear dynamics described by the following state space equations:

$$\begin{aligned} &x(k+1) =A(k) x(k)+n(k), \end{aligned}$$

(2.1)

$$\begin{aligned} &y(k) =B(k) x(k)+v(k), \end{aligned}$$

(2.2)

where $x(k)\in {\mathcal{R}}^{n}$, $y(k)\in {\mathcal{R}}^{m}$, ${n}(k)\in {\mathcal{R}}^{n}$, and ${v}(k)\in {\mathcal{R}}^{m}$. ${ n}(k)$ and ${ v}(k)$ are zero mean white noises with covariance matrices $E \{{n}(k) { n}^{T} (j)\} ={Q(k)}\delta _{kj}$, $E\{{ v}(k) { v}^{T} (j)\} ={ R(k)}\delta _{kj}$, respectively. The random processes ${n}(k)$, ${v}(k)$ for all k and the initial states ${{x}}(0)$ are considered mutually independent.

Lemma 2.1

([43])

For system (2.1)–(2.2), the LMMSE one-step predictor is given by

$$\begin{aligned} \begin{aligned} \hat{x}(k+1|k) =A(k) \hat{x}(k|k-1)+K_{p}(k)\bigl[y(k)-B(k) \hat{x}(k|k-1)\bigr], \\ \hat{x}(0|-1) =\mu _{0}, \end{aligned} \end{aligned}$$

(2.3)

where

$$\begin{aligned} &K_{p}(k) =A(k)P(k)B^{T}(k)R^{-1}_{\varepsilon (k)}, \end{aligned}$$

(2.4)

$$\begin{aligned} &R_{\varepsilon (k)} = B(k)P(k)B^{T}(k)+R(k), \end{aligned}$$

(2.5)

and $P(k)$ is obtained by solving the coming discrete Riccati equation

$$\begin{aligned} P(k+1)= A(k)P(k)A^{T}(k)+Q(k)-A(k)P(k)B^{T}(k)R^{-1}_{\varepsilon (k)}B(k)P(k)A ^{T}(k). \end{aligned}$$

(2.6)

Consider the discrete LQR problem for the following time-delay system:

$$\begin{aligned} x(k+1)=A(k)x(k)+B(k)u(k), \end{aligned}$$

(2.7)

associated with the quadratic performance index

$$\begin{aligned} J(N) =x^{T}(N+1) \overline{P}_{N+1} x(N + 1) + \sum _{k=0}^{N}x^{T}(k)Q(k) x(k)+\sum _{k=0}^{N}{u}^{T}(k){R}(k) {u}(k), \end{aligned}$$

(2.8)

where ${x}(k)\in {\mathcal{R}}^{n}$ and ${u}(k)\in {\mathcal{R}}^{m}$ are the state and the control signals, respectively. The initial state $x(0)$ is considered, $\overline{P}_{N+1}=\overline{P}^{T}_{N+1} \geq 0$ shows the penalty applied on the final state, the weighting matrices $R(k)$ and $Q(k)$ are considered as positive definite and non-negative definite matrices, respectively.

LQR problem: For the given system (2.7), calculate input signal samples $\{u(0),u(1),\ldots , u(N)\}$ so that the performance index $J(N)$ of (2.8) is minimized.

Lemma 2.2

([1])

The optimal control signal for an LQR problem with performance index (2.8) could be computed as

$$\begin{aligned} u(k) =-K^{T}(k)x(k), \end{aligned}$$

(2.9)

where the gain $K(k)$ is respectively given as follows:

$$\begin{aligned} &K(k) = A^{T}(k)\overline{P}(k+1)B(k)R^{-1}_{\mathbf{w}(k)}, \end{aligned}$$

(2.10)

$$\begin{aligned} &R_{\mathbf{w}(k)} = B^{T}(k)\overline{P}(k+1)B(k)+R(k), \end{aligned}$$

(2.11)

and $\overline{P}(k)$ is obtained from the following difference Riccati equation:

$$\begin{aligned} \begin{aligned} &\overline{P}(k) = A^{T}(k) \overline{P}(k+1)A(k)+Q(k)-A^{T}(k) \overline{P}(k+1)B(k)R^{-1}_{\mathbf{w}(k)}B^{T}(k) \overline{P}(k+1)A(k), \\ &\overline{P}(N+1) = \overline{P}_{N+1}. \end{aligned} \end{aligned}$$

(2.12)

The classical duality can be seen from Table 1, now we give a brief summary in the following theorem.

Table 1 Duality between estimation and control

Theorem 2.1

([1])

The LMMSE estimation problem presented in Lemma 2.1 and the LQR problem presented in Lemma 2.2 are dual.

Proof

For the classical duality principle, we present a simple explanation. Consider that the following transformations are performed in the right-hand side of (2.10), (2.11), and (2.12), respectively:

$$ A(k)\rightarrow A^{T}(k), \qquad B(k)\rightarrow B^{T}(k),\qquad \overline{P}(k+1) \rightarrow P(k). $$

Now, we obtain $K_{p}(k)$, $R_{\varepsilon (k)}$, $P(k+1)$ in the formulae (2.4), (2.5), and (2.6), respectively. The converse of the theorem could be proved similarly. □

3 Duality for time-delay linear systems

The classic duality principle states that the optimal estimation problem with LMMSE criterion is equal to an optimal control problem with a quadratic performance index in the inverse time and vice versa. In this section, we want to discuss the duality between LMMSE estimation and LQR for time-delay systems.

Considering the reorganized innovation method, the LMMSE problem for systems which have multiple observation channels but single observation delay is considered in [44], that is,

$$\begin{aligned} &x(k+1) =A(k)x(k)+n(k), \end{aligned}$$

(3.1)

$$\begin{aligned} &y_{i}(k) =B_{i}(k)x(k-l_{i})+v_{i}(k),\quad i=0,1 ,\ldots d, \end{aligned}$$

(3.2)

where $l_{i}$ is the measurement delay. Without loss of generality, $l_{i}$ is assumed to satisfy that $0=l_{0}< l_{1}<\cdots < l_{d}$. ${ v}_{i}(k)$ are white noises whose mean is zero and covariance matrices are $E\{{ v}_{i}(k){ v}_{j}^{T} (s)\} ={ R_{i}(k)}\delta _{i,j}\delta _{k,s}$. By the way, the LQR problem is considered in [51] for systems which have multiple input channels but a single input

$$\begin{aligned} x(k+1)=A(k)x(k)+\sum_{i=0}^{d}B_{i}(k)u_{i}(k-l_{i}), \end{aligned}$$

(3.3)

associated with this performance index

$$\begin{aligned} J(N) =&x^{T}(N+1) \overline{P}_{N+1} x(N + 1) + \sum _{k=0}^{N}x^{T}(k)Q(k) x(k)+\sum _{i=0}^{d}\sum_{k=0}^{N-l _{i}}{u}^{T}_{i}(k){R_{i}(k)} {u}_{i}(k), \end{aligned}$$

(3.4)

where $u(-i)$ ($0< i \leq l_{d}$) are the control inputs with recognized statistical properties.

Theorem 3.1

([51])

The LMMSE estimation problem for the given systems (3.1)–(3.2) is dual to the LQR problem for the given system (3.3) associated with performance (3.4).

However, note that systems studied in [44, 45] are a special case of systems which have only a single observation channel but multiple observation delays. The reorganized innovation could not be directly employed as a mathematical approach for solving the LMMSE estimation problem for these systems. According to the partial difference Riccati equation method [48], the LMMSE estimator could be designed for systems which have a single observation channel but multiple observation delays. These systems could be represented as

$$\begin{aligned} &x(k+1) =A(k)x(k)+n(k), \end{aligned}$$

(3.5)

$$\begin{aligned} &y(k) =\sum_{i=0}^{d} B_{i}(k)x(k-l_{i})+v(k). \end{aligned}$$

(3.6)

Theorem 3.2

([35])

For the given systems

$$\begin{aligned} x(k+1) =& A(k)x(k)+\sum_{i=0}^{d} B_{i}(k)u(k-l_{i}), \end{aligned}$$

(3.7)

associated with the following performance:

$$\begin{aligned} J(N) =&x^{T}(N+1) \overline{P}_{N+1} x(N + 1)+ \sum _{k=0}^{N}x^{T}(k)Q(k) x(k)+\sum_{k=0} ^{N}{u}^{T}(k){R}(k){u}(k), \end{aligned}$$

(3.8)

the LQR problem and the LMMSE estimation problem related to (3.5)–(3.6) are dual.

Note that both in (3.1)–(3.2) and in (3.5)-(3.6), the delays only appear in the measurement equation. In the following we will investigate the estimator design for systems with delay which appears both in the state equation and in the observation equation.

Lemma 3.1

([49])

For the given systems,

$$\begin{aligned} &x(k+1) =\sum_{i=0}^{d}A_{i}(k)x(k-h_{i})+n(k), \end{aligned}$$

(3.9)

$$\begin{aligned} &y(k) =\sum_{i=0}^{d}B_{i}(k)x(k-l_{i})+v(k), \end{aligned}$$

(3.10)

the LMMSE filter and smoother are represented with the following equations:

$$\begin{aligned} &\hat{x}(k+1|k) =\sum_{i=0}^{d}A_{i}(k) \hat{x}(k-h_{i}|k), \end{aligned}$$

(3.11)

$$\begin{aligned} &\hat{x}(k-j|k) =\hat{x}(k-j|k-1)+K_{j}(k)\varepsilon (k), \end{aligned}$$

(3.12)

$$\begin{aligned} &K_{j}(k) =\sum_{i=0}^{d} \widetilde{P}(k-j,k-l_{i},k-1)B_{i}^{T}(k)R ^{-1}_{\varepsilon (k)}, \end{aligned}$$

(3.13)

$$\begin{aligned} &R_{\varepsilon (k)} =\sum_{i=0}^{d}\sum _{j=0}^{d}B_{i}(k) \widetilde{P}(k - l_{i},k - l_{j},k - 1)B^{T}_{j}(k) + R(k), \end{aligned}$$

(3.14)

and $\widetilde{P}(\cdot ,\cdot ,\cdot )$ is computed based on the following partial difference Riccati equation:

$$\begin{aligned} &\widetilde{P}(k-i,k-j,k) =\widetilde{P}(k-i,k-j,k-1)-K_{i}(k)R_{ \varepsilon (k)}K^{T}_{j}(k), \end{aligned}$$

(3.15)

$$\begin{aligned} &\widetilde{P}(k+1,k-j,k) =\sum_{i=0}^{d}A_{i}(k) \widetilde{P}(k-h _{i},k-j,k), \end{aligned}$$

(3.16)

$$\begin{aligned} &\widetilde{P}(k+1,k+1,k) =\sum_{i=0}^{d} \sum_{j=0}^{d} A_{i}(k) \widetilde{P}( k - h_{i}, k - h_{j}, k ) A_{j}^{T} + Q(k) , \\ &\widetilde{P}(k-i,k-j,k) =\widetilde{P}^{T}(k-j,k-i,k). \end{aligned}$$

(3.17)

In the following, the aim is to establish the duality between the LMMSE estimation problem in Lemma 3.1 and the LQR problem for discrete linear systems including multiple time delays appearing in state and control input variables. To attain this aim, the LQR problem will be considered firstly, and then both results will be compared.

Suppose the discrete LQR problem for systems having a single input channel but multiple inputs, i.e.,

$$\begin{aligned} x(k+1)=\sum_{i=0}^{d}A_{i}(k)x(k-h_{i})+ \sum_{i=0}^{d}B_{i}(k)u(k-l _{i}), \end{aligned}$$

(3.18)

associated with the quadratic performance index

$$\begin{aligned} J(N) =&x^{T}(N+1) \overline{P}_{N+1} x(N + 1) + \sum _{k=0}^{N}x^{T}(k)Q(k) x(k)+\sum _{k=0}^{N}{u}^{T}(k){R}(k) {u}(k), \end{aligned}$$

(3.19)

where $\overline{P}_{N+1}=P^{T}_{N+1}\geq 0$ is the penalty applied on the final state, the weighting matrix $R(k)$ and $Q(k)$ are considered positive definite and non-negative definite, respectively. Moreover, the initial state $x(-i)$ ($0\leq i \leq h_{d}$) and the control signal $u(-i)$ ($0< i \leq l_{d}$) are considered to be known.

LQR problem: Find the control signal samples $\{u(0),u(1), \ldots ,u(N)\}$ such that the performance index $J(N)$ of (3.19) is minimized.

Remark 3.1

The LQR problem mentioned above can be regarded as an $N+1$ step decision-making problem in which the $N+1$ control signal samples $\{{u}(0);\ldots ;{u}(N)\}$ should be calculated so that the quadratic performance index (3.19) is minimized. The control law will be obtained by first finding the control for the last stage. Then the dynamic programming technique is employed to obtain the control law for each former stage and accordingly obtain the required control law for all the stages.

For convenience, we introduce the backward systems:

$$\begin{aligned} &{\mathbf{x}}(k) =\sum_{i=0}^{d}A^{T}_{i}(k) {\mathbf{x}}(k+1+h_{i})+ {\mathbf{n}}(k), \end{aligned}$$

(3.20)

$$\begin{aligned} &{\mathbf{y}}(k) = \sum_{i=0}^{d}B^{T}_{i}(k) \mathbf{ {x}}(k+1+l_{i})+ \mathbf{v}(k), \end{aligned}$$

(3.21)

$$\begin{aligned} &{\mathbf{x}}_{j}(k) =\sum_{i=j}^{d}A^{T}_{i}(k) {\mathbf{x}}(k+1+h _{i}), \end{aligned}$$

(3.22)

$$\begin{aligned} &{\mathbf{y}}_{j}(k) = \sum_{i=j}^{d}B^{T}_{i}(k) \mathbf{ {x}}(k+1+l _{i}), \end{aligned}$$

(3.23)

where ${\mathbf{v}}(k)$, ${\mathbf{n}}(k)$, and ${\mathbf{x}}(N+1)$ are uncorrelated white noises whose mean is zero and covariance matrices are $\langle {\mathbf{x}}(N+1), {\mathbf{x}}(N+1) \rangle = \overline{P}_{N+1}$, $\langle {\mathbf{n}}(k), {\mathbf{n}}(s) \rangle = {Q}(k)\delta _{ks}$, $\langle {\mathbf{v}}(k), {\mathbf{v}}(s) \rangle = R(k)\delta _{ks}$, respectively. We also set that ${\mathbf{x}}(N+1+i)=0$ for $i\geq 1$. Consider that $x(k)$ with normal face of (3.18) and $\mathbf{x}(k)$ with bold face of (3.20) are different.

Lemma 3.2

([36, 49])

The optimal control signals obtained from the LQR problem for system (3.18) and performance index (3.19) are

$$\begin{aligned} u(k) =-\overline{K}^{T}_{0}(k)x(k)-\sum ^{d}_{i=1}\sum_{j=h_{i-1}+1} ^{h_{i}} \overline{K}^{T}_{ij}(k) x(k-j) -\sum ^{d}_{i=1}\sum_{j=l_{i-1}+1} ^{l_{i}} \widetilde{K}^{T}_{ij}(k) u(k-j), \end{aligned}$$

(3.24)

in (3.24), the gains $\overline{K}_{ij}(k)$ and $\widetilde{K} _{ij}(k)$ could be obtained as follows:

$$\begin{aligned} &\overline{K}_{ij}(k) = \sum_{s=i}^{d} A^{T}_{s} (k)\overline{K}_{h _{s}+1-j}(k), \end{aligned}$$

(3.25)

$$\begin{aligned} &\widetilde{K}_{ij}(k) = \sum_{s=i}^{d}B^{T}_{s} (k)\overline{K}_{l _{s}+1-j}(k), \end{aligned}$$

(3.26)

while $\overline{K}_{j}(k)$, the smoothing gain of state $\mathbf{x}(k+j)$, could be calculated as

$$\begin{aligned} &\overline{K}_{j}(k) =\sum_{i=0}^{d} \overline{P}(k+j,k+1+l_{i},k+1)B _{i}(k) R^{-1}_{\mathbf{w}(k)}, \end{aligned}$$

(3.27)

$$\begin{aligned} &\overline{K}_{0}(k) =\sum_{i=0}^{d}A^{T}_{i}(k) \overline{K}_{h_{i}+1}(k), \end{aligned}$$

(3.28)

$$\begin{aligned} &R_{\mathbf{w}(k)} =\sum_{i=0}^{d} \sum _{j=0}^{d}B^{T}_{i}(k) \overline{P}(k+1+l_{i},k+1+l_{j},k+1)B_{j}(k)+R(k), \end{aligned}$$

(3.29)

and $\overline{P}(\cdot ,\cdot ,\cdot )$ is the solution of the following partial difference Riccati equation:

$$\begin{aligned} &\overline{P}(k+i,k+j,k) = \overline{P}(k+i,k+j,k+1)- \overline{K}_{i}(k)R_{ \mathbf{w}(k)}\overline{K}^{T}_{j}(k), \end{aligned}$$

(3.30)

$$\begin{aligned} &\overline{P}(k,k+j,k) = \sum _{i=0}^{d}A^{T}_{i}(k) \overline{P}(k+h_{i}+1,k+j,k), \end{aligned}$$

(3.31)

$$\begin{aligned} &\overline{P}(k,k,k) = \sum _{i=0}^{d}\sum_{j=0}^{d}A_{i}^{T}(k) \overline{P}(k + h_{i} + 1,k + h_{j} + 1,k)A_{j}(k)+Q(k), \end{aligned}$$

(3.32)

$$\begin{aligned} &\overline{P}(k+i,k+j,k) = \overline{P}^{T}(k+j,k+i,k). \end{aligned}$$

(3.33)

The initial conditions for this equation are as follows:

$$\begin{aligned} &\overline{P}(N+1,N+1,N+1)=\overline{P}_{N+1}, \\ &\overline{P}(i,j,k)=0,\quad i> N+1, \\ &\overline{P}(i,j,k)=0,\quad j> N+1. \end{aligned}$$

Remark 3.2

The LQR problem of the linear systems has been solved in [35], in which the multiple delays are contained in a single input channel and the controller is designed by means of a partial difference Riccati equation. Recently, we have extended the results of [35] to [36] by applying the dynamic programming technique in which the delays exist in both input and state. From Lemma 3.2, we notice that the controller gain can be obtained from a partial difference Riccati equation, where the dimension of the plant and the Riccati equation are the same. Compared with the previous augmentation method, the method in Lemma 3.2 is computationally efficient.

It can be seen from Lemma 3.2 that the controller gains can be transformed into solving the filtering and smoothing problems for backward systems (3.20)–(3.23). That is to say, the duality principle still holds for normal time-delay systems. Similar to the duality principle for delay-free systems, the duality principle for general time-delay systems will be introduced in the following.

It can be seen from Table 2 that the duality between estimation and control still holds for time-delay systems, now we provide a brief summary in Theorem 3.3.

Table 2 Duality between estimation and control

Theorem 3.3

The LMMSE estimation problem provided in Lemma 3.1 is dual to the LQR problem provided in Lemma 3.2.

Proof

Similar to the proof of the classical duality principle, we present a simple explanation. If we make the following transformations:

$$ A_{i}(k)\rightarrow A^{T}_{i}(k), \qquad B_{i}(k)\rightarrow B^{T}_{i}(k), \qquad \overline{P}(\cdot,\cdot,\cdot)\rightarrow \widetilde{P}(\cdot,\cdot,\cdot) $$

with

$$\begin{aligned} & k+j \rightarrow k-j,\qquad k+i \rightarrow k-i, \qquad k+1 \rightarrow k-1, \\ &k+1+l_{i} \rightarrow k-l_{i},\qquad k+1+l_{j} \rightarrow k-l_{j}, \\ & k+1+h_{i} \rightarrow k-h_{i},\qquad k+1+h_{j} \rightarrow k-h_{j} \end{aligned}$$

in the right-hand side of (3.27), (3.29), (3.30), (3.31), and (3.32), respectively, then we obtain $K_{j}(k)$, $R_{\varepsilon (k)}$, $\widetilde{P}(k-i,k-j,k)$, $\widetilde{P}(k+1,k-j,k)$, $\widetilde{P}(k+1,k+1,k)$ in the formulae (3.13), (3.14), (3.15), (3.16), and (3.17), respectively, and vice versa. □

4 Duality for linear time-delay systems subject to multiplicative noise

Consider the following time-delay multiplicative noise system:

$$\begin{aligned} &x(k+1) =\sum_{i=0}^{d}A_{i}(k)x(k-h_{i})+A(k) \eta (k)x(k)+n(k), \end{aligned}$$

(4.1)

$$\begin{aligned} &y(k) =\sum_{i=0}^{d}B_{i}(k)x(k-l_{i})+B(k) \omega (k)x(k)+v(k). \end{aligned}$$

(4.2)

No generality will be lost if the delays are regarded to be ascending: $0=h_{0}< h_{1}<\cdots < h_{d}$, $0=l_{0}< l_{1}<\cdots < l_{d}$. $\eta (k)$ and $\omega (k)$ are random zero mean process and ${ E}\{\eta (k)\eta (j)\} = \sigma \delta _{kj}$, ${ E}\{\omega (k) \omega (j)\} = \sigma \delta _{kj}$, in addition, the initial states ${{x}}(-i)$ ($i=0,1,\ldots ,\tau$, $\tau =\max (h_{d},l_{d})$) ensure $E\{{x}(-i)\}=\mu _{-i}$ and $E\{{x}(-i){x}^{T}(-j)\}=P_{0}(-i,-j)$. ${ n}(k)$ and ${ v}(k)$ are zero mean white noises with covariance matrices $E \{{n}(k) { n}^{T} (j)\} ={\overline{Q}(k)}\delta _{kj}$, $E \{{ v}(k){ v}^{T} (j)\} ={ \overline{R}(k)}\delta _{kj}$, respectively. $\omega (k)$, ${v}(k)$, and ${n}(k)$ are the random processes which are mutually independent for all k.

LMMSE problem: The goal is finding the LMMSE estimation $\hat{x}(k-l|k)$ ($l=-1, 0, \ldots ,h_{d}$) of the system state $x(k-l)$ when given observation samples $\{y(k),\ldots ,y(0)\}$, i.e., minimize the Euclidean 2-norm

$$\begin{aligned} J =&E\bigl\{ \bigl[x(k-l)-\hat{x}(k-l|k)\bigr]^{T}\bigl[x(k-l)- \hat{x}(k-l|k)\bigr]\bigr\} \\ =&E\bigl\{ \tilde{x}^{T}(k-l|k)\tilde{x}(k-l|k)\bigr\} \end{aligned}$$

(4.3)

at each time moment k. Before obtaining the LMMSE estimators of system (4.1)–(4.2), we first present a useful lemma.

Lemma 4.1

Based on system (2.1), for the given integer numbers i and j $(0 \leq i\leq h_{d},0 \leq j\leq h_{d})$, let $D_{i,j}(k)=E\{x(k-i)x ^{T}(k-j)\}$, then we have the following correlation functions:

$$\begin{aligned} D_{i,j}(k)=D^{T}_{j,i}(k)= \textstyle\begin{cases} D_{i-j,0}(k-j), \quad i>j, \\ D_{0,j-i}(k-i),\quad i\leq j, \end{cases}\displaystyle \end{aligned}$$

(4.4)

which could be calculated by

$$\begin{aligned} &D_{0,0}(k) = \overline{Q}(k)+\sigma A(k)D_{0,0}(k-1)A^{T}(k) +\sum_{i=0}^{d} A_{i}(k)D_{0,0}(k-1-h_{i})A^{T}_{i}(k) \\ &\hphantom{D_{0,0}(k) = } {}+\sum_{i=j+1}^{d}\sum _{j=0}^{d}A_{i}(k)D^{T}_{0,h_{i}-h _{j}} ( k - 1 - h_{j} )A^{T}_{j}( k ) \\ &\hphantom{D_{0,0}(k) = } {}+ \sum _{i=0}^{j-1}\sum_{j=1}^{d}A_{i}(k)D_{0,h_{j} - h_{i}}(k - 1 - h_{i})A^{T}_{j}( k ), \end{aligned}$$

(4.5)

$$\begin{aligned} &D_{0,s}(k) = \sum _{i=0}^{j}A_{i}(k)D_{0,s-1-h_{i}}( k - 1 - h_{i} ) \\ &\hphantom{D_{0,s}(k) = }{}+ \sum_{i=j+1}^{d}A_{i}(k)D^{T}_{0,h_{i}-s+1}(k-s),\quad h_{j} \leq s-1 < h _{j+1}, \\ &D_{i,j}(0) = P_{0}(-i,-j). \end{aligned}$$

(4.6)

Based on equations (4.1)–(4.2), the following innovation sequence $\varepsilon (k)$ is introduced:

$$\begin{aligned} \varepsilon (k) \triangleq & y(k)-\hat{y}(k|k-1)= \sum _{i=0}^{d}B_{i}(k) \tilde{x}(k-l_{i}|k-1)+B(k) \omega (k)x(k)+v(k), \end{aligned}$$

(4.7)

where $\hat{y}(k|k-1)$ is the projection of $y(k)$ onto the linear space $\mathbf{\ell }\{y(s)|_{0\leq s \leq k-1}\}$. Moreover, the cross covariance matrices for the estimation error are defined as

$$\begin{aligned} \widetilde{P}(i,j,k)=E\bigl\{ \bigl(x(i)-\hat{x}(i|k)\bigr) \bigl(x(j)-\hat{x}(j|k)\bigr)^{T}\bigr\} . \end{aligned}$$

(4.8)

The LMMSE smoother and filter will be derived by the innovation analysis approach in the following.

Theorem 4.1

The smoother and the LMMSE filter for systems (2.1)–(2.2) are obtained as follows:

$$\begin{aligned} &\hat{x}(k + 1|k) = \sum_{i=0}^{d}A_{i}(k) \hat{x}(k-h_{i}|k), \end{aligned}$$

(4.9)

$$\begin{aligned} &\hat{x}(k - j|k) = \hat{x}(k - j|k - 1) + K_{j}(k) \varepsilon ( k ),\quad j=0,\ldots ,h_{d}, \end{aligned}$$

(4.10)

where the initial state values are $\hat{x}(-k|0)=\mu _{-k}$ and $K_{j}(k)$ could be obtained by calculating

$$\begin{aligned} &K_{j}(k) =\sum_{i=0}^{d} \widetilde{P}(k-j,k-l_{i},k-1)B_{i}^{T}(k)R ^{-1}_{\varepsilon (k)}, \end{aligned}$$

(4.11)

$$\begin{aligned} &R_{\varepsilon (k)} =\sum_{i=0}^{d}\sum _{j=0}^{d}B_{i}(k) \widetilde{P}(k-l_{i},k-l_{j},k-1)B^{T}_{j}(k) +\sigma B(k)D_{0,0}(k)B ^{T}(k)+\overline{R}(k), \end{aligned}$$

(4.12)

while $D_{0,0}(k)$ can be calculated from (4.5)–(4.6), $\widetilde{P}(\cdot ,\cdot ,\cdot )$ is obtained by calculating the following partial difference Riccati equation:

$$\begin{aligned} &\widetilde{P}(k - i,k - j,k) =\widetilde{P}(k-i,k-j,k-1)-K_{i}(k)R_{\varepsilon (k)}K^{T}_{j}(k),\quad 0 \leq i \leq j \leq \tau , \end{aligned}$$

(4.13)

$$\begin{aligned} &\widetilde{P}(k + 1,k - j,k) = \sum_{i=0}^{d} A_{i}(k)\widetilde{P}(k - h_{i}, k - j,k),\quad 0 \leq j \leq \tau , \end{aligned}$$

(4.14)

$$\begin{aligned} &\widetilde{P}(k + 1,k + 1,k) = \sum_{i=0}^{d}\sum _{j=0}^{d}A_{i}(k) \widetilde{P}(k-h_{i},k-h_{j},k)A_{j}^{T}(k) \\ &\hphantom{\widetilde{P}(k + 1,k +1,k) =} {}+ \sigma A(k) D_{0,0}(k)A^{T}(k) + \overline{Q}(k), \end{aligned}$$

(4.15)

$$\begin{aligned} &\widetilde{P}(k - i,k - j,k) =\widetilde{P}^{T}(k-j,k-i,k), \\ &\widetilde{P}(- i,- j,0) = \widetilde{P}_{0}(-i,-j), \quad 0 \leq i \leq j, 0 \leq j \leq \tau . \end{aligned}$$

(4.16)

Proof

The projection theory [43] leads to

$$\begin{aligned} &\hat{x}(k+1|k) =\sum_{i=0}^{d}A_{i}(k) \hat{x}(k-h_{i}|k), \end{aligned}$$

(4.17)

$$\begin{aligned} &\hat{x}(k-j|k) =\hat{x}(k-j|k-1)+K_{j}(k)\varepsilon (k), \end{aligned}$$

(4.18)

where $K_{j}(k)$ is given as

$$ K_{j}(k)=E\bigl\{ x(k-j)\varepsilon ^{T}(k)\bigr\} R^{-1}_{\varepsilon (k)}. $$

Observe that $x(k-j)=\hat{x}(k-j|k-1)+\tilde{x}(k-j|k-1)$. Now, according to (4.2) and (4.7), we have

$$\begin{aligned} K_{j}(k) =&E\bigl\{ \tilde{x}(k-j|k-1)\varepsilon ^{T}(k) \bigr\} R^{-1}_{\varepsilon (k)} \\ =&E\Biggl\{ \tilde{x}(k-j|k-1)\Biggl[\sum_{i=0}^{d}B_{i}(k) \tilde{x}(k-l_{i}|k-1)+B(k) \omega (k)x(k)+v(k)\Biggr]^{T} \Biggr\} R^{-1}_{\varepsilon (k)} \\ =&\sum_{i=0}^{d}\widetilde{P}(k-j,k-l_{i},k-1)B_{i}^{T}(k)R^{-1}_{ \varepsilon (k)}. \end{aligned}$$

(4.19)

The covariance matrices given in (4.7) of the innovation $\varepsilon (k)$ will be calculated in the following, where Lemma 4.1 is utilized:

$$\begin{aligned} R_{\varepsilon (k)} =& E\bigl\{ \varepsilon (k)\varepsilon ^{T}(k)\bigr\} \\ =& E\Biggl\{ \Biggl[\sum _{i=0}^{d}B_{i}(k)\tilde{x}( k - l_{i} | k - 1 ) + B( k )\omega ( k ) x( k ) + v( k ) \Biggr]\\ &{}\times \Biggl[ \sum _{i=0}^{d} B_{i}( k )\tilde{x}( k - l_{i} | k - 1 ) + B(k)\omega (k)x(k) + v(k) \Biggr]^{T}\Biggr\} \\ =& \sum_{i=0}^{d} \sum_{j=0}^{d}B_{i}(k) \widetilde{P}(k-l _{i},k-l_{j},k-1)B^{T}_{j}(k) +\sigma B(k) D_{0,0}(k)B^{T}(k)+ \overline{R}(k), \end{aligned}$$

this means that (4.12) is true. Considering (4.18), we have

$$\begin{aligned} &\tilde{x}(k-j|k) =\tilde{x}(k-j|k-1)-K_{j}(k)\varepsilon (k), \end{aligned}$$

(4.20)

$$\begin{aligned} &\tilde{x}(k-i|k) =\tilde{x}(k-i|k-1)-K_{i}(k)\varepsilon (k). \end{aligned}$$

(4.21)

Based on (4.20)–(4.21), covariance matrices for the estimation error are as follows:

$$\begin{aligned} \begin{aligned} &\widetilde{P}(k-i,k-j,k) \\ &\quad = E \bigl\{ \tilde{x}(k-i|k)\tilde{x}^{T}(k-j|k)\bigr\} \\ &\quad = E\bigl\{ \tilde{x}(k-i|k-1)\tilde{x}^{T}(k-i|k-1)\bigr\} + E\bigl\{ K_{i}(k)\varepsilon (k)\varepsilon ^{T}(k)K^{T}_{j}(k) \bigr\} \\ &\qquad {}-E\bigl\{ \tilde{x}(k-i|k-1)\varepsilon ^{T}(k)\bigr\} K^{T}_{j}(k)-K_{i}(k)E\bigl\{ \varepsilon (k) \tilde{x}^{T}(k-j|k-1)\bigr\} \\ &\quad = \widetilde{P}(k-i,k-j,k-1)-K_{i}(k)R_{\varepsilon (k)}K^{T}_{j}(k), \end{aligned} \end{aligned}$$

which is (4.13). Incorporating (4.1) and (4.17) gives

$$\begin{aligned} \tilde{x}(k+1|k)=\sum_{i=0}^{d}A_{i}(k) \tilde{x}(k-h_{i}|k) + A(k) \eta (k)x(k) + n(k). \end{aligned}$$

(4.22)

Furthermore, one has

$$\begin{aligned} &\widetilde{P}(k+1,k-j,k) \\ &\quad =E\bigl\{ \tilde{x}(k+1|k)\tilde{x}^{T}(k-j|k)\bigr\} \\ &\quad =E\Biggl\{ \Biggl[\sum_{i=0}^{d}A_{i}(k) \tilde{x}(k-h_{i}|k)+A(k)\eta (k)x(k)+n(k)\Biggr] \tilde{x}^{T}(k-j|k)\Biggr\} \\ &\quad =\sum_{i=0}^{d}A_{i}(k) \widetilde{P}(k-h_{i},k-j,k), \\ &\widetilde{P}(k+1,k+1,k) \\ &\quad =E\bigl\{ \tilde{x}(k+1|k)\tilde{x}^{T}(k+1|k)\bigr\} \\ &\quad =E\Biggl\{ \Biggl[\sum_{i=0}^{d}A_{i}(k) \tilde{x}(k-h_{i}|k)+A(k)\eta (k)x(k)+n(k)\Biggr] \\ &\qquad {}\times\Biggl[ \sum _{j=0}^{d}A_{j}(k) \tilde{x}(k-h_{j}|k)+A(k)\eta (k)x(k)+n(k)\Biggr]^{T} \Biggr\} \\ &\quad =\sum_{i=0}^{d}\sum _{j=0}^{d}A_{i}(k) \widetilde{P}(k-h_{i},k-h_{j},k)A ^{T}_{j}(k) +\sigma A(k) D_{0,0}(k)A^{T}(k)+ \overline{Q}(k), \end{aligned}$$

therefore, (4.14) and (4.15) are true. Finally, (4.16) could be easily obtained from (4.8). Thus, the proof is completed. □

Remark 4.1

In accordance with the innovation analysis approach, the optimal filter and smoother have been derived based on an n-dimensional partial difference Riccati equation (4.13)–(4.15). The number of divisions and multiplications is considered as the operation count because the divisions and multiplications are more valuable compared with additions. Consider that these numbers for our proposed method and for augmentation method are denoted by $C_{\mathrm{new}}$ and $C_{\mathrm{aug}}$, respectively. According to [35], it could be verified that the order of $h_{d}$ in $C_{\mathrm{aug}}$ is 3, while the order of $h_{d}$ in $C_{\mathrm{new}}$ is 2. Thus, $C_{\mathrm{aug}}\gg C_{\mathrm{new}}$ when $h_{d}$ is large enough. Compared with the state augmentation method [42, 79], the partial difference Riccati equation approach can greatly save the computational cost for the large delay.

However, the estimation problem in Theorem 4.1 is not dual anymore to the LQR problem provided in Lemma 3.2 because there are not only additive noises but also multiplicative noises in the estimation problem in Theorem 4.1. According to the delay-free systems, the authors in [8] established the duality between the LMMSE estimation for multiplicative noise systems with additive noise and the LQR for deterministic systems with constraint condition [96, 97]. Motivated by this point, we obtain the following result about duality between control and estimation.

Theorem 4.2

If we impose the conditions on the weight matrices Q and R in Lemma 3.2

$$ \begin{aligned} &\overline{Q}(k)=\sigma A^{T}(k) \bar{D}_{0,0}(k+1)A(k)+Q(k),\\ &\overline{R}(k)=\sigma B^{T}(k) \bar{D}_{0,0}(k+1)B(k)+R(k), \end{aligned} $$

(4.23)

then the forward partial difference Riccati equation (4.13)–(4.15) in Theorem 4.1 is dual to the backward partial difference Riccati equation (3.30)–(3.32) in Lemma 3.2. Moreover, similar to Theorem 3.3, we can find that the LMMSE estimation problem presented in Theorem 4.1 is dual to the LQR problem provided in Lemma 3.2 with constraint conditions (4.23).

Remark 4.2

([83])

It is needed to emphasize that the duality given in Theorem 4.2 is significant. The main result is that we have successfully revealed the essential links between the estimation problem for time-delay systems subject to multiplicative noise and the LQR problem for the deterministic time-delay systems with constraint conditions. Particularly, Theorem 3.3 establishes the duality principle between the estimation problem for general time-delay discrete systems and the LQR problem for the deterministic general time-delay discrete systems under free conditions.

5 Duality for Markov jump systems

Consider special systems whose parameters are found by a Markov chain, where the chain $\vartheta (t), t=0,1,\ldots ,l$, could have values in the set $\tau =\{1,2,\ldots ,N\}$. Assume the process $\theta (t)=\vartheta (l-t)$ which derives the parameters of the system

$$\begin{aligned} x(t+1)=A_{\theta (t)}x(t)+B_{\theta (t)}u(t), \end{aligned}$$

(5.1)

with initial condition $x(0)=x_{0}$. As usual, $(x,\theta )$ stands for the state variable, u is the control variable, matrices $A_{i},B _{i}, i\in \tau$ are known and of appropriate dimensions.

In fact, the authors in [95] assumed a quadratic performance index for system (5.1) with linear state feedback, resulting in a time reversed Markov jump LQR problem. The linear quadratic problem tends to control the system output

$$\begin{aligned} y(t)=C_{\theta (t)}x(t)+D_{\theta (t)}u(t),\quad \forall t=0,1,\ldots , l. \end{aligned}$$

(5.2)

The quadratic performance index is given

$$\begin{aligned} E \Biggl\{ \sum_{t=0}^{l} \bigl\Vert y(t) \bigr\Vert ^{2}+ \bigl\Vert x(l+1) \bigr\Vert ^{2} \Biggr\} . \end{aligned}$$

(5.3)

Consider the standard LMMSE problem for Markov jump linear systems (MJLS) defined by

$$\begin{aligned} &z(t+1) =F_{\eta (t)}z(t)+G_{\eta (t)}\omega (t), \end{aligned}$$

(5.4)

$$\begin{aligned} &y(t) =L_{\eta (t)}z(t)+H_{\eta (t)}\omega (t), \\ &z(0) =z_{0}, \end{aligned}$$

(5.5)

where the variables $\omega (t)$ and $z_{0}$ are i.i.d. random variables ensuring $E\{\omega (t)\}=0$, $E\{\omega (t)\omega (t)^{T}\}=I$, $E\{z_{0}=0\}$, and $E\{z_{0}z^{T}_{0}\}=\varSigma$.

Theorem 5.1

([95])

Under the condition that $\theta (t)=\eta (l-t)$, the LMMSE estimation problem for the given systems (5.4)–(5.5) is dual to the LQR problem for the given system (5.1) associated with performance (5.3).

The result beautifully generalizes the classic duality principle between filtering and control to the Markov jump systems case; for details, please see [95].

6 Conclusion

Motivated by the classical duality between control and filtering, in this paper we have reviewed the duality between linear estimation and linear quadratic regulation problems for time-delay systems, multiplicative noise systems, and Markov jump systems. It has effectively demonstrated the fundamental relations between the estimation problem and the LQR problem once again. In future research, is it possible to generalize the classical duality principle between control and filtering for linear systems (their matrices can be transposed in the dual sense) to network control systems? It is worth our thinking.