1 Introduction

In modern society, the study on complex dynamics of financial systems has become a topic of focus in the microeconomic and macroeconomic fields. Numerous researchers pay much attention to this theme. For example, Gao and Ma [1] considered the chaos and Hopf bifurcation of a finance model. Ma and Chen [2, 3] investigated the bifurcation phenomenon and the global character for a nonlinear finance model. Ma and Wang discussed the Hopf bifurcation and topological horseshoe for a chaotic finance model.

Chaotic phenomenon often occur in many economics. Serletic [4] point out that chaos stands for a radical change of perspective on business cycles. In many cases, chaos will cause the instability of economical systems. Thus chaos control has become an important problem that must be solved for real human life. Generally speaking, the aim of chaotic control is to stabilize a chaotic attractor to an equilibrium point or a periodic solution. In recent years, there have been two main ways to control chaos. One was developed by Ott et al. [5] and another is the time-delayed feedback method proposed by Pyragas [6]. The latter is more convenient than the former. So we adopt the latter to control chaos in this article.

Fractional calculus has a history of over 300 years. The investigation progress on fractional calculus is very slow due to the lack of theoretical basis and realistic background. In recent years, fractional differential equations have been proved to be potentially useful in electroanalytical chemistry, robotics, bioengineering, viscoelasticity, medicine and so on [7–48]. Different from integer-order models, fractional-order models possess memory, namely, the fractional-order model depends on the history of the model.

In 2016, Yang et al. [49] studied the following financial model:

$$ \textstyle\begin{cases} \frac{du_{1}}{dt}=a_{1}(u_{1}+u_{2}), \\ \frac{du_{2}}{dt}=-u_{2}-a_{1}u_{1}u_{3}, \\ \frac{du_{3}}{dt}=a_{2}+a_{1}u_{1}u_{2}, \end{cases} $$
(1.1)

where \(a_{i}>0\) (\(i=1,2\)) is the constant, \(u_{1}\) represents the interest rate, \(u_{2}\) represents investment demand and \(u_{3}\) represents the price index. Based on the model (1.1) and considering that fractional differential equations have memory and hereditary properties, for practical dynamical process, we can modify system (1.1) as a fractional-order version:

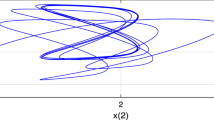
$$ \textstyle\begin{cases} \frac{d^{p}u_{1}}{dt^{p}}=a_{1}(u_{1}+u_{2}), \\ \frac{d^{p}u_{2}}{dt^{p}}=-u_{2}-a_{1}u_{1}u_{3}, \\ \frac{d^{p}u_{3}}{dt^{p}}=a_{2}+a_{1}u_{1}u_{2}, \end{cases} $$
(1.2)

where p represents the fractional order. In economic operation, the interest rate, investment demand and price index are under the impact of their memories. In addition, the process of economic operation has a close connection with the whole time information of the financial system. The model (1.2) has memory and hereditary properties for practical dynamical process, so we think that the model (1.2) shows some novelty and it is better than model (1.1). When \(p=0.8\) and \(a_{1}=1.79\), \(a_{2}=4\), system (1.2) is chaotic, which is shown in Fig. 1.

Figure 1
figure 1

Time history plots, variable relation plots and phase diagrams of system (1.2) with \(a_{1}=1.79\), \(a_{2}=4\)

Full size image

The main object of this paper is to discuss two topics: (1) designing a suitable time-delayed feedback controller to suppress the chaos of the system (1.2) and (2) the effect of time delay and the fractional order on the stability and the existence of Hopf bifurcation of controlled system are presented. During the past decades, the time-delayed feedback control technique has only been applied to the control of chaos and Hopf bifurcation of integer-order differential dynamical systems. There are relatively few works that deal with chaos and Hopf bifurcation control by applying time-delayed feedback controllers. Considering the introduction of fractional order for delayed differential systems, the corresponding characteristic equation will be more complex. Thus it is more difficult to analyze the distribution of roots of the characteristic equation of the involved fractional-order dynamical systems. The contributions of this article lie in four aspects:

  • The integer-order delayed financial model has been extended to a delayed fractional-order financial model, which can better describe the memory properties of the model.

  • The control technique is more complex than that for integer-order differential systems due to the introduction of the fractional order. A set of sufficient conditions that ensure the stability and the existence of Hopf bifurcation of the fractional-order delayed financial model are established. The study shows that the delay and fractional order have an important effect on the stability and the existence of Hopf bifurcation of involved controlled systems.

  • Up to now, there are few papers that focus on the Hopf bifurcation of fractional-order delayed financial model. The theoretical findings of this article will enrich and develop the Hopf bifurcation theory of fractional-order delayed differential equations and supplement the earlier publications.

  • The approach of this paper can provide a good reference in the study of some similar fractional-order delayed differential models.

The rest of this paper is organized as follows. In Sect. 2, several definitions and lemmas on fractional calculus are given. In Sect. 3, a time-delay feedback controller is designed to control the chaos of the chaotic fractional-order financial model. In Sect. 4, a numerical example is given to check the theoretical predictions. Finally, a brief conclusion is included.

2 Preliminary results

In this section, two definitions and two lemmas of fractional calculus are introduced.

Definition 2.1

([50])

The fractional integral of order δ for a function \(h(\xi )\) is defined as follows:

$$ {\mathcal {I}}^{\delta }h(\xi )=\frac{1}{\Gamma (\delta )} \int _{\xi _{0}}^{ \xi }(\xi -s)^{\delta -1}h(s)\,ds, $$

where \(\xi \geq \xi _{0}\), \(\delta >0\), \(\Gamma (\cdot)\) denotes the Gamma function and \(\Gamma (s)=\int _{0}^{\infty }\xi ^{s-1}e^{-\xi }\,d\xi \).

Definition 2.2

([50])

The Caputo fractional-order derivative of order δ for a function \(h(\xi )\in ([\xi _{0},\infty ),R)\) is defined as follows:

$$ {\mathcal {D}}^{\delta }h(\xi )=\frac{1}{\Gamma (n-\delta )} \int _{\xi _{0}}^{ \xi }\frac{ h^{(n)}(s)}{(\xi -s)^{\delta -n+1}}\,ds, $$

where \(\xi \geq \xi _{0}\) and n is a positive integer such that \(n-1\leq \delta < n\). In particular, when \(0<\delta <1\),

$$ {\mathcal {D}}^{\delta }h(\xi )=\frac{1}{\Gamma (1-\delta )} \int _{\xi _{0}}^{ \xi }\frac{ h^{\prime }(s)}{(\xi -s)^{\delta }}\,ds. $$

Lemma 2.1

([51])

Let there be given an autonomous system \({\mathcal {D}}^{\delta }z={\mathcal {A}}z\), \(z(0)=z_{0}\) where \(0<\delta <1\), \(z\in R^{n}\), \({\mathcal {A}}\in R^{n\times n}\). Suppose that \(\lambda _{i}\) (\(i=1,2,\ldots ,n\)) is the root of the characteristic equation of \({\mathcal {D}}^{\delta }z={\mathcal {A}}z\). Then system \({\mathcal {D}}^{\delta }z={\mathcal {A}}z\) is asymptotically stable ⇔ \(|\operatorname{arg}(\lambda _{i})| >\frac{\delta \pi }{2}\) (\(i=1,2,\ldots ,n\)). Especially, this system is stable ⇔ \(|\operatorname{arg}(\lambda _{i})| >\frac{\delta \pi }{2}\) (\(i=1,2,\ldots ,n\)) and those critical eigenvalues that satisfy \(|\operatorname{arg}(\lambda _{i})| =\frac{\delta \pi }{2}\) (\(i=1,2,\ldots ,n\)) possess geometric multiplicity one.

Lemma 2.2

([8])

For the given fractional-order delayed differential equation with Caputo derivative: \({\mathcal {D}}^{\delta }u(t)={\mathcal {C}}_{1}u(t)+{\mathcal {C}}_{2}u(t- \varrho )\), where \(u(t)=\phi (t)\), \(t\in [-\varrho ,0]\), \(\delta \in (0,1]\), \(u\in R^{n}\), \({ \mathcal {C}}_{1},{\mathcal {C}}_{2}\in R^{n\times n}\), \(\varrho \in R^{+(n \times n)}\). Then the characteristic equation of the system is \(\det |s^{\delta }I-{\mathcal {C}}_{1}-{\mathcal {C}}_{2}e^{-s\varrho }|=0\). If all the roots of the characteristic equation of the system have negative real roots, then the zero solution of the system is asymptotically stable.

3 Controller design for chaos control

Over the past few decades, many linear time-delay feedback methods are applied to control the Hopf bifurcation of integer-order models. However, the linear time-delay feedback controllers are very rare in controlling a Hopf bifurcation of fractional-order models. To make up for the deficiency, we design a linear time-delay feedback controller [52] which takes the form

$$ \kappa _{i}\bigl[u_{i}(t)-u_{i}(t-\varrho )\bigr]\quad (i=1,2), $$
(3.1)

where \(\kappa _{i}\) (\(i=1,2\)) is the feedback strength and ϱ is the time delay. \(\kappa _{i}, \varrho \in R\) and \(\varrho \geq 0\). Clearly, system (1.2) has two equilibrium points,

$$ E_{1} \biggl(-\sqrt{\frac{a_{2}}{a_{1}}}, \sqrt{ \frac{a_{2}}{a_{1}}}, \frac{1}{a_{1}} \biggr),\qquad E_{2} \biggl( \sqrt{\frac{a_{2}}{a_{1}}}, - \sqrt{\frac{a_{2}}{a_{1}}},\frac{1}{a_{1}} \biggr). $$

In this paper, we only consider the equilibrium point \(E_{1}\) and \(E_{2}\) can be handled in a similar approach. Adding the time-delayed feedback controller \(\kappa _{i}[u_{i}(t)-u_{i}(t-\varrho )]\) to the ith equation of system (1.2), we have

$$ \textstyle\begin{cases} \frac{du_{1}^{p}}{dt^{p}}=a_{1}(u_{1}+u_{2})+\kappa _{1}[u_{1}(t)-u_{1}(t- \varrho )], \\ \frac{du_{2}^{p}}{dt^{p}}=-u_{2}-a_{1}u_{1}u_{3}+ \kappa _{2}[u_{2}(t)-u_{2}(t-\varrho )], \\ \frac{du_{3}^{p}}{dt^{p}}=a_{2}+a_{1}u_{1}u_{2}. \end{cases} $$
(3.2)

The linear equation of (3.2) near the equilibrium point \(E_{1}\) takes the form

$$ \textstyle\begin{cases} \frac{du_{1}^{p}}{dt^{p}}=(a_{1}+\kappa _{1})u_{1}+a_{1}u_{2}- \kappa _{1}u_{1}(t-\varrho )], \\ \frac{du_{2}^{p}}{dt^{p}}=-u_{1}+(\kappa _{2}-1)u_{2}+ \sqrt{a_{1}a_{2}}u_{3}-\kappa _{2}u_{2}(t-\varrho ), \\ \frac{du_{3}^{p}}{dt^{p}}=\sqrt{a_{1}a_{2}}u_{1}-\sqrt{a_{1}a_{2}}u_{2}. \end{cases} $$
(3.3)

The corresponding characteristic equation of (3.3) is given by

$$ \det \begin{bmatrix} s^{p}-(a_{1}+\kappa _{1})+\kappa _{1}e^{-s\varrho } & -a_{1} & 0 \\ 1 & s^{p}-(\kappa _{2}-1)+\kappa _{2}e^{-s\varrho } & -\sqrt{a_{1}a_{2}} \\ -\sqrt{a_{1}a_{2}} & \sqrt{a_{1}a_{2}} & s^{p} \end{bmatrix} ,$$
(3.4)

which leads to

$$ {\mathcal {A}}_{1}(s)+{\mathcal {A}}_{2}(s)e^{-s\varrho }+{ \mathcal {A}}_{3}(s)e^{-2s \varrho }=0, $$
(3.5)

where

$$\begin{aligned}& {\mathcal {A}}_{1}(s)= s^{3p}-(\kappa _{1}-1+a_{1}+\kappa _{2})s^{2p}+ \bigl[a_{1}a_{2}- \kappa _{1}-(a_{1}+ \kappa _{1}) (\kappa _{2}-1)\bigr]s^{p} \\& \hphantom{{\mathcal {A}}_{1}(s)={}}{}+a_{1}a_{2}\kappa _{1}, \\& {\mathcal {A}}_{2}(s)=(\kappa _{1}+\kappa _{2})s^{2p}-\bigl[\kappa _{2}(a_{1}+ \kappa _{1})+\kappa _{1}(\kappa _{2}-1) \bigr]s^{p}+a_{1}a_{2}\kappa _{1}, \\& {\mathcal {A}}_{3}(s)=\kappa _{1}\kappa _{2}s^{p}. \end{aligned}$$

It follows from (3.5) that

$$ {\mathcal {A}}_{1}(s)e^{s\varrho }+{\mathcal {A}}_{2}(s)+{\mathcal {A}}_{3}(s)e^{-s \varrho }=0. $$
(3.6)

Let \(s=i\phi =\phi (\cos \frac{\pi }{2}+i\sin \frac{\pi }{2} )\) be a root of (3.6). Then

$$ \textstyle\begin{cases} {\mathcal {H}}_{1}(\phi )\cos \phi \sigma +{\mathcal {H}}_{2}( \phi )\sin \phi \sigma ={\mathcal {H}}_{3}(\phi ), \\ {\mathcal {G}}_{1}(\phi )\cos \phi \sigma +{\mathcal {G}}_{2}( \phi )\sin \phi \sigma ={\mathcal {G}}_{3}(\phi ), \end{cases} $$
(3.7)

where

$$\begin{aligned}& \begin{aligned} {\mathcal {H}}_{1}(\phi )={}&\phi ^{3p}\cos \frac{3p\pi }{2}-(\kappa _{1}-1+a_{1}+ \kappa _{2})\phi ^{2p}\cos p\pi +\bigl[a_{1}a_{2}- \kappa _{1} \\ &{}-(a_{1}+\kappa _{1}) (\kappa _{2}-1)+ \kappa _{1}\kappa _{2}\bigr] \phi ^{p}\cos \frac{p\pi }{2}+a_{1}a_{2}\kappa _{1}, \end{aligned} \\& \begin{aligned} {\mathcal {H}}_{2}(\phi )={}&{-}\phi ^{3p}\sin \frac{3p\pi }{2}+(\kappa _{1}-1+a_{1}+ \kappa _{2})\phi ^{2p}\sin p\pi -\bigl[a_{1}a_{2}- \kappa _{1} \\ &{}-(a_{1}+\kappa _{1}) (\kappa _{2}-1)+ \kappa _{1}\kappa _{2}\bigr] \phi ^{p}\sin \frac{p\pi }{2}, \end{aligned} \\& {\mathcal {H}}_{3}(\phi )=-(\kappa _{1}+\kappa _{2})\phi ^{2p}\cos p \pi +\bigl[\kappa _{2}(a_{1}+\kappa _{1})+\kappa _{1}(\kappa _{2}-1)\bigr]\phi ^{p} \cos \frac{p\pi }{2}-a_{1}a_{2}\kappa _{1}, \\& \begin{aligned} {\mathcal {G}}_{1}(\phi )={}&\phi ^{3p}\sin \frac{3p\pi }{2}-(\kappa _{1}-1+a_{1}+ \kappa _{2})\phi ^{2p}\cos p\pi +\bigl[a_{1}a_{2}- \kappa _{1} \\ &{}-(a_{1}+\kappa _{1}) (\kappa _{2}-1)+ \kappa _{1}\kappa _{2}\bigr] \phi ^{p}\sin \frac{p\pi }{2}, \end{aligned} \\& \begin{aligned} {\mathcal {G}}_{2}(\phi )={}&\phi ^{3p}\cos \frac{3p\pi }{2}-(\kappa _{1}-1+a_{1}+ \kappa _{2})\phi ^{2p}\cos p\pi +\bigl[a_{1}a_{2}- \kappa _{1} \\ &{}-(a_{1}+\kappa _{1}) (\kappa _{2}-1)- \kappa _{1}\kappa _{2}\bigr] \phi ^{p}\cos \frac{p\pi }{2}+a_{1}a_{2}(a_{1}+ \kappa _{1}), \end{aligned} \\& {\mathcal {G}}_{3}(\phi )=-(\kappa _{1}+\kappa _{2})\phi ^{2p}\sin p \pi +\bigl[\kappa _{2}(a_{1}+\kappa _{1})+\kappa _{1}(\kappa _{2}-1)\bigr]\phi ^{p} \sin \frac{p\pi }{2}. \end{aligned}$$

Let

$$ \textstyle\begin{cases} \alpha _{1}=\cos \frac{3p\pi }{2},\qquad \alpha _{2}=-(\kappa _{1}-1+a_{1}+ \kappa _{2})\cos p\pi , \\ \alpha _{3}=[a_{1}a_{2}-\kappa _{1}-(a_{1}+\kappa _{1})( \kappa _{2}-1)+\kappa _{1}\kappa _{2}]\cos \frac{p\pi }{2}, \\ \alpha _{4}=a_{1}a_{2}\kappa _{1},\qquad \alpha _{5}=-\sin \frac{3p\pi }{2}, \qquad \alpha _{6}=(\kappa _{1}-1+a_{1}+\kappa _{2})\sin p \pi , \\ \alpha _{7}=-[a_{1}a_{2}-\kappa _{1}-(a_{1}+\kappa _{1})( \kappa _{2}-1)+\kappa _{1}\kappa _{2}]\sin \frac{p\pi }{2}, \\ \alpha _{8}=-(\kappa _{1}+\kappa _{2})\cos p\pi ,\qquad \alpha _{9}=[\kappa _{2}(a_{1}+\kappa _{1})+\kappa _{1}(\kappa _{2}-1)] \cos \frac{p\pi }{2}, \\ \alpha _{10}=-a_{1}a_{2}\kappa _{1},\qquad \alpha _{11}=\sin \frac{3p\pi }{2},\qquad \alpha _{12}=-(\kappa _{1}-1+a_{1}+\kappa _{2})\cos p \pi , \\ \alpha _{13}=[a_{1}a_{2}-\kappa _{1}-(a_{1}+\kappa _{1})( \kappa _{2}-1)+\kappa _{1}\kappa _{2}]\sin \frac{p\pi }{2},\qquad \alpha _{14}= \cos \frac{3p\pi }{2}, \\ \alpha _{15}=-(\kappa _{1}-1+a_{1}+\kappa _{2})\cos p \pi , \\ \alpha _{16}=[a_{1}a_{2}-\kappa _{1}-(a_{1}+\kappa _{1})( \kappa _{2}-1)-\kappa _{1}\kappa _{2}]\cos \frac{p\pi }{2}, \\ \alpha _{17}=a_{1}a_{2}(a_{1}+\kappa _{1}), \qquad \alpha _{18}=-( \kappa _{1}+\kappa _{2})\sin p\pi , \\ \alpha _{19}=[\kappa _{2}(a_{1}+ \kappa _{1})+\kappa _{1}(\kappa _{2}-1)]\sin \frac{p\pi }{2}. \end{cases} $$
(3.8)

Then

$$ \textstyle\begin{cases} {\mathcal {H}}_{1}(\phi )=\alpha _{1}\phi ^{3p}+\alpha _{2} \phi ^{2p}+\alpha _{3}\phi ^{p}+\alpha _{4}, \\ {\mathcal {H}}_{2}(\phi )=\alpha _{5}\phi ^{3p}+\alpha _{6} \phi ^{2p}+\alpha _{7}\phi ^{p}, \\ {\mathcal {H}}_{3}(\phi )=\alpha _{8}\phi ^{2p}+\alpha _{9} \phi ^{p}+\alpha _{10}, \\ {\mathcal {G}}_{1}(\phi )=\alpha _{11}\phi ^{3p}+\alpha _{12} \phi ^{2p}+\alpha _{13}\phi ^{p}, \\ {\mathcal {G}}_{2}(\phi )=\alpha _{14}\phi ^{3p}+\alpha _{15} \phi ^{2p}+\alpha _{16}\phi ^{p}+\alpha _{17}, \\ {\mathcal {G}}_{3}(\phi )=\alpha _{18}\phi ^{2p}+\alpha _{19} \phi ^{p}. \end{cases} $$
(3.9)

By (3.7), one has

$$ \textstyle\begin{cases} \cos \phi \sigma = \frac{{\mathcal {H}}_{3}(\phi ){\mathcal {G}}_{2}(\phi )- {\mathcal {G}}_{3}(\phi ){\mathcal {H}}_{2}(\phi )}{{\mathcal {H}}_{1}(\phi ) {\mathcal {G}}_{2}(\phi )-{\mathcal {G}}_{1}(\phi ){\mathcal {H}}_{2}(\phi )}, \\ \sin \varphi \sigma = \frac{{\mathcal {H}}_{1}(\phi ){\mathcal {G}}_{3}(\phi )- {\mathcal {G}}_{1}(\phi ){\mathcal {H}}_{3}(\phi )}{{\mathcal {H}}_{1}(\phi ) {\mathcal {G}}_{2}(\phi )-{\mathcal {G}}_{1}(\phi ){\mathcal {H}}_{2}(\phi )}. \end{cases} $$
(3.10)

In view of the equation \(\cos ^{2} \phi \sigma +\sin ^{2} \phi \sigma =1\), one has

$$\begin{aligned}& \bigl[{\mathcal {H}}_{3}(\phi ){\mathcal {G}}_{2}( \phi )-{\mathcal {G}}_{3}( \phi ){\mathcal {H}}_{2}(\phi )\bigr]^{2}+\bigl[{\mathcal {H}}_{1}(\phi ){ \mathcal {G}}_{3}(\phi )-{\mathcal {G}}_{1}(\phi ){\mathcal {H}}_{3}( \phi )\bigr]^{2} \\& \quad =\bigl[{\mathcal {H}}_{1}(\phi ){\mathcal {G}}_{2}( \phi )-{\mathcal {G}}_{1}( \phi ){\mathcal {H}}_{2}(\phi )\bigr]^{2}. \end{aligned}$$
(3.11)

Since

$$\begin{aligned}& \bigl[{\mathcal {H}}_{3}(\phi ){\mathcal {G}}_{2}( \phi )-{\mathcal {G}}_{3}( \phi ){\mathcal {H}}_{2}(\phi )\bigr]^{2}=\bigl(l_{1}\phi ^{5p}+l_{2} \phi ^{4p}+l_{3} \phi ^{3p}+l_{4} \phi ^{2p}+l_{5}\phi ^{p}+l_{6} \bigr)^{2}, \\& \bigl[{\mathcal {H}}_{1}(\phi ){\mathcal {G}}_{3}( \phi )-{\mathcal {G}}_{1}( \phi ){\mathcal {H}}_{3}(\phi )\bigr]^{2}=\bigl(l_{7}\phi ^{5p}+l_{8} \phi ^{4p}+l_{9} \phi ^{3p}+l_{10} \phi ^{2p}+l_{11}\phi ^{p} \bigr)^{2}, \\& \bigl[{\mathcal {H}}_{1}(\phi ){\mathcal {G}}_{2}( \phi )-{\mathcal {G}}_{1}( \phi ){\mathcal {H}}_{2}(\phi )\bigr]^{2} \\& \quad =\bigl(l_{12}\phi ^{6p}+l_{13} \phi ^{5p}+l_{14} \phi ^{4p}+l_{15} \phi ^{3p}+l_{16}\phi ^{2p}+l_{17} \phi ^{p}+l_{18}\bigr)^{2}, \end{aligned}$$

where

$$ \textstyle\begin{cases} l_{1}=\alpha _{8}\alpha _{14}-\alpha _{5}\alpha _{18},\qquad l_{2}= \alpha _{8}\alpha _{15}+\alpha _{9}\alpha _{14}-\alpha _{6}\alpha _{18}- \alpha _{5}\alpha _{19}, \\ l_{3}=\alpha _{8}\alpha _{16}+\alpha _{9}\alpha _{15}+ \alpha _{10}\alpha _{14}-\alpha _{7}\alpha _{18}-\alpha _{6}\alpha _{19}, \\ l_{4}=\alpha _{8}\alpha _{17}+\alpha _{9}\alpha _{16}+ \alpha _{10}\alpha _{15}-\alpha _{7}\alpha _{19},\qquad l_{5}=\alpha _{10} \alpha _{16}, \qquad l_{6}=\alpha _{10}\alpha _{17}, \\ l_{7}=\alpha _{1}\alpha _{18}-\alpha _{8}\alpha _{11},\qquad l_{8}= \alpha _{1}\alpha _{19}+\alpha _{2}\alpha _{18}-\alpha _{9}\alpha _{11}- \alpha _{8}\alpha _{12}, \\ l_{9}=\alpha _{2}\alpha _{19}+\alpha _{3}\alpha _{18}- \alpha _{10}\alpha _{11}-\alpha _{9}\alpha _{12}-\alpha _{8}\alpha _{13}, \\ l_{10}=\alpha _{3}\alpha _{19}+\alpha _{4}\alpha _{18}- \alpha _{10}\alpha _{12}-\alpha _{9}\alpha _{13},\qquad l_{11}=\alpha _{4} \alpha _{19}-\alpha _{10}\alpha _{13}, \\ l_{12}=\alpha _{1}\alpha _{14}-\alpha _{3}\alpha _{11},\qquad l_{13}= \alpha _{1}\alpha _{15}+\alpha _{2}\alpha _{14}-\alpha _{6}\alpha _{11}- \alpha _{3}\alpha _{12}, \\ l_{14}=\alpha _{1}\alpha _{16}+\alpha _{2}\alpha _{15}+ \alpha _{3}\alpha _{14}-\alpha _{7}\alpha _{11}-\alpha _{6}\alpha _{12}- \alpha _{3}\alpha _{13}, \\ l_{15}=\alpha _{1}\alpha _{17}+\alpha _{2}\alpha _{16}+ \alpha _{3}\alpha _{15}+\alpha _{4}\alpha _{14}-\alpha _{7}\alpha _{12}- \alpha _{7}\alpha _{13}, \\ l_{16}=\alpha _{2}\alpha _{17}+\alpha _{3}\alpha _{16}+ \alpha _{4}\alpha _{15}-\alpha _{7}\alpha _{13}, \\ l_{17}=\alpha _{3}\alpha _{17}+\alpha _{4}\alpha _{16},\qquad l_{18}= \alpha _{4}\alpha _{17}, \end{cases} $$
(3.12)

we have

$$\begin{aligned}& b_{1}\phi ^{12p}+b_{2}\phi ^{11p}+b_{3}\phi ^{10p}+b_{4}\phi ^{9p}+b_{5} \phi ^{8p}+b_{6} \phi ^{7p}+b_{7}\phi ^{6p} \\& \quad {} +b_{8}\phi ^{5p}+b_{9}\phi ^{4p}+b_{10}\phi ^{3p}+b_{11}\phi ^{2p}+b_{12} \phi ^{p}+b_{13}=0, \end{aligned}$$
(3.13)

where

$$ \textstyle\begin{cases} b_{1}=l_{12}^{2},\qquad b_{2}=2l_{12}l_{13},\qquad b_{3}=l_{13}^{2}+2l_{12}l_{14}-l_{7}^{2}-l_{1}^{2}, \\ b_{4}=2(l_{12}l_{15}+l_{13}l_{14}-l_{7}l_{8}-l_{1}l_{2}), \\ b_{5}=l_{14}^{2}+2l_{12}l_{16}+2l_{13}l_{15}-l_{8}^{2}-2l_{7}l_{8}-l_{2}^{2}-2l_{1}l_{3}, \\ b_{6}=2[l_{12}l_{17}+l_{13}l_{16}+l_{14}l_{15}-l_{8}l_{9}-l_{7}l_{10}-l_{1}l_{4}-l_{2}l_{3}], \\ b_{7}=l_{15}^{2}+2l_{12}l_{18}+2l_{14}l_{16}+2l_{13}l_{17}-l_{9}^{2}-2l_{7}l_{11}-2l_{8}l_{10}-l_{3}^{2}-2l_{1}l_{5}-2l_{2}l_{4}, \\ b_{8}=2[l_{13}l_{18}+l_{14}l_{17}+l_{15}l_{16}-l_{8}l_{11}-l_{9}l_{10}-l_{1}l_{6}-l_{2}l_{5}-l_{3}l_{4}], \\ b_{9}=l_{16}^{2}+2l_{14}l_{18}+2l_{15}l_{17}-l_{10}^{2}-2l_{9}l_{11}-l_{4}^{2}-2l_{2}l_{6}-2l_{3}l_{5}, \\ b_{10}=2[l_{15}l_{18}+l_{16}l_{17}-l_{10}l_{11}-l_{3}l_{6}-l_{4}l_{5}], \\ b_{11}=l_{17}^{2}+2l_{16}l_{18}-l_{5}^{2}-2l_{4}l_{6},\qquad b_{12}=2(l_{17}l_{18}-2l_{5}l_{6}),\qquad b_{13}=l_{18}^{2}. \end{cases} $$
(3.14)

Denote

$$\begin{aligned} \chi (\phi ) =&b_{1}\phi ^{12p}+b_{2}\phi ^{11p}+b_{3}\phi ^{10p}+b_{4} \phi ^{9p}+b_{5}\phi ^{8p}+b_{6} \phi ^{7p}+b_{7}\phi ^{6p} \\ &{} +b_{8}\phi ^{5p}+b_{9}\phi ^{4p}+b_{10}\phi ^{3p}+b_{11} \phi ^{2p}+b_{12}\phi ^{p}+b_{13} \end{aligned}$$
(3.15)

and

$$\begin{aligned} \rho (\mu ) =&b_{1}\mu ^{12}+b_{2}\mu ^{11}+b_{3}\mu ^{10}+b_{4}\mu ^{9}+b_{5} \mu ^{8}+b_{6}\mu ^{7}+b_{7}\mu ^{6} \\ &{} +b_{8}\mu ^{5}+b_{9}\mu ^{4}+b_{10}\mu ^{3}+b_{11}\mu ^{2}+b_{12} \mu +b_{13}. \end{aligned}$$
(3.16)

The following assumption is given:

(\({\mathcal {A}}\)1):

\(\kappa _{1}\neq 0\).

Lemma 3.1

For (3.5), the following conclusions are true:

  1. (i)

    If \(b_{i}>0\) (\(i=1,2,3,\ldots ,12\)), then (3.5) possesses no root with zero real parts.

  2. (ii)

    If there exists a positive constant \(\mu _{0}\) such that \(\rho (\mu _{0})<0\), then (3.5) possesses at least two pairs of purely imaginary roots.

Proof

We will prove the two cases, respectively.

(i) By (3.15), one gets

$$\begin{aligned} \frac{d\chi (\phi )}{d\phi } =&12pb_{1}\phi ^{12p-1}+11pb_{2} \phi ^{11p-1}+10pb_{3} \phi ^{10p-1}+9pb_{4} \phi ^{9p-1}+8pb_{5}\phi ^{8p-1} \\ &{}+7pb_{6} \phi ^{7p-1}+6pb_{7}\phi ^{6p-1}+5pb_{8}\phi ^{5p-1}+4pb_{9}\phi ^{4p-1}+3pb_{10} \phi ^{3p-1} \\ &{}+2pb_{11}\phi ^{2p-1}+pb_{12} \phi ^{p-1}. \end{aligned}$$
(3.17)

Since \(b_{i}>0\) (\(i=1,2,3,\ldots ,13\)), we have \(\frac{d\chi (\phi )}{d\phi }>0\) \(\forall \phi >0\). In view of \(\chi (0)=b_{13}>0\), we know that (3.15) possesses no positive real root. In view of (\({\mathcal {A}}\)1), we can conclude that \(s=0\) is not the root of (3.5). The proof of (i) is completed.

(ii) Because \(\rho (0)=b_{13}>0\), \(\rho (\varepsilon _{0})<0\) (\(\varepsilon _{0}>0\)) and \(\lim_{\nu \rightarrow +\infty }\frac{\rho (\nu )}{d\nu }=+\infty \), one can know that \(\exists \varepsilon _{01}\in (0,\varepsilon _{0})\) and \(\varepsilon _{02}\in (\varepsilon _{0},+\infty )\) such that \(\rho (\varepsilon _{01})=\rho (\varepsilon _{02})=0\), which implies that (3.13) possesses at least two positive real roots. Then (3.5) possesses at least two pairs of purely imaginary roots. The proof of (ii) is finished. □

Without loss of generality, assume that (3.13) has six positive real roots identified by \(\phi _{l}\) (\(l=1,2,\ldots ,13\)). By (3.10), one gets

$$ \varrho _{l}^{k}=\frac{1}{\phi _{l}} \biggl[\arccos \biggl( \frac{{\mathcal {H}}_{3}(\phi _{l}){\mathcal {G}}_{2}(\phi _{l}) -{\mathcal {G}}_{3}(\phi _{l}){\mathcal {H}}_{2}(\phi _{l})}{{\mathcal {H}}_{1}(\phi _{l})G_{2}(\phi _{l})-{\mathcal {G}}_{1} (\phi _{l}){\mathcal {H}}_{2}(\phi _{l})} \biggr)+2k\pi \biggr], $$
(3.18)

where \(k=0, 1,2,\ldots \) , \(l=1,2,\ldots ,13\). Then \(\pm i\phi _{l}\) is a pair of purely imaginary roots of (3.5) when \(\varrho =\varrho _{l}^{k}\). Let

$$ \varrho _{0}=\min_{l=1,2,\ldots ,13}\bigl\{ \varrho _{l}^{0}\bigr\} , \qquad \phi _{0}= \phi |_{\varrho =\varrho _{0}}. $$
(3.19)

Now the following assumption is made:

(\({\mathcal {A}}\)2):

\({\mathcal {M}}_{1}{\mathcal {N}}_{1}+{\mathcal {M}}_{2}{\mathcal {N}}_{2}>0\), where

$$\begin{aligned}& {\mathcal {M}}_{1} = \kappa _{1}\kappa _{2}\phi _{0}^{p} \biggl(\cos \phi _{0}\varrho _{0}\cos \frac{p\pi }{2}+\sin \phi _{0}\varrho _{0} \sin \frac{p\pi }{2} \biggr) \\& \hphantom{{\mathcal {M}}_{1} ={}}{} + \phi _{0}\sin \phi _{0}\varrho _{0} \biggl[ \phi _{0}^{3p}\cos \frac{3p\pi }{2}-(\kappa _{1}-1+a_{1}+\kappa _{2})\phi _{0}^{2p}\cos p\pi \\& \hphantom{{\mathcal {M}}_{1} ={}}{}+ \bigl(a_{1}a_{2}-\kappa _{1}-(a_{1}+ \kappa _{1}) (\kappa _{2}-1)\bigr)\phi _{0}^{p}\cos \frac{p\pi }{2}+a_{1}a_{2} \kappa _{1} \biggr] \\& \hphantom{{\mathcal {M}}_{1} ={}}{}+\phi _{0}\cos \phi _{0}\varrho _{0} \biggl[\phi _{0}^{3p}\sin \frac{3p\pi }{2}-(\kappa _{1}-1+a_{1}+ \kappa _{2})\phi _{0}^{2p}\sin p\pi \\& \hphantom{{\mathcal {M}}_{1} ={}}{}+ \bigl(a_{1}a_{2}-\kappa _{1}-(a_{1}+ \kappa _{1}) (\kappa _{2}-1)\bigr)\phi _{0}^{p}\sin \frac{p\pi }{2} \biggr], \\& {\mathcal {M}}_{2} = \kappa _{1}\kappa _{2}\phi _{0}^{p} \biggl(\cos \phi _{0}\varrho _{0}\sin \frac{p\pi }{2}-\sin \phi _{0}\varrho _{0} \cos \frac{p\pi }{2} \biggr) \\& \hphantom{{\mathcal {M}}_{2} ={}}{}+ \phi _{0}\sin \phi _{0}\varrho _{0} \biggl[ \phi _{0}^{3p}\sin \frac{3p\pi }{2}-(\kappa _{1}-1+a_{1}+\kappa _{2})\phi _{0}^{2p}\sin p\pi \\& \hphantom{{\mathcal {M}}_{2} ={}}{} + \bigl(a_{1}a_{2}-\kappa _{1}-(a_{1}+ \kappa _{1}) (\kappa _{2}-1)\bigr)\phi _{0}^{p}\sin \frac{p\pi }{2} \biggr] \\& \hphantom{{\mathcal {M}}_{2} ={}}{}+ \phi _{0}\cos \phi _{0}\varrho _{0} \biggl[\phi _{0}^{3p}\cos \frac{3p\pi }{2} -(\kappa _{1}-1+a_{1}+\kappa _{2})\phi _{0}^{2p}\cos p\pi \\& \hphantom{{\mathcal {M}}_{2} ={}}{}+\bigl(a_{1}a_{2}- \kappa _{1}-(a_{1}+\kappa _{1}) (\kappa _{2}-1)\bigr)\phi _{0}^{p}\cos \frac{p\pi }{2}+a_{1}a_{2}\kappa _{1} \biggr], \\& {\mathcal {N}}_{1} = \biggl[3p\phi _{0}^{3p} \cos \frac{3p\pi }{2}-2p( \kappa _{1}-1+a_{1}+ \kappa _{2})\phi _{0}^{2p-1}\cos \frac{(2p-1)\pi }{2} \\& \hphantom{{\mathcal {N}}_{1} ={}}{} +p\bigl(a_{1}a_{2}-\kappa _{1}-(a_{1}+\kappa _{1}) (\kappa _{2}-1)\bigr)\phi _{0}^{p-1} \cos \frac{(p-1)\pi }{2} \biggr]\cos \phi _{0}\varrho _{0} \\& \hphantom{{\mathcal {N}}_{1} ={}}{}-\sin \phi _{0} \varrho _{0} \biggl[3p \phi _{0}^{3p}\sin \frac{3p\pi }{2}-2p(\kappa _{1}-1+a_{1}+ \kappa _{2})\phi _{0}^{2p-1}\sin \frac{(2p-1)\pi }{2} \\& \hphantom{{\mathcal {N}}_{1} ={}}{}+p \bigl(a_{1}a_{2}- \kappa _{1}-(a_{1}+ \kappa _{1}) (\kappa _{2}-1)\bigr)\phi _{0}^{p-1}\sin \frac{(p-1)\pi }{2} \biggr] \\& \hphantom{{\mathcal {N}}_{1} ={}}{} +\varrho _{0}\cos \phi _{0}\varrho _{0} \biggl[\phi _{0}^{3p}\cos \frac{3p\pi }{2}-(\kappa _{1}-1+a_{1}+\kappa _{2})\phi _{0}^{2p}\cos \frac{2p\pi }{2} \\& \hphantom{{\mathcal {N}}_{1} ={}}{}+ \bigl(a_{1}a_{2}-\kappa _{1}-(a_{1}+ \kappa _{1}) (\kappa _{2}-1)\bigr)\phi _{0}^{p} \cos \frac{p\pi }{2}+a_{1}a_{2} \kappa _{1} \biggr] \\& \hphantom{{\mathcal {N}}_{1} ={}}{}-\varrho _{0}\sin \phi _{0} \varrho _{0} \biggl[ \phi _{0}^{3p}\sin \frac{3p\pi }{2}-(\kappa _{1}-1+a_{1}+\kappa _{2}) \phi _{0}^{2p}\sin \frac{2p\pi }{2} \\& \hphantom{{\mathcal {N}}_{1} ={}}{} +\bigl(a_{1}a_{2}-\kappa _{1}-(a_{1}+ \kappa _{1}) (\kappa _{2}-1)\bigr) \phi _{0}^{p}\sin \frac{p\pi }{2} \biggr]+2p(\kappa _{1}+\kappa _{2}) \phi _{0}^{2p-1} \cos \frac{(2p-1)\pi }{2} \\& \hphantom{{\mathcal {N}}_{1} ={}}{} -p\bigl[\kappa _{2}(a-1+a_{2})-\kappa _{1}(\kappa _{2}-1)\bigr]\phi _{0}^{p-1} \cos \frac{(p-1)\pi }{2} \\& \hphantom{{\mathcal {N}}_{1} ={}}{} +p\kappa _{1}\kappa _{2}\phi _{0}^{p-1}\cos \frac{(p-1)\pi }{2}\cos \phi _{0}\varrho _{0}-p\kappa _{1}\kappa _{2}\phi _{0}^{p-1} \sin \frac{(p-1)\pi }{2} \sin \phi _{0}\varrho _{0} \\& \hphantom{{\mathcal {N}}_{1} ={}}{}+ \varrho _{0}\kappa _{1}\kappa _{2}\phi _{0}^{p} \cos \frac{p\pi }{2}\cos \phi _{0}\varrho _{0}+\varrho _{0}\kappa _{1} \kappa _{2}\phi _{0}^{p} \sin \frac{p\pi }{2}\sin \phi _{0}\varrho _{0}, \\& {\mathcal {N}}_{2} = \biggl[3p\phi _{0}^{3p} \cos \frac{3p\pi }{2}-2p( \kappa _{1}-1+a_{1}+ \kappa _{2})\phi _{0}^{2p-1}\cos \frac{(2p-1)\pi }{2} \\& \hphantom{{\mathcal {N}}_{2} ={}}{}+p\bigl(a_{1}a_{2}-\kappa _{1}-(a_{1}+\kappa _{1}) (\kappa _{2}-1)\bigr)\phi _{0}^{p-1} \cos \frac{(p-1)\pi }{2} \biggr]\sin \phi _{0}\varrho _{0} \\& \hphantom{{\mathcal {N}}_{2} ={}}{}-\cos \phi _{0} \varrho _{0} \biggl[3p \phi _{0}^{3p}\sin \frac{3p\pi }{2}-2p(\kappa _{1}-1+a_{1}+ \kappa _{2}) \phi _{0}^{2p-1}\sin \frac{(2p-1)\pi }{2} \\& \hphantom{{\mathcal {N}}_{2} ={}}{}+p \bigl(a_{1}a_{2}- \kappa _{1}-(a_{1}+ \kappa _{1}) (\kappa _{2}-1)\bigr)\phi _{0}^{p-1}\sin \frac{(p-1)\pi }{2} \biggr] \\& \hphantom{{\mathcal {N}}_{2} ={}}{} +\varrho _{0}\sin \phi _{0}\varrho _{0} \biggl[\phi _{0}^{3p}\cos \frac{3p\pi }{2}-(\kappa _{1}-1+a_{1}+\kappa _{2})\phi _{0}^{2p}\cos \frac{2p\pi }{2} \\& \hphantom{{\mathcal {N}}_{2} ={}}{}+ \bigl(a_{1}a_{2}-\kappa _{1}-(a_{1}+ \kappa _{1}) (\kappa _{2}-1)\bigr)\phi _{0}^{p} \cos \frac{p\pi }{2}+a_{1}a_{2} \kappa _{1} \biggr] \\& \hphantom{{\mathcal {N}}_{2} ={}}{}+\varrho _{0}\cos \phi _{0} \varrho _{0} \biggl[ \phi _{0}^{3p}\sin \frac{3p\pi }{2}-(\kappa _{1}-1+a_{1}+\kappa _{2}) \phi _{0}^{2p}\sin \frac{2p\pi }{2} \\& \hphantom{{\mathcal {N}}_{2} ={}}{} +\bigl(a_{1}a_{2}-\kappa _{1}-(a_{1}+ \kappa _{1}) (\kappa _{2}-1)\bigr) \phi _{0}^{p}\sin \frac{p\pi }{2} \biggr]+2p(\kappa _{1}+\kappa _{2}) \phi _{0}^{2p-1} \sin \frac{(2p-1)\pi }{2} \\& \hphantom{{\mathcal {N}}_{2} ={}}{} -p\bigl[\kappa _{2}(a-1+a_{2})-\kappa _{1}(\kappa _{2}-1)\bigr]\phi _{0}^{p-1} \sin \frac{(p-1)\pi }{2} \\& \hphantom{{\mathcal {N}}_{2} ={}}{} +p\kappa _{1}\kappa _{2}\phi _{0}^{p-1}\cos \frac{(p-1)\pi }{2}\sin \phi _{0}\varrho _{0} +p\kappa _{1}\kappa _{2}\phi _{0}^{p-1} \sin \frac{(p-1)\pi }{2} \cos \phi _{0}\varrho _{0} \\& \hphantom{{\mathcal {N}}_{2} ={}}{}- \varrho _{0}\kappa _{1}\kappa _{2}\phi _{0}^{p} \cos \frac{p\pi }{2}\sin \phi _{0}\varrho _{0} +\varrho _{0}\kappa _{1} \kappa _{2}\phi _{0}^{p} \sin \frac{p\pi }{2}\cos \phi _{0}\varrho _{0}. \end{aligned}$$

Lemma 3.2

Suppose that \(s(\varrho )=\nu (\varrho )+i\phi (\varrho )\) is the root of (3.5) at \(\varrho =\varrho _{0}\) satisfying \(\nu (\varrho _{0})=0\), \(\phi (\varrho _{0})=\phi _{0}\), then \(\operatorname {Re} [\frac{ds}{d\varrho } ] |_{\varrho =\varrho _{0}, \phi =\phi _{0}}>0\).

Proof

According to (3.6), one gets

$$ \frac{ds}{d\varrho }= \frac{{\mathcal {B}}_{1}(\varrho )}{{\mathcal {B}}_{2}(\varrho )}, $$
(3.20)

where

$$\begin{aligned}& \begin{aligned} {\mathcal {B}}_{1}(\varrho ) ={}& e^{-s\varrho }\kappa _{1}\kappa _{2}s^{p}-se^{s \varrho } \bigl[s^{3p}-(\kappa _{1}-1+a_{1}+\kappa _{2})s^{2p} \\ &{} +\bigl(a_{1}a_{2}-\kappa _{1}-(a_{1}+ \kappa _{1}) (\kappa _{2}-1)\bigr)s^{p}+a_{1}a_{2} \kappa _{1}\bigr], \end{aligned} \\& \begin{aligned} {\mathcal {B}}_{2}(\varrho ) ={}& \bigl\{ 3ps^{3p-1}-2p( \kappa _{1}-1+a_{1}+ \kappa _{2})s^{2p-1}+p \bigl[a_{1}a_{2}-\kappa _{1}-(a_{1}+ \kappa _{1}) ( \kappa _{2}-1)\bigr]s^{p-1} \bigr\} e^{s\varrho } \\ &{}+e^{s\varrho }\varrho \bigl[s^{3p}-(\kappa _{1}-1+a_{1}+\kappa _{2})s^{2p}+ \bigl(a_{1}a_{2}- \kappa _{1}-(a_{1}+ \kappa _{1}) (\kappa _{2}-1)\bigr)s^{p}+a_{1}a_{2} \kappa _{1}\bigr] \\ &{}+2p(\kappa _{1}+\kappa _{2})s^{2p-1}-p \bigl[\kappa _{2}(a_{1}+a_{2})- \kappa _{1}(\kappa _{2}-1)\bigr]s^{p-1} \\ &{}+p\kappa _{1}\kappa _{2}s^{p-1}e^{-s \varrho }-e^{-s\varrho } \varrho \kappa _{1}\kappa _{2}s^{p}. \end{aligned} \end{aligned}$$

Then

$$ \operatorname{Re} \biggl\{ \frac{ds}{d\sigma } \biggr\} =\operatorname{Re} \biggl\{ \frac{{\mathcal {B}}_{1}(\varrho )}{{\mathcal {B}}_{2}(\varrho )} \biggr\} . $$
(3.21)

Hence

$$ \operatorname{Re} \biggl\{ \frac{ds}{d\sigma } \biggr\} \bigg|_{\varrho =\varrho _{0}, \phi =\phi _{0}}=\operatorname{Re} \biggl\{ \frac{B_{1}(\varrho )}{B_{2}(\varrho )} \biggr\} \bigg|_{\varrho = \varrho _{0}, \phi =\phi _{0}}= \frac{{\mathcal {M}}_{1}{\mathcal {N}}_{1} +{\mathcal {M}}_{2}{\mathcal {N}}_{2}}{{\mathcal {N}}_{1}^{2}+{\mathcal {N}}_{2}^{2}}. $$
(3.22)

In terms of (\({\mathcal {A}}\)3), one has

$$ \operatorname{Re} \biggl\{ \biggl[\frac{ds}{d\varrho } \biggr]^{-1} \biggr\} \bigg|_{\varrho =\varrho _{0}, \phi =\phi _{0}}>0. $$

The proof of Lemma 3.2 is finished. □

Next we give an assumption as follows:

(\({\mathcal {A}}\)3):

\(\kappa _{1}>0\), \((1-a_{1})(a_{1}a_{2}-2\kappa _{1}\kappa _{2}-2a_{1} \kappa _{2}+a_{1}+\kappa _{1})>2a_{1}a_{2}\kappa _{1}\).

Lemma 3.3

If \(\varrho =0\) and (\({\mathcal {A}}\)3) hold true, then system (3.2) is asymptotically stable.

Proof

If \(\varrho =0\), then (3.5) takes the form

$$ \lambda ^{3}+(1-a_{1})\lambda ^{2}+(a_{1}a_{2}-2 \kappa _{1}\kappa _{2}-2a_{1} \kappa _{2}+a_{1}+\kappa _{1})\lambda +2a_{1}a_{2}\kappa _{1}=0. $$
(3.23)

It follows from (\({\mathcal {A}}\)3) that all the roots \(\lambda _{i}\) of (3.20) satisfy \(|\operatorname{arg}(\lambda _{i})|>\frac{p\pi }{2}\) (\(i=1,2\)). By Lemma 2.1, we know that system (3.2) with \(\varrho =0\) is asymptotically stable. The proof of Lemma 3.3 is finished. □

According to the analysis above and Lemmas 3.2 and 3.3, one has the following theorem.

Theorem 3.1

For system (3.2), assume that (\({\mathcal {A}}\)1)–(\({ \mathcal {A}}\)3) are satisfied, then the equilibrium point \(E_{1}\) is globally asymptotically stable for \(\varrho \in [0,\varrho _{0})\) and system (3.2) undergoes a Hopf bifurcation near the equilibrium point \(E_{1}\) when \(\varrho =\varrho _{0}\).

Remark 3.1

In [1–3, 53], the authors studied the Hopf bifurcation and chaotic behavior of integer-order finance systems. In this paper, we investigate the chaos control of fractional-order delayed finance systems. All the obtained results and analysis methods [1–3, 53] cannot be applied to (3.2) to obtain the stability and the existence of Hopf bifurcation for (3.2). For these reasons, the fruits of our research about the chaos control for (1.2) are completely innovative and are an important supplement to some previous research results.

Remark 3.2

Xu and Zhang [54] focused on the chaos control of the Qi system by linear time-delay feedback control. They do not involve fractional-order models. From this viewpoint, the results of this article also supplement the research of Xu and Zhang [54].

4 An example

Consider the fractional-order finance model:

$$ \textstyle\begin{cases} \frac{d^{0.8}u_{1}}{dt^{0.8}}=1.79(u_{1}+u_{2})+\kappa _{1}[u_{1}(t)-u_{1}(t- \varrho )], \\ \frac{d^{0.8}u_{2}}{dt^{0.8}}=-u_{2}-1.79u_{1}u_{3}+ \kappa _{2}[u_{2}(t)-u_{2}(t-\varrho )], \\ \frac{d^{0.8}u_{3}}{dt^{0.8}}=4+a_{1}u_{1}u_{2}. \end{cases} $$
(4.1)

Clearly, system (4.1) possesses the equilibrium point \((-1.4949, 1.4949, 0.5587)\). Let \(\kappa _{1}=\kappa _{2}=1\). Then the critical frequency \(\phi _{0}=0.3944\) and the bifurcation point \(\varrho _{0}= 1.1844\). Then all the conditions (\({\mathcal {A}}\)1)–(\({ \mathcal {A}}\)3) of Theorem 3.1 hold true. Figure 2 reveals that the equilibrium point \((-1.4949, 1.4949, 0.5587)\) of system (4.1) is locally asymptotically stable for \(\varrho \in [0, 1.1844)\). Figure 3 manifests that system (4.1) loses its stability and a Hopf bifurcation takes place when \(\varrho \in [1.1844,+\infty )\). The relationship of the three parameters p, \(\phi _{0}\) and \(\varrho _{0}\) of (4.1) is clearly presented in Table 1.

Figure 2
figure 2

\(\varrho =1.15<\varrho _{0}= 1.1844\). Time history plots, variable relation plots and phase diagrams of system (4.1). The equilibrium point \((-1.4949, 1.4949, 0.5587)\) of system (4.1) is asymptotically stable

Full size image
Figure 3
figure 3

\(\varrho =1.2677>\varrho _{0}= 1.1844\). Time history plots, variable relation plots and phase diagrams of system (4.1). A Hopf bifurcation of system (4.1) takes place around the equilibrium point \((-1.4949, 1.4949, 0.5587)\)

Full size image
Table 1 The relation of the three parameters p, \(\phi _{0}\), \(\varrho _{0}\) of (4.1)
Full size table

5 Conclusions

In this article, based on earlier studies, we propose a new fractional-order financial model. By designing a suitable time-delayed feedback controller, the chaotic behavior of the fractional-order financial model has been controlled. By adding the linear time-delayed feedback controller to both equations of fractional-order financial model and choosing the time delay as bifurcation parameter, we establish the sufficient conditions ensuring the stability and the existence of a Hopf bifurcation of a controlled fractional-order financial model. The investigation reveals that the equilibrium point of the involved system is locally asymptotically stable when the delay remains in an appropriate value, while the system will lose its stability and a Hopf bifurcation will occur when the delay exceeds the critical value. The study also shows that fractional-order and time delay have an important influence on the stability and the Hopf bifurcation of the controlled fractional-order financial model. The obtained results can help us grasp the laws of finance and interpret economical phenomena in theory.