1 Introduction

The classical KdV equation is a nonlinear partial differential equation to model waves on shallow water surfaces that was established by Korteweg and de Vries in 1895. This exactly solvable model has been the topic of many research works. Nowadays, unique applications of the classical KdV equation have been suggested by many scholars as it can be used to describe long internal waves in a density-stratified ocean, ion-acoustic waves in a plasma, and acoustic waves on a crystal lattice. The mathematical form of the classical KdV equation is given by [1]

$$ u_{t} + \alpha _{1} u_{xxx} + \alpha _{2} u u_{x} =0. $$

There are different variations of the classical KdV equation, some of those reported in the literature are [2, 3]:

$$\begin{aligned}& u_{t} + \alpha _{1} u_{xxx} + \alpha _{2} u^{2} u_{x} =0,\quad ( \text{modified KdV} ), \\& u_{t} + \alpha _{1} u_{xxx} + \alpha _{2} u^{n} u_{x} =0,\quad ( \text{generalized KdV} ), \end{aligned}$$

and the \((2 + 1)\)-dimensional KdV equation

$$ \textstyle\begin{cases} u_{t} - u_{xxx} +3 ( uv )_{x} =0,\\ u_{x} - v_{y} =0. \end{cases} $$

Many efforts have been devoted to studying the KdV-type equations, for example, Wazwaz [2] used different reliable methods to obtain solitons and periodic solutions of the KdV, modified KdV, and generalized KdV equations, and Wang [3] derived lump solutions of the \((2 + 1)\)-dimensional KdV equation by means of an ansatz based on the quadratic functions. Recently, the fractional forms of the KdV-type equations have been explored using a series of systematic methods in [4, 5].

Our aim of this paper is studying a new \((2 + 1)\)-dimensional mKdV equation involving the Caputo–Fabrizio time-fractional derivative as follows:

$$ {}_{0}^{\mathrm{CF}} D_{t}^{\alpha } u=6 u^{2} u_{x} -6 u^{2} u_{y} + u_{xxx} - u_{yyy} -3 u_{xxy} +3 u_{xyy},\quad 0< \alpha \leq 1, $$
(1)

through a systematic technique called the homotopy analysis transform method [6–11]. The classical form of the new 2D-mKdV Eq. (1) was first proposed by Wang and Kara [12] in 2019 using the extended Lax pair. Wang and Kara in [12] extracted a group of solitary wave solutions of the new 2D-mKdV equation (its classical form) through the Lie symmetry method.

Recently, nonlinear ODEs/PDEs involving the Caputo–Fabrizio fractional derivative have gained significant attention owing to their potential to describe many complicated physical phenomena. In this respect, Shah et al. [13] analyzed a nonlinear model of dengue fever disease with the CF fractional derivative using the Laplace Adomian decomposition method. Owolabi and Atangana [14] explored a series of nonlinear fractional parabolic differential equations involving the CF derivative thought a numerical scheme. In another work performed by Arshad et al. [15], the CD4+ T-cells model of HIV infection with the CF fractional derivative was studied using an effective numerical scheme. Shaikh et al. [16] employed the iterative Laplace transform method to analyze a group of fractional reaction-diffusion equations involving the CF derivative. More articles can be found in [17–45].

The rest of this paper is as follows: In Sect. 2, the Caputo–Fabrizio fractional operators are reviewed in detail. In Sect. 3, the Lipschitz condition for the kernel \(\psi (x,y, t;u)\) is proved, then the fixed-point theorem is formally applied to show the existence and uniqueness of the solution of the new 2D-mKdV equation involving the CF time-fractional derivative. In Sect. 4, an analytic approximation for the new 2D-mKdV equation involving the Caputo–Fabrizio time-fractional derivative is acquired using the HAT method. The results of this paper are summarized in the last section.

2 Basic definitions and features

This section presents the basic definitions and features of the Caputo–Fabrizio fractional operators. In this respect, first the Caputo–Fabrizio fractional derivative and integral are defined, then the Laplace transform of the Caputo–Fabrizio fractional derivative is given.

Definition 1

Suppose that \(u ( t ) \in H^{1} ( a,b )\), \(b>a\) and \(\alpha \in (0, 1]\). Then, the Caputo–Fabrizio fractional derivative of \(u ( t )\) of order α is given by [17]

$$ {}_{a}^{\mathrm{CF}} D_{t}^{\alpha } u ( t ) = \frac{M ( \alpha )}{1-\alpha } \int _{a}^{t} u ' ( \varepsilon ) e^{- \frac{\alpha }{1-\alpha } ( t-\varepsilon )} \,d\varepsilon , $$

where \(M ( \alpha )\) is a normalized function satisfying \(M ( 0 ) = M ( 1 ) =1\).

Definition 2

The Caputo–Fabrizio fractional integral of \(u ( t )\) of order α (\(\alpha \in (0, 1]\)) is given by [18]

$$ {}_{0}^{\mathrm{CF}} I_{t}^{\alpha } u ( t ) = \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} u ( t ) + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \int _{0}^{t} u ( \varepsilon ) \,d\varepsilon ,\quad t\geq 0. $$

Definition 3

The Laplace transform of \({}_{0}^{\mathrm{CF}} D_{t}^{\alpha } u ( t )\) is given as [17]

$$ \mathcal{L} \bigl[ {}_{0}^{\mathrm{CF}} D_{t}^{\alpha } u ( t ) \bigr] ( s ) = \frac{s \mathcal{L} [ u ( t ) ] ( s ) -u(0)}{s+\alpha ( 1-s )}, $$

and in the general case, we have

$$ \mathcal{L} \bigl[ {}_{0}^{\mathrm{CF}} D_{t}^{ ( \alpha +n )} u ( t ) \bigr] ( s ) = \frac{s^{n+1} \mathcal{L} [ u ( t ) ] ( s ) - s^{n} u(0)- s^{n-1} u ' (0)-\cdots - u^{ ( n )} (0)}{s+\alpha ( 1-s )}. $$

Theorem 1

The following Lipschitz condition holds for the Caputo–Fabrizio fractional derivative given in Definition 1:

$$ \bigl\Vert {}_{a}^{\mathrm{CF}} D_{t}^{\alpha } u ( t ) - {}_{a}^{\mathrm{CF}} D_{t}^{\alpha } v ( t ) \bigr\Vert \leq \lambda \bigl\Vert u ( t ) -v ( t ) \bigr\Vert . $$

Proof

In a similar manner as in [23], it is easy to show that

$$\begin{aligned} \bigl\Vert {}_{a}^{\mathrm{CF}} D_{t}^{\alpha } u ( t ) - {}_{a}^{\mathrm{CF}} D_{t}^{\alpha } v ( t ) \bigr\Vert &= \biggl\Vert \frac{M ( \alpha )}{1-\alpha } \int _{a}^{t} u ' ( \varepsilon ) e^{- \frac{\alpha }{1-\alpha } ( t-\varepsilon )} \,d\varepsilon - \frac{M ( \alpha )}{1-\alpha } \int _{a}^{t} v ' ( \varepsilon ) e^{- \frac{\alpha }{1-\alpha } ( t-\varepsilon )} \,d\varepsilon \biggr\Vert \\ &= \biggl\Vert \frac{M ( \alpha )}{1-\alpha } \biggl( \int _{a}^{t} u ' ( \varepsilon ) e^{- \frac{\alpha }{1-\alpha } ( t-\varepsilon )} \,d\varepsilon - \int _{a}^{t} v ' ( \varepsilon ) e^{- \frac{\alpha }{1-\alpha } ( t-\varepsilon )} \,d\varepsilon \biggr) \biggr\Vert \\ &= \biggl\Vert \frac{M ( \alpha )}{1-\alpha } e^{- \frac{\alpha }{1-\alpha } ( t-\varepsilon )} \biggl( \int _{a}^{t} \bigl( u ' ( \varepsilon ) - v ' ( \varepsilon ) \bigr) \,d\varepsilon \biggr) \biggr\Vert \\ &\leq \frac{M ( \alpha )}{1-\alpha } \mu e^{- \frac{\alpha }{1-\alpha } ( t-\alpha )} \bigl\Vert u ( t ) -v(t) \bigr\Vert \\ &=\lambda \bigl\Vert u ( t ) -v ( t ) \bigr\Vert . \end{aligned}$$

 □

3 The model and the existence and uniqueness of its solution

To start, let us consider

$$ \psi ( x,y,t;u ) =6 u^{2} u_{x} -6 u^{2} u_{y} + u_{xxx} - u_{yyy} -3 u_{xxy} + 3u_{xyy}. $$

This suggests that Eq. (1) can be rewritten as

$$ {}_{0}^{\mathrm{CF}} D_{t}^{\alpha } u ( x,y,t ) = \psi ( x,y,t;u ). $$
(2)

Applying the CF fractional integral to both sides of Eq. (2) results in

$$ u ( x,y,t ) -u ( x,y,0 ) = \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \psi ( x,y,t;u ) + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \int _{0}^{t} \psi ( x,y, \varepsilon ;u ) \,d \varepsilon . $$
(3)

In order to show that the kernel \(\psi ( x,y,t;u )\) satisfies the Lipschitz condition, we first consider bounded functions \(u(x,y, t)\) and \(v(x,y, t)\). Using the triangle property of norms, one can find

$$\begin{aligned}& \bigl\Vert \psi ( x,y,t;u ) -\psi ( x,y,t;v ) \bigr\Vert \\& \quad = \bigl\Vert \bigl( 6 u^{2} u_{x} -6 v^{2} v_{x} \bigr) - \bigl( 6 u^{2} u_{y} -6 v^{2} v_{y} \bigr) + ( u_{xxx} - v_{xxx} ) - ( u_{yyy} - v_{yyy} )\\& \qquad {} - ( 3 u_{xxy} -3 v_{xxy} ) +(3 u_{xyy} -3 v_{xyy} ) \bigr\Vert \\& \quad = \biggl\Vert 2 \frac{\partial }{\partial x} \bigl( u^{3} - \nu ^{3} \bigr) -2 \frac{\partial }{\partial y} \bigl( u^{3} - \nu ^{3} \bigr) + \frac{\partial ^{3}}{\partial x^{3}} ( u-v ) - \frac{\partial ^{3}}{\partial y^{3}} ( u-v ) \\& \qquad {}-3 \frac{\partial ^{3}}{\partial y\,\partial x^{2}} ( u-v ) +3 \frac{\partial ^{3}}{\partial y^{2} \,\partial x} ( u-v ) \biggr\Vert \\& \quad \leq 2 \biggl\Vert \frac{\partial }{\partial x} \bigl( u^{3} - \nu ^{3} \bigr) \biggr\Vert +2 \biggl\Vert \frac{\partial }{\partial y} \bigl( u^{3} - \nu ^{3} \bigr) \biggr\Vert + \biggl\Vert \frac{\partial ^{3}}{\partial x^{3}} ( u-v ) \biggr\Vert + \biggl\Vert \frac{\partial ^{3}}{\partial y^{3}} ( u-v ) \biggr\Vert \\& \qquad {} +3 \biggl\Vert \frac{\partial ^{3}}{\partial y\,\partial x^{2}} ( u-v ) \biggr\Vert + 3 \biggl\Vert \frac{\partial ^{3}}{\partial y^{2} \,\partial x} ( u-v ) \biggr\Vert \\& \quad \leq 2A \bigl\Vert u^{3} - \nu ^{3} \bigr\Vert +2B \bigl\Vert u^{3} - \nu ^{3} \bigr\Vert +C \Vert u-\nu \Vert +D \Vert u-\nu \Vert +3E \Vert u-\nu \Vert +3F \Vert u-\nu \Vert \\& \quad \leq (2A+2B) \bigl( \mu ^{2} +\mu \upsilon + \upsilon ^{2} \bigr) \Vert u-\nu \Vert +C \Vert u-\nu \Vert +D \Vert u-\nu \Vert +3E \Vert u-\nu \Vert +3F \Vert u-\nu \Vert \\& \quad = \bigl( ( 2A+2B ) \bigl( \mu ^{2} +\mu \upsilon + \upsilon ^{2} \bigr) +C+D+3E+3F \bigr) \Vert u-\nu \Vert ,\quad \Vert u \Vert \leq \mu , \Vert v \Vert \leq \upsilon . \end{aligned}$$

Therefore

$$ \bigl\Vert \psi ( x,y,t;u ) -\psi (x,y,t;v) \bigr\Vert \leq \lambda \Vert u-v \Vert , $$

which

$$ \lambda = \bigl( ( 2A+2B ) \bigl( \mu ^{2} +\mu \upsilon + \upsilon ^{2} \bigr) +C+D+3E+3F \bigr). $$

This confirms that the Lipschitz condition is satisfied for the kernel \(\psi ( x,y,t;u )\).

Now, based on the Eq. (3) and the fixed-point theorem, an iterative scheme is established as follows:

$$ u_{n+1} ( x,y,t ) = \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \psi ( x,y,t; u_{n} ) + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \int _{0}^{t} \psi ( x,y, \varepsilon ; u_{n} ) \,d\varepsilon , $$

where

$$ u_{0} ( x,y,t ) =u ( x,y,0 ). $$

It is clear that

$$\begin{aligned} e_{n} ( x,y,t )& = u_{n} ( x,y,t ) - u_{n-1} ( x,y,t ) \\ &= \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \bigl( \psi ( x,y,t; u_{n-1} ) -\psi ( x,y,t; u_{n-2} ) \bigr) \\ &\quad {}+ \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \int _{0}^{t} \bigl( \psi ( x,y,\varepsilon ; u_{n-1} ) -\psi ( x,y,\varepsilon ; u_{n-2} ) \bigr) \,d \varepsilon , \end{aligned}$$

and

$$ u_{n} ( x,y,t ) = \sum_{i=0}^{n} e_{i} ( x,y,t ). $$
(4)

Theorem 2

If the function\(u(x,y, t)\)is bounded, then

$$ \bigl\Vert e_{n} ( x,y,t) \bigr\Vert \leq \biggl( \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t \biggr)^{n} \bigl\Vert u ( x,y,0 ) \bigr\Vert . $$

Proof by induction

Suppose that \(n=1\). Then, one can write

$$\begin{aligned} \bigl\Vert e_{1} ( x,y,t ) \bigr\Vert &= \bigl\Vert u_{1} ( x,y,t ) - u_{0} ( x,y,t ) \bigr\Vert \\ &\leq \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \bigl\Vert \psi ( x,y,t; u_{0} ) -\psi ( x,y,t; u_{-1} ) \bigr\Vert \\ &\quad {}+ \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \int _{0}^{t} \bigl\Vert \psi ( x,y, \varepsilon ; u_{0} ) -\psi ( x,y, \varepsilon ; u_{-1} ) \bigr\Vert \,d \varepsilon \\ &\leq \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda \Vert u_{0} - u_{-1} \Vert + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \int _{0}^{t} \lambda \Vert u_{0} - u_{-1} \Vert \,d\varepsilon \\ &= \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda \bigl\Vert u ( x,y,0 ) \bigr\Vert + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \int _{0}^{t} \lambda \bigl\Vert u ( x,y,0 ) \bigr\Vert \,d\varepsilon \\ &= \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda \bigl\Vert u ( x,y,0 ) \bigr\Vert + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda \bigl\Vert u ( x,y,0 ) \bigr\Vert \int _{0}^{t} \,d\varepsilon \\ &= \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda \bigl\Vert u ( x,y,0 ) \bigr\Vert + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda \bigl\Vert u ( x,y,0 ) \bigr\Vert t \\ &= \biggl( \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t \biggr) \bigl\Vert u ( x,y,0 ) \bigr\Vert . \end{aligned}$$

Now, if the relation holds for \(n-1\), namely

$$ \bigl\Vert e_{n-1} ( x,y,t) \bigr\Vert \leq \biggl( \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t \biggr)^{n-1} \bigl\Vert u ( x,y,0 ) \bigr\Vert , $$

then, we will prove that

$$ \bigl\Vert e_{n} ( x,y,t) \bigr\Vert \leq \biggl( \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t \biggr)^{n} \bigl\Vert u ( x,y,0 ) \bigr\Vert . $$

To show this, we proceed as follows:

$$\begin{aligned} \bigl\Vert e_{n} ( x,y,t ) \bigr\Vert &= \bigl\Vert u_{n} ( x,y,t ) - u_{n -1} ( x,y,t ) \bigr\Vert \\ &\leq \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \bigl\Vert \psi ( x,y,t; u_{n -1} ) -\psi ( x,y,t; u_{n -2} ) \bigr\Vert \\ &\quad {}+ \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \int _{0}^{t} \bigl\Vert \psi ( x,y, \varepsilon ; u_{n -1} ) -\psi ( x,y, \varepsilon ; u_{n -2} ) \bigr\Vert \,d \varepsilon \\ &\leq \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda \Vert u_{n -1} - u_{n-2} \Vert + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \int _{0}^{t} \lambda \Vert u_{n -1} - u_{n-2} \Vert \,d\varepsilon \\ &= \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda \bigl\Vert e_{n-1} ( x,y,t) \bigr\Vert + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \int _{0}^{t} \lambda \bigl\Vert e_{n-1} ( x,y,\varepsilon ) \bigr\Vert \,d\varepsilon \\ &= \biggl( \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t \biggr)^{n-1} \bigl\Vert u ( x,y,0 ) \bigr\Vert \\ &\quad {}\times \biggl( \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda \int _{0}^{t} \,d\varepsilon \biggr) \\ &= \biggl( \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t \biggr)^{n-1} \\ &\quad {}\times\biggl( \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t \biggr) \bigl\Vert u ( x,y,0 ) \bigr\Vert \\ &= \biggl( \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t \biggr)^{n} \bigl\Vert u ( x,y,0 ) \bigr\Vert . \end{aligned}$$

 □

Theorem 3

If at\(t= t_{0}\)we have

$$ 0\leq \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t_{0} < 1, $$

then the solution of the new 2D-mKdV equation involving the CF time-fractional derivative exists.

Proof

Based on Eq. (4), one can write

$$\begin{aligned} \bigl\Vert u_{n} ( x,y,t ) \bigr\Vert &\leq \sum _{i=0}^{n} \bigl\Vert e_{i} ( x,y,t ) \bigr\Vert \\ &\leq \sum_{i=0}^{n} \biggl( \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t \biggr)^{i} \bigl\Vert u ( x,y,0 ) \bigr\Vert . \end{aligned}$$

For \(t= t_{0}\), one obtains

$$ \bigl\Vert u_{n} ( x,y,t ) \bigr\Vert \leq \bigl\Vert u ( x,y,0 ) \bigr\Vert \sum_{i=0}^{n} \biggl( \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t_{0} \biggr)^{i}. $$

Consequently,

$$ \lim_{n\rightarrow \infty } \bigl\Vert u_{n} ( x,y,t ) \bigr\Vert \leq \bigl\Vert u ( x,y,0 ) \bigr\Vert \sum_{i=0}^{\infty } \biggl( \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t_{0} \biggr)^{i}. $$

Since

$$ 0\leq \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t_{0} < 1, $$

the above series is convergent, and therefore, \(u_{n} ( x,y,t )\) exists and is bounded for any n.

Besides, by assuming

$$ R_{n} ( x,y,t ) =u ( x,y,t ) - u_{n} (x,y,t), $$

one can easily prove that

$$ \bigl\Vert R_{n} ( x,y,t ) \bigr\Vert \leq \biggl( \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t_{0} \biggr)^{n+1} \mu , $$

and so

$$ \lim_{n\rightarrow \infty } \bigl\Vert R_{n} ( x,y,t ) \bigr\Vert \leq \lim_{n\rightarrow \infty } \biggl( \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t_{0} \biggr)^{n+1} \mu . $$

But

$$ 0\leq \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t_{0} < 1, $$

thus

$$ \lim_{n\rightarrow \infty } \bigl\Vert R_{n} ( x,y,t ) \bigr\Vert =0\quad \text{or} \quad \lim_{n\rightarrow \infty } u_{n} (x,y,t) =u ( x,y,t ). $$

 □

Theorem 4

If at\(t= t_{0}\)we have

$$ 0\leq \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t_{0} < 1, $$

then the solution of the new 2D-mKdV equation involving the CF time-fractional derivative is unique.

Proof by contradiction

To start, let us consider two solutions, say \(u ( x,y,t )\) and \(v ( x,{y}, t )\), for the model (1). One can write

$$\begin{aligned}& \begin{aligned} u ( x,y,t ) -v ( x,y,t ) &= \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \bigl( \psi ( x,y,t;u ) -\psi ( x,y,t;v ) \bigr) \\ &\quad {}+ \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \int _{0}^{t} \bigl( \psi ( x,y, \varepsilon ;u ) - \psi ( x,y, \varepsilon ;v ) \bigr) \,d\varepsilon . \end{aligned} \end{aligned}$$

Consequently,

$$\begin{aligned} \bigl\Vert u ( x,y,t ) -v ( x,y,t ) \bigr\Vert &\leq \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \bigl\Vert \psi ( x,y,t;u ) -\psi ( x,y,t;v ) \bigr\Vert \\ &\quad {}+ \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \int _{0}^{t} \bigl\Vert \psi ( x,y, \varepsilon ;u ) -\psi ( x,y, \varepsilon ;v ) \bigr\Vert \,d\varepsilon \\ &\leq \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda \Vert u-v \Vert + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \int _{0}^{t} \lambda \Vert u-v \Vert \,d \varepsilon \\ &= \biggl( \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda \int _{0}^{t} \,d\varepsilon \biggr) \Vert u-v \Vert \\ &= \biggl( \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t \biggr) \Vert u-v \Vert . \end{aligned}$$

But

$$ 0\leq \frac{2 ( 1-\alpha )}{ ( 2-\alpha ) M(\alpha )} \lambda + \frac{2\alpha }{ ( 2-\alpha ) M(\alpha )} \lambda t_{0} < 1, $$

therefore

$$ \bigl\Vert u(x,y,t)-v(x,y,t) \bigr\Vert =0, $$

and so, the solution of the new 2D-mKdV equation involving the CF time-fractional derivative is unique. □

4 The new CF time-fractional 2D-mKdV equation and its analytical solutions

In the present section, first soliton solutions of the classical form of the model are extracted using an ansatz method, then the HAT method is used to acquire an analytic approximation for the new CF time-fractional 2D-mKdV equation.

4.1 Soliton solutions of the classical form of the model

To find soliton solutions, a test function is considered as follows:

$$ u(x,y,t)= A_{0} + A_{1} \operatorname{sech} ( \alpha _{1} x+ \alpha _{2} y+ \alpha _{3} t ). $$

By substituting the above function into the classical form of the model, we obtain a nonlinear algebraic system as follows:

$$\begin{aligned}& 6 A_{0}^{2} \alpha _{1} -6 A_{0}^{2} \alpha _{2} + \alpha _{1}^{3} -3 \alpha _{1}^{2} \alpha _{2} +3 \alpha _{2}^{2} \alpha _{1} - \alpha _{2}^{3} - \alpha _{3} =0, \\& 12 A_{0} A_{1} \alpha _{1} -12 A_{0} A_{1} \alpha _{2} =0, \\& 6 A_{1}^{2} \alpha _{1} -6 A_{1}^{2} \alpha _{2} -6 \alpha _{1}^{3} +18 \alpha _{1}^{2} \alpha _{2} -18 \alpha _{2}^{2} \alpha _{1} +6 \alpha _{2}^{3} =0, \end{aligned}$$

whose solution yields

$$ A_{0} =0, A_{1} =\mp \alpha _{1} \pm \alpha _{2}, \alpha _{3} = \alpha _{1}^{3} -3 \alpha _{1}^{2} \alpha _{2} +3 \alpha _{2}^{2} \alpha _{1} - \alpha _{2}^{3}. $$

Now, the following soliton solutions to the classical form of the model (1) can be constructed:

$$ u_{1,2} (x,y,t)= ( \mp \alpha _{1} \pm \alpha _{2} ) \operatorname{sech} \bigl( \alpha _{1} x+ \alpha _{2} y+ \bigl( \alpha _{1}^{3} -3 \alpha _{1}^{2} \alpha _{2} +3 \alpha _{2}^{2} \alpha _{1} - \alpha _{2}^{3} \bigr) t \bigr). $$

For \(\alpha _{1} =1\) and \(\alpha _{2} =-1\), the above solitons are reduced to

$$ u_{1,2} (x,y,t)= \mp 2 \operatorname{sech} ( x-y+8t ) =\mp 4 \frac{e^{x-y+8t}}{1+ e^{2 ( x-y+8t )}}. $$

4.2 The model and its analytic approximation

To obtain an analytic approximation, we apply the Laplace transform to both sides of Eq. (1). Such an operation results in

$$ \begin{aligned}[b] &\mathcal{L} \bigl[ u ( x,y,t ) \bigr] - \frac{u ( x,y,0 )}{s} - \biggl( \frac{s+\alpha ( 1-s )}{s} \biggr) \mathcal{L} \bigl[ 6 u^{2} ( x,y,t ) u_{x} ( x,y,t )\\ &\quad {} -6 u^{2} ( x,y,t ) u_{y} ( x,y,t ) + u_{xxx} ( x,y,t ) - u_{yyy} ( x,y,t )\\ &\quad {} -3 u_{xxy} ( x,y,t ) +3 u_{xyy} ( x,y,t ) \bigr] =0. \end{aligned} $$
(5)

Based on Eq. (5), the nonlinear operator can be defined as

$$ \begin{aligned} \varOmega \bigl[ \phi ( x,y,t;p ) \bigr] &=\mathcal{L} \bigl[ \phi ( x,y,t;p ) \bigr] - \frac{u_{0} ( x,y,t )}{s} \\ &\quad {}- \biggl( \frac{s+\alpha ( 1-s )}{s} \biggr) \mathcal{L} \bigl[ 6 \phi ^{2} ( x,y,t;p ) \phi _{x} ( x,y,t;p ) \\ &\quad {}-6 \phi ^{2} ( x,y,t;p ) \phi _{y} ( x,y,t;p ) + \phi _{xxx} ( x,y,t;p ) - \phi _{yyy} ( x,y,t;p ) \\ &\quad {}-3 \phi _{xxy} ( x,y,t;p ) +3 \phi _{xyy} ( x,y,t;p ) \bigr] \\ &=0. \end{aligned} $$

Now, the following mth order deformation equation is considered:

$$ \mathcal{L} \bigl[ u_{m} ( x,y,t ) - \chi _{m} u_{m-1} ( x,y,t ) \bigr] =h \mathcal{R}_{m} ( \vec{u}_{m-1} ), $$

where

$$ \mathcal{R}_{m} ( \vec{u}_{m-1} ) = \frac{1}{ ( m-1 ) !} \frac{\partial ^{m-1} \varOmega [ \phi ( x,y,t;p ) ]}{\partial p^{m-1}} \bigg\vert _{p=0} , $$

and

$$ \chi _{m} = \textstyle\begin{cases} 0& m \leq 1,\\ 1& m >1. \end{cases} $$

It is worth mentioning that by selecting

$$ u ( x,y,0 ) =- 4 \frac{e^{x-y}}{1+ e^{2 ( x-y )}} $$

and solving the resulting equations, one obtains

$$\begin{aligned}& u_{0} ( x,y,t ) = -4 \frac{e^{x-y}}{1+ e^{2 ( x-y )}}, \\& u_{1} ( x,y,t ) =-32 \frac{h e^{x-y} ( \alpha e^{2 ( x-y )} t-\alpha e^{2 ( x-y )} + e^{2 ( x-y )} -\alpha t+\alpha -1 )}{ ( e^{2 ( x-y )} +1 )^{2}}, \\& \vdots \end{aligned}$$

Therefore, the series solution of the new CF time-fractional 2D-mKdV equation is derived as

$$ u ( x,y,t ) = -4 \frac{e^{x-y}}{1+ e^{2 ( x-y )}} -32 \frac{h e^{x-y} ( \alpha e^{2 ( x-y )} t-\alpha e^{2 ( x-y )} + e^{2 ( x-y )} -\alpha t+\alpha -1 )}{ ( e^{2 ( x-y )} +1 )^{2}} +\cdots . $$

It is noteworthy that for \(\alpha =1\) and \(h=-1\), the above series converges to the following exact solution:

$$ u ( x,y,t ) =-4 \frac{e^{x-y+8t}}{1+ e^{2 ( x-y+8t )}}. $$

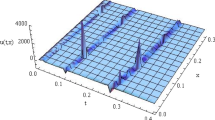
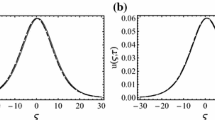
Figure 1 presents the 3-order approximation of the new CF time-fractional 2D-mKdV equation for \(\alpha =1, 0.99, \text{ and } 0.98\) against the exact solution. From this figure, a full agreement between the 3-order approximation (when \(\alpha =1\)) and the exact solution is obviously observed. The absolute error of the 3-order approximation (when \(\alpha =1\)) and the exact solution has been presented in Table 1. The results confirm the efficiency of the HAT method in deriving an analytic approximation with high accuracy. Finally, Fig. 2 shows the 3D plots of the exact solution and the 3-order approximation for \(\alpha =1, 0.99, \text{ and } 0.98\).

Figure 1
figure 1

The 3th order approximation against the exact solution (a) \(y=0.5\), \(t=0.01\), \(h=-1\), and \(\alpha =1, 0.99, \text{ and } 0.98\); (b) \(x=0.5\), \(t=0.01\), \(h=-1\), and \(\alpha =1, 0.99, \text{ and } 0.98\)

Full size image
Figure 2
figure 2

(a) The exact solution for \(t=0.01\) against (b, c, d) the 3-order approximation when (b) \(t=0.01\), \(h=-1\), and \(\alpha =1\); (c) \(t=0.01\), \(h=-1\), and \(\alpha =0.99\); (d) \(t=0.01\), \(h=-1\), and \(\alpha =0.98\)

Full size image
Table 1 The absolute error of the 3-order approximation and the exact solution
Full size table

It is believed that the analytic approximation given by the HAT method can precisely predict the dynamics of the dark soliton solution of the new 2D-mKdV equation involving the CF time-fractional derivative.

5 Conclusion

A thorough study on a nonlinear model involving the Caputo–Fabrizio time-fractional derivative was carried out successfully in the current paper. In this respect, a new 2D-mKdV equation designed with the CF time-fractional derivative was considered, and an analytic approximation for it was formally derived using a systematic approach, named the homotopy analysis transform method. The existence and uniqueness of the solution of the new 2D-mKdV equation involving the Caputo–Fabrizio time-fractional derivative were studied by proving the Lipschitz condition for the kernel \(\psi ( x, y, t; u )\) and applying the fixed-point theorem. A detailed study was finally accomplished to investigate the effect of the Caputo–Fabrizio operator on the dynamics of the obtained analytic approximation. The results presented herein confirm the efficiency of the HAT method in deriving an analytic approximation with high accuracy for nonlinear models involving the Caputo–Fabrizio time-fractional derivative. Our future work is to obtain an analytic approximation of the new 2D-mKdV equation with the Atangana–Baleanu time-fractional derivative and study the effect of the Atangana–Baleanu operator on the dynamics of the approximate solution.