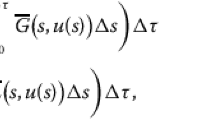Study on the estimates of Gronwall–Ou-Iang dynamic integral inequalities by means of diamond-α derivatives

Abstract

By the utilization of diamond-α derivatives, certain new generalizations of Ou-Iang type of dynamic integral inequalities of one independent variable on time scales are examined. The resulting inequalities are significant in the study of various fields of dynamic equations. A few mathematical applications are also presented.

1 Introduction

Integral inequalities have an extraordinarily advantageous position in strengthening the traditional differential and integral equations hypotheses. Gronwall [10] discussed the integral inequality

$$ y(v)\leq c+ \int _{a}^{v}f(\tau )y(\tau )\,d\tau ,\quad v\in [a,b], $$

for some $c\geq 0$. Ou-Iang inequalities and their subsequent developments have demonstrated to be valuable devices in the concept of stability, oscillation, and boundedness and in different fields of differential and integral equations. Like Gronwall’s inequality, Ou-Iang’s inequality is additionally utilized to obtain an explicit bound of unknown functions. An introduction to continuous and discrete OuIang inequalities can be found in [26, 27], and in [1, 7, 8, 13, 14, 24] one finds generalizations to numerous integrals. Pachpatte [19] introduced the following integral inequality:

$$ y^{2}(v)\leq c^{2}+2 \int _{0}^{v} \bigl[f(\tau )y^{2}(\tau )+g(\tau )y( \tau ) \bigr]\,d\tau , $$

c is a nonnegative constant and $v\in \mathbb{R}_{+}$.

It is noteworthy that the dynamic inequalities assume the role of a necessary key in the improvement of the subjective concept of dynamic equations on time scales. Hilger [12] started the advancement of analysis of time scales. The general impression is to show an equation for a dynamic equation or a dynamic inequality where the domain of the unknown function is supposed to be a time scale $\mathbb{T}$. The motivation behind the hypothesis of time scales is to unify continuous and discrete investigation. In the course of recent years, many authors completed an exhaustive examination of the properties and usage of various sorts of these types of inequalities on time scale; see [2, 3, 5, 9, 16–18, 23, 25] and the references therein. Bohner et al. [4] inspected the integral inequality on time scales of the kind

$$ y(v)\leq a(v)+p(v) \int _{v_{0}}^{v} \bigl[b(\tau )y(\tau )+q(\tau ) \bigr] \Delta \tau . $$

Consequently in 2010, Li [15] tested the subsequent nonlinear integral inequality of one independent variable associated with time scales

$$ y^{\gamma }(v)\leq a(v)+c(v) \int _{v_{0}}^{v} \bigl[f(\tau )y\bigl(\rho ( \tau ) \bigr)+n(\tau ) \bigr]\Delta \tau , $$

for $v\in v_{0}$ with initial conditions $y(v)=\varOmega (v)$, $v\in [\beta ,v_{0}]\cap \mathbb{T}$, $\varUpsilon (\rho (v))\leq (a(v))^{\frac{1}{\gamma }}$ for $v\in v_{0}$, $\rho (v)\leq v_{0}$, where $\gamma \geq 1$ is a constant, $\rho (v)\leq v$, $-\infty <\beta =\inf \{ \rho (v),v\in \mathbb{T}_{0} \} \leq v_{0}$ and $\varOmega (v)\in C_{\mathrm{rd}}([\beta ,v_{0}]\cap \mathbb{T},\mathbb{R}_{+})$. Meanwhile, Pachpatte [20] stepped forward to discover the extension of the integral inequality of the form

$$ y(v)\leq a(v)+ \int _{v_{0}}^{v} f(\tau ) \biggl[y(\tau )+ \int _{v_{0}}^{ \tau }m(\tau ,\sigma )y(\sigma )\Delta \sigma \biggr]\Delta \tau , $$

such that $m(\tau ,\sigma )\geq 0$, $m^{\Delta }(\tau ,\sigma )\geq 0$ for $v,\sigma \in \mathbb{T}$ and $\sigma \leq v$. Later, Haidong [11] proposed the generalization of the nonlinear integral inequality as follows:

$$\begin{aligned} y(v)&\leq a(v)+b(v) \int _{\alpha (v_{0})}^{\alpha (v)} \biggl[f_{1}(s)y(s)+f_{2}(s) \int _{\alpha (v_{0})}^{s}g(\tau )y(\tau )\Delta \tau \biggr] \Delta s \\ &\quad{} +\lambda b(T) \int _{\alpha (v_{0})}^{\alpha (T)} \biggl[f_{1}(s)y(s)+f_{2}(s) \int _{\alpha (v_{0})}^{s}g(\tau )y(\tau )\Delta \tau \biggr] \Delta s, \end{aligned}$$

where $\lambda \geq 0$. Despite the fact that diamond-α derivatives cannot be identified as a standard derivative due to the absence of an antiderivative [21], its powerful distinct-alike pattern allows for accessibility in computational situations. Although there has been done much work on the integral inequalities related to the delta derivative or the nabla derivative, yet we do not carry out any significant research of integral inequalities based on diamond-α derivatives on time scales. In view of the work listed above and utilizing a similar setting to Gronwall–Bellman type inequalities, in this paper, we generalize and sum up the accompanying nonlinear integral inequalities of one variable by virtue of diamond alpha derivatives on time scales. The obtained results are useful to investigate the qualitative properties of different issues of certain classes of integral equations and evolution equations.

2 Basics on diamond-α derivatives and integrals

In what follows, denote $\mathbb{R}_{+}=[0,\infty )$. A time scale $\mathbb{T}$ is a nonempty closed subset of the real line $\mathbb{R}$. For $v\in \mathbb{T}$, the forward and backward jump operators $\varpi , \varsigma :\mathbb{T}\rightarrow \mathbb{T}$ are defined by $\varpi (v)=\inf (v,\infty )_{\mathbb{T}}$, and $\varsigma (v)=\sup (-\infty ,v)_{\mathbb{T}}$ simultaneously, whereas the forward and backward graininess functions $\varrho , \chi :\mathbb{T}\rightarrow [0,\infty )$ are defined by $\varrho (v)=\varpi (v)-v$ and $\chi (v)=v-\varsigma (v)$, respectively. We have the set $\mathbb{T}^{k}=\mathbb{T}/(\varsigma (\sup \mathbb{T}),\mathbb{T}]$ and the set $\mathbb{T}_{k}=\mathbb{T}/[\inf \mathbb{T},\varpi (\inf \mathbb{T}))$. A function $p:\mathbb{T}\rightarrow \mathbb{R}$ is called regressive and ℜ defines the set of all regressive and rd-continuous functions if $1+\varrho (v)p(v)\neq 0$ for $v\in \mathbb{T}^{k}$. Also a function $q:\mathbb{T}\rightarrow \mathbb{R}$ is known as v-regressive provided $1-\chi (v)q(v)\neq 0$ for $v\in \mathbb{T}_{k}$ and $\Re _{v}$ are the set of all v-regressive and ld-continuous functions. The delta derivative of the function $j :\mathbb{T} \rightarrow \mathbb{R}$, denoted by $j^{\Delta }(t)$ is

$$ \bigl\vert j\bigl(\varpi (v)\bigr)-j(n)-j^{\Delta }(v) \bigl(\varpi (v)-n \bigr) \bigr\vert \le \epsilon \bigl\vert \varpi (v)-n \bigr\vert , \quad \forall \epsilon >0, $$

for $v\in \mathbb{T}^{k}$ with $n\in \aleph$ where ℵ is a neighborhood of v and the nabla derivative of j, defined by $j^{\nabla }(v)$ is

$$ \bigl\vert j(n)-j\bigl(\varsigma (v)\bigr)-j^{\nabla }(v) \bigl(n- \varsigma (v)\bigr) \bigr\vert \le \epsilon \bigl\vert n-\varsigma (v) \bigr\vert , \quad \forall \epsilon >0, $$

for $v\in \mathbb{T}_{k}$ such that $n\in \varLambda$ and Λ is a neighborhood of v. Similarly we have the $\diamond _{\alpha }$-derivative of n at $v\in \mathbb{T}_{k}^{k}$, denoted by $n^{\diamond _{\alpha }}(v)$ for all $\epsilon >0$, and there is a neighborhood $\aleph \subset \mathbb{T}$, for any $n\in \aleph$,

$$\begin{aligned}& \bigl\vert \alpha \bigl[ j\bigl(\varpi (v)\bigr)-j(n) \bigr] \bigl[ \varsigma (v)-n \bigr] +(1+\alpha ) \bigl[ j\bigl(\varsigma (v) \bigr)-j(n) \bigr]\bigl[\varpi (v)-n \bigr] \\& \quad\quad{} -n^{\diamond _{\alpha }}(v) \bigl[\varsigma (v)-n \bigr] \bigl[ \varpi (v)-n \bigr]\bigr\vert \\& \quad \leq \epsilon \bigl\vert \varsigma (v)-n \bigr\vert \bigl\vert \varpi (v)-n \bigr\vert . \end{aligned}$$

The function $e_{p}(v,v_{0})=\exp (\int _{v_{0}}^{v}\xi _{\varrho (\tau )}(p( \tau ))\Delta \tau )$ stands for the Δ-exponential function where $p\in \Re$ and the cylinder transformation is $\varepsilon _{h}(z)=\frac{1}{h}\log (1+zh)$, log is the principal logarithm function. Analogously, the ∇-exponential function is defined by $e^{\wedge }_{p}(v,v_{0})=\exp (\int _{v_{0}}^{v}\xi ^{\wedge }_{\chi }(\tau )(p(\tau ))\nabla \tau )$, $p\in \Re _{v}$ and the v-cylinder transformation is $\varepsilon ^{\wedge }_{h}(z)=-\frac{1}{h}\log (1-zh)$. In addition, ${}_{\alpha }e_{p}(v_{0},v)=\exp (\alpha \int _{v_{0}}^{v}\xi _{ \varrho (\tau )}(p(\tau ))\Delta \tau +(1-\alpha )\int _{v_{0}}^{v} \xi ^{\wedge }_{\chi }(\tau )(p(\tau ))\nabla \tau )$, which is a combination of the Δ and ∇ exponential functions. $C_{\mathrm{rd}}(\mathbb{T},\mathbb{R})$ denotes the class of real rd-continuous functions defined on a time scale $\mathbb{T}$. If $j\in C_{\mathrm{rd}}(\mathbb{T},\mathbb{R})$ is rd-continuous, i.e. it is continuous at right-dense points and left-sided limits exist at left-dense points in $\mathbb{T}$, then there exists a function $J(v)$ such that $J^{\Delta }(v)=j(v)$. The delta integral is defined by $\int _{a}^{b}j(v)\Delta v=J(b)-J(a)$. A function $m:\mathbb{T}\rightarrow \mathbb{R}$ is ld-continuous if it is continuous at left-dense points and right-sided limits exist at right-dense points in $\mathbb{T}$; the class of real ld-continuous functions on a time scale $\mathbb{T}$ is denoted by $C_{\mathrm{ld}}(\mathbb{T},\mathbb{R})$. If $m\in C_{\mathrm{ld}}(\mathbb{T},\mathbb{R})$, then there exists a function $M(v)$ such that $M^{\nabla }(v)=m(v)$. The nabla integral is denoted $\int _{a}^{b}m(v)\nabla v=M(b)-M(a)$. For the general primary ideas and background of time scale analysis, we refer to a book by Bohner et al. [6].

Presently, on time scales, we declare the essential lemmas that will be used later in the verifications of the paper.

Lemma 2.1

([22])

Let$r, v\in \mathbb{T}$. If the left-sided limits of$j:\mathbb{T}\rightarrow \mathbb{R}$exist at left-dense points and the right-sided limits of the function exist at right-dense points in$\mathbb{T}$, then$\int _{a}^{v}j(\tau )\diamond _{\alpha }(\tau )$is$\diamond _{\alpha }$-differentiable on$\mathbb{T}$, and

$$ \biggl( \int _{r}^{v}j(\tau )\diamond _{\alpha }(\tau ) \biggr)^{ \diamond _{\alpha }}=\bigl(1-2\alpha +2\alpha ^{2}\bigr)j(v)+\bigl( \alpha -\alpha ^{2}\bigr)j\bigl( \varpi (v)\bigr)+\bigl(\alpha -\alpha ^{2}\bigr)j\bigl(\varsigma (v)\bigr). $$

3 Results and discussion

The statements of our main results are as follows.

Lemma 3.1

Let$r,q\in \mathbb{T}$where$\mathbb{T}$be a regulated time scale subject to$\varpi (r)=r$. Further, $k \in C^{l}([r,q]_{\mathbb{T}},\mathbb{R})$with$k^{\Delta }(v), k^{\nabla }(v)\geq 0$and$b\in C(\mathbb{R}_{+}, \mathbb{R}_{+})$is a positive and non-decreasing function so that$H(u)=\int _{u_{0}}^{u}\frac{d\varOmega }{b(\varOmega )}<\infty$, $u_{0}>0$, $u\geq 0$, and if$H(u)=\int _{0}^{u}\frac{d\varOmega }{b(\varOmega )}=\infty$then

$$ (H\circ k) (v)\leq 2(H\circ k) (r)+2 \int _{r}^{v} \frac{k^{\diamond _{\alpha }}(\varOmega )}{b(k(\varsigma (\varOmega )))}, \quad v\in [r,q]_{\mathbb{T}}. $$

Proof

Clearly

$$ \frac{1}{b(k(\varsigma (v))+hz(v)k^{\nabla }(v))}\leq \frac{1}{b(k(\varsigma (v)))} $$

and

$$ \frac{1}{b(k(v)+h\varrho (v)k^{\Delta }(v))}\leq \frac{1}{b(k(v))}; $$

for $\alpha \in (0,1)$, we get

$$\begin{aligned}& \alpha k^{\Delta }(v) \int _{0}^{1} \frac{dh}{b(k(v)+h\varrho (v)k^{\Delta }(v))}+(1-\alpha )k^{\nabla }(v)) \int _{0}^{1}\frac{dh}{b(k(\varsigma (v))+hz(v)k^{\nabla }(v))} \\& \quad \leq \alpha \frac{k^{\Delta }(v)}{b(k(v))}+(1-\alpha ) \frac{k^{\nabla }(v)}{b(k(\varsigma (v)))} \end{aligned}$$

and

$$ (H\circ K)^{\diamond _{\alpha }}(v)\leq \frac{k^{\diamond _{\alpha }}(v)}{b(k(\varsigma (v)))}; $$

by [3, 22], and the assumption of r, we have

$$ \frac{1}{2}(H\circ k) (v)\leq (H\circ k) (r)+ \int _{r}^{v} \frac{k^{\diamond _{\alpha }}(\varOmega )}{b(k(\varsigma (\varOmega )))}. $$

 □

Theorem 3.2

Assume that the function$y(v)\in C([r,q]_{\mathbb{T}},\mathbb{R}_{+})$for all$v\in [r,q]_{\mathbb{T}}$. $\mathbb{T}$is regulated with$\varpi (r)=r$. Moreover, let$b,d,s\in C([r,q]_{\mathbb{T}},\mathbb{R}_{+})$be nonnegative functions and the relation

$$ y^{2}(v)\leq j^{2}+2 \int _{r}^{v}b(\tau ) \biggl[y^{2}(\tau )+ \int _{r}^{ \tau }d(\vartheta )y^{2}(\vartheta )\diamond _{\alpha }\vartheta \biggr]\diamond _{\alpha }\tau +2 \int _{r}^{v}s(\tau )y(\tau ) \diamond _{\alpha }\tau , $$

(1)

be satisfied for some$j>0$. Then there exist fixed constantsl, nsuch that

$$\begin{aligned} y(v)&\leq 4j+2l \int _{r}^{v_{0}} \bigl[\bigl(1-2\alpha +2\alpha ^{2}\bigr)s(\tau )+\bigl( \alpha -\alpha ^{2}\bigr)s\bigl( \varsigma (\tau )\bigr)+\bigl(\alpha -\alpha ^{2}\bigr)s\bigl( \varpi (v)\bigr) \bigr]\diamond _{\alpha }\tau \\ &\quad{} +2 \int _{r}^{v} \bigl[ \bigl[2l\bigl(1-2\alpha +2 \alpha ^{2}\bigr)^{2}+4l\bigl(\alpha - \alpha ^{2} \bigr)^{2} \bigr]b(\tau ) \\ &\quad{}+4l\bigl(1-2\alpha +2\alpha ^{2} \bigr) \bigl(\alpha - \alpha ^{2}\bigr)b\bigl(\varsigma (\tau )\bigr) \\ &\quad{} +4l\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi (\tau )\bigr)+2l\bigl( \alpha -\alpha ^{2}\bigr)b\bigl(\varpi ^{2}(v)\bigr) \\ &\quad{}+2l\bigl(\alpha -\alpha ^{2}\bigr)b\bigl( \varsigma ^{2}(\tau )\bigr) \bigr] \\ &\quad{}\times \biggl[2j+l \int _{r}^{\tau _{0}} \bigl[\bigl(1-2\alpha +2\alpha ^{2}\bigr)s( \vartheta )+\bigl(\alpha -\alpha ^{2}\bigr)s \bigl(\varsigma (\vartheta )\bigr) \\ &\quad{}+\bigl(\alpha - \alpha ^{2}\bigr)s \bigl(\varpi (\vartheta )\bigr) \bigr]\diamond _{\alpha }\vartheta \biggr]^{2}{}_{\alpha }e_{\varLambda }(v,r)\diamond _{\alpha }\tau , \end{aligned}$$

(2)

where

$$\begin{aligned} \varLambda (v)&= 2 \bigl[ \bigl[2nl\bigl(1-2\alpha +2\alpha ^{2} \bigr)^{2}+4nl\bigl( \alpha -\alpha ^{2}\bigr)^{2} \bigr]b\bigl(\varpi ^{2}(v)\bigr) \\ &\quad{}+4nl\bigl(1-2\alpha +2 \alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi (v) \bigr) +4nl\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi ^{3}(v)\bigr) \\ &\quad{}+2nl\bigl( \alpha - \alpha ^{2}\bigr)b\bigl(\varpi ^{4}(v)\bigr)+2nl\bigl(\alpha -\alpha ^{2}\bigr)b(v) \\ &\quad{} +n\bigl(1-2\alpha +2\alpha ^{2}\bigr)d\bigl(\varpi ^{2}(v)\bigr)+n\bigl(\alpha -\alpha ^{2}\bigr)d\bigl( \varpi (v)\bigr)+n\bigl(\alpha -\alpha ^{2}\bigr)d\bigl(\varpi ^{3}(v)\bigr) \bigr]. \end{aligned}$$

(3)

Proof

Let $v_{0}\in [r,q]$ and define a non-decreasing function $z(v)$ in $[r,v_{0}]$ by

$$ z(v)=j^{2}+2 \int _{r}^{v}b(\tau ) \biggl[y^{2}(\tau )+ \int _{r}^{\tau }d( \vartheta )y^{2}( \vartheta )\diamond _{\alpha }\vartheta \biggr] \diamond _{\alpha }\tau +2 \int _{r}^{v}s(\tau )y(\tau )\diamond _{ \alpha }\tau , $$

(4)

for $v\in [r,v_{0}]_{\mathbb{T}}$, then (1) can be modified as

$$ y^{2}(v)\leq z(v)\quad \Rightarrow \quad y(v)\leq \sqrt{z(v)}; $$

(5)

since $z^{\Delta }(v), z^{\nabla }(v)\geq 0$, from (5) and Lemma 2.1, we deduce

$$\begin{aligned} 0&\leq z^{\diamond _{\alpha }}(v) \\ &=2\bigl(1-2\alpha +2\alpha ^{2}\bigr)b(v) \biggl[y^{2}(v)+ \int _{r}^{v}d(\tau )y^{2}(\tau )\diamond _{\alpha } \tau \biggr]+2\bigl(1-2\alpha +2\alpha ^{2} \bigr)s(v)y(v) \\ &\quad{} +2\bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varsigma (v)\bigr) \biggl[y^{2}\bigl(\varsigma (v)\bigr)+ \int _{r}^{\varsigma (v)}d(\tau )y^{2}(\tau )\diamond _{\alpha }\tau \biggr]+2\bigl(\alpha -\alpha ^{2}\bigr)s\bigl( \varsigma (v)\bigr)y\bigl(\varsigma (v)\bigr) \\ &\quad{} +2\bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi (v)\bigr) \biggl[y^{2}\bigl(\varpi (v)\bigr)+ \int _{r}^{ \varpi (v)}d(\tau )z(\tau )\diamond _{\alpha }\tau \biggr] \\ &\quad{}+2\bigl(\alpha - \alpha ^{2}\bigr)s\bigl( \varpi (v)\bigr)y\bigl(\varpi (v)\bigr), \\ &\leq 2\bigl(1-2\alpha +2\alpha ^{2}\bigr)b(v) \biggl[z(v)+ \int _{r}^{v}d(\tau )z( \tau )\diamond _{\alpha }\tau \biggr]+2\bigl(1-2\alpha +2\alpha ^{2}\bigr)s(v) \sqrt{z(v)} \\ &\quad{} +2\bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varsigma (v)\bigr) \biggl[z\bigl(\varsigma (v)\bigr)+ \int _{r}^{ \varsigma (v)}d(\tau )z(\tau )\diamond _{\alpha }\tau \biggr]+2\bigl( \alpha -\alpha ^{2}\bigr)s\bigl( \varsigma (v)\bigr)\sqrt{z\bigl(\varsigma (v)\bigr)} \\ &\quad{} +2\bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi (v)\bigr) \biggl[z\bigl(\varpi (v)\bigr)+ \int _{r}^{ \varpi (v)}d(\tau )z(\tau )\diamond _{\alpha }\tau \biggr] \\ &\quad{}+2\bigl(\alpha - \alpha ^{2}\bigr)s\bigl( \varpi (v)\bigr)\sqrt{z\bigl(\varpi (v)\bigr)}, \end{aligned}$$

$z(v)$ is non-decreasing, therefore the above inequality by using $z(\varsigma (v))\geq z(v)\geq z(\varpi (v))$ implies that

$$\begin{aligned} & \frac{z^{\diamond _{\alpha }}(v)}{2\sqrt{z(\varpi (v))}} \\ &\quad \leq \bigl(1-2 \alpha +2\alpha ^{2}\bigr)b(v) \biggl[\sqrt{z(v)}+ \int _{r}^{v}d(\tau )\sqrt{z( \tau )}\diamond _{\alpha }\tau \biggr]+\bigl(1-2\alpha +2\alpha ^{2}\bigr)s(v) \\ &\quad \quad{} +\bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varsigma (v)\bigr) \biggl[\sqrt{z\bigl(\varsigma (v)\bigr)}+ \int _{r}^{\varsigma (v)}d(\tau )\sqrt{z(\tau )}\diamond _{\alpha } \tau \biggr]+\bigl(\alpha -\alpha ^{2}\bigr)s\bigl( \varsigma (v)\bigr) \\ &\quad \quad{} +\bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi (v)\bigr) \biggl[\sqrt{z\bigl(\varpi (v)\bigr)}+ \int _{r}^{ \varpi (v)}d(\tau )\sqrt{z(\tau )}\diamond _{\alpha }\tau \biggr]+\bigl( \alpha -\alpha ^{2}\bigr)s\bigl( \varpi (v)\bigr), \end{aligned}$$

(6)

$z(v)$ is bounded as it is regulated in $[r,q]_{\mathbb{T}}$ and composed of $C([r,q]_{\mathbb{T}}, \mathbb{R}_{+})$ and never will be zero. For a constant $l=\max_{v \in [r,v_{0}]_{\mathbb{T}}} \frac{\sqrt{z(\varpi (v))}}{\sqrt{z(\varsigma (v))}}$, we multiply (6) by l, hence

$$\begin{aligned} & \frac{z^{\diamond _{\alpha }}(v)}{2\sqrt{z(\varpi (v))}} \\ &\quad \leq l\bigl(1-2 \alpha +2\alpha ^{2}\bigr)b(v) \biggl[\sqrt{z(v)}+ \int _{r}^{v}d(\tau )\sqrt{z( \tau )}\diamond _{\alpha }\tau \biggr]+l\bigl(1-2\alpha +2\alpha ^{2}\bigr)s(v) \\ &\quad \quad{} +l\bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varsigma (v)\bigr) \biggl[\sqrt{z\bigl(\varsigma (v)\bigr)}+ \int _{r}^{\varsigma (v)}d(\tau )\sqrt{z(\tau )}\diamond _{\alpha } \tau \biggr]+l\bigl(\alpha -\alpha ^{2}\bigr)s\bigl( \varsigma (v)\bigr) \\ &\quad \quad{} +l\bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi (v)\bigr) \biggl[\sqrt{z\bigl(\varpi (v)\bigr)}+ \int _{r}^{ \varpi (v)}d(\tau )\sqrt{z(\tau )}\diamond _{\alpha }\tau \biggr]+l\bigl( \alpha -\alpha ^{2}\bigr)s\bigl( \varpi (v)\bigr), \end{aligned}$$

which by integrating from r to v, using Lemma 3.1 and $z(r)=j^{2}$, leads to

$$\begin{aligned} \sqrt{z(v)}&\leq 2j+l \int _{r}^{v_{0}} \bigl[\bigl(1-2\alpha +2\alpha ^{2}\bigr)s( \tau )+\bigl(\alpha -\alpha ^{2}\bigr)s\bigl( \varsigma (\tau )\bigr)+\bigl(\alpha -\alpha ^{2}\bigr)s\bigl( \varpi (v)\bigr) \bigr]\diamond _{\alpha }\tau \\ &\quad{} +2l\bigl(1-2\alpha +2\alpha ^{2}\bigr) \int _{r}^{v}b(\tau ) \biggl[\sqrt{z(\tau )}+ \int _{r}^{\tau }d(\vartheta )\sqrt{z(\vartheta )} \diamond _{\alpha } \vartheta \biggr]\diamond _{\alpha }\tau \\ &\quad{} +2l\bigl(\alpha -\alpha ^{2}\bigr) \int _{r}^{v}b\bigl(\varsigma (\tau )\bigr) \biggl[ \sqrt{z\bigl( \varsigma (\tau )\bigr)}+ \int _{r}^{\varsigma (\tau )}d(\vartheta )\sqrt{z( \vartheta )} \diamond _{\alpha }\vartheta \biggr]\diamond _{\alpha } \tau \\ &\quad{} +2l\bigl(\alpha -\alpha ^{2}\bigr) \int _{r}^{v}b\bigl(\varpi (\tau )\bigr) \biggl[ \sqrt{z\bigl( \varpi (\tau )\bigr)}+ \int _{r}^{\varpi (\tau )}d(\vartheta )\sqrt{z( \vartheta )} \diamond _{\alpha }\vartheta \biggr]\diamond _{\alpha } \tau . \end{aligned}$$

(7)

Take the right hand side of (7) as $G(v)$, then $\sqrt{z(v)} \leq G(v)$,

$$ G(r)=2j+l \int _{r}^{v_{0}} \bigl[\bigl(1-2\alpha +2\alpha ^{2}\bigr)s(\tau )+\bigl( \alpha -\alpha ^{2}\bigr)s\bigl( \varsigma (\tau )\bigr)+\bigl(\alpha -\alpha ^{2}\bigr)s\bigl( \varpi (v)\bigr) \bigr]\diamond _{\alpha }\tau $$

(8)

and

$$\begin{aligned} G^{\diamond _{\alpha }}(v)&\leq \bigl[2l\bigl(1-2\alpha +2\alpha ^{2} \bigr)^{2}+4l\bigl( \alpha -\alpha ^{2}\bigr)^{2} \bigr] \biggl[b(v) \biggl(G(v)+ \int _{r}^{v}d(\tau )G( \tau )\diamond _{\alpha }\tau \biggr) \biggr] \\ &\quad{} +4l\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varsigma (v)\bigr) \biggl(G\bigl(\varsigma (v)\bigr)+ \int _{r}^{\varsigma (v)}d(\tau )G(\tau ) \diamond _{\alpha }\tau \biggr) \\ &\quad{} +4l\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi (v)\bigr) \biggl(G\bigl( \varpi (v)\bigr)+ \int _{r}^{\varpi (v)}d(\tau )G(\tau )\diamond _{\alpha } \tau \biggr) \\ &\quad{} +2l\bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varsigma ^{2}(v)\bigr) \biggl(G\bigl(\varsigma ^{2}(v)\bigr)+ \int _{r}^{\varsigma ^{2}(v)}d(\tau )G(\tau )\diamond _{\alpha }\tau \biggr) \\ &\quad{} +2l\bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi ^{2}(v)\bigr) \biggl(G\bigl(\varpi ^{2}(v)\bigr)+ \int _{r}^{\varpi ^{2}(v)}d(\tau )G(\tau )\diamond _{\alpha }\tau \biggr), \end{aligned}$$

(9)

here $G^{\diamond _{\alpha }}(v)\geq 0$ and by the delta and nabla derivative, i.e $G^{\Delta }(v), G^{\nabla }(v)\geq 0$, we observe that $G(\varpi ^{2}(v))\geq G(\varpi (v))\geq G(v)\geq G(\varsigma (v)) \geq G(\varsigma ^{2}(v))$. Therefore (9) yields

$$\begin{aligned} G^{\diamond _{\alpha }}(v)&\leq \bigl[ \bigl[2l\bigl(1-2\alpha +2\alpha ^{2} \bigr)^{2}+4l\bigl( \alpha -\alpha ^{2}\bigr)^{2} \bigr]b(v)+4l\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha - \alpha ^{2}\bigr)b\bigl(\varsigma (v)\bigr) \\ &\quad{} +4l\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi (v)\bigr) \\ &\quad{}+2l\bigl( \alpha -\alpha ^{2}\bigr)b\bigl(\varpi ^{2}(v)\bigr)+2l\bigl(\alpha -\alpha ^{2}\bigr)b\bigl( \varsigma ^{2}(v)\bigr) \bigr] \\ &\quad{}\times \biggl[G\bigl(\varpi ^{2}(v)\bigr)+ \int _{r}^{\varpi ^{2}(v)}d(\tau )G(\tau ) \diamond _{\alpha }\tau \biggr]. \end{aligned}$$

(10)

Put $\varPi (v)=G(\varpi ^{2}(v))+\int _{r}^{\varpi ^{2}(v)}d(\tau )G(\tau ) \diamond _{\alpha }\tau$. By the definition of $\varPi (v)$ and from (10), we obtain

$$\begin{aligned} \varPi ^{\diamond _{\alpha }}(v)&\leq \bigl[ \bigl[2l\bigl(1-2\alpha +2\alpha ^{2}\bigr)^{2}+4l\bigl( \alpha -\alpha ^{2} \bigr)^{2} \bigr]b\bigl(\varpi ^{2}(v)\bigr) \\ &\quad{}+4l\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl( \alpha -\alpha ^{2}\bigr)b\bigl( \varpi (v)\bigr) +4l\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi ^{3}(v)\bigr) \\ &\quad{}+2l\bigl( \alpha - \alpha ^{2}\bigr)b\bigl(\varpi ^{4}(v)\bigr)+2l\bigl(\alpha - \alpha ^{2}\bigr)b(v) \bigr]\varPi (v) \\ &\quad{} +\bigl(1-2\alpha +2\alpha ^{2}\bigr)d\bigl(\varpi ^{2}(v)\bigr)G\bigl(\varpi ^{2}(v)\bigr)+\bigl( \alpha - \alpha ^{2}\bigr)d\bigl(\varpi (v)\bigr)G\bigl(\varpi (v)\bigr) \\ &\quad{} +\bigl(\alpha -\alpha ^{2}\bigr)d\bigl(\varpi ^{3}(v)\bigr)G\bigl(\varpi ^{3}(v)\bigr), \end{aligned}$$

(11)

$\varPi ^{\diamond _{\alpha }}(v)\geq 0$, $\varPi ^{\Delta }(v), \varPi ^{\nabla }(v)\geq 0$, obviously $G(\varpi ^{2}(v))\leq \varPi (v)$, also $\varPi (\varpi (v))\geq \varPi (v)\geq \varPi (\varsigma (v))$ and $\varPi (\varpi (v))\geq G(\varpi ^{3}(v))$. Therefore, from (11), we get

$$\begin{aligned} \frac{\varPi ^{\diamond _{\alpha }}(v)}{\varPi (\varpi (v))}&\leq \bigl[2l\bigl(1-2 \alpha +2\alpha ^{2} \bigr)^{2}+4l\bigl(\alpha -\alpha ^{2}\bigr)^{2} \bigr]b\bigl(\varpi ^{2}(v)\bigr) \\ &\quad{}+4l\bigl(1-2 \alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi (v) \bigr) +4l\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi ^{3}(v)\bigr) \\ &\quad{}+2l\bigl( \alpha - \alpha ^{2}\bigr)b\bigl(\varpi ^{4}(v)\bigr)+2l\bigl(\alpha - \alpha ^{2}\bigr)b(v) \\ &\quad{} +\bigl(1-2\alpha +2\alpha ^{2}\bigr)d\bigl(\varpi ^{2}(v)\bigr)+\bigl(\alpha -\alpha ^{2}\bigr)d\bigl( \varpi (v)\bigr)+\bigl(\alpha -\alpha ^{2}\bigr)d\bigl(\varpi ^{3}(v)\bigr), \end{aligned}$$

there exists a fixed constant $n=\max_{v \in [r,v_{0}]_{\mathbb{T}}} \frac{\varPi (\varpi (v))}{\varPi (\varsigma (v))}$, multiplying the last inequality by n, we have

$$\begin{aligned} \frac{\varPi ^{\diamond _{\alpha }}(v)}{\varPi (\varpi (v))}&\leq \bigl[2nl\bigl(1-2 \alpha +2\alpha ^{2} \bigr)^{2}+4nl\bigl(\alpha -\alpha ^{2}\bigr)^{2} \bigr]b\bigl(\varpi ^{2}(v)\bigr) \\ &\quad{}+4nl\bigl(1-2 \alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi (v) \bigr) \\ &\quad{} +4nl\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi ^{3}(v)\bigr)+2nl\bigl( \alpha - \alpha ^{2}\bigr)b\bigl(\varpi ^{4}(v)\bigr) \\ &\quad{}+2nl\bigl(\alpha -\alpha ^{2}\bigr)b(v) +n\bigl(1-2\alpha +2\alpha ^{2}\bigr)d\bigl(\varpi ^{2}(v)\bigr)+n\bigl(\alpha -\alpha ^{2}\bigr)d\bigl( \varpi (v)\bigr) \\ &\quad{}+n\bigl(\alpha -\alpha ^{2}\bigr)d\bigl(\varpi ^{3}(v)\bigr), \end{aligned}$$

which by using (8) gives the estimate

$$ \begin{aligned}[b] \varPi (v)&\leq \biggl[2j+l \int _{r}^{v_{0}} \bigl[\bigl(1-2\alpha +2\alpha ^{2}\bigr)s( \tau )+\bigl(\alpha -\alpha ^{2}\bigr)s\bigl( \varsigma (\tau )\bigr) \\ &\quad{}+\bigl(\alpha -\alpha ^{2}\bigr)s\bigl( \varpi ( \tau )\bigr) \bigr]\diamond _{\alpha }\tau \biggr]^{2}{}_{\alpha }e_{ \varLambda }(v,r), \end{aligned} $$

(12)

where $\varLambda (v)$ is defined in (3). From (10) and (12), we obtain

$$\begin{aligned} G^{\diamond _{\alpha }}(v)&\leq \bigl[ \bigl[2l\bigl(1-2\alpha +2\alpha ^{2} \bigr)^{2}+4l\bigl( \alpha -\alpha ^{2}\bigr)^{2} \bigr]b(v)+4l\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha - \alpha ^{2}\bigr)b\bigl(\varsigma (v)\bigr) \\ &\quad{} +4l\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi (v)\bigr)+2l\bigl( \alpha -\alpha ^{2}\bigr)b\bigl(\varpi ^{2}(v)\bigr) \\ &\quad{}+2l\bigl(\alpha -\alpha ^{2}\bigr)b\bigl( \varsigma ^{2}(v)\bigr) \bigr] \\ &\quad{}\times \biggl[2j+l \int _{r}^{v_{0}} \bigl[\bigl(1-2\alpha +2\alpha ^{2}\bigr)s(\tau )+\bigl( \alpha -\alpha ^{2}\bigr)s\bigl( \varsigma (\tau )\bigr) \\ &\quad{}+\bigl(\alpha -\alpha ^{2}\bigr)s\bigl( \varpi (v)\bigr) \bigr]\diamond _{\alpha }\tau \biggr]^{2}{}_{\alpha }e_{ \varLambda }(v,r), \end{aligned}$$

or equivalently

$$\begin{aligned} & \frac{1}{2} G(v) \\ &\quad \leq 2j+l \int _{r}^{v_{0}} \bigl[\bigl(1-2\alpha +2\alpha ^{2}\bigr)s( \tau )+\bigl(\alpha -\alpha ^{2}\bigr)s\bigl( \varsigma (\tau )\bigr)+\bigl(\alpha -\alpha ^{2}\bigr)s\bigl( \varpi (v)\bigr) \bigr]\diamond _{\alpha }\tau \\ &\quad \quad{} + \int _{r}^{v} \bigl[ \bigl[2l\bigl(1-2\alpha +2 \alpha ^{2}\bigr)^{2}+4l\bigl(\alpha - \alpha ^{2} \bigr)^{2} \bigr]b(\tau )+4l\bigl(1-2\alpha +2\alpha ^{2} \bigr) \bigl(\alpha - \alpha ^{2}\bigr)b\bigl(\varsigma (\tau )\bigr) \\ &\quad \quad{} +4l\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi (\tau )\bigr)+2l\bigl( \alpha -\alpha ^{2}\bigr)b\bigl(\varpi ^{2}(v)\bigr)+2l\bigl(\alpha -\alpha ^{2}\bigr)b\bigl( \varsigma ^{2}(\tau )\bigr) \bigr] \\ &\quad \quad{}\times \biggl[2j+l \int _{r}^{\tau _{0}} \bigl[\bigl(1-2\alpha +2\alpha ^{2}\bigr)s( \vartheta )+\bigl(\alpha -\alpha ^{2}\bigr)s \bigl(\varsigma (\vartheta )\bigr) \\ &\quad \quad{}+\bigl(\alpha - \alpha ^{2}\bigr)s \bigl(\varpi (\vartheta )\bigr) \bigr]\diamond _{\alpha }\vartheta \biggr]^{2}{}_{\alpha }e_{\varLambda }(v,r)\diamond _{\alpha }\tau . \end{aligned}$$

The conclusion in (2) can be obtained by substituting the last inequality in $\sqrt{z(v)}\leq G(v)$ and (5). □

The following theorem is useful.

Theorem 3.3

Suppose that$y(v)$, b, d, ϖ, r, qare as mentioned in Theorem 3.2and$\psi (v)\in C(\mathbb{R}_{+},\mathbb{R}_{+})$is non-decreasing. If

$$ y^{2}(v)\leq j^{2}+2 \int _{r}^{v}b(\tau )y^{2}(\tau )\diamond _{ \alpha }\tau +2 \int _{r}^{v}b(\tau ) \biggl( \int _{r}^{\tau }d( \vartheta )y(\vartheta )\psi \bigl(y(\vartheta )\bigr)\diamond _{\alpha } \vartheta \biggr)\diamond _{\alpha }\tau , $$

(13)

where$j>0$, then for fixed constants$l_{1},n_{1} >0$we have

$$\begin{aligned} y(v)&\leq 4j+2 \int _{r}^{v} \biggl[ \bigl(\bigl[2l_{1} \bigl(1-2\alpha +2\alpha ^{2}\bigr)^{2}+4l_{1} \bigl( \alpha -\alpha ^{2}\bigr)^{2}\bigr]b(\tau ) \\ &\quad{}+4l_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl( \alpha - \alpha ^{2}\bigr)b\bigl(\varsigma (\tau )\bigr) \\ &\quad{} +4l_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl( \alpha -\alpha ^{2}\bigr)b\bigl(\varpi (\tau )\bigr)+2l_{1} \bigl( \alpha -\alpha ^{2}\bigr)^{2}b\bigl(\varsigma ^{2}(\tau )\bigr) \\ &\quad{}+2l_{1}\bigl(\alpha - \alpha ^{2} \bigr)^{2}b\bigl(\varpi ^{2}(\tau )\bigr) \bigr) \\ &\quad{}\times \biggl(\varUpsilon ^{-1} \biggl[2\varUpsilon (2j)+ \int _{r}^{\tau } \bigl(\bigl[4n_{1}l_{1} \bigl(1-2 \alpha +2\alpha ^{2}\bigr)^{2}+8n_{1}l_{1} \bigl(\alpha -\alpha ^{2}\bigr)^{2}\bigr]b\bigl( \varpi ^{2}(\vartheta )\bigr) \\ &\quad{} +8n_{1}l_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi ( \vartheta )\bigr) \\ &\quad{}+8n_{1}l_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl( \varpi ^{3}(\vartheta )\bigr) \\ &\quad{} +4n_{1}l_{1}\bigl(\alpha -\alpha ^{2} \bigr)^{2}b\bigl(\varpi ^{4}(\vartheta )\bigr)+4n_{1}l_{1} \bigl( \alpha -\alpha ^{2}\bigr)^{2}b\bigl(\varpi (\vartheta ) \bigr) \\ &\quad{}+2n_{1}\bigl(1-2\alpha +2 \alpha ^{2}\bigr)d\bigl( \varpi ^{2}(\vartheta )\bigr) \\ &\quad{} +2n_{1}\bigl(\alpha -\alpha ^{2}\bigr)d\bigl( \varpi (\vartheta )\bigr)++2n_{1}\bigl(\alpha - \alpha ^{2} \bigr)d\bigl(\varpi ^{3}(\vartheta )\bigr) \bigr)\diamond _{\alpha } \vartheta \biggr] \biggr) \biggr]\diamond _{\alpha }\tau , \end{aligned}$$

(14)

where$\varUpsilon (u)= \int _{1}^{u}\frac{dp}{p+\psi (p)}$, $u>0$.

Proof

Let $v_{1}\in [r,q]$ and a non-decreasing function $z_{1}(v)$ be defined by

$$ z_{1}(v)=j^{2}+2 \int _{r}^{v}b(\tau )y^{2}(\tau )\diamond _{\alpha } \tau +2 \int _{r}^{v}b(\tau ) \biggl( \int _{r}^{\tau }d(\vartheta )y( \vartheta )\psi \bigl(y(\vartheta )\bigr)\diamond _{\alpha }\vartheta \biggr) \diamond _{\alpha }\tau , $$

(15)

(13) can be restated as

$$ y^{2}(v)\leq z_{1}(v)\quad \Rightarrow \quad y(v)\leq \sqrt{z_{1}(v)}; $$

(16)

as $z_{1}^{\Delta }(v), z_{1}^{\nabla }(v)\geq 0$, it is noticed from Lemma 2.1 that

$$\begin{aligned} z_{1}^{\diamond _{\alpha }}(v)&=2\bigl(1-2\alpha +2\alpha ^{2} \bigr)b(v)y^{2}(v)+2\bigl(1-2 \alpha +2\alpha ^{2}\bigr)b(v) \biggl[ \int _{r}^{v}d(\tau )y(\tau )\psi \bigl(y( \tau ) \bigr)\diamond _{\alpha }\tau \biggr] \\ &\quad{} +2\bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varsigma (v) \bigr)y^{2}\bigl(\varsigma (v)\bigr)+2\bigl( \alpha -\alpha ^{2}\bigr)b\bigl(\varsigma (v)\bigr) \biggl[ \int _{r}^{\varsigma (\tau )}d( \tau )y(\tau )\psi \bigl(y(\tau ) \bigr)\diamond _{\alpha }\tau \biggr] \\ &\quad{} +2\bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi (v) \bigr)y^{2}\bigl(\varpi (v)\bigr) \\ &\quad{} +2\bigl(\alpha - \alpha ^{2} \bigr)b\bigl(\varpi (v)\bigr) \biggl[ \int _{r}^{\varpi (\tau )}d(\tau )y( \tau )\psi \bigl(y(\tau ) \bigr)\diamond _{\alpha }\tau \biggr], \end{aligned}$$

$z_{1}(v)\geq 0$, $z_{1}(\varsigma (v))\geq z_{1}(v)\geq z_{1}(\varpi (v))$. Further, $z_{1}(v)$ is bounded and regulated in $[r,q]_{\mathbb{T}}$ and belong to $C([r,q]_{\mathbb{T}}, \mathbb{R}_{+})$ which does not tend to zero. Consider a constant $l_{1}=\max_{v \in [r,v_{1}]_{\mathbb{T}}} \frac{\sqrt{z_{1}(\varpi (v))}}{\sqrt{z_{1}(\varsigma (v))}}$, multiplying the previous inequality by $l_{1}$,

$$\begin{aligned} \frac{z_{1}^{\diamond _{\alpha }}(v)}{2\sqrt{z_{1}(\varpi (v))}}&\leq l_{1}\bigl(1-2\alpha +2\alpha ^{2} \bigr)b(v) \biggl[\sqrt{z_{1}(v)}+ \int _{r}^{v}d( \tau )\psi \bigl( \sqrt{z_{1}(\tau )}\bigr)\diamond _{\alpha }\tau \biggr] \\ &\quad{} +l_{1}\bigl(\alpha -\alpha ^{2}\bigr)b\bigl( \varsigma (v)\bigr) \biggl[\sqrt{z_{1}\bigl( \varsigma (v)\bigr)}+ \int _{r}^{\varsigma (v)}d(\tau )\psi \bigl( \sqrt{z_{1}( \tau )}\bigr)\diamond _{\alpha }\tau \biggr] \\ &\quad{} +l_{1}\bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi (v)\bigr) \biggl[\sqrt{z_{1}\bigl(\varpi (v)\bigr)}+ \int _{r}^{\varpi (v)}d(\tau )\psi \bigl( \sqrt{z_{1}(\tau )}\bigr)\diamond _{ \alpha }\tau \biggr], \end{aligned}$$

(17)

integrating (17) from r to v, using Lemma 3.1 and $z_{1}(r)=j^{2}$, we have

$$\begin{aligned} \sqrt{z(v)}&\leq 2j+2l_{1}\bigl(1-2\alpha +2\alpha ^{2} \bigr) \int _{r}^{v}b( \tau ) \biggl[\sqrt{z(\tau )}+ \int _{r}^{\tau }d(\vartheta )\psi \bigl(\sqrt{z( \vartheta )}\bigr)\diamond _{\alpha }\vartheta \biggr]\diamond _{\alpha } \tau \\ &\quad{} +2l_{1}\bigl(\alpha -\alpha ^{2}\bigr) \int _{r}^{v}b\bigl(\varsigma (\tau )\bigr) \biggl[ \sqrt{z\bigl(\varsigma (\tau )\bigr)}+l \int _{r}^{\varsigma (\tau )}d( \vartheta )\psi \bigl(\sqrt{z( \vartheta )}\bigr)\diamond _{\alpha }\vartheta \biggr]\diamond _{\alpha }\tau \\ &\quad{} +2l_{1}\bigl(\alpha -\alpha ^{2}\bigr) \int _{r}^{v}b\bigl(\varpi (\tau )\bigr) \biggl[ \sqrt{z\bigl(\varpi (\tau )\bigr)}+ \int _{r}^{\varpi (\tau )}d(\vartheta )\psi \bigl( \sqrt{z( \vartheta )}\bigr)\diamond _{\alpha }\vartheta \biggr]\diamond _{ \alpha }\tau \\ &\leq G_{1}(v), \end{aligned}$$

(18)

where

$$\begin{aligned} G_{1}(v)&=2j+2l_{1}\bigl(1-2\alpha +2\alpha ^{2} \bigr) \int _{r}^{v}b(\tau ) \biggl[\sqrt{z(\tau )}+ \int _{r}^{\tau }d(\vartheta )\psi \bigl(\sqrt{z( \vartheta )}\bigr)\diamond _{\alpha }\vartheta \biggr]\diamond _{\alpha } \tau \\ &\quad{} +2l_{1}\bigl(\alpha -\alpha ^{2}\bigr) \int _{r}^{v}b\bigl(\varsigma (\tau )\bigr) \biggl[ \sqrt{z\bigl(\varsigma (\tau )\bigr)}+l \int _{r}^{\varsigma (\tau )}d( \vartheta )\psi \bigl(\sqrt{z( \vartheta )}\bigr)\diamond _{\alpha }\vartheta \biggr]\diamond _{\alpha }\tau \\ &\quad{} +2l_{1}\bigl(\alpha -\alpha ^{2}\bigr) \int _{r}^{v}b\bigl(\varpi (\tau )\bigr) \biggl[ \sqrt{z\bigl(\varpi (\tau )\bigr)} \\ &\quad{}+ \int _{r}^{\varpi (\tau )}d(\vartheta )\psi \bigl( \sqrt{z( \vartheta )}\bigr)\diamond _{\alpha }\vartheta \biggr]\diamond _{ \alpha }\tau . \end{aligned}$$

(19)

By following the same steps from (8)–(10) to (19) with some alterations, we conclude

$$\begin{aligned} G_{1}^{\diamond _{\alpha }}(v)&\leq \bigl[ \bigl[2l_{1}\bigl(1-2 \alpha +2 \alpha ^{2}\bigr)^{2}+4l_{1}\bigl(\alpha -\alpha ^{2}\bigr)^{2} \bigr]b(v)+4l_{1}\bigl(1-2 \alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b \bigl(\varsigma (v)\bigr) \\ &\quad{} +4l_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl( \alpha -\alpha ^{2}\bigr)b\bigl(\varpi (v)\bigr)+2l_{1}\bigl( \alpha -\alpha ^{2}\bigr)b\bigl(\varpi ^{2}(v) \bigr) \\ &\quad{}+2l_{1}\bigl(\alpha -\alpha ^{2}\bigr)b\bigl( \varsigma ^{2}(v)\bigr) \bigr] \varPi _{1}(v), \end{aligned}$$

(20)

where $\varPi _{1}(v)=G_{1}(\varpi ^{2}(v))+\int _{r}^{\varpi ^{2}(v)}d(\tau ) \psi (G_{1}(\tau ))\diamond _{\alpha }\tau$ and $G_{1}(\varpi ^{2}(v))\leq \varPi _{1}(v)$. In view of $\varPi _{1}(v)\geq 0$, $\varPi _{1}^{\Delta }(v), \varPi _{1}^{\nabla }(v)\geq 0$, apparently $\varPi _{1}(\varpi (v))\geq \varPi _{1}(v)\geq \varPi _{1}(\varsigma (v))$, $\varPi _{1}(\varpi (v))\geq G_{1}(\varpi ^{3}(v))$. Thus from (20), we acquire

$$\begin{aligned} & \frac{\varPi _{1}^{\diamond _{\alpha }}(v)}{\varPi _{1}(v)+\varPi _{1}(\varpi (v))} \\ &\quad \leq \bigl[2l_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr)^{2}+4l_{1}\bigl(\alpha -\alpha ^{2}\bigr)^{2} \bigr]b\bigl(\varpi ^{2}(v) \bigr) \\ &\quad \quad{}+4l_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha - \alpha ^{2}\bigr)b\bigl(\varpi (v)\bigr) \\ &\quad \quad{} +4l_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl( \alpha -\alpha ^{2}\bigr)b\bigl(\varpi ^{3}(v) \bigr)+2l_{1}\bigl( \alpha -\alpha ^{2}\bigr)b\bigl(\varpi ^{4}(v)\bigr)+2l_{1}\bigl(\alpha -\alpha ^{2} \bigr)b(v) \\ &\quad \quad{} +\bigl(1-2\alpha +2\alpha ^{2}\bigr)d\bigl(\varpi ^{2}(v)\bigr)+\bigl(\alpha -\alpha ^{2}\bigr)d\bigl( \varpi (v)\bigr)+\bigl(\alpha -\alpha ^{2}\bigr)d\bigl(\varpi ^{3}(v)\bigr). \end{aligned}$$

(21)

Multiply (21) by a fixed constant $n_{1}$ so that $n_{1}=\max_{v \in [r,v_{0}]_{\mathbb{T}}} \frac{\varPi _{1}(\varpi (v))}{\varPi _{1}(v)+\varPi _{1}(\varsigma (v))}$, then, by using the definition of ϒ and the fact that $\varUpsilon (\varPi _{1}(r)=2j$, we have

$$\begin{aligned} \varPi _{1}(v)&\leq \varUpsilon ^{-1} \biggl[2\varUpsilon (2j)+ \int _{r}^{v} \bigl(\bigl[4n_{1}l_{1} \bigl(1-2\alpha +2\alpha ^{2}\bigr)^{2}+8n_{1}l_{1} \bigl(\alpha - \alpha ^{2}\bigr)^{2}\bigr]b\bigl(\varpi ^{2}(\tau )\bigr) \\ &\quad{} +8n_{1}l_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi ( \tau )\bigr) \\ &\quad{}+8n_{1}l_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl( \varpi ^{3}(\tau )\bigr) \\ &\quad{} +4n_{1}l_{1}\bigl(\alpha -\alpha ^{2} \bigr)^{2}b\bigl(\varpi ^{4}(\tau )\bigr)+4n_{1}l_{1} \bigl( \alpha -\alpha ^{2}\bigr)^{2}b\bigl(\varpi (\tau ) \bigr) \\ &\quad{}+2n_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr)d\bigl( \varpi ^{2}(\tau )\bigr) \\ &\quad{} +2n_{1}\bigl(\alpha -\alpha ^{2}\bigr)d\bigl( \varpi (\tau )\bigr)++2n_{1}\bigl(\alpha - \alpha ^{2}\bigr)d \bigl(\varpi ^{3}(\tau )\bigr)\diamond _{\alpha }\tau \bigr) \biggr]. \end{aligned}$$

(22)

From (20) and (22), we obtain

$$\begin{aligned} G_{1}^{\diamond _{\alpha }}(v)&\leq \bigl[ \bigl[2l_{1}\bigl(1-2 \alpha +2 \alpha ^{2}\bigr)^{2}+4l_{1}\bigl(\alpha -\alpha ^{2}\bigr)^{2} \bigr]b(v)+4l_{1}\bigl(1-2 \alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b \bigl(\varsigma (v)\bigr) \\ &\quad{} +4l_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl( \alpha -\alpha ^{2}\bigr)b\bigl(\varpi (v)\bigr)+2l_{1}\bigl( \alpha -\alpha ^{2}\bigr)b\bigl(\varpi ^{2}(v) \bigr) \\ &\quad{}+2l_{1}\bigl(\alpha -\alpha ^{2}\bigr)b\bigl( \varsigma ^{2}(v)\bigr) \bigr] \\ &\quad{}\times \biggl[\varUpsilon ^{-1} \biggl(2\varUpsilon (2j)+ \int _{r}^{v} \bigl[\bigl[4n_{1}l_{1} \bigl(1-2 \alpha +2\alpha ^{2}\bigr)^{2}+8n_{1}l_{1} \bigl(\alpha -\alpha ^{2}\bigr)^{2}\bigr]b\bigl( \varpi ^{2}(\tau )\bigr) \\ &\quad{} +8n_{1}l_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi ( \tau )\bigr) \\ &\quad{}+8n_{1}l_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl( \varpi ^{3}(\tau )\bigr) \\ &\quad{} +4n_{1}l_{1}\bigl(\alpha -\alpha ^{2} \bigr)^{2}b\bigl(\varpi ^{4}(\tau )\bigr)+4n_{1}l_{1} \bigl( \alpha -\alpha ^{2}\bigr)^{2}b\bigl(\varpi (\tau ) \bigr) \\ &\quad{}+2n_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr)d\bigl( \varpi ^{2}(\tau )\bigr) \\ &\quad{} +2n_{1}\bigl(\alpha -\alpha ^{2}\bigr)d\bigl( \varpi (\tau )\bigr)++2n_{1}\bigl(\alpha - \alpha ^{2}\bigr)d \bigl(\varpi ^{3}(\tau )\bigr)\diamond _{\alpha }\tau \bigr] \biggr) \biggr], \end{aligned}$$

which by the integration from r to v, using Lemma 3.1, (5) and $G_{1}(r)=2j$, produces the required bound in (14). □

Remark 3.4

If $j^{2}=a(v)$, $a(v)$ is a non-decreasing function, $y^{2}(v)=u(v)$, $r=v_{0}$, $d(v)=k(\tau ,v)$, $2b(v)=f(v)$ and $\psi (y(v))=1$, then Theorem 3.3 is converted into Theorem 3 in [20] with delta derivatives on time scales.

Remark 3.5

Put $j^{2}=a(v)$, $y^{2}(v)=u(v)$, $r=v_{0}$, $d(v)=0$ and $2b(v)=f(v)$, then Theorem 3.3 changes into Corollary 3.11 in [4] related to delta derivatives.

4 Applications

Here, we will derive some applications of the established inequalities to discuss certain characteristics of the solutions of nonlinear dynamic integro-differential equation on time scales of the type

$$ x^{\diamond _{\alpha }}(\xi )=H \biggl(\xi ,x(\xi ), \int _{0}^{\xi }N\bigl( \xi ,\sigma ,x(\sigma )\bigr) \diamond _{\alpha }\sigma \biggr),\quad x(0)=x_{0}, \xi \in \mathbb{T}^{k}, $$

(23)

where $x_{0}$ is a constant, and $H:\mathbb{T}^{k}\times \mathbb{R}\times \mathbb{R}\rightarrow \mathbb{R}$, $N:\mathbb{T}^{k}\times \mathbb{T}^{k}\times \mathbb{R}\rightarrow \mathbb{R}$ are continuous functions.

The boundedness on the solution of (23) can be addressed in the first example.

Example 1

Suppose that $x(\xi )$ is a solution of (23), and the functions H and B in (23) satisfy the following conditions:

$$\begin{aligned}& \bigl\vert H(\xi ,x,z) \bigr\vert \leq b(\xi ) \vert x \vert + \vert z \vert , \end{aligned}$$

(24)

$$\begin{aligned}& \bigl\vert N(\xi ,\sigma ,x) \bigr\vert \leq b(\xi )d(\sigma ) \bigl\vert \psi (x) \bigr\vert , \end{aligned}$$

(25)

then

$$\begin{aligned} \bigl\vert x(\xi ) \bigr\vert &\leq 4 \vert x_{0} \vert +2 \int _{0}^{\xi } \biggl[ \bigl(\bigl[2l_{1} \bigl(1-2 \alpha +2\alpha ^{2}\bigr)^{2}+4l_{1} \bigl(\alpha -\alpha ^{2}\bigr)^{2}\bigr]b(\tau ) \\ &\quad{} +4l_{1}\bigl(1-2 \alpha +2\alpha ^{2}\bigr) \bigl(\alpha - \alpha ^{2}\bigr)b\bigl(\varsigma (\tau )\bigr) \\ &\quad{} +4l_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl( \alpha -\alpha ^{2}\bigr)b\bigl(\varpi (\tau )\bigr)+2l_{1} \bigl( \alpha -\alpha ^{2}\bigr)^{2}b\bigl(\varsigma ^{2}(\tau )\bigr) \\ &\quad{} +2l_{1}\bigl(\alpha - \alpha ^{2} \bigr)^{2}b\bigl(\varpi ^{2}(\tau )\bigr) \bigr) \\ &\quad{}\times \biggl(\varUpsilon ^{-1} \biggl[2\varUpsilon \bigl(2 \vert x_{0} \vert \bigr)+ \int _{0}^{\tau } \bigl(\bigl[4n_{1}l_{1} \bigl(1-2\alpha +2\alpha ^{2}\bigr)^{2}+8n_{1}l_{1} \bigl(\alpha - \alpha ^{2}\bigr)^{2}\bigr]b\bigl(\varpi ^{2}(\vartheta )\bigr) \\ &\quad{} +8n_{1}l_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl(\varpi ( \vartheta )\bigr) \\ &\quad{} +8n_{1}l_{1}\bigl(1-2\alpha +2\alpha ^{2}\bigr) \bigl(\alpha -\alpha ^{2}\bigr)b\bigl( \varpi ^{3}(\vartheta )\bigr) \\ &\quad{} +4n_{1}l_{1}\bigl(\alpha -\alpha ^{2} \bigr)^{2}b\bigl(\varpi ^{4}(\vartheta )\bigr)+4n_{1}l_{1} \bigl( \alpha -\alpha ^{2}\bigr)^{2}b\bigl(\varpi (\vartheta ) \bigr) \\ &\quad{} +2n_{1}\bigl(1-2\alpha +2 \alpha ^{2}\bigr)d\bigl( \varpi ^{2}(\vartheta )\bigr) \\ &\quad{} +2n_{1}\bigl(\alpha -\alpha ^{2}\bigr)d\bigl( \varpi (\vartheta )\bigr)++2n_{1}\bigl(\alpha - \alpha ^{2} \bigr)d\bigl(\varpi ^{3}(\vartheta )\bigr) \bigr)\diamond _{\alpha } \vartheta \biggr] \biggr) \biggr]\diamond _{\alpha }\tau , \end{aligned}$$

(26)

where b, d, ψ, ϒ, $l_{1}$, $n_{1}$ are given in Theorem 3.3.

Proof. Multiplying both sides of (23) by $x(\xi )$, substituting $\xi =\gamma$ and then integrating from 0 to ξ, we get

$$ x^{2}(\xi )= x_{0}^{2}+2 \int _{0}^{\xi } \biggl[x(\gamma )H \biggl( \gamma ,x( \gamma ), \int _{0}^{\gamma }N\bigl(\gamma ,\sigma ,x(\sigma )\bigr) \diamond _{\alpha }\sigma \biggr) \biggr]\diamond _{\alpha }\gamma , $$

it follows from (24) and (25) that

$$\begin{aligned}& \bigl\vert x(\xi ) \bigr\vert ^{2}\leq \vert x_{0} \vert ^{2}+2 \int _{0}^{\xi } \biggl\vert \biggl[x(\gamma )H \biggl(\gamma ,x(\gamma ), \int _{0}^{\gamma }N\bigl(\gamma ,\sigma ,x( \sigma ) \bigr)\diamond _{\alpha }\sigma \biggr) \biggr] \biggr\vert \diamond _{ \alpha }\gamma , \end{aligned}$$

(27)

$$\begin{aligned}& \begin{aligned}[b] \bigl\vert x(\xi ) \bigr\vert ^{2}\leq {}&\vert x_{0} \vert ^{2}+2 \int _{0}^{\xi }b(\gamma ) \bigl\vert x(\gamma ) \bigr\vert ^{2} \diamond _{\alpha }\gamma \\ &{}+2 \int _{0}^{\xi }b(\gamma ) \biggl( \int _{0}^{ \gamma }d(\sigma ) \bigl\vert x(\sigma ) \bigr\vert \bigl\vert \psi \bigl(x(\sigma )\bigr) \bigr\vert \diamond _{\alpha } \sigma \biggr)\diamond _{\alpha }\gamma . \end{aligned} \end{aligned}$$

(28)

The desired estimation in (26) follows from the suitable implementation of Theorem 3.3 to $\vert x(\xi ) \vert$ in (28).

The uniqueness of the solution of (23) is studied in the second example.

Example 2

Assume that

$$\begin{aligned}& \bigl\vert H(\xi ,x,z)-H(\xi ,\bar{x},\bar{z}) \bigr\vert \leq b(\xi ) \vert x-\bar{x} \vert + \vert z- \bar{z} \vert ], \end{aligned}$$

(29)

$$\begin{aligned}& \bigl\vert N(\xi ,\sigma ,x)-N(\xi ,\sigma ,\bar{x}) \bigr\vert \leq b(\xi )d(\sigma ) \vert x- \bar{x} \vert , \end{aligned}$$

(30)

then (23) has at most one positive solution on $\xi \in \mathbb{T}^{k}$.

Proof. Let $x(\xi )$ and $\bar{x}(\xi )$ be two solutions of (23) and applying (27), (28), (29), we obtain

$$\begin{aligned} & \bigl\vert x^{2}(\xi )-\bar{x}^{2}(\xi ) \bigr\vert \\ &\quad \leq 2 \int _{0}^{\xi }b(\gamma ) \bigl\vert x^{2}( \gamma )-\bar{x}^{2}(\gamma ) \bigr\vert \diamond _{\alpha }\gamma \\ &\quad \quad{} +2 \int _{0}^{\xi }b(\gamma ) \biggl( \int _{0}^{\gamma }d(\sigma ) \bigl\vert x( \sigma )- \bar{x}(\sigma ) \bigr\vert \bigl\vert \psi \bigl(x(\sigma )\bigr)-\psi \bigl( \bar{x}(\sigma )\bigr) \bigr\vert \diamond _{\alpha }\sigma \biggr)\diamond _{\alpha }\gamma . \end{aligned}$$

(31)

By making use of a similar procedure to Theorem 3.3 with appropriate modifications to the function $\vert x^{2}(\xi )-\bar{x}^{2}(\xi ) \vert$ in (31), we obtain

$$ \bigl\vert x^{2}(\xi )-\bar{x}^{2}(\xi ) \bigr\vert \leq 0, \quad v\in I. $$

Hence $x=\bar{x}$ on $\xi \in \mathbb{T}^{k}$.