1 Introduction

In the last few decades, a number of successful applications of RNNs have been witnessed in many areas, including associative memory, prediction and optimal control, and pattern recognition [1–8]. During the implementation of the operation, time delay is inevitably inherent in the transmission process among neurons on account of limited propagation speed and limited switching of the amplifier [9–13]. In addition, because of the existence of a large number of parallel channels with different coaxial process sizes and lengths, there maybe exist distributions of conduction velocities delays and propagation delays along with these paths. In these cases, we cannot only model the signal propagation with discrete delays due to it not being instantaneous. Thus, it is more suitable to add continuous distribution delays into the neural network model. Moreover, these delays sometimes may produce the desired excellent performance, such as processing moving images between neurons when signals are transmitted, exhibiting chaotic phenomena applied to secure communication. Therefore, it is quite necessary to discuss the dynamical behavior of the neural networks with mixed distributive and discrete delays. And there has been a lot of literature on mixed constant delays [14–19] and time-varying delays [19–24].

Recently, Liu et al. [25] proposed the asynchronous delays, and investigated the exponential stability for complex-valued recurrent neural networks with discrete asynchronous delays. Afterwards, Li et al. [26] presented the stability preservation in discrete analogue of an impulsive Cohen–Grossberg neural network with discrete asynchronous delays. In the implementation of the operation, time delays are not just discrete asynchronous, but also distributive asynchronous, or even mixed asynchronous. In fact, for a driver, there is not only one kind of delay; his eyes, hands and feet all have delays in responding to the operation. Since the delays are different for different drivers, it needs to be coordinated in the driver’s brain central nervous system. Therefore, the stability analysis of neural networks with distributive and discrete asynchronous delays is a challenge that we should look forward to discussing.

Inspired by the challenge above, we investigated the exponential stability of RNNs with mixed asynchronous time-varying delays. The main contribution was to find some novel sufficient conditions which make the discussed system’s balance point unique and the global exponential asymptotically stable. The rest arrangement of this article are as follows. In the second section, the RNN model with some reasonable assumption is given. The main results are given and proved in the third section. The corollaries and comparisons with the existing literature are given in the fourth section. Section 5 gives a numerical example with comprehensible simulation to illustrate the effectiveness of the main results. In the end of this paper, the conclusion is drawn.

2 Model description

In the present article, we investigate a class of RNNs of n (\(n \geq 2\)) interconnected neurons as follows:

$$ \textstyle\begin{cases} \frac{\mathrm{d}x_{i}(t)}{\mathrm{d}t} =-a_{i}x_{i}(t)+\sum_{j=1}^{n}b_{ij}f_{j}(x_{j}(t))+ \sum_{j=1}^{n}c_{ij}f_{j}(x_{j}(t-\tau _{ij}(t))) \\ \hphantom{\frac{\mathrm{d}x_{i}(t)}{\mathrm{d}t} ={}}{}+\sum_{j=1}^{n}d_{ij} \int _{t-h_{ij}(t)}^{t}f_{j}(x_{j}(s))\,ds+u_{i}, \\ \hphantom{\frac{\mathrm{d}x_{i}(t)}{\mathrm{d}t} ={}}{} t \geq 0, i=1,2,\ldots ,n, \end{cases} $$
(1)

where \(x_{i}(t)\) is the state variate at time t related to the ith neuron; \(a_{i}\) is a positive behaved constant; \(f_{j}(\cdot )\) stands for activation function of the jth neuron, and it is a globally Lipschitz continuous and differentiable nonlinear function such that

$$\begin{aligned}& \bigl\vert f_{i}(x)-f_{i}(y) \bigr\vert \leq l_{i} \vert x-y \vert ,\quad l_{i} \geq 0, \forall x,y \in \mathbb{R}, \end{aligned}$$
(2)
$$\begin{aligned}& \bigl\vert f_{i}(\cdot ) \bigr\vert \leq M_{i},\quad M_{i} \ge 0; \end{aligned}$$
(3)

\(b_{ij}\), \(c_{ij}\), and \(d_{ij}\) are the corresponding connection weights associated with the neurons without delays, with discrete delays, and with distributed delays, respectively; \(\tau _{ij}(t)\) corresponds to the discrete asynchronous transmission time-varying delay along with the axon of the unit j to the unit i at time t such that

$$ \tau _{ij}(t)\geq 0, \qquad \max_{1\leq j\leq n}\sup _{t \geq 0}\tau _{ij}(t)\leq \tau _{i}, \qquad 0 \leq \frac{\mathrm{d}\tau _{ij}(t)}{\mathrm{d}t}\leq \alpha < 1,\quad i=1,2, \ldots ,n; $$
(4)

\(h_{ij}(t)\) corresponds to the distributed asynchronous transmission time-varying delay along with the axon of the unit j to the unit i at time t, and satisfies

$$ h_{ij}(t)\geq 0, \qquad \max_{1\leq j\leq n}\sup _{t \geq 0}h_{ij}(t)\leq h_{i}, \quad i=1,2, \ldots ,n; $$
(5)

\(u_{i}\) is a constant, and represents the external input of the ith neuron.

For model (1), its initial conditions are assumed to be

$$ x_{i}(s)=\varphi _{i}(s),\quad \forall s \in [-\overline{ \tau _{i}}, 0], $$
(6)

where \(\varphi _{i}(s)\) is real-valued continuous function, and

$$ \overline{\tau _{i}}=\max \{\tau _{i},h_{i} \},\quad \forall i\in \{1,2, \ldots ,n\}. $$
(7)

Remark 1

\(\tau _{ij}(t)\) and \(h_{ij}(t)\) above receive different information between different nodes at time t, which means that the time-varying delays are asynchronous in system (1). Therefore, model (1) is more general than Refs. [22, 26].

Assume that \(x^{*}\) is a balance of model (1), and \(x_{i}^{*}\) is its ith component. Then Eq. (1) becomes

$$ a_{i}x_{i}^{*}=\sum _{j=1}^{n}b_{ij}f_{j} \bigl(x_{j}^{*}\bigr)+\sum_{j=1}^{n}c_{ij}f_{j} \bigl(x_{j}^{*}\bigr)+ \sum_{j=1}^{n}d_{ij}h_{ij}(t)f_{j} \bigl(x_{j}^{*}\bigr)+u_{i}. $$
(8)

By Ref. [20], we can define the global exponential asymptotic stability of \(x^{*}\).

Definition 1

The equilibrium point \(x^{*}\) in model (1) is said to have global exponential asymptotic stability, if there are \(M \geq 1\) and \(\gamma > 0\) such that each solution of Eq. (1) satisfies

$$ \sum_{i=1}^{n} \bigl\vert x_{i}(t)-x_{i}^{*} \bigr\vert \leq M e^{-\gamma t} \sum_{i=1}^{n} \sup _{s\in \varOmega } \bigl\vert \varphi _{i}(s)-x_{i}^{*} \bigr\vert , $$
(9)

where \(\varphi _{i}(s)\) is the initial continuous function, and Ω is a set of real numbers.

3 Main results and proofs

In this section, we will show that there is a unique balance point \(x^{*}\) in the neural networks (1), and it shows global exponential asymptotic stability.

Theorem 1

Suppose that (2), (3), and (5) hold. If for eachi, \(i\in \{1,2,\ldots ,n \}\), one has

$$ l_{i}\sum_{j=1}^{n}\bigl( \vert c_{ji} \vert + \vert b_{ji} \vert + \vert d_{ji} \vert h_{j}\bigr)< a_{i} , $$
(10)

then the equilibrium point\(x^{*}\)exists and is unique in system (1).

Proof

On account of \(a_{i} > 0\), (8) can turn into

$$ \textstyle\begin{cases} x_{i}^{*}=\frac{1}{a_{i}}[\sum_{j=1}^{n}b_{ij}f_{j}(x_{j}^{*})+\sum_{j=1}^{n}c_{ij}f_{j}(x_{j}^{*})+ \sum_{j=1}^{n}d_{ij}h_{ij}(t)f_{j}(x_{j}^{*})+u_{i}], \\ \quad t \geq 0, i=1,2,\ldots ,n. \end{cases} $$
(11)

Let

$$ g_{i}(x_{1}, x_{2},\ldots,x_{n})= \frac{1}{a_{i}}\Biggl[\sum_{j=1}^{n}b_{ij}f_{j}(x_{j})+ \sum_{j=1}^{n}c_{ij}f_{j}(x_{j})+ \sum_{j=1}^{n}d_{ij}h_{ij}(t)f_{j}(x_{j})+u_{i} \Biggr]. $$

Then we know that \(x_{i}^{*}\) is a fixed point of the mapping \(g_{i}(x)\) from Eq. (11). Hence the equilibrium point of Eq. (1) can be determined by the fixed points of functions \(g_{1}(x), g_{2}(x), \ldots \) , and \(g_{n}(x)\) within a specific range. Let \(x(t)\) be the vector \((x_{1}(t), x_{2}(t),\ldots ,x_{n}(t))^{T} \), and Φ be a hypercube set defined by

$$ \varPhi =\Biggl\{ x(t) \Bigm| \bigl\vert x_{i}(t) \bigr\vert \leq \frac{1}{a_{i}}\Biggl[\sum_{j=1}^{n} \bigl( \vert b_{ij} \vert + \vert c_{ij} \vert + \vert d_{ij} \vert h_{i}\bigr)M_{j}+ \vert u_{i} \vert \Biggr],i=1,2, \ldots ,n\Biggr\} . $$
(12)

By the hypotheses (3) and (5), we can get

$$\begin{aligned} \bigl\vert g_{i}\bigl(x_{1}^{*}, x_{2}^{*},\ldots ,x_{n}^{*}\bigr) \bigr\vert =& \Biggl\vert \frac{1}{a_{i}}\Biggl[ \sum _{j=1}^{n}b_{ij}f_{j} \bigl(x_{j}^{*}\bigr)+\sum_{j=1}^{n}c_{ij}f_{j} \bigl(x_{j}^{*}\bigr)+ \sum_{j=1}^{n}d_{ij}h_{ij}(t)f_{j} \bigl(x_{j}^{*}\bigr)+u_{i}\Biggr] \Biggr\vert \\ \leq &\frac{1}{a_{i}}\Biggl[\sum_{j=1}^{n} \vert b_{ij} \vert M_{j}+\sum _{j=1}^{n} \vert c_{ij} \vert M_{j}+ \sum_{j=1}^{n} \vert d_{ij} \vert h_{i}M_{j}+ \vert u_{i} \vert \Biggr] \\ \leq &\frac{1}{a_{i}}\Biggl[\sum_{j=1}^{n} \bigl( \vert b_{ij} \vert + \vert c_{ij} \vert + \vert d_{ij} \vert h_{i}\bigr)M_{j}+ \vert u_{i} \vert \Biggr]. \end{aligned}$$
(13)

Let \(g(x)\) be the vector function \((g_{1}(x),g_{2}(x),\ldots ,g_{n}(x))^{T}\). From the continuity of \(f_{i}\), we know that \(g(x)\) is a continuous mapping from set Φ to Φ. By Brouwer’s fixed point theorem, there is at least one \(x^{*}\in \varPhi \) such that

$$ g_{i}\bigl(x^{*}\bigr)=x_{i}^{*},\quad \forall i\in \{1,2,\ldots ,n\}. $$

It follows that there is at least one equilibrium point in Eq. (1).

Next, we will show the uniqueness of the equilibrium point in Eq. (1).

Let \(y^{*}=(y_{1}^{*}, y_{2}^{*},\ldots ,y_{n}^{*})^{T}\) be also an equilibrium point of model (1). From (2), (3), and (8), we can obtain

$$\begin{aligned} \bigl\vert y_{i}^{*}-x_{i}^{*} \bigr\vert =&\frac{1}{a_{i}} \Biggl\vert \sum _{j=1}^{n}\bigl(c_{ij}+b_{ij}+d_{ij}h_{ij}(t) \bigr) \bigl(f_{j}\bigl(y_{j}^{*} \bigr)-f_{j}\bigl(x_{j}^{*}\bigr)\bigr) \Biggr\vert \\ \leq &\frac{1}{a_{i}}\sum_{j=1}^{n} \bigl( \vert c_{ij} \vert + \vert b_{ij} \vert + \vert d_{ij} \vert h_{ij}(t)\bigr)l_{j} \bigl\vert y_{j}^{*}-x_{j}^{*} \bigr\vert \\ \leq &\frac{1}{a_{i}}\sum_{j=1}^{n}l_{j} \bigl( \vert c_{ij} \vert + \vert b_{ij} \vert + \vert d_{ij} \vert h_{i}\bigr) \bigl\vert y_{j}^{*}-x_{j}^{*} \bigr\vert . \end{aligned}$$
(14)

Summing over all the neurons that satisfy the inequality (14), we get

$$\begin{aligned} \sum_{i=1}^{n} \bigl\vert y_{i}^{*}-x_{i}^{*} \bigr\vert \leq & \sum_{i=1}^{n}\sum _{j=1}^{n} \frac{1}{a_{i}}l_{j} \bigl( \vert c_{ij} \vert + \vert b_{ij} \vert + \vert d_{ij} \vert h_{i}\bigr) \bigl\vert y_{j}^{*}-x_{j}^{*} \bigr\vert \\ \leq &\sum_{i=1}^{n}\sum _{j=1}^{n}\frac{1}{a_{i}}l_{i} \bigl( \vert c_{ji} \vert + \vert b_{ji} \vert + \vert d_{ji} \vert h_{j}\bigr) \bigl\vert y_{i}^{*}-x_{i}^{*} \bigr\vert . \end{aligned}$$
(15)

It follows that

$$ \sum_{i=1}^{n} \bigl\vert y_{i}^{*}-x_{i}^{*} \bigr\vert \Biggl[a_{i}-l_{i}\sum _{j=1}^{n}\bigl( \vert c_{ji} \vert + \vert b_{ji} \vert + \vert d_{ji} \vert h_{j}\bigr)\Biggr] = 0. $$
(16)

According to the condition (10), we can get

$$ x_{i}^{*}=y_{i}^{*},\quad i=1,2, \ldots ,n, $$

implying that there exists a unique equilibrium in model (1). □

Theorem 2

Suppose that (2)–(5), and (10) hold, and we have\(\beta \geq 1\)and\(q > 0\)such that

$$ \beta =\max_{1 \leq i \leq n}\Biggl\{ 1+\sum _{j=1}^{n} \vert c_{ji} \vert l_{i} \tau _{j}\frac{e^{q\tau _{j}}}{1-\alpha }+\sum _{j=1}^{n} \vert d_{ji} \vert l_{i}\biggl( \frac{1}{q^{2}}+\frac{q h_{j}-1}{q^{2}}e^{qh_{j}} \biggr)\Biggr\} . $$
(17)

If the equilibrium point\(x^{*}\)and each solution of Eq. (1) with the initial conditions (6) satisfy

$$ \sum_{i=1}^{n} \bigl\vert x_{i}(t)-x_{i}^{*} \bigr\vert \leq \beta e^{-qt} \sum_{i=1}^{n} \sup_{s\in [-\overline{\tau _{i}}, 0]} \bigl\vert \varphi _{i}(s)-x_{i}^{*} \bigr\vert , $$
(18)

then\(x^{*}\)is the global exponential asymptotic stability.

Proof

By Theorem 1, model (1) exists a unique balance point under the assumptions (2), (3), (5), and (10), and we denote it as \(x^{*}\). Then from Eq. (1), we have

$$\begin{aligned} \frac{\mathrm{d} \vert x_{i}(t)-x_{i}^{*} \vert }{\mathrm{d}t} \leq & -a_{i} \bigl\vert x_{i}(t)-x_{i}^{*} \bigr\vert + \sum _{j=1}^{n} \vert b_{ij} \vert l_{j} \bigl\vert x_{j}(t)-x_{j}^{*} \bigr\vert +\sum_{j=1}^{n} \vert c_{ij} \vert l_{j}\bigl|x_{j}\bigl(t- \tau _{ij}(t)\bigr)-x_{j}^{*} \bigr\vert \\ &{}+\sum_{j=1}^{n} \vert d_{ij} \vert \int _{t-h_{ij}(t)}^{t}l_{j}|x_{j}(s)-x_{j}^{*}|\,ds. \end{aligned}$$
(19)

Assumed that

$$ y_{i}(t)=e^{qt} \bigl\vert x_{i}(t)-x_{i}^{*} \bigr\vert ,\quad t\geq -\overline{\tau _{i}}, i=1,2, \ldots ,n. $$

Then the derivative along with (19) is

$$\begin{aligned} \frac{\mathrm{d}y_{i}(t)}{\mathrm{d}t} =& qe^{qt} \bigl\vert x_{i}(t)-x_{i}^{*} \bigr\vert +e^{qt} \frac{\mathrm{d} \vert x_{i}(t)-x_{i}^{*} \vert }{\mathrm{d}t} \\ \leq & -(a_{i}-q)y_{i}(t) +e^{qt}\sum _{j=1}^{n} \vert b_{ij} \vert l_{j} \bigl\vert x_{j}(t)-x_{j}^{*} \bigr\vert +e^{qt} \sum_{j=1}^{n} \vert c_{ij} \vert l_{j}\bigl|x_{j}\bigl(t- \tau _{ij}(t)\bigr)-x_{j}^{*} \bigr\vert \\ &{}+e^{qt}\sum_{j=1}^{n} \vert d_{ij} \vert \int _{t-h_{ij}(t)}^{t}l_{j}\bigl|x_{j}(s)-x_{j}^{*}\bigr|\,ds. \end{aligned}$$
(20)

Since

$$\begin{aligned} e^{qt} \int _{t-h_{ij}(t)}^{t} \bigl\vert x_{j}(s)-x_{j}^{*} \bigr\vert \,ds \leq & e^{qt} \int _{t-h_{i}}^{t} \bigl\vert x_{j}(s)-x_{j}^{*} \bigr\vert \,ds \\ =&e^{qt} \int _{0}^{h_{i}} \bigl\vert x_{j}(u+t-h_{i})-x_{j}^{*} \bigr\vert \,du \\ =& \int _{0}^{h_{i}}e^{q(h_{i}-u)}y_{j}(u+t-h_{i})\,du, \end{aligned}$$
(21)

we substitute (21) into (20), and get

$$\begin{aligned} \frac{\mathrm{d}y_{i}(t)}{\mathrm{d}t} \leq & -(a_{i}-q)y_{i}(t) +e^{qt} \sum_{j=1}^{n} \vert b_{ij} \vert l_{j} \bigl\vert x_{j}(t)-x_{j}^{*} \bigr\vert +e^{qt}\sum_{j=1}^{n} \vert c_{ij} \vert l_{j}\bigl|x_{j}\bigl(t- \tau _{ij}(t)\bigr)-x_{j}^{*} \bigr\vert \\ &{}+\sum_{j=1}^{n}|d_{ij}|l_{j} \int _{0}^{h_{i}}e^{q(h_{i}-u)}y_{j}(u+t-h_{i})\,du. \end{aligned}$$
(22)

Consider a Lyapunov function \(V(t)=V(y_{1}, y_{2},\ldots ,y_{n})(t)\) defined by

$$\begin{aligned} V(t) =& \sum_{i=1}^{n} \Biggl\{ y_{i}(t)+\sum_{j=1}^{n} \vert c_{ij} \vert l_{j} \frac{e^{q\tau _{i}}}{1-\alpha } \int _{(t-\tau _{ij}(t))}^{t} y_{j}(s)\,ds \\ &{}+\sum_{j=1}^{n} \vert d_{ij} \vert l_{j} \int _{0}^{h_{i}}e^{q(h_{i}-u)} \int _{u+t-h_{i}}^{t}y_{j}(w)\,dw\,du \Biggr\} . \end{aligned}$$
(23)

Taking the derivative of \(V(t)\) along with (19), we get

$$\begin{aligned} \frac{\mathrm{d}V(t)}{\mathrm{d}t} =& \sum_{i=1}^{n} \Biggl\{ \frac{\mathrm{d}y_{i}(t)}{\mathrm{d}t}+\sum_{j=1}^{n} \vert c_{ij} \vert l_{j} \frac{e^{q\tau _{i}}}{1-\alpha } \bigl(y_{j}(t)-y_{j}\bigl(t-\tau _{ij}(t) \bigr) \bigl(1- \dot{\tau }_{ij}(t)\bigr)\bigr) \\ &{}+\sum_{j=1}^{n} \vert d_{ij} \vert l_{j} \int _{0}^{h_{i}}e^{q(h_{i}-u)} \bigl(y_{j}(t)-y_{j}(u+t-h_{i})\bigr)\,du \Biggr\} \\ \leq & -\sum_{i=1}^{n} \Biggl\{ (a_{i}-q)y_{i}(t)-\sum_{j=1}^{n} \vert b_{ij} \vert l_{j}y_{j}(t)- \sum _{j=1}^{n} \vert c_{ji} \vert l_{i}\frac{e^{q\tau _{i}}}{1-\alpha }y_{j}(t) \\ &{}-\sum_{j=1}^{n} \vert d_{ij} \vert l_{j} \int _{0}^{h_{i}}e^{q(h_{i}-u)}y_{j}(t)\,du \Biggr\} \\ =& -\sum_{i=1}^{n} \Biggl\{ (a_{i}-q)-\sum_{j=1}^{n} \vert b_{ji} \vert l_{i}-\sum _{j=1}^{n} \vert c_{ji} \vert l_{i} \frac{e^{q\tau _{j}}}{1-\alpha } \\ &{}-\sum_{j=1}^{n} \vert d_{ji} \vert l_{i}\frac{e^{qh_{j}}-1}{q}\Biggr\} y_{i}(t). \end{aligned}$$
(24)

Let \(F_{i}(q_{i})\) be an auxiliary continuous function related to index i, defined by

$$ F_{i}(q_{i})=a_{i}-q_{i}-l_{i} \sum_{j=1}^{n} \vert b_{ji} \vert -l_{i}\sum_{j=1}^{n} \vert c_{ji} \vert \frac{e^{q_{i}\tau _{j}}}{(1-\alpha )^{q_{i}/q}} -l_{i}\sum _{j=1}^{n} \vert d_{ji} \vert \Biggl[h_{j}+ \sum_{k=2}^{\infty } \frac{q_{i}^{k-1}h_{j}^{k}}{k!}\Biggr], $$
(25)

where \(q_{i}\) is a positive real number, and i is a positive nature number not bigger than n. In view of the hypothesis (10), one has

$$ F_{i}(0)=a_{i}-l_{i}\sum _{j=1}^{n} \vert b_{ji} \vert -l_{i}\sum_{j=1}^{n} \vert c_{ji} \vert -l_{i} \sum _{j=1}^{n} \vert d_{ji} \vert h_{j}>0. $$
(26)

From the continuity of \(F_{i}\), there exists \(q_{i}^{*}\in (0,+\infty )\) such that

$$ F_{i}\bigl(q_{i}^{*}\bigr)>0, \quad i=1,2,\ldots ,n. $$

Without loss of generality, let \(q=\max_{1\leq i\leq n}\{q_{1}^{*},q_{2}^{*},\ldots ,q_{n}^{*} \}\). Then

$$\begin{aligned} F_{i}(q) =&a_{i}-q-l_{i}\sum _{j=1}^{n} \vert b_{ji} \vert -l_{i}\sum_{j=1}^{n} \vert c_{ji} \vert \frac{e^{q\tau _{j}}}{1-\alpha } -l_{i}\sum _{j=1}^{n} \vert d_{ji} \vert \Biggl[h_{j}+ \sum_{k=2}^{\infty } \frac{q^{k-1}h_{j}^{k}}{k!}\Biggr] \\ =&(a_{i}-q)-\sum_{j=1}^{n} \vert b_{ji} \vert l_{i}-\sum _{j=1}^{n} \vert c_{ji} \vert l_{i} \frac{e^{q\tau _{j}}}{1-\alpha }-\sum_{j=1}^{n} \vert d_{ji} \vert l_{i} \frac{e^{qh_{j}}-1}{q} >0. \end{aligned}$$
(27)

Therefore, by (24) and (27), one can see that the derivative of \(V(t)\) is smaller than 0 for \(t\in [0, + \infty ]\). Based on the definition of \(V(t)\) and the assumption (4), we obtain

$$ \sum_{i=1}^{n}e^{qt} \bigl\vert x_{i}(t)-x_{i}^{*} \bigr\vert \leq V(t)\leq V(0), $$
(28)

where

$$\begin{aligned} V(0) =&\sum_{i=1}^{n} \Biggl\{ y_{i}(0)+\sum_{j=1}^{n} \vert c_{ij} \vert l_{j} \frac{e^{q\tau _{i}}}{1-\alpha } \biggl\vert \int _{-\tau _{ij}(0)}^{0} y_{j}(s)\,ds \biggr\vert \\ &{}+ \sum_{j=1}^{n} \vert d_{ij} \vert l_{j} \int _{0}^{h_{i}}e^{q(h_{i}-u)} \int _{u-h_{i}}^{0}y_{j}(w)\,dw\,du \Biggr\} \\ \leq &\sum_{i=1}^{n} \Biggl\{ y_{i}(0)+\sum_{j=1}^{n} \vert c_{ij} \vert l_{j}\tau _{i} \frac{e^{q\tau _{i}}}{1-\alpha }\sup_{s\in [-\tau _{i}, 0]}y_{j}(s) \\ &{}+ \sum _{j=1}^{n} \vert d_{ij} \vert l_{j} \int _{0}^{h_{i}}e^{q(h_{i}-u)}(h_{i}-u)\,du \sup_{s\in [-h_{i}, 0]}y_{j}(s)\Biggr\} \\ =&\sum_{i=1}^{n} \Biggl\{ y_{i}(0)+\sum_{j=1}^{n} \vert c_{ij} \vert l_{j}\tau _{i} \frac{e^{q\tau _{i}}}{1-\alpha }\sup_{s\in [-\tau _{i}, 0]}y_{j}(s) \\ &{}+ \sum _{j=1}^{n} \vert d_{ij} \vert l_{j}\biggl(\frac{1}{q^{2}}+\frac{q h_{i}-1}{q^{2}}e^{qh_{i}} \biggr) \sup_{s\in [-h_{i}, 0]}y_{j}(s)\Biggr\} \\ \leq &\sum_{i=1}^{n} \Biggl\{ 1+\sum _{j=1}^{n} \vert c_{ji} \vert l_{i}\tau _{j} \frac{e^{q\tau _{j}}}{1-\alpha } \\ &{}+\sum _{j=1}^{n} \vert d_{ji} \vert l_{i}\biggl( \frac{1}{q^{2}}+\frac{q h_{j}-1}{q^{2}}e^{qh_{j}} \biggr)\Biggr\} \sup_{s \in [-\overline{\tau _{i}}, 0]} \bigl\vert \varphi _{i}(s)-x^{*} \bigr\vert \\ \leq & \beta \sum_{i=1}^{n}\sup _{s\in [- \overline{\tau _{i}}, 0]} \bigl\vert \varphi _{i}(s)-x^{*} \bigr\vert . \end{aligned}$$
(29)

Combining (17), (28), and (29), one can derive the inequality (18), and thus the equilibrium point \(x^{*}\) of Eq. (1) has the global exponential asymptotic stability on account of Definition 1. □

Remark 2

The constant \(\beta \geq 1\), which plays a significant role in the index of convergence of model (1), relies on the distributive delay \(h_{j}\) and delay \(\tau _{j}\) for \(j=1,2,\ldots ,n\). If either the discrete delay \(\tau _{j}\) or the distribution delay \(h_{j}\) of (17) is sufficiently large, namely, the discrete asynchronous delays \(\tau _{ij}(t)\) of (4) and distributed asynchronous delays \(h_{ij}(t)\) of (5) are sufficiently large, then β will be large enough, and thus the convergence time towards the equilibrium point will be longer. Therefore, the convergence time of model (1) can be shortened only if the two delays are reduced appropriately in the process of operation coordination.

4 Corollaries and comparisons

By Theorem 1 and Theorem 2, we will have the following corollaries. Meanwhile, we also will compare the conclusions of this paper with the existing literature.

When \(h_{ij}(t)=0\) for \(i, j\in \{1,2,\ldots ,n\}\), Eq. (1) changes into the following neural networks:

$$ \frac{\mathrm{d}x_{i}(t)}{\mathrm{d}t} =-a_{i}x_{i}(t)+\sum _{j=1}^{n}b_{ij}f_{j} \bigl(x_{j}(t)\bigr)+ \sum_{j=1}^{n}c_{ij}f_{j} \bigl(x_{j}\bigl(t-\tau _{ij}(t)\bigr)\bigr)+ u_{i}, \quad t \ge 0, $$
(30)

and its initial conditions are

$$ x_{i}(s)=\varphi _{i}(s),\quad \forall s \in [-\tau _{i}, 0], $$
(31)

where i is a positive integer not bigger than n.

Corollary 1

Assume that (2) and (3) are true. If for eachi, \(i\in \{1,2,\ldots ,n \}\), one has

$$ l_{i}\sum_{j=1}^{n}\bigl( \vert c_{ji} \vert + \vert b_{ji} \vert \bigr)< a_{i}, $$
(32)

then the equilibrium point\(x^{*}\)exists and is unique in the system (30).

Corollary 2

Suppose that (2)–(4), and (32) hold. If there exist two constants\(\beta \geq 1\)and\(q > 0\)such that

$$ \beta =\max_{1 \leq i \leq n}\Biggl\{ 1+\sum _{j=1}^{n} \vert c_{ji} \vert l_{i} \tau _{j}\frac{e^{q\tau _{j}}}{1-\alpha }\Biggr\} , $$
(33)

and the equilibrium point\(x^{*}\)and each solution of Eq. (30) with the initial conditions (31) satisfy

$$ \sum_{i=1}^{n} \bigl\vert x_{i}(t)-x_{i}^{*} \bigr\vert \leq \beta e^{-qt} \sum_{i=1}^{n} \sup_{s\in [-\tau _{i}, 0]} \bigl\vert \varphi _{i}(s)-x_{i}^{*} \bigr\vert , $$
(34)

then\(x^{*}\)is the global exponential asymptotic stability.

Remark 3

By Ref. [26], the equilibrium point of model (30) with discrete asynchronous time-varying delay is the same to that without delays. Meanwhile \(h_{ij}(t)\neq 0\), by Theorem 1, the equilibrium point of model (1) will be affected by \(h_{ij}(t)\), \(t>0\).

When \(\tau _{ij}(t)=0\) for \(i, j\in \{1,2,\ldots ,n\}\), Eq. (1) turns into the following neural networks:

$$\begin{aligned} \frac{\mathrm{d}x_{i}(t)}{\mathrm{d}t} =&-a_{i}x_{i}(t)+\sum _{j=1}^{n}b_{ij}f_{j} \bigl(x_{j}(t)\bigr)+ \sum_{j=1}^{n}c_{ij}f_{j} \bigl(x_{j}(t)\bigr) \\ &{}+\sum_{j=1}^{n}d_{ij} \int _{t-h_{ij}(t)}^{t}f_{j} \bigl(x_{j}(s)\bigr)\,ds+u_{i},\quad t \ge 0, \end{aligned}$$
(35)

and its initial conditions are

$$ x_{i}(s)=\varphi _{i}(s),\quad \forall s \in [-h_{i}, 0], $$
(36)

where i is a natural number, belonging to the set \(\{1,2,\ldots ,n\}\).

Corollary 3

Suppose that (2), (3), and (5) hold. If for eachi, \(i\in \{1,2,\ldots ,n \}\), we have

$$ l_{i}\sum_{j=1}^{n}\bigl( \vert b_{ji} \vert + \vert d_{ji} \vert h_{j}\bigr)< a_{i}, $$
(37)

then the equilibrium point\(x^{*}\)exists and is unique in the system (35).

Corollary 4

Suppose that (2), (3), (5), and (36) hold. If we have\(\beta \geq 1\)and\(q > 0\)such that

$$ \beta =\max_{1 \leq i \leq n}\Biggl\{ 1+\sum _{j=1}^{n} \vert d_{ji} \vert l_{i}\biggl( \frac{1}{q^{2}}+\frac{q h_{j}-1}{q^{2}}e^{qh_{j}} \biggr)\Biggr\} , $$
(38)

and the equilibrium point\(x^{*}\)and each solution of Eq. (35) with the initial conditions (36) satisfy

$$ \sum_{i=1}^{n} \bigl\vert x_{i}(t)-x_{i}^{*} \bigr\vert \leq \beta e^{-qt} \sum_{i=1}^{n} \sup_{s\in [-h_{i}, 0]} \bigl\vert \varphi _{i}(s)-x_{i}^{*} \bigr\vert , $$
(39)

then\(x^{*}\)has the global exponential asymptotic stability.

When \(\tau _{ij}(t)=\tau (t)\) and \(h_{ij}(t)= h(t)\) for \(i, j\in \{1,2,\ldots ,n\}\), let \(\sup_{t\geq 0}\tau (t)\leq \tau \), and \(\sup_{t\geq 0}h(t)\leq h\). Hence Eq. (1) changes into

$$ \textstyle\begin{cases} \frac{\mathrm{d}x_{i}(t)}{\mathrm{d}t} =-a_{i}x_{i}(t)+\sum_{j=1}^{n}b_{ij}f_{j}(x_{j}(t))+ \sum_{j=1}^{n}c_{ij}f_{j}(x_{j}(t-\tau (t))) \\ \hphantom{\frac{\mathrm{d}x_{i}(t)}{\mathrm{d}t} ={}}{}+\sum_{j=1}^{n}d_{ij} \int _{t-h(t)}^{t}f_{j}(x_{j}(s))\,ds+u_{i}, \\ \hphantom{\frac{\mathrm{d}x_{i}(t)}{\mathrm{d}t} ={}}{}i=1,2,\ldots ,n, t \ge 0, \end{cases} $$
(40)

and its initial conditions are

$$ \textstyle\begin{cases} x_{i}(s)=\varphi _{i}(s), \quad \forall s \in [-\overline{\tau }, 0], \\ \quad i=1,2,\ldots ,n, t \ge 0, \end{cases} $$
(41)

where \(\varphi _{i}(s)\) is real-valued continuous functions, and

$$ \overline{\tau }=\max_{t\geq 0}\{\tau , h\}. $$
(42)

Corollary 5

Suppose that (2), (3), and (5) hold. If for eachi, \(i\in \{1,2,\ldots ,n \}\), we have

$$ l_{i}\sum_{j=1}^{n}\bigl( \vert b_{ji} \vert + \vert c_{ji} \vert + \vert d_{ji} \vert h\bigr)< a_{i}, $$
(43)

then the equilibrium point\(x^{*}\)exists and is unique in the system (40).

Corollary 6

Suppose that (2)–(5), and (43) hold, and we have\(\beta \geq 1\)and\(q > 0\)such that

$$ \beta =\max_{1 \leq i \leq n}\Biggl\{ 1+\sum _{j=1}^{n} \vert c_{ji} \vert l_{i} \tau \frac{e^{q\tau }}{1-\alpha }+\sum_{j=1}^{n} \vert d_{ji} \vert l_{i}\biggl( \frac{1}{q^{2}}+\frac{q h-1}{q^{2}}e^{qh}\biggr)\Biggr\} . $$
(44)

If the equilibrium point\(x^{*}\)and each solution of Eq. (40) with the initial conditions (41) satisfy

$$ \sum_{i=1}^{n} \bigl\vert x_{i}(t)-x_{i}^{*} \bigr\vert \leq \beta e^{-qt} \sum_{i=1}^{n} \sup_{s\in [-\overline{\tau }, 0]} \bigl\vert \varphi _{i}(s)-x_{i}^{*} \bigr\vert , $$
(45)

then\(x^{*}\)has the global exponential asymptotic stability.

Remark 4

The system (40) is one of the RNNs with distributive and discrete delays, which occur to the literature [22]. In this paper, we show the balance \(x^{*}\) of Eq. (40) is the global exponential asymptotic stability via the Lyapunov function method, which is different from the method used in the literature [22].

5 Simulation example

Example

We consider the following two-dimensional neural network model:

$$ \textstyle\begin{cases} \frac{\mathrm{d}x_{1}(t)}{\mathrm{d}t} =-5x_{1}(t)+0.2f_{1}(x_{1}(t))+0.3f_{2}(x_{2}(t))+1.7f_{1}(x_{1}(t- \tau _{11}(t))) \\ \hphantom{\frac{\mathrm{d}x_{1}(t)}{\mathrm{d}t} ={}}{} +0.8f_{2}(x_{2}(t-\tau _{12}(t))) +0.3\int _{t-h_{11}(t)}^{t}f_{1}(x_{1}(s))\,ds \\ \hphantom{\frac{\mathrm{d}x_{1}(t)}{\mathrm{d}t} ={}}{}+0.2 \int _{t-h_{12}(t)}^{t}f_{2}(x_{2}(s))\,ds+2.5, \\ \frac{\mathrm{d}x_{2}(t)}{\mathrm{d}t} =-7x_{2}(t)+0.1f_{1}(x_{1}(t))+0.4f_{2}(x_{2}(t)) +0.8f_{1}(x_{1}(t- \tau _{21}(t))) \\ \hphantom{\frac{\mathrm{d}x_{2}(t)}{\mathrm{d}t} ={}}{} +0.9f_{2}(x_{2}(t-\tau _{22}(t))) -0.2\int _{t-h_{21}(t)}^{t}f_{1}(x_{1}(s))\,ds \\ \hphantom{\frac{\mathrm{d}x_{2}(t)}{\mathrm{d}t} ={}}{}+0.4 \int _{t-h_{22}(t)}^{t}f_{2}(x_{2}(s))\,ds+1.5, \end{cases} $$
(46)

where \(f_{i}(x_{i}(t))=\tanh (x_{i}(t))\), \(\tau _{11}(t)=\tau _{21}(t)=0.49+0.49\sin (0.02t)\), \(\tau _{12}(t)=\tau _{22}(t)=0.48+0.48\cos (0.03t)\), \(h_{11}(t)=h_{21}(t)=1.5+e^{-t}\), and \(h_{12}(t)=h_{22}(t)=3+e^{-t}\). For the initial condition is considered that \(x_{1}(s)=\ln (s+3.9)\), \(x_{2}(s)=0.4e^{s}-0.7\), \(s\in [-4,0]\).

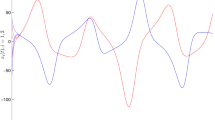
After comparison and simple calculation, we know that Eq. (46) represents a two-dimensional RNN with discrete and distributed asynchronous time-varying delays, and satisfies all the assumptions of Theorem 1 and Theorem 2. In Fig. 1, we illustrate state trajectories of \(x_{1}\) and \(x_{2}\) of model (46), which show that model (46) has a unique and exponential asymptotically stable equilibrium point.

Figure 1
figure 1

State trajectories of model (46)

Full size image

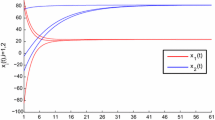
In Fig. 2, we illustrate state trajectories of \(x_{1}\) and \(x_{2}\) of model (46) under three other different initial conditions: \(x_{1}(s)=0.4\), \(x_{2}(s)=0.7\); \(x_{1}(s)=-0.5+e^{s}\), \(x_{2}(s)=0.4e^{s}\) and \(x_{1}(s)=-0.9\), \(x_{2}(s)=-0.3\), which demonstrate that exponential convergence of model (46) is global. Therefore, Figs. 1 and 2 show fully the effectiveness of our results in this paper.

Figure 2
figure 2

State trajectories of model (46) under three other initial conditions

Full size image

Taking out the distributed delay, model (46) turns into a two-dimensional RNN with discrete asynchronous time-varying delays. Figure 3 illustrates its state trajectories, which are marked as x1-discrete and x2-discrete, respectively. Meanwhile, Fig. 3 also shows the sate trajectories of \(x_{1}\) and \(x_{2}\) of model (46) without delays. From Fig. 3, we see that the dynamical behaviors of Eq. (46) without distributed delay and Eq. (46) without delay are converging toward the same equilibrium point.

Figure 3
figure 3

State trajectories of model (46) without distributed delay, or without delay

Full size image

Removing the discrete delay, model (46) becomes a two-dimensional RNN with distributive asynchronous time-varying delays. Figure 4 illustrates its state trajectories, which are marked as x1-distributed and x2-distributed, respectively. Meanwhile, Fig. 4 also demonstrate the sate trajectories of \(x_{1}\) and \(x_{2}\) of model (46) without delays. From Fig. 4, we see that the trajectories of Eq. (46) with distributive asynchronous time-varying delays and Eq. (46) without delay are different, which implies that the dynamical behavior of model (46) is affected by the distributed asynchronous time-varying delay.

Figure 4
figure 4

State trajectories of model (46) without discrete delay, or without delay

Full size image

In Fig. 5, we illustrate the state trajectories of model (46) with delays (i): \(\tau _{11}(t)=\tau _{21}(t)=0.49+0.49\sin (0.02t)\), \(\tau _{12}(t)=\tau _{22}(t)=0.48+0.48\cos (0.03t)\), \(h_{11}(t)=h_{21}(t)=1.5+e^{-t}\), \(h_{12}(t)=h_{22}(t)=3+e^{-t}\), and model (46) with delays (ii): \(\tau _{11}(t)=\tau _{21}(t)=0.11+0.11\sin (0.02t)\), \(\tau _{12}(t)=\tau _{22}(t)=0.09+0.09\cos (0.03t)\), \(h_{11}(t)=h_{21}(t)=0.1+e^{-t}\), \(h_{12}(t)=h_{22}(t)=0.2+e^{-t}\), which are marked as x1-big and x2-big, and x1-small and x2-small, respectively. Obviously, the maximum of all delays in (i) is bigger than that in (ii). From Fig. 5, we see that the stability convergence time of neural networks with big upper bound delay is longer than that of neural networks with small upper bound delay.

Figure 5
figure 5

State trajectories of model (46) with different asynchronous time-varying delays

Full size image

6 Conclusion

In the present paper, we discuss the RNNs with mixed asynchronous time-varying delays. By the Lyapunov function method, some algebra conditions are given to make the investigated model have a unique and global exponential asymptotically stable balance point. Meanwhile, we also show that the balance point of the neural networks with distributive asynchronous time-varying delays is different from that without distributed delays. Finally, one numerical example and its simulation are given to demonstrate the effectiveness of our results. The considered neural networks in this paper can be further discussed as regards their discrete-time analogue, and also can be investigated as regards their dynamical characteristics by adding pulses.