Finite-time adaptive neural network control for fractional-order chaotic PMSM via command filtered backstepping

Abstract

A finite-time adaptive neural network position tracking control method is considered for the fractional-order chaotic permanent magnet synchronous motor (PMSM) via command filtered backstepping in this paper. Firstly, a neural network with a fractional-order parametric update law is utilized to cope with the nonlinear and unknown functions. Then the command filtered technique is introduced to address the repeated derivative problem in backstepping. In addition, a novel finite-time control method is proposed by employing the fractional-order terminal sliding manifolds, designing the error compensation mechanism and the new virtual control laws. The finite-time convergence of the tracking error can be guaranteed by the proposed controller. Finally, the designed control method is verified by simulation results.

1 Introduction

Fractional calculus is an evolving theory in many relevant sciences which is opening new areas in mathematics. It is a generalization of conventional differentiation and integration to arbitrary order [1]. Due to its potential applications and interesting properties, the fractional calculus has captured considerable attention from scholars in many fields [2–5]. Currently, many interesting results associated with the fractional calculus have been given [6–8]. The research shows that the fractional-order controllers are more advantageous than that of traditional integer-order ones. And also, some meaningful results have been reported on the stability problems in the scope of fractional calculus. For instance, by utilizing the fractional-order Lyapunov stability criterion, the robust consensus tracking problem is investigated in [9] for fractional-order multiagent systems with external disturbances and heterogeneous unknown nonlinearities. Based on the Chebyshev neural network (NN) technique, an adaptive synchronization approach is proposed in [10] for a class of fractional-order micro-electro-mechanical systems with chaotic oscillation. Therefore, the research of fractional-order system is a meaningful work.

The permanent magnet synchronous motor (PMSM) has received wide acceptance for industry applications, owing to the superiorities of reliable operation, simple structure and high power density [11, 12]. The PMSM is a type of synchronous motor in which the field excitation generated in the stator windings is created by the rare-earth permanent magnet of the rotor. PMSM has been used in various areas such as robotics, wind generator, electric vehicles, pumps and ship electric propulsion systems. However, the multivariable and coupled mathematical model of PMSM can exhibit chaotic behavior while systemic parameters exceeding a certain critical value [13]. The chaotic motion for PMSM is not acceptable since it may lead to the controlled system collapse [14]. Recently, a large number of control design schemes for chaotic systems have been investigated. The OGY approach is considered to be an efficient tool for stabilizing chaotic systems [15]. The main weakness with this method is that it depends on an uncertain systemic parameter which is generally unmeasurable in real PMSM system. In order to avoid this problem, time-delay feedback control is a better choice for controlling unsteady periodic orbits of nonlinear systems with chaotic behavior [16]. One of the limitations with this approach is that the time-delay parameter is difficult to determine. Sliding mode control (SMC) is deemed to be a basic method for chaos control. In [17], an adaptive SMC approach combined composite feedback control technique is investigated to synchronize two different unknown dynamic nonlinear systems with disturbances and time-varying delay. However, the chattering phenomenon is the drawback of SMC in electrical power circuits. NN control scheme displays a great merit for controlling chaotic systems with uncertain parts. An NNs-based adaptive control strategy is presented in [18] to address the tracking control issue for input-delayed systems with state constraint. However, this method depends on precise mathematic model.

Adaptive backstepping technique has shown its advantages in controlling the nonlinear systems which does not satisfy matching conditions [19]. For the PMSM drive system with chaotic oscillation, the problem of position tracking control is addressed in [20] by using backstepping-based nonlinear adaptive control scheme. An adaptive SMC approach by fusing NN and backstepping is presented in [21] to control chaos of the PMSM. In [22], an adaptive fuzzy output feedback control method combined with the backstepping technique is considered for the PMSM with external load disturbance and parametric uncertainties. For a type of multi-input and multi-output (MIMO) uncertain nonlinear input-saturated systems, a fuzzy control method via backstepping technique is investigated in [23] to track a given trajectory. In [24], the tracking control issue for PMSM system with unknown parameters is studied by employing adaptive fuzzy finite-time control method. However, all the previously mentioned methods mainly focus on inter-order systems. Fractional differential equations can describe many natural behaviors briefly and accurately from the standpoint of modeling. Many researchers have devoted their efforts to the study of fractional-order PMSM systems [25–27]. In [25], the fractional-order model of PMSM is proposed by Yu et al. in the frequency domain, the experiment results have shown that the fractional differential equation presents more precise model for PMSM than conventional integer differential equation. Moreover, the stabilization problem for fractional-order PMSM is investigated by Guo and Mani et al. in [26, 27]. For fractional-order chaotic system, the synchronization issue is considered by using backstepping strategy in [28]. In [29], an adaptive fuzzy backstepping control method is investigated to converge the tracking error for a class of lower triangular structured fractional-order nonlinear uncertain systems. However, this work does not involve the finite-time convergence issue for nonlinear systems.

The finite-time control approach has several merits such as higher precision performance, faster response and better disturbance rejection property [30]. In [31], a finite-time hybrid adaptive intelligent backstepping SMC scheme is provided to suppress chaos for fractional-order chaotic systems. An adaptive NN terminal sliding mode output control approach for fractional-order nonlinear system with unknown actuator faults is proposed in [32] to obtain finite-time stability. One of the limitations with these methods is that the ‘explosion of complexity’ problem is unsolved in their works. Fortunately, dynamic surface control (DSC) technology affords an effective way to solve this issue. In [33], the NNs based adaptive DSC method is introduced to guarantee the convergence of the tracking error. However, this method ignores the effect of filtering errors induced by the DSC. Recently, command filtering-based backstepping technique combined an error compensation mechanism is an efficient method for solving the above problems [34]. For a class of high-order nonlinear systems, a finite-time tracking control problem is addressed in [35] by introducing the virtual control laws combined with finite-time filter. For the nonlinear saturated systems, a Levant differentiator combined fuzzy control approach is presented in [36] to ensure the finite-time convergence of the tracking error. However, the difference between this kind of the PMSM system and pure mathematical models is significant. Besides, the methods proposed in [33, 35, 36] are not applicable for fractional-order systems. To what degree new schemes can achieve finite-time convergence of the tracking error in the fractional-order PMSM system remains further study.

Motivated by the above discussions, a finite-time adaptive NN control approach is presented in this article. Compared with the existing achievements, the noteworthy contributions of this paper are summarized as:

• (1) The issue of the repeated derivative in backstepping is handled by utilizing command filters. Meanwhile, the filtering errors are compensated in finite time by introducing a fractional-order error compensating system.

• (2) A novel finite-time virtual signals are designed by employing appropriate terminal sliding surfaces such that the finite-time signal tracking is obtained.

• (3) In the field of fractional calculus, we integrate adaptive NNs, command filtered backstepping, fractional-order error compensating mechanism and terminal sliding surface technique into finite-time controller, which can solve the tracking problem for fractional-order PMSM with chaotic motion in finite time.

2 Fractional-order PMSM and preliminaries

Consider the equation of PMSM as follows [20]:

$$ \textstyle\begin{cases} \frac{d\varTheta }{dt}=w, \\ \frac{dw}{d{t}}=\sigma (i_{q}-w)-T_{L}, \\ \frac{di_{q}}{d{t}}=-{i_{q}}-{i_{d}w}+\gamma {w}+u_{q}, \\ \frac{di_{d}}{d{t}}=-{i_{d}}+{i_{q}}{w}+u_{d}, \end{cases} $$

(1)

where Θ, w, $i_{q}$ and $i_{d}$ denote system state variables, which mean the rotor position, the angular speed, the q-axis and d-axis currents. σ and γ stand for the dimensionless operating parameters. $T_{L}$ is load torque, $u_{q}$ and $u_{d}$ represent the $d-q$ axis voltages.

Let $x_{1}=\varTheta$, $x_{2}=w$, $x_{3}=i_{q}$ and $x_{4}=i_{d}$. The PMSM can be extended to the fractional domain as [26, 37]

$$ \textstyle\begin{cases} {}^{C}_{0}D_{t}^{\alpha }x_{1}=x_{2}, \\ {}^{C}_{0}D_{t}^{\alpha }x_{2}=\sigma ({x_{3}}-{x_{2}})-T_{L}, \\ {}^{C}_{0}D_{t}^{\alpha }x_{3}=-{x_{3}}-{x_{2}}{x_{4}}+\gamma {x_{2}}+u_{q}, \\ {}^{C}_{0}D_{t}^{\alpha }x_{4}=-{x_{4}}+{x_{2}}{x_{3}}+u_{d}, \end{cases} $$

(2)

where α stands for the fractional order.

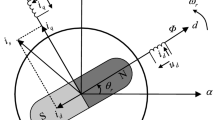
It should be mentioned that the dynamics of the system (2) are usually highly nonlinear on account of the coupling between the currents and the angular speed. Meanwhile, the parameter uncertainties may also influence the dynamic performance of the PMSM. Related research proves that the fractional-order PMSM exhibits chaos oscillation when σ and γ over a certain critical value in the case of zero external inputs. For instance, the fractional-order PMSM presents chaos with $\sigma =5.46$ and $\gamma =26.5$. Figure 1 shows the chaotic attractor with $\alpha =0.98$. It is clear that the chaotic behavior can break the stable performance of the fractional-order PMSM system.

Figure 1

Typical strange attractor in the case of $\alpha =0.98$, $\sigma =5.46$ and $\gamma =26.5$

To remove the chaos in fractional-order PMSM, we use $u_{q}$ and $u_{d}$ as the control signals. The objective is to construct $u_{q}$ and $u_{d}$ such that the rotor position $x_{1}$ follows the desired value $x_{d}$ and the tracking error performs finite-time convergence. For convenience of the controller design, we introduce some properties of fractional-order differential and integral equations.

The Caputo definition of fractional-order derivative of the function $f(t)\in C^{n}([0, \infty ], R)$ is given as [9]

$$ {}^{C}_{0}D_{t}^{\alpha }f(t)= \frac{1}{\varGamma (m-\alpha )} \int _{0}^{t} \frac{f^{(m)}(\tau )}{(t-\tau )^{\alpha +1-m}}\,d\tau, $$

(3)

where $\alpha \in (m-1, m]$, $m\in Z^{+}$, $t\in [0, \infty )$, and $\varGamma (\cdot )$ indicates the Gamma function.

The fractional-order integral is expressed by

$$ {}_{0}I_{t}^{\alpha }f(t)= \frac{1}{\varGamma (\alpha )} \int _{0}^{t} \frac{f(\tau )}{(t-\tau )^{1-\alpha }}\,d\tau . $$

(4)

Lemma 1

([7])

If$x(t)$is a derivable continuous function, then

$$ \frac{1}{2}{{}^{C}_{0}D_{t}^{\alpha }} \bigl(x^{T}(t)x(t)\bigr)\le x^{T}(t){}^{C}_{0}D_{t}^{ \alpha }x(t). $$

(5)

Lemma 2

([38])

Let the origin$x=0$be an equilibrium point of a fractional-order non-autonomous system

$$ {{}^{C}_{0}D_{t}^{\alpha }}x(t)=f \bigl(t,x(t)\bigr), $$

(6)

where$\alpha \in (0, 1)$and$f(t,x(t))$is a Lipschitz continuous function. Suppose that there exists a Lyapunov function$V(t,x(t))$and class-Kfunctions$g_{i}$ ($i=1, 2, 3$) satisfying

$$ \begin{aligned} &g_{1}\bigl( \bigl\Vert x(t) \bigr\Vert \bigr) \le V\bigl(t, x(t)\bigr) \le g_{2}\bigl( \bigl\Vert x(t) \bigr\Vert \bigr), \\ &{{}^{C}_{0}D_{t}^{\alpha }}V\bigl(t, x(t) \bigr) \le -g_{3}\bigl( \bigl\Vert x(t) \bigr\Vert \bigr), \end{aligned} $$

(7)

then$x(t)$can converge to the equilibrium point$x=0$of the system (6) as$t\to +\infty$.

Lemma 3

([39])

Suppose that$V(x)$isC-regular, and$x(t) : [0, +\infty )\to R^{n}$is an absolutely continuous function on any compact interval of$[0, +\infty )$. Let$\nu (t)=V(x(t))$and$\frac{1}{2}<\eta <1$. If the inequality

$$ {{}^{C}_{0}D_{t}^{\alpha }}\nu (t)\le -\lambda \nu ^{2\eta -1}(t) $$

(8)

holds for$t\ge 0$and$\alpha \in (0, 1)$, then

$$ \lim_{t\to T^{*}}\nu (t)=0, \quad \nu (t)=0, t \ge T^{*}, $$

(9)

and

$$ \lim_{t\to T^{*}}x(t)=0, \quad x(t)=0, t\ge T^{*}, $$

(10)

where

$$ T^{*}= \biggl[\nu ^{\alpha (1+\alpha )-2\eta }(0) \frac{\varGamma (1-\frac{2\eta }{1+\alpha })\varGamma (1+\alpha )}{\lambda \varGamma (2+\alpha )\varGamma (1+\alpha -\frac{2\eta }{1+\alpha })} \biggr]^{\frac{1}{\alpha }} . $$

(11)

Remark 1

So far, a great number of control methods for dynamical systems with chaotic motion have been developed such as OGY technique, time-delay feedback control, fuzzy control and feedback linearization methods (see [15, 16, 22, 26] and the references therein). Nevertheless, the above control approaches have some limitations. The OGY approach needs a variable parameter for dynamical system which is generally unmeasurable. The employed method of time-delay feedback control suffers from the fact that it is hard to choose the time delay. The fuzzy control method presents the inference rules in an unsystematic form. For the feedback linearization approach, the accurate mathematical model is required. In [12, 18, 20, 32–34], the adaptive NN scheme shows a distinct advantage in dealing with nonlinear systems with uncertain function. Therefore, the adaptive NN technique is adopted to address the unknown nonlinear functions in this paper.

Lemma 4

([33])

Suppose that$\varphi (x)$is a continuous smooth function which is defined on a compact setΩ. Then there exists an ideal radial basis function (RBF) NN$\phi ^{T}P(x)$for a given$\varepsilon >0$such that

$$ \sup_{x\in \varOmega } \bigl\vert \varphi (x)-{\phi }^{T}P(x) \bigr\vert \le \varepsilon, $$

(12)

where$\phi =[\phi _{1}, \phi _{2}, \ldots , \phi _{n}]^{T}$is the weight vector with$n>1$and$P(x)=[p_{1}(x), p_{2}(x), \ldots , p_{n}(x)]^{T}$stands for the basis function vector and$p_{i}(x)$is Gaussian function with

$$ p_{i}(x)=\exp \biggl[\frac{-(x-\mu _{i})^{T}(x-\mu _{i})}{q_{i}^{2}} \biggr],\quad i=1,2,\ldots ,n , $$

(13)

where$q_{i}$represents the width of Gaussian function and$\mu _{i}$means the center vector.

3 Finite-time controller design

The finite-time adaptive NN control scheme via backstepping is shown in this section.

The tracking error variables are defined as

$$ \textstyle\begin{cases} z_{1}=x_{1}-x_{,}d \\ z_{2}=x_{2}-a_{1,c}, \\ z_{3}=x_{3}-a_{2,c}, \\ z_{4}=x_{4}, \end{cases} $$

(14)

where $x_{d}$ means the reference signal, $a_{i,c}$ denotes the output of the finite-time command filter with virtual signal $a_{i}$ as the input for $i=1, 2$.

The compensated tracking errors are constructed as follows:

$$ v_{i}=z_{i}-\xi _{i}, \quad i=1, \ldots , 4, $$

(15)

where $\xi _{i}$ is the error compensating signal.

Remark 2

It should be noted that the errors caused by the command filters will degrade the control performance. Compared with adaptive NN output tracking control method designed in [32], our approach considers the repeated derivatives in backstepping. Meanwhile, we also employ an error compensation system to lessen the errors generated by the filters.

The error compensating signals are designed as

$$ \textstyle\begin{cases} {{}^{C}_{0}D_{t}^{\alpha }}\xi _{1}= -k_{1}\xi _{1}+\xi _{2}+a_{1,c}-a_{1}-g_{1}\operatorname{sign}( \xi _{1}), \\ {{}^{C}_{0}D_{t}^{\alpha }}\xi _{2}= -k_{2}\xi _{2}-\xi _{1}+\xi _{3}+a_{2,c}-a_{2}-g_{2}\operatorname{sign}( \xi _{2}), \\ {{}^{C}_{0}D_{t}^{\alpha }}\xi _{3}= -k_{3}\xi _{3}-\xi _{2}-g_{3}\operatorname{sign}( \xi _{3}), \\ {{}^{C}_{0}D_{t}^{\alpha }}\xi _{4}= -k_{4}\xi _{4}-g_{4}\operatorname{sign}(\xi _{4}), \end{cases} $$

(16)

with $k_{i}$ and $g_{i}$ being positive constants for $i=1, \ldots , 4$.

Remark 3

It should be mentioned that error compensating signals are finite-time stability by determining the properly parameters $k_{i}$ and $g_{i}$. A finite-time compensation approach for the filtering error is introduced in [24, 35, 36], however, this research focuses on the integer domain. We expand the compensation mechanism to fractional-order framework.

3.1 Terminal sliding manifolds

The sliding surfaces for system (2) can be chosen as

$$ \begin{aligned} &s_{i}=v_{i}+c_{i} \chi _{i}, \\ &{{}^{C}_{0}D_{t}^{\alpha }}\chi _{i}=v_{i}^{p_{i}/q_{i}}-d_{i}\chi _{i}, \end{aligned} $$

(17)

where $i=1, \ldots , 4$, $c_{i}>0$, $d_{i}>0$, $p_{i}$ and $q_{i}$ are positive odd constants with $q_{i}>p_{i}$, $\chi _{i}$ is a continuous function.

From sliding mode method, one has $s_{i}=0$ when the system operates in the sliding surface. Then, utilizing (17), we have

$$ {{}^{C}_{0}D_{t}^{\alpha }} \chi _{i}=l_{i}\chi _{i}^{p_{i}/q_{i}}-d_{i} \chi _{i}, $$

(18)

where $l_{i}=-c_{i}^{p_{i}/q_{i}}$. Integrating both sides of (18), one has

$$ \begin{aligned}[b] \chi _{i}(t)&=\chi _{i}(0)+{{}_{0}I_{t}^{\alpha }} \bigl(l_{i}\chi _{i}^{p_{i}/q_{i}}-d_{i} \chi _{i}\bigr) \\ &=\chi _{i}(0)+\frac{1}{\varGamma (\alpha )} \int _{0}^{t}(t-\tau )^{ \alpha -1} \bigl(l_{i}\chi _{i}^{p_{i}/q_{i}}-d_{i}\chi _{i}\bigr) \,d\tau . \end{aligned} $$

(19)

Therefore, it can be concluded that the solution of the equation (18) is existent.

Theorem 1

Consider the dynamics system (18). Its states will go to zero in finite time.

Proof

Construct the Lyapunov functional candidate $V_{\chi _{i}}$ as

$$ V_{\chi _{i}}=\frac{1}{2}\chi _{i}^{2} . $$

(20)

From Lemma 1, the fractional-order derivative of $V_{\chi _{i}}$ can be written as

$$ \begin{aligned}[b] {{}^{C}_{0}D_{t}^{\alpha }}V_{\chi _{i}} &\le \chi _{i}{{}^{C}_{0}D_{t}^{ \alpha }} \chi _{i}=\chi _{i}\bigl(-c_{i}^{p_{i}/q_{i}} \chi _{i}^{p_{i}/q_{i}}-d_{i} \chi _{i}\bigr) \\ &= -c_{i}^{p_{i}/q_{i}}\chi _{i}^{1+p_{i}/q_{i}}-d_{i} \chi _{i}^{2} \\ &\le 0. \end{aligned} $$

(21)

According to Lemma 2, we see that the dynamics system (18) is asymptotically stable. In what follows, the finite-time convergence of states in the system (18) will be proved.

From inequality (21), we have

$$ {{}^{C}_{0}D_{t}^{\alpha }}V_{\chi _{i}} \le -c_{i}^{p_{i}/q_{i}}\chi _{i}^{1+p_{i}/q_{i}}=-c_{i}^{p_{i}/q_{i}} \sqrt{2}^{\frac{p_{i}+q_{i}}{q_{i}}}V_{\chi _{i}}^{ \frac{(p_{i}+q_{i})}{2q_{i}}} . $$

(22)

According to Lemma 3, we can see that the dynamics system (18) is stable. Moreover, the finite-time convergence of states is obtained. This completes the proof. □

3.2 Control law design

Step 1: Select the Lyapunov functional candidate as

$$ V_{1}=\frac{1}{2}s_{1}^{2} . $$

(23)

Taking the derivative $V_{1}$, one has

$$ {{}^{C}_{0}D_{t}^{\alpha }}V_{1} \le s_{1}\bigl(x_{2}-{{}^{C}_{0}D_{t}^{\alpha }}x_{d}-{{}^{C}_{0}D_{t}^{ \alpha }} \xi _{1}+c_{1}\bigl(v_{1}^{p_{1}/q_{1}}-d_{1} \chi _{1}\bigr)\bigr) . $$

(24)

Substituting the derivative of $\xi _{1}$ into (24) yields

$$ \begin{aligned}[b] {{}^{C}_{0}D_{t}^{\alpha }}V_{1}& \le s_{1}\bigl({x_{2}-{{}^{C}_{0}D_{t}^{ \alpha }}x_{d}+c_{1} \bigl(v_{1}^{p_{1}/q_{1}}-d_{1}\chi _{1}\bigr)} \\ &\quad {}+k_{1}\xi _{1}-\xi _{2}-(a_{1,c}-a_{1})+g_{1} \operatorname{sign}(\xi _{1})\bigr). \end{aligned} $$

(25)

Then the virtual control signal $a_{1}$ is constructed as

$$ \begin{aligned}[b] a_{1}&=-k_{1}z_{1}-k_{1}c_{1} \chi _{1}+c_{2}\chi _{2}+{{}^{C}_{0}D_{t}^{ \alpha }}x_{d}- \hat{\varepsilon }_{1}\operatorname{sign}(s_{1}) \\ &\quad {}-c_{1}\bigl(v_{1}^{p_{1}/q_{1}}-d_{1} \chi _{1}\bigr)-g_{1}\operatorname{sign}(\xi _{1})-b_{1}s_{1}^{p_{1}/q_{1}}, \end{aligned} $$

(26)

where $b_{1}>0$, $\hat{\varepsilon }_{1}$ represents the estimation of $\varepsilon _{1}$ and $\varepsilon _{1}=0$.

The following command filter is used to obtain $a_{1,c}$:

$$\begin{aligned} \textstyle\begin{cases} {{}^{C}_{0}D_{t}^{\alpha }}\zeta _{1}=\iota , \\ \iota =-R_{1} \vert \zeta _{1}-a_{1} \vert ^{\frac{1}{2}}\operatorname{sign}(\zeta _{1}-a_{1})+ \zeta _{2}, \\ {{}^{C}_{0}D_{t}^{\alpha }}\zeta _{2}=-R_{2}\operatorname{sign}(\zeta _{2}-\iota ), \end{cases}\displaystyle \end{aligned}$$

(27)

where $a_{1,c}=\zeta _{1}$ denotes the output of filter.

Thus, substituting (26) into (25) yields

$$ {{}^{C}_{0}D_{t}^{\alpha }}V_{1} \le -k_{1}s_{1}^{2}+s_{1}s_{2}- \hat{\varepsilon }_{1} \vert s_{1} \vert -b_{1}s_{1}^{1+p_{1}/q_{1}} . $$

(28)

Step 2: Select the Lyapunov function $V_{2}$ as

$$ V_{2}=V_{1}+\frac{1}{2}s_{2}^{2} . $$

(29)

Taking its derivative, one has

$$ \begin{aligned}[b] {{}^{C}_{0}D_{t}^{\alpha }}V_{2}& \le {{}^{C}_{0}D_{t}^{\alpha }}V_{1}+s_{2}{{}^{C}_{0}D_{t}^{ \alpha }}s_{2} \\ &={{}^{C}_{0}D_{t}^{\alpha }}V_{1}+s_{2} \bigl(\sigma ({x_{3}}-{x_{2}})-T_{L}-{{}^{C}_{0}D_{t}^{ \alpha }}a_{1,c} \\ &\quad {}-{{}^{C}_{0}D_{t}^{\alpha }}\xi _{2}+c_{2}\bigl(v_{2}^{p_{2}/q_{2}}-d_{2} \chi _{2}\bigr)\bigr). \end{aligned} $$

(30)

Substituting (28) into (30), we can show the following form:

$$ \begin{aligned}[b] {{}^{C}_{0}D_{t}^{\alpha }}V_{2}& \le -k_{1}s_{1}^{2}+s_{2} \bigl(x_{3}+s_{1}+f_{2}-{{}^{C}_{0}D_{t}^{ \alpha }} \xi _{2} \\ &\quad {}+c_{2}\bigl(v_{2}^{p_{2}/q_{2}}-d_{2} \chi _{2}\bigr)\bigr)-\hat{\varepsilon }_{1} \vert s_{1} \vert -b_{1}s_{1}^{1+p_{1}/q_{1}}, \end{aligned} $$

(31)

where $f_{2}(Z_{2})=\sigma ({x_{3}}-{x_{2}})-T_{L}-{{}^{C}_{0}D_{t}^{\alpha }}a_{1,c}-x_{3}$ and $Z_{2}=[x_{1}, x_{2}, x_{3}, x_{4}, x_{d}]^{T}$.

Remark 4

It should be mentioned that the external load torque $T_{L}$ and the parameter σ are unknown. We cannot achieve the control signal directly. To avoid this problem, the RBF NN is introduced to adaptively approximate the unknown part $f_{2}$.

From Lemma 4, for a given $\varepsilon _{2}>0$, the existence of a RBF NN is ensured and it satisfies $f_{2}=\phi _{2}^{T}P_{2}(Z_{2})+\delta _{2}(Z_{2})$, where $\delta _{2}(Z_{2})$ stands for the approximation error with $\vert \delta _{2}(Z_{2}) \vert \le \varepsilon _{2}$.

The virtual control signal $a_{2}$ is designed as

$$ \begin{aligned}[b] a_{2}&=-k_{2}z_{2}-k_{2}c_{2} \chi _{2}-z_{1}-c_{1}\chi _{1}+c_{3} \chi _{3} \\ &\quad {}-c_{2}\bigl(v_{2}^{p_{2}/q_{2}}-d_{2} \chi _{2}\bigr)-g_{2}\operatorname{sign}(\xi _{2})- \hat{\phi }_{2}^{T}P_{2}(Z_{2}) \\ &\quad {}-\hat{\varepsilon }_{2}\operatorname{sign}(s_{2})-b_{2}s_{2}^{p_{2}/q_{2}}, \end{aligned} $$

(32)

where $b_{2}>0$, $\hat{\phi }_{2}$ means the estimation of $\phi _{2}$, $\hat{\varepsilon }_{2}$ denotes the estimation of $\varepsilon _{2}$.

Similarly, one can obtain the output $a_{2,c}$ of the filter with $a_{2}$ being its input. Thus, from (16), (30) and (32), the derivative of $V_{2}$ is given in the following form:

$$ \begin{aligned}[b] {{}^{C}_{0}D_{t}^{\alpha }}V_{2}& \le -\sum_{i=1}^{2}k_{i}s_{i}^{2}+s_{2}s_{3}- \sum_{i=1}^{2}b_{i}s_{i}^{1+p_{i}/q_{i}} \\ &\quad {}+s_{2}\tilde{\phi }_{2}^{T}P_{2}(Z_{2})+ \delta _{2}s_{2}-\sum_{i=1}^{2} \hat{\varepsilon }_{i} \vert s_{i} \vert , \end{aligned} $$

(33)

where $\tilde{\phi }_{2}=\phi _{2}-\hat{\phi }_{2}$.

Step 3: Construct the Lyapunov function candidate $V_{3}$ as

$$ V_{3}=V_{2}+\frac{1}{2}s_{3}^{2} . $$

(34)

By differentiating $V_{3}$, it follows that

$$ \begin{aligned}[b] {{}^{C}_{0}D_{t}^{\alpha }}V_{3}& \le {{}^{C}_{0}D_{t}^{\alpha }}V_{2}+s_{3}{{}^{C}_{0}D_{t}^{ \alpha }}s_{3} \\ &={{}^{C}_{0}D_{t}^{\alpha }}V_{2}+s_{3} \bigl(-{x_{3}}-{x_{2}} {x_{4}}+\gamma {x_{2}}+u_{q} \\ &\quad {}-{{}^{C}_{0}D_{t}^{\alpha }}a_{2,c}-{{}^{C}_{0}D_{t}^{\alpha }} \xi _{3}+c_{3}\bigl(v_{3}^{p_{3}/q_{3}}-d_{3} \chi _{3}\bigr)\bigr). \end{aligned} $$

(35)

Substituting (33) into (35), we get

$$ \begin{aligned}[b] {{}^{C}_{0}D_{t}^{\alpha }}V_{3}& \le -\sum_{i=1}^{2}k_{i}s_{i}^{2}+s_{3} \bigl(s_{2}+u_{q}+f_{3}-{{}^{C}_{0}D_{t}^{ \alpha }} \xi _{3} \\ &\quad {}+c_{3}\bigl(v_{3}^{p_{3}/q_{3}}-d_{3} \chi _{3}\bigr)\bigr)-\sum_{i=1}^{2}b_{i}s_{i}^{1+p_{i}/q_{i}} \\ &\quad {}+s_{2}\tilde{\phi }_{2}^{T}P_{2}(Z_{2})+ \delta _{2}s_{2}-\sum_{i=1}^{2} \hat{\varepsilon }_{i} \vert s_{i} \vert , \end{aligned} $$

(36)

where $f_{3}(Z_{3})=-{x_{3}}-{x_{2}}{x_{4}}+\gamma {x_{2}}-{{}^{C}_{0}D_{t}^{ \alpha }}a_{2,c}$ and $Z_{3}=Z_{2}$.

Remark 5

It is clear that the function $f_{3}$ involves the nonlinear term $-x_{2}x_{4}$ and the differential part $-{{}^{C}_{0}D_{t}^{\alpha }}a_{2,c}$, these will increase the complexity of the control law $u_{q}$. In order to avoid this problem, the RBF NN is adopted to estimate the nonlinear function $f_{3}$.

Similarly, for a given $\varepsilon _{3}$, there exists a RBF NN satisfying $f_{3}=\phi _{3}^{T}P_{3}(Z_{3})+\delta _{3}(Z_{3})$, where $\vert \delta _{3}(Z_{3}) \vert \le \varepsilon _{3}$.

Furthermore, the control signal $u_{q}$ can be given by

$$ \begin{aligned}[b] u_{q}&=-k_{3}z_{3}-k_{3}c_{3} \chi _{3}-c_{2}\chi _{2}-z_{2}-c_{3} \bigl(v_{3}^{p_{3}/q_{3}}-d_{3} \chi _{3}\bigr) \\ &\quad {}-g_{3}\operatorname{sign}(\xi _{3})-\hat{\phi }_{3}^{T}P_{3}(Z_{3})- \hat{ \varepsilon }_{3}\operatorname{sign}(s_{3})-b_{3}s_{3}^{p_{3}/q_{3}}, \end{aligned} $$

(37)

where $b_{3}>0$, $\hat{\phi }_{3}$ means the estimation of $\phi _{3}$, $\hat{\varepsilon }_{3}$ denotes the estimation of $\varepsilon _{3}$.

By taking (16), (36) and (37) into account, it can be verified that

$$ \begin{aligned}[b] {{}^{C}_{0}D_{t}^{\alpha }}V_{3}& \le -\sum_{i=1}^{3}k_{i}s_{i}^{2}- \sum_{i=1}^{3}b_{i}s_{i}^{1+p_{i}/q_{i}} \\ &\quad {}+\sum_{i=2}^{3} \bigl(s_{i}\tilde{\phi }_{i}^{T}P_{i}(Z_{i})+ \delta _{i}s_{i}\bigr)- \sum_{i=1}^{3} \hat{\varepsilon }_{i} \vert s_{i} \vert , \end{aligned} $$

(38)

where $\tilde{\phi _{3}}=\phi _{3}-\hat{\phi }_{3}$.

Step 4: Consider the Lyapunov function candidate $V_{4}$ as

$$ V_{4}=V_{3}+\frac{1}{2}s_{4}^{2} . $$

(39)

Differentiating $V_{4}$ yields

$$ \begin{aligned}[b] {{}^{C}_{0}D_{t}^{\alpha }}V_{4}& \le {{}^{C}_{0}D_{t}^{\alpha }}V_{3}+s_{4} \bigl(-{x_{4}}+{x_{2}} {x_{3}}+u_{d} \\ &\quad {}-{{}^{C}_{0}D_{t}^{\alpha }}\xi _{4}+c_{4}\bigl(v_{4}^{p_{4}/q_{4}}-d_{4} \chi _{4}\bigr)\bigr). \end{aligned} $$

(40)

Then substituting (38) into (40) results in

$$ \begin{aligned}[b] {{}^{C}_{0}D_{t}^{\alpha }}V_{4}& \le -\sum_{i=1}^{3}k_{i}s_{i}^{2}+s_{4} \bigl(f_{4}+u_{d}-{{}^{C}_{0}D_{t}^{ \alpha }} \xi _{4} \\ &\quad {}+c_{4}\bigl(v_{4}^{p_{4}/q_{4}}-d_{4} \chi _{4}\bigr)\bigr)-\sum_{i=1}^{3}b_{i}s_{i}^{1+p_{i}/q_{i}} \\ &\quad {}+\sum_{i=2}^{3} \bigl(s_{i}\tilde{\phi }_{i}^{T}P_{i}(Z_{i})+ \delta _{i}s_{i}\bigr)- \sum_{i=1}^{3} \hat{\varepsilon }_{i} \vert s_{i} \vert , \end{aligned} $$

(41)

where $f_{4}(Z_{4})=-x_{4}+x_{2}x_{3}$ and $Z_{4}=Z_{3}$.

Similarly, there exists a RBF NN $\phi _{4}^{T}P_{4}(Z_{4})$ for a given $\varepsilon _{4}>0$ such that $f_{4}=\phi _{4}^{T}P_{4}(Z_{4})+\delta _{4}(Z_{4})$, where $\vert \delta _{4}(Z_{4}) \vert \le \varepsilon _{4}$.

Then the control law $u_{d}$ can be constructed as

$$ \begin{aligned}[b] u_{d}&=-k_{4}z_{4}-k_{4}c_{4} \chi _{4}-c_{4}\bigl(v_{4}^{p_{4}/q_{4}}-d_{4} \chi _{4}\bigr)-g_{4}\operatorname{sign}(\xi _{4}) \\ &\quad {}-\hat{\phi }_{4}^{T}P_{4}(Z_{4})- \hat{\varepsilon }_{4}\operatorname{sign}(s_{4})-b_{4}s_{4}^{p_{4}/q_{4}}, \end{aligned} $$

(42)

where $b_{4}>0$, $\hat{\phi }_{4}$ means the estimation of $\phi _{4}$, $\hat{\varepsilon }_{4}$ denotes the estimation of $\varepsilon _{4}$.

By taking (16), (41) and (42) into account, it follows that

$$ \begin{aligned}[b] {{}^{C}_{0}D_{t}^{\alpha }}V_{4}& \le -\sum_{i=1}^{4}k_{i}s_{i}^{2}- \sum_{i=1}^{4}b_{i}s_{i}^{1+p_{i}/q_{i}} \\ &\quad {}+\sum_{i=2}^{4} \bigl(s_{i}\tilde{\phi }_{i}^{T}P_{i}(Z_{i})+ \delta _{i}s_{i}\bigr)- \sum_{i=1}^{4} \hat{\varepsilon }_{i} \vert s_{i} \vert , \end{aligned} $$

(43)

where $\tilde{\phi _{4}}=\phi _{4}-\hat{\phi }_{4}$.

4 Stability analysis

In this section, the stability of the designed controller is analyzed.

Theorem 2

For the fractional-order PMSM with chaotic motion, load torque disturbance and parameters uncertainties, the controllers with virtual signals$a_{1}$ (26), $a_{2}$ (32), control signals$u_{q}$ (37), $u_{d}$ (42), compensating signals (16), command filter (27) and adaptive laws (48) can ensure the tracking errors converge to zero in finite time.

Proof

Construct the Lyapunov function in the following form:

$$ V=V_{4}+\frac{1}{2m_{i}}\sum _{i=2}^{4}\tilde{\phi }_{i}^{T} \tilde{\phi }_{i}+\frac{1}{2r_{i}}\sum_{i=1}^{4} \tilde{\varepsilon }_{i}^{2}, $$

(44)

where $\tilde{\varepsilon }_{i}=\varepsilon _{i}-\hat{\varepsilon }_{i}$, $m_{i}$ and $r_{i}$ are positive constants.

The derivative of V can be written as

$$ \begin{aligned}[b] {{}^{C}_{0}D_{t}^{\alpha }}V& \le -\sum_{i=1}^{4}k_{i}s_{i}^{2}- \sum_{i=1}^{4}b_{i}s_{i}^{1+p_{i}/q_{i}} \\ &\quad {}+\sum_{i=2}^{4} \bigl(s_{i}\tilde{\phi }_{i}^{T}P_{i}(Z_{i})+ \delta _{i}s_{i}\bigr)- \sum_{i=1}^{4} \hat{\varepsilon }_{i} \vert s_{i} \vert \\ &\quad {}-\frac{1}{m_{i}}\sum_{i=2}^{4} \tilde{\phi }_{i}^{T}{{}^{C}_{0}D_{t}^{ \alpha }} \hat{\phi }_{i}-\frac{1}{r_{i}}\sum_{i=1}^{4} \tilde{\varepsilon }_{i}{{}^{C}_{0}D_{t}^{\alpha }} {\hat{\varepsilon }}_{i}. \end{aligned} $$

(45)

By utilizing the inequality $|\delta _{i}|\le \varepsilon _{i}$, one has

$$ \delta _{i}s_{i}\le \vert \delta _{i}s_{i} \vert \le \vert \delta _{i} \vert \vert s_{i} \vert \le \varepsilon _{i} \vert s_{i} \vert . $$

(46)

Thus, substituting (46) into (45), it can be verified that

$$ \begin{aligned}[b] {{}^{C}_{0}D_{t}^{\alpha }}V& \le -\sum_{i=1}^{4}k_{i}s_{i}^{2}- \sum_{i=1}^{4}b_{i}s_{i}^{1+p_{i}/q_{i}} \\ &\quad {}+\frac{1}{m_{i}}\sum_{i=2}^{4} \tilde{\phi }_{i}^{T}\bigl(m_{i}s_{i}P_{i}(Z_{i})-{{}^{C}_{0}D_{t}^{ \alpha }} {\hat{\phi }}_{i}\bigr) \\ &\quad {}+\frac{1}{r_{i}}\sum_{i=1}^{4} \tilde{\varepsilon }_{i}\bigl(r_{i} \vert s_{i} \vert -{{}^{C}_{0}D_{t}^{\alpha }} {\hat{ \varepsilon }}_{i}\bigr). \end{aligned} $$

(47)

According to (47), the adaptive laws are constructed in the following form:

$$ \begin{aligned} &{{}^{C}_{0}D_{t}^{\alpha }} {\hat{\phi }}_{i}=m_{i}s_{i}P_{i}(Z_{i}), \\ &{{}^{C}_{0}D_{t}^{\alpha }} {\hat{ \varepsilon }}_{i}=r_{i} \vert s_{i} \vert . \end{aligned} $$

(48)

From (47) and (48), it can be derived that

$$ {{}^{C}_{0}D_{t}^{\alpha }}V \le -\sum_{i=1}^{4}k_{i}s_{i}^{2}- \sum_{i=1}^{4}b_{i}s_{i}^{1+p_{i}/q_{i}}. $$

(49)

Then we define

$$\begin{aligned}& \varpi =[s_{1}, \ldots , s_{4}, {\hat{\phi }}_{2}, {\hat{\phi }}_{3}, { \hat{\phi }}_{4}, \tilde{\varepsilon }_{1}, \tilde{\varepsilon }_{2}, \tilde{ \varepsilon }_{3}, \tilde{\varepsilon }_{4}]^{T} , \end{aligned}$$

(50)

$$\begin{aligned}& \beta _{\max }=\max \biggl\{ 1, \frac{1}{m_{2}}, \frac{1}{m_{3}}, \frac{1}{m_{4}}, \frac{1}{r_{1}}, \frac{1}{r_{2}}, \frac{1}{r_{3}}, \frac{1}{r_{4}} \biggr\} , \end{aligned}$$

(51)

$$\begin{aligned}& \beta _{\min }=\min \biggl\{ 1, \frac{1}{m_{2}}, \frac{1}{m_{3}}, \frac{1}{m_{4}}, \frac{1}{r_{1}}, \frac{1}{r_{2}}, \frac{1}{r_{3}}, \frac{1}{r_{4}} \biggr\} . \end{aligned}$$

(52)

Obviously, we have the following inequality:

$$ \frac{1}{2\beta _{\max }} \Vert \varpi \Vert ^{2}\le V \le \frac{1}{2\beta _{\min }} \Vert \varpi \Vert ^{2} . $$

(53)

Thus, there exists a κ-function ρ such that

$$ {{}^{C}_{0}D_{t}^{\alpha }}V \le -\rho \bigl( \Vert \varpi \Vert \bigr) . $$

(54)

Then, referring to Lemma 2, we see that the compensated tracking errors go to zero asymptotically.

Now it is time to prove that the sliding motion happens in finite time. Construct the Lyapunov function candidate as

$$ V_{s}=\frac{1}{2}s_{4}^{2} \le V . $$

(55)

The inequality (49) can be rewritten as

$$ \begin{aligned}[b] {{}^{C}_{0}D_{t}^{\alpha }}V& \le -\sum_{i=1}^{4}k_{i}s_{i}^{2}- \sum_{i=1}^{4}b_{i}s_{i}^{1+p_{i}/q_{i}} \\ &\le -b_{4}s_{4}^{1+p_{4}/q_{4}}=-\sqrt{2}^{\frac{p_{4}+q_{4}}{q_{4}}}b_{4}V_{s}^{ \frac{p_{4}+q_{4}}{2q_{4}}}. \end{aligned} $$

(56)

Furthermore, there exists a positive constant n such that [3]

$$ nV^{\frac{p_{4}+q_{4}}{2q_{4}}}\le V_{4}^{\frac{p_{4}+q_{4}}{2q_{4}}} . $$

(57)

Substituting (57) into (56), it can be derived that

$$ \begin{aligned}[b] {{}^{C}_{0}D_{t}^{\alpha }}V& \le -\sqrt{2}^{\frac{p_{4}+q_{4}}{q_{4}}}{b_{4}}V_{s}^{ \frac{p_{4}+q_{4}}{2q_{4}}} \\ &\le -\sqrt{2}^{\frac{p_{4}+q_{4}}{q_{4}}}nb_{4}V^{ \frac{p_{4}+q_{4}}{2q_{4}}}. \end{aligned} $$

(58)

According to Lemma 3, we can conclude that the sliding motion occurs in finite time. Since $v_{i}=z_{i}-\xi _{i}$, then if we can show that $\xi _{i}$ goes to zero in finite time, this also means that the tracking errors $z_{i}$ will go to zero within finite time.

In what follows, select the Lyapunov function candidate $V_{\xi }$ to prove that $\xi _{i}$ ($i=1, \ldots , 4$) go to zero within finite time:

$$ V_{\xi }=\frac{1}{2}\sum _{i=1}^{4}\xi _{i}^{2}. $$

(59)

Then the time derivative of $V_{\xi }$ can be written as

$$ \begin{aligned}[b] {{}^{C}_{0}D_{t}^{\alpha }}V_{\xi }& \le \sum_{i=1}^{4}\xi _{i}{{}^{C}_{0}D_{t}^{ \alpha }} \xi _{i} \\ &= -\sum_{i=1}^{4}k_{i}\xi _{i}^{2}+\sum_{i=1}^{2} \xi _{i}(a_{i,c}-a_{i}) \\ &\quad{}-\sum_{i=1}^{4}g_{i}\xi _{i}\operatorname{sign}(\xi _{1}). \end{aligned} $$

(60)

According to [40], we know that the command filters can guarantee $|a_{i,c}-a_{i}|\le \psi _{i}$ in finite time. Then we have

$$\begin{aligned} {{}^{C}_{0}D_{t}^{\alpha }}V_{\xi } &\le -\sum_{i=1}^{4}k_{i}\xi _{i}^{2}+ \sum_{i=1}^{2} \xi _{i}(a_{i,c}-a_{i}) \\ &\quad{}-\sum_{i=1}^{4}g_{i}\xi _{i}\operatorname{sign}(\xi _{1}) \\ &\le -\sum_{i=1}^{4}k_{i}\xi _{i}^{2}+\sum_{i=1}^{2} \vert \xi _{i} \vert \bigl\vert (a_{i,c}-a_{i}) \bigr\vert \\ &\quad{}-\sum_{i=1}^{4}g_{i} \vert \xi _{i} \vert \\ &\le -(\sqrt{2}g_{0}-2\sqrt{2}\bar{\psi }) \vert \xi _{i} \vert \\ &=-(\sqrt{2}g_{0}-2\sqrt{2}\bar{\psi })V_{\xi }^{1/2}, \end{aligned}$$

(61)

where $g_{0}=\min (g_{i})$, $\bar{\psi }=\max (\psi _{i})$. Then, if we select appropriate parameter $g_{0}$ such that $\sqrt{2}g_{0}-2\sqrt{2}\bar{\psi }>0$, then $\xi _{i}$ will go to zero in finite time. The proof is completed. □

Remark 6

Compared with the backstepping based adaptive control strategy considered in [2, 12, 20, 22–24, 28, 29, 33, 34], the following superiorities are obtained. First, the designed error compensating mechanism in [22, 23, 34] can only achieve asymptotic stability. In this paper, we employ the sign functions as in (16) such that the finite-time convergent of the error compensation system can be guaranteed. Second, the conventional control laws constructed in [2, 12, 20, 22, 29] can only guarantee the tracking errors are bounded. However, the controllers (26), (32), (37) and (42) provided in this paper can guarantee that the tracking errors are finite-time stable, which can ensure the fractional-order PMSM system with fast convergence performance. Third, the finite-time tracking control method proposed in [24] for PMSMs does not cover the generalized fractional-order system. However, our method can solve the finite-time control issue for fractional-order PMSM. Fourth, the adaptive NN technique via backstepping developed in [12, 33, 34] does not take into account the approximation errors. In this paper, the adaptive law ${{}^{C}_{0}D_{t}^{\alpha }}{\hat{\varepsilon }}_{i}=r_{i}\vert s_{i} \vert$ in (48) is constructed to compensate the approximation errors, which can ensure the closed-loop system with high quality tracking performance.

5 Simulation results

5.1 Performance analysis

Simulation results are given to show the effectiveness of the constructed finite-time adaptive NN control for the fractional-order PMSM in this section. Let the reference signal be $x_{d}=\sin (t)$. The simulation is conducted under the condition of $x_{1}(0)=0.2$, $x_{2}(0)=x_{3}(0)=0$, $x_{4}(0)=10$ and the external disturbance

$$\begin{aligned} T_{L}= \textstyle\begin{cases} 1.5\mbox{ Nm} & 0\le t \le 10, \\ 3\mbox{ Nm} & t>10. \end{cases}\displaystyle \end{aligned}$$

(62)

The control parameters of the designed controllers are selected as $k_{1}=25$, $k_{2}=20$, $k_{3}=25$, $k_{4}=50$, $c_{1}=0.01$, $c_{2}=0.02$, $c_{3}=0.01$, $c_{4}=0.01$, $d_{1}=60$, $d_{2}=50$, $d_{3}=55$, $d_{4}=60$, $b_{1}=5$, $b_{2}=10$, $b_{3}=10$, $b_{4}=10$, $m_{2}=m_{3}=m_{4}=1500$, $r_{1}=0.1$, $r_{2}=0.2$, $r_{3}=0.1$, $r_{4}=0.5$.

Furthermore, the RBF NNs are adopted as the following way. The RBF NNs $\phi _{2}^{T}P_{2}(Z_{2})$, $\phi _{3}^{T}P_{3}(Z_{3})$, $\phi _{4}^{T}P_{4}(Z_{4})$ cover nine nodes with centers $\mu _{i}$ spaced evenly in the range $[-8, 8]$ and the widths are set to be 2, respectively.

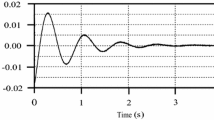
Previous study shows that the fractional-order PMSM occurs chaos without controllers. The trajectory tracking of the fractional-order PMSM is shown in Figs. 2–5 with the designed controllers being applied. The time curves of the output response $x_{1}$ and the desired signal $x_{d}$ are depicted in Fig. 2(a). As we can see, the state $x_{1}$ can track the desired value $x_{d}$ precisely. A change of load torque disturbance does not result in performance degradation. The amplitude of the tracking error between $x_{1}$ and $x_{d}$ reduces to zero in finite time. Figure 2(b) displays the curve of tracking error, it shows that the rotor position tracking error goes to zero rapidly. The time curves of $s_{i}$, $i=1,2,3$ are provided in Figs. 3–4. From both Figs. 3 and 4, one sees that the sliding motion obtains in a short time. Therefore, a conclusion can be achieved that our method has good convergence properties.

Figure 2

The trajectory tracking of $\sin (t)$ in the case of $\alpha =0.98$. (a) $x_{1}$ and $x_{d}$. (b) The tracking error

Figure 3

The time evolution of $s_{1}$

Figure 4

Sliding mode surfaces $s_{2}$ and $s_{3}$

Figure 5

$d-q$ axis currents

The curves of $d-q$ axis currents are given in Fig. 5. The results of trajectory tracking performance for different α are shown in Fig. 6. Figure 6(a) is the curve of the position, and the tracking error is given in Fig. 6(b). The time evolution of $s_{1}$ is displayed in Fig. 6(c). It can be obviously observed that the fractional-order PMSM system achieves finite-time stability despite the orders are different, which means that the proposed controllers are effective for fractional-order PMSM system.

Figure 6

The trajectory tracking performance for different α. (a) $x_{1}$ and $x_{d}$. (b) The tracking error. (c) The time evolution of $s_{1}$

Figure 7 exhibits the performance of the controller when perturbation of the parameter γ occurs. As the system parameter γ alters a little, the system is still stable. That is to say, the designed controllers show good robustness for the system with parameter perturbations and uncertainties in the whole process.

Figure 7

The trajectory tracking performance for different γ

Although there exist chaotic motion, load torque disturbance, parameter perturbations and uncertainties, the proposed method is an efficient approach to obtaining the finite-time stability for fractional-order chaotic PMSM system.

5.2 Scheme contrast

To display the superiority of the finite-time controller presented in this paper, the result is given comparing with [34] under the condition of $\alpha =0.98$. For the fractional-order PMSM system, the neural networks command filtered backstepping controller (NCBC) proposed in [34] can be constructed as

$$\begin{aligned}& a_{1f}=-k_{1f}z_{1}+{{}^{C}_{0}D_{t}^{\alpha }}x_{d}, \end{aligned}$$

(63)

$$\begin{aligned}& a_{2f}=-k_{2f}z_{2}- \frac{1}{2}v_{2}-z_{1}-\frac{1}{2l_{2}^{2}} \hat{\theta }_{f}P_{2f}^{T}P_{2f}, \end{aligned}$$

(64)

$$\begin{aligned}& u_{qf}=-k_{3f}z_{3}- \frac{1}{2}v_{3}-z_{2}-\frac{1}{2l_{3}^{2}} \hat{\theta }_{f}P_{3f}^{T}P_{3f} , \end{aligned}$$

(65)

$$\begin{aligned}& u_{df}=-k_{4f}z_{4}- \frac{1}{2}v_{4}-\frac{1}{2l_{4}^{2}} \hat{\theta }_{f}P_{4f}^{T}P_{4f} . \end{aligned}$$

(66)

The command filter has the following form:

$$\begin{aligned} \textstyle\begin{cases} {}^{C}_{0}D^{\alpha }\varphi _{1}=w_{n}\varphi _{2}, \\ {}^{C}_{0}D^{\alpha }\varphi _{2}=-\zeta w_{n}\varphi _{2}-w_{n}( \varphi _{1}-q), \end{cases}\displaystyle \end{aligned}$$

(67)

where $\varphi _{1}$ indicates the output of the filter with q being the input.

The adaptive law is designed as

$$ {{}^{C}_{0}D_{t}^{\alpha }} \theta _{f}=\sum_{i=2}^{4} \frac{h}{2l_{i}^{2}}v_{i}^{2}P_{i}^{T}P_{i}-m_{f} \hat{\theta }_{f}, $$

(68)

where $k_{if}>0$ for $i=1, \ldots , 4$, h and $l_{i}$ for $i=2,3,4$ are positive constants, $P_{if}$ denote the NNs basis function.

Compared with the NCBC proposed in [34], our method can realize finite-time signal tracking. Figure 8 depicts the trajectory tracking contrast between NCBC and the proposed control strategy. It reveals that our scheme is more accurate than the NCBC. Therefore, it is concluded that the fractional-order chaotic PMSM possesses better performance by utilizing the proposed control strategy.

Figure 8

Trajectory tracking contrast between NCBC and the proposed control strategy. (a) $x_{1}$ and $x_{d}$. (b) The tracking error

Remark 7

The NCBC method proposed in [34] cannot guarantee the tracking error coverages to zero in finite time. Through these comparisons, we can know that our method can solve the tracking problem for fractional-order PMSM in finite time.

Remark 8

So far, to the best of our knowledge, no results are available for finite-time control of fractional-order PMSM. Compared with the existing literature, the finite-time tracking control issue is considered in this paper for fractional-order chaotic PMSM.

6 Conclusions

In this brief, a finite-time adaptive NN control method is presented to deal with the position tracking issue of fractional-order PMSM with chaotic motion, load torque disturbance, parameter perturbations and uncertainties. The finite-time adaptive control approach consists of adaptive NNs, command filters, backstepping, fractional-order error compensating mechanism and terminal sliding surface technique. With the aid of adaptive NNs, the unknown function can be estimated by designed weight adaptive laws. The command filters with a compensating mechanism not only solve the ‘explosion of complexity’ problem in backstepping, but also reduce the filtering errors. Meanwhile, the fractional-order terminal sliding manifolds are integrated into control signals to ensure finite-time stability of the tracking error. Our simulation results show the superior performance of the proposed control strategy for the fractional-order chaotic PMSM. In future work, we will study the finite-time tracking control problem for incommensurate fractional-order PMSM system with unmeasured states and input saturation.