1 Introduction

Chaos phenomena, which have attracted increasing attention of scholars from many fields, intensively exist in many actual nonlinear systems. More and more interesting results have been reported on this theme because it has possible applications in some domains, such as control, information processing, and secure communication [1,2,3,4,5,6,7,8,9]. Up to now, the synchronization and control of chaotic systems has become a hot research topic. A number of methods have been developed for the chaotic systems, for example, pinning control [10], adaptive control [11, 12], sliding mode control (SMC) [13, 14], backstepping control, and many others. Among these control methods, backstepping control is an effective control method to handle the SISO chaotic systems with triangular structure. In the backstepping control design, in each step, a virtual control input should be designed, and finally, in the last step, the controller will be designed. The backstepping control approach has some interesting control performance, for example, global stability, easy to be implemented [15].

On the other hand, fractional calculus has received more and more attention. During the past two decades, nonlinear systems described by fractional differential equations have had many applications in robotics, engineering, biophysics, electron-analytical chemistry [16,17,18,19,20,21,22,23,24,25,26,27,28]. Compared with the classical integer-order calculus, the fractional-order one is more accurate in describing many practical problems [29,30,31,32,33]. In particular, by using the fractional controller, one can expand the freedom of the controlled system by one more degree and obtain better control performance. The stability for the uncertain fractional-order chaotic systems was obtained via SMC in [34, 35], where a key assumption is that the models of the chaotic systems should be known in advance. Synchronization and control of fractional-order chaotic systems has become a hot research topic. In [11], adaptive fuzzy controller was designed for fractional-order chaotic systems with dead-zone. In [17], a fractional sliding surface was designed to synchronize two non-identical fractional-order NNs, where the prior knowledge of the uncertain gain matrices is needed.

It is well known that system models were usually partly known even fully unknown in practical applications, and these system uncertainties always affect the control performance and the closed-loop stability if they are not handled well [36,37,38,39,40,41,42,43,44,45]. To handle this type of problem, fuzzy logic system (FLS) and neural network (NN) were used for estimating system uncertainties. One major benefit of the aforementioned methods consists in that they can tackle mismatched system uncertainties that cannot be linearly parameterized. That is to say, adaptive fuzzy control (AFC) and adaptive NN control are interesting and effective issues [46,47,48]. By using dynamic fuzzy NN method and backstepping technique, the control of uncertain chaotic systems was addressed in [49]. Ref. [50] researched the control of a class of strict-feedback nonlinear systems with functional uncertainties by using NN learning control method. Base on the adaptive fuzzy backstepping technique, the control of uncertain fractional-order nonlinear systems was investigated in [15]. It should be mentioned that in the proposed method of [15], a fuzzy system should be used to approximate a fractional-order term, which may decrease the control performance and need large control energy.

Motivated by the above analysis, we aim to present the stability analysis of a FOCH chaotic system with unknown external disturbances by using the backstepping technique. Firstly, the system uncertainties are approximated by NNs; secondly, based on the fractional Lyapunov stability theory, a fractional adaptation law that ensures that the states of a system converge to a small region of zero is designed; finally, the NN backstepping controller is implemented step by step. The main contribution of the proposed method includes the following: (1) Adaptive NN control together with backstepping control method is proposed for fractional-order chaotic systems, and the prior knowledge of the system model is not needed. (2) In each step, a fractional-order signal is constructed to cancel the approximation error of the unknown nonlinear function. That is to say, the aforementioned problem of [15] is solved in this paper.

2 Preliminaries

2.1 Fractional calculus concept

In this part, we will give some results about the fractional calculus that will be used later.

Definition 1

([51])

The fractional integral of a smooth function \(\mu (\nu )\) can be given as

$$ \mathbb{D}^{-\rho }\mu (\nu )=\frac{1}{\varGamma (\rho )} \int ^{\nu }_{0}( \nu -\zeta )^{\rho -1}\mu (\zeta )\,d\zeta , $$
(1)

where \(\varGamma (\rho )=\int ^{+\infty }_{0}\nu ^{\rho -1}e^{-\nu }\,d \nu \).

Definition 2

([51])

The ρth Caputo derivative of \(\mu (\nu )\) is defined as

$$ \mathbb{D}^{\rho }\mu (\nu )=\frac{1}{\varGamma (n-\rho )} \int ^{\nu } _{0}(\nu -\zeta )^{(n-\rho -1)}\mu ^{(n)}(\zeta )\,d\zeta , $$
(2)

where \(n-1\leq \rho < n\), \(n\in \mathbb{N}\). For convenience, we always suppose that \(\rho \in (0,1]\) in this paper.

Definition 3

([51])

The Mittag-Leffler function can be given by

$$ E_{\alpha _{1},\alpha _{2}}(\nu )=\sum^{\infty }_{i=0} \frac{\nu ^{i}}{ \varGamma (\alpha _{1}i)+\alpha _{2}}, $$
(3)

where \(\alpha _{1}, \alpha _{2} >0\) and \(\nu \in \mathbb{C}\).

Lemma 1

([52])

Let \(\mu (\nu )=0\) be an equilibrium point of the fractional order system

$$ \mathbb{D}^{\rho }\mu (\nu )=g\bigl(\nu ,\mu (\nu )\bigr). $$
(4)

If there exists a Lyapunov function \(V(\nu ,\mu (\nu ))\) and a class-\(\mathcal{K}\) function \(\lambda _{i}\) satisfying

$$\begin{aligned}& \lambda _{1}\bigl( \bigl\Vert \mu (\nu ) \bigr\Vert \bigr)\leq V \bigl(\nu ,\mu (\nu )\bigr)\leq \lambda _{2}\bigl( \bigl\Vert \mu ( \nu ) \bigr\Vert \bigr), \end{aligned}$$
(5)
$$\begin{aligned}& \mathbb{D}^{\rho }V\bigl(\nu ,\mu (\nu )\bigr)\leq -\lambda _{3}\bigl( \bigl\Vert \mu (\nu ) \bigr\Vert \bigr), \end{aligned}$$
(6)

then system (4) is Mittag-Leffler stable.

Lemma 2

([53])

Suppose that \(\mu (\nu )\in \mathbb{R}^{n}\) is a smooth function. Then the following inequalities hold:

$$ \mathbb{D}^{\rho }\mu ^{2}(\nu )\leq 2\mu (\nu ) \mathbb{D}^{\rho } \mu (\nu ), \quad \forall \nu \in \mathbb{R}^{+}. $$
(7)

Lemma 3

([54])

Assume that \(g(\nu )\) is a positive definite smooth function, it holds

$$ \mathbb{D}^{\rho }g(\nu )\leq -\varrho _{1}g(\nu )+\varrho _{2}, $$
(8)

where \(\varrho _{1}, \varrho _{2} \in \mathbb{R}\) are two positive parameters, then \(g(\nu )\) will eventually be as small as possible under proper values of the coefficients.

2.2 Characterization of the NN

A three-layer MIMO NN will be used to approximate unknown system uncertainty, which has the structure as shown in Fig. 1.

Figure 1
figure 1

NN structure

Full size image

Let η, k, and m be the number of neurons in the input layer, hidden layer, and output layer, respectively. Thus, the mathematical model of the above NN is expressed by

$$ y_{p}(s,w_{p})=\sum _{j=1}^{k}\omega _{pj}\varphi _{pj} \Biggl(\sum_{i=1} ^{\eta }v_{ji}s_{i}+ \theta _{j} \Biggr)=w^{T}_{p}\omega _{p}(\cdot ), $$
(9)

in which \(p=1,\ldots,m\),

w p = [ ω p 1 ⋮ ω p k ] , ω p = [ φ p 1 ( ∑ i = 1 η v 1 i s i + Π 1 ) ⋮ φ p h ( ∑ i = 1 η v h i s i + Π k ) ] ,

\(y_{k}\) represents the output. Usually, the function \(\varphi (\cdot )\) can be defined as

$$ \varphi (\xi )=\frac{e^{\xi }-e^{-\xi }}{e^{\xi }+e^{-\xi }}. $$

Denote

ϕ= [ w 1 T w 2 T ⋮ w m T ] ,φ= [ ω 1 ( ⋅ ) 0 ⋯ 0 0 ω 2 ( ⋅ ) ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ ω m ( ⋅ ) ] andy= [ y 1 y 2 ⋮ y m ] ,

NN (9) can be expressed by

$$ y=\phi ^{T}\varphi . $$
(10)

NN (10) can be used to approximate unknown function \(\varPsi (\eta (s))\) by

$$ \varPsi \bigl(\eta (s)\bigr)=\phi ^{*T}\varphi \bigl(\eta (s)\bigr)+ \varsigma \bigl(\eta (s)\bigr), $$
(11)

with \(\varsigma (\eta (s))\) being the approximation error. Let us define the optimal approximate error \(\phi ^{*}\) as follows:

$$ \phi ^{*}=\operatorname{arg}\min_{\phi } \bigl[ \max \bigl\vert \phi ^{T}\varphi \bigl(\eta (s)\bigr)- \varPsi \bigl(\eta (s)\bigr) \bigr\vert \bigr]. $$

3 Main results

Consider the FOCH chaotic system, which can be expressed as follows [55]:

$$ \textstyle\begin{cases} \mathbb{D}^{\alpha } u_{1}(s) = u_{2}(s)+\frac{10}{7}(u_{1}(s)-u_{1} ^{3}(s)), \\ \mathbb{D}^{\alpha } u_{2}(s) =10u_{1}(s)-u_{2}(s)+u _{3}(s),\\ \mathbb{D}^{\alpha } u_{3}(s) =-\frac{100}{7}u_{2}(s)+ \vartheta (s)+w(s), \end{cases} $$
(12)

where \(u_{i}\) is the state variable, \(\vartheta (s)\) is an unknown nonlinear function, and \(w(s)\) is the control input.

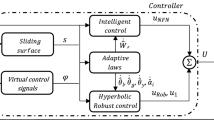
Our objective is to design an adaptive NN controller such that the system is asymptotically stable. The backstepping design procedure is given by n steps as follows.

For system (12), let \(\bar{\xi }_{1}(t)=u_{1}(s)\), then

$$ \mathbb{ D}^{\alpha }\bar{\xi }_{1}(s)=u_{2}(s)+ \frac{10}{7}\bigl(u_{1}(s)-u ^{3}_{1}(s) \bigr). $$
(13)

Introducing a virtual controller \(\eta _{1}(s)\), then we have

$$ \bar{\xi }_{2}(t)=u_{2}(s)-\eta _{1}(s). $$
(14)

Choose \(\eta _{1}(s)\) as

$$ \eta _{1}(s)=-k_{1}\bar{\xi _{1}}(s)-\frac{10}{7}\bigl(u_{1}(s)-u^{3}_{1}(s) \bigr). $$
(15)

Substituting (14) and (15) into Eq. (13), we can get

$$ \mathbb{D}^{\alpha }\bar{\xi }_{1}(s)=\bar{\xi }_{2}(s)-k_{1}\bar{\xi _{1}}(s). $$
(16)

Differentiating \(\bar{\xi }_{2}(s)\) yields

$$ \mathbb{D}^{\alpha }\bar{\xi }_{2}(s)=10u_{1}(s)-u_{2}(s)+u_{3}(s)- \mathbb{D}^{\alpha }\eta _{1}(s). $$
(17)

Let

$$ \bar{\xi }_{3}(s)=u_{3}(s)-\eta _{2}(s), $$
(18)

then (17) is rearranged by

$$ \mathbb{D}^{\alpha }\bar{\xi }_{2}(s)=10u_{1}(s)-u_{2}(s)+ \bar{\xi } _{3}(s)+\eta _{2}(s)-\mathbb{D}^{\alpha } \eta _{1}(s). $$
(19)

We choose \(\eta _{2}(s)\) as

$$ \eta _{2}(s)=-k_{2}\bar{\xi _{s}}(t)-\bar{\xi _{1}}(s)-10u_{1}(s)+u_{2}(s)+ \mathbb{D}^{\alpha }\eta _{1}(s), $$
(20)

which implies that

$$ \mathbb{D}^{\alpha }\bar{\xi }_{2}(s)=\bar{\xi }_{3}(s)-k_{2}\bar{\xi _{2}}(s)-\bar{\xi _{1}}(s). $$
(21)

From (18), we have

$$ \mathbb{D}^{\alpha }\bar{\xi }_{3}(s)=- \frac{100}{7}u_{2}(s)+\vartheta (s)+w(s)-\mathbb{D}^{\alpha } \eta _{2}(s). $$
(22)

Based on the above discussion, the main results are given as follows.

Theorem 1

Consider system (12). If \(\vartheta (s)\) is known, and the controller is given as

$$ w(s)=\frac{100}{7}u_{2}(s)-k_{3}\bar{\xi }_{3}(s)-\bar{\xi }_{2}(s)- \vartheta (s)+ \mathbb{D}^{\alpha }\eta _{2}(s), $$

then the system is globally asymptotically stable, where \(\eta _{i}(s)\) is the designed virtual controller, \(k_{1}\), \(k_{2}\), \(k_{3}\) are three positive constants.

Proof

Consider the following Lyapunov function:

$$ V(s)=\frac{1}{2}\bar{\xi }^{2}_{1}(s)+ \frac{1}{2}\bar{\xi }^{2}_{2}(s)+ \frac{1}{2} \bar{\xi }^{2}_{3}(s). $$
(23)

It follows from Lemma 2 that

$$ \mathbb{D}^{\alpha }V(s)=\bar{\xi }_{1}(s) \mathbb{D}^{\alpha }\bar{ \xi }_{1}(s)+\bar{\xi }_{2}(s)\mathbb{D}^{\alpha }\bar{\xi }_{2}(s)+\bar{ \xi }_{3}(s)\mathbb{D}^{\alpha }\bar{\xi }_{3}(s). $$
(24)

Substituting (16), (21), and (22) into (24), we have

$$ \begin{aligned}[b] \mathbb{D}^{\alpha }V(s) &=-k_{1}\bar{\xi }^{2}_{1}(s)-k_{2} \bar{ \xi }^{2}_{2}(s)+\bar{\xi }_{2}(s)\bar{\xi }_{3}(s) \\ &\quad{} +\bar{\xi } _{3}(s) \biggl[-\frac{100}{7}u_{2}(s)+ \vartheta (s)+w(s)-\mathbb{D} ^{\alpha }\eta _{2}(s) \biggr]. \end{aligned} $$
(25)

Final controller can be chosen as

$$ w(s)=\frac{100}{7}u_{2}(s)-k_{3}\bar{ \xi }_{3}(s)-\bar{\xi }_{2}(s)- \vartheta (s)+ \mathbb{D}^{\alpha }\eta _{2}(s), $$
(26)

which yields

$$ \begin{aligned}[b] \mathbb{D}^{\alpha }V(s) &=-k_{1}\bar{\xi }^{2}_{1}(s)-k_{2} \bar{ \xi }^{2}_{2}(s)-k_{3}\bar{\xi }^{2}_{3}(s) \\ &\leq -\sigma V(s), \end{aligned} $$
(27)

where \(\sigma =2\min \{k_{1}, k_{2}, k_{3}\}\). □

Therefore, it follows from Lemmas 1 and 3 that system (12) is globally asymptotically stable.

However, since \(\vartheta (s)\) is unknown, the controller \(w(s)\) cannot be achieved directly. Now, the adaptive NN backstepping controller is designed as follows.

By employing NNs (10), the unknown function \(\vartheta (s)\) can be approximated by

$$ \vartheta (s)=\phi ^{*T}\varphi (s)+\varsigma (s). $$
(28)

The following inequalities will be used:

$$\begin{aligned}& \begin{aligned}[b] \bar{\xi }_{3}(s)\phi ^{*T}\varphi (s) &\leq \frac{1}{2}\bar{\xi }^{2} _{3}(s)\phi ^{*T}\phi ^{*}\varphi ^{T}(t)\varphi (s)+\frac{1}{2} \\ &\leq \frac{1}{2}\bar{\xi }^{2}_{3}(s)\varPi \varphi ^{T}(s)\varphi (s)+ \frac{1}{2}, \end{aligned} \end{aligned}$$
(29)
$$\begin{aligned}& \bar{\xi }_{3}(s)\varsigma (s)\leq \frac{1}{2} \bar{\xi }^{2}_{3}(s)+ \frac{1}{2}\varsigma ^{*2}, \end{aligned}$$
(30)

where \(\varPi = \Vert \phi ^{*} \Vert ^{2}\), \(\tilde{\varPi }=\varPi -\hat{\varPi }\) with Π̂ being the estimation of Π.

To achieve the control, we choose \(w(t)\) as

$$ w(s) =\frac{100}{7}u_{2}(s)-k_{3} \bar{\xi }(s)-\bar{\xi }_{2}(s)- \frac{1}{2}\bar{\xi }_{3}\hat{\varPi }\varphi ^{T}(s)\varphi (s)+ \mathbb{D}^{\alpha }\eta _{2}(s), $$
(31)

and the adaptation law is given as

$$ \mathbb{D}^{\alpha }\hat{\varPi }=\frac{1}{2}\bar{\xi }^{2}_{3}\varphi ^{T}(s)\varphi (s)-\hat{\varPi }. $$
(32)

Based on the above detailed procedure, we can obtain the following theorem.

Theorem 2

Consider the fractional-order chaotic system (12). If the NN controller and the fractional adaptation laws are designed as

$$\begin{aligned}& w(s)=\frac{100}{7}u_{2}(s)-k_{3}\bar{\xi }(s)-\bar{ \xi }_{2}(s)- \frac{1}{2}\bar{\xi }_{3}\hat{\varPi } \varphi ^{T}(s)\varphi (s)+ \mathbb{D}^{\alpha }\eta _{2}(s), \\& \mathbb{D}^{\alpha }\hat{\varPi }=\frac{1}{2}\bar{\xi }^{2}_{3}\varphi ^{T}(s)\varphi (s)-\hat{\varPi }, \end{aligned}$$

respectively, then the states of system (12) will converge to a small neighborhood of zero.

Proof

Define the Lyapunov function as

$$ V(s)=\frac{1}{2}\bar{\xi }^{2}_{1}(s)+ \frac{1}{2}\bar{\xi }^{2}_{2}(s)+ \frac{1}{2} \bar{\xi }^{2}_{3}(s)+\frac{1}{2}\tilde{\varPi }^{2}. $$
(33)

Using using (25), (28), (31), and Lemma 2, we have

$$ \begin{aligned}[b] \mathbb{D}^{\alpha }V(s) &=-k_{1}\bar{\xi }^{2}_{1}(s)-k_{2} \bar{ \xi }^{2}_{2}(s)-k_{3}\bar{\xi }^{2}_{3}(s)+\bar{\xi }_{3}(s)\phi ^{*T} \varphi (s) \\ &\quad{} +\bar{\xi }_{3}(s)\varsigma (s) -\frac{1}{2}\bar{ \xi }^{2}_{3}\hat{\varPi }\varphi ^{T}(s)\varphi (s)-\tilde{\varPi } \dot{\hat{\varPi }}. \end{aligned} $$
(34)

Substituting (29), (30), and (32) into (34) yields

$$\begin{aligned} \mathbb{D}^{\alpha }V(s) &\leq -k_{1}\bar{\xi }^{2}_{1}(s)-k_{2} \bar{ \xi }^{2}_{2}(s)-k_{3}\bar{\xi }^{2}_{3}(s)+\frac{1}{2}\bar{\xi }^{2} _{3}(s)\varPi \varphi ^{T}(s)\varphi (s)+\frac{1}{2} \\ &\quad{} +\frac{1}{2}\bar{ \xi }^{2}_{3}(s)+ \frac{1}{2}\varsigma ^{*2} -\frac{1}{2}\bar{\xi }^{2} _{3}\hat{\varPi }\varphi ^{T}(s)\varphi (s)-\tilde{\varPi }\biggl[\frac{1}{2}\bar{ \xi }^{2}_{3} \varphi ^{T}(s)\varphi (s)-\hat{\varPi }\biggr] \\ &=-k_{1}\bar{ \xi }^{2}_{1}(s)-k_{2} \bar{\xi }^{2}_{2}(s)-\biggl(k_{3}- \frac{1}{2}\biggr)\bar{ \xi }^{2}_{3}(s)+ \frac{1}{2}+\frac{1}{2}\varsigma ^{*2}+\tilde{\varPi } \hat{\varPi }. \end{aligned}$$
(35)

Note that

$$ \tilde{\varPi }\hat{\varPi }=\tilde{\varPi }(\varPi -\tilde{ \varPi })\leq \frac{1}{2}\varPi ^{2}-\frac{1}{2}\tilde{ \varPi }^{2}, $$
(36)

then (35) can be rearranged as

$$ \begin{aligned}[b] \mathbb{D}^{\alpha }V(s) &\leq -k_{1}\bar{\xi }^{2}_{1}(s)-k_{2} \bar{ \xi }^{2}_{2}(s)-\biggl(k_{3}- \frac{1}{2}\biggr)\bar{\xi }^{2}_{3}(s) \\ &\quad{} + \frac{1}{2}+\frac{1}{2}\varsigma ^{*2}+ \frac{1}{2}\varPi ^{2}-\frac{1}{2} \tilde{\varPi }^{2} \\ &\leq -\rho _{1}V(s)+\rho _{2}, \end{aligned} $$
(37)

where \(\rho _{1}=\min \{2k_{1}, 2k_{2}, 2k_{3}-1, 1\}\), \(\rho _{2}= \frac{1}{2}+\frac{1}{2}\varsigma ^{*2}+\frac{1}{2}\varPi ^{2}\).

Thus, according to (37) and Lemma 3, the states of system (12) will remain in a small neighborhood of zero. □

Remark 1

In this work, NN approximation-based adaptive control method is used. In fact, the NN approximation-based adaptive control method has attracted more and more scholars’ attention in the past years. Compared with the conventional control method, the NN control method has some satisfactory merits. Firstly, the complexity of modeling practical systems can be greatly simplified. As a result, the controller design problem for many nonlinear systems subject to functional uncertainties can be alleviated. Secondly, according to the practical persistently exciting condition of NNs, parameter convergence is easier to be achieved and it can also improve the control performance. In addition, a NN control method treats the similar or the same mission as a new one and recalculates adaptive parameters to ensure the stability of the controlled system without the prior knowledge; however, the traditional adaptive control needs not only the adaptability but also the capabilities of accurate parameter estimation and knowledge storage with reusage for other similar or same missions.

Remark 2

To update the parameters of the NNs, the fractional-order adaptation law (32) is given. From the proof of Theorem 2, we know that the fractional-order adaptation law plays an important role in the stability analysis of fractional-order systems. Compared with the traditional law, the fractional one has one more degree. In fact, the traditional law can be seen as an exceptional case of the fractional one, i.e., \(\alpha =1\).

Remark 3

In this paper, backstepping control approach is used. This is a technique of designing stabilizing controls for systems with triangular form. This type of systems is constructed from subsystems that radiate out from an irreducible subsystem that can be stabilized using some other method. That is to say, the triangular systems have recursive structure, and the controller can be implemented at the known-stable system and back to stabilize each outer subsystem. It is worth mentioning that there are many control approaches, such as feedback control, adaptive control, impulsive control, that can be used to control fractional-order chaotic systems. However, the aforementioned control methods can not be used as a recursive algorithm.

4 Circuit realization for the FOCH chaotic system

In this section, we will build an electronic circuit for the FOCH chaotic system. In the literature [56], the approximation of \(\frac{1}{t^{0.9}}\) is given by

$$ \frac{1}{t^{0.9}}\approx \frac{2.2675(t+1.292)(t+215.4)}{(t+0.01292)(t+2.154)(t+359.4)}. $$
(38)

Base on this approximation, a unit circuit is designed to implement the function \(\frac{1}{t^{0.9}}\) which is shown in Fig. 2. Here, the chain fractance consists of three resistors \(R_{x}\), \(R_{y}\), \(R_{z}\) and three capacitors \(C_{x}\), \(C_{y}\), \(C_{z}\). The transfer function \(\operatorname{FC}(t)\) of this chain fractance is written as follows:

$$ \operatorname{FC}(t)=\frac{\frac{C_{0}}{C_{x}}}{t+\frac{1}{R_{x}C_{x}}}+\frac{\frac{C _{0}}{C_{y}}}{t+\frac{1}{R_{y}C_{y}}}+ \frac{\frac{C_{0}}{C_{z}}}{t+\frac{1}{R _{z}C_{z}}}. $$
(39)

Let \(C_{0}=1\ \mu \mathrm{F}\), from (38) and (39), we can gain \(R_{x}=62.84 \ \mathrm{M}\varOmega \), \(R_{y}=250\ \mathrm{k}\varOmega \), \(R_{z}=205\ \mathrm{k}\varOmega \), \(C_{x}=1.23 \ \mu \mathrm{F}\), \(C_{y}=1.835\ \mu \mathrm{F}\), \(C_{z}=1.1\ \mu \mathrm{F}\), \(\operatorname{FC}(t)\approx \frac{1}{t^{0.9}}\).

Figure 2
figure 2

Unit circuit for realizing \(\frac{1}{t^{0.9}}\)

Full size image

s

To realize the FOCH chaotic system, an electronic circuit is designed using R–C components, analog multipliers and operational amplifiers. The circuit diagram is depicted in Fig. 3, its mathematical equations are given as the following form:

$$ \textstyle\begin{cases} \mathbb{D}^{\alpha } u_{1} = \frac{R_{b}}{R_{c}R_{g}C_{1}}u_{2}+\frac{R _{b}}{R_{c}C_{1}}(\frac{1}{R_{f}}u_{1}-\frac{R_{e}}{R_{a}R_{d}}u_{1} ^{3}), \\ \mathbb{D}^{\alpha } u_{2} =\frac{R_{i}}{R_{h}R_{j}C_{2}}u _{1}-\frac{R_{i}R_{l}}{R_{j}R_{k}R_{m}C_{2}}u_{2}+\frac{R_{i}}{R_{j}R _{n}C_{2}}u_{3},\\ \mathbb{D}^{\alpha } u_{3} =-\frac{R_{l}R_{p}}{R _{k}R_{o}R_{q}C_{3}}u_{2}, \end{cases} $$
(40)

where \(C_{1}\), \(C_{2}\), \(C_{3}\) are three fractional capacitors, they are implemented by \(R_{x}\), \(R_{y}\), \(R_{z}\), \(C_{x}\), \(C_{y}\), \(C_{z}\). In order to satisfy FOCH chaotic system (12), we choose the values of resistors and capacitors as follows:

$$\begin{aligned}& R_{a}=R_{f}=R_{o}=7 \ \mathrm{k}\varOmega ,\quad\quad R_{b}=R_{i}=R_{p}=1 \ \mathrm{k}\varOmega ,\quad\quad R_{c}=100 \ \mathrm{k}\varOmega , \quad\quad R_{j}=4 \ \mathrm{k}\varOmega \\& R_{d}=R_{e}=R_{g}=R_{k}=R_{l}=R_{q}=10 \ \mathrm{k}\varOmega , \quad\quad R_{h}=R_{m}=R_{n}=250 \ \mathrm{k}\varOmega \\& C_{1}=C_{2}=C_{3}=1\ \mu \mathrm{F}. \end{aligned}$$
Figure 3
figure 3

Simulation circuit of FOCH chaotic system (12)

Full size image

5 Simulation studies

The validity of the proposed method will be indicated by simulation results in this part.

For FOCH system (12), let the initial condition be \(u_{1}(0)=1.0\), \(u_{2}(0)=-1.0\), \(u_{3}(0)=0.5\), where \(\alpha =0.9\). Let \(\omega (s)\equiv \vartheta (s) \equiv 0 \), the dynamical behavior of system (12) is depicted in Fig. 4.

Figure 4
figure 4

Dynamical behavior of system (12) with \(\omega (s)=0\)

Full size image

Let the unknown nonlinear function be \(\vartheta (s) = u_{1}(s)u_{3}(s)+u _{2}(s)\), and the control parameters are given as \(k_{1}=k_{2}=k_{3}=1\).

Figure 5 gives the response of the output variable \(u_{1}\), from which we can see that the output variable converges to a small region of the origin rapidly. The smoothness of the control input \(\omega (s)\) and the NN \(\phi (s)\) are given in Fig. 6 and Fig. 7, respectively. The initial value of the NN is random. It is indicated that the proposed method has good control performance.

Figure 5
figure 5

Time response of state variables of \(u_{1}\)

Full size image
Figure 6
figure 6

Control input ω

Full size image
Figure 7
figure 7

NN parameters ϕ

Full size image

To test the robustness of this method, we add external disturbance to system (12): \(d_{1}(t)=3\sin t\), \(d_{2}(t)=3\cos t\), \(d_{3}(t)=3.5 \sin t-3\cos t\). The simulation results are shown in Fig. 8. From Fig. 8, we can see that the variables quickly converge to the origin with very small fluctuations. That is to say, our control method has very good robustness.

Figure 8
figure 8

Simulation trajectories of system (12) with external disturbance

Full size image

6 Conclusions

This paper provides an adaptive NN control approach for a class of fractional-order chaotic systems. The NNs are used to approximate unknown system uncertainties and external disturbances. By using the backstepping control technique, a NN controller is constructed. It is proven that the proposed controller combined with fractional-order parameter adaptation law can guarantee the stability of the closed-loop system. Noting that the proposed controller has a complicated form, how to design a backstepping controller resolving the “explosion of terms” problem is our future research direction.