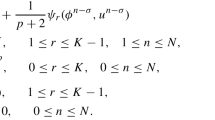Abstract
In this study, we have proposed an efficient numerical algorithm based on third degree modified extended B-spline (EBS) functions for solving time-fractional diffusion wave equation with reaction and damping terms. The Caputo time-fractional derivative has been approximated by means of usual finite difference scheme and the modified EBS functions are used for spatial discretization. The stability analysis and derivation of theoretical convergence validates the authenticity and effectiveness of the proposed algorithm. The numerical experiments show that the computational outcomes are in line with the theoretical expectations. Moreover, the numerical results are proved to be better than other methods on the topic.
Similar content being viewed by others
1 Introduction
The study of fractional calculus is considered to be an extension of classical calculus which has been given significant attentions in last couple of decades. Many applications of fractional differential equations are found in electro-chemistry, biomedical engineering, hydrology, probability theory and finance [1,2,3,4,5,6]. Fractional-order differential equations appear in mathematical modeling of several natural phenomena such as diffusion procedures, viscoelasticity, thermo-elasticity, seepage of a liquid, dynamical processes in self-similar and porous structures, wave propagation, anomalous diffusion transport, signal processing, control theory of dynamical systems, rheology and optics [7,8,9,10,11]. The time-fractional diffusion-wave equation (DWE) is one of them. This mathematical model is formulated from the classical DWE after replacing the second order time derivative by fractional derivative of order α (\(1<\alpha \leq 2\)). Consider the following time-fractional DWE with Caputo’s fractional derivative involving reaction and damping terms:
controlled by the following constraints:
where \(f(z,t)\), \(\phi _{i}\), \(\psi _{i}\) (\(i=0,1\)) are smooth functions with second order continuous derivatives and β, γ are coefficients of the reaction and damping terms, respectively. The Caputo fractional derivative \(\frac{\partial ^{\alpha }}{\partial t^{\alpha }}u(z,t)\) of order \(\alpha \in (1,2]\) is defined as
where Γ denotes the gamma function.
The study of exact and approximate solutions of differential/integral equations has always remained an attractive area of research. The existence and behavior of unique solutions for some fractional-order quadratic Volterra equations and nonlinear integral equations has been discussed in [12,13,14,15,16]. In the last couple of decades many researchers studied the approximate solution of fractional-order DWE. Ding et al. [17] presented two numerical algorithms based on usual finite difference formulation for solving time-fractional DWE. Bhrawy et al. [18] employed the spectral tau method composed with the shifted Jacobi matrix for numerical treatment of second order fractional DWE. A numerical algorithm based on radial basis functions for solving fractional DWE was developed by Avazzadeh et al. [19]. A triangular function algorithm based on the operational matrix of a fractional-order integration was discussed by Ebadian et al. [20] for solving a time-fractional DWE. Osama et al. [21] employed the Sinc-Legendre collocation method to explore the numerical solution of a time-fractional DWE by reducing the problem into system of linear algebraic equations. Hooshmandasl et al. [22] numerically solved the fractional sub-diffusion and time-fractional DWE by employing the Galerkin technique depending on the fractional-order Legendre functions.
Chatterjee et al. [23] used Bernstein polynomials to approximate truncated series for nonlinear fractional-order DWE. A numerical algorithm based on Chebyshev wavelets was formulated by Zhou and Xu [24] to obtain the approximate solution for time-fractional DWE. Numerous researchers have developed various methods for solving a time-fractional DWE; see [14, 25,26,27]. Recently, Kanwal et al. [28] presented a Ritz–Galerkin method together with two-dimensional Genocchi polynomials to establish the numerical solutions of a time-fractional DWE and a time-fractional Klein–Gordon equation.
Various numerical methods based on spline functions have also been employed by researchers in pursue of reliable solutions for fractional-order differential equations [29,30,31]. The B-spline functions provide decent approximations in contrast with rest of numerical schemes due to the nominal, compact support and \(C^{2}\) continuity [32]. The approximate solution of a time-fractional DWE via cubic trigonometric B-splines was explored in [33]. Sayevand et al. [34] employed the B-spline collocation technique for a numerical investigation of time-fractional diffusion problems arising in transport dynamic systems. Shukla and Tamsir [35] proposed differential quadrature method based on third degree EBS test functions for solving Fisher’s reaction–diffusion equation. Recently, Mohyud-Din et al. [32] discretized the spatial derivatives using extended cubic B-spline (ECBS) functions for solving a time-fractional advection–diffusion equation (ADE).
In the present paper, the application of modified ECBS functions has been presented for a numerical treatment of a time-fractional DWE involving reaction and damping terms. For temporal discretization, a usual finite difference approach consorted with Caputo’s time-fractional derivative has been used, while spatial derivatives are described by modified ECBS functions.
The section-wise organization of the paper is as follows: In Sect. 2, derivation of space derivatives via modified ECBS functions has been discussed. The temporal discretization is explained in Sect. 3. The description of numerical method is presented in Sect. 4. The stability and convergence analysis of the proposed scheme is given in Sect. 5. To corroborate the efficiency and validity of the present approach, the experimental results and comparisons are displayed in Sect. 6. Finally, concluding remarks are presented in Sect. 7.
2 Modified extended cubic B-spline functions
Consider a partition \(a=z_{0}< z_{1}<\cdots <z_{N}=b\) of the interval \([a,b]\) into subintervals \([z_{i-1},z_{i}]\) with equal spacing \(h=\frac{1}{N}(b-a)\), \(i=1:1:N\).
Let \(U(z,t)\) denote the ECBS solution to the problem (1)–(3) s.t.
where \(\alpha _{i}^{n}(t)\) are time dependent constants, to be determined, and the ECBS blending functions of degree 4, \(\eta _{i}(z)\), are defined as [32, 36]
In the above formulation, μ is a free parameter which is used to change the shape of the B-spline curve and \(-m(m-2)\leq \mu \leq 1\), m is the degree of ECBS [35]. For \(\mu =0\), the ECBS functions reduce to ordinary cubic B-spline functions. Further, \(\eta _{-1},\eta _{0}, \ldots ,\eta _{N+1}\) are taken in such a way that it forms spline basis over \([a,b]\). The values of ECBS functions and their derivative at nodal points are displayed in Table 1. The approximate solution \(U_{i}^{n}=U(z_{i},t^{n})\) with its first and second derivative in terms of the time parameter \(\alpha _{i}\) can be expressed as
where \(c_{1}=\frac{4-\mu }{24}\), \(c_{2}=\frac{16+2\mu }{24}\), \(c_{3}=\frac{1}{2h}\), \(c_{4}=\frac{2+\mu }{2h^{2}}\), \(c_{5}=\frac{-4-2 \mu }{2h^{2}}\).
In the present study, the ECBS functions are modified in such a way that they preserve the diagonal dominance property. The modification in ECBS functions is as follows [37]:
where \(\{B_{0},B_{1}, \ldots , B_{N}\}\) are the modified ECBS basis over the spatial domain \([a,b]\).
3 Temporal discretization
The second order differential operator approximation in time direction, using a finite difference scheme, is given by
where \(t_{n}=n\times \Delta t\), \(n=0:1:M\) and \(T=M\times \Delta t\). The Caputo fractional derivative term \(\frac{\partial ^{\alpha }u(z,t)}{ \partial t^{\alpha }}\) given in Eq. (1) is discretized by making use of Eqs. (4) and (9) to obtain an efficient approximation as follows:
Hence
where \(b_{r} = (r+1)^{2-\alpha }-(r)^{2-\alpha }\), \(s = t_{n+1}- \tau \) and the truncation error \(e_{\Delta t}^{n+1}\) is bounded such that
where σ is a constant.
Lemma 3.1
The following properties are fulfilled by the coefficients \(b_{r} \) [34]:
-
\(b_{r}>0 \) and \(b_{0}=1 \), \(r=1:1:n\),
-
\(b_{0}>b_{1}>b_{2}>\cdots > b_{r}\), \(b_{r} \rightarrow 0 \) as \(r\rightarrow \infty \),
-
\(-b_{r}+(2b_{r}-b_{r-1})+\sum_{r=1}^{n-1} (-b_{r-1}+2b_{r}-b_{r+1})+(2b _{0}-b_{1})=1\).
Using Eq. (10) in Eq. (1), we get the following form:
Assuming \(\rho = \frac{1}{\varGamma (3-\alpha ) (\Delta t)^{\alpha }}\), \(\beta _{0} =\frac{\beta }{\Delta t}\), \(u^{n+1}=u(z,t_{n+1})\), the above expression takes the following form:
where \(n=0:1:M\). We use the initial condition to eliminate \(u^{-1}\), which will occur for \(n=0\), i.e.
In particular, taking \(n=0\), the scheme takes the following form:
Using Eq. (14), the above equation simply leads to the following form:
4 Description of the numerical scheme
Using the ECBS approximations given in Eq. (7) in Eq. (13), the implicit finite difference formulation yields the following recurrence relation:
The above system together with Eq. (15) gives \((N+1)\) linear equations with \((N+1)\) unknowns. We obtain a tri-diagonal \((N+1) \times (N+1)\) matrix system as
where \(p=(\rho +\beta _{0}+\gamma )c_{1}- c_{4}\), \(q=(\rho +\beta _{0}+ \gamma )c_{2}- c_{5}\) and \(q_{i}^{n+1}=2b_{n} \Delta t \phi _{1}(z)+f _{i}^{n+1}\). First of all, it is essential to find the initial vector \(\alpha ^{0}=[\alpha _{0}^{0},\alpha _{1}^{0}, \ldots ,\alpha _{N}^{0}]^{T}\) to initiate the iteration procedure. Making use of the initial conditions, we have
In matrix notation, the above tri-diagonal system is expressed as
5 Stability and convergence
This section is for the discussion of the stability analysis and theoretical convergence of the proposed scheme.
5.1 Stability analysis
The numerical scheme is stable when the errors vanish as the computational procedure continues [38]. The Fourier method has been employed to investigate the stability of the presented numerical algorithm for solving time-fractional DWE. Let \(\varPhi _{i} ^{n}\) be the growth factor of the fourier mode and \(\tilde{\varPhi }_{i} ^{n}\) be its approximation. Define the error term \(\epsilon _{i}^{n}\) as
and \(\epsilon ^{n}=[\epsilon _{1}^{n}, \epsilon _{2}^{n}, \cdot , \epsilon _{N-1}^{n}]^{T}\).
It is sufficient to analyze stability of the scheme presented in Eq. (16) for force-free case \((f=0)\) only. The round-off error equation has been obtained from Eqs. (20) and (16) as
The initial/boundary conditions are satisfied by the error equation such as
and
Now, we define the mesh function as follows:
Expressing \(\epsilon ^{n}(z)\) in the Fourier series form:
where
Using the norm definition, we have
Using the Parseval equality, \(\int _{a}^{b}|\epsilon ^{n}|^{2} \,dz = \sum_{-\infty }^{\infty } |\xi _{n}(m)|^{2}\), we obtain the following relation:
Suppose the solution in the Fourier series form is presented as follows:
where \(i=\sqrt{-1}\) and \(\lambda ={\frac{2\pi m }{b-a}}\). Using Eq. (28) in Eq. (21) and then dividing by \(e^{i \lambda j h}\), we obtain
Using the relation \(e^{i \lambda h }+e^{-i \lambda h } = 2 \cos ( \lambda h)\) and collecting the like terms, we get
where \(\omega =1+\frac{2(\gamma c_{1}- c_{4})\cos (\lambda h)+(\gamma c_{2}- c_{5})}{(\rho +\beta _{0})(2 c_{1} \cos (\lambda h)+c_{2})}\), and we see that clearly \(\omega \geq 1\).
Lemma 5.1
Let \(\xi _{n}\) be the solution of Eq. (30), then \(|\xi _{n}| \leq 2|\xi _{0}|\), \(n=0:1:T \times M \).
Proof
We prove this result by induction.
For \(n=0\), Eq. (30) implies
Suppose that the result \(|\xi _{n}|\leq 2 |\xi _{0}|\) is true for \(n=1:1:T \times M-1\), and from Eq. (30), we obtain
□
Theorem 1
The implicit collocation scheme (16) is unconditionally stable.
Proof
By making use of Eq. (27) and Lemma 5.1, we get
From the aforementioned relations we conclude that the proposed scheme (16) is unconditionally stable. □
5.2 Convergence analysis
We follow Kadalbajoo and Arora [39] to examine the convergence of the proposed scheme. First of all, we state a theorem due to Boor [40] and Hall [41] which plays a key role for the convergence analysis of the proposed scheme.
Theorem 2
Let, \(u(z,t)\) belongs to \(C^{4}[a,b]\), f belongs to \(C^{2}[a,b]\) and \(\varPi =\{a=z_{0},z_{1}, \ldots , z_{N}=b\}\) be a partition such that \(z_{i}=ih\), \(i= 1:1:N\). Let \(\tilde{U}(z,t)\) denote the unique spline approximation to the present problem at the knots \(z \in \varPi \), then \(\forall t\geq 0\), ∃ \(a_{j}\), free of h, s.t.
Lemma 5.2
The modified ECBS set \(\{\eta _{0}, \eta _{1}, \ldots , \eta _{N}\}\) presented in Eq. (8) satisfy the inequality,
Proof
Using the triangular inequality, we have
For any nodal point \(z_{i}\), we get
Furthermore, for a point \(z \in [z_{i},z_{i+1}]\), we obtain
where
Since \(-8 \leq \mu \leq 1\), we have \(1 \leq \frac{20+\mu }{12} \leq \frac{7}{4}\).
Hence,
□
Theorem 3
The numerical approximation \(U(z,t)\) to the closed form solution \(u(z,t)\) exists for the time-fractional problem (1)–(3). Also, if \(f \in C^{2}[0,1]\), we have
where h is sufficiently small and \(\kappa >0\) is, a constant, free of h.
Proof
Let \(\tilde{U}(z,t)=\sum_{i=0}^{N} d_{i}(t) \eta _{i}(z)\) be the computed spline for the approximate solution \(U(z,t)\) and exact solution \(u(z,t)\). Using the triangular inequality, the expression can be written as
Using (31), we have
Let \(Lu(z_{i},t)=LU(z_{i},t)=f(z_{i},t)\), \(i=0:1:N \), be the collocation conditions, then
At any time level n, the given problem in the form of the difference equation \(L(\tilde{U}(z_{i},t)-U(z_{i},t))\) can be written as follows:
Also, the boundary conditions take the following form:
where
and
It is evident from (31) that we have
We define \(\varOmega ^{n}=\max \{|\varOmega _{i}^{n}|;0 \leq i \leq N \}\), \(\tilde{e}_{i}^{n}=|\nu _{i}^{n}|\) and \(\tilde{e}^{n}=\max \{|e _{i} ^{n}|;0 \leq i \leq N \}\).
For \(n=0\), Eq. (35) together with (14) takes the following form:
Using the initial condition, \(e^{0}=0\), we have
Taking absolute values of \(\varOmega _{i}^{n}\) and \(\nu _{i}^{n}\) with a sufficiently small mesh size h, we have
where \(a_{1}\) is independent of h.
Using the induction technique, assume that \(\tilde{e}_{i}^{s}\leq a _{s} h^{2}\) is true for \(s=1,2, \ldots , n\).
Let \(a=\max \{a_{s}: 0\leq s \leq n \}\), then Eq. (35) becomes
Hence,
Thus, for all values of n, we have
Now,
Taking the infinite norm and using Lemma 5.1, we obtain
From Eq. (38), Eq. (34) takes the following form:
where \(\kappa =a_{0}h^{2}+1.75a\). □
From the aforementioned theorem and Eq. (11) we conclude that the proposed numerical approach is convergent. Hence,
where κ and σ are constants.
6 Numerical examples
To examine the accuracy of the proposed computational scheme, some test examples are considered for the time-fractional DWE. The \(L_{2}\) and \(L_{\infty }\) norms are used to calculate the absolute errors of the proposed method as in [42]. We have
The experimental order of convergence (EOC) is calculated to be [43]
The numerical results obtained from the modified ECBS method are compared with given exact solutions and the numerical methods available in the literature. The software package MATHEMATICA 9.0 is used to run the simulation.
Example 1
Consider the time-fractional DWE [33]
with the conditions
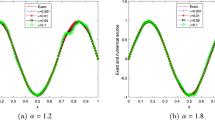
The boundary conditions can be extracted from the true solution \(u(z,t)=(t^{2}-t)\sin (\pi z)\). A comparison of maximum absolute error for Example 1 with the Hermite formula (HF) [44] and the cubic trigonometric B-spline method (CuTBSM) [33] is presented in Table 2. The numerically approximated solution with \(t=0.2\) and \(\alpha =1.5\), in the spatial domain \(0\leq z\leq 1\) using different combinations of h and Δt, is investigated. The results obtained by modified ECBS method are self-explanatory as compared to the outcomes of HF [44] and CuTBSM [33]. Also the results elaborated in Table 3 show a far better agreement with the analytical exact solution than the other methods at \(t=0.4\), \(\alpha =1.7\) for different choices of h and Δt. The EOC is portrayed in Table 4. The error norms \(L_{2}\) and \(L_{\infty }\) are also compared with the method given in [33]. In Fig. 1, the approximate solution at different time levels is shown in one frame when \(-1\leq z\leq 1\). The three dimensional visuals given in Fig. 2 elucidate our claim about accuracy of the proposed scheme for \(N=32\), \(\Delta t=0.01 \) and \(t=2\). The 3D absolute error graph is displayed in Fig. 3 for \(N=20\), \(t=1\), \(\Delta t=0.01 \) and \(\alpha =1.3\).
Exact and approximate solutions for Example 1 at \(t=2,4,6\) when \(N=10\), \(\alpha =1.5\) and \(-1\leq z \leq 1\)
Exact and approximate solutions for Example 1, when \(N=32\), \(\alpha =1.5\) and \(\Delta t= 0.01\)
Absolute error graph for Example 1 at \(t=1\) when \(N=20\), \(\alpha =1.3\) and \(0\leq z \leq 1\)
Example 2
Consider the time-fractional DWE involving damping term [45]
with the initial/boundary conditions
and
The analytical exact solution is \(u(z,t)=t^{3} e^{z}\). In Table 5, the approximate results returned by our method are compared with the implicit numerical method (INM) proposed in [45] for \(\alpha =1.85\), \(t=1\) and \(\Delta t=h^{2}\). The graphical representation of exact and numerical solutions at different time levels is captured in Fig. 4. Figure 5 depicts the physical behavior of exact and numerical solutions at \(N=50\), \(\alpha =1.25\) and \(t=1\). The comparison of the results shows a reflexive behavior of the approximate solution to the analytical exact solution. Figure 6 shows a 3D absolute error graph for \(\alpha =1.5\), \(t=1\), \(\Delta t=0.01\) and \(N=16\).
Exact and approximate solutions for Example 2 at \(t=0.2,0.3,0.4,0.5\) when \(N=10\), \(\alpha =1.85\) and \(\Delta t=0.001\)
Exact and approximate solutions for Example 2, when \(N=50\), \(\alpha =1.25\), \(t=2\) and \(\Delta t= 0.01\)
Absolute error graph for Example 2 at \(t=1\) when \(N=16\), \(\alpha =1.5\) and \(0\leq z \leq 1\)
Example 3
Consider a time-fractional DWE with a reaction term [19]
subject to the initial/boundary constraints
The exact solution is \(u(z,t)=t^{2} \sinh (z)\). In Table 6, the numerical results obtained by means of the modified ECBS method are compared with the radial basis function (RBF) method introduced in [19] and CuTBSM developed in [33]. The absolute computational errors corresponding to \(N=50\), \(\mu =-0.0196\), \(\alpha =1.25\) and \(\alpha =1.5\) are reported in Table 6. The numerical solutions obtained by the proposed numerical method at different time levels are depicted in Fig. 7. The 3D space-time graphs of exact and approximate solutions for \(N=50\), \(\alpha =1.6\), \(t=1\) and \(\Delta t= 0.01\) are displayed in Fig. 8. The three dimensional pictorizations of the absolute error for \(N=50\), \(\alpha =1.5\), \(t=1\) and \(\Delta t= 0.01\) are given in Fig. 9.
Exact and approximate solutions for Example 3 at \(t=2,4,6,8,10\) when \(N=10\), \(\alpha =1.5\) and \(\Delta t=0.01\)
Exact and approximate solutions for Example 3, when \(N=50\), \(\alpha =1.6\) and \(\Delta t= 0.01\), \(t=1\)
Absolute error graph for Example 3 at \(t=1\) when \(N=50\), \(\alpha =1.5\) and \(0\leq z \leq 1\)
7 Conclusion
An efficient fully implicit numerical algorithm, based on extended modified cubic B-spline functions, has been presented for solving a time-fractional diffusion-wave equation with reaction and damping terms. The Caputo time-fractional derivative is approximated by the usual finite difference formulation, whereas modified extended B-spline functions are employed to interpolate the solution curves in the space direction. The proposed numerical scheme is proved to be unconditionally stable. The theoretical and experimental convergence is of order 2. The computational outcomes are proved to be more reliable than the results found in RBF [19], CuTBSM [33], HF [44] and INM [45].
References
Miller, K.S., Ross, B.: An Introduction to the Fractional Calculus and Fractional Differential Equations (1993)
Podlubny, I.: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Mathematics in Science and Engineering, vol. 198 (1998)
Mainardi, F.: Fractional Calculus, pp. 291–348 (1997)
Benson, D.A., Wheatcraft, S.W., Meerschaert, M.M.: Application of a fractional advection–dispersion equation. Water Resour. Res. 36(6), 1403–1412 (2000)
Meerschaert, M.M., Tadjeran, C.: Finite difference approximations for fractional advection–dispersion flow equations. J. Comput. Appl. Math. 172(1), 65–77 (2004)
Meerschaert, M.M., Scalas, E.: Coupled continuous time random walks in finance. Phys. A, Stat. Mech. Appl. 370(1), 114–118 (2006)
Koeller, R.: Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 51(2), 299–307 (1984)
Shivanian, E., Jafarabadi, A.: Applications of Fractional Calculus in Physics (2000)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)
Aleroev, T., Aleroeva, H., Huang, J., Nie, N., Tang, Y., Zhang, S.: Features of seepage of a liquid to a chink in the cracked deformable layer. Int. J. Model. Simul. Sci. Comput. 1(3), 333–347 (2010)
Machado, J.T., Kiryakova, V., Mainardi, F.: Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 16(3), 1140–1153 (2011)
Mishra, L.N., Sen, M.: On the concept of existence and local attractivity of solutions for some quadratic Volterra integral equation of fractional order. Appl. Math. Comput. 285, 174–183 (2016)
Mishra, V.N.: Some problems on approximations of functions in Banach spaces. Ph.D. thesis (2007)
Mishra, V., Vishal, K., Das, S., Ong, S.H.: On the solution of the nonlinear fractional diffusion-wave equation with absorption: a homotopy approach. Z. Naturforsch. A 69(3–4), 135–144 (2014)
Deepmala: A study on fixed point theorems for nonlinear contractions and its applications. Ph.D. thesis (2014)
Esbo, M.R., Vazifeshenas, Y., Asboei, A.K., Mohammadyari, R., Vandana, V.: Numerical simulation of twisted tapes fitted in circular tube consisting of alternate axes and regularly spaced tapes. Acta Sci., Technol. 40, e37348 (2018)
Ding, H., Li, C.: Numerical algorithms for the fractional diffusion-wave equation with reaction term. Abstr. Appl. Anal. 2013, Article ID 493406 (2013)
Bhrawy, A., Doha, E.H., Baleanu, D., Ezz-Eldien, S.S.: A spectral tau algorithm based on Jacobi operational matrix for numerical solution of time fractional diffusion-wave equations. J. Comput. Phys. 293, 142–156 (2015)
Avazzadeh, Z., Hosseini, V., Chen, W.: Radial basis functions and FDM for solving fractional diffusion-wave equation. Iran. J. Sci. Technol., Sci. 38(3), 205–212 (2014)
Ebadian, A., Fazli, H.R., Khajehnasiri, A.A.: Solution of nonlinear fractional diffusion-wave equation by traingular functions. SeMA J. 72(1), 37–46 (2015)
Osama, H., Fadhel, S., Mohammed, G.: Numerical solution for the time-fractional diffusion-wave equations by using sinc-Legendre collocation method. Math. Theory Model. 5(1), 49–57 (2015)
Hooshmandasl, M., Heydari, M., Cattani, C.: Numerical solution of fractional sub-diffusion and time-fractional diffusion-wave equations via fractional-order Legendre functions. Eur. Phys. J. Plus 131(8), 268 (2016)
Chatterjee, A., Basu, U., Mandal, B.: Numerical algorithm based on Bernstein polynomials for solving nonlinear fractional diffusion-wave equation. Int. J. Adv. Appl. Math. Mech. 5, 9–15 (2017)
Zhou, F., Xu, X.: Numerical solution of time-fractional diffusion-wave equations via Chebyshev wavelets collocation method. Adv. Math. Phys. 2017, Article ID 2610804 (2017)
Mitkowski, W.: Approximation of fractional diffusion-wave equation. Acta Mech. Autom. 5, 65–68 (2011)
Delic, A.: Fractional in time diffusion-wave equation and its numerical approximation. Filomat 30(5), 1375–1385 (2016)
Ferreira, M., Vieira, N.: Fundamental solutions of the time fractional diffusion-wave and parabolic Dirac operators. J. Math. Anal. Appl. 447(1), 329–353 (2017)
Kanwal, A., Phang, C., Iqbal, U.: Numerical solution of fractional diffusion wave equation and fractional Klein–Gordon equation via two-dimensional Genocchi polynomials with a Ritz–Galerkin method. Computation 6(3), 40 (2018)
Khalid, N., Abbas, M., Iqbal, M.K.: Non-polynomial quintic spline for solving fourth-order fractional boundary value problems involving product terms. Appl. Math. Comput. 349, 393–407 (2019)
Amin, M., Abbas, M., Iqbal, M.K., Baleanu, D.: Non-polynomial quintic spline for numerical solution of fourth-order time fractional partial differential equations. Adv. Differ. Equ. 2019(1), 183 (2019)
Yaseen, M., Abbas, M.: An efficient computational technique based on cubic trigonometric B-splines for time fractional Burgers’ equation. Int. J. Comput. Math. (2019). https://doi.org/10.1080/00207160.2019.1612053
Mohyud-Din, S.T., Akram, T., Abbas, M., Ismail, A.I., Ali, N.H.: A fully implicit finite difference scheme based on extended cubic B-splines for time fractional advection–diffusion equation. Adv. Differ. Equ. 2018(1), 109 (2018)
Yaseen, M., Abbas, M., Nazir, T., Baleanu, D.: A finite difference scheme based on cubic trigonometric B-splines for a time fractional diffusion-wave equation. Adv. Differ. Equ. 2017(1), 274 (2017)
Sayevand, K., Yazdani, A., Arjang, F.: Cubic B-spline collocation method and its application for anomalous fractional diffusion equations in transport dynamic systems. J. Vib. Control 22(9), 2173–2186 (2016)
Shukla, H., Tamsir, M.: Extended modified cubic B-spline algorithm for nonlinear Fisher’s reaction–diffusion equation. Alex. Eng. J. 55(3), 2871–2879 (2016)
Wasim, I., Abbas, M., Iqbal, M.K.: A new extended B-spline approximation technique for second order singular boundary value problems arising in physiology. J. Math. Comput. Sci. 19(4), 258–267 (2019)
Mittal, R., Jain, R.: Numerical solutions of nonlinear Burgers’ equation with modified cubic B-splines collocation method. Appl. Math. Comput. 218(15), 7839–7855 (2012)
Boyce, W.E., DiPrima, R.C., Meade, D.B.: Elementary Differential Equations and Boundary Value Problems, vol. 9 (1992)
Kadalbajoo, M.K., Arora, P.: B-spline collocation method for the singular-perturbation problem using artificial viscosity. Comput. Math. Appl. 57(4), 650–663 (2009)
de Boor, C.: On the convergence of odd-degree spline interpolation. J. Approx. Theory 1(4), 452–463 (1968)
Hall, C.: On error bounds for spline interpolation. J. Approx. Theory 1(2), 209–218 (1968)
Abbas, M., Majid, A.A., Ismail, A.I.M., Rashid, A.: The application of cubic trigonometric B-spline to the numerical solution of the hyperbolic problems. Appl. Math. Comput. 239, 74–88 (2014)
Wasim, I., Abbas, M., Amin, M.: Hybrid B-spline collocation method for solving the generalized Burgers–Fisher and Burgers–Huxley equations. Math. Probl. Eng. 2018, Article ID 6143934 (2018)
Khader, M.M., Adel, M.H.: Numerical solutions of fractional wave equations using an efficient class of fdm based on the Hermite formula. Adv. Differ. Equ. 2016(1), 34 (2016)
Liu, F., Meerschaert, M.M., McGough, R.J., Zhuang, P., Liu, Q.: Numerical methods for solving the multi-term time-fractional wave-diffusion equation. Fract. Calc. Appl. Anal. 16(1), 9–25 (2013)
Acknowledgements
The authors are grateful to the anonymous reviewers for their helpful, valuable comments and suggestions in the improvement of this manuscript.
Availability of data and materials
Not applicable.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
All authors equally contributed to this work. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Khalid, N., Abbas, M., Iqbal, M.K. et al. A numerical algorithm based on modified extended B-spline functions for solving time-fractional diffusion wave equation involving reaction and damping terms. Adv Differ Equ 2019, 378 (2019). https://doi.org/10.1186/s13662-019-2318-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2318-7