1 Introduction

Fractional calculus (FC) was firstly put forward by L’Hopital. FC has received a lot of devotion and appreciation during the last few decades, due to its capability to provide an exact description for various nonlinear complex phenomena. The differential systems with fractional order have lately gained popularity in developing procedure of models and investigation of dynamical systems. The fractional calculus is the generalization of the traditional calculus having nonlocal and genetic consequences in the material properties.

The fundamental properties of fractional calculus have been described by many researchers [1,2,3,4]. FC plays a vital role and acts as an essential tool in analysing and solving problems situated in diverse areas of science and technology, like fluid and continuum mechanics [5], chaos theory [6], biotechnology [7], electrodynamics [8], and many other fields [9,10,11]. The solution for differential equations having arbitrary order and describing the above phenomena plays a pivotal part in labelling the behaviour of complex problems arising in nature [12,13,14,15,16,17,18,19,20,21,22].

In the twentieth century, Whitham [23], Broer [24] and Kaup [25] studied the equations, which elucidate the propagation of shallow water waves having distinct dispersion relation, called Whitham–Broer–Kaup (WBK) equations. Consider the coupled WBK equations of fractional order [26]:

$$ \textstyle\begin{cases} D_{t}^{\alpha } u+u u_{x} + v_{x} +b u_{xx} =0, \\ D_{t}^{\alpha } v+u v_{x} +v u_{x} +a u_{xxx} -b v_{xx} =0, \end{cases}\displaystyle 0< \alpha \leq 1, $$
(1)

where \(u=u ( x,t )\) is the horizontal velocity and \(v=v ( x,t ) \) is the height that deviates from equilibrium position of the liquid. Here, α is the order of the time-fractional derivative. Further, a and b are constants which represent distinct diffusion powers, i.e. if \(a=1\) and \(b=0\), then Eq. (1) becomes a modified Boussinesq equation. Similarly, for \(a=0\) and \(b=1\), the system signifies conventional long wave equation. These equations arise in hydrodynamics to illustrate the propagation of waves in dissipative and nonlinear media, and they are advisable for problems arising in the leakage of water in porous subsurface stratum and widely used in ocean and coastal engineering. Moreover, Eq. (1) is the foundation of numerous models utilized to portray the unconfined subsurface like drainage and groundwater flow problems.

Last thirty years has been the testimony for discovery of plenty of new schemes to solve nonlinear fractional differential equations in parallel to the developments of new computational algorithms with symbolic programming. In connection with this, Liao proposed a technique called homotopy analysis method (HAM), which is based on construction of a homotopy which continuously deforms an initial guess approximation to the exact solution of the given problem [27]. It does not require any discretization, linearization and perturbation. However, it requires huge computation and more computer memory to solve complex nonlinear problems situated in connected areas of science and technology. Hence, it necessitates an amalgamation of transformation techniques to overcome these confines.

In the present investigation, we applied the q-homotopy analysis transform method to find an approximated analytical solution for coupled modified Boussinesq and approximate long wave equations of fractional order. These equations have been studied and analysed by several authors via distinct techniques like Adomian decomposition method (ADM) [28], variational iteration method (VIM) [29], coupled fractional reduced differential transform method (CFRDTM) [26], Laplace Adomian decomposition method (LADM) [30] and other techniques [31,32,33]. In these cited papers, authors used a difficult solution procedure to find the solution, whereas the solution procedure of the future technique is very simple and straightforward. Further, these methods require huge computation and have a highly complicated solution procedure to solve coupled differential equations. The proposed method is a modified technique which is an elegant mixture of q-HAM and Laplace transform. Hence, it does not require discretization, linearization or perturbation; in addition, it will decrease huge mathematical computations, more computer memory and is free from obtaining difficult integrals, polynomials and physical parameters. The future technique has many sturdy properties including a straightforward solution procedure, promising large convergence region, and is free from any assumption, discretization and perturbation. The present method gives highly approximate results with a few iterations. The advantage of this method is its capability of combining two powerful methods for obtaining exact and approximate analytical solutions for nonlinear equations. It is worth revealing that the Laplace transform with semi-analytical techniques requires less C.P.U. time to evaluate solution for nonlinear complex models and phenomena arising in science and technology. The q-HATM solution involves two auxiliary parameters ℏ and n, which helps us adjust and control the convergence of the solution, which quickly tends to the analytical solution in a small acceptable region. It is worth to mention that the proposed scheme can decrease the computation time and work as compared with other traditional techniques while maintaining great efficiency.

Recently, due to consistency and efficacy of q-HATM, it has been eminently used by many researchers to analyse various kinds of nonlinear problem. For example, authors in [34] analysed and found the approximated analytical solution for a fractional model of vibration equation and elucidated the exactness of q-HATM. In [35] the solution for fractional Drinfeld–Sokolov–Wilson equation was investigated with the aid of the proposed scheme. The cancer chemotherapy effect model with fractional order was analysed by the authors in [36]. Bulut and his co-authors analysed HIV infection of CD4+T lymphocyte cells of fractional model [37]. The efficiency of considered algorithm was presented while finding the solution for fractional telegraph equation in [38]. Authors in [39] analysed the model of Lienard’s equation, and many others have studied and found the solution for many complex problems arising in the related fields of science [40,41,42,43,44,45]. The time-fractional derivative shows new characteristics in comparison with the standard time derivative, we can study these types of properties with the aid of the proposed technique. Also, the above literature survey shows that the future technique is highly systematic and accurate and can be employed to study the nonlinear mathematical models of arbitrary order, and the application of arbitrary order derivative gives very interesting and useful consequences. Motivated by these investigations, we find the approximated analytical solution for coupled nonlinear differential equations describing the shallow water waves through distinct dispersion relation. Also, we try to capture the behaviour of coupled surface for the obtained solution, and we made an attempt to analyse the nature of q-HATM solution for diverse values of fractional order.

2 Preliminaries

In this segment, we present basic definitions and notions which will be used in the present framework.

Definition 1

Let \(f ( t ) \in C_{\mu }\) (\(\mu \geq - 1 \)) be a function. Then the Riemann–Liouville fractional integral of \(f ( t )\) with order \(\alpha >0\) is presented as

$$ \begin{aligned}&J^{\alpha } f ( t )= \frac{1}{\varGamma ( \alpha )} \int _{0}^{t} ( t - x )^{\alpha - 1} f ( \vartheta )\,dx, \\ & J^{0} f ( t ) = f ( t ). \end{aligned} $$
(2)

Definition 2

The Caputo fractional derivative of \(f\in C_{- 1} ^{n}\) is defined as

$$ D_{t}^{\alpha } f ( t ) = \textstyle\begin{cases} \frac{d^{n} f ( t )}{d t^{n}}, &\alpha = n \in \mathbb{N}, \\ \frac{1}{\varGamma ( n-\alpha )} \int _{0}^{t} ( t- x )^{n- \alpha - 1} f^{( n )} ( x )\,dx, &n- 1< \alpha < n, n \in \mathbb{N}. \end{cases} $$
(3)

Definition 3

The Laplace transform (LT) of a Caputo fractional derivative \(D_{t}^{\alpha } f ( t )\) is represented as

$$ L \bigl[ D_{t}^{\alpha } f ( t ) \bigr] = s^{\alpha } F ( s ) - \sum_{r =0}^{n - 1} s^{\alpha - r - 1} f^{ ( r )} \bigl( 0^{+} \bigr)\quad ( n - 1< \alpha \leq n ), $$
(4)

where \(F ( s )\) represents the LT of \(f ( t )\).

3 Basic idea of q-HATM

Consider the nonlinear differential equation of arbitrary order

$$ D_{t}^{\alpha } \mathcal{U} ( x, t ) + R \mathcal{U} ( x, t ) + N \mathcal{U} ( x, t ) = f ( x, t ),\quad n - 1< \alpha \leq n, $$
(5)

where R is the bounded linear differential operator in x and t (i.e. for a number \(\varepsilon >0\), we have \(\Vert R \mathcal{U} \Vert \leq \varepsilon \Vert \mathcal{U} \Vert \)), N specifies the nonlinear differential operator and is Lipschitz continuous with \(\mu >0\) satisfying \(\vert N \mathcal{U}- N \mathcal{V} \vert \leq \mu \vert \mathcal{U}-\mathcal{V} \vert \), and \(f ( x, t ) \) denotes the source term. On applying LT to Eq. (5), we have

$$ s^{\alpha } L \bigl[ \mathcal{U} ( x, t ) \bigr] - \sum _{k =0}^{n - 1} s^{\alpha - k - 1} \mathcal{U}^{ ( k )} ( x,0 ) + L \bigl[ R \mathcal{U} ( x, t ) \bigr] + L \bigl[ N \mathcal{U} ( x, t ) \bigr] = L \bigl[ f ( x, t ) \bigr]. $$
(6)

On simplification, Eq. (6) reduces to

$$ L \bigl[ \mathcal{U} ( x, t ) \bigr] - \frac{1}{s^{ \alpha }} \sum _{k =0}^{n - 1} s^{\alpha - k - 1} \mathcal{U}^{k} ( x,0 ) + \frac{1}{s^{\alpha }} \bigl\{ L \bigl[ R \mathcal{U} ( x, t ) \bigr] + L \bigl[ N \mathcal{U} ( x, t ) \bigr] - L \bigl[ f ( x, t ) \bigr] \bigr\} =0. $$
(7)

According to the homotopy analysis method [27], the nonlinear operator is a real function \(\varphi ( x, t; q )\) defined as

$$\begin{aligned} N \bigl[ \varphi ( x, t; q ) \bigr] =& L \bigl[ \varphi ( x, t; q ) \bigr] - \frac{1}{s^{\alpha }} \sum_{k =0}^{n - 1} s^{\alpha - k - 1} \varphi ^{ ( k )} ( x, t; q ) \bigl( 0^{+} \bigr) \\ &{} + \frac{1}{s^{\alpha }} \bigl\{ L \bigl[ R\varphi ( x, t; q ) \bigr] + L \bigl[ N\varphi ( x, t; q ) \bigr] -L \bigl[ f ( x, t ) \bigr] \bigr\} ,\quad \forall q \in \biggl[ 0, \frac{1}{ n} \biggr]. \end{aligned}$$
(8)

The homotopy constructed for \(H ( x, t )\) is as shown below:

$$ ( 1 - nq ) L \bigl[ \varphi ( x, t; q ) - \mathcal{U}_{0} ( x, t ) \bigr] = \hslash qH ( x, t ) N \bigl[ \varphi ( x, t; q ) \bigr], $$
(9)

where L symbolizes LT, \(\hslash \neq 0\) is an auxiliary parameter, \(\mathcal{U}_{0} ( x, t )\) is the initial guess and \(\varphi ( x, t; q )\) is an unknown function. For \(q =0\) and \(q = \frac{ 1}{n}\), the following results respectively hold true:

$$ \varphi ( x, t;0 ) = \mathcal{U}_{0} ( x, t ),\qquad \varphi \biggl( x, t; \frac{1}{n} \biggr) = \mathcal{U} ( x, t ). $$
(10)

Thus, by increasing q from 0 to \(\frac{1}{n}\), the solution \(\varphi ( x, t; q )\) converges from \(\mathcal{U}_{0} ( x, t )\) to \(\mathcal{U} ( x, t )\). Now, by applying the Taylor theorem [46], the function \(\varphi ( x, t; q )\) is expanding in a series form near to q, we have

$$ \varphi ( x, t; q ) = \mathcal{U}_{0} ( x, t ) + \sum _{m =1}^{\infty } \mathcal{U}_{m} ( x, t ) q^{m}, $$
(11)

where

$$ \mathcal{U}_{m} ( x, t ) = \frac{1}{m !} \frac{\partial ^{m} \varphi ( x, t; q )}{\partial q^{m}} \bigg| _{q =0}. $$
(12)

On choosing the initial guess \(\mathcal{U}_{0} ( x, t )\), the auxiliary parameter n, the auxiliary linear operator, ℏ and \(H ( x, t )\), series (11) converges at \(q = \frac{1}{n}\). Later, it provides solutions for Eq. (5) which is of the form

$$ \mathcal{U} ( x, t ) = \mathcal{U}_{0} ( x, t ) + \sum _{m =1}^{\propto } \mathcal{U}_{m} ( x, t ) \biggl( {\frac{1}{n}} \biggr)^{m}. $$
(13)

Now, differentiating Eq. (9) m-times in terms of q, then multiplying by \(\frac{1}{m !} \) and then taking \(q =0\), we have

(14)

where

$$ \vec {\mathcal{U}}_{m} = \bigl\{ \mathcal{U}_{0} ( x, t ), \mathcal{U}_{1} ( x, t ), \dots , \mathcal{U}_{m} ( x, t ) \bigr\} . $$
(15)

On employing inverse LT for Eq. (14), one can get

(16)

where

(17)

and

(18)

In Eq. (17), \(\mathcal{H}_{m}\) denotes homotopy polynomial defined as

$$ \mathcal{H}_{m} = \frac{1}{m!} \biggl[ \frac{\partial ^{m} \varphi ( x, y, t;q )}{\partial q^{m}} \biggr]_{q=0}\quad \text{and}\quad \varphi ( x, y, t;q ) = \varphi _{0} +q \varphi _{1} + q^{2} \varphi _{2} +\cdots . $$
(19)

By Eqs. (16) and (17), we have

(20)

Lastly, on simplifying Eq. (20), we get the iterative terms of \(\mathcal{ U}_{m} ( x,t )\). The series solution of q-HATM is presented by

$$ \mathcal{U} ( x,t ) = \sum_{m=0}^{\infty } \mathcal{U} _{m} ( x,t ). $$
(21)

4 Convergence analysis of q-HATM solution

Theorem 1

(Uniqueness theorem)

The solution for the nonlinear fractional differential equation (5) obtained by q-HATM is unique for every \(\beta \in ( 0,1 )\), where \(\beta = ( n+ \hslash )+ \hslash ( \varepsilon +\mu ) T\).

Proof

For Eq. (5), the solution is defined by

$$ \mathcal{U} ( x,t ) = \sum_{m=0}^{\infty } \mathcal{U} _{m} ( x,t ), $$

where

(22)

Suppose \(\mathcal{U}\) and \(\mathcal{U}^{\blacksquare}\) are the two solutions of Eq. (4), then it is sufficient to show \(\mathcal{U} = \mathcal{U}^{\blacksquare}\) to prove the theorem. Now, by Eq. (21), we obtain

$$ \bigl\vert \mathcal{U} - \mathcal{U}^{\blacksquare} \bigr\vert = \biggl\vert ( n+ \hslash ) \bigl( \mathcal{U} - \mathcal{U}^{\blacksquare} \bigr) + \hslash L^{-1} \biggl( \frac{1}{s ^{\alpha }} L \bigl( N \bigl( \mathcal{U} - \mathcal{U}^{ \blacksquare} \bigr) +R \bigl( \mathcal{U} - \mathcal{U}^{ \blacksquare} \bigr) \bigr) \biggr) \biggr\vert , $$

then by using the convolution theorem for LT, we have

$$\begin{aligned} \bigl\vert \mathcal{U} - \mathcal{U}^{\blacksquare} \bigr\vert \leq& ( n+ \hslash ) \bigl\vert \mathcal{U} - \mathcal{U}^{\blacksquare} \bigr\vert + \hslash \int _{0}^{t} \bigl( \bigl\vert N \bigl( \mathcal{U} - \mathcal{U}^{\blacksquare} \bigr) \bigr\vert + \bigl\vert R \bigl( \mathcal{U} - \mathcal{U}^{ \blacksquare} \bigr) \bigr\vert \bigr) \frac{ ( t- \xi ) ^{\alpha }}{\varGamma ( \alpha +1 )} \,d\xi \\ \leq& ( n+ \hslash ) \bigl\vert \mathcal{U} - \mathcal{U}^{\blacksquare} \bigr\vert + \hslash \int _{0}^{t} \bigl( \varepsilon \bigl\vert \bigl( \mathcal{U} - \mathcal{U}^{ \blacksquare} \bigr) \bigr\vert +\mu \bigl\vert \bigl( \mathcal{U} - \mathcal{U}^{\blacksquare} \bigr) \bigr\vert \bigr) \frac{ ( t- \xi )^{\alpha }}{\varGamma ( \alpha +1 )} \,d\xi . \end{aligned}$$

With the aid of integral mean value theorem, the above equation reduces to

$$ \bigl\vert \mathcal{U} - \mathcal{U}^{\blacksquare} \bigr\vert \leq ( n+ \hslash ) \bigl\vert \mathcal{U} - \mathcal{U}^{\blacksquare} \bigr\vert + \hslash \bigl( \varepsilon \bigl\vert \bigl( \mathcal{U} - \mathcal{U}^{\blacksquare} \bigr) \bigr\vert + \mu \bigl\vert \bigl( \mathcal{U} - \mathcal{U}^{\blacksquare} \bigr) \bigr\vert \bigr) T. $$

Here, \(\beta = ( n+ \hslash ) + \hslash ( \varepsilon +\mu ) T\), thus

$$ \bigl\vert \mathcal{U} - \mathcal{U}^{\blacksquare} \bigr\vert \leq \beta \bigl\vert \mathcal{U} - \mathcal{U}^{\blacksquare} \bigr\vert \quad \Rightarrow\quad ( 1-\beta ) \bigl\vert \mathcal{U} - \mathcal{U}^{\blacksquare} \bigr\vert \leq 0. $$

Since \(0<\beta <1\), then \(\mathcal{U} - \mathcal{U}^{\blacksquare} =0 \Rightarrow \mathcal{ U} = \mathcal{U}^{\blacksquare}\).

Hence, the solution for Eq. (5) is unique. □

Theorem 2

(Convergence theorem)

Let X be a Banach space and \(F:X\rightarrow X\) be a nonlinear mapping. Assume that

$$ \bigl\Vert F ( \mathcal{U} ) -F( \mathcal{V}) \bigr\Vert \leq \beta \Vert \mathcal{U} -\mathcal{V} \Vert , \quad \forall a, b\in X, $$

then F has a fixed point in view of Banach’s fixed point theory [47]. Moreover, for the arbitrary selection of \(a_{0}, b_{0} \in X\), the sequence generated by the q-HATM converges to a fixed point of F and

$$ \Vert \mathcal{U}_{m} - \mathcal{U}_{n} \Vert \leq \frac{ \beta ^{n}}{1-\beta } \Vert \mathcal{U}_{1} - \mathcal{U}_{0} \Vert , \quad \forall a, b\in X. $$

Proof

For all continuous functions, let us consider a Banach space (\(C [ I ]\), \(\Vert \boldsymbol{\cdot } \Vert \)) on I with norm given by \(\Vert g ( \lambda ) \Vert = \max_{\lambda \in I } \vert g ( \lambda ) \vert \). First, we prove that \(\{ \mathcal{U}_{n} \}\) is a Cauchy sequence in X.

Now consider

$$\begin{aligned} \Vert \mathcal{U}_{m } - \mathcal{U}_{n } \Vert =& \max _{\lambda \in I } \vert \mathcal{U} _{m } - \mathcal{U}_{n } \vert \\ =& \max_{\lambda \in I } \biggl\vert ( n+ \hslash ) ( \mathcal{U}_{m -1} - \mathcal{U}_{ n -1} ) \\ &{}+ \hslash L ^{-1} \biggl( \frac{1}{ s ^{\alpha }} L \bigl( N ( \mathcal{U}_{m -1} - \mathcal{U}_{n -1} ) + R ( \mathcal{U}_{m -1} - \mathcal{U}_{ n -1} ) \bigr) \biggr) \biggr\vert \\ \leq& \max_{\lambda \in I } [ ( n+ \hslash ) \bigl\vert ( \mathcal{U}_{m -1} - \mathcal{U}_{n -1} ) \bigr\vert + \hslash L ^{-1} \biggl( \frac{1}{s ^{\alpha }} L \bigl(N \vert \mathcal{U} _{m -1} - \mathcal{U}_{n -1} \vert \\ &{}+ R \bigl( \vert \mathcal{U}_{m -1} - \mathcal{U}_{n -1} \vert \bigr) \bigr)\biggr). \end{aligned}$$
(23)

By the convolution theorem for LT, Eq. (22) becomes

$$\begin{aligned} \Vert \mathcal{U}_{m} - \mathcal{U}_{n} \Vert \leq& \max_{\lambda \in I } [ ( n+ \hslash ) \bigl\vert ( \mathcal{U}_{m-1} - \mathcal{U}_{n-1} ) \bigr\vert \hslash \int _{0}^{t} \bigl( \bigl\vert N ( \mathcal{U}_{m-1} - \mathcal{U}_{n-1} ) \bigr\vert \\ &{}+ \bigl\vert R ( \mathcal{U}_{m-1} - \mathcal{U}_{n-1} ) \bigr\vert \bigr) \frac{ ( t- \xi )^{\alpha }}{\varGamma ( \alpha +1 )} \,d\xi \\ \leq& \max_{\lambda \in I } [ ( n+ \hslash ) \bigl\vert ( \mathcal{U}_{m-1} - \mathcal{U} _{n-1} ) \bigr\vert +\hslash \int _{0}^{t} \bigl( \bigl\vert N ( \mathcal{U}_{m-1} - \mathcal{U}_{n-1} ) \bigr\vert \\ &{}+ \bigl\vert R ( \mathcal{U}_{m-1} - \mathcal{U}_{n-1} ) \bigr\vert \bigr) \frac{ ( t- \xi )^{\alpha }}{\varGamma ( \alpha +1 )} \,d\xi . \end{aligned}$$
(24)

With the aid of integral mean value theorem, the above inequality reduces to

$$\begin{aligned} \Vert \mathcal{U}_{m} - \mathcal{U}_{n} \Vert \leq& \max_{\lambda \in I } \bigl[ ( n+ \hslash ) \bigl\vert ( \mathcal{U}_{m-1} - \mathcal{U} _{n-1} ) \bigr\vert +\hslash \bigl( \varepsilon \vert \mathcal{U} _{m-1} - \mathcal{U}_{n-1} \vert +\mu \vert \mathcal{U} _{m-1} - \mathcal{U}_{n-1} \vert \bigr) T \bigr] \\ \leq& \beta \Vert \mathcal{U}_{m-1} - \mathcal{U}_{n-1} \Vert . \end{aligned}$$

For \(m=n+1\), one can get

$$\begin{aligned} \Vert \mathcal{U}_{n+1} - \mathcal{U}_{n} \Vert \leq& \beta \Vert \mathcal{U}_{n} - \mathcal{U}_{n-1} \Vert \leq \beta ^{2} \Vert \mathcal{U}_{n-1} - \mathcal{U}_{n-2} \Vert \leq \beta ^{3} \Vert \mathcal{U}_{n-2} - \mathcal{U}_{n-3} \Vert \leq \cdots \\ \leq& \beta ^{n} \Vert \mathcal{U}_{1} - \mathcal{U} _{0} \Vert . \end{aligned}$$

In view of the triangular inequality, we have

$$\begin{aligned} \Vert \mathcal{U}_{m} - \mathcal{U}_{n} \Vert \leq& \Vert \mathcal{U} _{n+1} - \mathcal{U}_{n} \Vert + \Vert \mathcal{U}_{n+2} - \mathcal{U}_{n+1} \Vert +\cdots + \Vert \mathcal{U}_{m} - \mathcal{U}_{m-1} \Vert \\ \leq& \bigl[ \beta ^{n} + \beta ^{n+1} +\cdots + \beta ^{m-1} \bigr] \Vert \mathcal{U}_{1} - \mathcal{U}_{0} \Vert = \beta ^{n} \bigl[ 1+\beta +\cdots + \beta ^{m-n-1} \bigr] \Vert \mathcal{U} _{1} - \mathcal{U}_{0} \Vert \\ \leq& \beta ^{n} \biggl[ \frac{1- \beta ^{m-n-1}}{1-\beta } \biggr] \Vert \mathcal{U}_{1} - \mathcal{U}_{0} \Vert . \end{aligned}$$

Clearly, \(1- \beta ^{m-n-1} <1\) (since \(0<\beta <1\)). Therefore, the above inequality becomes

$$ \Vert \mathcal{U}_{m} - \mathcal{U}_{n} \Vert \leq \frac{ \beta ^{n}}{1-\beta } \Vert \mathcal{U}_{1} - \mathcal{U}_{0} \Vert . $$
(25)

But \(\Vert \mathcal{U}_{1} - \mathcal{U}_{0} \Vert < \infty \); consequently, as \(m\rightarrow \infty \), then \(\Vert \mathcal{U} _{m} - \mathcal{U}_{n} \Vert \rightarrow 0\).

It provides \(\{ \mathcal{U}_{n} \}\) is a Cauchy sequence in \(C [ I ]\), and every Cauchy sequence is a convergent sequence. Hence \(\{ \mathcal{U}_{n} \}\) is a convergent sequence. □

5 Error analysis of the proposed algorithm

The error analysis of the proposed scheme obtained with the help of q-HATM is presented in this segment.

Theorem 3

If we can obtain a real number \(0<\rho <1\) fulfilling \(\Vert \mathcal{U}_{m+1} ( x,t ) \Vert \leq \rho \Vert \mathcal{U}_{m} ( x,t ) \Vert \) for all m. Moreover, if the truncated series \(\sum_{m=0}^{i} \mathcal{U}_{m} ( x,t )\) is used as an approximate solution of \(\mathcal{ U} ( x,t )\), then the maximum absolute truncated error can be obtained by

$$ \Biggl\Vert \mathcal{U} ( x,t ) - \sum_{m=0}^{i} \mathcal{U}_{m} ( x,t ) \Biggr\Vert \leq \frac{\rho ^{i+1}}{1- \rho } \bigl\Vert \mathcal{U}_{0} ( x,t ) \bigr\Vert . $$

Proof

We have

$$\begin{aligned} \Biggl\Vert \mathcal{U} ( x,t ) - \sum_{m=0}^{i} \mathcal{U}_{m} ( x,t ) \Biggr\Vert =& \Biggl\Vert \sum _{m=i+1} ^{\infty } \mathcal{U}_{m} ( x,t ) \Biggr\Vert \\ \leq& \sum_{m=l+1}^{\infty } \bigl\Vert \mathcal{U}_{m} ( x,t ) \bigr\Vert \\ \leq& \sum_{m=i+1}^{\infty } \rho ^{m} \bigl\Vert \mathcal{U}_{0} ( x,t ) \bigr\Vert \\ \leq& \rho ^{i+1} \bigl[ 1+ \rho ^{1} + \rho ^{2} +\cdots \bigr] \bigl\Vert \mathcal{U} _{0} ( x,t ) \bigr\Vert \\ \leq& \frac{\rho ^{i+1}}{1-\rho } \bigl\Vert \mathcal{U}_{0} ( x,t ) \bigr\Vert , \end{aligned}$$

which proves our required result. □

6 Illustrative examples

Here, we consider two coupled examples to present the efficiency and applicability q-HATM.

Example 6.1

Consider the modified Boussinesq (MB) equations of fractional order [26, 28, 31]:

$$ \textstyle\begin{cases} D_{t}^{\alpha } u=-u \frac{\partial u}{\partial x} - \frac{\partial v}{ \partial x}, \\ D_{t}^{\alpha } v=-u \frac{\partial v}{\partial x} -v \frac{\partial u}{\partial x} - \frac{\partial ^{3} u}{\partial x^{3}}, \end{cases}\displaystyle 0< \alpha \leq 1, $$
(26)

with the initial conditions

$$ u ( x,0 ) =\omega -2 \ell \coth \bigl[ \ell ( x+c ) \bigr], \qquad v ( x,0 ) =-2 \ell ^{2} \operatorname{csch}^{2} \bigl[ \ell ( x+c ) \bigr]. $$
(27)

The exact solution for classical order MB equations is

$$ u ( x,t ) = \omega -2 \ell \coth \bigl[ \ell ( x+c-\omega t ) \bigr], \qquad v ( x,t ) = - 2 \ell ^{2} \operatorname{csch}^{2} \bigl[ \ell ( x+c-\omega t ) \bigr]. $$

By performing LT on Eq. (26) and using Eq. (27), we have

$$ \begin{aligned}&L \bigl[ u ( x,t ) \bigr] - \frac{1}{s} \bigl( \omega -2 \ell \coth \bigl[ \ell ( x+c ) \bigr] \bigr) + \frac{1}{s^{\alpha }} L \biggl\{ u \frac{\partial u}{\partial x} + \frac{\partial v}{\partial x} \biggr\} =0, \\ & L \bigl[ v ( x,t ) \bigr] - \frac{1}{s} \bigl( -2 \ell ^{2} \operatorname{csch}^{2} \bigl[ \ell ( x+c ) \bigr] \bigr) + \frac{1}{s^{\beta }} L \biggl\{ u \frac{\partial v}{\partial x} +v \frac{ \partial u}{\partial x} + \frac{\partial ^{3} u}{\partial x^{3}} \biggr\} =0. \end{aligned} $$
(28)

Define the nonlinear operators as follows:

$$ \begin{aligned}&N^{1} \bigl[ \varphi _{1} ( x,t;q ), \varphi _{2} (x,t;q)\bigr] =L \bigl[ \varphi _{1} ( x,t;q ) \bigr] - \frac{1}{s} \bigl( \omega -2 \ell \coth \bigl[ \ell ( x+c ) \bigr] \bigr) \\ &\hphantom{N^{1} [ \varphi _{1} ( x,t;q ), \varphi _{2} (x,t;q)] =}{} + \frac{1}{s^{ \alpha }} L \biggl\{ \varphi _{1} ( x,t;q ) \frac{\partial \varphi _{1} ( x,t;q )}{\partial x}+ \frac{\partial \varphi _{2} ( x,t;q )}{\partial x} \biggr\} , \\ & N^{2}\bigl[\varphi_{1}(x,t;q),\varphi_{2}(x,t;q) \bigr]= L \bigl[ \varphi _{2} ( x,t;q ) \bigr] - \frac{1}{s} \bigl( -2 \ell ^{2} \operatorname{csch}^{2} \bigl[ \ell ( x+c ) \bigr] \bigr) \\ &\hphantom{N^{2}[\varphi_{1}(x,t;q),\varphi_{2}(x,t;q)]=}{}+ \frac{1}{s^{\beta }} L \biggl\{ \varphi _{1} ( x,t;q ) \frac{\partial \varphi _{2} ( x,t;q )}{\partial x} + \varphi _{2} ( x,t;q ) \frac{ \partial \varphi _{1} ( x,t;q )}{\partial x} \\ &\hphantom{N^{2}[\varphi_{1}(x,t;q),\varphi_{2}(x,t;q)]=}{} + \frac{\partial ^{3} \varphi _{1} ( x,t;q )}{ \partial x^{3}} \biggr\} . \end{aligned} $$
(29)

By applying the proposed numerical scheme, mth order deformation equation for \(H ( x,t ) =1\) is given as

(30)

where

(31)

By employing inverse LT on Eq. (30), we get

(32)

On solving the above equation, we have

$$\begin{aligned}& u_{0} ( x,t ) =\omega -2 \ell \coth \bigl[ \ell ( x+c ) \bigr], \\& v_{0} ( x,t ) =- 2 \ell ^{2} \operatorname{csch}^{2} \bigl[ \ell ( x+c ) \bigr], \\& u_{1} ( x,t ) = \frac{2\hslash \ell ^{2} \omega \operatorname{csch} ^{2} [ \ell ( x+c ) ] t^{\alpha }}{ \varGamma [ \alpha +1 ]}, \\& v_{1} ( x,t ) = \frac{4 \hslash \ell ^{3} \omega \coth [\ell ( x+c ) ] \operatorname{csch}^{2} [ \ell ( x+c ) ] t^{ \alpha }}{\varGamma [ \alpha +1 ]}, \\& u_{2} ( x,t ) = \frac{2(n+\hslash )\hslash \ell ^{2} \omega \operatorname{csch}^{2} [ \ell ( x+c ) ] t^{\alpha }}{\varGamma [ \alpha +1 ]} \\& \hphantom{u_{2} ( x,t ) =}{}- \frac{4 \hslash ^{2} \ell ^{3} \omega ^{2} \coth [\ell ( x+c ) ] \operatorname{csch} ^{2} [ \ell ( x+c ) ] t^{2\alpha }}{ \varGamma [ 2\alpha +1 ]}, \\& v_{2} ( x,t ) = \frac{4(n+\hslash )\hslash \ell ^{3} \omega \coth [\ell ( x+c ) ] \operatorname{csch} ^{2} [ \ell ( x+c ) ] t^{\alpha }}{ \varGamma [ \alpha +1 ]} \\& \hphantom{v_{2} ( x,t ) =}{} - \frac{4 \hslash ^{2} \ell ^{4} \omega ^{2} ( 2+ \cosh [ 2 \ell ( x+c ) ] ) \operatorname{csch}^{4} [ \ell ( x+c ) ] t^{2\alpha }}{\varGamma [ 2\alpha +1 ]}, \\& u_{3} ( x,t ) = \frac{2 ( \hslash +n )^{2} \hslash \ell ^{2} \omega \operatorname{csch}^{2} [ \ell ( x+c ) ] t^{\alpha }}{\varGamma [ 1+\alpha ]} \\& \hphantom{u_{3} ( x,t ) =}{}- \frac{8 ( \hslash +n ) \hslash ^{2} \ell ^{3} \omega ^{2} \coth [ \ell ( x+c ) ] \operatorname{csch}^{2} [ \ell ( x+c ) ] t^{2\alpha }}{ \varGamma [ 1+2\alpha ]} \\& \hphantom{u_{3} ( x,t ) =}{}+ \frac{2\hslash ^{3} \ell ^{4} \omega ^{2} \operatorname{csch}^{5} [ \ell ( x+c ) ] t^{3\alpha }}{\varGamma [ \alpha +1 ]^{2} \varGamma [ 3\alpha +1 ]} ( -4l \cosh \bigl[ \ell ( x+c ) \bigr] \varGamma [ 1+2\alpha ] \\& \hphantom{u_{3} ( x,t ) =}{} + \varGamma [ 1+\alpha ]^{2} \bigl( 8 \ell \cosh \bigl[ \ell ( x+c ) \bigr] \\& \hphantom{u_{3} ( x,t ) =}{} +\omega \bigl( \bigl( 3 \sinh \bigl[ \ell ( x+c ) \bigr] +\sinh \bigl[ 3 \ell ( x+c ) \bigr] \bigr) \bigr) \bigr), \\& v_{3} ( x,t )= \frac{4 ( \hslash +n )^{2} \hslash \ell ^{3} \omega \coth [ \ell ( x+c ) ] \operatorname{csch}^{2} [ \ell ( x+c ) ] t^{\alpha }}{\varGamma [ \alpha +1 ]} \\& \hphantom{v_{3} ( x,t )=}{} - \frac{8 ( \hslash +n ) \hslash ^{2} \ell ^{5} \omega ( 2+\cosh [ 2 \ell ( x+c ) ] ) \operatorname{csch} ^{4} [ \ell ( x+c ) ] t^{2 \alpha }}{ \varGamma [ 2 \alpha +1 ]} \\& \hphantom{v_{3} ( x,t )=}{}+ \frac{2 \hslash ^{3} \ell ^{5} \omega ^{2} \operatorname{csch}^{6} [ \ell ( x+c ) ] t^{3 \alpha }}{\varGamma [ \alpha +1 ]^{2} \varGamma [ 3 \alpha +1 ]} (-4l \bigl( 3+2 \cosh \bigl[ 2 \ell ( x+c ) \bigr] \bigr) \varGamma [ 2 \alpha +1 ] \\& \hphantom{v_{3} ( x,t )=}{}+ \varGamma [ \alpha +1 ]^{2} (24 \ell +16 \ell \cosh \bigl[ 2 \ell ( x+c ) \bigr] \\& \hphantom{v_{3} ( x,t )=}{}+10 \omega \sinh \bigl[ 2 \ell ( x+c ) \bigr] + \omega \sinh \bigl[ 4 \ell ( x+c ) \bigr]. \end{aligned}$$

In this way, the remaining term can be obtained. Then, for system of Eq. (26), the q-HATM series solution is presented as follows:

$$ \begin{aligned}&u ( x,t ) = u_{0} ( x,t ) + \sum _{m=1}^{ \infty } u_{m} ( x,t ) \biggl( \frac{1}{n} \biggr)^{m}, \\ &v ( x,t ) = v_{0} ( x,t ) + \sum_{m=1}^{ \infty } v_{m} ( x,t ) \biggl( \frac{1}{n} \biggr)^{m}. \end{aligned} $$
(33)

Example 6.2

Consider the approximate long wave (ALW) equations with arbitrary order [26, 28, 33]:

$$ \textstyle\begin{cases} D_{t}^{\alpha } u=-u \frac{\partial u}{\partial x} - \frac{\partial v}{ \partial x} - \frac{1}{2} \frac{\partial ^{2} v}{\partial x^{2}}, \\ D_{t}^{\alpha } v=-u \frac{\partial v}{\partial x} -v \frac{ \partial u}{\partial x} + \frac{1}{2} \frac{\partial ^{2} v}{\partial x^{2}}, \end{cases}\displaystyle 0< \alpha \leq 1, $$
(34)

with the initial conditions

$$ \begin{aligned}&u ( x,0 ) =\omega -\ell \coth \bigl[ \ell ( x+c ) \bigr], \\ &v ( x,0 ) =- \ell ^{2} \operatorname{csch}^{2} \bigl[ \ell ( x+c ) \bigr]. \end{aligned}$$
(35)

The exact solution for classical order ALW equations is

$$ \begin{aligned}&u ( x,t ) = \omega -\ell \coth \bigl[ \ell ( x+c-\omega t ) \bigr], \\ & v ( x,t ) = - \ell ^{2} \operatorname{csch}^{2} \bigl[ \ell ( x+c-\omega t ) \bigr]. \end{aligned}$$

By performing LT on Eq. (34) and using Eq. (35), we have

$$ \begin{aligned}&L \bigl[ u ( x,t ) \bigr] - \frac{\omega -\ell \coth [ \ell ( x+c ) ]}{s} + \frac{1}{s ^{\alpha }} L \biggl\{ u \frac{\partial u}{\partial x} + \frac{\partial v}{\partial x} + \frac{1}{2} \frac{\partial ^{2} u}{\partial x^{2}} \biggr\} =0, \\ & L \bigl[ v ( x,t ) \bigr] - \frac{- \ell ^{2} \operatorname{csch}^{2} [ \ell ( x+c ) ]}{s} + \frac{1}{s^{\alpha }} L \biggl\{ u \frac{\partial v}{ \partial x} +v \frac{\partial u}{\partial x} - \frac{1}{2} \frac{ \partial ^{2} v}{\partial x^{2}} \biggr\} =0. \end{aligned} $$
(36)

Define the nonlinear operators as

$$\begin{aligned}& \begin{aligned}&N^{1} \bigl[ \varphi _{1} ( x,t;q ), \varphi _{2} ( x,t;q ) \bigr] \\ & \quad =L \bigl[ \varphi _{1} ( x,t;q ) \bigr] - \frac{\omega -\ell \coth [ \ell ( x+c ) ]}{s} \\ & \qquad {} + \frac{1}{s^{\alpha }} L \biggl\{ \varphi _{1} ( x,t;q ) \frac{\partial \varphi _{1} ( x,t;q )}{ \partial x} + \frac{\partial \varphi _{2} ( x,t;q )}{ \partial y} + \frac{1}{2} \frac{\partial ^{2} \varphi _{1} ( x,t;q )}{\partial x^{2}} \biggr\} , \\ &N^{2} \bigl[ \varphi _{1} ( x,t;q ), \varphi _{2} ( x,t;q ) \bigr] \\ &\quad =L \bigl[ \varphi _{2} ( x,t;q ) \bigr] - \frac{- \ell ^{2} \operatorname{csch}^{2} [ \ell ( x+c ) ]}{s} \\ & \qquad {} + \frac{1}{s ^{\alpha }} L\biggl\{ \varphi _{1} ( x,t;q ) \frac{\partial \varphi _{2} ( x,t;q )}{\partial x} + \varphi _{2} ( x,t;q ) \frac{\partial \varphi _{1} ( x,t;q )}{ \partial x} - \frac{1}{2} \frac{\partial ^{2} \varphi _{2} ( x,t;q )}{\partial x^{2}} \biggr\} . \end{aligned} \end{aligned}$$
(37)

Now, for \(H ( x,t ) =1\), the mth order deformation equation is presented as follows:

(38)

where

(39)

By employing inverse LT on Eq. (38), we obtain

(40)

On simplification, we obtain

$$\begin{aligned}& u_{0} ( x,t ) =\omega -\ell \coth \bigl[ \ell ( x+c ) \bigr], \\& v_{0} ( x,t ) =- \ell ^{2} \operatorname{csch}^{2} \bigl[ \ell ( x+c ) \bigr], \\& u_{1} ( x,t ) = \frac{\hslash \ell ^{2} \omega \operatorname{csch} ^{2} [ \ell ( x+c ) ] t^{\alpha }}{ \varGamma [ \alpha +1 ]}, \\& v_{1} ( x,t ) = \frac{2 \hslash \ell ^{3} \omega \coth [\ell ( x+c ) ] \operatorname{csch}^{2} [ \ell ( x+c ) ] t^{ \alpha }}{\varGamma [ \alpha +1 ]}, \\& u_{2} ( x,t ) = \frac{(n+\hslash )\hslash \ell ^{2} \omega \operatorname{csch}^{2} [ \ell ( x+c ) ] t^{\alpha }}{\varGamma [ \alpha +1 ]} \\& \hphantom{u_{2} ( x,t ) =}{}- \frac{2 \hslash ^{2} \ell ^{3} \omega ^{2} \coth [\ell ( x+c ) ] \operatorname{csch} ^{2} [ \ell ( x+c ) ] t^{2\alpha }}{ \varGamma [ 2\alpha +1 ]}, \\& v_{2} ( x,t ) = \frac{2(n+\hslash )\hslash \ell ^{3} \omega \coth [\ell ( x+c ) ] \operatorname{csch} ^{2} [ \ell ( x+c ) ] t^{\alpha }}{ \varGamma [ \alpha +1 ]} \\& \hphantom{v_{2} ( x,t ) =}{}- \frac{2 \hslash ^{2} \ell ^{4} \omega ^{2} ( 2+ \cosh [ 2 \ell ( x+c ) ] ) \operatorname{csch}^{4} [ \ell ( x+c ) ] t^{2 \alpha }}{\varGamma [ 2 \alpha +1 ]}, \\& u_{3} ( x,t ) = \frac{ ( \hslash +n )^{2} \hslash \ell ^{2} \omega \operatorname{csch}^{2} [ \ell ( x+c ) ] t^{\alpha }}{\varGamma [ 1+\alpha ]} \\& \hphantom{u_{3} ( x,t ) =}{} - \frac{4 ( \hslash +n ) \hslash ^{2} \ell ^{3} \omega ^{2} \coth [ \ell ( x+c ) ] \operatorname{csch}^{2} [ \ell ( x+c ) ] t^{2\alpha }}{ \varGamma [ 1+2\alpha ]} \\& \hphantom{u_{3} ( x,t ) =}{}+ \frac{\hslash ^{3} \ell ^{4} t^{3\alpha } \omega ^{2} \operatorname{csch}^{5} [ \ell ( x+c ) ]}{\varGamma [ \alpha +1 ]^{2} \varGamma [ 3\alpha +1 ]} (-2k \cosh \bigl[ \ell ( x+c ) \bigr] \varGamma [ 1+2 \alpha ] \\& \hphantom{u_{3} ( x,t ) =}{}+ \varGamma [ 1+\alpha ]^{2} \bigl( 4 \ell \cosh \bigl[ \ell ( x+c ) \bigr] +\omega \bigl( 3 \sinh \bigl[ \ell ( x+c ) \bigr] + \sinh \bigl[ 3 \ell ( x+c ) \bigr] \bigr) \bigr), \\& v_{3} ( x,t ) = \frac{2 ( \hslash +n )^{2} \hslash \ell ^{3} \omega \coth [ \ell ( x+c ) ] \operatorname{csch}^{2} [ \ell ( x+c ) ] t^{\alpha }}{\varGamma [ \alpha +1 ]} \\& \hphantom{v_{3} ( x,t ) =}{}- \frac{4 ( \hslash +n ) \hslash ^{2} \ell ^{5} t^{2 \beta } \omega ( 2+\cosh [ 2 \ell ( x+c ) ] ) \operatorname{csch}^{4} [ \ell ( x+c ) ]}{ \varGamma [ 2\alpha +1 ]} \\& \hphantom{v_{3} ( x,t ) =}{}+ \frac{\hslash ^{3} \ell ^{5} t^{3\alpha } \omega ^{2} \operatorname{csch}^{6} [ \ell ( x+c ) ]}{\varGamma [ \alpha +1 ]^{2} \varGamma [ 3\alpha +1 ]} (-2l \bigl( 3+2 \cosh \bigl[ 2 \ell ( x+c ) \bigr] \bigr) \varGamma [ 2\alpha +1 ] \\& \hphantom{v_{3} ( x,t ) =}{}+ \varGamma [ \alpha +1 ]^{2} \bigl( 12 \ell +8 \ell \cosh \bigl[ 2 \ell ( x+c ) \bigr] \\& \hphantom{v_{3} ( x,t ) =}{} +10 \omega \sinh \bigl[ 2 \ell ( x+c ) \bigr] + \omega \sinh \bigl[ 4 \ell ( x+c ) \bigr] \bigr). \\& \vdots \end{aligned}$$

Following the same procedure, the remaining terms can be obtained. Eventually, for Eq. (34), the q-HATM solutions are presented as follows:

$$ \begin{aligned}&u ( x,t ) = u_{0} ( x,t ) + \sum _{m=1}^{ \infty } u_{m} ( x,t ) \biggl( \frac{1}{n} \biggr)^{m}, \\ &v ( x,t ) = v_{0} ( x,t ) + \sum_{m=1}^{ \infty } v_{m} ( x,t ) \biggl( \frac{1}{n} \biggr)^{m}. \end{aligned} $$
(41)

7 Numerical results and discussion

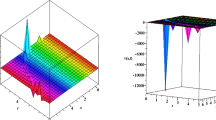
Here, the numerical simulation has been conducted in order to prove that the future algorithm leads to greater accuracy. We can see from the obtained results that the future scheme gives remarkable exactness in comparison to the technique presented in the literature [26, 29, 30], which is cited for both the examples in Tables 1–4. Figs. 1 and 2 explore the comparison of the obtained solutions with exact solutions and absolute error for Example 6.1. Figures 3 and 4 are the response to the obtained solutions for FMB equation with diverse Brownian motion and standard motion (\(\alpha =1 \)). Figures 5 and 6 depict the q-HATM solutions for distinct ℏ, which aids us to adjust and control the convergence region. Figures 7–8 present the importance of asymptotic parameter n with ℏ in q-HATM solution.

Figure 1
figure 1

Behaviour of (a) Approximate solution (b) Exact solution (c) Absolute error \(= \vert u_{\mathrm{exa.}} - u_{\mathrm{app.}} \vert \) for Example 6.1 at \(\omega = 0.005\), \(\ell =0.1\), \(c=10\), \(n=1\), \(\alpha =1\) and \(\hslash =-1\)

Full size image
Figure 2
figure 2

Behaviour of (a) Approximate solution (b) Exact solution (c) Absolute error \(= \vert v_{\mathrm{exa.}} - v_{\mathrm{app.}} \vert \) for Example 6.1 at \(\omega = 0.005\), \(\ell =0.1\), \(c=10\), \(n=1\), \(\alpha =1\) and \(\hslash =-1\)

Full size image
Figure 3
figure 3

Nature of \(u ( x,t )\) with t for Example 6.1 at \(\omega = 0.005\), \(\hslash =-1\), \(\ell =0.1\), \(c=10\), \(x=1\) and \(n=1\) with diverse α

Full size image
Figure 4
figure 4

Nature \(v ( x,t )\) with t for Example 6.1 at \(\omega = 0.005\), \(\ell =0.1\), \(c=10\), \(\hslash =-1\), \(x=1\) and \(n=1\) with diverse α

Full size image
Figure 5
figure 5

Plot of \(u ( x,t )\) with diverse ℏ when \(\omega = 0.005\), \(\ell =0.1\), \(c=10\), \(n=5\), \(\alpha =1\) and \(x=1\) for Example 6.1

Full size image
Figure 6
figure 6

Nature of \(v ( x,t )\) with distinct ℏ at \(\omega = 0.005\), \(\ell =0.1\), \(c=10\), \(n=1\), \(\alpha =1\) and \(x=1\) for Example 6.1

Full size image
Figure 7
figure 7

ℏ-curves drown for \(u ( x,t )\) at \(n =1\) (left) and \(n =2\) (right) with different α when \(\omega = 0.005\), \(\ell =0.1\), \(c=10\), \(x=1\) and \(t=0.01\) for Example 6.1

Full size image
Figure 8
figure 8

ℏ-curve drown for \(v ( x,t )\) at \(n =1\) (left) and \(n =2\) (right) with different α when \(\omega = 0.005\), \(\ell =0.1\), \(c=10\), \(x=1\) and \(t=0.01\) for Example 6.1

Full size image
Table 1 Comparative study in terms of absolute error between ADM [28], VIM [29], CFRDTM [26] and q-HATM for the approximate solution \(u(x,t)\) at \(\omega = 0.005\), \(\ell =0.1\), \(c=10\), \(n=1\), \(\hslash =-1\) and \(\alpha =1\) for Example 6.1
Full size table
Table 2 Comparative study in terms of absolute error between ADM [28], VIM [29], CFRDTM [26] and q-HATM for the approximate solution \(v(x,t)\) at \(\omega = 0.005\), \(\ell =0.1\), \(c=10\), \(\hslash =-1\), \(n=1\), \(\hslash =-1\) and \(\alpha =1\) for Example 6.1
Full size table
Table 3 Comparative study between ADM [28], VIM [29], LADM [30], CRFDTM [26] and q-HATM for the approximate solution \(u(x,t)\) at \(\omega =0.005\), \(\ell= 0.1\), \(c=10\), \(\alpha =1 \) and \(\hslash =-1\) for Example 6.2
Full size table
Table 4 Comparative study between ADM [28], VIM [29], LADM [30], CRFDTM [26] and q-HATM for the approximate solution \(v(x,t)\) at \(\omega =0.005\), \(\ell= 0.1\), \(c=10\), \(\alpha =1 \) and \(\hslash =-1\) for Example 6.2
Full size table

Moreover, Figs. 10 and 11 show the nature of obtained solutions in comparison with exact solutions for Example 6.2. In particular, Figs. 10(c) and 11(c) reveal the exactness of the obtained solution in absolute error. Figures 12 and 13 explore the behaviour of obtained solution for distinct α i.e. \(\alpha =1, 0.75\) and 0.50. Figures 14 and 15 cite the nature of obtained solutions for distinct ℏ, and these aid us to control the convergence region. Finally, Figs. 16–17 signify the ℏ-curves and the horizontal line illustrates the region of convergence for FALW equation. The coupled surface of the MB and ALW equations considered in Example 6.1 and Example 6.2 are respectively shown in Figs. 9 and 18, which helps us understand the nature of coupled equations.

Figure 9
figure 9

Coupled surface of \(u ( x,t )\) and \(v ( x,t )\) for Example 6.1 at \(\omega = 0.005\), \(\ell =0.1\), \(c=10\), \(n=1\), \(\alpha =1\) and \(\hslash =-1\)

Full size image
Figure 10
figure 10

Behaviour of (a) Approximate solution (b) Exact solution (c) Absolute error \(= \vert u_{\mathrm{exa}.} - u_{\mathrm{app}.} \vert \) at \(\omega = 0.005\), \(\ell =0.1\), \(c=10\), \(n=1\), \(\alpha =1\) and \(\hslash =-1\) for Example 6.2

Full size image
Figure 11
figure 11

Behaviour of (a) Approximate solution (b) Exact solution (c) Absolute error \(= \vert v_{\mathrm{exa.}} - v_{\mathrm{app.}} \vert \) at \(\omega = 0.005\), \(\ell =0.1\), \(c=10\), \(n=1\), \(\alpha =1\) and \(\hslash =-1\) for Example 6.2

Full size image
Figure 12
figure 12

Plot of \(u ( x,t )\) with respect to t at diverse values of α when \(\omega = 0.005\), \(\ell =0.1\), \(c=10\), \(n=1\), \(\hslash =-1\) and \(x=1\) for Example 6.2

Full size image
Figure 13
figure 13

Response of \(v ( x,t )\) with t at diverse α when \(\omega = 0.005\), \(\ell =0.1\), \(c=10\), \(n=1\), \(\hslash =-1 \) and \(x=1\) for Example 6.2

Full size image
Figure 14
figure 14

Nature of \(u ( x,t )\) with distinct ℏ for Example 6.2 at \(\omega = 0.005\), \(\ell =0.1\), \(c=10\), \(n=5\), \(\alpha =1\) and \(x=1\)

Full size image
Figure 15
figure 15

Nature of \(v ( x,t )\) with distinct ℏ for Example 6.2 at \(\ell =0.1\), \(c=10\), \(n=3\), \(\alpha =1\) and \(x=1\)

Full size image
Figure 16
figure 16

ℏ-curves drown for \(u ( x,t )\) at \(n =1\) (left) and \(n =2\) (right) for Example 6.2 at \(\omega = 0.005\), \(\ell =0.1\), \(c=10\), \(x=1\) and \(t=0.01\) with diverse α

Full size image
Figure 17
figure 17

ℏ-curves drown for \(v ( x,t )\) at \(n =1\) (left) and \(n =2\) (right) with different α for Example 6.1 when \(\omega = 0.005\), \(\ell =0.1\), \(c=10\), \(x=1\) and \(t=0.01\)

Full size image
Figure 18
figure 18

Nature of coupled q-HATM solutions \(u ( x,t )\) and \(v ( x,t )\) for Example 6.2 when at \(n=1\), \(\alpha =1\), \(\hslash =-1\), \(\omega = 0.005\), \(\ell =0.1\) and \(c=10\)

Full size image

8 Conclusion

In the present work, the q-HATM is employed advantageously to find the solution for coupled modified Boussinesq and approximate long wave equations of fractional order. Two examples are considered in order to illustrate and validate the efficiency of the considered algorithm. The convergence and error analysis have been offered in the present framework to show the consistency and applicability. The numerical simulation has been conducted for both considered fractional coupled systems in terms of absolute error. From the cited tables and plots, we can see that the proposed technique is effective and more exact in comparison to other methods and contains the results of CFRDTM as a special case (\(n=1\) and \(\hslash =-1\)). Moreover, the algorithm controls and manipulates the series solution which quickly converges to the analytical solution in a small admissible domain. Hence, we can conclude that the proposed algorithm is very powerful and well-organized to study the coupled system arising in physical phenomena, both fractional and integer order derivatives analytically and numerically describe the real world problems in a systematic and better manner.