Computable solution of fractional kinetic equations using Mathieu-type series

Abstract

The Mathieu series appeared in the study of elasticity of solid bodies in the work of Émile Leonard Mathieu. Since then numerous authors have studied various problems arising from the Mathieu series in several diverse ways. In this line, our aim is to study the solution of fractional kinetic equations involving generalized Mathieu-type series. The generality of this series will help us to deduce results related to a fractional kinetic equation involving another form of Mathieu series. To obtain the solution, we use the Laplace transform technique. Besides, a graphical representation is given to observe the behavior of the obtained solutions.

1 Introduction and preliminaries

Fractional calculus (FC) is a useful mathematical tool to study fractional order integrals and derivatives. The fractional calculus has been developed and used in different areas of science and engineering. The concept of fractional differential equations and their applications have played a significant role in many diverse fields such as applied science, physics, biology, chemistry, and engineering. The kinetic equations designate a system of differential equations, which describe the rate of change of the chemical composition of a star for each order in terms of the reaction rates for production and destruction. During the last several decades, fractional kinetic equations in various forms have been broadly and usefully employed when describing and solving several important problems of physics and astrophysics (see, e.g., [2, 7,8,9,10,11, 13,14,15,16, 20, 24,25,26,27,28,29, 31] and the references therein). The special functions and their applications appear in the solutions of fractional integral and differential equations and are related to comprehensive problems in the several areas of mathematics and mathematical physics. In view of the effectiveness and great importance of the fractional kinetic equations in certain astrophysical problems, the authors develop a generalized form of the fractional kinetic equations along with Mathieu-type series. The broad generality of Mathieu-type series will allow us to deduce many special cases of the main results.

In [14], Haubold and Mathai explored the kinetic equation describing the rate of change of detraction, production, and reaction, which is given as

$$ \frac{dN}{dt}=p(N_{t})-d(N_{t}), $$

(1)

where $d=d(N)$ is the rate of destruction, $p=p(N)$ the rate of production, $N=N(t)$ the rate of reaction, and $N_{t}$ denotes the function given by $N_{t}(t^{*})=N(t-t^{*})$, $t>0$. A particular case of (1), when special fluctuations or inhomogeneities in quantity $N(t)$ are decayed, is given by the equation

$$ \frac{dN}{dt}=-c_{i}N_{i}(t) $$

(2)

with basic condition $N_{i}(t=0)=N_{0}$ describing the variety of density of species i at time $t=0$ and $c_{i}>0$. Neglecting index i and integrating, (2) becomes

$$ N(t)-N_{0}=-c_{0}{ }_{0}D_{t}^{-1}N(t), $$

(3)

where ${}_{0}D_{t}^{-1}$ is the standard integral operator.

Further, a fractional generalization of (3) was given by Haubold and Mathai [14] in the following form:

$$ N(t)-N_{0}=-c^{\nu }{_{0}D_{t}^{-\nu }N(t)}, $$

(4)

where ${}_{0}D_{t}^{-\nu }$ represents the Riemann–Liouville integral operator defined as

$$ {}_{0}D_{t}^{-\nu }=\frac{1}{\varGamma (\nu )} \int _{0}^{t}(-s+t)^{\nu -1}f(s)\,ds \quad \bigl( \Re (\nu )>0, t>0\bigr). $$

(5)

Saxena et al. [26] investigated solutions of three generalized forms of (4) in terms of the following generalized Mittag-Leffler function (see, e.g., [40]):

$$ E_{\nu ,\mu }(z)=\sum_{r=0}^{\infty } \frac{z^{r}}{\varGamma (\nu {r}+ \mu )}\quad \bigl(\Re (\nu )>0, \mu \in \mathbb{C}\bigr). $$

(6)

We here recall just one of them (see [26, Theorem 2]). The equation

$$ N(t)-N_{0}t^{\mu -1} E_{\nu ,\mu }\bigl(-d^{\nu }t^{\nu } \bigr)=-c^{\nu }{ } _{0}D_{t}^{-\nu } N(t) $$

(7)

is solved by

$$\begin{aligned} N(t)=N_{0}\frac{t^{\mu -\nu -1}}{c^{\nu }-d^{\nu }}\bigl[E_{\nu ,\mu - \nu } \bigl(-d^{\nu }t^{\nu }\bigr)-E_{\nu ,\mu -\nu }\bigl(-d^{\nu }t^{\nu } \bigr)\bigr], \end{aligned}$$

(8)

where $\mu ,\nu ,c,d \in \mathbb{R^{+}}$; $c\neq d$.

Sexena et al. [28] investigated the following generalized fractional kinetic equation:

$$ N(t)-N_{0}t^{\mu -1} E^{\gamma }_{\nu ,\mu } \bigl(-d^{\nu }t^{\nu }\bigr)=-c ^{\nu }{ }_{0}D_{t}^{-\nu } N(t) \quad \bigl(\mu ,\nu ,\gamma , c \in \mathbb{R^{+}}\bigr), $$

(9)

and its solution is

$$ N(t)=N_{0}t^{\mu -1}E^{\gamma +1}_{\nu ,\mu } \bigl(-c^{\nu }t^{\nu }\bigr), $$

(10)

where $E_{\nu ,\mu }^{\gamma }(z)$ is an extension of the generalized Mittag-Leffler function (6) (see [23]):

$$ E_{\nu ,\mu }^{\gamma }(z)=\sum _{r=0}^{\infty }\frac{(\gamma )_{r} { }z^{r}}{\varGamma (\nu {r}+\mu )}\quad \bigl(\Re (\nu )>0; \mu , \gamma \in \mathbb{C}\bigr) $$

(11)

and $(\eta )_{\varepsilon }$ denotes the Pochhammer symbol which is defined (for $\eta ,\varepsilon \in \mathbb{C}$) in terms of the gamma function Γ as

$$ (\eta )_{\varepsilon }:= \frac{\varGamma (\eta +\varepsilon )}{ \varGamma ( \eta )} = \textstyle\begin{cases} 1 &\bigl(\varepsilon =0; \eta \in \mathbb{C}\setminus \{0\} \bigr), \\ \eta (\eta +1) \cdots ( \eta +n-1)& (\varepsilon =n \in {\mathbb{N}}; \eta \in \mathbb{C}). \end{cases} $$

(12)

Saxena and Kalla [25] investigated the following fractional kinetic equation:

$$ N(t)-N_{0}f(t)=-c^{\nu }{_{0}D_{t}^{-\nu }N(t)} \quad \bigl(\nu ,c\in \mathbb{R^{+}}\bigr), $$

(13)

where $f\in {L(0,\infty )}$. Applying the Laplace transform (LT) to (13), we have

$$ L\bigl[N(t) : s\bigr]=N_{0}\frac{F(s)}{c^{\nu }s^{-\nu }+1}=N_{0}F(s) \biggl( \sum_{n\geq {0}}\bigl(-c^{\nu } \bigr)^{n}s^{-n\nu } \biggr)\quad \biggl(n\in {N _{0}}, \biggl\vert \frac{c}{s} \biggr\vert \biggr). $$

(14)

Suppose that $f(t)$ is a real- (or complex-) valued function of the (time) variable $t>0$ and s is real or complex parameter. The Laplace transform of the function $f(t)$ is defined by

$$\begin{aligned} F(s) &=L \bigl\lbrace N(t); s \bigr\rbrace = \int _{0}^{\infty }e^{-st}f(t)\,dt \quad \bigl(\Re (s)>0\bigr) \\ &=\lim_{\varepsilon \rightarrow \infty } \int _{0}^{\varepsilon }e^{-st}f(t)\,dt, \end{aligned}$$

(15)

whenever the limit exits (as a finite number). The convolution of two functions $f(t)$ and $g(t)$, which are defined for $t>0$, plays an important role in a number of different physical applications. The Laplace convolution of functions $f(t)$ and $g(t)$ is given by the following integral:

$$\begin{aligned} (f\ast g) (t)= \int _{0}^{t}f(u)g(1-u)\,du=(g\ast f) (t), \end{aligned}$$

(16)

which exists if the functions f and g are at least piecewise continuous. One of the most significant properties possessed by the convolution in connection with the Laplace transform is that the Laplace transform of the convolution of two functions is the product of their transforms (see, e.g., [20, 30, 32, 33]).

The Laplace Convolution Theorem

If f and g are piecewise continuous on $[0,\infty )$ and of exponential order α when $t \rightarrow \infty$, then

$$\begin{aligned} L \bigl\lbrace (f\ast g) (t):s \bigr\rbrace = L \bigl\lbrace f (t):s \bigr\rbrace \cdot L \bigl\lbrace g(t):s \bigr\rbrace \quad \bigl(\Re (s)>0\bigr). \end{aligned}$$

(17)

We find

$$\begin{aligned} L \bigl\lbrace _{0}D^{-\nu }_{t}f(t) : s \bigr\rbrace &=\frac{1}{ \varGamma (\nu )} L \bigl\lbrace t^{\nu -1} \ast f(t) : s \bigr\rbrace \\ &=\frac{1}{\varGamma (\nu )} L \bigl\lbrace t^{\nu -1} : s \bigr\rbrace L \bigl\lbrace f(t) : s \bigr\rbrace =\frac{1}{s^{\nu }}L \bigl\lbrace f(t) : s \bigr\rbrace , \end{aligned}$$

(18)

by using the following well-known identity:

$$\begin{aligned} &L \bigl\lbrace t^{\nu }: s \bigr\rbrace =\frac{\varGamma (\nu +1)}{s ^{\nu +1}} \end{aligned}$$

(19)

$$\begin{aligned} &\quad \Longleftrightarrow\quad L^{-1} \biggl( \frac{1}{s^{\nu +1}} \biggr) = \frac{t ^{\nu }}{\varGamma (\nu +1)}, \end{aligned}$$

(20)

in which $L^{-1}$ denotes the inverse Laplace transform.

Recently, many papers investigated the solution of generalized fractional kinetic equations involving a variety of special functions by using Laplace and Sumudu transformations. For instance, for generalized fractional kinetic equations with $f(t)$ in (13) replaced by certain forms of generalized Mittag-Leffler function (11), Saxena et al. [29] presented their corresponding solutions. Moreover, Chaurasia and Kumar [7] investigated the solution of generalized fractional kinetic equations involving M-series, and Choi and Kumar [9] gave their corresponding solutions involving Aleph function. Furthermore, Agarwal et al. [1, 2] investigated solutions of fractional kinetic equations with $f(t)$ in (13) replaced by certain forms of k-Mittag-Leffler function and k-Bessel function. Subsequently, Nisar and Qi [22] presented solution of fractional kinetic equations with $f(t)$ in (13) replaced by certain forms of generalized k-Bessel function.

The following familiar infinite series was introduced by Mathieu [21]:

$$ S(l)=\sum_{k=1}^{\infty } \frac{2k}{(k^{2}+l^{2})} \quad \bigl(l \in \mathbb{R^{+}}\bigr). $$

(21)

An integral representation of (21) is given by (see [12])

$$ S(l)=\frac{1}{l} \int _{0}^{\infty }\frac{t\sin (lt)}{e^{t}-1}\,dt. $$

(22)

Numerous interesting problems and solutions handling integral representations and related to the following generalization of the Mathieu series with fractional power

$$ S_{\mu }(l)=\sum_{k=1}^{\infty } \frac{2k}{(k^{2}+l^{2})^{\mu }} \quad \bigl(l \in \mathbb{R^{+}}; \mu \leq 1\bigr) $$

(23)

can be found in the works by Cerone and Lenard [6] as well as Tomovski and Trencevski [37]. Extending the work of Cerone and Lenard [6], Srivastava and Tomovski [34] defined a family of generalized Mathieu series

$$ S^{(\rho ,\sigma )}_{\mu }(l,d)=S^{(\rho ,\sigma )}_{\mu } \bigl(l, \lbrace d _{k} \rbrace _{k=1}^{\infty }\bigr)= \sum_{k=1}^{\infty }\frac{2d^{ \sigma }_{k}}{(d^{\rho }_{k}+l^{2})^{\mu }} \quad \bigl(l,d, \rho ,\sigma , \mu \in \mathbb{R^{+}}\bigr), $$

(24)

where the positive sequence $d= \lbrace d_{k} \rbrace _{k=1}^{\infty }= \lbrace d_{1},d_{2},\dots \rbrace$ ($\lim_{k\rightarrow \infty }d_{k}=\infty$) is such that the infinite series $\sum_{k=1}^{\infty }\frac{1}{d^{\mu {\rho }-\sigma } _{k}}$ is convergent.

In the sequel, Tomovski and Mehrez [35] proposed a generalization of definition (24) in the following power series:

$$\begin{aligned} S^{(\rho ,\sigma )}_{\mu ,\tau }(l,d;u) =&S^{(\rho ,\sigma )}_{\mu , \tau } \bigl(l, \lbrace d_{k} \rbrace _{k=1}^{\infty }; u\bigr) \\ =& \sum_{k=1}^{\infty }\frac{2d^{\sigma }_{k}(\tau )_{k}}{(d^{\rho }_{k}+l ^{2})^{\mu }} \frac{u^{k}}{k!} \quad \bigl(l,d,\rho ,\sigma ,\mu \in \mathbb{R^{+}}; \vert u \vert \leq {1}\bigr). \end{aligned}$$

(25)

Evidently, the case $d_{k} = k$, $\rho =2$, $\sigma =1=\tau$ and μ replaced with $\mu +1$ corresponds to the Mathieu series defined by Tomovski and Pogány [36]:

$$ S^{(2,1)}_{\mu +1,1}(l,k;u)=S_{\mu }(l; u)= \sum_{k=1}^{\infty }\frac{2ku ^{k}}{(k^{2}+l^{2})^{\mu +1}} \quad \bigl(l,\mu \in \mathbb{R^{+}}; \vert u \vert \leq {1}\bigr). $$

(26)

Due to the great importance of fractional kinetic equations involving special functions, in this paper, we aim to investigate solution of generalized fractional kinetic equations (13) with $f(t)$ replaced by several generalized Mathieu-type series, by mainly using the Laplace and Sumudu transforms. The results presented here, being general, are also shown to reduce to fractional kinetic equations involving simpler special functions. The manuscript is organized as follows. In Sect. 2, the solution of fractional kinetic equations involving Mathieu-type series is established, and in Sect. 3, a graphical interpretation and nature of the solution are discussed. Section 4 is focused on some examples, and in Sect. 5 concluding remarks are given.

2 Solution of fractional kinetic equations

In this section, we obtain the solution of generalized fractional kinetic equation (13) involving generalized Mathieu-type series (25) by applying the Laplace transform technique.

Theorem 2.1

For all $\nu , c, h >{0}$; $c\neq {h}$, if $\mu , \rho , \sigma , \tau , l \in {\mathbb{R}^{+}}$, $|ht|\leq {1}$, then equation

$$ N(t)-N_{0}{ }S^{(\rho ,\sigma )}_{\mu ,\tau }\bigl(l, \lbrace d_{k} \rbrace _{k=1}^{\infty }; ht \bigr)=-c^{\nu }{_{0}D_{t}^{-\nu }}N(t) $$

(27)

has the solution

$$ N(t)=N_{0}{}\sum_{k=1}^{\infty } \frac{2d^{\sigma }_{k} (\tau )_{k}}{(d _{k}^{\rho }+l^{2})^{\mu }}(ht)^{k}{}E_{\nu , {k}+1}\bigl(-c^{\nu }t^{ \nu } \bigr). $$

(28)

Proof

Applying the Laplace transform to (27) and using (25) and (18) gives

$$ N^{*}(s)=N_{0} \Biggl( \int _{0}^{\infty } e^{-st}\sum _{k=1}^{\infty }\frac{2d ^{\sigma }_{k} (\tau )_{k}}{(d_{k}^{\rho }+l^{2})^{\mu }} \frac{(ht)^{k}}{k!} \Biggr)\,dt-c^{\nu }s^{-\nu }N^{*}(s), $$

(29)

where $N^{*}(s)=L \lbrace N(t);s \rbrace$.

Under the given assumptions, computing the integral in (29) term by term and using $L \lbrace t^{\lambda };s \rbrace =\frac{ \varGamma (\lambda +1)}{s^{\lambda +1}}$, we have

$$ \biggl( 1+ \biggl( \frac{c}{s} \biggr)^{\nu } \biggr) N^{*}(s)=N_{0} \sum_{k=1}^{\infty } \frac{2d^{\sigma }_{k} (\tau )_{k}}{(d_{k}^{ \rho }+l^{2})^{\mu }} \frac{h^{k}}{k!}\frac{\varGamma (1+{k})}{s^{1+ {k}}}. $$

Employing the geometric series expansion of $( 1+ ( \frac{c}{s} )^{\nu } )^{-1}$ for $c<|s|$, we have

$$\begin{aligned} N^{*}(s) ={}&N_{0} \sum _{k=1}^{\infty }\frac{2d^{\sigma }_{k} (\tau )_{k}}{(d _{k}^{\rho }+l^{2})^{\mu }} \frac{h^{k}}{s^{1+{k}}} \\ & {}\times \sum_{r=0}^{\infty }(-1)^{r} \biggl(\frac{c}{s} \biggr) ^{\nu {r}}. \end{aligned}$$

(30)

Taking the inverse Laplace transform and applying the relation $L^{-1}\{s^{-\nu };t\}=\frac{t^{\nu -1}}{\varGamma (\nu )}$, $\Re ( \nu )>0$, we get

$$\begin{aligned} N(t) &=L^{-1} \bigl\lbrace N^{*}(s);t \bigr\rbrace \\ &=N_{0} \sum_{k=1}^{\infty } \frac{2d^{\sigma }_{k} (\tau )_{k}}{(d _{k}^{\rho }+l^{2})^{\mu }}(ht)^{k} \Biggl\lbrace \sum _{r=0}^{\infty }\frac{(-1)^{r}(ct)^{ \nu {r}}}{\varGamma (\nu {r}+1+k)} \Biggr\rbrace \\ &=N_{0} \sum_{k=1}^{\infty } \frac{2d^{\sigma }_{k} (\tau )_{k}}{(d _{k}^{\rho }+l^{2})^{\mu }}(ht)^{k}E_{\nu ,k+1}\bigl(-c^{\nu }t^{\nu } \bigr). \end{aligned}$$

 □

In view of relation (26), we state the following consequence of Theorem 2.1.

Corollary

For all $\nu , c, h >{0}$; $c\neq {h}$, if $\mu , l \in {\mathbb{R} ^{+}}$, $|ht|\leq {1}$, then equation

$$ N(t)-N_{0}{ } {}S_{\mu ,\tau }(l, k; ht)=-c^{\nu }{_{0}D_{t}^{-\nu }}N(t) $$

(31)

has the solution

$$ N(t)=N_{0}\sum_{k=1}^{\infty } \frac{2k}{(k^{2}+l^{2})^{\mu +1}} (ht)^{k} E _{\nu , k+1}\bigl(-c^{\nu }t^{\nu } \bigr). $$

(32)

Theorem 2.2

Assume that $\nu , c, w >{0}$ and $\mu , \rho , \sigma , \tau , l \in {\mathbb{R}^{+}}$, $|wt|\leq {1}$, then equation

$$N(t)-N_0{S}_{\mu ,\tau }^{(\rho ,\sigma )}(l,{\{d_k\}}_{k=1}^{\mathrm{\infty }};w{t}^{\nu })=-\left[\sum _{r=1}^n\left(\begin{array}{c}n\\ r\end{array}\right){c^{\nu r}}_0{D}_t^{-\nu r}\right]N(t)$$

(33)

has the solution

$$ N(t)=N_{0}t^{\alpha -1}\sum _{k=1}^{\infty }\frac{2d^{\sigma }_{k} ( \tau )_{k} \varGamma (\nu {}k+1)}{(d_{k}^{\rho }+l^{2})^{\mu }} \frac{(wt ^{\nu })^{k}}{k!}E^{n}_{\nu ,1+\nu {k}} \bigl(-c^{\nu }{}t^{\nu }\bigr). $$

(34)

Proof

Applying LT to both sides of (33) and then using (25) and (15), we get

$$ L \bigl\lbrace N(t); s \bigr\rbrace =N_{0} L \bigl\lbrace S^{( \rho ,\sigma )}_{\mu ,\tau }\bigl(l, \lbrace d_{k} \rbrace _{k=1}^{\infty }; wt^{\nu }\bigr); s \bigr\rbrace -L \left \lbrace \left [\sum_{r=1}^{n} \begin{pmatrix} n \\ r \end{pmatrix} c^{\nu {r}}{_{0}D_{t}^{-\nu {r}}} \right ]N(t);s \right\rbrace $$

which, upon solving for $N^{*}(s)$, yields

$$\begin{aligned}& N^{*}(s)-N_{0} \sum_{k=1}^{\infty } \frac{2d^{\sigma }_{k} (\tau )_{k}}{(d _{k}^{\rho }+l^{2})^{\mu }} \frac{w^{k}}{k!}\frac{\varGamma (1+\nu {k})}{s ^{1+\nu {k}}} \\& \quad =- \biggl[ ^{n}C_{1} \biggl( \frac{c}{s} \biggr)^{\nu }+{}^{n}C_{2} \biggl( \frac{c}{s} \biggr)^{2\nu }+\cdots +{}^{n}C_{n} \biggl( \frac{c}{s} \biggr)^{n\nu } \biggr] N^{*}(s) =- \biggl( \frac{c}{s} \biggr)^{n\nu }N^{*}(s), \\& N^{*}(s)=N_{0} \sum_{k=1}^{\infty } \frac{2d^{\sigma }_{k} (\tau )_{k}}{(d _{k}^{\rho }+l^{2})^{\mu }} \frac{w^{k}}{k!}\frac{\varGamma (1+\nu {k})}{s ^{1+\nu {k}}} \biggl( 1+ \biggl( \frac{c}{s} \biggr) ^{\nu } \biggr) ^{-n}. \end{aligned}$$

Employing the binomial formula

$$ (1-u)^{-\lambda }=\sum_{r=0}^{\infty } \frac{(\lambda )_{r}}{r!}u^{r}, $$

which obviously converges for all $|u|<1$, we have

$$ N^{*}(s)=N_{0} \sum _{k=1}^{\infty }\frac{2d^{\sigma }_{k} (\tau )_{k}}{(d _{k}^{\rho }+l^{2})^{\mu }} \frac{w^{k}}{k!} \frac{\varGamma (1+\nu {k})}{s ^{1+\nu {k}}} \Biggl\lbrace \sum_{j=0}^{\infty }(-1)^{j} \frac{(n)_{j}}{j!}\bigl(-c^{\nu }s^{-\nu }\bigr)^{j} \Biggr\rbrace . $$

(35)

If we now take the inverse LT of (35) and use (11), after easy simplification, the result (34) readily follows. □

In view of relation (26), we establish the following consequence of Theorem 2.2.

Corollary

Assume that $\nu , \alpha , c, w >{0}$, and let $\mu , l \in {\mathbb{R} ^{+}}$, $|wt|\leq {1}$, then equation

$$N(t)-N_0{t}^{\alpha -1}{S}_{\mu }(l;w{t}^{\nu })=-\left[\sum _{r=1}^n\left(\begin{array}{c}n\\ r\end{array}\right){c^{\nu r}}_0{D}_t^{-\nu r}\right]N(t)$$

(36)

has the solution

$$ N(t)=N_{0}\sum_{k=1}^{\infty } \frac{2k\varGamma (\nu k+1)}{(k^{2}+l^{2})^{ \mu +1}} \frac{(wt^{\nu })^{k}}{k!}E^{n}_{\nu ,1+\nu {k}} \bigl(-c^{\nu }t ^{\nu }\bigr). $$

(37)

Theorem 2.3

For all $\nu >0$, $c>{0}$, $\mu , \rho , \sigma , \tau , l \in {\mathbb{R} ^{+}}$, $|t|\leq {1}$, the equation

$$ N(t)-N_{0}{ }S^{(\rho ,\sigma )}_{\mu ,\tau }\bigl(l, \lbrace d_{k} \rbrace _{k=1}^{\infty }; c^{\nu }t^{\nu }\bigr)=-c^{\nu }{_{0}D_{t}^{-\nu }}N(t) $$

(38)

has the solution

$$ N(t)=N_{0}\sum_{k=1}^{\infty } \frac{2d^{\sigma }_{k} (\tau )_{k} \varGamma (\nu k+1)}{(d_{k}^{\rho }+l^{2})^{\mu }} \frac{(c^{\nu }t^{ \nu })^{k}}{k!} E_{\nu , \nu {k}+1}\bigl(-c^{\nu }t^{\nu } \bigr). $$

(39)

Proof

This can be proved by the same procedure as in the proof of Theorem 2.1. So we omit all details. □

Using relation (26), we state the following consequence of Theorem 2.3.

Corollary

For all $\nu >0$, $c>{0}$, $\mu , l \in {\mathbb{R}^{+}}$, $|t|\leq {1}$, the equation

$$ N(t)-N_{0}{ }S_{\mu }\bigl(l;c^{\nu }t^{\nu } \bigr)=-c^{\nu }{_{0}D_{t}^{- \nu }}N(t) $$

(40)

has the solution

$$ N(t)=N_{0}\sum_{k=1}^{\infty } \frac{2k\varGamma (\nu k+1)}{(k^{2}+l^{2})^{ \mu +1}} \frac{(c^{\nu }t^{\nu })^{k}}{k!}E_{\nu , \nu {k}+1}\bigl(-c^{ \nu }t^{\nu } \bigr). $$

(41)

3 Graphical representations

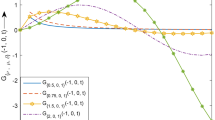
Figures 1–5 represents the graph of solution (28) by considering some fractional values, and observe that, by choosing small values for ν, the graph is increasing in nature, and if we choose larger values for ν, then it is gradually decreasing. The graphical results confirm that the region of convergence of solutions depends continuously on the fractional parameter ν. Hence, by observing the nature of the solutions for various parameters and time interval, it is concluded that $N(t)$ can be negative as well as positive. A similar observation can be obtained for the solutions (34) and (39).

Figure 1

Solution (13) for $N(t)$ and t

Figure 2

Solution (13) for $N(t)$ and t

Figure 3

Solution (13) for $N(t)$ and t

Figure 4

Solution (13) for $N(t)$ and t

Figure 5

Solution (13) for $N(t)$ and t

4 Example

A detailed account of Mathieu-type series and their applications can be found in the monographs by various authors [21, 35,36,37]. An integral transform, called the Sumudu transform, was defined and studied by Watugala [38] to facilitate the process of solving differential and integral equations in the time domain, and for the use in various applications of system control engineering and applied mathematics. In [3, 4], some fundamental properties of the Sumudu transform are investigated. It turns out that the Sumudu transform has very special and useful properties, and it is useful in solving problems of science and control engineering governing kinetic equations. The Sumudu transform is defined on the set of functions

$$ A= \bigl\lbrace f(t)| \exists {} M,{} \delta _{1}, \delta _{2}, \bigl\vert f(t) \bigr\vert < Me ^{ \vert t \vert /\delta _{j}} \text{ if } t \in (-1)^{j}\times [0,\infty ) \bigr\rbrace , $$

by

$$ G(u)=S\bigl(f(t) ; u\bigr)= \int _{0}^{\infty }e^{-t}f(ut)\,dt,\quad u \in (-\delta _{1},\delta _{2}), $$

where M is a real finite number and $\delta _{1}$ and $\delta _{2}$ can be finite or infinite. For more details, see [38, 39].

By using the convolution theorem for the Sumudu transform [3,4,5], (5) can be written in the following form:

$$ S \bigl\lbrace {} _{0}D_{t}^{-\nu } f(t) \bigr\rbrace = S \biggl\lbrace \frac{t ^{\nu -1}}{\varGamma (\nu )} \biggr\rbrace \cdot S \bigl\lbrace f(t) \bigr\rbrace =u ^{\nu }G(u). $$

(42)

It is easy to see that the Sumudu transform of the function $f(t)=t^{\varepsilon }$ is given by

$$ S\bigl[f(t)\bigr]= \int _{0}^{\infty } (ty)^{\varepsilon }e^{-t}\,dt=u^{\varepsilon } \varGamma (\varepsilon +1) \quad \bigl(\Re (\varepsilon )>-1\bigr). $$

(43)

The Laplace transform is a very potent mathematical tool which is used to solve diverse engineering and science problems. The Sumudu transform (which is not so well-known as the Laplace transform) was proposed in the early 1990s, and it has some interesting advantages over other integral transforms, especially regarding the “unity” feature which could become convenient when solving differential equations. As a comparison, the Sumudu transform is a simple variant of the Laplace transform. This paper focuses on the effectiveness of both transforms to obtain the solutions of fractional kinetic equations. The Sumudu transform is essentially identical with the Laplace transform. Given an initial $f(t)$, its Laplace transform $F(s)$ can be translated into the Sumudu transform $F_{s}(u)$ of f by means of the relation

$$\begin{aligned} S(u)=\frac{F ( \frac{1}{u} ) }{u}, \end{aligned}$$

and its inverse is

$$\begin{aligned} F(s)=\frac{S ( \frac{1}{s} ) }{s}. \end{aligned}$$

For more details about the Sumudu transform and its properties in comparison to the Laplace transform, the interested readers can check [17,18,19].

Due to the importance of the above observation, in this section, we first define the Sumudu transform of Mathieu-type series (25) and further determine the solution of fractional kinetic equations by applying Sumudu transform technique as given in the following Examples 4.1, 4.2, and 4.3.

The following integral gives the Sumudu transform of Mathieu-type series (25):

$$ \int _{0}^{\infty }e^{-t}(ut)^{\varepsilon -1}S^{(\rho ,\sigma )}_{ \mu ,\tau } \bigl(l, \lbrace d_{k} \rbrace _{k=1}^{\infty }; w(ut)^{ \nu }\bigr)\,dt=u^{\varepsilon -1} \sum_{k=1}^{\infty } \frac{2d^{\sigma } _{k}(\tau )_{k}}{(d^{\rho }_{k}+l^{2})^{\mu }}\frac{\varGamma (\varepsilon +\nu {k})}{k!}(uw)^{k}, $$

(44)

where $\Re (u)>|w|^{-1/\Re (\nu )}$, $\Re (\varepsilon )>0$, $u\in (-\delta _{1},\delta _{2})$, $|f(t)|< Me^{|t|/\delta _{j}}$ and $l,d,\rho , \sigma , \mu \in \mathbb{R^{+}}$.

Using the same procedure of analysis as in Theorems 2.1, 2.2, and 2.3, we can find the solutions of generalized fractional kinetic equations involving Mathieu-type series, which are given in the following three examples.

Example 4.1

If $\varepsilon , \nu , c,h >{0}$, $\Re (s)>0$ with $|s|< c^{-1}$, $c\neq {h}$ and $\mu , \rho , \sigma , \tau , l \in {\mathbb{R}^{+}}$, then the solution of the generalized fractional kinetic equation

$$ N(t)-N_{0}{ } {t^{\varepsilon -1}}S^{(\rho ,\sigma )}_{\mu ,\tau } \bigl(l, \lbrace d_{k} \rbrace _{k=1}^{\infty }; ht^{\nu }\bigr)=-c^{ \nu }{_{0}D_{t}^{-\nu }}N(t) $$

(45)

is given by

$$ N(t)=N_{0}t^{\varepsilon -2}\sum _{k=1}^{\infty }\frac{2d^{\sigma } _{k} (\tau )_{k} \varGamma (\nu k+\varepsilon )}{(d_{k}^{\rho }+l^{2})^{ \mu }} \frac{(c^{\nu }t^{\nu })^{k}}{k!} E_{\nu , \varepsilon + \nu {k}-1}\bigl(-c^{\nu }t^{\nu }\bigr). $$

(46)

Example 4.2

If $\nu , c, w >{0}$ and $\mu , \rho , \sigma , \tau , l \in {\mathbb{R} ^{+}}$; $|s|< c^{-1}$, $c\neq {w}$, then the solution of the generalized fractional kinetic equation

$$ N(t)-N_{0}{ }t^{\varepsilon -1}{ }S^{(\rho ,\sigma )}_{\mu ,\tau } \bigl(l, \lbrace d_{k} \rbrace _{k=1}^{\infty }; wt^{\nu }\bigr)=-\left [\sum_{r=1}^{n} \begin{pmatrix} n \\ r \end{pmatrix} c^{\nu {r}}{_{0}D_{t}^{-\nu {r}}} \right ] N(t) $$

(47)

is given by

$$ N(t)=N_{0}{ }t^{\varepsilon -2}\sum _{k=1}^{\infty }\frac{2d^{\sigma } _{k} (\tau )_{k} \varGamma (\nu {}k+\varepsilon )}{(d_{k}^{\rho }+l^{2})^{ \mu }} \frac{(wt^{\nu })^{k}}{k!}E^{n}_{\nu , \nu {k}+\varepsilon -1} \bigl(-c ^{\nu }{}t^{\nu }\bigr). $$

(48)

Example 4.3

If $\nu >0$, $c>{0}$, $\mu , \rho , \sigma , \tau , l \in {\mathbb{R} ^{+}}$ and $|s|< {c^{-1}}$, then the solution of the generalized fractional kinetic equation

$$ N(t)-N_{0}{ }t^{\varepsilon -1}{ }S^{(\rho ,\sigma )}_{\mu ,\tau } \bigl(l, \lbrace d_{k} \rbrace _{k=1}^{\infty }; c^{\nu }t^{\nu }\bigr)=-c ^{\nu }{_{0}D_{t}^{-\nu }}N(t) $$

(49)

is given by

$$ N(t)=N_{0}{ }t^{\varepsilon -2}\sum _{k=1}^{\infty }\frac{2d^{\sigma } _{k} (\tau )_{k} \varGamma (\nu k+\varepsilon )}{(d_{k}^{\rho }+l^{2})^{ \mu }} \frac{(c^{\nu }t^{\nu })^{k}}{k!} E_{\nu , \nu {k}+\varepsilon -1}\bigl(-c^{\nu }t^{\nu }\bigr). $$

(50)

5 Conclusion

In the current study, we have obtained the solution of generalized fractional kinetic equations involving generalized Mathieu-type series with the help of Laplace and Sumudu transform techniques. The results of Sect. 2 are general in character and are likely to find certain applications in the theory of fractional calculus and special functions. From the graphical analysis, we conclude that $N(t) > 0$ or $N(t) < 0$ for distinct values of the parameters. By suitably specializing the values of the parameters of generalized Mathieu-type series (25), our main results can yield several new solutions of generalized fractional kinetic equations corresponding to the Mathieu series given by various authors [6, 21, 34, 37]. Therefore, the investigated results in this paper would at once give many results involving diverse special functions occurring in the problems of astrophysics, mathematical physics, and engineering.