1 Introduction

Neural networks are playing a more and more important role in the reconstruction of images, signal processing, optimization problems, artificial intelligence, etc. However, neural networks can arise chaotic behaviors due to an unpredictable disturbance. To control the chaos arising in the neural networks, a variety of synchronization schemes have been proposed, including projective synchronization [22], event-based synchronization [13], exponential synchronization [8, 15], finite-time synchronization [29, 36], generalized synchronization [2, 10], pinning synchronization [9, 31], lag synchronization [26, 32], adaptive synchronization [3, 11, 18, 24, 27, 36], impulsive synchronization [14, 17, 28, 30, 31], and so on. Recently, another important topic is the fractional calculus, which depicts arbitrary non-integer-order differentiation and integration. The fractional-order neural networks have been proposed in theory and practice due to the great significance of the fractional calculus. Stability analysis of a fractional-order system with impulses was performed in [21]. Synchronization schemes were proposed for the fractional-order neural networks with delays (see, e.g., [33, 35]). Memristor-based fractional-order cellular neural networks were studied in [7, 20].

Fuzzy logic theory is a powerful tool to deal with synthesis of integer-order complex systems (see [4,5,6, 23, 25, 38]). However, they have not considered the effects of fuzzy logic on the fractional-order neural networks. There are few papers considering the stability and synchronization of Takagi–Sugeno (T-S) fuzzy neural networks. Recently, state estimation was given for T-S fuzzy delayed Hopfield neural networks in [1]. Adaptive fuzzy sliding mode control scheme was proposed for the uncertain fractional-order chaotic systems [16]. Finite stability analysis was performed for a memristor-based fractional-order fuzzy cellular neural networks in [37]. In [19], impulsive synchronization was proposed for fractional T-S fuzzy networks by utilizing the comparison principle. In [22], the authors studied the adaptive projective synchronization for fractional-order T-S fuzzy neural networks with uncertain parameters. In the previous works, they considered the projective synchronization and the impulsive synchronization of fractional-order T-S fuzzy neural networks. However, different from their consideration and method, we construct a different Lyapunov function and employ the linear matrix inequality. Some sufficient conditions are obtained to guarantee the master–slave synchronization of fractional-order T-S neural networks. This is the highlight of this paper.

This paper is organized as follows. Definitions and lemmas are presented in the next section. Section 3 is devoted to obtaining the sufficient conditions for synchronization of fractional-order neural networks. Finally, an example and its simulations are given.

2 Preliminaries

In this section, the assumptions, definitions, and some lemmas are given. Two definitions of the Caputo fractional-order integrals and derivatives are introduced.

Definition 2.1

For a function \(x(t)\) and non-integer real number \(\alpha>0\), the Caputo fractional integral is defined as

$$I^{\alpha}x(t)=\frac{1}{\varGamma(\alpha)} \int_{t_{0}}^{t} (t-\tau )^{\alpha-1}x(\tau)\,d\tau, $$

where the gamma function \(\varGamma(\cdot)\) satisfies \(\varGamma(s)=\int _{0}^{\infty} t^{s-1}e^{-t}\,dt\), \(t_{0}\) is the initial time, \(t\geq t_{0}\).

Definition 2.2

For a function \(x(t)\) and non-integer real number \(\alpha>0\), the Caputo fractional derivative is defined as

$$D^{\alpha}x(t)=\frac{1}{\varGamma(n-\alpha)} \int_{t_{0}}^{t} (t-\tau )^{n-\alpha-1}x^{(n)}( \tau)\,d\tau, $$

where \(t_{0}\) is the initial time, \(t\geq t_{0}\), \(n-1 < \alpha<n \in Z^{+}\).

We need the following lemmas.

Lemma 2.1

([12])

For the Caputo fractional-order derivative, when \(n-1 < \alpha<n, n \in N^{+}\), we have

$$D^{-\alpha}\bigl(D^{\alpha}\bigr)f(t)=f(t)-\sum _{i=1}^{n-1}\frac {f^{i}(t_{0})}{i!}(t-t_{0})^{i}. $$

In particular, when \(0< \alpha<1\),

$$D^{-\alpha}\bigl(D^{\alpha}\bigr)f(t)=f(t)-f(t_{0}),\qquad D^{-\alpha }\bigl(I^{\alpha}\bigr)f(t)=f(t). $$

Lemma 2.2

([1])

For any matrices \(X\in R^{ m\times n}\), \(Y\in R^{ m\times n}\), \(\varLambda =\varLambda^{T}>0\), \(\varLambda\in R^{n \times n}\), the inequality \(X^{T}Y+Y^{T}X \leq X^{T}\varLambda X+Y^{T}\varLambda^{-1}Y\) holds.

Lemma 2.3

([34])

Given constant matrices \(\varXi_{1}\), \(\varXi_{2}\), \(\varXi_{3}\), where \(\varXi _{1}=\varXi_{1}^{T}\), \(\varXi_{2}=\varXi_{2}^{T}\), and \(\varXi_{2}>0\), then \(\varXi _{1}+\varXi_{3}^{T}\varXi_{2}^{-1}\varXi_{3}<0\) if and only if

$$\begin{aligned} \begin{pmatrix} \varXi_{1} &\varXi_{3}^{T} \\ \varXi_{3}& -\varXi_{2} \end{pmatrix} < 0,\quad \textit{or} \quad \begin{pmatrix} -\varXi_{2} & \varXi_{3}^{T} \\ \varXi_{3} & \varXi_{1} \end{pmatrix} < 0. \end{aligned}$$

3 Model formulations and synchronization schemes

In this section, we discuss the master–slave synchronization of fractional-order T-S fuzzy delayed neural networks. The aim is to achieve the synchronization of the T-S fuzzy master–slave systems by using a state feedback controller. Consider a vector form of the neural network as follows:

$$\begin{aligned} D^{\alpha}x(t)=C x(t)+A f\bigl(x(t)\bigr)+B g\bigl(u(t-\tau) \bigr)+I(t). \end{aligned}$$
(1)

If we take (1) as the master system, the corresponding slave system can be given as

$$\begin{aligned} D^{\alpha}v(t)=C v(t)+A f\bigl(v(t)\bigr)+B g\bigl(v(t-\tau) \bigr)-U(t)+I(t), \end{aligned}$$
(2)

where \(x(t)=[u_{1}(t),\ldots,u_{n}(t)]^{T}\in R^{n}\) is the state vector, \(v(t)=[v_{1}(t),\ldots,v_{n}(t)]^{T}\in R^{n}\) is the output vector, \(C=\operatorname{diag}(-c_{1},\ldots,-c_{n})\) (\(c_{k}>0\), \(k=1,\ldots,n\)) is the self-feedback matrix, \(U(t)\) is a suitable controller, A and B \(\in R^{n\times n}\), \(I(t)=[\xi_{1}(t),\xi_{2}(t),\ldots,\xi _{n}(t)]^{T}\in R^{n}\) is the external input vector, \(f(x(t))=[f_{1}(u_{1}(t)),\ldots,f_{n}(u_{n}(t))]^{T}\) and \(g(u(t-\tau ))=[g_{1}(u_{1}(t-\tau)),\ldots,g_{n}(u_{n}(t-\tau))]^{T}\) denotes the output vector at time t and \(t-\tau\), respectively.

Motivated by [1], we define the fuzzy rule k as follows:

IF \(\omega_{1}\) is \(\mu_{k1}\) and ⋯ \(\omega_{s}\) is \(\mu_{ks}\), THEN

$$\begin{aligned} &D^{\alpha}x(t)=C_{k} x(t)+A_{k} f \bigl(x(t)\bigr)+B_{k} g\bigl(u(t-\tau)\bigr)+I_{k}(t), \end{aligned}$$
(3)
$$\begin{aligned} &D^{\alpha}v(t)=C_{i} v(t)+A_{k} f \bigl(v(t)\bigr)+B_{k} g\bigl(v(t-\tau)\bigr)-U(t)+I_{k}(t). \end{aligned}$$
(4)

The meaning of parameters \(\omega_{k},\mu_{kq}\) (\(k=1,2,\ldots ,r\), \(q=1,2,\ldots,s\)), r is the same as in [1]. Using a standard fuzzy inference method, we have from (3)–(4) that

$$\begin{aligned} &D^{\alpha}u(t)=\sum_{k=1}^{r}h_{k}( \omega)\bigl[C_{k} u(t)+A_{k} f\bigl(u(t) \bigr)+B_{k} g\bigl(u(t-\tau)\bigr)+I_{k}(t)\bigr], \end{aligned}$$
(5)
$$\begin{aligned} &D^{\alpha}v(t)=\sum_{k=1}^{r}h_{k}( \omega)\bigl[C_{k} v(t)+A_{k} f\bigl(v(t) \bigr)+B_{k} g\bigl(v(t-\tau)\bigr)-U(t)+I_{k}(t)\bigr], \end{aligned}$$
(6)

where \(h_{k}(\omega)=\frac{\omega_{k}(\omega)}{\sum_{k=1}^{s}\omega_{k}(\omega)}\) satisfies

$$\begin{aligned} h_{k}(\omega)\geq0,\qquad \sum_{i=1}^{n}h_{k}( \omega)=1. \end{aligned}$$
(7)

Throughout this paper, we make the following assumption.

Assumption 3.1

The neuron activation functions \(f_{j}(x)\) and \(g_{j}(x)\) satisfy the following Lipschitz conditions:

$$\bigl\vert f_{j}(x)-f_{j}(y) \bigr\vert \leq l_{j} \vert x-y \vert $$

and

$$\bigl\vert g_{j}(x)-g_{j}(y) \bigr\vert \leq h_{j} \vert x-y \vert $$

for all \(x,y \in\mathbb{R}\), where \(l_{j}>0\), \(h_{j}>0\) are Lipschitz constants.

Let \(e(t)=v(t)-u(t)\) be the synchronization error, select the control input function

$$\begin{aligned} U(t)=\varPhi\bigl(v(t)-u(t)\bigr), \end{aligned}$$
(8)

where \(\varPhi=\operatorname{diag}(\phi_{1},\phi_{2}, \ldots,\phi_{n})\) is the controller feedback matrix.

Then we can obtain the error system as follows:

$$\begin{aligned} D^{\alpha}e(t)={}&\sum_{k=1}^{r}h_{k}( \omega)\bigl\{ (C_{k}-\varPhi) e(t)+A_{k} \bigl[f\bigl(v(t) \bigr)-A_{k} f\bigl(u(t)\bigr)\bigr] \\ &{}+B_{k}\bigl[ g\bigl(v(t-\tau)\bigr)-B_{k} g \bigl(u(t-\tau)\bigr)\bigr]\bigr\} . \end{aligned}$$
(9)

Theorem 3.1

If there exist positive definite matrices \(P, Q, R, S\), and V such that

$$\begin{aligned} \begin{pmatrix} \varPsi& 0 & V & PA_{k} & P B_{k} \\ 0 & H-R & -V & 0 & 0 \\ V & -V & -\frac{1}{\tau}Q & 0 & 0 \\ A_{k}^{T}P & 0 & 0 & -E & 0 \\ B_{k}^{T}P& 0 & 0 & 0 & -E \end{pmatrix} < 0 \end{aligned}$$
(10)

for all k (\(k=1,2,\ldots,r\)), where \(\varPsi=(C_{k}-\varPhi)^{T}P+P(C_{k}-\varPhi )+L+\tau Q+R+S\), \(L=\operatorname{diag}\{l_{1}^{2},l_{2}^{2},\ldots,l_{n}^{2}\}\), \(H=\operatorname{diag}\{h_{1}^{2},h_{2}^{2},\ldots,h_{n}^{2}\}\), E is an identity matrix, then the fractional-order T-S fuzzy system (5) synchronizes to system (6).

Proof

We define the following Lyapunov function:

$$\begin{aligned} V(t)={}&D^{\alpha-1}\bigl[e^{T}(t)P e(t)\bigr]+ \int_{-\tau}^{0} \int_{t+\theta }^{t}e(\varpi)^{T}Qe(\varpi)\,d\varpi \,d\theta \\ &{}+\biggl[ \int_{-\tau}^{0}e(t+\sigma)\,d\sigma\biggr]^{T}V \biggl[ \int_{-\tau }^{0}e(t+\sigma)\,d\sigma\biggr] \\ &{}+ \int_{-\tau}^{0} e^{T}(t+\sigma) R e(t+ \sigma)\,d\sigma, \end{aligned}$$
(11)

where

$$\begin{aligned} e(t)=\bigl(e_{1}(t),e_{2}(t), \ldots,e_{n}(t)\bigr)^{T}. \end{aligned}$$
(12)

Calculation on the derivative along (9) leads to

$$\begin{aligned} \dot{V}(t)={}&D^{\alpha}\bigl[e^{T}(t)Pe(t)\bigr]+\tau e^{T}(t)Qe(t)\\ &{}- \int_{t-\tau }^{t}e^{T}(\sigma)Qe(\sigma)\,d \sigma+e^{T}(t)Re(t) \\ &{}-e^{T}(t-\tau)Re(t-\tau)+\bigl[e(t)-e(t-\tau)\bigr]^{T}V \biggl[ \int_{t-\tau }^{t}e(\sigma)\,d\sigma\biggr] \\ &{}+\biggl[ \int_{t-\tau}^{t}e(\sigma)\,d\sigma\biggr]^{T}V \bigl[e(t)-e(t-\tau)\bigr] \\ ={}&\sum_{k=1}^{r}h_{k}(\omega) \bigl[e^{T}(t) \bigl(C_{k}^{T}-\varPhi ^{T}\bigr)+\bigl(f\bigl(v(t)\bigr)-f\bigl(u(t)\bigr) \bigr)^{T}A_{k}^{T}+\bigl(g\bigl(v(t-\tau)\bigr) \\ &{}-g\bigl(u(t-\tau)\bigr)\bigr)^{T}B_{k}^{T} \bigr]Pe(t)+e^{T}(t)P\sum_{k=1}^{r}h_{k}( \omega )\bigl[(C_{k}-\varPhi)e(t) \\ &{}+A_{k}\bigl(f\bigl(v(t)\bigr)-f\bigl(u(t)\bigr)\bigr)+B_{k} \bigl(g\bigl(v(t-\tau)\bigr)-g\bigl(u(t-\tau)\bigr)\bigr)\bigr] \\ &{}+\tau e^{T}(t)Qe(t)- \int_{t-\tau}^{t}e^{T}(\sigma)Qe(\sigma)\,d \sigma +e^{T}(t)Re(t)-e^{T}(t-\tau)Re(t-\tau) \\ &{}+\bigl[e(t)-e(t-\tau)\bigr]^{T}V \biggl[ \int_{t-\tau }^{t}e(\sigma)\,d\sigma\biggr]\\ &{} +\biggl[ \int_{t-\tau}^{t}e(\sigma)\,d\sigma\biggr]^{T}V \bigl[e(t)-e(t-\tau)\bigr] \\ ={}&\sum_{k=1}^{r}h_{k}(\omega) \bigl\{ e^{T}(t)\bigl[(C_{k}-\varPhi)^{T}P+P(C_{k}- \varPhi )\bigr]e(t)+\bigl(f\bigl(v(t)\bigr) \\ &{}-f\bigl(u(t)\bigr)\bigr)^{T}A_{k}^{T}Pe(t)+e^{T}(t)PA_{k} \bigl(f\bigl(v(t)\bigr)-f\bigl(u(t)\bigr)\bigr)+\bigl(g\bigl(v(t-\tau )\bigr) \\ &{}-g\bigl(u(t-\tau)\bigr)\bigr)^{T}B_{k}^{T}Pe(t)+e^{T}(t)PB_{k} \bigl(g\bigl(v(t-\tau)\bigr)-g\bigl(u(t-\tau )\bigr)\bigr)\bigr\} \\ &{}+\tau e^{T}(t)Qe(t)- \int_{t-\tau}^{t}e^{T}(\sigma)Qe(\sigma)\,d \sigma +e^{T}(t)Re(t)-e^{T}(t-\tau)Re(t-\tau) \\ &{}+\bigl[e(t)-e(t-\tau)\bigr]^{T}V\biggl[ \int_{t-\tau}^{t}e(\sigma)\,d\sigma\biggr]\\ &{}+\biggl[ \int_{t-\tau }^{t}e(\sigma)\,d\sigma\biggr]^{T}V \bigl[e(t)-e(t-\tau)\bigr]. \end{aligned}$$

In view of Lemma 2.2, we obtain

$$\begin{aligned} &\bigl(f\bigl(v(t)\bigr)-f\bigl(u(t)\bigr)\bigr)^{T}A_{k}^{T}Pe(t)+e^{T}(t)PA_{k} \bigl(f\bigl(v(t)\bigr)-f\bigl(u(t)\bigr)\bigr) \\ &\quad \leq\sum_{j=1}^{n} l^{2}_{j}e^{2}_{j}(t)+e^{T}(t)PA_{k}A_{k}^{T}Pe(t) \\ &\quad \leq e^{T}(t) \bigl(L+PA_{i}A_{k}^{T}P \bigr)e(t), \end{aligned}$$

and

$$\begin{aligned} &\bigl(g\bigl(v(t-\tau)\bigr)-g\bigl(u(t-\tau)\bigr)\bigr)^{T}B_{k}^{T}Pe(t)+e^{T}(t)PB_{k} \bigl(g\bigl(v(t-\tau )\bigr)-g\bigl(u(t-\tau)\bigr)\bigr) \\ &\quad \leq\sum_{j=1}^{n} h^{2}_{j}e^{2}_{j}(t- \tau )+e^{T}(t)PB_{k}B_{k}^{T}Pe(t) \\ &\quad \leq e^{T}(t-\tau)He(t-\tau)+e^{T}(t)PB_{k}B_{k}^{T}Pe(t), \end{aligned} $$

where \(L=\operatorname{diag}\{l_{1}^{2},l_{2}^{2},\ldots,l_{n}^{2}\}\), \(H=\operatorname{diag}\{ h_{1}^{2},h_{2}^{2},\ldots,h_{n}^{2}\}\). Thus, we have

$$\begin{aligned} \dot{V}(t)\leq{}&\sum_{k=1}^{r}h_{k}( \omega)\bigl\{ e^{T}(t)\bigl[(C_{k}-\varPhi )^{T}P+P(C_{k}- \varPhi)\bigr]e(t)+e^{T}(t)Le(t) \\ &{}+e^{T}(t)PA_{k}A_{k}^{T}Pe(t)+e^{T}(t- \tau)He(t-\tau )+e^{T}(t)PB_{k}B_{k}^{T}Pe(t) \bigr\} \\ &{}+\tau e^{T}(t)Qe(t)- \int_{t-\tau}^{t}e^{T}(\sigma)Qe(\sigma)\,d \sigma +e^{T}(t)Re(t)-e^{T}(t-\tau)Re(t-\tau) \\ &{}+\bigl[e(t)-e(t-\tau)\bigr]^{T}V\biggl[ \int_{t-\tau}^{t}e(\sigma)\,d\sigma\biggr]+\biggl[ \int_{t-\tau }^{t}e(\sigma)\,d\sigma\biggr]^{T}V \bigl[e(t)-e(t-\tau)\bigr]. \end{aligned}$$

By using the inequality

$$\biggl[ \int_{t-\tau}^{t}e(\sigma)\,d\sigma\biggr]^{T}Q \biggl[ \int_{t-\tau}^{t}e(\sigma )\,d\sigma\biggr]\leq\tau \int_{t-\tau}^{t}e(\sigma)^{T}Qe(\sigma)\,d \sigma, $$

we have

$$\int_{t-\tau}^{t}e(\sigma)^{T}Qe(\sigma)\,d \sigma\geq\frac{1}{\tau}\biggl[ \int _{t-\tau}^{t}e(\sigma)\,d\sigma\biggr]^{T}Q \biggl[ \int_{t-\tau}^{t}e(\sigma)\,d\sigma\biggr]. $$

Thus,

$$\begin{aligned} \dot{V}(t)\leq{}&\sum_{k=1}^{r}h_{k}( \omega)\bigl\{ e^{T}(t)\bigl[(C_{k}-\varPhi )^{T}P+P(C_{k}- \varPhi)\bigr]e(t)+e^{T}(t)Le(t)+e^{T}(t)PA_{k}A_{k}^{T}Pe(t) \\ &{}+e^{T}(t- \tau)He(t-\tau )+e^{T}(t)PB_{k}B_{k}^{T}Pe(t) \bigr\} +\tau e^{T}(t)Qe(t) \\ &{}-\frac{1}{\tau}\biggl[ \int_{t-\tau}^{t}e(\sigma)\,d\sigma \biggr]^{T}Q \biggl[ \int_{t-\tau}^{t}e(\sigma)\,d\sigma\biggr]+e^{T}(t)Re(t)-e^{T}(t-\tau)Re(t-\tau) \\ &{}+\bigl[e(t)-e(t-\tau)\bigr]^{T}V \biggl[ \int_{t-\tau }^{t}e(\sigma)\,d\sigma\biggr] +\biggl[ \int_{t-\tau}^{t}e(\sigma)\,d\sigma\biggr]^{T}V \bigl[e(t)-e(t-\tau)\bigr] \\ ={}&\sum_{k=1}^{r}h_{k}(\omega) \bigl\{ e^{T}(t)\bigl[(C_{k}-\varPhi)^{T}P+P(C_{k}- \varPhi )+L+PA_{k}A_{k}^{T}P \\ &{}+P B_{k}B_{k}^{T}P+\tau Q+R\bigr]e(t)\bigr\} +e^{T}(t-\tau) (H-R)e(t-\tau) \\ &{}-\frac{1}{\tau}\biggl[ \int_{t-\tau}^{t}e(\sigma)\,d\sigma\biggr]^{T}Q \biggl[ \int_{t-\tau }^{t}e(\sigma)\,d\sigma\biggr]+\bigl[e(t)-e(t- \tau)\bigr]^{T}V\biggl[ \int_{t-\tau}^{t}e(\sigma )\,d\sigma\biggr] \\ &{}+\biggl[ \int_{t-\tau}^{t}e(\sigma)\,d\sigma\biggr]^{T}V \bigl[e(t)-e(t-\tau)\bigr] \\ ={}&\sum_{k=1}^{r}h_{k}(\omega) \left\{ \begin{pmatrix} e(t) \\ e(t-\tau) \\ \int_{t-\tau}^{t}e(\sigma)\,d\sigma \end{pmatrix} ^{T} \begin{pmatrix} \varPi& 0 & V \\ 0 & H-R & -V \\ V & -V & -\frac{1}{\tau}Q \end{pmatrix} \begin{pmatrix} e(t) \\ e(t-\tau) \\ \int_{t-\tau}^{t}e(\sigma)\,d\sigma \end{pmatrix} \right.\\ &\left.\vphantom{\begin{pmatrix} e(t) \\ e(t-\tau) \\ \int_{t-\tau}^{t}e(\sigma)\,d\sigma \end{pmatrix}}{}-e(t)^{T}Se(t)\right\}, \end{aligned}$$

where

$$\varPi=(C_{k}-\varPhi)^{T}P+P(C_{k}-\varPhi )+L+PA_{k}A_{k}^{T}P+PB_{k}B_{k}^{T}P+ \tau Q+R+S. $$

Note that, by Lemma 2.3, the matrix inequality

$$\begin{aligned} \begin{pmatrix} \varPsi& 0 & V & PA_{k} & P B_{k} \\ 0 & -R & -V & 0 & 0 \\ V & -V & -\frac{1}{\tau}Q & 0 & 0 \\ A_{k}^{T}P & 0 & 0 & -E & 0 \\ B_{k}^{T}P& 0 & 0 & 0 & -E \end{pmatrix} < 0 \end{aligned}$$

implies that the following inequality holds:

$$\begin{aligned} \begin{pmatrix} \varPi& 0 & V \\ 0 & H-R & -V \\ V & -V & -\frac{1}{\tau}Q \end{pmatrix} < 0. \end{aligned}$$
(13)

Therefore,

$$\dot{V}(t)< \sum_{k=1}^{r}h_{k}( \omega)\bigl\{ -e(t)^{T}Se(t)\bigr\} =-e(t)^{T}Se(t)< 0. $$

This implies that the fractional-order T-S fuzzy neuron system (5) synchronizes to system (6). □

Remark 3.1

We construct a skillful Lyapunov function with the Caputo fractional-order integral, definite integral, and double integral in the proof of Theorem 3.1.

4 Numerical example

In this section, as an example, we consider a fractional-order T-S fuzzy delayed neural networks with two neurons.

Fuzzy Rule 1

IF \(\omega_{1}\) is \(\mu_{11}\) and ⋯ \(\omega_{s}\) is \(\mu_{1s}\), THEN

$$\begin{aligned} &D^{\alpha}u(t)=C_{1} u(t)+A_{1} f \bigl(u(t)\bigr)+B_{1}g\bigl(u(t-\tau)\bigr)+I_{1}(t), \end{aligned}$$
(14)
$$\begin{aligned} &D^{\alpha}v(t)=C_{1} v(t)+A_{1} f \bigl(v(t)\bigr)+B_{1}g\bigl(v(t-\tau)\bigr)-\varPhi e(t)+I_{1}(t). \end{aligned}$$
(15)

Fuzzy Rule 2

IF \(\omega_{1}\) is \(\mu_{21}\) and ⋯ \(\omega_{s}\) is \(\mu_{2s}\), THEN

$$\begin{aligned} &D^{\alpha}u(t)=C_{2} u(t)+A_{2} f \bigl(u(t)\bigr)+B_{2}g\bigl(u(t-\tau)\bigr)+I_{2}(t), \end{aligned}$$
(16)
$$\begin{aligned} &D^{\alpha}v(t)=C_{2} v(t)+A_{2} f \bigl(v(t)\bigr)+B_{2}g\bigl(v(t-\tau)\bigr)-\varPhi e(t)+I_{2}(t). \end{aligned}$$
(17)

Using a standard fuzzy inference method, system (12)–(13) is inferred as follows:

$$\begin{aligned} &D^{\alpha}u(t)=\sum_{k=1}^{2}h_{k}( \omega)\bigl[C_{k} u(t)+A_{k} f\bigl(u(t) \bigr)+B_{k}g\bigl(u(t-\tau)\bigr)+I_{k}(t)\bigr], \end{aligned}$$
(18)
$$\begin{aligned} &D^{\alpha}v(t)=\sum_{k=1}^{2}h_{k}( \omega)\bigl[C_{k} v(t)+A_{k} f\bigl(v(t) \bigr)+B_{k}g\bigl(v(t-\tau)\bigr)-\varPhi e(t)+I_{k}(t)\bigr], \end{aligned}$$
(19)

with \(r=2\),

$$\begin{aligned} &f_{1}\bigl(u_{1}(t)\bigr)=g_{1} \bigl(u_{1}(t)\bigr)=\frac{1}{1+e^{-u_{1}(t)}}, \\ &f_{2}\bigl(u_{2}(t)\bigr)=g_{2} \bigl(u_{2}(t)\bigr)=\frac{1}{1+e^{-u_{2}(t)}}. \end{aligned}$$

Correspondingly,

$$\begin{aligned} &u(t)= \begin{pmatrix} u_{1} (t)\\ u_{2} (t) \end{pmatrix} , \qquad v(t)= \begin{pmatrix} v_{1} (t)\\ v_{2} (t) \end{pmatrix} , \\ &A_{1}=B_{1}= \begin{pmatrix} -1 & 0.4 \\ 0 & -0.1 \end{pmatrix} , \qquad C_{1}= \begin{pmatrix} -4.5 & 0 \\ 0 & -0.5 \end{pmatrix} , \\ &A_{2}=B_{2}= \begin{pmatrix} 1 & -0.8 \\ 0.4 & 0.5 \end{pmatrix} ,\qquad C_{2}= \begin{pmatrix} -2.1 & 0 \\ 0 & -2.8 \end{pmatrix} , \\ &\varPhi= \begin{pmatrix} 11 & 0 \\ 0 & 11 \end{pmatrix} ,\qquad I_{1}(t)= \begin{pmatrix} \sin2t \\ -\cos t \end{pmatrix} , \qquad I_{2}(t)= \begin{pmatrix} \sin t \\ \cos t \end{pmatrix} . \end{aligned}$$

Taking \(h_{1}(\omega)=\sin^{2}(10 \tanh\frac{\pi(t+2)}{2})\), \(h_{2}(\omega )=\cos^{2}(10 \tanh\frac{\pi(t+2)}{2})\). Select \(\tau=1\), \(\alpha =0.9\), and the initial conditions of \(u(t)\) and \(v(t)\)

$$\begin{aligned} x(0)= \begin{pmatrix} -4.2\\ 1.2 \end{pmatrix} , \qquad y(0)= \begin{pmatrix} 2.1\\ -1.7 \end{pmatrix} . \end{aligned}$$

Based on these parameters, we obtain the solution of the linear matrix inequality (10) by using Matlab LMI toolbox:

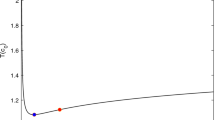
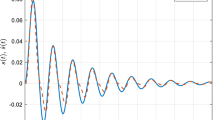
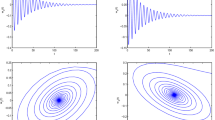
$$\begin{aligned} &P= \begin{pmatrix} 0.1490 & 0.0001 \\ 0.0001 & 0.1490 \end{pmatrix} , \qquad Q= \begin{pmatrix} 1.0569 & 0.003 \\ 0.003 & 1.0569 \end{pmatrix} , \\ &R= \begin{pmatrix} 1.0986 & 0.0003 \\ 0.0003 & 1.1114 \end{pmatrix} , \qquad S= \begin{pmatrix} 0.9998 & 0.0009 \\ 0.009 & 1.0384 \end{pmatrix} , \\ &V= \begin{pmatrix} 0.1206 & 0 \\ 0 & 0.1206 \end{pmatrix} . \end{aligned}$$

Obviously, P, Q, R, S, and V are positive definite matrices. The simulation results for the synchronization of our drive-master systems are shown in Figs. 1–3. In this numerical example, we employed the first type of Lagrange interpolation approximation to draw the image of the fractional-order Caputo derivative.

Figure 1
figure 1

Dynamics of states \(u_{1}(t)\) and \(v_{1}(t)\)

Full size image
Figure 2
figure 2

Dynamics of states \(u_{2}(t)\) and \(v_{2}(t)\)

Full size image
Figure 3
figure 3

Dynamics of states \(e_{1}(t)\) and \(e_{2}(t)\)

Full size image