1 Introduction

In recent years, many approximation-based adaptive fuzzy or neural backstepping controllers have been developed for uncertain nonlinear systems; see [1–19]. Among them, to eliminate the problem of ‘explosion of complexity’ inherent in the existing method, in [13] a control design strategy was developed for a class of nonlinear systems in strict-feedback form with arbitrary uncertainty. To deal with the state unmeasured problem, a novel control scheme was introduced in [18]. To address the control problem of nonsmooth hysteresis nonlinearity in the actuator, adaptive neural controllers were constructed for nonlinear strict-feedback systems with unknown hysteresis in [19]. It should be noted that the control schemes mentioned are under the presupposition that the systems have a nonstrict-feedback structure.

In the nonlinear systems without strict-feedback structure, the unknown nonlinear functions involve all the state variables, so they cannot be approximated with current states. To deal with such a structural restriction, in [20] a variable separation method was proposed. The control scheme in [20] assured that the tracking performance is achieved as time variable goes to infinity. Besides the proposed control scheme, many efforts have been made in relaxing such a restriction of system structure; see [21–25]. In practical application, the actuator component is usually employed to execute control actions on the plant. However, the actuation mechanism may suffer from failures, which results in the actuator losses of partial or total effectiveness. To prevent the emergence of performance deterioration and instability of the closed-loop system caused by actuator faults, accommodating actuator failures should be taken into account in the control design.

In recent years, many control schemes have been proposed to accommodate actuator failures; see, for example, [26–32]. By applying backstepping technique for the linear systems, a systematic actuator failure compensation control was presented in [26]. Then, in [27] the proposed control method was extended to nonlinear systems with actuator failures; in [28] the problem of accommodating actuator failures was investigated for a lass of uncertain nonlinear systems with hysteresis input as a follow-up extension. In practice, the failure pattern in an actuator may change repeatedly, which makes failure parameters suffer from an infinite number of jumps. Consequently, the considered Lyapunov function would experience infinite number of jumps. In [29], this problem was addressed by applying a new tuning function under the frame of adaptive control. However, the proposed control strategy can only apply to the strict-feedback systems.

Motivated by the aforementioned researches, in this paper, we focus on the problem of adaptive compensation for an infinite number of actuator failures in neural tracking control for a class of nonstrict-feedback systems. The main contributions in this paper can be summarized as follows.

  1. (1)

    The control scheme in this paper relaxes the restriction of system structure so that a better approach is proposed to deal with the problem of compensation for an infinite number of actuator failures, which is more meaningful in practical application in comparison with [29].

  2. (2)

    In this paper, combining neural networks and a new piecewise Lyapunov function analysis, we establish an adaptive control scheme for a class of uncertain nonlinear systems with a nonstrict-feedback structure.

The remainder of the paper is organized as follows. In the next section, the problem description and preliminaries are presented. Section 3 shows the major result. In Section 4, the simulation result expounds the validity of the proposed control scheme. Finally, we give a simple summary.

2 Preliminaries and problem description

2.1 A. System description

We consider the following nonstrict-feedback system form:

$$\begin{aligned}& \dot{x}_{i}=x_{i+1}+f_{i}(x), \quad1\leq i\leq n-1, \\& \dot{x}_{n}=\sum_{j=1}^{m}b_{j}{ \sigma}_{j}(x)u_{j}+f_{n}(x), \\& y=x_{1} , \end{aligned}$$

where \(x=[x_{1},x_{2},\ldots,x_{n}]^{T}\) are the state vectors, \(f_{i}\) (\(i=1,2,\ldots,n\)) are unknown smooth nonlinear functions, \(u_{j}\in R\) for \(j=1,\ldots,m\) is the output of the jth actuator, y denotes the system output, \(b_{j}\) (\(j=1,\ldots,m\)) are unknown control coefficients, and \({\sigma}_{j}(x)\) (\(j=1,\ldots,m\)) are known continuous functions.

For simplicity, the internal dynamics in actuators can be negligible. Let \(\check{u}_{j}\) (\(j = 1,\ldots,m\)) be jth actuator input, and then the normal actuator is described as \(u_{j}=\check{u}_{j}\). However, in practical applications, the actuation components may suffer from failures or faults. The actuator failure model in this paper is given as follows:

$$\begin{aligned} &u_{j}=\kappa_{j,k}(t)\check{u}_{j}+u_{fj,k}(t), \end{aligned}$$
(1)
$$\begin{aligned} &\kappa_{j,k}(t)u_{fj,k}(t)=0,\quad j=1,\ldots,m, \end{aligned}$$
(2)

where \(t \in[t_{k}, t_{k+1})\) for \(k = 0, 1, \ldots\) , and \(t_{k}\) denotes the unknown failure time instant at which the failure parameter jumps occur. In (2)-(3), \(0 \leq\kappa _{j,k}(t)\leq1\) is called the efficiency factor, and \(u_{fj,k}(t)\) is the stuck value. Note that the proposed model covers two classes of typical actuator failures, that is, partial loss of effectiveness (PLOE) faults (\(0 < \kappa_{j,k} < 1\)) and total loss of effectiveness (TLOE) faults (\(\kappa_{j,k} = 0\)), as detailed in [33].

Remark 1

The unknown time-varying value \(u_{fj,k}(t)\) can be linearly parameterized as \(u_{fj,k}(t) = u_{j0,k}+\Sigma_{i=1}^{q_{j}}\zeta _{ji,k}\phi_{ji}(t)\) with known functions \(\phi_{ji}(t)\) and unknown constants \(u_{j0,k}\) and \(\zeta_{ji,k}\).

Control objective: design the control input \(\check{u}_{j}\) to compensate for the actuator failures modeled as (2)-(3) such that all the closed-loop signals are bounded and the system output y tracks the given reference signal \(y_{d}\) with a tracking error converging to a residual around zero. The following assumptions are general in the literature on the adaptive actuator failure compensation control.

Assumption 1

The number of failed actuators undergoing TLOE faults simultaneously is allowed to be at most \({m-1}\), and achieving control objective with the remaining actuators is still possible.

Assumption 2

The reference signal \(y_{d}(t)\) and its first nth-order time derivatives \(y_{d}(t)\) (\(i = 1, \ldots, n\)) are known, smooth, and bounded.

Assumption 3

\(\operatorname{sign}(b_{j})\) are known for \(j = 1, 2,\ldots,m\).

Assumption 4

The conditions \({\sigma}_{j}(\cdot)\neq0\), \(0 < b_{0} \leq \vert b_{j}\vert \leq b_{M}\), and \(\vert u_{fj,k}(t)\vert \leq u_{fM}\) are satisfied. In addition, for the PLOE faults, \(0 < \kappa_{0} \leq \kappa_{j,k}(t) < 1\). Note that \(b_{0}\), \(b_{M}\), \(u_{fM}\), and \(\kappa_{0}\) are known constants.

Assumption 5

The failure parameters \(\kappa_{j,k}(t)\) and \(u_{fj,k}(t)\) are smooth and continuous over \([t_{k}, t_{k+1})\). Moreover, their change rates are bounded, that is, \(\sup_{t\in[t_{k},t_{k+1})} \vert \dot{\kappa}_{j,k}(t)\vert \leq d_{1}\) and \(\sup_{t\in[t_{k},t_{k+1})} \vert \dot{u}_{fj,k}(t)\vert \leq d_{2}\), where \(d_{1}\) and \(d_{2}\) denote two unknown positive constants.

2.2 B. RBF neural networks

In the following design, the radial basis function (RBF) neural networks will be utilized to approximate an unknown function \(f(\zeta)\) defined on some compact set Ξ. For sufficiently large nodes number κ, the RBF neural networks \(\xi^{*T}\Phi(\zeta)\) can approximate any continuous function \(f(\zeta)\) over a compact set \(\Xi\subset R^{q}\) to arbitrary accuracy \(\varepsilon>0\) as follows:

$$\begin{aligned} f(\zeta)={\xi^{*}}^{T}\varphi(\zeta)+\epsilon(\zeta), \quad \forall \zeta\in\Xi\subset R^{q}, \end{aligned}$$

where the approximation error \(\epsilon(\zeta)\) satisfies \(\vert \epsilon(\zeta)\vert \leq\varepsilon\), \(\varphi (\zeta)=[ \varphi_{1}(\zeta), \varphi_{2}(\zeta), \dots, \varphi_{\kappa}( \zeta)]^{T}\) is the basis function vector, and \(\xi^{*}=[\xi_{1}, \xi _{2}, \dots, \xi_{\kappa}]^{T} \in R^{\kappa}\) is defined as

$$\begin{aligned} \xi^{*}:=\arg\min_{\xi\in R^{\kappa}}\Bigl\{ \sup _{\zeta\in\Xi}\bigl\vert f( \zeta)-\xi^{T}\varphi(\zeta) \bigr\vert \Bigr\} , \end{aligned}$$

where \(\xi\in R^{\kappa}\) denotes the weight vector. In this research, the following Gaussian basis functions \(\phi_{i}(\zeta)\) will be used:

$$ \varphi_{i}(\zeta)=\exp\biggl[-\frac{(\zeta-\iota _{i})^{T}(\zeta-\iota _{i})}{\omega_{i}^{2}} \biggr],\quad i=1, 2, \ldots, \kappa, $$
(3)

where \(\iota_{i}=[\iota_{i1}, \iota_{i2}, \ldots, \iota_{iq}]^{T}\) denotes the center of the receptive field, and \(\omega_{i}\) represents the width of the Gaussian function.

Lemma 1

([34])

Let \(f(\chi)\) be a continuous function defined on a compact set Ω. Then, for every \(\varepsilon>0\), there exists a neural network \(\theta^{T}\Re( \chi)\) such that

$$\begin{aligned}& \sup_{\chi\in\Omega}\bigl\vert f(\chi)- \theta^{T}\Re (\chi)\bigr\vert \leq\varepsilon . \end{aligned}$$
(4)

Lemma 2

([35])

For any \(\omega\in{R}\) and \(\varepsilon>0\), the following holds:

$$\begin{aligned} 0\leq \vert \omega \vert -{\omega}\tanh\biggl(\frac {\omega}{\varepsilon} \biggr)\leq \delta\varepsilon \end{aligned}$$
(5)

with \(\delta=0.2785\).

3 Adaptive tracking control design and stability analysis

In this section, based on a backstepping technique and neural networks, we design an adaptive actuator failure compensation control scheme. The control goal of this manuscript is to establish an adaptive controller such that the system output y follows a desired reference signal \(y_{d}\).

3.1 A. Adaptive tracking control design

Before implementing the design, a set of uncertain constants is defined as

$$\begin{aligned}& W_{i}=M_{i}\Vert \theta_{i} \Vert _{2}^{2}=M_{i}\theta_{i}^{T} \theta_{i}, \quad i=1, \ldots,n, \end{aligned}$$
(6)

where \(\theta_{i}=[\theta_{i,1},\ldots,\theta_{i,N_{i}}]\) and \(N_{i}\) are the weight vector and the number of neurons in ith hidden layer, respectively. The operator \(\Vert \cdot \Vert _{2}\) represents the Euclidean norm of a column vector. From the definition we know that \(W_{i}\) is an unknown constant. The adaptive parameter \(\hat{W}_{i}\) is utilized to estimate \(W_{i}\), and the estimated error is \(\tilde{W} _{i} = W_{i}-\hat{W}_{i}\). The computation in adaptation mechanism utilized in the literature can be reduced from \(\Sigma_{i=1}^{n}M_{i}\) to n.

The coordinate transformations are defined as follows:

$$ \begin{gathered} {z}_{1}={x}_{1}-{y}_{d}, \\ {z}_{i}={x}_{i}-\alpha_{i-1}-y_{d}^{(i-1)}, \quad i=2,\ldots,n, \end{gathered} $$
(7)

where \(\alpha_{i-1}\) is an intermediate controller.

Denote

$$\begin{aligned} \check{u}_{j}=\frac{\operatorname{sign}(b_{j})}{{\sigma }_{j}}\hat{ \tau}^{T}v, \end{aligned}$$
(8)

where \(\hat{\tau}=[\hat{\tau}_{1},\hat{\tau}_{2,1},\ldots, \hat{\tau}_{2,m}]\) is the estimate of \({\tau}\in R^{1+m}\) designed latter, and \(v=[\alpha_{n}+y_{d}^{(n)},{\sigma}_{1},\ldots,{\sigma }_{m}]\).

To ensure the boundedness of the jumping size of the Lyapunov function at failure instants, we design the adaptation laws for updating parameter estimators with projection operation.

The adaptive laws are selected as

$$\begin{aligned}& \dot{\hat{W_{i}}}=\sum_{i=1}^{n} \frac {l}{2a_{i}}z_{i}^{2}-{\wp} _{1} \hat{W}_{i}, \quad i=1,2,\ldots,n, \end{aligned}$$
(9)
$$\begin{aligned}& \dot{\hat{\varepsilon}}=\sum_{i=1}^{n}hz_{i} \tanh\frac{z_{i}}{ \varsigma}-{\wp}_{2}\hat{\varepsilon}, \end{aligned}$$
(10)
$$\begin{aligned}& \dot{\hat{\tau}}=\operatorname{Proj}(-\Gamma_{\tau}vz_{n}), \quad \hat{\tau}(0)\in \Omega_{\tau}, \end{aligned}$$
(11)

where h, \({\wp}_{1}\), and \({\wp}_{2}\) are positive design constants, and \(\Gamma_{\tau} \in R^{(1+m)(1+m)}\) is chosen to be symmetric and positive definite (for convenience, we can select \(\Gamma_{\tau}=diag \{r_{1},r_{2},\dots,r_{1+m}\}\) with positive constants \(r_{i}\)), \(\operatorname{Proj}(\cdot)\) denotes the projection operator, and \(\Omega_{\tau}\) is a known convex compact set given by

$$\begin{aligned} \Omega_{\tau}=\biggl\{ (\gamma_{1}, \gamma_{2,1},\ldots,\gamma _{2,m})\Big| \frac{1}{mb _{M}} \leq \frac{1}{b_{0}\kappa_{0}} \mbox{ and }\biggl\vert \gamma_{2,j}\leq \frac{b _{M}u_{fM}}{b_{0}\kappa_{0}}\biggr\vert , j=1,\ldots,m \biggr\} ; \end{aligned}$$
(12)

\(\alpha_{i-1}\) is the virtual controller designed as

$$\begin{aligned} \alpha_{i}=-{\lambda}_{i}{z}_{i}- \frac {1}{2a_{i}^{2}}z_{i}\hat{W} _{i}-\hat{\varepsilon}\tanh \frac{z_{i}}{\varsigma}, \end{aligned}$$
(13)

where \(\lambda_{i}\), \(a_{i}\), and l are positive design constants.

With the developed projection-based tuning function approach, we further propose new piecewise Lyapunov function analysis to establish the closed-loop system stability.

3.2 B. Stability analysis

Theorem 1

Consider the closed-loop adaptive system consisting of nonlinear plant (1) with actuator failures (2)-(3) and the proposed control scheme (9)-(14). Moreover, the nonstrict-feedback nonlinear system (1) satisfies Assumptions  1-4. Then:

  1. (1)

    All the signals of the closed-loop system are bounded;

  2. (2)

    The tracking error converges to a small neighborhood of zero.

Proof

Consider the following Lyapunov function candidate:

$$\begin{aligned} \bar{V}_{k} =&\frac{1}{2}\sum _{i=1}^{n}z_{i}^{2}+ \frac{1}{2l} \tilde{W}^{2}+\frac{1}{2h}\tilde{ \varepsilon}^{2}+\frac{1}{2}\sum_{j=1}^{m} \vert b_{j}\vert \kappa_{j,k}(t)\tilde{\tau }^{T}\Gamma_{\tau}^{-1} \tilde{\tau}, \end{aligned}$$
(14)

where \(\tilde{\varepsilon}_{i}\) is used to estimate \(\varepsilon_{i}\), \(\tilde{\varepsilon}_{i} = \varepsilon_{i}-\hat{\varepsilon}_{i}\) refers to the estimated error, and \(\tilde{\tau}_{i} = \tau_{i}- \hat{\tau}_{i}\) is the estimated error of \(\tau_{i}\). We define \(\tau(t)\in R^{1+m}\) by

$$\begin{aligned}& \tau_{1}(t)=\frac{1}{\sum_{j=1}^{m}\vert b_{j}\vert \kappa_{j,k}(t)}, \end{aligned}$$
(15)
$$\begin{aligned}& \tau_{2,j}(t)=-\frac{b_{j}u_{fj,k}(t)}{\sum_{j=1}^{m}\vert b_{j}\vert \kappa _{j,k}(t)}, \end{aligned}$$
(16)

where \(j=1,\ldots,m\).

Note that all \(\Re_{1}\), \(\Re_{2} \in\Omega_{\tau}\) satisfy

$$\begin{aligned} \Vert \Re_{1}-\Re_{2}\Vert \leq\sqrt{\biggl( \frac{1}{b_{0}\kappa _{0}}-\frac{1}{mb _{M}}\biggr)^{2}+\frac{4mb_{m}^{2}u_{fM}^{2}}{b_{0}^{2}\kappa_{0}^{2}}}= \hbar. \end{aligned}$$

From the related properties of a projection operator in [17] we can derive that \(\hat{\tau}(t)\in\Omega_{\tau}\). We get

$$\begin{aligned} \bigl\Vert \tilde{\tau}(t)\bigr\Vert =\bigl\Vert \tau (t)- \hat{\tau}(t)\bigr\Vert \leq\hbar. \end{aligned}$$
(17)

The time derivative of V̄ is

$$\begin{aligned} \dot{\bar{V}}_{k} =&z_{1}(z_{2}+ \alpha_{1}+\varphi_{1})+\sum_{i=2} ^{n-1}z_{i}({z}_{i+1}+\alpha_{i}+ \varphi_{i}-\dot{\alpha}_{i-1}) \\ &{}+\dot{\phi}+z_{n}\Biggl(\sum_{j=1}^{m} \vert b_{j}\vert \kappa _{j,k}(t)\hat{\tau} ^{T}v+\sum_{j=1}^{m}b_{j}{ \sigma}_{j}u_{fj,k}(t)+\varphi_{n}- \dot{ \alpha}_{n-1}-y_{d}^{(n)}\Biggr), \end{aligned}$$
(18)

where

$$\begin{aligned} \phi=\frac{1}{2l}\tilde{W}^{2}+\frac{1}{2h}\tilde{ \varepsilon}^{2}+ \frac{1}{2}\sum_{j=1}^{m} \vert b_{j}\vert \kappa _{j,k}(t)\tilde{ \tau}^{T} \Gamma_{\tau}^{-1}\tilde{\tau}. \end{aligned}$$

It follows that

$$\begin{aligned} \dot{\phi} =&-\frac{1}{l}\tilde{W}\dot{\hat{W}}- \frac{1}{h} \tilde{\varepsilon}\dot{\hat{\varepsilon}}-\sum _{j=1}^{m}\vert b_{j}\vert \kappa_{j,k}(t)\tilde{\tau}^{T}\Gamma^{-1}_{\tau} \dot{\hat{\tau}} \\ & {}+\sum_{j=1}^{m}\frac{\vert b_{j}\vert \dot{\kappa_{j,k}}(t)}{2} \tilde{\tau}^{T}\Gamma^{-1}_{\tau}\tilde{\tau}+\sum _{j=1}^{m}\vert b _{j}\vert \kappa_{j,k}(t)\tilde{\tau}^{T}\Gamma^{-1}_{\tau} \dot {\tau}. \end{aligned}$$
(19)

Define unknown functions as

$$\begin{aligned}& \begin{aligned}[b] &P_{i}\bigl(x,\hat{W}, \hat{\varepsilon},y_{d},\ldots,y_{d}^{(i-1)}\bigr) \\ &\quad =\frac{\partial\alpha_{i-1}}{\partial\hat{W}}\sum_{j=1}^{i-1} \frac{l}{2a _{j}^{2}}z_{j}^{2}-z_{i} \frac{l}{2a_{i}^{2}}\sum_{j=2}^{i}\biggl\vert z_{j}\frac{ \partial\alpha_{j-1}}{\partial\hat{W}}\biggr\vert -\frac{\partial \alpha_{i-1}}{ \partial\hat{W}}{ \wp}_{1}\hat{W} \\ &\quad\quad{} +\frac{\partial\alpha_{i-1}}{\partial\hat{\varepsilon}}\sum_{j=1} ^{i-1}hz_{j}\tanh\frac{z_{j}}{\varsigma}+h\tanh\frac{z_{i}}{\varsigma } \sum_{j=2}^{i}z_{j} \frac{\partial\alpha_{j-1}}{\partial \hat{\varepsilon}}-\frac{\partial\alpha_{i-1}}{\partial \hat{\varepsilon}}{\wp}_{2}\hat{\varepsilon}, \end{aligned} \end{aligned}$$
(20)
$$\begin{aligned}& f_{1}(x)=\varphi_{1}(x), \end{aligned}$$
(21)
$$\begin{aligned}& f_{i}\bigl(x,\hat{W},\hat{\varepsilon},y_{d}, \ldots,y_{d}^{(i-1)}\bigr)=z _{i-1}+ \varphi_{i}-\sum_{j=1}^{i-1} \frac{\partial\alpha_{i-1}}{ \partial{x_{j}}}(x_{j+1}+\varphi_{j}) \end{aligned}$$
(22)
$$\begin{aligned}& \hphantom{f_{i}\bigl(x,\hat{W},\hat{\varepsilon},y_{d}, \ldots,y_{d}^{(i-1)}\bigr)}\quad{}-\sum_{j=1}^{i-1} \frac{\partial\alpha_{i-1}}{\partial{y_{d}}^{(j-1)}}y_{d}^{(j)}-P _{i}\bigl(x, \hat{W},\hat{\varepsilon},y_{d},\ldots,y_{d}^{(i-1)} \bigr), \\& \hphantom{f_{i}\bigl(x,\hat{W},\hat{\varepsilon},y_{d}, \ldots,y_{d}^{(i-1)}\bigr)}\quad i= 2, \ldots,n. \end{aligned}$$
(23)

From (9)-(10) and (20)-(22) we have

$$\begin{aligned} \sum_{i=2}^{n}z_{i} \biggl(P_{i}-\frac{\partial\alpha _{i-1}}{\partial \hat{W}}\dot{\hat{W}}-\frac{\partial\alpha_{i-1}}{\partial \hat{\varepsilon}}\dot{ \hat{\varepsilon}}\biggr) \leq0. \end{aligned}$$
(24)

Moreover, according to (8) and (17), we have

$$\begin{aligned} \sum_{j=1}^{m}\vert b_{j}\vert \kappa _{j,k}(t)\tau^{T}v+\sum _{j=1}^{m}b_{j} { \sigma}_{j}u_{fj,k}(t)-\alpha_{n}-y_{d}^{(n)}=0. \end{aligned}$$
(25)

It follows that

$$\begin{aligned} \dot{\bar{V}}_{k}(t)\leq\sum _{i=1}^{n}(\alpha _{i}+f_{i})- \sum_{j=1} ^{m}\vert b_{j} \vert \kappa_{j,k}(t)\tilde{\tau }^{T}vz_{n}+\dot{ \phi}. \end{aligned}$$
(26)

Since \({f}_{i}(x)\) contain the unknown functions \(\varphi_{i}\), they cannot be implemented in practice. According to Lemma 1, for any given constant \(\varepsilon_{i}>0\), there exists a neural network \(\theta^{T}_{i}\Re_{i}\) such that

$$\begin{aligned} \vert z_{i}\vert f_{i}(x) \leq \frac {1}{2a_{i}^{2}}z_{i}^{2}\Vert \theta_{i} \Vert ^{2} \Re_{i}^{T}\Re_{i}+ \frac{1}{2}a_{i}^{2}+\vert z_{i}\vert \varepsilon. \end{aligned}$$
(27)

Combining with the condition \(\Re_{i}^{T}\Re_{i} \leq M_{i}\) and Lemma 2, we have

$$\begin{aligned} \vert z_{i}\vert f_{i}(x) \leq \frac {1}{2a_{i}^{2}}z_{i}^{2}W+\frac{1}{2}a_{i} ^{2}+z_{i}\varepsilon\tanh\frac{z_{i}}{\varsigma}+0.2785\varsigma \varepsilon, \end{aligned}$$
(28)

where

$$\begin{aligned}& W=\max\bigl\{ \Vert \theta_{1}\Vert ^{2} \Re _{1}^{T}\Re_{1},\ldots, \Vert \theta_{i} \Vert ^{2}\Re_{i}^{T} \Re_{i}\bigr\} , \end{aligned}$$
(29)
$$\begin{aligned}& \varepsilon=\max\{\varepsilon_{1},\ldots,\varepsilon_{n} \}. \end{aligned}$$
(30)

Substituting (27) and (11) into (25), we have

$$\begin{aligned} \dot{\bar{{V}}}_{k} \leq&\sum _{i=1}^{n}\lambda _{i}z_{i}^{2}+ \sum_{i=1}^{n}\frac{1}{2a_{i}^{2}}z_{i}^{2} \tilde{W}+\sum_{i=1}^{n} \frac{1}{2}a_{i}^{2}+\sum _{i=1}^{n}z_{i}\tilde{\varepsilon}\tanh \frac{z _{i}}{\varsigma}+\sum_{i=1}^{n}0.2785 \varsigma\varepsilon \\ & {}-\sum_{j=1}^{m}\vert b_{j}\vert \kappa_{j,k}(t)\tilde {\tau}^{T}vz _{n}+\dot{\phi}. \end{aligned}$$
(31)

By Assumption 5 and by (17) and (18) we get

$$\begin{aligned}& \Vert \dot{\tau}_{1}\Vert \leq \frac{ mb_{M}d_{1}}{b_{0}^{2}\kappa_{0}^{2}}, \end{aligned}$$
(32)
$$\begin{aligned}& \Vert \dot{\tau}_{2,j}\Vert \leq\frac {mb_{M}^{2}d_{2}+mb_{M}^{2}u_{fM}d _{1}}{b_{0}^{2}\kappa_{0}^{2}},\quad j=1,\ldots,m. \end{aligned}$$
(33)

It follows that

$$\begin{aligned} \bigl\Vert \dot{\tau}(t)\bigr\Vert \leq\frac {mb_{M}d_{1}}{b_{0}^{2}\kappa_{0}^{2}}+ \frac{mb _{M}^{2}d_{2}+mb_{M}^{2}u_{fM}d_{1}}{b_{0}^{2}\kappa_{0}^{2}}=\varpi . \end{aligned}$$
(34)

According to (9), (10), and (12), we have

$$\begin{aligned} \dot{\bar{V}}_{k} \leq&\sum _{i=1}^{n}\lambda _{i}z_{i}^{2}- \frac{\tau _{1}}{2l}\tilde{W}^{2}-\frac{\tau_{2}}{2h}\tilde{ \varepsilon}^{2}+\frac{mb _{M}}{2}\tau_{M}^{2}+ \frac{\tau_{1}}{2l}W^{2}+\frac{\tau_{2}}{2h} \varepsilon^{2}+ \sum_{i=1}^{n}\frac{1}{2}a_{i}^{2}(0.2785 \varsigma \varepsilon)+\varpi_{0} \\ & {}-\sum_{j=1}^{m}\frac{\vert b_{j}\vert \kappa _{j,k}(t)}{2\lambda_{\max}( \Gamma_{\tau}^{-1})} \tilde{\tau}^{T}\Gamma_{\tau}^{-1} \tilde{\tau}, \end{aligned}$$
(35)

where

$$\begin{aligned} \varpi_{0}=\frac{mb_{M}d_{1}}{2}\hbar^{2}\bigl\Vert \Gamma _{\tau}^{-1}\bigr\Vert _{F}+mb _{M}\hbar\bigl\Vert \Gamma_{\tau}^{-1}\bigr\Vert _{F}\varpi. \end{aligned}$$
(36)

Then, it follows that

$$\begin{aligned} \dot{\bar{V}}_{k}(t) \leq-A\bar{V}_{k}+B, \end{aligned}$$
(37)

where

$$\begin{aligned}& A=\min\biggl\{ 2\lambda_{i}, \tau_{1}, \tau_{2}, \frac{1}{\lambda _{\max}( \Gamma_{\tau}^{-1})}\biggr\} , \end{aligned}$$
(38)
$$\begin{aligned}& \begin{aligned}[b] B&=\frac{\tau_{1}}{2l}W^{2}+ \frac{\tau_{2}}{2h}\varepsilon^{2}+\sum_{i=1}^{n} \frac{1}{2}a_{i}^{2}(0.2785\varsigma\varepsilon)+ \frac{mb _{M}}{2}\tau_{M}^{2}+\varpi_{0}t_{k}, \\ &\quad t_{k} \leq t \leq t_{k+1}, k=0,1, \ldots. \end{aligned} \end{aligned}$$
(39)

To establish the closed-loop system stability for all the time under the case of actuator failures or faults, we need to consider the overall Lyapunov function defined as

$$\begin{aligned} V(t)= \bar{V}(t)_{k}, \quad t \in[t_{k},t_{k+1}), k=0,1,\ldots, \end{aligned}$$
(40)

where \(t_{0}=0\) is the initial time instant. Note that \(V(t)\) is not a continuous function, and it experiences a sudden jump at each failure instant \(t_{k+1}\) (\(k=0,1,\ldots\)). The jumping size at instant \(t_{k}\) is computed as

$$\begin{aligned}& V\bigl(t_{k+1}^{+}\bigr)-V \bigl(t_{k+1}^{-}\bigr) \\& \quad=\sum_{j=1}^{m}\frac{\vert b_{j}\vert \kappa _{j,k+1}(t_{k+1}^{+})}{2} \tilde{\tau}^{T}\bigl(t_{k+1}^{+}\bigr) \Gamma_{\tau}^{-1}\tilde{\tau}\bigl(t_{k+1} ^{+}\bigr) \\& \quad\quad {}-\sum_{j=1}^{m} \frac{\vert b_{j}\vert \kappa _{j,k+1}(t_{k+1}^{-})}{2} \tilde{\tau}^{T}\bigl(t_{k+1}^{-} \bigr)\Gamma_{\tau}^{-1}\tilde{\tau}\bigl(t_{k+1} ^{-}\bigr) \\& \quad \leq\frac{mb_{M}}{2}\bigl\Vert \Gamma_{\tau}^{-1} \bigr\Vert _{F}\hbar^{2}=\Lambda. \end{aligned}$$
(41)

Let \(H(t)=e^{at}V(t)\). Then it follows that

$$\begin{aligned} \dot{H}=Ae^{at}V(t)+e^{at}\dot{V}(t)\leq Be^{At}. \end{aligned}$$
(42)

Integrating both sides of (42) over \([t_{k},t_{k+1})\), we have

$$\begin{aligned} H\bigl(t_{k+1}^{-}\bigr)\leq H \bigl(t_{k+1}^{+}\bigr)+ \int ^{t_{k+1}}_{t_{k}}Be^{At}\,dt. \end{aligned}$$
(43)

From (41)-(43) we have

$$\begin{aligned} H\bigl(t_{k+1}^{+}\bigr) \leq H \bigl(t_{k}^{+}\bigr)+ \int ^{t_{k+1}}_{t_{k}}Be^{At}\,dt+e ^{at_{k+1}}\Lambda. \end{aligned}$$
(44)

We denote by \(\aleph(t, T)\) the number of jumps of the overall Lyapunov \(V(t)\) during \((t,T)\) for \(t \geq0\). Let \(T^{\flat} = \min\{t_{k+1} - t_{k}\}\), \(k = 0, 1,\ldots\) . Then it follows that

$$\begin{aligned}& \begin{aligned}[b] H\bigl(T^{-}\bigr)&=H \bigl[t^{+}_{\aleph(0,T)}\bigr]+ \int^{T}_{t_{\aleph(0,T)}}Be^{At}\,dt \Lambda \\ &\leq V(0)+ \int^{T}_{0}Be^{At}\,dt+e^{AT} \sum_{k=1}^{\aleph(0,T)}e ^{a(t_{k}-T)}\Lambda, \end{aligned} \end{aligned}$$
(45)
$$\begin{aligned}& \begin{aligned} &\aleph(t_{k}, T)T^{\flat} \leq T-t_{k}, \quad k = 1, \ldots,\aleph(0, T) \\ &t_{k}-T \leq-\aleph(t_{k}, T)T^{\flat}. \end{aligned} \end{aligned}$$
(46)

Then we have

$$\begin{aligned} e^{AT}\sum_{k=1}^{\aleph(0,T)}e^{a(t_{k}-T)} \Lambda \leq& e^{AT} \sum_{k=1}^{\aleph(0,T)}e^{-a\aleph(t_{k},T)T^{\flat}} \Lambda \\ =&\frac{1-e^{-aT^{\flat}\aleph(0,T)}}{1-e^{-aT^{\flat}}}e^{aT} \Lambda. \end{aligned}$$
(47)

It follows that

$$\begin{aligned}& V\bigl(T^{-}\bigr) \leq\biggl(V(0)- \frac{B}{A}-\frac{\Lambda }{1-e^{-aT^{\flat}}}\biggr)e ^{-aT}+\biggl( \frac{B}{A}+\frac{\Lambda}{1-e^{-aT^{\flat}}}\biggr), \quad \forall T > 0. \end{aligned}$$
(48)

Then all closed-loop signals are bounded. Note that \(\Sigma_{i=1}^{n} \leq2V(t)\), and let \(T \rightarrow\infty\). The bound of the tracking error can be derived as

$$\begin{aligned} \lim_{t\rightarrow\infty}\bigl\Vert z(t)\bigr\Vert \leq \sqrt{\frac{2B}{A}+\frac{2 \Lambda}{1-e^{-AT^{\flat}}}}. \end{aligned}$$
(49)

 □

Remark 2

Inequality (28) makes a vital contribution to the backstepping design because it builds the relation between \(x_{i}\) and \(z_{i}\), which makes a backstepping-based design procedure viable.

Remark 3

The adaptive parameters \(\hat{W}_{i}\), ε̂, τ̂ are utilized to estimate \(W_{i}\), ε, τ, respectively. \(\tilde{W}_{i} = W _{i}-\hat{W}_{i}\), \(\tilde{\varepsilon}=\epsilon-\hat{\varepsilon}\), and \(\tilde{\tau}=\tau-\hat{\tau}\) denote the estimated errors. Note that the failure parameter \(\kappa_{j,k}\) is allowed to be time varying during each time interval \([t_{k}, t_{k+1})\) for \(k = 0,1,\ldots\) and \(b_{j}\) (\(j=1,\ldots,m\)) are unknown control coefficients. The instability cannot be ensured when \([t_{k}, t_{k+1})\) and \(b_{j}\) are not contained in the Lyapunov function.

Remark 4

The failure-related parameters τ contained in the Lyapunov function (15) will undergo a sudden jump at unknown time instant \(t_{k}\), and it follows that decreasing of the Lyapunov function, shown as in (38), is only valid at the time interval \([t_{k}, t_{k+1})\) during which the Lyapunov function \(\bar{V}_{k}(t)\) is differentiable. To establish the closed-loop system stability under the case of actuator failures or faults, we consider the overall Lyapunov function defined in (41).

4 Simulation example

In this section, we use two examples to expound our design scheme and testify the results obtained.

4.1 A. Example 1

The nonlinear system is given as

$$ \begin{gathered} \dot{x}_{1}=x_{2}+2x_{1}^{2}, \\ \dot{x}_{2}=x_{1}x_{2}+2\frac{1-e^{-x_{2}}}{1+e^{-x_{2}}}+b_{1}u _{1}+b_{2}u_{2}, \\ y=x_{1}, \\ \dot{\xi}=Z(\xi,x_{1},x_{2}), \\ Z(\xi,x_{1},x_{2})=-\xi+x_{2}+ \tan^{-1}x_{2} \\ \hphantom{Z(\xi,x_{1},x_{2})=} {}+\frac{2+x_{2}^{2}}{1+x_{2}^{2}}\biggl[x_{1}x_{2}+ \frac{2-2e^{-x_{2}}}{1+e ^{-x_{2}}}\biggr], \end{gathered} $$
(50)

where y is the system output, and \(u_{j}\) (\(j = 1 , 2\)) are control inputs to the plant. The parameters \(b_{1} = 1\) and \(b_{2} = 1.1\) are unknown for controller design. The last subsystem system \(\dot{\xi} = Z(\xi, x_{1}, x_{2})\) represents the zero dynamics for the system. From [36, 37] we have that \(\xi= Z(\xi, x_{1}, x _{2})\) is input-to-state stable with respect to \([x_{1}, x_{2}]\), which implies that the state variable ξ is bounded if \(x_{1}(t), x_{2}(t) \in\ell_{\infty}\). The system is initialized as \(x_{1}(0) = 0.2\), \(x _{2}(0) = 0\), \(\xi(0) = 0\), and \(u_{1}(0) = u_{2}(0) = 0\). In the simulation, the failure case studied is given by

$$\begin{aligned}& u_{1}=\cos\bigl(0.05\bigl(t-hT^{\flat}\bigr) \bigr)u_{c1} \end{aligned}$$
(51)
$$\begin{aligned}& u_{2}=u_{c2}, t\in\bigl[hT^{\flat},(h+1)T^{\flat} \bigr], \quad h=0,2,4,\ldots, \end{aligned}$$
(52)
$$\begin{aligned}& u_{1}=5\sin(0.05t), \end{aligned}$$
(53)
$$\begin{aligned}& u_{2}=0.6u_{c2}, t\in\bigl[hT^{\flat},(h+1)T^{\flat} \bigr], \quad h=1,3,5,\ldots , \end{aligned}$$
(54)

where \(\check{u}_{j}\) is the jth actuator input for \(j = 1,2\), and \(T^{\flat} = 10\mbox{ s}\) denotes the minimum length of time intervals between two successive jumps of failure parameters. It is seen that during the time interval \([hT^{\flat},(h+1)T^{\flat})\), \(h = 0, 2, 4,\ldots\) , the first actuator suffers from PLOE faults with a time-varying efficiency indicator \(\kappa_{1,h}(t) = \cos(0.05(t - hT^{\flat}))\), whereas the second actuator works normally, and during \([hT^{\flat},(h+1)T^{ \flat})\), \(h = 1, 3, 5,\ldots\) , the first actuator output is stuck at an unknown time-varying value, that is, \(u_{1} = 5\sin(0.05t)\), whereas the second actuator loses 40% of the effectiveness of its input. The boundary information \(b_{0} = 0.6\), \(b_{M} = 2\), \(\kappa_{0} = 0.6\), and \(u_{fM} = 6\) is employed to construct the projection adaptation law (13), and then the compact set \(\Omega_{\tau}\) in (13) is computed as

$$\begin{aligned} \Omega_{\tau} =&[\tau_{1},\tau_{2,1}, \tau _{2,2}]^{T}|0.25\leq\tau _{1}\leq2.7778, -33.33\leq\tau_{2,1} \leq33.33, j=1,2]. \end{aligned}$$
(55)

To make all the signals bounded and y follow a given signal \(y_{d}=0.25\sin(1.5t)\), we select the scheme

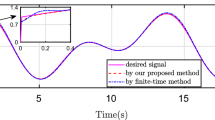
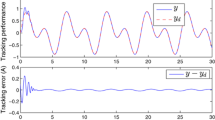
$$\begin{aligned}& z_{1}=y-y_{d}, \\& z_{2}=x_{2}-\alpha_{1}-\dot{y_{d}}, \\& \alpha_{1}=-5z_{1}-2.222\hat{W}z_{1}-\hat{ \varepsilon}(2.7778z_{1}), \\& \alpha_{2}=-3.6z_{2}-3.472\hat{W}z_{2}-\hat{ \varepsilon}(2.7778z _{2}), \\& \dot{\hat{W}}=44.444z_{1}^{2}+69.445z_{2}^{2} \tanh(2.7778z_{2})-0.05 \hat{\varepsilon}, \\& \dot{\dot{\tau}}=\operatorname{Proj}(-\Gamma_{\tau}vz_{n}), \quad \hat{0}\in\Omega _{\tau}, \\& \check{u}_{j}=\hat{\tau}_{1}(\alpha_{2}+ \ddot{y}_{d})+\hat{\tau} _{2,1}+\hat{\tau}_{2,2}, \quad j=1,2, \end{aligned}$$

with \(\Gamma_{\tau} = 25I_{3}\), where \(I_{3}\) denotes the \(3\times3\) identity matrix. The initial parameter estimates are set as \(\hat{W}(0) = 1\), \(\hat{\varepsilon}(0) = 0.1\), and \(\hat{\tau}(0) = [1.5, 0.3, 0.6]^{T}\). Figures 1-3 demonstrate the corresponding simulation results.

Figure 1
figure 1

y and \(\pmb{y_{r}}\) .

Full size image
Figure 2
figure 2

\(\pmb{y-y_{r}}\) .

Full size image
Figure 3
figure 3

\(\pmb{u_{1}}\) and \(\pmb{u_{2}}\) .

Full size image

4.2 B. Example 2

We consider the subsystem of the cascade chemical reactor system as in [37, 38]:

$$ \begin{gathered} \dot{x}_{1}=x_{2}+ \phi_{1}+{x_{3}}\triangle, \\ \dot{x}_{2}=\phi_{2}+b_{1}u_{1}+b_{2}u_{2}, \\ y=x_{1} . \end{gathered} $$
(56)

In the system,

$$\begin{aligned} \phi_{1}=\frac{(q+q_{R})T^{d}_{1}}{V}-\frac{x_{1}+T^{d}_{2}}{V}(q+q _{R})-\frac{C_{A_{2}}^{d}{\alpha}\lambda}{\rho{c_{\rho}}}e^{-\frac{E _{a}}{R(x_{1}+T_{2}^{d})}}-\frac{UA}{\rho{c_{\rho}}V} \bigl(x_{1}+T_{2} ^{d}-T_{j2}^{d} \bigr), \end{aligned}$$
(57)

and

$$\begin{aligned} \phi_{2}=\frac{UA}{\rho{c_{\rho}}V}\biggl[\frac{q_{j2}}{V_{j}} \biggl(T_{j20} ^{d}-\frac{\rho{c_{\rho}}Vx_{2}}{UA}-T_{j2}^{d} \biggr)+\frac{UA}{\rho_{j} {c_{j}}V_{j}}\biggl(x_{1}+T_{2}^{d}- \frac{\rho{c_{\rho}}Vx_{2}}{UA}-T_{j2} ^{d}\biggr)\biggr], \end{aligned}$$

where q and \(q_{1}=q+q_{R}\) are the flows of reactants, \(b_{1} = \frac{UAq _{j2}}{\rho{c_{\rho}}VV_{j}}\) and \(b_{2} = \frac{UAq_{j2}}{\rho {c_{\rho}}VV_{j}}\) denote the control coefficients, V represents the volume of the reactor. The system parameters are given in Table 1. The system is initialized as \(x_{1}(0) = 0.05\), \(x_{2}(0) = 0\), \(x_{3}(0)=0\), and \(u_{1}(0) = u_{2}(0) = 0\). In the simulation, the failure case studied is given by

$$\begin{aligned}& u_{1}=u_{c1}, \\ & u_{2}=u_{c2},\quad t\in\bigl[hT^{\flat},(h+1)T^{\flat} \bigr], h=0,2,4,\ldots, \\ & u_{1}=0.6u_{c1}, \end{aligned}$$
(58)
$$\begin{aligned}& u_{2}=1, \quad t\in\bigl[hT^{\flat},(h+1)T^{\flat} \bigr], h=1,3,5,\ldots , \end{aligned}$$
(59)

where \(\check{u}_{j}\) is the jth actuator input for \(j = 1,2\), and \(T^{\flat} = 10\mbox{ s}\) denotes the minimum length of time intervals between two successive jumps of failure parameters; \(b_{0} = 0.06\), \(b_{M} = 2\), \(\kappa_{0} = 0.06\), and \(u_{fM} = 6\) are employed to construct the projection adaptation law (13), and then the compact set \(\Omega_{\tau}\) in (13) is computed as

$$\begin{aligned} \Omega_{\tau} =&[\tau_{1},\tau_{2,1}, \tau _{2,2}]^{T}|0.25\leq\tau _{1}\leq2.7778, -33.33\leq\tau_{2,1} \leq33.33, j=1,2]. \end{aligned}$$
(60)
Table 1 Parameters of the cascade chemical reactor system
Full size table

To make all the signals bounded and y follow a given signal \(y_{d}=0\), we select the scheme

$$\begin{aligned}& z_{1}=y-y_{d}, \\& z_{2}=x_{2}-\alpha_{1}-\dot{y_{d}}, \\& \alpha_{1}=-5z_{1}-2.222\hat{W}z_{1}-\hat{ \varepsilon}(2.7778z_{1}), \\& \alpha_{2}=-3.6z_{2}-3.472\hat{W}z_{2}-\hat{ \varepsilon}(2.7778z _{2}), \\& \dot{\hat{W}}=44.444z_{1}^{2}+69.445z_{2}^{2} \tanh(2.7778z_{2})-0.05 \hat{\varepsilon}, \\& \dot{\dot{\tau}}=\operatorname{Proj}(-\Gamma_{\tau}vz_{n}),\quad \hat {0}\in\Omega _{\tau}, \\& \check{u}_{j}=\hat{\tau}_{1}(\alpha_{2}+ \ddot{y}_{d})+\hat{\tau} _{2,1}+\hat{\tau}_{2,2}, \quad j=1,2, \end{aligned}$$

with \(\Gamma_{\tau} = 25I_{3}\), where \(I_{3}\) denotes the \(3\times3\) identity matrix. The initial parameter estimates are set as \(\hat{W}(0) = 1\), \(\hat{\varepsilon}(0) = 0.1\), and \(\hat{\tau}(0) = [1.5, 0.3, 0.6]^{T}\). Figures 4-6 demonstrate the corresponding simulation results.

Figure 4
figure 4

y and \(\pmb{y_{r}}\) .

Full size image
Figure 5
figure 5

\(\pmb{y-y_{r}}\) .

Full size image
Figure 6
figure 6

\(\pmb{u_{1}}\) and \(\pmb{u_{2}}\) .

Full size image

4.3 C. Conclusions

In this papedr, we investigate the issue of adaptive finite-time tracking for a class of nonlinearity systems with hysteresis. On the basis of the approximation capability of fuzzy logic systems, we give an adaptive law and an intermediate control function. Moreover, we proved that the aforementioned approach can make the system SGPFS.

In comparison with the tuning function control schemes in [39–44], which also focus on adaptive actuator failure compensation problem, the framework of our control is further simplified by using RBFNN, as seen in (9)-(13). Moreover, with respect to the previous fault-tolerant controllers such as [45, 46], our scheme additionally contains an optimized neural network adaptation mechanism, which renders that there are only two estimates, that is, \(\hat{W_{i}}\) and ε need to be computed online. The control scheme in [47] is under the presupposition that the systems have a nonstrict-feedback structure. Our control scheme relaxes the restriction of system structure so that the method in this note is more meaningful. In this sense, the presented study is more computationally attractive and thus feasible in practical implementation in comparison with other existing results.