Abstract
This paper is dedicated to neural networks-based adaptive finite-time control design of switched nonlinear systems in the time-varying domain. More specifically, by employing the approximation ability of neural networks system, an integrated adaptive controller is constructed. The main aim is to make sure the closed-loop system in arbitrary switching signals is semi-global practical finite-time stable (SGPFS). A backstepping design with a common Lyapunov function is proposed. Unlike some existing control schemes with actuator failures, the key is dealing with the time-varying fault-tolerant job for the switched system. It is also proved that all signals in the system are bounded and the tracking error can converge in a small field of the origin in finite time. A practical example is presented to illustrate the validity of the theory.
Similar content being viewed by others
1 Introduction
With the quick development of society, there are increasingly complex control problems [1]. Apart from the characteristics of non-linearity [2], being time-varying and showing uncertainty, the problems also have the characteristics of complex structure [3], complex behavior [4] and multi-subsystem integration [5]. Thus, a switched system as a special class of hybrid control system has been widely investigated in various fields [6], since its first introduction by Liberzon and Daniel et al. [7]. A switched system is composed of a set of subsystems and switched strategy, which coordinates the operation of each subsystem [8]. There are some characteristics of the switched system, for instance, even if all subsystems are unstable, an appropriate switched function can ensure system globally asymptotic stability [9]. Assuming subsystems are stable, under the circumstances of the switched control strategy, is strictly consistent, and the system performance is also improved [10]. Similarly, all the subsystems are globally exponential stable, the switched systems are also instable [11]. In a nutshell, in order to solve the existing control problems, a switched nonlinear system has sparked a heated discussion [12].
There are many means to make the nonlinear switched system stable. Based on the common Lyapunov function method, switched systems can be made stable under an arbitrary switched signal [13,14,15,16]. Using the average dwell time method, the locally exponentially stable of the closed-loop system can be guaranteed in [17, 18]. By an adaptive backstepping control method, the input-to-state stability of the system can be obtained [19, 20]. The finite-time practical control problem was developed for nonlinear switched systems subjected to nonlinear input [21]. The control design of cascade switched systems with uncertainties was investigated in [22]. The authors of [23] studied the control and stabilization problem for normal nonlinear switched systems with unknown dynamics. Then, by a fuzzy logical system (FLS) method a radial basis function (RBF) NNs method is used for the analysis of the system; see [24,25,26,27,28,29,30]. Applying FLS to identify the unknown functions, this technique can ensure all switched signals are bounded [26]. A switched system has been widely applied in substation switching, traffic control and electromechanical integration in recent years, which is the driving force for this paper.
Most control schemes are focused on the faultless system, such as the results of [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. As is well known, actuator faults [31,32,33,34,35,36] occur frequently in techniques. When the system encounters actuator failure, it can damage the stability of the system and even crash the system. Therefore, this emphasizes the importance of designing fault-tolerant control in practical applications. Furthermore, by using the approximation ability of FLS in [37], an adaptive controller has been created to deal with the system uncertainty and unknown actuator failure [31]. Thus, as an effective solution, designing appropriate fault-tolerant controllers has been widely used in fault handling. An adaptive fault-tolerant controller was designed for large systems with actuator failures [38]. The developed control scheme can be used to avoid the problem of “explosion of complexity” [35]. Then several output feedback control strategies have been developed for nonlinear switched systems with actuator faults, by using filter observers, adaptive methods and a backstepping technique [39,40,41,42,43]. For instance, an adaptive compensation controller was constructed by utilizing the backstepping technique [39]. An adaptive distributed controller was proposed to ensure the realization of tracking error [41]. However, the fault-tolerant control strategies in [32,33,34,35,36,37,38,39,40,41,42,43] can guarantee system performances in infinite time.
In practice, fault-tolerant control in a finite time can reduce the defect caused by the system faults. As a consequence, when faults occur, the tracking error of the nonlinear system also need to converge to a small domain of the origin in finite time. The practical finite-time stable of nonlinear systems was discussed in [44]. Adopting the sliding-mode control method, the closed-loop system reached a small domain of the sliding surface in finite time [45]. An adaptive controller was designed to ensure the boundedness of the closed-loop system, while ensuring the state of the system was adjusted to the origin in finite time [46]. Considering the time-varying actuator failure in this paper, NNs are used to approximate the unknown function, this adds more difficulty in controller design for the switched systems. Hence, a new type adaptive NNs under time-varying actuator failure should be proposed in finite time.
On the basis of the above analysis and by comparing with existing achievements on adaptive control for nonlinear systems, this paper is committed to cope with the adaptive finite-time tracking control problem of nonlinear systems under time-varying actuator failure. The main contributions of this paper are as follows:
(1) In this paper, unknown actuator failure leads to time-varying control gains, which is more general than those currently known. Besides, unknown functions are approximated by the RBF NNS. (2) All the signals in the closed-loop system are proved to show boundedness under arbitrary switching and designed controllers can guarantee stability of switched nonlinear systems in finite time. (3) The system considered includes strict-feedback switched nonlinear systems (when \(g=1\)), so the system is more comprehensive and universal.
The rest of this paper is organized as follows: Sect. 2 gives the problem formulation and preliminaries. One introduces the RBF NNs and gets the main results in Sect. 3. Section 4 provides an example to illustrate the proposed results, and the conclusion is presented in Sect. 5.
2 Problem formulation and preliminary knowledge
Consider a class of strict-feedback switching nonlinear systems described as
where \({\bar{x}_{j}=[x_{1}, x_{2},\ldots, x_{j}]}^{T} \in R^{j}\), \(j=1,\ldots, n-1\). \(x=[x_{1}, x_{2},\ldots, x_{n}]^{T}\in R^{n}\) denotes a state vector, \(u_{\eta (t)}\in R\) and \(y \in R\) denote the system input and output, respectively. \(\eta (t):[0,\infty )\rightarrow D=\{1,\ldots, \iota \}\) stands for a piecewise continuous switching signal, ι is the subsystem number, \(\eta (t)=m\) (\(m\in D\)) when the mth subsystem is active, \(f_{j,m}(\bar{x}_{j})\) are unknown smooth nonlinear functions of the mth subsystem, \(g_{j}(\bar{x}_{j})\) are the known smooth nonlinear functions.
One supposes \(u_{\eta (t)}\) has encounter actuator faults. And the actuator failure model is described as follows:
where \(\rho _{m}(t,t_{\rho })\in [0,1]\) stands for an actuation effectiveness, \(a_{m}\) represents the actual input signal of the mth subsystem, \(u_{b}(t,t_{b})\) denotes an uncontrollable time-varying additive actuation fault, \(t_{\rho }\) reveals a time instant at which the loss of actuation effectiveness fault occurs, and \(t_{b}\) shows the moment when there is the additive actuation fault.
Remark 1
The scheme of control and stabilization was presented for nonlinear switched systems without the time-varying actuation fault [22, 23]. In research on existing finite-time control for switched nonlinear systems in [30, 47], it was supposed that time-invariance or \(u_{m}=a_{m}\) was founded on healthy actuation. Nonetheless, unknown actuator failure causes the control gain time-varying in application, and the actuation element may encounter failure or faults, which let us consider both effectiveness and the additive actuation fault simultaneously.
Thence, compared with the methods in [22, 23, 30, 47], in the above paper, efficiency loss and additional actuator failure cannot occur simultaneously, the developed fault model (2) can remedy this weakness. It means that two kinds of faults may occur at the same time, expanding the range of application.
Next, some definitions and lemmas which are essential in our subsequent development are given.
Definition 1
([48])
For the nonlinear system \(\dot{\wp }=f({\wp , b})\), if for all \(\wp (t_{0})=\wp _{0}\), there exist \(a>0\) and \(T(a, \wp _{0})<\infty \), such that \(\Vert \wp (t) \Vert < a\), for all \(t\geq t_{0}+T\), then the solution is semi-global practical finite-time stable (SGPFS), where ℘, b are the state vector and input vector, respectively.
Lemma 1
([49])
Suppose \(V(x)\)is a \(C^{1}\)smooth positive-definite function (defined on \(U\subset R^{n}\)) and \(\dot{V}(x)+\lambda V^{\alpha }(x)\)is a negative semi-definite function on \(U\subset R^{n}\)for \(\alpha \in (0, 1)\)and \(\lambda \in R^{+}\), then there exists an area \(U_{0}\subset R^{n}\)such that any \(V(x)\)which starts from \(U_{0}\subset R^{n}\)can reach \(V(x)\equiv 0\)in finite time. Moreover, if \(T_{\mathrm{reach}}\)is the time needed to reach \(V(x)\equiv 0\), then
where \(V(x_{0})\)is the initial value of \(V(x)\).
Lemma 2
([29])
Consider the nonlinear system \(\dot{\wp }=f(\wp ,u)\), for smooth positive-definite function \(V(\wp )\), suppose that there exist scalars \(\lambda >0\), \(0<\alpha <1\), and \(0<\eta <\infty \)such that
therefore, the nonlinear system \(\dot{\wp }=f(\wp ,u)\)is SGPFS.
Lemma 3
([50])
For \(\forall (x,y)\in R^{2}\), the Young inequality is \(xy\leqslant \frac{a ^{p}}{p} \Vert x \Vert ^{p}+\frac{1}{qa^{q}} \Vert y \Vert ^{q}\), where \(a>0\), \(p>1\), \(q>1\), and \((p- 1)(q - 1)= 1\).
Assumption 1
Unknown time-varying functions \(\rho _{m}(t,t_{\rho })\), \(u_{b}(t, t_{b})\) are bounded. That is, there exist some positive constants \(\rho _{ \min }\) and \(u_{m}\) such that \(\rho _{\min }<\rho _{m}(t, t_{\rho })<1\) and \(\vert u_{b}(t, t_{b}) \vert \leqslant \bar{u}_{b}\).
Assumption 2
\(y_{d}\) and its first nth-order time derivatives \(y_{d}^{(i)}\) (\(i=1,\ldots, n\)) are smooth and bounded.
Remark 2
As Assumption 1 claimed, the control gain \(\rho _{m}(t, t_{\rho })\) and uncontrollable additive actuation fault \(u_{b}(t, t _{b})\) are assumed to be unknown, which makes the previous finite-time stability criterion unavailable. For the subsequent stability analysis, one has Assumption 2, which is used in tracking control of nonlinear systems (see [31, 40]).
3 RBF NNs and the main results
Under the following design, the RBF NNs will be utilized to approximate the unknown function \(f(\varpi )\). The basis function \(S_{i}(\varpi )\) are the Gaussian functions with the form
where \(\jmath _{i}=[\jmath _{i1}, \jmath _{i2},\ldots, \jmath _{i\kappa }]^{T}\) and \(\ell _{i}\) are the centers and the widths of NNs, respectively, \(\kappa >1\) is the NNs node number.
As mentioned in [27], for the continuous nonlinear function \(f(\varpi )\) defined on any compact set \(\varOmega _{\varpi }\subset R^{n}\), there exist NNs \(H^{*T}S(\varpi )\) and arbitrary \(\varepsilon >0\), such that
where \(\varpi \in R^{n}\), \(H^{*}\in R^{\kappa }\) are the input variable and the ideal constant weight vector, respectively. And the smooth basis vector of RBF NNs is \(S(\varpi )\), where \(S(\varpi )=[S_{1}(\varpi ),\ldots, S_{\kappa }(\varpi )]^{T}\).
On account of the universal approximation theory of RBF NNs, for an unknown function \(f(\varpi )\), it can be approximated as
where \(\varepsilon (\varpi )\) is named the approximation error, and is supposed to be bounded by ε̄, thus \(\varepsilon ( \varpi )\leq \bar{\varepsilon }\) with \(\bar{\varepsilon }>0\), for all \(\varpi \in \varOmega _{\varpi }\).
For the system (1), our aim is to design an adaptive controller in finite time. Next, one defines \(P_{i}= \Vert H_{i}^{*} \Vert ^{2}\), \(i=1, 2,\ldots, n\), where \(H_{i}^{*}\) is the weight vector of NNs. Let \(P_{i}\) be estimated as \(\hat{P_{i}}\), the estimation error be expressed by \(\widetilde{P_{i}}=P_{i}-\hat{P_{i}}\). Then we have the common coordinate transformation
where \(y_{d}\), \(\alpha _{j-1}\) express the reference signal and virtual controller to be designed later, respectively.
Step 1: For the system (1) and \(\xi _{1}=x_{1}-y _{d}\), the differential of \(\xi _{1}\) is
where \(S_{1}(z_{1})\), \(z_{1}=x_{1}\) are the RBF and input vector of NNs, respectively, \(\varepsilon _{1,\eta }^{*}\) is the approximate error.
Then, by the Lyapunov function and Lemma 3, one gets
From the above analysis, the first-order derivative of \(V_{1}\) is
We design the virtual controller \(\alpha _{1}\) and adaptive law \(\dot{\hat{P}}_{1}\) as
where \(\beta _{1}>0\) is a constant.
Then (5) can be rewritten as
By Lemma 3, one knows
then \(\dot{V}_{1}\) can be further expressed as
Step j (\(j=2,\ldots,n-1\)). Based on \(\xi _{j}=x_{j}-\alpha _{j-1}\), one gets
where \(z_{j}=[x_{1},\ldots,x_{j}]^{T}\) is the input vector of NNs, and
Applying Lemma 3 again, one has
Adopting a similar procedure to Step 1, the time derivative of \(V_{j}\) is
The virtual controller and the adaptive law are designed thus:
Consider the following fact:
Then (10) can be replaced by
Step n: By Lemma 3, one obtains
By (13), one knows
Performing in the same way as in Step j, from the above analysis, the time derivative of \(V_{n}\) is
The actual fault-tolerant controller and adaptive laws are developed as
Then, by putting (16)–(18) into (15), one has
From (19) and Lemma 3, one obtains
Then one gets
Hitherto, one gets the following theorem to summarize the main result of this paper.
Theorem 1
For the switched nonlinear strict-feedback system (1) affected by actuator failure (2), RBF NNs are developed to approximate the nonlinear system, the designed virtual controllers (11), the subsystems controllers (16), and the adaptive laws (17), it is guaranteed that all the signals in a closed-loop system are bounded and SGPFS, i.e., the outputycan track the given signal \(y_{d}\)in finite-time.
Proof
Consider Lyapunov function as follows:
Together with (20), if \(\beta _{n}>1\), then
where
For (22), the integral of inequality from 0 to t, the following inequality can be obtained:
From (21) and (23), one has \(\xi _{i}\), \(\tilde{P}_{i}\), \(i=1,\ldots, n\) and \(\tilde{u}_{b}\), \(b\in \iota \) are bounded for initial conditions. Moreover, based on \(\tilde{P}_{i}=P _{i}-\hat{P}_{i}\), thus \(\hat{P}_{i}\) is bounded because of the boundedness of \(P_{i}\). Similarly, \(\hat{u}_{b}\) is also bounded. Therefore, all the signals in the closed-loop system are bounded under arbitrary switching signals.
Next, denote \(\vert \tilde{P}_{i} \vert \leqslant P_{iM}\) and \(\vert \tilde{u}_{b} \vert \leqslant u_{bM}\).
Step 1: In this section, from the Lyapunov function
By (6), one has
Step j (\(j=2,\ldots,n-1\)). We use the Lyapunov function
By (11), the first-order derivative of \(V_{\xi j}\) is
Step n: The Lyapunov function is as follows:
by Lemma 3, one knows
Substitute (16) into the derivative of \(V_{\xi n}\), and define \(\beta _{i}>P_{iM}\), \(i=1,\ldots,n-1\), \(\beta _{n}>P_{nM}+2\), then
where \(\bar{c}=[(c+1)/2]\), \(\bar{d}=\frac{1}{2}\bar{u}_{b}^{2}+ \frac{1}{2}u_{bM}^{2}\).
Thus choosing the following common Lyapunov function:
from the above analysis procedure, one obtains
by Lemma 2, \(\xi _{i}\) (\(i=1,\ldots, n\)) are SGPFS, i.e., the output tracks the reference signal and \(y(t)\) tracks the given signal to a small compact set in finite time.
Then by Lemma 1, the convergence time satisfies
where \(V_{\xi }(0)\) is the initial value of \(V_{\xi }\).
This completes the proof. □
Remark 3
The actuator faults which contain both the loss of effectiveness and the additive faults can be written as \(u_{m}=\rho _{m}(t,t_{\rho })a_{m}+u _{b}(t,t_{b})\), the parameters \(\rho _{m}(t, t_{\rho })\), \(u_{b}(t,t_{b})\) are time-varying. In order to ensure the stability of the closed-loop systems, one chooses the parameters satisfying \(\beta _{n}>1\), \(0< c<1\). The tracking error can converge in finite time, we claim, the parameters are chosen as \(\beta _{i}>P_{iM}\), \(i=1,\ldots,n-1\) and \(\beta _{n}>P_{nM}+2\), where the other parameters are chosen to be positive.
4 Numerical example
A continuous stirred tank reactor (CSTR) with two modes feed stream in [51] is the example to verify our results, which is modeled as a switched nonlinear system,
where \(f_{1, 1}=f_{2, 1}=(5/6)x_{2}-x_{2}\), \(f_{1, 2}=-0.02x_{1}-(5/6)x _{2}\), \(f_{2, 2}=-0.01x_{1}-(5/6)x_{2}\), \(g_{1}(\bar{x}_{1})=g_{1}( \bar{x}_{2})=1\), \(\eta ={1,2}\). One chooses the reference signal \(y_{d}\) as
and the actuator fault \(u_{m}\) as
where \(m=\{1, 2\}\), \(\rho _{1}=0.4+0.1\exp (-0.2t)\), \(\rho _{2}=0.6+0.1\sin (-t)\), \(u_{b}(t,t_{b})=0.5\sin (t)\), and \(a_{1}\), \(a_{2}\) represent the input signal.
From Theorem 1, the virtual controller, actual controllers and the adaptive laws are given as
where \(\xi _{1}=x_{1}-y_{d}\), \(\xi _{2}=x_{2}-\alpha _{1}\), \(\beta _{1}=1.25\), \(\beta _{2}=3.75\), \(c=0.45\), \(\gamma _{1}=0.3\), \(\gamma _{2}=0.6\), \(\lambda =0.2\).
Further, \(z_{1}=x_{1}\), \(z_{2}=[x_{1}, x_{2}]^{T}\) are input vectors of RBF NNs. The centers \(\jmath _{1}\), \(\jmath _{2}\) are spaced on \([-2, 2]\) simultaneously, the widths are defined as \(\ell _{1}=\ell _{2}=2\), the initial values of the system states are \(x_{1}(0)=0.01\), \(x _{2}(0)=0.2\), respectively, and \(\hat{\xi }_{1}(0)=0.01\), \(\hat{\xi } _{2}(0)=0.02\), \(\hat{u}_{1}(0)=\hat{u}_{2}(0)=0.04\) denote the initial values of the actuator fault.
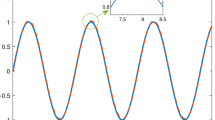
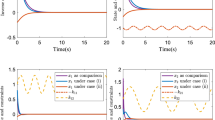
By the above analysis, Fig. 1 expresses the arbitrarily chosen switching signal. From Fig. 2, a good tracking performance is obtained. The subsystem controllers \(u_{1}\), \(u_{2}\) are given in Figs. 3 and 5. Figures 4 and 6 correspond to the adaptive law. From the above figures, it is shown that all the signals in the closed-loop system are bounded. Then, in order to illustrate the effectiveness of our method, with the other parameters unchanged, we verify whether the system has good tracking performance when the reference signal is selected as \(y_{d}=0.1(\sin (1.5t)+\sin (t))\). From Fig. 7, one can see the tracking performance is nice. Thus our method is effective.
5 Conclusion
This paper deals with the problem of adaptive finite-time stability for a class of strict-feedback switched nonlinear systems. One takes the backstepping technique and the RBF NNs method, an adaptive finite-time control strategy is formed. In this paper, the actuator failure model is time-varying, and the control scheme can ensure system performances SGPFS in finite-time. Although some progresses have been made in this article, the established adaptive control result is based on a backstepping method. Recently, we notice that there are many other approaches to obtain a controller for nonlinear switched systems, such as stated in [22, 23]; an adaptive control algorithm or a robust sliding-mode control strategy is also an effective tool to model the nonlinearities. In future, we will also make more efforts to obtain something unique in using RBF NNs, such as nonlinear system with time-varying state constraints.
References
Liu, X., Li, Y., Zhang, W.: Stochastic linear quadratic optimal control with constraint for discrete-time systems. Appl. Math. Comput. 228, 264–270 (2004)
Wang, Y., Pan, Z., Li, Y., Zhang, W.: \(H_{\infty}\) control for nonlinear stochastic Markov systems with time-delay and multiplicative noise. J. Syst. Sci. Complex. 30(6), 1–23 (2017)
Chang, Z., Meng, X., Zhang, T.: A new way of investigating the asymptotic behaviour of a stochastic SIS system with multiplicative noise. Appl. Math. Lett. 87, 80–86 (2019)
Zhang, Y., Zhao, M., Su, J., Lu, X., Lv, K.: Novel model for cascading failure based on degree strength and its application in directed gene logic networks. Comput. Math. Methods Med. 2018, Article ID 8950794 (2018)
Liu, X., Li, Y., Li, Y.: Adaptive tracking control for a class of uncertain switched stochastic nonlinear systems. Adv. Differ. Equ. 2019(33), 33 (2019)
Zhu, Y., Zheng, W.: Multiple Lyapunov functions analysis approach for discrete-time switched piecewise-affine systems under dwell-time constraints. IEEE Trans. Autom. Control (2019). https://doi.org/10.1109/TAC.2019.2938302
Liberzon, D.M., Hespanha, J.P., Morse, A.S.: Stability of switched systems: a Lie-algebraic condition. Syst. Control Lett. 37(3), 117–122 (1999)
Sun, Z., Ge, S.S.: Analysis and synthesis of switched linear control systems. Automatica 41(2), 181–195 (2005)
Lin, H., Antsaklis, P.J.: Stability and stabilizability of switched linear systems: a survey of recent results. IEEE Trans. Autom. Control 54(2), 308–322 (2009)
Geromel, J.C., Deaecto, G.S., Daafouz, J.: Suboptimal switching control consistency analysis for switched linear systems. IEEE Trans. Autom. Control 58(7), 1857–1861 (2013)
Liberzon, D.: Switching in Systems and Control. Birkhäuser, Boston (2003)
Zhu, Y., Zheng, W., Zhou, D.: Quasi-synchronization of discrete-time Lur’e-type switched systems with parameter mismatches and relaxed PDT constraints. IEEE Trans. Cybern. (2019). https://doi.org/10.1109/TCYB.2019.2930945
Li, Y., Tong, S.: Adaptive neural networks prescribed performance control design for switched interconnected uncertain nonlinear systems. IEEE Trans. Neural Netw. 29(7), 3059–3068 (2018)
Vu, L., Liberzon, D.M.: Common Lyapunov functions for families of commuting nonlinear systems. Syst. Control Lett. 54(5), 405–416 (2005)
Luo, Y., Song, B., Liang, J., Dobaie, A.M.: Finite-time state estimation for jumping recurrent neural networks with deficient transition probabilities and linear fractional uncertainties. Neurocomputing 260, 265–274 (2017)
Sui, S., Tong, S.: Fuzzy adaptive quantized output feedback tracking control for switched nonlinear systems with input quantization. Fuzzy Sets Syst. 290, 56–78 (2016)
De Persis, C., De Santis, R., Morse, A.S.: Switched nonlinear systems with state-dependent dwell-time. Syst. Control Lett. 50(4), 291–302 (2003)
Wang, H., Wang, Z., Liu, Y., Tong, S.: Fuzzy tracking adaptive control of discrete-time switched nonlinear systems. Fuzzy Sets Syst. 316, 35–48 (2017)
Zhou, Q., Li, H., Wang, L., Lu, R.: Prescribed performance observer-based adaptive fuzzy control for nonstrict-feedback stochastic nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 48(10), 1747–1758 (2018)
Zhang, X., Liu, X., Li, Y.: Adaptive fuzzy tracking control for nonlinear strict-feedback systems with unmodeled dynamics via backstepping technique. Neurocomputing 235, 182–191 (2017)
Aghababa, M.P.: Stabilization of a class of cascade nonlinear switched systems with application to chaotic systems. Int. J. Robust Nonlinear Control 28(11), 3640–3656 (2018)
Aghababa, M.P.: Lyapunov control method for mismatched uncertainty and gain variation compensation in switched systems. IEEE Trans. Syst. Man Cybern. Syst. https://doi.org/10.1109/TSMC.2019.2930303
Aghababa, M.P.: Twofold sliding controller design for uncertain switched nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. https://doi.org/10.1109/TSMC.2019.2895099
Wang, F., Chen, B., Sun, Y., Lin, C.: Finite time control of switched stochastic nonlinear systems. Fuzzy Sets Syst. 365, 140–152 (2019)
Tong, S., Sun, K., Sui, S.: Observer-based adaptive fuzzy decentralized optimal control design for strict-feedback nonlinear large-scale systems. IEEE Trans. Fuzzy Syst. 26(2), 569–584 (2018)
Wang, L., Li, H., Zhou, Q., Lu, R.: Adaptive fuzzy control for nonstrict feedback systems with unmodeled dynamics and fuzzy dead zone via output feedback. IEEE Trans. Syst. Man Cybern. Syst. 47(47), 2400–2412 (2017)
Cui, G., Wang, Z., Zhuang, G., Li, Z., Chu, Y.: Adaptive decentralized NN control of large-scale stochastic nonlinear time-delay systems with unknown dead-zone inputs. Neurocomputing 158, 194–203 (2015)
Liu, Y., Lu, S., Tong, S., Chen, X., Chen, C.L., Li, D.J.: Adaptive control-based barrier Lyapunov functions for a class of stochastic nonlinear systems with full state constraints. Automatica 87(87), 83–93 (2018)
Wang, F., Chen, B., Lin, C., Zhang, J., Meng, X.: Adaptive neural network finite-time output feedback control of quantized nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 48(6), 1839–1848 (2018)
Wu, J., Chen, W., Li, J.: Global finite-time adaptive stabilization for nonlinear systems with multiple unknown control directions. Automatica 69(69), 298–307 (2016)
Wang, F., Zhang, X.: Adaptive finite time control of nonlinear systems under time-varying actuator failures. IEEE Trans. Syst. Man Cybern. Syst. 49(9), 1845–1852 (2019)
Shao, Z.: Adaptive compensation control based on MMST grouping for a class of MIMO nonlinear systems with actuator failures. Acta Autom. Sin. 88(3), 2445–2455 (2014)
Tang, X., Tao, G., Joshi, S.M.: Adaptive actuator failure compensation for parametric strict feedback systems and an aircraft application. Automatica 39(11), 1975–1982 (2003)
Jin, X., Yang, G.: Robust adaptive fault-tolerant compensation control with actuator failures and bounded disturbances. Acta Autom. Sin. 35(3), 305–309 (2009)
Wang, L., Basin, M.V., Li, H., Lu, R.: Observer-based composite adaptive fuzzy control for nonstrict-feedback systems with actuator failures. IEEE Trans. Fuzzy Syst. 26(4), 2336–2347 (2018)
Ye, D., Yang, G.: Adaptive fault-tolerant tracking control against actuator faults with application to flight control. IEEE Trans. Control Syst. Technol. 14(6), 1088–1096 (2006)
Wang, L., Mendel, J.M.: Fuzzy basis functions, universal approximation, and orthogonal least-squares learning. IEEE Trans. Fuzzy Syst. 3(5), 807–814 (1992)
Tong, S., Huo, B., Li, Y.: Observer-based adaptive decentralized fuzzy fault-tolerant control of nonlinear large-scale systems with actuator failures. IEEE Trans. Fuzzy Syst. 22(1), 1–15 (2014)
Zhang, Z., Chen, W.: Adaptive output feedback control of nonlinear systems with actuator failures. Inf. Sci. 179(24), 4249–4260 (2009)
Lai, G., Wen, C., Liu, Z., Zhang, Y., Chen, C.L., Xie, S.: Adaptive compensation for infinite number of actuator failures based on tuning function approach. Automatica 87(87), 365–374 (2018)
Zhang, Y., Liang, H., Ma, H., Zhou, Q., Yu, Z.: Distributed adaptive consensus tracking control for nonlinear multi-agent systems with state constraints. Appl. Math. Comput. 326, 16–32 (2018)
Ma, H., Zhou, Q., Bai, L., Liang, H.: Observer-based adaptive fuzzy fault-tolerant control for stochastic nonstrict-feedback nonlinear systems with input quantization. IEEE Trans. Syst. Man Cybern. Syst. 49(99), 287–298 (2019)
Shen, Q., Jiang, B., Cocquempot, V.: Adaptive fuzzy observer-based active fault-tolerant dynamic surface control for a class of nonlinear systems with actuator faults. IEEE Trans. Fuzzy Syst. 22(2), 338–349 (2014)
Aghababa, M.P.: Finite time control of a class of nonlinear switched systems in spite of unknown parameters and input saturation. Nonlinear Anal. Hybrid Syst. 31, 220–232 (2019)
Hu, Q., Huo, X., Xiao, B.: Reaction wheel fault tolerant control for spacecraft attitude stabilization with finite-time convergence. Int. J. Robust Nonlinear Control 23(15), 1737–1752 (2012)
Song, Z., Zhai, J.: Finite-time adaptive control for a class of switched stochastic uncertain nonlinear systems. J. Franklin Inst. Eng. Appl. Math. 354(12), 4637–4655 (2017)
Liu, L., Liu, Y.J., Tong, S.: Neural networks-based adaptive finite-time fault-tolerant control for a class of strict-feedback switched nonlinear systems. IEEE Trans. Cybern. 99, 1–10 (2018)
Zhu, Z., Xia, Y., Fu, M.: Attitude stabilization of rigid spacecraft with finite-time convergence. Int. J. Robust Nonlinear Control 21(6), 686–702 (2011)
Bhat, S.P., Bernstein, D.S.: Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 38(3), 751–766 (2000)
Deng, H., Krstic, M.: Stochastic nonlinear stabilization-I: a backstepping design. Syst. Control Lett. 32(3), 143–150 (1997)
Ma, R., Zhao, J.: Backstepping design for global stabilization of switched nonlinear systems in lower triangular form under arbitrary switchings. Automatica 46(11), 1819–1823 (2010)
Acknowledgements
We are thankful to the reviewers for their useful corrections and suggestions, which improved the quality of this paper.
Funding
This work was supported by the National Natural Science Foundation of China (No. 61972236), Shandong Provincial Natural Science Foundation (No. ZR2018MF013), the Research Fund for the Taishan Scholar Project of Shandong Province of China, SDUST Research Fund (No. 2015TDJH105) and the Fund for Postdoctoral Application Research Project of Qingdao (2016118).
Author information
Authors and Affiliations
Contributions
The main idea of this paper was proposed by the first and last authors, while the second and last authors reviewed and modified the paper. Furthermore, all authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liu, X., Shi, X. & Li, Y. Neural networks-based adaptive finite-time control of switched nonlinear systems under time-varying actuator failures. Adv Differ Equ 2019, 482 (2019). https://doi.org/10.1186/s13662-019-2396-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2396-6