1 Introduction

The last few decades, fractional differential equations systems are widely used for modelling the complex real world problems occurring in science and engineering applications [1–17]. Fractional differential equation systems involve non-integer order differential operators. There are some different definitions of a fractional derivative in the literature. Some of them are defined as follows. For \(0<\alpha<1\), the Caputo fractional derivative of f is [18]

$$ D^{(\alpha)}f(t)=\frac{1}{\Gamma(1-\alpha)} \int_{a}^{t} (t-x)^{\alpha}f'(x)\,dx. $$
(1.1)

The Riemann-Liouville derivative of f is [18]

$$\begin{aligned} D^{(\alpha)}f(t)=\frac{1}{\Gamma(1-\alpha)}\biggl(\frac{d}{dt}\biggr) \int_{a}^{t} (t-x)^{\alpha}f(x)\,dx. \end{aligned}$$
(1.2)

The Caputo-Fabrizio derivative of f is [19]

$$\begin{aligned} D^{(\alpha)}f(t)=\frac{M(\alpha)}{(1-\alpha)} \int_{a}^{t} f(x)\exp\biggl[-\frac{\alpha(t-x)}{(1-\alpha)} \biggr]\,dx. \end{aligned}$$
(1.3)

The Atangana-Baleanu derivative of f is [20]

$$\begin{aligned} D^{(\alpha)}f(t)=\frac{B(\alpha)}{(1-\alpha)} \int_{a}^{t} f'(x)E_{\alpha}\biggl[-\frac{\alpha(t-x)^{\alpha}}{(1-\alpha)}\biggr]\,dx. \end{aligned}$$
(1.4)

The conformable derivative also called alpha derivative of f is [21]

$$D^{\alpha}_{x}\bigl(f(x)\bigr)=\lim_{\epsilon\rightarrow0} \frac{f(x+\epsilon x^{1-\alpha})-f(x)}{\epsilon}. $$

Its extension, the beta derivative of f is [22]

$$D^{\beta}_{x}\bigl(f(x)\bigr)=\lim_{\epsilon\rightarrow0} \frac{f(x+\epsilon(x+\frac{1}{\Gamma(\beta)} )^{1-\beta })-f(x)}{\epsilon}. $$

In this study, the Caputo definition of fractional order derivative is considered. Unfortunately, most of the fractional differential equations systems do not have exact analytic solutions, therefore approximation and numerical techniques must be applied for obtaining the solution of such systems. For this purpose, different numerical techniques are applied to fractional differential equations systems. For instance we have the Adomian decomposition method [23, 24], the variational iteration method [12, 25], the differential transform method [26], the homotopy perturbation method [27–29], the homotopy analysis method [30], and the fractional natural decomposition method [31].

It is revealed by [32] that sinc methods give a much better rate of convergence and more efficient results than classical polynomial methods in the presence of singularities. In the present paper, a sinc collocation method is proposed to find the approximate solution of the following system:

$$ \textstyle\begin{cases} \sum_{i=0}^{2}\mu_{i}(x)u^{(i)}(x)+\mu_{\alpha_{1}}(x)u^{(\alpha_{1})}(x)+\sum _{i=0}^{2}\xi_{i}(x)v^{(i)}(x)+\xi_{\beta_{1}}(x)v^{(\beta_{1})}(x)=f_{1}(x),\\ \sum_{i=0}^{2}\gamma_{i}(x)u^{(i)}(x)+\gamma_{\alpha_{2}}(x)u^{(\alpha _{2})}(x)+\sum_{i=0}^{2}\eta_{i}(x)v^{(i)}(x)+\eta_{\beta_{1}}(x)v^{(\beta _{2})}(x)=f_{2}(x),\\ u(a)=u(b)=0,\qquad v(a)=v(b)=0, \end{cases} $$
(1.5)

where \(\cdot^{(\alpha)}\) is the Caputo fractional derivative and \(0<\alpha _{i},\beta_{i}<1\) for \(i=1,2\). In the next section we give some background on fractional calculus and the sinc collocation method. In Section 3 we give some theorems to show the approximation of the proposed method. Then, in Section 4, we illustrate the findings with two numerical examples. Finally in the last section the paper is concluded.

2 Preliminaries

In this section, some preliminaries and notations related to fractional calculus and sinc basis functions are given. For more details we refer the reader to monographs [1–7, 33–35].

Definition 1

Let \(f:[a,b]\rightarrow\mathbb{R}\) be a function, α a positive real number, n the integer satisfying \(n-1\leq\alpha< n\), and Γ the Euler gamma function. Then the left Caputo fractional derivative of order α of \(f(x)\) is given as

$$ f^{(\alpha)}(x)=\frac{1}{\Gamma(n-\alpha)} \int_{a}^{x} (x-t)^{n-\alpha-1}f^{(n)}(t)\,dt. $$
(2.1)

Theorem 1

Let be \(\alpha>0\) and \(n \in\mathbb{N}\) such that \(n-1< \alpha\leq n\) and \(f(x)\in C^{n}[a,b]\) then

$$f^{(\alpha)}(x)=I^{(n-\alpha)}f^{(n)}(x). $$

Theorem 2

Let be \(\alpha>0\) and \(D^{(\alpha)}\) is Riemann-Liouville fractional derivative. If f is continuous, then

$$D^{(\alpha)}I^{(\alpha)}f(x)=f(x). $$

Definition 2

The sinc function is defined on the whole real line \(-\infty< x<\infty\) by

$$\operatorname{sinc}(x) = \textstyle\begin{cases} \frac{\sin(\pi x)}{\pi x}, & x\neq0,\\ 1, & x=0. \end{cases} $$

Definition 3

For \(h>0\) and \(k=0,\pm1,\pm2,\ldots\) the translated sinc function with space node is given by

$$S(k,h) (x)=\operatorname{sinc}\biggl(\frac{x-kh}{h}\biggr) = \textstyle\begin{cases} \frac{\sin(\pi\frac{x-kh}{h})}{\pi\frac{x-kh}{h}}, & x\neq kh,\\ 1, & x=kh. \end{cases} $$

Definition 4

If \(f(x)\) is defined on the real line, then for \(h>0\) the series

$$C(f,h) (x)=\sum_{k=-\infty}^{\infty}f(kh) \operatorname{sinc}\biggl(\frac{x-kh}{h}\biggr) $$

is called the Whittaker cardinal expansion of f whenever this series converges.

In general, approximations can be constructed for infinite, semi-infinite and finite intervals. To construct an approximation on the interval \((a,b)\) the conformal map

$$ \phi(z)=\ln\biggl(\frac{z-a}{b-z}\biggr) $$
(2.2)

is employed. This map carries \(D_{E}\) the eye-shaped domain in the z-plane

$$D_{E}=\biggl\{ z=x+iy: \biggl\vert \operatorname{arg}\biggl(\frac{z-a}{b-z} \biggr) \biggr\vert < d\leq\frac{\pi}{2}\biggr\} $$

onto the infinite strip \(D_{S}\)

$$D_{S}\equiv\biggl\{ w=u+iv: \vert v \vert < d\leq\frac{\pi}{2} \biggr\} . $$

The basis functions on the interval \((a,b)\) are derived from the composite translated sinc functions

$$S_{k}(z)=S(k,h) (z)\circ \phi(z)=\operatorname{sinc}\biggl( \frac{\phi(z)-kh}{h}\biggr) $$

for \(z\in D_{E}\). The inverse map of \(w=\phi(z)\) is

$$z=\phi^{-1}(w)=\frac{a+be^{w}}{1+e^{w}}. $$

The sinc grid points \(z_{k}\in(a,b)\) in \(D_{E}\) will be denoted by \(x_{k}\) because they are real. For the evenly spaced nodes \(\{kh\}_{k=-\infty }^{\infty}\) on the real line, the image which corresponds to these nodes is denoted by

$$x_{k}=\phi^{-1}(kh)=\frac{a+be^{kh}}{1+e^{kh}},\quad k=0,\pm1, \pm2,\ldots. $$

Definition 5

Let \(D_{E}\) be a simply connected domain in the complex plane \(\mathbb {C}\), and let \(\partial D_{E}\) denote the boundary of \(D_{E}\). Let a, b be points on \(\partial D_{E}\) and ϕ be a conformal map \(D_{E}\) onto \(D_{S}\) such that \(\phi(a)=-\infty\) and \(\phi(b)=\infty\). If the inverse map of ϕ is denoted by φ, define

$$\Gamma=\bigl\{ \phi^{-1}(u)\in D_{E}:-\infty< u< \infty\bigr\} $$

and \(z_{k}=\varphi(kh)\), \(k=0,\pm1,\pm2,\ldots\) .

Definition 6

Let \(B(D_{E})\) be the class of functions F that are analytic in \(D_{E}\) and satisfy

$$\int_{\psi(L+u)} \bigl\vert F(z) \bigr\vert \,dz\rightarrow0,\quad \text{as } u=\mp\infty, $$

where

$$L=\biggl\{ iy: \vert y \vert < d\leq\frac{\pi}{2}\biggr\} , $$

and those on the boundary of \(D_{E}\) satisfy

$$T(F)= \int_{\partial D_{E}} \bigl\vert F(z)\,dz \bigr\vert < \infty. $$

Theorem 3

Let Γ be \((0,1)\), \(F\in B(D_{E})\), then, for \(h>0\) sufficiently small,

$$\begin{aligned} \int_{\Gamma}F(z)\,dz-h\sum_{j=-\infty}^{\infty} \frac{F(z_{j})}{\phi'(z_{j})}=\frac{i}{2} \int_{\partial D}\frac{F(z)k(\phi,h)(z)}{\sin(\pi\phi(z)/h)}\,dz\equiv I_{F}, \end{aligned}$$
(2.3)

where

$$\bigl\vert k(\phi,h) \bigr\vert _{z\in\partial D}= \bigl\vert e^{[\frac{i\pi\phi(z)}{h}\operatorname{sgn}(\operatorname{Im}\phi(z))]} \bigr\vert _{z\in\partial D}=e^{\frac{-\pi d}{h}}. $$

Proof

See [18]. □

For the term of fractional in (1.1), the infinite quadrature rule must be truncated to a finite sum. The following theorem indicates the conditions under which an exponential convergence results.

Theorem 4

If there exist positive constants α, β and C such that

$$ \biggl\vert \frac{F(x)}{\phi'(x)} \biggr\vert \leq C \textstyle\begin{cases} e^{-\alpha \vert \phi(x) \vert }, & x\in\psi((-\infty,\infty)),\\ e^{-\beta \vert \phi(x) \vert }, & x\in\psi((0,\infty)), \end{cases} $$
(2.4)

then the error bound for the quadrature rule (2.3) is

$$ \Biggl\vert \int_{\Gamma}F(x)\,dx-h\sum_{j=-M}^{N} \frac{F(x_{j})}{\phi'(x_{j})} \Biggr\vert \leq C\biggl(\frac{e^{-\alpha Mh}}{\alpha}+ \frac{e^{-\beta Nh}}{\beta}\biggr)+ \vert I_{F} \vert . $$
(2.5)

Proof

See [18]. □

The infinite sum in (2.3) is truncated with the use of (2.4) to arrive at the inequality (2.5). Making the selections

$$h=\sqrt{\frac{\pi d}{\alpha M}} $$

and

$$N\equiv\biggl[\biggl\lfloor \frac{\alpha M}{\beta}+1 \biggr\rfloor \biggr] $$

where \([\lfloor\cdot \rfloor]\) is an integer part of the statement and M is the integer value which specifies the grid size, then

$$ \int_{\Gamma}F(x)\,dx=h\sum_{j=-M}^{N} \frac{F(x_{j})}{\phi'(x_{j})}+O\bigl(e^{-(\pi\alpha \,d M)^{1/2}}\bigr). $$
(2.6)

We used these theorems to approximate the arising integral in the formulation of the term fractional in (1.1).

Lemma 1

Let ϕ be the conformal one-to-one mapping of the simply connected domain \(D_{E}\) onto \(D_{S}\), given by (2.2). Then

$$\begin{aligned}& \delta_{jk}^{(0)} =\bigl[S(j,h)\circ \phi(x)\bigr]\big\vert _{x=x_{k}} \textstyle\begin{cases} 1, & j=k,\\ 0, & j\neq k, \end{cases}\displaystyle \\& \delta_{jk}^{(1)} =h\frac{d}{d\phi}\bigl[S(j,h)\circ \phi(x) \bigr]\bigg\vert _{x=x_{k}} \textstyle\begin{cases} 0, & j=k,\\ \frac{(-1)^{k-j}}{k-j}, & j\neq k, \end{cases}\displaystyle \\& \delta_{jk}^{(2)} =h^{2}\frac{d^{2}}{d\phi^{2}} \bigl[S(j,h)\circ \phi(x)\bigr]\bigg\vert _{x=x_{k}} \textstyle\begin{cases} -\frac{\pi^{2}}{3}, & j=k,\\ \frac{-2(-1)^{k-j}}{(k-j)^{2}}, & j\neq k. \end{cases}\displaystyle \end{aligned}$$

Proof

See [36]. □

3 The sinc-collocation method

We assume approximate solutions for problem (1.1) by the finite expansion of the sinc basis functions

$$ \textstyle\begin{cases} u_{n}(x)=\sum_{k=-M}^{N}c_{k}S_{k}(x), & n=M+N+1,\\ v_{n}(x)=\sum_{k=-M}^{N}d_{k}S_{k}(x), & n=M+N+1, \end{cases} $$
(3.1)

where \(S_{k}(x)\) is the function \(S(k,h)\circ\phi(x)\). Here, the unknown coefficients are determined by the sinc-collocation method via the following theorems.

Theorem 5

Let be a function \(f(x)=\sum_{k=-M}^{N}c_{k}S_{k}(x)\) defined as the finite expansion of sinc basis functions, then the first and second derivatives of \(f(x)\) are given by

$$\begin{aligned}& \frac{d}{dx}f(x) = \sum_{k=-M}^{N}c_{k} \phi'(x)\frac{d}{d\phi}S_{k}(x) , \end{aligned}$$
(3.2)
$$\begin{aligned}& \frac{d^{2}}{dx^{2}}f(x) = \sum_{k=-M}^{N}c_{k} \biggl(\phi''(x)\frac{d}{d\phi}S_{k}(x)+ \bigl(\phi'\bigr)^{2}\frac{d^{2}}{d\phi^{2}}S_{k}(x) \biggr), \end{aligned}$$
(3.3)

respectively.

Similarly, the order α derivative of \(f(x)\) for \(0<\alpha<1\) is given by the following theorem.

Theorem 6

If ψ is a conformal map for the interval \([a,x]\), then the order α Caputo derivative of \(f(x)\) for \(0<\alpha<1\) is given by

$$ f^{(\alpha)}(x)=\sum_{k=-M}^{N}c_{k}S_{k}^{(\alpha)}(x), $$
(3.4)

where

$$S_{k}^{(\alpha)}(x)\approx\frac{h_{L}}{\Gamma(1-\alpha)}\sum _{r=-L}^{L}\frac{(x-x_{r})S'_{k}(x_{r})}{\psi'(x_{r})}. $$

Proof

We use the definition of the Caputo fractional derivative given in (2.1), writing

$$f^{(\alpha)}(x)=\sum_{k=-M}^{N}c_{k}S_{k}^{(\alpha)}(x), $$

where

$$S_{k}^{(\alpha)}(x)=\frac{1}{\Gamma(1-\alpha)} \int_{a}^{x}(x-t)^{-\alpha}S'_{k}(t)\,dt. $$

Now we use the quadrature rule given in (2.6) to compute the above integral, which is divergent on the interval \([a,x]\). For this purpose, a conformal map and its inverse image that denotes the sinc grid points are given by

$$\psi(t)=\ln\biggl(\frac{t-a}{x-t}\biggr) $$

and

$$x_{r}=\psi^{-1}(rh_{L})=\frac{a+xe^{rh_{L}}}{1+e^{rh_{L}}}, $$

where \(h_{L}=\pi/\sqrt{L}\). Then, according to equality (2.6), we write

$$S_{k}^{(\alpha)}(x)\approx\frac{h_{L}}{\Gamma(1-\alpha)}\sum _{r=-L}^{L}\frac{(x-x_{r})S'_{k}(x_{r})}{\psi'(x_{r})}. $$

This completes the proof. □

Using in terms of (1.1) the approximations given in (3.1)-(3.4), multiplying the resulting equation by \(\{(1/\phi ')^{2}\}\), we obtain the following linear system:

$$\begin{aligned} \textstyle\begin{cases} \sum_{k=-M}^{N}[c_{k}\{\sum_{i=0}^{2}g_{i}(x)\frac{d^{i}}{d\phi^{i}}S_{k} +g_{3}(x)S_{k}^{(\alpha_{1})}\} +d_{k}\{\sum_{i=0}^{2}p_{i}(x)\frac{d^{i}}{d\phi^{i}}S_{k} +p_{3}(x)S_{k}^{(\beta_{1})}\}]\\ \quad = (f_{1}(x)(\frac{1}{\phi'(x)})^{2}),\\ \sum_{k=-M}^{N}[c_{k}\{\sum_{i=0}^{2}r_{i}(x)\frac{d^{i}}{d\phi^{i}}S_{k} +r_{3}(x)S_{k}^{(\alpha_{2})}\} +d_{k}\{\sum_{i=0}^{2}q_{i}(x)\frac{d^{i}}{d\phi^{i}}S_{k} +q_{3}(x)S_{k}^{(\beta_{2})}\}]\\ \quad = (f_{2}(x)(\frac{1}{\phi'(x)})^{2}), \end{cases}\displaystyle \end{aligned}$$

where

$$\begin{aligned}& g_{0}(x) = \mu_{0}(x) \biggl(\frac{1}{\phi'(x)} \biggr)^{2}, \\& g_{1}(x) = \biggl[\mu_{1}(x) \biggl(\frac{1}{\phi'(x)} \biggr)-\mu_{2}(x) \biggl(\frac{1}{\phi'(x)}\biggr)' \biggr], \\& g_{2}(x) = \mu_{2}(x), \\& g_{3}(x) = \mu_{\alpha_{1}}(x) \biggl(\frac{1}{\phi'(x)} \biggr)^{2}, \\& p_{0}(x) = \xi_{0}(x) \biggl(\frac{1}{\phi'(x)} \biggr)^{2}, \\& p_{1}(x) = \biggl[\xi_{1}(x) \biggl(\frac{1}{\phi'(x)} \biggr)-\xi_{2}(x) \biggl(\frac{1}{\phi'(x)}\biggr)' \biggr], \\& p_{2}(x) = \xi_{2}(x), \\& p_{3}(x) = \xi_{\beta_{1}}(x) \biggl(\frac{1}{\phi'(x)} \biggr)^{2}, \\& r_{0}(x) = \gamma_{0}(x) \biggl(\frac{1}{\phi'(x)} \biggr)^{2}, \\& r_{1}(x) = \biggl[\gamma_{1}(x) \biggl(\frac{1}{\phi'(x)} \biggr)-\gamma_{2}(x) \biggl(\frac{1}{\phi'(x)}\biggr)' \biggr], \\& r_{2}(x) = \gamma_{2}(x), \\& r_{3}(x) = \gamma_{\alpha_{2}}(x) \biggl(\frac{1}{\phi'(x)} \biggr)^{2}, \end{aligned}$$

and

$$\begin{aligned}& q_{0}(x) = \eta_{0}(x) \biggl(\frac{1}{\phi'(x)} \biggr)^{2}, \\& q_{1}(x) = \biggl[\eta_{1}(x) \biggl(\frac{1}{\phi'(x)} \biggr)-\eta_{2}(x) \biggl(\frac{1}{\phi'(x)}\biggr)' \biggr], \\& q_{2}(x) = \eta_{2}(x), \\& q_{3}(x) = \eta_{\beta_{2}}(x) \biggl(\frac{1}{\phi'(x)} \biggr)^{2}. \end{aligned}$$

By using Lemma 1, we know that

$$\delta_{jk}^{(0)}=\delta_{kj}^{(0)},\qquad \delta_{jk}^{(1)}=-\delta_{kj}^{(1)},\qquad \delta_{jk}^{(2)}=\delta_{kj}^{(2)} , $$

then we obtain the following theorem setting \(x=x_{j}\) in the above systems.

Theorem 7

If the assumed approximate solution of boundary value problem (1.1) is (3.1), then the discrete sinc-collocation system for the determination of the unknown coefficients is given by

$$ \textstyle\begin{cases} \sum_{k=-M}^{N}[c_{k}\{\sum_{i=0}^{2}\frac{g_{i}(x_{j})(-1)^{i}}{h^{i}}\delta_{jk}^{(i)} +g_{3}(x_{j})S_{k}^{(\alpha_{1})}(x_{j})\} \\\quad {}+d_{k}\{\sum_{i=0}^{2}\frac{p_{i}(x_{j})(-1)^{i}}{h^{i}}\delta_{jk}^{(i)} +p_{3}(x_{j})S_{k}^{(\beta_{1})}(x_{j})\}] =(f_{1}(x_{j})(\frac{1}{\phi'(x_{j})})^{2}),\\ \sum_{k=-M}^{N}[c_{k}\{\sum_{i=0}^{2}\frac{r_{i}(x_{j})(-1)^{i}}{h^{i}}\delta_{jk}^{(i)} +r_{3}(x_{j})S_{k}^{(\alpha_{2})}(x_{j})\} \\\quad {}+d_{k}\{\sum_{i=0}^{2}\frac{q_{i}(x_{j})(-1)^{i}}{h^{i}}\delta_{jk}^{(i)} +q_{3}(x_{j})S_{k}^{(\beta_{2})}(x_{j})\}] =(f_{2}(x_{j})(\frac{1}{\phi'(x_{j})})^{2}),\\ \textit{for } j=-M,-M+1,\ldots,N. \end{cases} $$
(3.5)

Now we define some notations to represent in the matrix-vector form for system (3.5). Let \(\mathbf{D}(y)\) denote a diagonal matrix whose diagonal elements are \(y(x_{-M}),y(x_{-M+1}),{\ldots},y(x_{N})\) and non-diagonal elements are zero, let \(\mathbf{G}_{\alpha}=S_{k}^{(\alpha )}(x_{j})\) denote a matrix and also let \(\mathbf{I}^{(i)}\) denote the matrices

$$I^{(i)}=\bigl[\delta_{jk}^{(i)}\bigr],\quad i=0,1,2, $$

where D, \(\mathbf{G}_{\alpha}\), \(\mathbf{I}^{(0)}\), \(\mathbf {I}^{(1)}\) and \(\mathbf{I}^{(2)}\) are square matrices of order \(n\times n\). In order to calculate the unknown coefficients \(c_{k}\) in linear system (3.5), we rewrite this system by using the above notations in matrix-vector form as

$$ \mathbf{A}\mathbf{c}=\mathbf{B} $$
(3.6)

where

Now we have a linear system of n equations in the n unknown coefficients given by (3.6). When it is solved, we can obtain the unknown coefficients that are necessary for an approximate solution in (3.1).

4 Computational examples

In this section, two problems that have homogeneous boundary conditions will be tested by using the present method via Mathematica10 on a personal computer. In all the examples, we take \(d=\pi/2\), \(L=M=N\).

Example 1

Consider system of fractional boundary value problem in the following form:

$$\textstyle\begin{cases} u''(x)-v'(x)+v^{(0.4)}(x)+v(x)=f_{1}(x),\\ v''(x)-u'(x)+u^{(0.6)}(x)+u(x)=f_{2}(x), \end{cases} $$

subject to the homogeneous boundary conditions

$$u(0)=u(1)=0, \qquad v(0)=v(1)=0, $$

where

$$\begin{aligned}& f_{1}(x) = 11 x^{2}+3x-1 -\frac{2x^{1.6}}{\Gamma(2.6)}+ \frac{x^{0.6}}{\Gamma(1.6)}, \\& f_{2}(x) = x^{4}-4x^{3}-x-1+\frac{24x^{3.4}}{\Gamma(4.4)}- \frac{x^{0.4}}{\Gamma(1.4)}, \end{aligned}$$

whose exact solutions are

$$u(x)=x\bigl(x^{3}-1\bigr), \qquad v(x)=x(1-x). $$

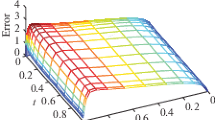
The numerical solutions which are obtained by using the sinc-collocation method (SCM) for this problem are presented in Table 1 and Table 2. In addition to, the graphics of the exact and approximate solutions for different values of N are given in Figure 1 and Figure 2.

Figure 1
figure 1

Graphs of exact and approximate solutions for u in Example  1 .

Full size image
Figure 2
figure 2

Graphs of exact and approximate solutions for v in Example  1 .

Full size image
Table 1 Maximum absolute error for Example  1
Full size table
Table 2 Numerical results for Example  1 when \(\pmb{N=40}\)
Full size table

Example 2

Consider the system of the fractional boundary value problem in the following form:

$$\textstyle\begin{cases} u''(x)+(2x-1)u'(x)+u^{(0.3)}(x)+\cos(\pi x)v(x)=f_{1}(x),\\ v''(x)+v^{(0.7)}(x)+x u(x)=f_{2}(x), \end{cases} $$

subject to the homogeneous boundary conditions

$$u(0)=u(1)=0, \qquad v(0)=v(1)=0, $$

where

$$\begin{aligned}& f_{1}(x) = 6 x^{3}-7x^{2}+8x-2+(1-2x)\cos(\pi x)+ \frac{6x^{2.7}}{\Gamma(3.7)}-\frac{2x^{1.7}}{\Gamma(2.7)}, \\& f_{2}(x) = x^{4}-x^{3}-2+\frac{x^{0.3}}{\Gamma(1.3)}- \frac{2x^{1.3}}{\Gamma(2.3)}, \end{aligned}$$

whose exact solutions are

$$u(x)=x^{2}(x-1), \qquad v(x)=x(1-x) $$

The numerical solutions which are obtained by using the sinc-collocation method (SCM) for this problem are presented in Table 3 and Table 4. In addition, the graphics of the exact and approximate solutions for different values of N are given in Figure 3 and Figure 4.

Figure 3
figure 3

Graphs of exact and approximate solutions for u in Example  2 .

Full size image
Figure 4
figure 4

Graphs of exact and approximate solutions for v in Example  2 .

Full size image
Table 3 Maximum absolute error for Example  2
Full size table
Table 4 Numerical results for Example  2 when \(\pmb{N=40}\)
Full size table

5 Conclusion

This study focuses on the application of the sinc-collocation method to obtain the approximate solutions of the system of fractional order differential equations (1.1). The proposed method is applied to some special examples in order to illustrate the applicability and accuracy of the proposed method for equation (1.1). Obtained numerical solutions are compared with exact solutions and results are presented in tables and by graphics. Regarding the findings, it can be concluded that the sinc-collocation method is an effective and convenient method for obtaining the approximate solution of a system differential equations of fractional order.