Sinc-Galerkin method for approximate solutions of fractional order boundary value problems

Abstract

In this paper we present an approximate solution of a fractional order two-point boundary value problem (FBVP). We use the sinc-Galerkin method that has almost not been employed for the fractional order differential equations. We expand the solution function in a finite series in terms of composite translated sinc functions and some unknown coefficients. These coefficients are determined by writing the original FBVP as a bilinear form with respect to some base functions. The bilinear forms are expressed by some appropriate integrals. These integrals are approximately solved by sinc quadrature rule where a conformal map and its inverse are evaluated at sinc grid points. Obtained results are presented as two new theorems. In order to illustrate the applicability and accuracy of the present method, the method is applied to some specific examples, and simulations of the approximate solutions are provided. The results are compared with the ones obtained by the Cubic splines. Because there are only a few studies regarding the application of sinc-type methods to fractional order differential equations, this study is going to be a totally new contribution and highly useful for the researchers in fractional calculus area of scientific research.

1 Introduction

Fractional calculus is one of the most novel types of calculus having a broad range of applications in many different scientific and engineering disciplines. Order of the derivatives in the fractional calculus might be any real number which separates the fractional calculus from the ordinary calculus where the derivatives are allowed only positive integer numbers. Therefore fractional calculus might be considered as an extension of ordinary calculus. Fractional calculus is a highly useful tool in the modeling of many sorts of scientific phenomena including image processing, earthquake engineering, biomedical engineering and physics. In the references [1] and [2] (amongst many others), fundamental concepts of fractional calculus and applications of it to different scientific and engineering areas are studied in a quite neat manner. Interested reader can read those references in conjunction with the present paper to have a detailed information of this significantly useful type of calculus.

Even though fractional calculus is a highly useful and important topic, a general solution method which could be used at almost every sorts of problems has not yet been established. Most of the solution techniques in this area have been developed for particular sorts of problems. As a result, a single standard method for problems regarding fractional calculus has not emerged. Therefore, finding reliable and accurate solution techniques along with fast implementation methods is useful and active research area. Some well-known methods for the analytical and numerical solutions of fractional differential and integral equations might be listed as power series method [3], differential transform method [4] and [5], homotopy analysis method [6], variational iteration method [7] and homotopy perturbation method [8]. Typical numerical methods including collocation, finite differences and elements are among the most popular numerical techniques, and detailed information about most of these techniques can be obtained from, for instance, [9–11] and the aforementioned references.

In this paper we propose a new solution technique for approximate (or alternatively saying numerical) solution of a fractional order two-point boundary value problem (FBVP). We use the sinc-Galerkin method that has almost not been employed for the fractional order differential equations. We expand the solution function in a finite series in terms of composite translated sinc functions and some unknown coefficients. These coefficients are determined by writing the original FBVP as a bilinear form with respect to some basis functions. Bearing in mind the methodology of the sinc-Galerkin method, these bilinear forms are expressed by some integrals. These integrals are approximately solved by the sinc quadrature rule where a conformal map and its inverse are evaluated at sinc grid points. Finally, it is proved that some new results are obtained as a new contribution to the subject.

Although there are several studies about the applications of sinc function-based methods to deterministic boundary value problems such as [12] and [13], the applicability of the sinc functions-based methods has not been investigated in detail at the numerical solutions of fractional order differential equations. The most significant methods employing sinc functions at the numerical solution of differential equations might be given as the sinc-Nyström method [14] and the method presented in [15].

The rest of this paper is organized as follows. Section 2 reviews the underlying ideas and basic theorems of fractional calculus and sinc-Galerkin technique. In Section 3 we apply the sinc-Galerkin method to a general two-point boundary value problem. In the same section, the obtained results are presented as two new theorems. In Section 4 we present three specific examples in order to illustrate the applicability and accuracy of the present method. Simulations of the approximate solutions are provided. The results are compared with the ones obtained by the Cubic splines. Because there are only a few studies regarding the application of sinc-type methods to fractional order differential equations, this study is going to be a totally new contribution and highly useful for the researchers in fractional calculus area of scientific research. We illustrate the results in the simulations and tables. We complete the paper with a conclusion section where we briefly overview the present paper and discuss some future extensions of this research.

2 Preliminaries

2.1 Fractional calculus

In this section, firstly we present the definitions of the Riemann-Liouville and the Caputo of fractional derivative. Also, we give the definition of integration by parts of fractional order by using these definitions.

Definition 2.1 [16]

Let be a function, α be a positive real number, n be the integer satisfying $n-1\le \alpha <n$, and Γ be the Euler gamma function. Then:

• i. The left and right Riemann-Liouville fractional derivatives of order α of $f(x)$ are given as

  $${}_{a}D_x^{\alpha }f(x)=\frac{1}{\mathrm{\Gamma }(n-\alpha )}\frac{d^n}{d{x}^n}{\int }_a^x{(x-t)}^{n-\alpha -1}f(t)dt$$

  (2.1)

and

$${}_{x}D_b^{\alpha }f(x)=\frac{{(-1)}^n}{\mathrm{\Gamma }(n-\alpha )}\frac{d^n}{d{x}^n}{\int }_x^b{(t-x)}^{n-\alpha -1}f(t)dt,$$

(2.2)

respectively.

• ii. The left and right Caputo fractional derivatives of order α of $f(x)$ are given as

  $${}_a{}^{C}D_x^{\alpha }f(x)=\frac{1}{\mathrm{\Gamma }(n-\alpha )}{\int }_a^x{(x-t)}^{n-\alpha -1}{f}^{(n)}(t)dt$$

  (2.3)

and

$${}_x{}^{C}D_b^{\alpha }f(x)=\frac{1}{\mathrm{\Gamma }(n-\alpha )}{\int }_x^b{(-1)}^n{(t-x)}^{n-\alpha -1}{f}^{(n)}(t)dt,$$

(2.4)

respectively.

Now we can write the definition of integration by parts of fractional order by using the relations given in (2.1)-(2.4).

Definition 2.2 [16]

If $0<\alpha <1$ and f is a function such that $f(a)=f(b)=0$, we can write

$${\int }_a^{b}g{(x)}_a^C{D}_x^{\alpha }f(x)dx={\int }_a^{b}f{(x)}_x{D}_b^{\alpha }g(x)dx$$

(2.5)

and

$${\int }_a^{b}g{(x)}_x^C{D}_b^{\alpha }f(x)dx={\int }_a^{b}f{(x)}_a{D}_x^{\alpha }g(x)dx.$$

2.2 Sinc basis functions properties and quadrature interpolations

In this section, we recall notations and definitions of the sinc function, state some known results, and derive useful formulas that are important for this paper.

The sinc basis functions

Definition 2.3 [17]

The function defined all by

$$sinc(z)=\{\begin{array}{ll}\frac{sin(\pi z)}{\pi z},& z\ne 0,\\ 1,& z=0,\end{array}$$

(2.6)

is called the sinc function.

Definition 2.4 [17]

Let f be a function defined on ℝ, and let $h>0$. Define the series

$$C(f,h)(x)=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}f(kh)sinc\left(\frac{x-kh}{h}\right),$$

(2.7)

where from (2.6)

$$S(k,h)(x)=sinc\left(\frac{x-kh}{h}\right)=\{\begin{array}{ll}\frac{sin(\pi \frac{x-kh}{h})}{\pi \frac{x-kh}{h}},& x\ne kh,\\ 1,& x=kh.\end{array}$$

Whenever the series in (2.7) converges, it is called the Whittaker cardinal function of f. They are based on the infinite strip $D_s$ in the complex plane

$$D_s\equiv \{w=u+iv:|v|<d\le \frac{\pi }{2}\}.$$

In general, approximations can be constructed for infinite, semi-infinite and finite intervals. Define the function

$$w=\varphi (z)=ln\left(\frac{z}{1-z}\right)$$

(2.8)

which is a conformal mapping from $D_E$, the eye-shaped domain in the z-plane, onto the infinite strip $D_S$, where

$$D_E=z=\{x+iy:|arg\left(\frac{z}{1-z}\right)|<d\le \frac{\pi }{2}\}.$$

This is shown in Figure 1. For the sinc-Galerkin method, the basis functions are derived from the composite translated sinc functions

$$S_k(z)=S(k,h)(z)o\varphi (z)=sinc\left(\frac{\varphi (z)-kh}{h}\right)$$

(2.9)

for$z\in D_E$. The function $z={\varphi }^{-1}(w)=\frac{e^w}{1+e^w}$ is an inverse mapping of $w=\varphi (z)$. We may define the range of ${\varphi }^{-1}$ on the real line as

$$\mathrm{\Gamma }=\{{\varphi }^{-1}(u)\in D_E:-\mathrm{\infty }<u<\mathrm{\infty }\},$$

the evenly spaced nodes ${\{kh\}}_{k=-\mathrm{\infty }}^{\mathrm{\infty }}$ on the real line. The image which corresponds to these nodes is denoted by

$$x_k={\varphi }^{-1}(kh)=\frac{e^{kh}}{1+e^{kh}}.$$

Figure 1

The domains ${\mathit{D}}_{\mathit{E}}$ and ${\mathit{D}}_{\mathit{S}}$ .

Sinc function interpolation and quadratures

Definition 2.5 [18]

Let $D_E$ be a simply connected domain in the complex plane C, and let $\partial D_E$ denote the boundary of $D_E$. Let a, b be points on $\partial D_E$ and ϕ be a conformal map $D_E$ onto $D_S$ such that $\varphi (a)=-\mathrm{\infty }$ and $\varphi (b)=\mathrm{\infty }$. If the inverse map of ϕ is denoted by φ, define

$$\mathrm{\Gamma }=\{{\varphi }^{-1}(u)\in D_E:-\mathrm{\infty }<u<\mathrm{\infty }\}$$

and $z_k=\phi (kh)$, $k=\pm 1,\pm 2,\dots$ .

Definition 2.6 [18]

Let $B(D_E)$ be the class of functions F that are analytic in $D_E$ and satisfy

$${\int }_{\psi (L+u)}|F(z)|dz\to 0,\text{as }u=\mp \mathrm{\infty },$$

where

$$L=\{iy:|y|<d\le \frac{\pi }{2}\},$$

and those on the boundary of $D_E$ satisfy

$$T(F)={\int }_{\partial D_E}|F(z)dz|<\mathrm{\infty }.$$

Theorem 2.7 [18]

Let Γ be $(0,1)$, $F\in B(D_E)$, then for $h>0$ sufficiently small,

$${\int }_{\mathrm{\Gamma }}F(z)dz-h\sum _{j=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{F(z_j)}{{\varphi }^{\prime }(z_j)}=\frac{i}{2}{\int }_{\partial D}\frac{F(z)k(\varphi ,h)(z)}{sin(\pi \varphi (z)/h)}dz\equiv I_F,$$

(2.10)

where

$$|k(\varphi ,h){|}_{z\in \partial D}=|e^{[\frac{i\pi \varphi (z)}{h}sgn(Im\varphi (z))]}{|}_{z\in \partial D}=e^{\frac{-\pi d}{h}}.$$

For the sinc-Galerkin method, the infinite quadrature rule must be truncated to a finite sum. The following theorem indicates the conditions under which an exponential convergence results.

Theorem 2.8 [18]

If there exist positive constants α, β and C such that

$$\left|\frac{F(x)}{{\varphi }^{\prime }(x)}\right|\le C\{\begin{array}{ll}{e}^{-\alpha |\varphi (x)|},& x\in \psi ((-\mathrm{\infty },\mathrm{\infty })),\\ e^{-\beta |\varphi (x)|},& x\in \psi ((0,\mathrm{\infty })),\end{array}$$

(2.11)

then the error bound for quadrature rule (2.10) is

$$|{\int }_{\mathrm{\Gamma }}F(x)dx-h\sum _{j=-M}^N\frac{F(x_j)}{{\varphi }^{\prime }(x_j)}|\le C(\frac{e^{-\alpha Mh}}{\alpha }+\frac{e^{-\beta Nh}}{\beta })+|I_F|.$$

(2.12)

The infinite sum in (2.10) is truncated with the use of (2.11) to arrive at inequality (2.12). Making the selections

where is an integer part of the statement and M is the integer value which specifies the grid size, then

$${\int }_{\mathrm{\Gamma }}F(x)dx=h\sum _{j=-M}^N\frac{F(x_j)}{{\varphi }^{\prime }(x_j)}+O\left(e^{-{(\pi \alpha dM)}^{\frac{1}{2}}}\right).$$

(2.13)

We used these theorems to approximate the integrals that arise in the formulation of the discrete systems corresponding to a second-order boundary value problem.

3 The sinc-Galerkin method

Consider the linear two-point boundary value problem

$${\mu }_2(x)y^{″}+{\mu }_1(x)y^{\prime }+\lambda {(x)}_0^C{D}_x^{\alpha }y+{\mu }_0(x)y=f(x),0<x<1,0<\alpha <1,$$

(3.1)

with the boundary conditions

$$y(0)=y(1)=0,$$

where ${}_0{}^{C}D_x$ is the Caputo fractional derivative operator.

An approximate solution for $y(x)$ is represented by the formula

$$y_n(x)=\sum _{k=-M}^M{c}_k{S}_k(x),n=2M+1,$$

(3.2)

where $S_k(x)$ is the function $S(k,h)o\varphi (x)$ defined in (2.9) for some fixed step size h. The unknown coefficients $c_k$ in (3.2) are determined by orthogonalizing the residual with respect to the basis functions, i.e.,

$$〈{\mu }_2(x)y^{″},S_k〉+〈{\mu }_1(x)y^{\prime },S_k〉+〈\lambda {(x)}_0^C{D}_x^{\alpha }y,S_k〉+〈{\mu }_0(x)y,S_k〉=〈f(x),S_k〉.$$

(3.3)

The inner product used for the sinc-Galerkin method is defined by

$$〈f,\eta 〉={\int }_a^{b}f(x)\eta (x)w(x)dx,$$

where $w(x)$ is a weight function and it is convenient to take

$$w(x)=\frac{1}{{\varphi }^{\prime }(x)}$$

for the case of second-order problems.

A complete discussion on the choice of the weight function can be found in [17].

Lemma 3.1 [19]

Let ϕ be the conformal one-to-one mapping of the simply connected domain $D_E$ onto $D_S$ given by (2.8). Then

$$\begin{array}{c}{\delta }_{jk}^{(0)}=[S(j,h)o\varphi (x)]{|}_{x=x_k}=\{\begin{array}{ll}1,& j=k,\\ 0,& j\ne k,\end{array}\hfill \\ {\delta }_{jk}^{(1)}=h\frac{d}{d\varphi }[S(j,h)o\varphi (x)]{|}_{x=x_k}=\{\begin{array}{ll}0,& j=k,\\ \frac{{(-1)}^{k-j}}{k-j},& j\ne k,\end{array}\hfill \\ {\delta }_{jk}^{(2)}=h^2\frac{d^2}{d{\varphi }^2}[S(j,h)o\varphi (x)]{|}_{x=x_k}=\{\begin{array}{ll}-\frac{{\pi }^2}{3},& j=k,\\ \frac{-2{(-1)}^{k-j}}{{(k-j)}^2},& j\ne k.\end{array}\hfill \end{array}$$

The method of approximating the integrals in (3.3) begins by integrating by parts to transfer all derivatives from y to $S_k$. The following theorems, which can easily be proved by using Lemma 3.1 and Definition 2.2, are used to solve equation (3.1).

Theorem 3.2 [20]

The following relations hold:

$$〈{\mu }_2(x)y^{″},S_k〉\cong h\sum _{k=-M}^M\sum _{i=0}^2\frac{y(x_k)}{{\varphi }^{\prime }(x_k)h^i}{\delta }_{jk}^{(i)}{g}_{2,i},$$

(3.4)

$$〈{\mu }_1(x)y^{\prime },S_k〉\cong -h\sum _{k=-M}^M\sum _{i=0}^1\frac{y(x_k)}{{\varphi }^{\prime }(x_k)h^i}{\delta }_{jk}^{(i)}{g}_{1,i}$$

(3.5)

and

$$〈G,S_k〉\cong h\frac{G(x_k)w(x_k)}{{\varphi }^{\prime }(x_k)},$$

(3.6)

where

$$\begin{array}{r}{g}_{2,2}=({\mu }_{2}w){\left({\varphi }^{\prime }\right)}^2,g_{2,1}=({\mu }_{2}w){\varphi }^{″}+2{({\mu }_{2}w)}^{\prime }{\varphi }^{\prime },g_{2,0}={({\mu }_{2}w)}^{″},\\ g_{1,1}=({\mu }_{1}w){\varphi }^{\prime },g_{1,0}={({\mu }_{1}w)}^{\prime }\end{array}$$

and

$$G={\mu }_{0}y\mathit{\text{or}}f(x).$$

Theorem 3.3 For $0<\alpha <1$, the following relation holds:

$$\begin{array}{c}〈\lambda {(x)}_0^C{D}_x^{\alpha }y(x),S_k〉\hfill \\ \cong -\frac{h_M}{\mathrm{\Gamma }(1-\alpha )}\sum _{k=-M}^M\frac{y(x_k)}{{\varphi }^{\prime }(x_k)}\frac{d}{dx}\left[h_L\sum _{r=-L}^L\frac{{(x_r-x)}^{-\alpha }K(x_r)}{{\xi }^{\prime }(x_r)}\right]{|}_{x=x_k},-M\le j\le M,\hfill \end{array}$$

(3.7)

where $K(x)=\lambda (x)S_k(x)w(x)$, $\xi (t)=ln(\frac{t-x}{1-t})$.

Proof The inner product with sinc basis element is given by

$$〈\lambda {(x)}_0^C{D}_x^{\alpha }y(x),S_k〉={\int }_0^1{(\lambda (x)S_k(x)w(x))}_0^C{D}_x^{\alpha }y(x)dx.$$

Using Definition 2.2, we can write

$${\int }_0^1{(\lambda (x)S_k(x)w(x))}_0^C{D}_x^{\alpha }y(x)dx={\int }_0^{1}y{(x)}_x^R{D}_1^{\alpha }(K(x))dx,$$

(3.8)

where $K(x)=\lambda (x)S_k(x)w(x)$. By the definition of the Riemann-Liouville fractional derivative given in (2.2), we have

$${}_x{}^{R}D_1^{\alpha }(K(x))=-\frac{1}{\mathrm{\Gamma }(1-\alpha )}\frac{d}{dx}{\int }_x^1{(t-x)}^{-\alpha }K(t)dt.$$

(3.9)

We will use the sinc quadrature rule given with equation (2.13) to compute it because the integral given in (3.9) is divergent on the interval $[x,1]$. For this purpose, a conformal map and its inverse image that denotes the sinc grid points are given by

$$\xi (t)=ln\left(\frac{t-x}{1-t}\right)$$

and

$$x_r={\xi }^{-1}(r{h}_L)=\frac{e^{r{h}_L}+x}{1+e^{r{h}_L}},$$

respectively. Then, according to equality (2.13), we write

$$-\frac{1}{\mathrm{\Gamma }(1-\alpha )}\frac{d}{dx}{\int }_x^1{(t-x)}^{-\alpha }K(t)dt\cong -\frac{1}{\mathrm{\Gamma }(1-\alpha )}\frac{d}{dx}\left[h_L\sum _{r=-L}^L\frac{{(x_r-x)}^{-\alpha }K(x_r)}{{\xi }^{\prime }(x_r)}\right],$$

where $h_L=\pi /\sqrt{L}$. Thus, the right-hand side of (3.8) can be rewritten as follows:

$${\int }_0^{1}y{(x)}_x^R{D}_1^{\alpha }(K(x))dx\cong -\frac{1}{\mathrm{\Gamma }(1-\alpha )}{\int }_0^1(y(x)\frac{d}{dx}\left[h_L\sum _{r=-L}^L\frac{{(x_r-x)}^{-\alpha }K(x_r)}{{\xi }^{\prime }(x_r)}\right])dx.$$

(3.10)

To apply the sinc quadrature rule given in (2.13) on the right-hand side of (3.10), a conformal map and its inverse image are given by

$$\varphi (t)=ln\left(\frac{t}{1-t}\right)$$

and

$$x_k={\varphi }^{-1}(kh)=\frac{e^{kh}}{1+e^{kh}},$$

respectively. Consequently, when the rule is applied, it is obtained

$$\begin{array}{c}〈\lambda {(x)}_0^C{D}_x^{\alpha }y(x),S_k〉\hfill \\ \cong -\frac{h}{\mathrm{\Gamma }(1-\alpha )}\sum _{k=-M}^M\frac{y(x_k)}{{\varphi }^{\prime }(x_k)}\frac{d}{dx}\left[h_L\sum _{r=-L}^L\frac{{(x_r-x)}^{-\alpha }K(x_r)}{{\xi }^{\prime }(x_r)}\right]{|}_{x=x_k},-M\le j\le M,\hfill \end{array}$$

where $h=\pi /\sqrt{M}$. This completes the proof. □

Replacing each term of (3.3) with the approximation defined in (3.4)-(3.7), replacing $y(x_k)$ with $c_k$ and dividing by h, we obtain the following theorem.

Theorem 3.4 If the assumed approximate solution of boundary value problem (3.1) is (3.2), then the discrete sinc-Galerkin system for the determination of the unknown coefficients ${\{c_k\}}_{k=-M}^M$ is given by

$$\begin{array}{c}\sum _{k=-M}^M\{\sum _{i=0}^2\frac{1}{h^i}{\delta }_{jk}^{(i)}\frac{g_{2,i}(x_k)}{{\varphi }^{\prime }(x_k)}{c}_k-\sum _{i=0}^1\frac{1}{h^i}{\delta }_{jk}^{(i)}\frac{g_{1,i}(x_k)}{{\varphi }^{\prime }(x_k)}{c}_k\hfill \\ -\frac{1}{\mathrm{\Gamma }(1-\alpha )}\frac{c_k}{{\varphi }^{\prime }(x_k)}\frac{d}{dx}\left[h_L\sum _{r=-L}^L\frac{{(x_r-x)}^{-\alpha }K(x_r)}{{\xi }^{\prime }(x_r)}\right]{|}_{x=x_k}\}+\frac{{\mu }_0(x_j)w(x_j)}{{\varphi }^{\prime }(x_j)}{c}_j\hfill \\ =\frac{f(x_j)w(x_j)}{{\varphi }^{\prime }(x_j)},-M\le j\le M.\hfill \end{array}$$

4 Examples

In this section, three problems that have homogeneous and nonhomogeneous boundary conditions will be tested by using the present method. In all the examples, we take $d=\pi /2$, $\alpha =\beta =1/2$, $N=M$.

Example 4.1 Consider the linear fractional boundary value problem

$$y^{″}(x){+}_0^C{D}_x^{0.5}y(x)=f(x),$$

subject to the homogeneous boundary conditions

$$y(0)=y(1)=0,$$

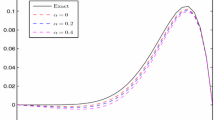
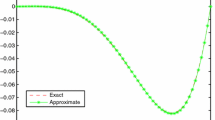
where$f(x)=2+\frac{1}{\mathrm{\Gamma }(0.5)}(2.65x^{1.5}-2x^{0.5})$. The exact solution of this problem is $y(x)=x(x-1)$. The numerical solutions which are obtained by using the sinc-Galerkin method (SGM) for this problem are presented in Table 1 and Table 2. Also, graphs of exact and approximate solutions for different values of L and M are presented in Figure 2.

Figure 2

Graphs of exact and approximate solutions for different values of L and M .

Table 1 Numerical results for $\mathit{L}\mathbf{=}\mathbf{5}$ , $\mathit{M}\mathbf{=}\mathbf{5}$

Table 2 Numerical results for $\mathit{L}\mathbf{=}\mathbf{40}$ , $\mathit{M}\mathbf{=}\mathbf{100}$

Example 4.2 [21]

Consider the linear fractional boundary value problem

$$y^{″}(x)+{0.5}_0^C{D}_x^{0.3}y(x)+y(x)=f(x),$$

subject to the homogeneous boundary conditions

$$y(0)=y(1)=0,$$

where$f(x)=4x^2(5x-3)+0.5x^{3.7}(\frac{120}{\mathrm{\Gamma }(5.7)}x-\frac{24}{\mathrm{\Gamma }(4.7)})+x^4(x-1)$. The exact solution of this problem is $y(x)=x^4(x-1)$. The numerical solutions which are obtained by using the sinc-Galerkin method (SGM) for this problem are presented in Table 3. In addition to this, in Table 4, the solutions are compared with the numerical solutions computed by using the Cubic splines (CS) in [21]. Also, graphs of exact and approximate solutions for different values of L and M are presented in Figure 3.

Figure 3

Graphs of exact and approximate solutions for different values of L and M .

Table 3 Numerical results for $\mathit{L}\mathbf{=}\mathbf{40}$ , $\mathit{M}\mathbf{=}\mathbf{100}$

Table 4 Numerical results for $\mathit{L}\mathbf{=}\mathbf{5}$ , $\mathit{M}\mathbf{=}\mathbf{5}$

Example 4.3 Consider the linear fractional boundary value problem

$$y^{″}(x)-x{y}^{\prime }(x){+}_0^C{D}_x^{0.5}y(x)=f(x),$$

subject to the nonhomogeneous boundary conditions

$$y(0)=0,y(1)=2,$$

where$f(x)=-3x^3-2x^2+6x+2+\frac{1}{\mathrm{\Gamma }(0.5)}(2.67x^{1.5}+3.2x^{2.5})$. The exact solution of this problem is $y(x)=x^2(x+1)$. First we convert the nonhomogeneous boundary conditions to homogeneous conditions by considering the transformation $u(x)=y(x)-2x$. This change of variable yields the following boundary value problem:

$$u^{″}(x)-x{u}^{\prime }(x){+}_0^C{D}_x^{0.5}u(x)=-3x^3-2x^2+8x+2+\frac{1}{\mathrm{\Gamma }(0.5)}(2.67x^{1.5}+3.2x^{2.5}-4x^{0.5})$$

with the homogeneous boundary conditions

$$u(0)=u(1)=0.$$

The numerical solutions which are obtained by using the sinc-Galerkin method (SGM) for this problem are presented in Table 5 and Table 6. Also, graphs of exact and approximate solutions for different values of L and M are presented in Figure 4.

Figure 4

Graphs of exact and approximate solutions for different values of L and M .

Table 5 Numerical results for $\mathit{L}\mathbf{=}\mathbf{5}$ , $\mathit{M}\mathbf{=}\mathbf{5}$

Table 6 Numerical results for $\mathit{L}\mathbf{=}\mathbf{50}$ , $\mathit{M}\mathbf{=}\mathbf{100}$

5 Conclusion

In this paper the sinc-Galerkin method has been employed to obtain approximate solutions of a general fractional order two-point boundary value problem. The method uses typical techniques of the Galerkin method such as series expansion but exploits the advantages of the sinc functions which make it much more efficient than the traditional interpolation-based numerical techniques. In order to illustrate the applicability and accuracy of the method to the real scientific problems, the method has been applied to some special examples, and simulations of the approximate solutions have been provided. The computational results have been compared with the ones obtained by the Cubic splines. Experimental results indicate the strength of the present method. In the future we plan to extend the present numerical solution algorithm to some other linear and nonlinear fractional boundary value problems.