1 Introduction

In this paper, we will study the convergence of iterative learning control of the following fractional system:

$$ \textstyle\begin{cases} {}^{c}\mathrm{D}^{\alpha}_{t} x(t)=Ax(t)+f(x(t),u(t),t),& t\in J=[0,b],\\ x(0)=x_{0},\\ y(t)=g(x(t),u(t),t), \end{cases} $$
(1)

where \({}^{c}\mathrm{D}^{\alpha}_{t}\) denotes the Caputo fractional derivative of order α, \(0<\alpha<1\). \(A\in R^{n\times n}\), the functions f, g are continuous and \(u(t)\) is a control vector.

Iterative learning control (ILC) was described by Uchiyama in 1978 in Japanese, but only few people noticed it. Arimoto et al. developed the ILC idea and studied the effective algorithm until 1984, they made it to be the iterative learning control theory, and more and more people paid attention to it.

Fractional calculus and fractional difference equations have attracted lots of authors in the past years [1–22], because they have been proved to be valuable tools in the modeling of many phenomena in engineering, physics, science, controllability, and they also provide an excellent tool to describe the hereditary properties of various materials and processes. The work on fractional order systems in iterative learning control appeared in 2001, and extensive attention has been paid to this field and great progress has been made in the following 15 years [14, 15, 23–32]; many fractional nonlinear systems were researched [33–37] and some operators have been studied [38, 39]. In [40], the author discussed the controllability of fractional control systems with control delay, and only used the Mittag-Leffler function to deduce the solution. Because it is exponentially bounded, we think that it should to be extensive studied and applied.

Motivated by the above mentioned works, we pay attention to and consider the system (1), the rest of this paper is organized as follows. In Section 2, we will show some definitions and preliminaries which will be used in the following parts. In Section 3, we give some results for P-type ILC for some fractional system. In Section 4, some simulation examples are given to illustrate our main results. In this paper, the norm for the n-dimensional vector \(x=(x_{1},x_{2},\ldots,x_{n})^{T}\) is defined as \(\Vert x \Vert =\max_{1 \leq i \leq n } \vert x_{i} \vert \).

2 Preliminaries

In this section, we will give some definitions and preliminaries which will be used in the paper.

Definition 2.1

The integral

$$I^{\alpha}_{t}f(t)=\frac{1}{\Gamma(\alpha)} \int^{t}_{0}(t-s)^{\alpha -1}f(s)\,ds,\quad \alpha>0, $$

is called a Riemann-Liouville fractional integral of order α, where Γ is the gamma function.

For a function \(f(t)\) given in the interval \([0,\infty)\), we have the expression

$${}^{\mathrm{RL}}D^{\alpha}_{t}f(t)=\frac{1}{\Gamma(n-\alpha)}\biggl( \frac{d}{dt}\biggr)^{n} \int ^{t}_{0}(t-s)^{n-\alpha-1}f(s)\,dt, $$

where \(n=[\alpha]+1\), \([\alpha]\) denotes the integer part of number α, is called the Riemann-Liouville fractional derivative of order \(\alpha>0\).

Definition 2.2

Caputo’s derivative for a function \(f:[0,\infty)\rightarrow R \) can be written as

$$^{c}D^{\alpha}_{t}f(t)= {}^{\mathrm{RL}}D^{\alpha}_{t} \Biggl[f(t)-\sum_{k=0}^{n-1} \frac {t^{k}}{k!}f^{(k)}(0)\Biggr],\quad n=[\alpha]+1, $$

where \([\alpha]\) denotes the integer part of real number α.

Definition 2.3

The definition of the two-parameter function of the Mittag-Leffler type is described by

$$E_{\alpha,\beta}(z)=\sum_{k=0}^{\infty} \frac{z^{k}}{\Gamma(\alpha k+\beta)},\quad \alpha>0,\beta>0,z\in C, $$

if \(\beta=1\), we get the Mittag-Leffler function of one parameter,

$$E_{\alpha}(z)=\sum_{k=0}^{\infty} \frac{z^{k}}{\Gamma(\alpha k+1)}. $$

Now, according to [36, 37, 40–42], we shall give Lemma 2.4.

Lemma 2.4

The general solution of equation (1) is given by

$$ x(t)= S_{\alpha,1}(A,t)x_{0}+ \int_{0}^{t}S_{\alpha,\alpha}(A,t-s)f \bigl(x(s),u(s),s\bigr)\,ds, $$
(2)

where

$$S_{\alpha,\beta}(A,t)=\sum_{k=0}^{\infty} \frac{A^{k}t^{\alpha k+\beta -1}}{\Gamma(\alpha k+\beta)}. $$

Lemma 2.5

Lemma 2.4 in [43]

The operators \(S_{\alpha,1}(t)\) and \(S_{\alpha,\alpha}(t)\) are exponentially bounded, we have the constants \(C_{1}=\frac{1}{\alpha }\), \(C_{2}=\frac{1}{\alpha} \Vert A \Vert ^{\frac{1-\alpha}{\alpha}}\),

$$ \bigl\Vert S_{\alpha,1}(A,t) \bigr\Vert \leq C_{1} e^{ \Vert A \Vert ^{\frac{1}{\alpha}}t},\qquad \bigl\Vert S_{\alpha,\alpha }(A,t) \bigr\Vert \leq C_{2} e^{ \Vert A \Vert ^{\frac{1}{\alpha }}t}. $$
(3)

Lemma 2.6

[34] Generalized Gronwall inequality

Let \(u(t)\) be a continuous function on \(t\in [0,T]\) and let \(v(t-s)\) be continuous and nonnegative on the interval \(0\leq s \leq T\). Moreover, let \(W(t)\) be a positive continuous and non-decreasing function on \(t \in[0,T]\). If

$$u(t)\leq W(t)+ \int_{0}^{t}v(t-s)u(s)\,ds,\quad t\in[0,T], $$

then

$$u(t)\leq W(t)e ^{\int_{0}^{t}v(t-s)\,ds},\quad t \in[0,T]. $$

3 P-type ILC for some fractional system

In this section, we consider the following fractional equation:

$$ \textstyle\begin{cases} {}^{c}\mathrm{D}^{\alpha}_{t} x^{k}(t)=Ax^{k}(t)+f(x^{k}(t),u^{k}(t),t),& t\in J=[0,b], \\ y^{k}(t)=g(x^{k}(t),u^{k}(t),t). \end{cases} $$
(4)

\(x^{k}\) denotes the kth iteration of x, \(u^{k}\) denotes the kth iteration of u, k is the number of iterations, \(k\in\{0,1,2,\ldots \} \).

Firstly, we will make the following assumptions on the data of our problem.

H(1):

The function \(f:R^{n}\times R^{n}\times J\rightarrow R^{n}\) satisfies:

  1. (i)

    f is measurable for all \(t\in J\);

  2. (ii)

    for \(1\leq i\leq n\), there exists a constant \(L_{f}>0\) such that

    $$\bigl\vert f\bigl(x_{i}^{k}(t),u_{i}^{k}(t),t \bigr)-f\bigl(\overline{x}_{i}^{k}(t),\overline {u}_{i}^{k}(t),t\bigr) \bigr\vert \leq L_{f} \bigl( \bigl\vert x_{i}^{k}(t)-\overline {x}_{i}^{k}(t) \bigr\vert + \bigl\vert u_{i}^{k}(t)-\overline {u}_{i}^{k}(t) \bigr\vert \bigr) $$

    for all \(x_{i}^{k},u_{i}^{k},\overline{x}_{i}^{k},\overline{u}_{i}^{k}\in R\).

H(2):

\(g:R^{n}\times R^{n}\times J\rightarrow R^{n}\), for \(\beta _{j}>0\), \(j=1,2,3,4\),

$$\textstyle\begin{cases} \beta_{1}\leq g_{iu}^{k}:=\frac{\partial g(x_{i}^{k}(t),u_{i}^{k}(t),t)}{\partial u_{i}^{k}(t)} \leq\beta_{2},\\ \beta_{3}\leq g_{ix}^{k}:=\frac{\partial g(x_{i}^{k}(t),u_{i}^{k}(t),t)}{\partial x_{i}^{k}(t)} \leq\beta_{4}, \end{cases} $$

we also denote \(\triangle x_{i}^{k}(t):=x_{i}^{k+1}(t)-x_{i}^{k}(t)\), \(\triangle u_{i}^{k}(t):=u_{i}^{k+1}(t)-u_{i}^{k}(t)\); \(e_{i}^{k}(t):=y_{i}^{d}(t)-y_{i}^{k}(t)\) is the tracking error function, \(y^{d}(t)=(y_{1}^{d},y_{2}^{d},\ldots,y_{n}^{d})^{T}\) is the objective function.

3.1 Open-loop case

For equation (4), we consider the following Open-loop P-type ILC, \(t\in [0,b]\), \(1\leq i\leq n\):

$$ \textstyle\begin{cases} x _{i}^{k+1}(t)=x _{i}^{k}(t)+\gamma e_{i}^{k}(t),\\ u _{i}^{k+1}(t)=u _{i}^{k}(t)+\delta_{1} e_{i}^{k}(t), \end{cases} $$
(5)

where γ and \(\delta_{1}\) are the parameters which will be determined.

Theorem 3.1

Assume that the hypotheses H(1), H(2) are satisfied, let \(y_{k}(\cdot)\) be the output of equation (4), for the arbitrary input \(u_{0}(\cdot)\), if

$$\begin{aligned}& \rho= \bigl\vert \bigl(1-\delta_{1} g_{iu}^{k} \bigl(\xi_{1}(0),\xi _{2}(0),0\bigr)-\gamma g_{ix}^{k}\bigl(\xi_{1}(0),\xi_{2}(0),0 \bigr)\bigr) \bigr\vert < 1, \\& \operatorname{max}\bigl\{ \vert 1-\delta_{1} \beta_{1}- \gamma\beta_{3} \vert , \vert 1-\delta_{1} \beta_{1}-\gamma\beta_{4} \vert , \vert 1- \delta_{1} \beta_{2}-\gamma\beta_{3} \vert , \vert 1-\delta _{1} \beta_{2}-\gamma\beta_{4} \vert \bigr\} < 1, \end{aligned}$$
(6)
$$\begin{aligned}& \vert 1-\delta_{1} \beta_{1} \vert + \delta_{1} \beta_{4} \bigl(b L_{f}C_{2}e^{ \Vert A \Vert ^{\frac{1}{\alpha}}b} \bigr)^{2}< 1, \end{aligned}$$
(7)
$$\begin{aligned}& \gamma b \beta_{4}L_{f}C_{1} C_{2} \bigl(e^{ \Vert A \Vert ^{\frac {1}{\alpha}}b}\bigr)^{2}< 1, \end{aligned}$$
(8)

the open-loop P-type ILC (5) guarantees that \(\lim_{k\to\infty} y_{i}^{k}(t)=y_{i}^{d}(t)\), or \(\lim_{k\to\infty} \Vert e^{k}(t) \Vert =0\), \(t\in J\).

Proof

Firstly, we know that \(e_{i}^{k}(t):=y_{i}^{d}(t)-y_{i}^{k}(t)\), by using the mean value theorem, we get

$$\begin{aligned} e_{i}^{k+1}(t) =&e_{i}^{k}(t)+y_{i}^{k}(t)-y_{i}^{k+1}(t) \\ =&e_{i}^{k}(t)+g\bigl(x_{i}^{k}(t),u_{i}^{k}(t),t \bigr)-g\bigl(x_{i}^{k+1}(t),u_{i}^{k+1}(t),t \bigr) \\ =&e_{i}^{k}(t)-\bigl[g\bigl(x_{i}^{k+1}(t),u_{i}^{k+1}(t),t \bigr)-g\bigl(x_{i}^{k}(t),u_{i}^{k+1}(t),t \bigr)\bigr] \\ &{}-\bigl[g\bigl(x_{i}^{k}(t),u_{i}^{k+1}(t),t \bigr)-g\bigl(x_{i}^{k}(t),u_{i}^{k}(t),t \bigr)\bigr] \\ =&e_{i}^{k}(t)-g_{ix}^{k}\bigl( \xi_{1}(t),\xi_{2}(t),t\bigr)\triangle x_{i}^{k}(t)-g_{iu}^{k} \bigl(\xi_{1}(t),\xi_{2}(t),t\bigr)\triangle u_{i}^{k}(t) \\ =&\bigl(1-g_{iu}^{k}\bigl(\xi_{1}(t), \xi_{2}(t),t\bigr)\delta _{1}\bigr)e_{i}^{k}(t)-g_{ix}^{k} \bigl(\xi_{1}(t),\xi_{2}(t),t\bigr)\triangle x_{i}^{k}(t), \end{aligned}$$
(9)

where \(\xi_{1}(t)\) lies in the segment with the end point \(x _{i}^{k}(t)\) and \(x _{i}^{k+1}(t)\), \(\xi_{2}(t)\) lies in the segment with the end point \(u _{i}^{k}(t)\) and \(u _{i}^{k+1}(t)\).

(I) \(t=0\). By using (5) and (6), we get

$$\begin{aligned} \bigl\vert e_{i}^{k+1}(0) \bigr\vert =& \bigl\vert e_{i}^{k}(0)-g_{ix}\bigl(\xi _{1}(0), \xi_{2}(0),0\bigr)\triangle x_{i}^{k}(0)-g_{iu} \bigl(\xi_{1}(0),\xi _{2}(0),0\bigr)\triangle u_{i}^{k}(0) \bigr\vert \\ =& \bigl\vert \bigl(1-\delta_{1} g_{iu}^{k} \bigl(\xi_{1}(0),\xi_{2}(0),0\bigr)-\gamma g_{ix}^{k}\bigl(\xi_{1}(0),\xi_{2}(0),0 \bigr)\bigr)\bigr\vert \bigl\vert e_{i}^{k}(0) \bigr\vert \\ \leq& \rho \bigl\vert e_{i}^{k}(0) \bigr\vert , \end{aligned}$$

so

$$\lim_{k\to\infty} \bigl\Vert e^{k}(0) \bigr\Vert =0. $$

(II) \(t\in(0,b)\). According to assumptions H(1), H(2) and (3), we can show that

$$\begin{aligned} \bigl\vert \triangle x_{i}^{k}(t) \bigr\vert =& \bigl\vert x_{i}^{k+1}(t)-x_{i}^{k}(t) \bigr\vert \\ =&\biggl\vert S_{\alpha,1}(A,t)x_{i}^{k+1}(0)+ \int_{0}^{t}S_{\alpha,\alpha }(A,t-s)f \bigl(x_{i}^{k+1}(s),u_{i}^{k+1}(s),s \bigr)\,ds \\ &{}-S_{\alpha,1}(A,t)x_{i}^{k}(0)+ \int_{0}^{t}S_{\alpha,\alpha }(A,t-s)f \bigl(x_{i}^{k}(s),u_{i}^{k}(s),s \bigr)\,ds\biggr\vert \\ \leq& \bigl\vert S_{\alpha,1}(A,t)\bigr\vert \bigl\vert \triangle x_{i}^{k}(0) \bigr\vert +L_{f} \int_{0}^{t} \bigl\vert S_{\alpha,\alpha}(A,t-s) \bigr\vert \bigl( \bigl\vert \triangle x_{i}^{k}(s) \bigr\vert + \bigl\vert \triangle u_{i}^{k}(s) \bigr\vert \bigr)\,ds \\ \leq& C_{1} e^{ \Vert A \Vert ^{\frac{1}{\alpha}}t} \bigl\vert \triangle x_{i}^{k}(0) \bigr\vert +L_{f}C_{2} \int_{0}^{t}e^{ \Vert A \Vert ^{\frac{1}{\alpha}}(t-s)} \bigl\vert \triangle u_{i}^{k}(s) \bigr\vert \,ds \\ &{}+L_{f}C_{2} \int_{0}^{t}e^{ \Vert A \Vert ^{\frac{1}{\alpha}}(t-s)} \bigl\vert \triangle x_{i}^{k}(s) \bigr\vert \,ds \\ \leq&C_{1} e^{ \Vert A \Vert ^{\frac{1}{\alpha}}t} \bigl\vert \triangle x_{i}^{k}(0) \bigr\vert +b L_{f}C_{2}e^{ \Vert A \Vert ^{\frac{1}{\alpha}}b} \bigl\Vert \triangle u^{k} \bigr\Vert \\ &{}+L_{f}C_{2} \int_{0}^{t}e^{ \Vert A \Vert ^{\frac{1}{\alpha }}(t-s)} \bigl\vert \triangle x_{i}^{k}(s) \bigr\vert \,ds, \end{aligned}$$

let \(W(t)=C_{1} e^{ \Vert A \Vert ^{\frac{1}{\alpha}}t} \vert \triangle x_{i}^{k}(0) \vert +b L_{f}C_{2}e^{ \Vert A \Vert ^{\frac{1}{\alpha}}b} \Vert \triangle u^{k} \Vert \), invoking Lemma 2.5 and Lemma 2.6, we get

$$\begin{aligned} \bigl\vert \triangle x_{i}^{k}(t) \bigr\vert \leq \bigl(C_{1} e^{ \Vert A \Vert ^{\frac{1}{\alpha}}t} \bigl\vert \triangle x_{i}^{k}(0) \bigr\vert +b L_{f}C_{2}e^{ \Vert A \Vert ^{\frac{1}{\alpha}}b} \bigl\Vert \triangle u^{k} \bigr\Vert \bigr)b L_{f}C_{2}e^{ \Vert A \Vert ^{\frac{1}{\alpha}}b}. \end{aligned}$$

In light of (9),

$$\begin{aligned}& \begin{aligned} \bigl\vert e_{i}^{k+1}(t) \bigr\vert & \leq \bigl\vert \bigl(1-\delta_{1} g_{iu}^{k} \bigl(\xi_{1}(t),\xi_{2}(t),t\bigr)\bigr)e_{i}^{k}(t) \bigr\vert +\beta _{4} \bigl\vert \triangle x_{i}^{k}(t) \bigr\vert \\ &\leq \bigl\vert \bigl(1-\delta_{1} g_{iu}^{k} \bigl(\xi_{1}(t),\xi _{2}(t),t\bigr)\bigr)e_{i}^{k}(t) \bigr\vert + b \beta_{4}L_{f}C_{1} C_{2} \bigl(e^{ \Vert A \Vert ^{\frac{1}{\alpha }}b}\bigr)^{2} \bigl\vert \triangle x_{i}^{k}(0) \bigr\vert \\ &\quad {}+\beta_{4} \bigl(b L_{f}C_{2}e^{ \Vert A \Vert ^{\frac{1}{\alpha }}b} \bigr)^{2} \bigl\Vert \triangle u^{k} \bigr\Vert , \end{aligned} \\& \begin{aligned} \bigl\Vert e^{k+1} \bigr\Vert &\leq \bigl\vert \bigl(1-\delta_{1} g_{iu}^{k}\bigl( \xi_{1}(t),\xi_{2}(t),t\bigr)\bigr) \bigr\vert \bigl\Vert e^{k} \bigr\Vert +\beta_{4} \bigl\Vert \triangle x^{k}(t) \bigr\Vert \\ &\leq \bigl\vert \bigl(1-\delta_{1} g_{iu}^{k} \bigl(\xi_{1}(t),\xi _{2}(t),t\bigr)\bigr) \bigr\vert \bigl\Vert e^{k} \bigr\Vert + b \beta_{4}L_{f}C_{1} C_{2} \bigl(e^{ \Vert A \Vert ^{\frac{1}{\alpha }}b}\bigr)^{2} \bigl\Vert \triangle x^{k}(0) \bigr\Vert \\ &\quad {}+\beta_{4} \bigl(b L_{f}C_{2}e^{ \Vert A \Vert ^{\frac{1}{\alpha }}b} \bigr)^{2} \bigl\Vert \triangle u^{k} \bigr\Vert \\ &\leq \bigl\vert 1-\delta_{1} g_{iu}^{k}\bigl( \xi_{1}(t),\xi _{2}(t),t\bigr))+\delta_{1} \beta_{4} \bigl(b L_{f}C_{2}e^{ \Vert A \Vert ^{\frac{1}{\alpha}}b} \bigr)^{2} \bigr\vert \bigl\Vert e^{k} \bigr\Vert \\ &\quad {}+ \gamma b \beta_{4}L_{f}C_{1} C_{2} \bigl(e^{ \Vert A \Vert ^{\frac {1}{\alpha}}b}\bigr)^{2} \bigl\Vert \triangle e^{k}(0) \bigr\Vert , \end{aligned} \end{aligned}$$

where

$$\begin{gathered} \eta_{1}= \vert 1-\delta_{1} \beta_{1} \vert +\delta_{1} \beta_{4} \bigl(b L_{f}C_{2}e^{ \Vert A \Vert ^{\frac{1}{\alpha}}b}\bigr)^{2}< 1, \\ \eta_{2}=\gamma b \beta_{4}L_{f}C_{1} C_{2} \bigl(e^{ \Vert A \Vert ^{\frac{1}{\alpha}}b}\bigr)^{2}< 1, \end{gathered} $$

From (7) and (8), we have

$$\lim_{k\to\infty} \bigl\Vert e^{k} \bigr\Vert =0, $$

the proof is completed. □

3.2 Closed-loop case

For equation (4), we consider the closed-loop P-type ILC, \(t\in[0,b]\):

$$ \textstyle\begin{cases} x _{i}^{k+1}(t)=x _{i}^{k}(t)+\gamma e_{i}^{k}(t),\\ u _{i}^{k+1}(t)=u _{i}^{k}(t)+\delta_{2} e_{i}^{k+1}(t), \end{cases} $$
(10)

we set

$$\begin{aligned}& \eta_{3}= \biggl\vert \frac{\beta_{4}\delta_{2}}{1+\delta_{2}\beta _{1}} \biggr\vert \bigl(b L_{f}C_{2}e^{ \Vert A \Vert ^{\frac{1}{\alpha }}b}\bigr)^{2},\qquad \eta_{4}= \biggl\vert \frac{1}{1+\delta_{2}\beta_{1}} \biggr\vert , \end{aligned}$$
(11)
$$\begin{aligned}& \eta_{5}= \biggl\vert \frac{\beta_{4}}{1+\delta_{2}\beta_{1}} \biggr\vert b L_{f}C_{1} C_{2} \bigl(e^{ \Vert A \Vert ^{\frac{1}{\alpha }}b} \bigr)^{2}. \end{aligned}$$
(12)

Theorem 3.2

Assume that the hypotheses H(1), H(2) are satisfied, let \(y_{k}(\cdot )\) be the output of the system (4), \(y_{d}(t)\) be the given function, for the arbitrary input \(u_{0}(\cdot)\), if

$$\begin{aligned}& \operatorname{max}\biggl\{ \biggl\vert \frac{1-\gamma\beta_{3}}{1+\delta_{2}\beta_{1}} \biggr\vert , \biggl\vert \frac{1-\gamma\beta_{3}}{1+\delta_{2}\beta_{2}} \biggr\vert , \biggl\vert \frac{1-\gamma\beta_{4}}{1+\delta_{2}\beta_{1}} \biggr\vert , \biggl\vert \frac{1-\gamma\beta_{4}}{1+\delta_{2}\beta_{2}} \biggr\vert \biggr\} < 1, \end{aligned}$$
(13)
$$\begin{aligned}& \frac{\eta_{4}}{1-\eta_{3}}< 1,\qquad \frac{\eta_{5}}{1-\eta_{3}}< 1, \end{aligned}$$
(14)

the closed-loop P-type ILC (10) guarantees that \(\lim_{k\to\infty} y_{i}^{k}(t)=y_{i}^{d}(t)\), or \(\lim_{k\to\infty} \Vert e^{k}(t) \Vert =0\), \(t\in J\).

Proof

According to H(1), H(2) and (10),

$$\begin{aligned}& \begin{aligned} \bigl\vert e_{i}^{k+1}(0) \bigr\vert &= \bigl\vert e_{i}^{k}(0)-g_{ix}^{k}\bigl( \xi_{1}(0),\xi_{2}(0),0\bigr)\triangle x_{i}^{k}(0)-g_{iu}^{k} \bigl(\xi_{1}(0),\xi_{2}(0),0\bigr)\triangle u_{i}^{k}(0) \bigr\vert \\ &= \bigl\vert \bigl(1- \gamma g_{ix}^{k}\bigl( \xi_{1}(0),\xi_{2}(0),0\bigr)\bigr)\bigr\vert \bigl\vert e_{i}^{k}(0) \bigr\vert - \delta_{2}g_{iu}^{k} \bigl(\xi_{1}(0),\xi _{2}(0),0\bigr) \bigl\vert e_{i}^{k+1}(0) \bigr\vert , \end{aligned} \\& \bigl\vert e_{i}^{k+1}(0) \bigr\vert = \biggl\vert \frac{1- \gamma g_{ix}^{k}(\xi_{1}(0),\xi_{2}(0),0)}{1+\delta_{2}g_{iu}^{k}(\xi _{1}(0),\xi_{2}(0),0)}\biggr\vert \big\vert e_{i}^{k}(0) \big\vert . \end{aligned}$$

It can easily be seen from (3), \(\lim_{k\to\infty} \Vert e^{k}(0) \Vert _{L^{2}}=0\).

For \(t\in(0,b]\), we obtain

$$\begin{aligned}& e_{i}^{k+1}(t)=\frac{1}{1+\delta_{2}g_{iu}^{k}(\xi_{1}(t),\xi _{2}(t),t)}\bigl(e_{k}(t)-g_{ix}^{k} \bigl(\xi_{1}(t),\xi_{2}(t),t \bigr)\triangle x_{i}^{k}(t)\bigr), \\& \begin{aligned} \bigl\Vert e^{k+1} \bigr\Vert &= \biggl\vert \frac{1}{1+\delta _{2}g_{iu}^{k}(\xi_{1}(t),\xi_{2}(t),t)} \biggr\vert \bigl\Vert e^{k} \bigr\Vert -\biggl\vert \frac{g_{ix}^{k}(\xi_{1}(t),\xi_{2}(t),t)}{ 1+\delta_{2}g_{iu}^{k}(\xi_{1}(t),\xi_{2}(t),t)}\biggr\vert \bigl\Vert \triangle x^{k} \bigr\Vert _{L^{2}} \\ &\leq \eta_{4} \bigl\Vert e^{k} \bigr\Vert + \biggl\vert \frac{\beta _{4}}{1+\delta_{2}\beta_{1}} \biggr\vert \bigl(b L_{f}C_{1} C_{2} \bigl(e^{ \Vert A \Vert ^{\frac{1}{\alpha}}b}\bigr)^{2} \bigl\Vert \triangle x^{k}(0) \bigr\Vert \\ &\quad {}+\bigl(b L_{f}C_{2}e^{ \Vert A \Vert ^{\frac{1}{\alpha}}b} \bigr)^{2} \bigl\Vert \triangle u^{k} \bigr\Vert \bigr) \\ &\leq \eta_{4} \bigl\Vert e^{k} \bigr\Vert + \eta_{5} \bigl\Vert \triangle x^{k}(0) \bigr\Vert + \eta_{3} \bigl\Vert e^{k+1} \bigr\Vert . \end{aligned} \end{aligned}$$

Therefore

$$\bigl\Vert e^{k+1} \bigr\Vert \leq\frac{\eta_{4}}{1-\eta_{3}} \bigl\Vert e^{k} \bigr\Vert +\frac{\eta_{5}}{1-\eta_{3}} \bigl\Vert e^{k}(0) \bigr\Vert , $$

it implies that \(\lim_{k\to\infty} \Vert e^{k} \Vert =0\), \(t\in J\), which completes the proof. □

4 Simulations

In this section, we will give two simulation examples to demonstrate the validity of the algorithm.

4.1. Consider the following Open-loop P-type ILC system:

$$ \textstyle\begin{cases} {}^{c}\mathrm{D}^{0.5}_{t} x_{1}^{k}(t)=(x_{1}^{k}(t))^{2}+x_{1}^{k}(t)+0.1u_{1}^{k}(t),& t\in J=[0,1.8], \\ x(0)=0.5,\\ y_{1}^{k}(t)=x_{1}^{k}(t)+0.5u_{1}^{k}(t), \end{cases} $$
(15)

with the iterative learning control

$$\textstyle\begin{cases} x _{1}^{k+1}(t)=x_{1}^{k}(t)+0.5e_{1}^{k}(t),\\ u _{1}^{k+1}(t)=u _{1}^{k}(t)+ 0.5e_{1}^{k}(t), \end{cases} $$

we set \(f=(x_{1}^{k}(t))^{2}\) and the initial control \(u_{0}(\cdot)=0\), \(y_{1}^{d}(t)=5t^{2}(3-2t)\), \(t\in[0,1.8]\), and set \(L_{f}=0.01\), \(\beta _{1}=0.2\), \(\beta_{2}=0.7\), \(\beta_{3}=0.5\), \(\beta_{4}=0.1\), \(\gamma=0.5\), \(\delta_{1}=0.5\), all conditions of Theorem 3.1 are satisfied.

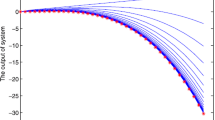
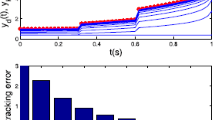
The simulation result can be seen from Figure 1 and Figure 2, for the Open-loop P-type ILC system (15), with the increase of the number of iterations, it can track the desired trajectory gradually by using the algorithm. Firstly, we use the single iteration rate to get the result, from Figure 1, we find that late in the iteration, the output of the system jumps around the desired trajectory, so we adopt the correction method, that is, when \(e^{j}>0\), \(u^{j}=u^{j}-0.5\times e^{j}\) or \(e^{j}<0\), \(u^{j}=u^{j}+0.5\times e^{j} \), j is the number of iteration, the result approaches the desired trajectory stably and quickly; from Figure 2, the tracking error tends to zero at the 14th iteration, so the iterative learning control is feasible and the efficiency is higher.

Figure 1
figure 1

“***” denotes the desired trajectory, “ooo” denotes the output of the system.

Full size image
Figure 2
figure 2

“***” denotes the desired trajectory, “—” denotes the output of the system.

Full size image

4.2. Consider the following Closed-loop P-type ILC system:

$$ \textstyle\begin{cases} {}^{c}\mathrm{D}^{0.5}_{t} x_{1}^{k}(t)=(x_{1}^{k}(t))^{2}+x_{1}^{k}(t)+0.2u_{1}^{k}(t),& t\in J=[0,1.8],\\ x(0)=0.5,\\ y_{1}^{k}(t)=x_{1}^{k}(t)+u_{1}^{k}(t), \end{cases} $$
(16)

with the iterative learning control

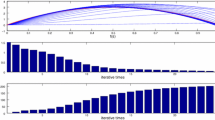
$$\textstyle\begin{cases} x _{1}^{k+1}(t)=x _{1}^{k}(t)+ 0.5e_{1}^{k}(t),\\ u _{1}^{k+1}(t)=u_{1}^{k}(t)+ e_{1}^{k+1}(t), \end{cases} $$

we set the initial control \(u_{0}(\cdot)=0\), \(y_{1}^{d}(t)=12t^{2}\), \(t\in [0,1.8]\), and \(L_{f}=0.015\), \(\beta_{1}=0.25\), \(\beta_{2}=0.6\), \(\beta_{3}=0.5\), \(\beta _{4}=0.1\), \(\gamma=0.5\), \(\delta_{2}=1\), all conditions of Theorem 3.2 are satisfied. We also use the correction method, that is, when \(e^{j}>0\), \(u^{j}=u^{j}-m\times e^{j}\) or \(e^{j}<0\), \(u^{j}=u^{j}+m\times e^{j} \), j is the number of iteration, m is the parameters, we set \(m=0.7,1,1.2\) and the output of the system is shown in Figure 3, Figure 5 and Figure 7, the tracking error is shown in Figure 4, Figure 6 and Figure 8.

Figure 3
figure 3

“***” denotes the desired trajectory, “—” denotes the output of the system.

Full size image
Figure 4
figure 4

Number of iterations and the tracking error.

Full size image
Figure 5
figure 5

“***” denotes the desired trajectory, “—” denotes the output of the system.

Full size image
Figure 6
figure 6

Number of iterations and the tracking error.

Full size image
Figure 7
figure 7

“***” denotes the desired trajectory, “—” denotes the output of the system.

Full size image
Figure 8
figure 8

Number of iterations and the tracking error.

Full size image

From Figure 3-Figure 8 and Table 1, we find the tracking error tends to zero within six iterations, so the output of the system can track the desired trajectory almost perfectly. By comparing three cases, when \(m=1\), the iteration number is only 2, and the tracking error is 0.001, the tracking performance is best and improved over the iteration domain.

Table 1 The iteration number and the tracking error and the running time table
Full size table

5 Conclusions

In this paper, the convergence of iterative learning control for some fractional equation was discussed. Based on our results, the Open-loop and Closed-loop P-type ILC law were proposed, by using the Gronwall inequality, the sufficient conditions of convergence for the two types of iterative learning control were showed. Simulation results showed that the algorithm is effective. In the future, we will study iterative learning control for some fractional equation with impulse or delay.