Abstract
We investigate state estimation for a class of discrete-time recurrent neural networks with leakage delay and time-varying delay. The design method for the state estimator to estimate the neuron states through available output measurements is given. A novel delay-dependent sufficient condition is obtained for the existence of state estimator such that the estimation error system is globally asymptotically stable. Based a novel double summation inequality and reciprocally convex approach, an improved stability criterion is obtained for the error-state system. Two numerical examples are given to demonstrate the effectiveness of the proposed design methods. The simulation results show that the leakage delay has a destabilizing influence on a neural network system.
Similar content being viewed by others
1 Introduction
Neural networks have become a hot research topic in the past few years, and many problems such as feedback control [1], stability [2–13], dissipativity and passivity [14–17] are being taken to treat in various dynamic neural networks systems. Since only partial information about the neuron states is available in the network output of large-scale complex networks, it is important and necessary to estimate the neuron states through available measurements. The state estimation problem is studied for neural networks with time-varying delays in [18]. A novel delay partition approach in [19] was proposed to study the state estimation problem of recurrent neural networks. The \(H_{\infty}\) state estimation for static neural networks is studied in [20, 21].
Most of works on state estimation for neural networks are focused on the continuous-time cases [18–27]. However, discrete-time neural networks play an important role when implementing the dynamic system in a digital way. In recent years, some significant results about state estimation problem for discrete-time neural networks have been obtained in [28–34]. For example, the robust state estimation problem for discrete-time bidirectional associative memory (BAM) neural networks is studied in [28]. A sufficient condition is obtained such that the error estimate system for discrete-time BAM neural networks is globally exponentially stable in [29]. Wu et al. [33] studied the state estimation for discrete-time neural networks with time-varying delay. A typical time delay called leakage delay has a tendency to destabilize a system. Since the leakage delay has a great impact on the dynamical behavior of neural networks, it is necessary to take the effect of leakage delay on state estimation of neural networks into account. Recently, the neural networks with leakage delay have received much attention [8–13, 16, 35, 36]. However, there are few research results on the state estimation for discrete-time neural networks with leakage delay in the existing literature.
Motivated by the above discussion, we consider the problem of state estimation for discrete-time recurrent neural networks with leakage delay. This paper aims to design a state estimator via the available output measurement such that the estimation error system is asymptotically stable. The major contributions of this paper can be summarized as follows: (1) A state estimator and a delay-dependent stability criterion for the error system of discrete-time neural networks with leakage delay in terms of linear matrix inequalities (LMIs) are developed. (2) Based on a novel double summation inequality, reciprocally convex method, and three zero-value equalities, a less conservative stability criterion with less computational complexity is derived in terms of LMIs.
Notation
Throughout this paper, \(\mathbb{Z}\) denotes the set of integers, \(\mathbb{R}^{n}\) is the n-dimensional Euclidean vector space, and \(\mathbb{R}^{m\times n}\) denotes the set of all \(m\times n\) real matrices. The superscript T stands for the transpose of a matrix; \(I_{n}\) and \(0_{m\times n}\) represent the \(n\times n\) identity matrix and \({m\times n}\) zero matrix, respectively; \(\|\cdot\|\) refers to the Euclidean vector norm or the induced matrix norm. The symbol ∗ denotes the symmetric term in a symmetric matrix, and \(\operatorname{Sym}\{X\}=X+X^{T}\).
2 Problem formulation and preliminaries
Consider the following discrete-time recurrent neural networks with leakage delay:
where \(x(k)=[x_{1}(k),x_{2}(k),\ldots,x_{n}(k)]^{T}\in\mathbb{R}^{n}\) is the state vector, \(g(x(k))=[g_{1}(x_{1}(k)), g_{2}(x_{2}(k)), \ldots ,g_{n}(x_{n}(k))]^{T}\in\mathbb{R}^{n}\) denotes the activation function, \(A=\operatorname{diag}\{a_{1},a_{2},\ldots,a_{n}\}\) is the state feedback matrix with entries \(|a_{i}|<1\), \(W_{0}\in\mathbb{R}^{n\times n}\) and \(W_{1}\in\mathbb{R}^{n\times n }\) are the interconnection weight matrices, J denotes an external input vector, \(y(k)\in\mathbb{R}^{m}\) is the measurement output, \(\phi(k,\cdot)\) is the neuron-dependent nonlinear disturbance on the network outputs, C is a known constant matrix of appropriate dimension, \(\tau(k)\) denotes the time-varying delay satisfying \(0<\tau_{1}\leq\tau (k)\leq\tau_{2}\), where \(\tau_{1}\), \(\tau_{2}\) are known positive integers, and σ is a known positive integer representing the leakage delay.
Assumption 1
[37]
For any \(u, v\in\mathbb{R}\), \(u\neq v\), each activation function \(g_{i}(\cdot)\) in (1) satisfies
where \(l_{i}^{-}\) and \(l_{i}^{+}\) are known constants.
Assumption 2
[34]
The function \(\phi(k,\cdot)\) is assumed to be globally Lipschitz continuous, that is,
where L is a known constant matrix of appropriate dimension.
Now, the full-order state estimator for system (1) is of the form
where \(\hat{x}(k)\) is the estimation of the state vector \(x(k)\), \(\hat{y}(k)\) is the estimation of the measurement output vector \(y(k)\), and \(K\in\mathbb{R}^{ n \times m}\) is the estimator gain matrix to be designed later.
Let the error state vector be \(e(k)=x(k)-\hat{x}(k)\). Then we can obtain the following error-state system from (1) and (2):
where \(f(k)=g(x(k))-g(\hat{x}(k))\) and \(\psi(k)=\phi(k,x(k))-\phi(k,\hat {x}(k))\).
From Assumption 1 it can be easily seen that \(l_{i}^{-}\leq\frac{f_{i}(k)}{e_{i}(k)}\leq l_{i}^{+}\) for all \({e_{i}(k)} \neq0\), \(i=1,2,\ldots,n\).
Before proceeding further, we introduce the following three lemmas.
Lemma 1
[38]
For any vectors \(\xi_{1}\), \(\xi _{2}\) in \(\mathbb{R}^{m}\), given a positive definite matrix Q in \(\mathbb{R}^{n\times n}\), any matrices \(W_{1}\), \(W_{2}\) in \(\mathbb {R}^{n\times m}\), and a scalar α in the interval \((0,1)\), if there exists a matrix X in \(\mathbb{R}^{n\times n}\) such that \(\bigl [{\scriptsize\begin{matrix}{} Q & X \cr \ast& Q \end{matrix}} \bigr ]>0 \), then the following inequality holds:
Lemma 2
[39]
For a given matrix \(Z>0\), any sequence of discrete-time variables y in \([-h,0]\cap\mathbb {Z}\rightarrow\mathbb{R}^{n}\), the following inequality holds:
where \(y(k)=x(k)-x(k-1)\), \(\Theta_{0}=x(0)-\frac{1}{h+1}\sum_{i=-h}^{0}x(i)\), \(\Theta_{1}=x(0)+\frac{2}{h+1}\sum_{i=-h}^{0}x(i)-\frac{6}{(h+1)(h+2)}\sum_{i=-h}^{0}\sum_{k=i}^{0}x(k)\).
Lemma 3
[40]
For given matrix \(Z>0\), three nonnegative integers a, b, k satisfying \(a\leq b\leq k\), define the function \(\omega(k,a,b)\) as
Then, the following summation inequality holds:
where \(\Delta x(s)=x(s+1)-x(s)\), \(\nu_{0}=x(k-a)-x(k-b)\), and \(\nu_{1}=x(k-a)+x(k-b)-\omega(k,a,b)\).
3 Main results
In this section, we consider the asymptotic stability of the error-state system (3). For simplicity, \(e_{i}\in R^{17n\times n}\) (\(i=1,2,\ldots,17\)) are defined as block entry matrices (e.g., \(e_{3}=[0_{n\times 2n},I_{n},0_{n\times14n}]^{T}\)). The other notations are defined as
Theorem 1
For given integers \(0<\tau_{1} <\tau_{2}\), \(0<\sigma\), the error-state system (3) is asymptotically stable if there exist symmetric positive definite matrices \(P\in\mathbb {R}^{5n\times5n}\), \(S_{1}\in\mathbb{R}^{n\times n}\), \(S_{2}\in\mathbb{R}^{2n\times2n}\), \(Q_{1}\in\mathbb{R}^{2n\times2n}\), \(Q_{2}\in\mathbb{R}^{2n\times2n}\), \(\mathcal{N}_{1}\in\mathbb{R}^{2n\times2n}\), \(\mathcal{N}_{2}\in \mathbb{R}^{2n\times2n}\), positive diagonal matrices \(H_{i}\in\mathbb{R}^{n\times n}\) (\(i=1,2,3,4\)), a scalar \(\epsilon>0\), symmetric matrices \(Z_{i}\in\mathbb{R}^{n\times n}\) (\(i=1,2,3\)), and matrices \(\mathcal{M}\in\mathbb{R}^{2n\times2n}\), \(X\in\mathbb{R}^{n\times n}\), \(Y\in\mathbb{R}^{n\times n}\) satisfying the following LMIs:
Furthermore, the estimator gain matrix is given by \(K=X^{-1}Y\).
Proof
Consider the Lyapunov-Krasovskii functional for system (3) as follows:
where
Define the forward difference of \(V(k)\) as \(\Delta{V(k)}=V(k+1)-V(k)\). Calculating \(\Delta V_{i}(k)\) (\(i=1, 2, 3, 4\)), we have
Using Jensen’s inequality in [37], we get
So
Obviously,
Inspired by the work of [41], for any symmetric matrices \(Z_{i}\) of appropriate dimension (\(i=1,2,3\)), we introduce the following zero equalities:
Using these zero equalities and the Jensen inequality, we have
By Lemma 1, since \(\Omega_{3}\geq0\), we get
The difference \(\Delta V_{4}(k)\) can be rebounded as
By Assumption 1, for any positive diagonal matrices \(H_{i}=\operatorname{diag}\{h_{i1},\ldots,h_{in}\}\) (\(i=1,2,3,4\)), the following inequality holds:
From Assumption 2, for any positive scalar ϵ, we can deduce that
On the other hand, to design the gain matrix K, for any matrix X of appropriate dimension, we use the following zero equality to avoid the nonlinear matrix inequality
Therefore, from (7)-(16), the following inequality holds:
Obviously, if \(\Xi<0\) and \(\xi(k)\neq0\), then \(\Delta V(k)<0\), which indicates that the error-state system (3) is asymptotically stable. This completes the proof of Theorem 1. □
Remark 1
Differently from methods in [28–33], we introduce three zero equalities (10)-(12) to reduce the conservatism of the stability criterion. In [19], the authors used the inequality \(-PX^{-1}P\leq-2P+X\) (\(X\geq0\)) to deal with the problem of nonlinear matrix inequality. In this paper, by employing the zero equality (16), the nonlinear matrix inequality can be avoided. At the same time, the method in our work can provide much flexibility in solving linear matrix inequalities.
Remark 2
In order to estimate \(-\sum_{j=t-h_{M}}^{t-h_{m}-1}\eta_{1}(j)^{T}R_{1}\eta_{1}(j)\), the authors in [28] divided the sum into two parts, \(-\sum_{j=t-h_{M}}^{t-h(t)-1}\eta_{1}^{T}(j)R_{1}\eta_{1}(j)\) and \(-\sum_{j=t-h(t)}^{t-h_{m}-1}\eta_{1}^{T}(j)R_{1}\eta_{1}(j)\), and then simply estimated them respectively. In [30], \(\sum_{i=k+1-\tau(k)}^{k-1}e^{T}(i)Qe(i)\) was approximated with \(\sum_{i=k+1-\tau_{m}}^{k-1}e^{T}(i)Qe(i)\). So the methods in [28, 30] may bring some conservatism. In this paper, the reciprocally convex approach and some inequality techniques are employed to deal with this kind of terms. Tighter upper bounds for these terms are obtained.
Recently, Nam et al. [40] obtained a discrete Wirtinger-based inequality. Based on this inequality, we will reconsider the asymptotic stability of the error-state system (3). For simplicity, \(\tilde {e}_{i}\in R^{18n\times n}\) (\(i=1,2,\ldots,18\)) are defined as block entry matrices (e.g., \(\tilde{e}_{3}=[0_{n\times2n},I_{n},0_{n\times 15n}]^{T}\)). The other notations are defined as
Theorem 2
For given integers \(0<\tau_{1} <\tau_{2}\), \(0<\sigma\), the error-state system (3) is asymptotically stable if there exist symmetric positive definite matrices \(P\in\mathbb {R}^{5n\times5n}\), \(S_{1}\in\mathbb{R}^{n\times n}\), \(S_{2}\in\mathbb{R}^{n\times n}\), \(Q_{1}\in\mathbb{R}^{2n\times2n}\), \(Q_{2}\in\mathbb{R}^{2n\times2n}\), \(\mathcal{N}_{1}\in\mathbb{R}^{2n\times2n}\), \(\mathcal{N}_{2}\in \mathbb{R}^{2n\times2n}\), \(Q_{3}\in\mathbb{R}^{n\times n}\), positive diagonal matrices \(H_{i}\in\mathbb{R}^{n\times n}\) (\(i=1,2,3,4\)), a scalar \(\epsilon>0\), symmetric matrices \(Z_{i}\in\mathbb{R}^{n\times n}\) (\(i=1,2,3\)), and matrices \(\mathcal{M}\in\mathbb{R}^{2n\times2n}\), \(X\in\mathbb{R}^{n\times n}\), \(Y\in\mathbb{R}^{n\times n}\) satisfying the following LMIs:
Then, the estimator gain matrix is given by \(K=X^{-1}Y\), and the other parameters are defined as in Theorem 1.
Proof
Defined a Lyapunov-Krasovskii functional as
where
where \(y(u)=e(u)-e(u-1)\).
By arguments similar to those in Theorem 1, we have
Calculating the forward difference of \(V_{2}(k)\) yields
Lemma 3 gives
where \(\zeta_{1}=e(k)-e(k-\sigma)\), \(\zeta_{2}=e(k)+e(k-\sigma)-\frac {1}{\sigma}(2\sum_{s=k-\sigma}^{k-1}e(s)+e(k)-e(k-\sigma))\).
So
Calculating \(\Delta V_{5}(k)\), we get
By Lemma 2 we obtain the following inequality:
where \(\zeta_{3}=e(k)-\frac{1}{\tau_{1}+1}\sum_{s=k-\tau _{1}}^{k}e(s)\), and
Hence,
Following a similar procedure as from (14) to (16), we gather from (21) to (23) that
Inequality (18) implies
Therefore, the error-state system (3) is asymptotically stable. This completes the proof of Theorem 2. □
Remark 3
In 2015, Nam et al. [40] derived a discrete version of the Wirtinger-based integral inequality. Combining this new inequality with the reciprocally convex technique, a less conservative stability condition for the linear discrete systems with an interval time-varying delay is obtained in [40]. Using the Wirtinger-based summation inequality obtained in [40], we derive Theorem 2, which is less conservative than Theorem 1. Recently, Zhang et al. [7] investigate the delay-variation-dependent stability of discrete-time systems with a time-varying delay. A novel augmented Lyapunov functional is constructed. A generalized free-weighing matrix approach is proposed to estimate the summation terms appearing in the forward difference of the Lyapunov functional. The generalized free-weighing matrix approach encompasses the Jensen-based inequality approach and the Wirtinger-based inequality approach as particular cases. Our results may be further improved by using the generalized free-weighing matrix approach.
Remark 4
In order to reduce the conservatism of the stability criterion, we modify the Lyapunov-Krsovskii functional in the proof of Theorem 1. The Lyapunov-Krsovskii functional term \(\sum_{s=-\tau_{1}+1}^{0}\sum_{j=s}^{0}\sum_{u=k+j}^{k}y^{T}(u)Q_{3}y(u)\) is taken into account,
in the proof of Theorem 1 is replaced by
A new asymptotic stability criterion - Theorem 2 is derived. Theorem 2 in this paper is less conservative than Theorem 1.
If the leakage delay disappears, that is \(\sigma=0\), then the error-state system (3) reduces to
From Theorem 2, the following stability criterion for the error-state system (25) can be obtained. For simplicity, \(\check{e}_{i}\in R^{16n\times n}\) (\(i=1,2,\ldots,16\)) are defined as block entry matrices (e.g., \(\check {e}_{3}=[0_{n\times2n},I_{n},0_{n\times13n}]^{T}\)). The other notations are defined as
Corollary 1
For given integers \(0<\tau_{1} <\tau_{2}\) and diagonal matrices \(L_{m}=\operatorname{diag}\{l_{1}^{-},\ldots,l_{n}^{-}\}\) and \(L_{p}=\operatorname{diag}\{ l_{1}^{+},\ldots,l_{n}^{+}\}\), the error-state system (25) is asymptotically stable for \(\tau_{1}\leq \tau(k)\leq\tau_{2}\) if there exist symmetric positive definite matrices \(P\in\mathbb {R}^{5n\times5n}\), \(Q_{1}\in\mathbb{R}^{2n\times2n}\), \(Q_{2}\in\mathbb{R}^{2n\times2n}\), \(\mathcal{N}_{1}\in\mathbb{R}^{2n\times2n}\), \(\mathcal{N}_{2}\in \mathbb{R}^{2n\times2n}\), \(Q_{3}\in\mathbb{R}^{n\times n}\), positive diagonal matrices \(H_{i}\in\mathbb{R}^{n\times n}\) (\(i=1,2,3,4\)), a scalar \(\epsilon>0\), symmetric matrices \(Z_{i}\in\mathbb{R}^{n\times n}\) (\(i=1,2,3\)), and matrices \(\mathcal{M}\), X, Y of appropriate dimensions satisfying the following LMIs:
Then, the estimator gain matrix is given by \(K=X^{-1}Y\), and the other parameters are defined as in Theorem 1.
Proof
Choose the following Lyapunov-Krasovskii functional for system (25):
where
where \(y(u)=e(u)-e(u-1)\).
From (7), (9), (13), and (23), the forward difference of \(V_{i}(k)\) (\(i=1, 2, 3, 4\)) satisfies
Combining (29) with (26) gives
So the error-state system (25) is asymptotically stable. This completes the proof. □
Remark 5
A novel Lyapunov-Krasovskii functional in Corollary 1 is constructed, which includes the Lyapunov-Krasovskii functional term \(V_{4}(k)=\sum_{s=-\tau_{1}+1}^{0}\sum_{j=s}^{0}\sum_{u=k+j}^{k}y^{T}(u) \times Q_{3}y(u)\). However, this Lyapunov-Krasovskii functional term was not taken into account in [30, 33]. The Jensen inequality was employed to estimate an upper bound of \(-\sum_{s=-\tau_{1}+1}^{0}\sum_{j=k+s}^{k}y^{T}(j)Q_{3}y(j)\) in the forward difference of the Lyapunov-Krasovskii functional in [34]. Since the Jensen inequality ignored some terms, the estimation methods in [34] may bring conservatism to some extent. In this paper, by employing a novel double summation inequality in Lemma 2, a tight upper bound of \(-\sum_{s=-\tau _{1}+1}^{0}\sum_{j=k+s}^{k}y^{T}(j)Q_{3}y(j)\) is given. The stability criterion in [34] needs \(56n^{2}+16n\) decision variables. However, the number of decision variables in Corollary 1 is \(28.5n^{2}+12.5n\). Therefore, Corollary 1 has lower computational complexity.
4 Numerical examples
In this section, we give two numerical examples to demonstrate the effectiveness of our stability criteria.
Example 1
Consider the discrete-time error-state system (3) with leakage delay and the following parameters:
Let the activation function \(g(x)=\bigl [{\scriptsize\begin{matrix}{} g_{1}(x_{1})\cr g_{2}(x_{2})\end{matrix}} \bigr ]=\bigl [{\scriptsize\begin{matrix}{} \tanh (0.3x_{1})\cr \tanh (0.4x_{2}) \end{matrix}} \bigr ]\). Then \(L_{m}=\operatorname{diag}\{0,0\}\) and \(L_{P}=\{0.3,0.4\}\).
By solving the LMIs in Theorem 1 and Theorem 2, the allowable upper bounds of \(\tau_{2}\) for different \(\tau_{1}\) and σ are listed in Table 1 and Table 2, respectively. For the case \(\tau_{1}=2\), \(\tau _{2}=11\), and \(\sigma=2\), by Theorem 2, the corresponding gain matrix is
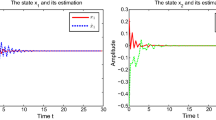
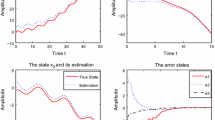
Furthermore, the state dynamics trajectories of \((x(t),\hat{x}(t))\) and error dynamics trajectories of \(e(t)\) are shown in Figures 1 and 2, respectively.
Remark 6
From Table 1 or Table 2, it can be easily seen that the error-state system (3) is globally asymptotically stable when the leakage delay \(\sigma=1\mbox{ and }2\). But when \(\sigma\geq3\), the LMIs in Theorem 1 and Theorem 2 are infeasible as shown in Table 1 and Table 2. Table 1 and Table 2 also show that Theorem 2 is less conservative than Theorem 1 when \(\sigma=2\).
Remark 7
Figure 1 and Figure 2 show the simulation results. For the case \(\sigma=2\), Figure 1 shows that the state trajectories of \((x(t),\hat{x}(t))\) and the error state \(e(t)\) converge to zero smoothly. Figure 2 shows that the state trajectories of \((x(t),\hat{x}(t))\) and the error state \(e(t)\) do not converge to an equilibrium point in case of \(\sigma=5\). Hence, the effect of leakage delay in the dynamical system cannot be neglected.
Example 2
Consider the discrete-time error-state system (25) with the following parameters:
Let the activation function be \(g(x)=\tanh (0.5x)\), we obtain \(L_{m}=\operatorname{diag}\{0,0,0\}\) and \(L_{P}=\{0.5,0.5,0.5\}\). Since all conditions in Corollary 1 are satisfied, the error-state system (25) with given parameters is globally asymptotically stable. For different values of \(\tau_{1}\), the allowed maximum time-delay bounds obtained by Corollary 1 are listed in Table 3. From Table 3, it can be confirmed that Corollary 1 gives larger delay upper bounds than those obtained by the stability criteria in [30, 33]. Although the allowed delay upper bounds obtained by Corollary 1 are the same as those obtained in [34], the stability criterion in [34] requires 552 decision variables. The number of decision variables (NoDV) in Corollary 1 is 294, which means that Corollary 1 has lower computational complexity.
For the case \(\tau_{1}=8\), \(\tau_{2}=34\), by solving the LMIs in Corollary 1, the corresponding state gain matrix is
5 Conclusions
In this paper, we have investigated the problem of delay-dependent state estimation for discrete-time recurrent neural networks with leakage delay and time-varying delay. By constructing two new Lyapunov-Krasovskii functionals, some new delay-dependent stability criteria for designing state estimator of the discrete-time networks are established. Moreover, the simulation results show that the effect of leakage delay in dynamical neural networks cannot be ignored. The effectiveness of the developed results has been verified via two examples.
References
He, Y, Wu, M, Liu, GP, She, JH: Output feedback stabilization for a discrete-time system with a time-varying delay. IEEE Trans. Autom. Control 53(10), 2372-2377 (2008)
Liu, XG, Wu, M, Martin, R, Tang, ML: Stability analysis for neutral systems with mixed delays. J. Comput. Appl. Math. 202, 478-497 (2007)
Guo, S, Tan, XH, Huang, L: Stability and bifurcation in a discrete system of two neurons with delays. Nonlinear Anal., Real World Appl. 9, 1323-1335 (2008)
Chen, P, Tang, XH: Existence and multiplicity of solutions for second-order impulsive differential equations with Dirichlet problems. Appl. Math. Comput. 218, 11775-11789 (2012)
Zang, YC, Li, JP: Stability in distribution of neutral stochastic partial differential delay equations driven by α-stable process. Adv. Differ. Equ. 2014, 13 (2014)
Xu, Y, He, ZM: Exponential stability of neutral stochastic delay differential equations with Markovian switching. Appl. Math. Lett. 52, 64-73 (2016)
Zhang, CK, He, Y, Jiang, L, Wu, M, Zeng, HB: Delay-variation-dependent stability of delayed discrete-time systems. IEEE Trans. Autom. Control (2015). doi:10.1109/TAC.2015.2503047
Banu, LJ, Balasubramaniam, P, Ratnavelu, K: Robust stability analysis for discrete-time uncertain neural networks with leakage time-varying delay. Neurocomputing 151, 806-816 (2015)
Balasubramaniam, P, Kalpana, M, Rakkiyappan, R: Global asymptotic stability of BAM fuzzy cellular neural networks with time delays in the leakage term, discrete and unbounded distributed delays. Math. Comput. Model. 53(5), 839-853 (2011)
Liu, B: Global exponential stability for BAM neural networks with time-varying delays in the leakage terms. Nonlinear Anal., Real World Appl. 14(1), 559-566 (2013)
Li, X, Cao, J: Delay-dependent stability of neural networks of neutral type with time delay in the leakage term. Nonlinearity 23(7), 1709-1726 (2010)
Chen, X, Song, Q: Global stability of complex-valued neural networks with both leakage time delay and discrete time delay on time scales. Neurocomputing 121, 254-264 (2013)
Li, X, Fu, X: Effect of leakage time-varying delay on stability of nonlinear differential systems. J. Franklin Inst. 350, 1335-1344 (2013)
Nagamani, G, Radhika, T: A quadratic convex combination approach on robust dissipativity and passivity analysis for Takagi-Sugeno fuzzy Cohen-Grossberg neural networks with time-varying delays. Math. Methods Appl. Sci. 39(13), 3880-3896 (2016)
Ramasamy, S, Nagamani, G, Zhu, QX: Robust dissipativity and passivity analysis for discrete-time stochastic T-S fuzzy Cohen-Grossberg Markovian jump neural networks with mixed time delays. Nonlinear Dyn. (2016). doi:10.1007/s11071-016-2862-6
Nagamani, G, Radhika, T, Balasubramaniam, P: A delay decomposition approach for robust dissipativity and passivity analysis of neutral-type neural networks with leakage time-varying delay. Complexity 21, 248-264 (2016)
Nagamani, G, Ramasamy, S, Balasubramaniam, P: Robust dissipativity and passivity analysis for discrete-time stochastic neural networks with time-varying delay. Complexity 21(3), 47-58 (2016)
Wang, Z, Ho, DWC, Liu, X: State estimation for delayed neural networks. IEEE Trans. Neural Netw. 16(1), 279-284 (2005)
Huang, H, Feng, G: State estimation of recurrent neural networks with time-varying delay: a novel delay partition approach. Neurocomputing 74, 792-796 (2011)
Liu, Y, Lee, SM, Kwon, OM, Park, JH: A study on \(H_{\infty}\) state estimation of static neural networks with time-varying delays. Appl. Math. Comput. 226, 589-597 (2014)
Shu, YJ, Liu, XG: Improved results on \(H_{\infty}\) state estimation of static neural networks with interval time-varying delay. J. Inequal. Appl. 2016, 48 (2016)
He, Y, Wang, QG, Wu, M, Lin, C: Delay-dependent state estimation for delayed neural networks. IEEE Trans. Neural Netw. 17(4), 1077-1081 (2006)
Liang, J, Lan, J: Robust state estimation for stochastic genetic regulatory networks. Int. J. Syst. Sci. 41(1), 47-63 (2010)
Wang, Z, Liu, Y, Liu, X: State estimation for jumping recurrent neural networks with discrete and distributed delays. Neural Netw. 22(1), 41-48 (2009)
Chen, Y, Bi, W, Li, W, Wu, Y: Less conservatived results of state estimation for neural networks with time-varying delay. Neurocomputing 73, 1324-1331 (2010)
Sakthivel, R, Vadivel, P, Mathiyalagan, K, Arunkumar, A, Sivachitra, M: Design of state estimator bidirectional associative memory neural network with leakage delays. Inf. Sci. 296, 263-274 (2015)
Lakshmanan, S, Park, JH, Jung, HY, Balasubramaniam, P: Design of state estimator for neural networks with leakage, discrete and distributed delays. Appl. Math. Comput. 218, 11297-11310 (2012)
Arunkumar, A, Sakthivel, R, Mathiyalagan, K, Marshal Anthoni, S: Robust state estimation for discrete-time BAM neural networks with time-varying delay. Neurocomputing 131, 171-178 (2014)
Qiu, SB, Liu, XG, Shu, YJ: New approach to state estimator for discrete-time BAM neural networks with time-varying delay. Adv. Differ. Equ. 2015, 189 (2015)
Mou, S, Gao, H, Qiang, W, Fei, Z: State estimation for discrete-time neural networks with time-varying delays. Neurocomputing 72, 643-647 (2008)
Kan, X, Wang, Z, Shu, H: State estimation for discrete-time delayed neural networks with fractional uncertainties and sensor saturations. Neurocomputing 117, 64-71 (2013)
Lu, CY: A delay-range-dependent approach to design state estimators for discrete-time recurrent neural networks with interval time-varying delay. IEEE Trans. Circuits Syst. II, Express Briefs 55(11), 1163-1167 (2008)
Wu, Z, Shi, P, Su, H, Chu, J: State estimation for discrete-time neural networks with time-varying delay. Int. J. Syst. Sci. 43(4), 647-655 (2012)
Park, MJ, Kwon, OM, Park, JH, Lee, SM, Cha, EJ: \(H_{\infty}\) state estimation for discrete-time neural networks with interval time-varying and probabilistic diverging disturbances. Neurocomputing 153, 255-270 (2015)
Gopalsamy, P: Leakage delays in BAM. J. Math. Appl. 325(2), 1117-1132 (2007)
Peng, S: Global attractive periodic solutions of BAM neural networks with continuously distributed delays in the leakage terms. Nonlinear Anal., Real World Appl. 11(3), 2141-2151 (2010)
Kwon, OM, Park, MJ, Park, JH, Lee, SM, Cha, EJ: New criteria on delay-dependent stability for discrete-time neural networks with time-varying delays. Neurocomputing 121, 185-194 (2013)
Park, P, Ko, JW, Jeong, C: Reciprocally convex approach to stability of systems with time-varying delays. Automatica 47(1), 235-238 (2011)
Wang, FX, Liu, XG, Tang, ML, Shu, YJ: Stability analysis of discrete-time systems with variable delays via some new summation inequalities. Adv. Differ. Equ. 2016, 95 (2016)
Nam, PT, Pathirana, PN, Trinh, H: Discrete Wirtinger-based inequality and its application. J. Franklin Inst. 352(5), 1893-1905 (2015)
Kwon, OM, Park, MJ, Park, JH, Lee, SM, Cha, EJ: Improved robust stability criteria for uncertain discrete-time systems with interval time-varying delays via new zero equalities. IET Control Theory Appl. 6(16), 2567-2575 (2012)
Acknowledgements
The authors would like to thank the reviewers for their valuable comments and constructive suggestions. This work is partly supported by National Natural Science Foundation of China under grants nos. 61271355 and 61375063, the ZNDXYJSJGXM under grant no. 2015JGB21, and the Educational Department of Hunan Province of China under grant no. 15C0243.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally and significantly in writing this paper. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Qiu, SB., Liu, XG. & Shu, YJ. A study on state estimation for discrete-time recurrent neural networks with leakage delay and time-varying delay. Adv Differ Equ 2016, 234 (2016). https://doi.org/10.1186/s13662-016-0958-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-016-0958-4