1 Introduction

We consider the following nonlinear fractional q-difference equation with integral boundary conditions:

$$ \begin{aligned} &D_{q}^{\alpha}u(t)+h(t) f\bigl(t,u(t)\bigr)=0,\quad t\in(0,1), \\ &D_{q}^{j}u(0)=0,\quad 0\leq j\leq n-2,\qquad u(1)=\mu\int _{0}^{1} g(s)u(s)\, d_{q}s, \end{aligned} $$
(1.1)

where \(\alpha\in(n-1,n]\) are a real number and \(n\geq3\) is an integer, \(D_{q}^{\alpha}\) are the fractional q-derivative of the Riemann-Liouville type, \(\mu>0\) and \(0< q<1\) are two constants, g, h are two given continuous functions, and \(f:[0,1]\times[0,\infty)\rightarrow[0,\infty )\)is continuous and \(f(t,0)\not\equiv0\) on \([0,1]\). To the best of authors’ knowledge, there is still little utilization of the monotone iterative method to study the existence of positive solutions for boundary value problems of nonlinear fractional q-difference equations with integral boundary conditions.

The monotone iterative method is an interesting and effective technique for investigating the existence of solutions/positive solutions for nonlinear boundary value problems. This method has been paid more and more attention due to the advantage that the first term of the iterative sequences may be taken to be a constant function or a simple function; see [1–8] and the references therein. For instance, by means of the monotone iterative technique and the method of lower and upper solutions, Xu and Liu [9] studied the maximal and minimal solutions for a coupled system of fractional differential-integral equations with two-point boundary conditions. In [10], by means of monotone iterative technique, Zhang et al. investigated the existence and uniqueness of the positive solution for a fractional differential equation with derivatives. By applying the monotone iteration method, Zhang et al. [11] obtained the positive extremal solutions and iterative schemes for approximating the solution of fractional differential equations with nonlinear terms depending on the lower-order derivatives on a half-line.

Since 2010, fractional q-difference equations have gained considerable popularity and importance due to the fact that they can describe the natural phenomena and the mathematical model more accurately. For some recent contributions on the topic, see [12–18] and the references incited therein. For example, under different conditions, Graef and Kong [19, 20] investigated the existence of positive solutions for boundary value problems with fractional q-derivatives in terms of different ranges of λ, respectively. By applying the nonlinear alternative of Leray-Schauder type and Krasnoselskii fixed point theorems, the author [21] established sufficient conditions for the existence of positive solutions for nonlinear semipositone fractional q-difference system with coupled integral boundary conditions. By applying some standard fixed point theorems, Agarwal et al. [22] and Ahmad et al. [23] showed some existence results for sequential q-fractional integrodifferential equations with q-antiperiodic boundary conditions and nonlocal four-point boundary conditions, respectively. In [24], relying on the contraction mapping principle and a fixed point theorem due to O’Regan, Ahmad et al. were concerned with new boundary value problems of nonlinear q-fractional differential equations with nonlocal and sub-strip type boundary conditions. In [25], Yang et al. obtained the existence and uniqueness of positive solutions for a class of nonlinear q-fractional boundary value problems and established the iterative schemes for approximating the solutions.

Motivated by the results mentioned above and the effectiveness and feasibility of monotone iterative method, we consider the existence of positive solutions for fractional q-difference boundary value problem (1.1). In Section 2, we present some preliminaries and lemmas that will be used to prove our main results. The main theorems are formulated and proved in Section 3. At last, an explicit example is given to illustrate the main result in Section 4.

2 Preliminaries

For the convenience of the reader, we present some necessary definitions and lemmas of fractional q-calculus theory. These details can be found in the recent literature; see [26] and references therein.

Definition 2.1

([26])

Let \(\alpha\geq0\), \(0< q<1\), and f be function defined on \([0,1]\). The fractional q-integral of the Riemann-Liouville type is \((I_{q}^{0}f)(x)=f(x)\) and

$$ \bigl(I_{q}^{\alpha}f\bigr) (x)=\frac{1}{\Gamma_{q}(\alpha)}\int _{0}^{x}(x-qt)^{(\alpha -1)}f(t)\, d_{q}t,\quad \alpha>0, x\in[0,1], $$

where \(\Gamma_{q}(\alpha)=(1-q)^{(\alpha-1)}(1-q)^{1-\alpha}\), \(0< q<1\), and satisfies the relation \(\Gamma_{q}(\alpha+1)=[\alpha]_{q}\Gamma_{q}(\alpha )\), with

$$ [\alpha]_{q}=\frac{q^{\alpha}-1}{q-1},\qquad (1-q)^{(0)}=1,\qquad (1-q)^{(n)}=\prod_{k=0}^{n-1} \bigl(1-q^{k+1}\bigr),\quad n\in\mathbb{N}. $$

More generally, if \(\alpha\in\mathbb{R}\), then \((1-q)^{(\alpha)}=\prod_{n=0}^{\infty}((1-q^{n+1})/(1-q^{1+\alpha +n}) )\).

For \(0< q<1\), the q-derivative of a real valued function f is here defined by

$$ (D_{q} f) (x)=\frac{f(x)-f(qx)}{(1-q)x}, \quad x\neq0\quad \mbox{and}\quad (D_{q}f) (0)=\lim_{x\rightarrow0}(D_{q}f) (x), $$

and q-derivatives of higher order by

$$ \bigl(D_{q}^{0}f\bigr) (x)=f(x) \quad \mbox{and}\quad \bigl(D_{q}^{n}f\bigr) (x)=D_{q} \bigl(D_{q}^{n-1}f\bigr) (x), \quad n\in\mathbb{N}. $$

Definition 2.2

([26])

The fractional q-derivative of the Riemann-Liouville type of order \(\alpha\geq0\) is defined by \(D_{q}^{0}f(x)=f(x)\) and

$$ \bigl(D_{q}^{\alpha}f\bigr) (x)=\bigl(D_{q}^{m}I_{q}^{m-\alpha}f \bigr) (x),\quad \alpha>0, $$

where m is the smallest integer greater than or equal to α.

Lemma 2.3

([26])

Let \(\alpha,\beta\geq0\), and f be a function defined on \([0,1]\). Then the next formulas hold:

  1. (1)

    \((I_{q}^{\beta}I_{q}^{\alpha}f)(x)=I_{q}^{\alpha+\beta}f(x)\),

  2. (2)

    \((D_{q}^{\alpha}I_{q}^{\alpha}f)(x)=f(x)\).

Lemma 2.4

([12])

Let \(\alpha>0\) and p be a positive integer. Then the following equality holds:

$$ \bigl(I_{q}^{\alpha}D_{q}^{p} f\bigr) (x)=\bigl(D_{q}^{p} I_{q}^{\alpha}f\bigr) (x)-\sum_{k=0}^{p-1}\frac {x^{\alpha-p+k}}{\Gamma_{q}(\alpha+k-p+1)} \bigl(D_{q}^{k}f\bigr) (0). $$

For the our analysis, we need the following assumptions:

  1. (H1)

    \(g:[0,1]\rightarrow[0,\infty)\) is continuous and \(\sigma=\mu \int_{0}^{1}s^{\alpha-1}g(s)\, d_{q}s<1\), \(\theta=\mu\int_{0}^{1}s^{\alpha}g(s)\, d_{q}s\).

  2. (H2)

    \(h:[0,1]\rightarrow[0,\infty)\) is continuous and \(0<\int_{0}^{1}(1-qs)^{(\alpha-1)} h(s)\, d_{q}s<\infty\).

Now we derive the corresponding Green’s function for boundary value problem (1.1), and obtain some properties of the Green’s function.

Lemma 2.5

For any \(x\in C[0,1]\), then the boundary value problem

$$ \begin{aligned} &D_{q}^{\alpha}u(t)+x(t)=0,\quad t\in(0,1), \\ &D_{q}^{j}u(0)=0,\quad 0\leq j\leq n-2,\qquad u(1)=\mu\int _{0}^{1} g(s)u(s)\, d_{q}s, \end{aligned} $$
(2.1)

has an unique solution given by

$$ u(t)=\int_{0}^{1}G(t,qs)x(s)\, d_{q}s, $$
(2.2)

where

$$\begin{aligned}& G(t,s)=H(t,s)+\frac{\mu t^{\alpha-1}}{1-\sigma}\int_{0}^{1}H( \tau,s)g(\tau )\, d_{q}\tau, \end{aligned}$$
(2.3)
$$\begin{aligned}& H(t,s)=\frac{1}{\Gamma_{q}(\alpha)}\left \{ \textstyle\begin{array}{l@{\quad}l} t^{\alpha-1}(1-s)^{(\alpha-1)}-(t-s)^{(\alpha-1)}, & 0\leq s\leq t\leq 1, \\ t^{\alpha-1}(1-s)^{(\alpha-1)}, & 0\leq t\leq s\leq1. \end{array}\displaystyle \right . \end{aligned}$$
(2.4)

Proof

In view of Definition 2.2 and Lemma 2.3, we see that

$$ \bigl(D_{q}^{\alpha}u\bigr) (t)=-x(t)\quad \Longleftrightarrow\quad \bigl(I_{q}^{\alpha}D_{q}^{n}I_{q}^{n-\alpha}u\bigr) (t)=- \bigl(I_{q}^{\alpha}x\bigr) (t). $$
(2.5)

From (2.5) and Lemma 2.4, we can reduce (2.1) to the following equivalent integral equations:

$$ u(t)=c_{1}t^{\alpha-1}+c_{2}t^{\alpha-2}+ \cdots+c_{n}t^{\alpha-n}-\int_{0}^{t} \frac{(t-qs)^{(\alpha-1)}}{\Gamma_{q}(\alpha)}x(s)\, d_{q}s. $$
(2.6)

From \(D_{q}^{j}u(0)=0\), \(0\leq j\leq n-2\), we have \(c_{n}=c_{n-1}=\cdots= c_{2}=0\). Thus, (2.6) reduces to

$$ u(t)=c_{1}t^{\alpha-1}-\int_{0}^{t} \frac{(t-qs)^{(\alpha-1)}}{\Gamma_{q}(\alpha )}x(s)\, d_{q}s. $$
(2.7)

Using the integral boundary condition: \(u(1)=\mu\int_{0}^{1}g(s)u(s)\, d_{q}s\) in (2.7), we obtain

$$ c_{1}=\mu\int_{0}^{1}g(s)u(s) \, d_{q}s+\int_{0}^{1} \frac{(1-qs)^{(\alpha-1)}}{\Gamma _{q}(\alpha)}x(s)\, d_{q}s. $$
(2.8)

Combining (2.7) and (2.8), we have

$$\begin{aligned} u(t) =&t^{\alpha-1} \biggl(\mu\int_{0}^{1}g(s)u(s) \, d_{q}s +\int_{0}^{1} \frac{(1-qs)^{(\alpha-1)}}{\Gamma_{q}(\alpha)}x(s)\, d_{q}s \biggr) \\ &{}-\int_{0}^{t}\frac{(t-qs)^{(\alpha-1)}}{\Gamma_{q}(\alpha)}x(s)\, d_{q}s \\ =&\mu t^{\alpha-1}\int_{0}^{1}g(s)u(s)\, d_{q}s+\int_{0}^{1}H(t,qs)x(s)\, d_{q}s. \end{aligned}$$
(2.9)

Multiplying both sides of (2.9) by \(g(t)\) and integrating the resulting identity with respect to t from 0 to 1, we obtain

$$\begin{aligned} \int_{0}^{1}g(t)u(t)\, d_{q}t =&\int _{0}^{1}g(t) \biggl(\mu t^{\alpha-1}\int _{0}^{1}g(s)u(s)\, d_{q}s+\int _{0}^{1}G_{1}(t,qs)x(s)\, d_{q}s \biggr)\, d_{q}t \\ =&\mu\int_{0}^{1} t^{\alpha-1}g(t)\, d_{q}t\int_{0}^{1}g(s)u(s)\, d_{q}s \\ &{}+\int_{0}^{1}g(t)\int_{0}^{1}H(t,qs)x(s) \, d_{q}s\, d_{q}t. \end{aligned}$$

Solving for \(\int_{0}^{1}g(t)u(t)\, d_{q}t\), we have

$$ \int_{0}^{1}g(t)u(t)\, d_{q}t=\frac{1}{1-\sigma}\int_{0}^{1}g(t) \int_{0}^{1}H(t,qs)x(s)\, d_{q}s\, d_{q}t. $$
(2.10)

Combining (2.9) and (2.10), we get

$$\begin{aligned} u(t)&=\int_{0}^{1}H(t,qs)x(s)\, d_{q}s+ \frac{\mu t^{\alpha-1}}{1-\sigma}\int_{0}^{1}g(t)\int _{0}^{1}H(t,qs)x(s)\, d_{q}s\, d_{q}t \\ &=\int_{0}^{1}G(t,qs)x(s)\, d_{q}s. \end{aligned}$$

This completes the proof of the lemma. □

Lemma 2.6

([21])

The function \(H(t,s)\) defined by (2.4) has the following properties:

$$ \frac{q^{\alpha-1} t^{\alpha-1}(1-t)(1-qs)^{(\alpha-1)}s}{\Gamma _{q}(\alpha)}\leq H(t,qs)\leq\frac{q[\alpha-1]_{q}(1-qs)^{(\alpha -1)}s}{\Gamma_{q}(\alpha)}. $$
(2.11)

Lemma 2.7

The function \(G(t,s)\) defined by (2.3) satisfies the following inequalities:

$$ G(t,qs)\leq\frac{t^{\alpha-1}(1-qs)^{(\alpha-1)}}{(1-\sigma)\Gamma _{q}(\alpha)}, \qquad \psi(t)\varphi(s)\leq G(t,qs)\leq\varphi(s),\quad \forall t,s\in[0,1], $$
(2.12)

where \(\delta=\mu\int_{0}^{1}g(t)\, d_{q}t\), σ, θ are given in (H1), and

$$\begin{aligned}& \psi(t)= \frac{q^{\alpha-2}(1-\theta)t^{\alpha-1}(1-t)}{[\alpha -1]_{q}(1-\sigma+\delta)}, \\& \varphi(s)= \frac{q[\alpha-1]_{q}(1-\sigma+\delta)(1-qs)^{(\alpha -1)}s}{(1-\sigma)\Gamma_{q}(\alpha)},\quad t,s\in[0,1]. \end{aligned}$$

Proof

It is evident by (2.4) that

$$ H(t,qs)\leq\frac{t^{\alpha-1}(1-qs)^{(\alpha-1)}}{\Gamma_{q}(\alpha)},\quad t,s\in[0,1]. $$
(2.13)

Thus, by (2.3), (2.4), and (2.13), we have

$$\begin{aligned} G(t,qs)&=H(t,qs)+\frac{\mu t^{\alpha-1}}{1-\sigma}\int_{0}^{1}H( \tau ,qs)g(\tau)\, d_{q}\tau \\ &\leq\frac{t^{\alpha-1}(1-qs)^{(\alpha-1)}}{\Gamma_{q}(\alpha)}+\frac{\mu t^{\alpha-1}}{1-\sigma}\int_{0}^{1} \frac{\tau^{\alpha-1}(1-qs)^{(\alpha -1)}}{\Gamma_{q}(\alpha)}g(\tau)\, d_{q}\tau \\ &=\frac{t^{\alpha-1}(1-qs)^{(\alpha-1)}}{(1-\sigma)\Gamma_{q}(\alpha)}. \end{aligned}$$

For any \(t,s\in[0,1]\), by (2.3), (2.4), and the right inequality of (2.11), we get

$$\begin{aligned} G(t,qs) =&H(t,qs)+\frac{\mu t^{\alpha-1}}{1-\sigma}\int_{0}^{1}H( \tau ,qs)g(\tau)\, d_{q}\tau \\ \leq&\frac{q[\alpha-1]_{q}(1-qs)^{(\alpha-1)}s}{\Gamma_{q}(\alpha)} +\frac{\mu t^{\alpha-1}}{1-\sigma}\int_{0}^{1} \frac{q[\alpha -1]_{q}(1-qs)^{(\alpha-1)}s}{\Gamma_{q}(\alpha)}g(\tau)\, d_{q}\tau \\ \leq&\frac{q[\alpha-1]_{q}(1-qs)^{(\alpha-1)}s}{\Gamma_{q}(\alpha)} +\frac{q[\alpha-1]_{q}\delta(1-qs)^{(\alpha-1)}s}{(1-\sigma)\Gamma _{q}(\alpha)}=\varphi(s). \end{aligned}$$

On the other hand, by (2.3), (2.4), and the left inequality of (2.11), we have

$$\begin{aligned} G(t,qs) =&H(t,qs)+\frac{\mu t^{\alpha-1}}{1-\sigma}\int_{0}^{1}H( \tau ,qs)g(\tau)\, d_{q}\tau \\ \geq&\frac{q^{\alpha-1} t^{\alpha-1}(1-t)(1-qs)^{(\alpha-1)}s}{\Gamma _{q}(\alpha)} +\frac{\mu t^{\alpha-1}}{1-\sigma}\int_{0}^{1} \frac{q^{\alpha-1} \tau ^{\alpha-1}(1-\tau)(1-qs)^{(\alpha-1)}s}{\Gamma_{q}(\alpha)}g(\tau)\, d_{q}\tau \\ =&\frac{q^{\alpha-1} t^{\alpha-1}(1-t)(1-qs)^{(\alpha-1)}s}{\Gamma _{q}(\alpha)}+\frac{q^{\alpha-1} t^{\alpha-1}(\sigma-\theta )(1-qs)^{(\alpha-1)}s}{(1-\sigma)\Gamma_{q}(\alpha)} \\ \geq&\frac{q^{\alpha-1} t^{\alpha-1}(1-t)(1-qs)^{(\alpha-1)}s}{\Gamma _{q}(\alpha)} \biggl(1+\frac{\sigma-\theta}{1-\sigma} \biggr)=\psi(t)\varphi(s) \geq0. \end{aligned}$$

Then the proof is completed. □

3 Main results

Consider the Banach space \(\mathscr{E}=C[0,1]\) with norm \(\|u\|=\max_{0\leq t\leq1}|u(t)|\) and define the cone \(\mathscr{K}\subset\mathscr{E}\) by

$$ \mathscr{K}=\bigl\{ u\in\mathscr{E}: u(t)\geq0,u(t)\geq\psi(t)\|u\|,t\in [0,1] \bigr\} , $$

where \(\psi(t)\) is defined as Lemma 2.7. We also define the operator \(\mathscr{T}:\mathscr{K}\rightarrow\mathscr{E}\) by

$$ (\mathscr{T}u) (t)=\int_{0}^{1}G(t,qs)h(s)f \bigl(s,u(s)\bigr)\, d_{q}s,\quad t\in[0,1]. $$

It is easy to prove that problem (1.1) is equivalent to the fixed point equation \(\mathscr{T}u=u\), \(u\in\mathscr{C}\).

Lemma 3.1

Assume that (H1) and (H2) hold. \(\mathscr{T}\) is a completely continuous operator and \(\mathscr{T}(\mathscr {K})\subseteq\mathscr{K}\).

Proof

In view of (2.12) we conclude that \(\mathscr {T}(\mathscr{K})\subseteq\mathscr{K}\). Applying the Arzela-Ascoli theorem and standard arguments, we conclude that \(\mathscr{T}\) is a completely continuous operator. The proof is completed. □

For convenience, we denote

$$ \Lambda= \biggl(\frac{1}{(1-\sigma)\Gamma_{q}(\alpha)}\int_{0}^{1}(1-qs)^{(\alpha-1)} h(s)\, d_{q}s \biggr)^{-1}. $$
(3.1)

By the condition (H2) we deduce that \(\Lambda>0\) is well defined.

Theorem 3.2

Assume that (H1) and (H2) hold. In addition, we assume that there exists \(a>0\) such that

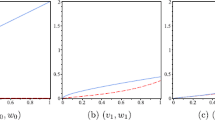
$$ f(t,x)\leq f(t,y)\leq\Lambda a,\quad \textit{for }0\leq x\leq y\leq a, t\in[0,1], $$
(3.2)

where Λ is given by (3.1). Then problem (1.1) has two positive solutions \(v^{\ast}\) and \(w^{\ast}\) satisfying \(0\leq\|v^{\ast}\| \leq\|w^{\ast}\|\leq a\). In addition, the iterative sequences \(v_{k+1}=\mathscr{T}v_{k}\), \(w_{k+1}=\mathscr{T}w_{k}\), \(k=0,1,2,\ldots\) , converge to positive solutions \(v^{\ast}\) and \(w^{\ast}\), respectively, where \(v_{0}(t)=0\), \(w_{0}(t)=at^{\alpha-1}\), \(t\in[0,1]\). Moreover,

$$\begin{aligned} v_{0}(t)&\leq v_{1}(t)\leq\cdots\leq v_{k}(t)\leq \cdots v^{\ast}(t)\leq w^{\ast}(t) \\ &\leq\cdots\leq w_{k}(t)\leq\cdots\leq w_{1}(t)\leq w_{0}(t), \quad t\in[0,1]. \end{aligned}$$

Proof

We will divide our proof into four steps.

Step 1. Let \(\mathscr{K}_{a}=\{u\in\mathscr{K}:\|u\|\leq a\}\), then \(\mathscr{T}(\mathscr{K}_{a})\subseteq\mathscr{K}_{a}\). In fact, if \(u\in\mathscr{K}_{a}\), then we have \(0\leq u(s)\leq\|u\|\leq a\), for \(s\in[0,1]\). Thus by (2.12) and (3.2), we get

$$\begin{aligned} (\mathscr{T}u) (t)&=\int_{0}^{1}G(t,qs)h(s)f \bigl(s,u(s)\bigr)\, d_{q}s \\ &\leq\int_{0}^{1}\frac{t^{\alpha-1}(1-qs)^{(\alpha-1)}}{(1-\sigma)\Gamma _{q}(\alpha)}h(s)f(s,a)\, d_{q}s \\ &\leq\frac{\Lambda a}{(1-\sigma)\Gamma_{q}(\alpha)}\int_{0}^{1}(1-qs)^{(\alpha -1)}h(s) \, d_{q}s=a,\quad t\in[0,1], \end{aligned}$$

which implies that \(\|u\|\leq a\), thus \(\mathscr{T}(\mathscr {K}_{a})\subseteq\mathscr{K}_{a}\).

Step 2. The iterative sequence \(\{v_{k}\}\) is increasing, and there exists \(v^{\ast}\in\mathscr{K}_{a}\) such that \(\lim_{k\rightarrow\infty}\|v_{k}-v^{\ast}\|=0\), and \(v^{\ast}\) is a positive solution of problem (1.1).

Obviously, \(v_{0}\in\mathscr{K}_{a}\). Since \(\mathscr{T}:\mathscr {K}_{a}\rightarrow\mathscr{K}_{a}\), we have \(v_{k}\in\mathscr{T}(\mathscr {K}_{a})\subseteq\mathscr{K}_{a}\), \(k=1,2,\ldots\) . Since \(\mathscr{T}\) is completely continuous, we assert that \(\{v_{k}\} _{k=1}^{\infty}\) is a sequentially compact set. Since \(v_{1}=\mathscr{T}v_{0}=\mathscr{T}0\in\mathscr{K}_{a}\), we obtain

$$ a\geq v_{1}(t)=(\mathscr{T}v_{0}) (t)\geq(\mathscr{T}0) (t) \geq0=v_{0}(t),\quad t\in[0,1]. $$

It follows from (3.2) that \(\mathscr{T}\) is nondecreasing, and then

$$ v_{2}(t)=(\mathscr{T}v_{1}) (t)\geq(\mathscr{T}v_{0}) (t)=v_{1}(t),\quad t\in[0,1]. $$

Thus, by the induction, we have

$$ v_{k+1}(t)\geq v_{k}(t), \quad t\in[0,1], k=0,1,2,\ldots. $$

Hence, there exists \(v^{\ast}\in\mathscr{K}_{a}\) such that \(\lim_{k\rightarrow\infty}\|v_{k}-v^{\ast}\|=0\). By the continuity of \(\mathscr {T}\) and equation \(v_{k+1}=\mathscr{T}v_{k}\), we get \(v^{\ast}=\mathscr {T}v^{\ast}\). Moreover, since the zero function is not a solution of problem (1.1), \(\|v^{\ast}\|>0\). It follows from the definition of the cone \(\mathscr{K}_{a}\) that we have \(v^{\ast}(t)\geq\psi(t)\|v^{\ast}\| >0\), \(t\in(0,1)\), i.e. \(v^{\ast}(t)\) is a positive solution of problem (1.1).

Step 3. The iterative sequence \(\{w_{k}\}\) is decreasing, and there exists \(w^{\ast}\in\mathscr{K}_{a}\) such that \(\lim_{k\rightarrow\infty}\|w_{k}-w^{\ast}\|=0\), and \(w^{\ast}\) is a positive solution of problem (1.1).

Obviously, \(w_{0}\in\mathscr{K}_{a}\). Since \(\mathscr{T}:\mathscr {K}_{a}\rightarrow\mathscr{K}_{a}\), we have \(w_{k}\in\mathscr{T}(\mathscr {K}_{a})\subseteq\mathscr{K}_{a}\), \(k=1,2,\ldots\) . Since \(\mathscr{T}\) is completely continuous, we assert that \(\{w_{k}\} _{k=1}^{\infty}\) is a sequentially compact set. Since \(w_{1}=\mathscr{T}w_{0}\in\mathscr{K}_{a}\), by (2.12) and (3.2), we obtain

$$\begin{aligned} (\mathscr{T}w_{0}) (t)&=\int_{0}^{1}G(t,qs)h(s)f \bigl(st,w_{0}(s)\bigr)\, d_{q}s \\ &\leq\int_{0}^{1}\frac{t^{\alpha-1}(1-qs)^{(\alpha-1)}}{(1-\sigma)\Gamma _{q}(\alpha)}h(s)f(s,a)\, d_{q}s \\ &\leq\frac{\Lambda at^{\alpha-1}}{(1-\sigma)\Gamma_{q}(\alpha)}\int_{0}^{1}(1-qs)^{(\alpha-1)}h(s) \, d_{q}s \\ &=at^{\alpha-1}=w_{0}(t), \quad t\in[0,1]. \end{aligned}$$

Thus we obtain \(w_{1}(t)\leq w_{0}(t)\), \(t\in[0,1]\), which together with (3.2) implies that

$$\begin{aligned} w_{2}(t)&=(\mathscr{T}w_{1}) (t)=\int_{0}^{1}G(t,qs)h(s)f \bigl(s,w_{1}(s)\bigr)\, d_{q}s \\ &\leq\int_{0}^{1}G(t,qs)h(s)f\bigl(s,w_{0}(s) \bigr)\, d_{q}s \\ &=(\mathscr{T}w_{0}) (t)=w_{1}(t), \quad t\in[0,1]. \end{aligned}$$

Thus, by the induction, we have

$$ w_{k+1}(t)\leq w_{k}(t),\quad t\in[0,1], k=0,1,2,\ldots. $$

Hence, there exists \(w^{\ast}\in\mathscr{K}_{a}\) such that \(\lim_{k\rightarrow\infty}\|w_{k}-w^{\ast}\|=0\). Applying the continuity of \(\mathscr{T}\) and the definition of \(\mathscr{K}\), we can concluded that \(w^{\ast}(t)\) is a positive solution of problem (1.1).

Step 4. From \(w_{0}(t)\leq w_{0}(t)\), \(t\in[0,1]\), we get

$$\begin{aligned} v_{1}(t)&=(\mathscr{T}w_{0}) (t)=\int_{0}^{1}G(t,qs)h(s)f \bigl(s,w_{0}(s)\bigr)\, d_{q}s \\ &\leq\int_{0}^{1}G(t,qs)h(s)f\bigl(s,w_{0}(s) \bigr)\, d_{q}s \\ &=(\mathscr{T}w_{0}) (t)=w_{1}(t), \quad t\in[0,1]. \end{aligned}$$

By the induction, we have

$$ v_{k}(t)\leq w_{k}(t), \quad t\in[0,1], k=0,1,2,\ldots. $$

The proof is complete. □

Corollary 3.3

Assume that (H1) and (H2) hold. Suppose further that \(f(t,u)\) is nondecreasing in u for each \(t\in[0,1]\) and

$$ \lim_{u\rightarrow+\infty}\max_{0\leq t\leq1}\frac{f(t,u)}{u}< \Lambda. $$

The conclusion of Theorem  3.2 is valid.

Remark 3.4

The iterative schemes in Theorem 3.2 start off with the zero function and a known simple function which is helpful for computational purpose, respectively.

Remark 3.5

Of course, \(w^{\ast}=v^{\ast}\) may happen and then problem (1.1) has only one solution in \(\mathscr{K}_{a}\). For example, in the case the Lipschitz condition is satisfied by the functions involved, the solutions \(v^{\ast}\) and \(w^{\ast}\) coincide, and then problem (1.1) will have a unique solution in \(\mathscr{K}_{a}\).

4 An example

Example 4.1

Consider the fractional q-difference equation with integral boundary conditions

$$ \begin{aligned} &D_{q}^{7/2} u(t)+t \bigl(3u^{2}+6t+2\bigr)=0,\quad t\in(0,1), \\ &D_{q}^{j}u(0)=0, \quad 0\leq j\leq2,\qquad u(1)=\int _{0}^{1} su(s)\, d_{q}s. \end{aligned} $$
(4.1)

Here, \(q=1/2\), \(\alpha=7/2\), \(\mu=1\), \(g(t)=h(t)=t\), and \(f(t,u)=3u^{2}+6t+2\). It is easy to see that (H1) and (H2) hold. If we let \(a=2\), by simple computation, we have

$$\begin{aligned} \Lambda&= \biggl(\frac{1}{(1-\sigma)\Gamma_{q}(\alpha)}\int_{0}^{1}(1-qs)^{(\alpha-1)} h(s)\, d_{q}s \biggr)^{-1} \\ &=\frac{(32-\sqrt{2})\Gamma_{1/2}(7/2)\Gamma_{1/2}(11/2)}{16-\sqrt{2}} \end{aligned}$$

and

$$ f(t,u)\leq f(t,2)\leq f(1,2)=20< 22.4819\approx\Lambda a, \quad (t,x)\in [0,1] \times[0,a]. $$

Then (3.2) is satisfied. Consequently, Theorem 3.2 guarantees that problem (4.1) has at least two positive solutions \(v^{\ast}\) and \(w^{\ast}\), satisfying \(0\leq \|v^{\ast}\|\leq\|w^{\ast}\|\leq a\).