1 Introduction

Fractional calculus and its implementations have grown in prominence due to their usefulness in representing a variety of complex phenomena in science and engineering [1–5]. One of the most important and distinctive issues in fractional calculus is the study of pantograph-type differential equations. It is a particular class of functional differential equations with proportional delay. It occurs in a variety of pure and applied mathematics areas, including quantum physics, electrodynamics, number theory, control systems and probability. Various researchers have used analytical and numerical methods to investigate the pantograph-type fractional differential equations (FDEs) [6–9]. Using fixed point techniques, some researchers proved the existence and uniqueness of the solution to some nonlinear classes of pantograph-type FDEs with a wider range of boundary conditions [10–15].

Sequential FDEs provide a flexible framework for describing complex systems with multiple memory-dependent processes. The sequential nature allows for the inclusion of fractional derivatives of various orders, providing a nuanced representation of system dynamics. This representation provides a richer mathematical framework for modelling diverse physical and engineering systems. This is advantageous in applications such as materials science, viscoelasticity and biological systems. Qualitative analysis of sequential FDEs is found in [16–20].

The generalised fractional derivative is a powerful tool for simulating complex real-world problems due to its increased precision. The Hilfer fractional derivative is a generalisation of Riemann–Liouville and Caputo fractional derivatives [1]. Sousa and Oliveira [21] provided the ψ-Hilfer fractional derivative with respect to another function. The advantage of the ψ-Hilfer fractional derivative is the freedom to select the differentiation operator and the kernel function ψ. Boundary value problems (BVPs) provide a natural framework for capturing real-world conditions and constraints [22–25]. BVPs involving the ψ-Hilfer fractional derivative were studied in [26–30].

In [12], a sequential pantograph problem involving the ϕ-Caputo derivative was taken into consideration, and the existence results were studied using Darbo’s fixed point theorem and the measure of noncompactness. Motivated by the above-mentioned works, we investigate the ψ-Hilfer sequential pantograph fractional BVP of the form

$$\begin{aligned} \textstyle\begin{cases} {^{H}}D^{\phi _{1},\eta _{1}:\psi}_{a^{+}} ( {^{H}}D^{\phi _{2}, \eta _{2}:\psi}_{a^{+}} x(t) + f(t,x(t)) )= g(t,x(t),x(\lambda t),{^{H}}D^{ \alpha,\beta;\psi}_{a^{+}}x(\lambda t)), \\ x(a)= 0, \qquad x(b) = \sum_{i=1}^{m} \omega _{i} x(\theta _{i}),\quad t \in \mathcal{S} = [a,b], \end{cases}\displaystyle \end{aligned}$$
(1)

where \({^{H}}D^{\phi _{1},\eta _{1}:\psi}_{a^{+}} \), \({^{H}}D^{\phi _{2},\eta _{2}:\psi}_{a^{+}} \) and \({^{H}}D^{\alpha,\beta;\psi}_{a^{+}}\) are the ψ-Hilfer fractional derivatives of order \(\phi _{1}\), \(\phi _{2}\) and α respectively, with \(0<\alpha < \phi _{1},\phi _{2} < 1\) and type \(0\leq \eta _{1},\eta _{2},\beta \leq 1\), \(\omega _{i} \in \mathcal{R^{+}}\), \(\theta _{i} \in \mathcal{S}\), \(g: \mathcal{S} \times \mathcal{R} \times \mathcal{R} \times \mathcal{R} \rightarrow \mathcal{R} \) and \(f: \mathcal{S} \times \mathcal{R} \rightarrow \mathcal{R}\) are continuous functions on a Banach space.

The article is structured as follows: Sect. 2 presents the fundamental concepts, theorems and lemmas that support our investigation. In Sect. 3, the solution of BVP (1) is obtained. The existence and uniqueness of the solution to (1) are established in Sect. 4. In Sect. 5, an example is given.

2 Preliminaries

Let \(C([a,b],\mathcal{R})\) represent the space of all continuous functions from \([a,b]\longrightarrow \mathcal{R}\) and \(AC([a,b],\mathcal{R})\) be the space of all absolutely continuous functions from \([a,b]\longrightarrow \mathcal{R}\).

Definition 1

[2] Let \((a,b) ( {- \infty \leq a < b \leq \infty}) \) be a finite or infinite interval of the real line \(\mathcal{R}\) and ϑ> 0. Let \(\psi (t)\) be an increasing and positive monotone function on \((a,b] \), having a continuous derivative \(\psi ^{\prime}(t)\) on \((a,b)\). The ψ-Riemann–Liouville fractional integral \(I^{\vartheta;\psi}_{a^{+}}(\cdot ) \) of a function \(h \in AC^{n}([a,b],\mathcal{R})\) with respect to another function ψ on [a,b] is defined by

$$\begin{aligned} I^{\vartheta;\psi}_{a^{+}} h(t) = \frac{1}{\Gamma (\vartheta )} \int ^{t}_{a} \psi ^{\prime }(s) \bigl(\psi (t)- \psi (s)\bigr)^{\vartheta -1} h(s) \,ds,\quad t>a>0, \end{aligned}$$

where \(\Gamma (.)\) represents the gamma function.

Definition 2

[2] Let \(\psi ^{\prime}(t) \neq 0\) and \(\vartheta >0\), \(n \in \mathbb{N}\). The Riemann–Liouville fractional derivative of order ϑ of a function \(h \in AC^{n}([a,b],\mathcal{R})\) with respect to another function ψ is defined by

$$\begin{aligned} \begin{aligned} D^{\vartheta,\rho;\psi}_{a^{+}} h(t) = {}& \biggl( \frac{1}{\psi ^{\prime}(t)}\frac {d}{dt} \biggr)^{n} I^{n-\vartheta; \psi}_{a^{+}} h(t) \\ ={}& \frac{1}{\Gamma (n-\vartheta )} \biggl(\frac{1}{\psi ^{\prime}(t)} \frac {d}{dt} \biggr)^{n} \int ^{t}_{a} \psi ^{\prime }(s) \bigl(\psi (t)- \psi (s)\bigr)^{n-\vartheta -1} h(s) \,ds, \end{aligned} \end{aligned}$$

where \(n=[\vartheta ]+1, [\vartheta ]\) represents the integer part of the real number ϑ.

Definition 3

[21] Let \(n-1 < \vartheta < n \) with \(n \in \mathbb{N}, [a,b] \) is the interval such that \({- \infty \leq a < b \leq \infty} \) and \(h,\psi \in C^{n}([a,b],\mathcal{R}) \) are two functions such that \(\psi (t) \) is increasing and \(\psi ^{\prime}(t) \neq 0 \) for all \(t \in [a,b] \). The ψ-Hilfer fractional derivative \(^{H}D^{\vartheta,\rho;\psi}_{a^{+}} (\cdot )\) of a function h of order ϑ and type \(0 \leq \rho \leq 1 \) is defined by

$$\begin{aligned} ^{H}D^{\vartheta,\rho;\psi}_{a^{+}} h(t) = I^{\rho (n-\vartheta ); \psi}_{a^{+}} \biggl(\frac{1}{\psi ^{\prime}(t)}\frac {d}{dt} \biggr)^{n} I^{(1-\rho )(n-\vartheta );\psi}_{a^{+}} h(t), \end{aligned}$$

where \(n=[\vartheta ]+1, [\vartheta ]\) represents the integer part of the real number ϑ with \(\gamma =\vartheta +\rho (n-\vartheta )\).

Lemma 1

[2] Let \(\vartheta,\tau >0\). Then we have the following semigroup property:

$$\begin{aligned} I^{\vartheta;\psi}_{a^{+}} I^{\tau;\psi}_{a^{+}} h(t)= I^{ \vartheta +\tau;\psi}_{a^{+}} h(t),\quad t>a. \end{aligned}$$

Lemma 2

[21] If \(h \in C^{n}([a,b],\mathcal{R}), n-1 < \vartheta < n \) and \(0 \leq \rho \leq 1 \) and \(\gamma =\vartheta +\rho (n-\vartheta )\), then

$$\begin{aligned} I^{\vartheta;\psi}_{a^{+}} {^{H}}D^{\vartheta,\rho;\psi}_{a^{+}} h(t)= h(t)- \sum_{k=1}^{n} \frac{(\psi (t)-\psi (a))^{\gamma -k}}{\Gamma (\gamma -k+1)} h^{[n-k]}_{ \psi} I^{(1-\rho )(n-\vartheta );\psi}_{a^{+}} h(a) \end{aligned}$$

for all \(t \in \mathcal{S}\), where \(h^{[n]}_{\psi} h(t)= (\frac{1}{\psi ^{\prime}(t)} \frac{d}{dt} )^{n} h(t)\).

Proposition 3

[2, 21] Let \(\vartheta \geq 0\), \(l>0\) and \(t>a\). Then the ψ-fractional integral and derivative of a power function are given by

  1. 1.

    \(I^{\vartheta;\psi}_{a^{+}} (\psi (t)-\psi (a))^{l-1}(t) = \frac{\Gamma (l)}{\Gamma (l+\vartheta )} (\psi (t)-\psi (a))^{l+ \vartheta -1} \);

  2. 2.

    \(D^{\vartheta,\rho;\psi}_{a^{+}} (\psi (t)-\psi (a))^{l-1}(t) = \frac{\Gamma (l)}{\Gamma (l-\vartheta )} (\psi (t)-\psi (a))^{l- \vartheta -1} \);

  3. 3.

    \(^{H}D^{\vartheta,\rho;\psi}_{a^{+}} (\psi (t)-\psi (a))^{l-1}(t) = \frac{\Gamma (l)}{\Gamma (l-\vartheta )} (\psi (t)-\psi (a))^{l- \vartheta -1} \), \(l>\gamma =\vartheta +\rho (n-\vartheta )\).

Lemma 4

[30] Let \(n-1 < \vartheta < n, m-1< \alpha < m \leq n, m,n \in \mathbb{N}, 0 \leq \beta \leq 1 \) and \(\vartheta \geq \alpha +\beta (m-\alpha )\). If \(h \in {C^{m}}(\mathcal{S}, \mathcal{R})\), then

$$\begin{aligned} {^{H}}D^{\alpha,\beta;\psi}_{a^{+}} I^{\vartheta;\psi}_{a^{+}} h(t)= I^{\vartheta -\alpha;\psi}_{a^{+}} h(t). \end{aligned}$$

Lemma 5

(Banach contraction principle)

[31] If C is a closed non-empty subset of a Banach space B, then any contraction mapping \(\mathcal{U}: C \rightarrow C \) has a unique fixed point.

Theorem 6

(Krasnosel’skii’s fixed point theorem)

[32] Let D be a closed, bounded, convex and non-empty subset of a Banach space \((B,\Vert \cdot \Vert )\). Suppose that \(\mathcal{U}_{1}, \mathcal{U}_{2}\) are operators from D to D such that

  1. 1.

    \(\mathcal{U}_{1}x + \mathcal{U}_{2}y \in D, \forall x, y \in D \);

  2. 2.

    \(\mathcal{U}_{1}\) is continuous and compact;

  3. 3.

    \(\mathcal{U}_{2}\) is a contraction mapping.

Then there exists \(z \in D \) such that \(z = \mathcal{U}_{1}z + \mathcal{U}_{2}z \).

3 An auxiliary result

System (1) relies on a lower-order fractional derivative of the state function. Therefore, we shall conduct the analysis in a special working space given by

$$\begin{aligned} &\mathcal{J}= \bigl\{ x\vert x(t) \in C\bigl([a,b],\mathcal{R} \bigr),{^{H}}D^{ \alpha,\beta;\psi}_{a^{+}} x(t) \in C\bigl([a,b], \mathcal{R}\bigr) \bigr\} \quad \text{with the norm}\\ &\quad \Vert x \Vert _{\mathcal{J}}= \max \bigl\{ \underset{t \in \mathcal{S}}{ \sup} \bigl\Vert x(t) \bigr\Vert , \underset{t \in \mathcal{S}}{\sup} \bigl\Vert {^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x(t) \bigr\Vert \bigr\} . \end{aligned}$$

The requirement that functions \(x(t)\) and \({^{H}}D^{\alpha,\beta;\psi}_{a^{+}} x(t)\) are continuous implies smoothness and regularity. We can verify from [33] that \(\mathcal{J}\) is a Banach space. \(\mathcal{J}\) also ensures that the solution is well posed and can be analysed within a rigorous mathematical framework.

For proving the existence results, Krasnosel’skii’s fixed point approach is more suitable for the above-considered special working space.

To demonstrate the existence and uniqueness of (1), it is essential to prove the following lemma.

Lemma 7

Let \(0<\alpha < \phi _{1},\phi _{2} < 1\), \(0\leq \eta _{1},\eta _{2},\beta \leq 1\), \(\gamma _{1}=\phi _{1}+ \eta _{1}(1-\phi _{1}), \gamma _{2}=\phi _{2}+\eta _{2}(1-\phi _{2})\), \(a \geq 0\) and \(\curlywedge \neq 0 \). Then, for \(g: \mathcal{S} \times \mathcal{J} \times \mathcal{J} \times \mathcal{J} \rightarrow \mathcal{J} \), \(f: \mathcal{S} \times \mathcal{J} \rightarrow \mathcal{J} \), the solution of the sequential pantograph fractional BVP (1) is given by

$$\begin{aligned} \begin{aligned} x(t)={}&I^{\phi _{1}+\phi _{2};\psi}_{a^{+}} g \bigl(t,x(t),x( \lambda t),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x(\lambda t)\bigr)- I^{ \phi _{2};\psi}_{a^{+}} f\bigl(t,x(t)\bigr) \\ & {}+ \frac{(\psi (t)-\psi (a))^{\gamma _{1}+\phi _{2}-1}}{\Gamma (\gamma _{1}+\phi _{2}) \cdot \curlywedge} \Biggl[ \sum_{i=1}^{m} \omega _{i} I^{\phi _{1}+\phi _{2}; \psi}_{a^{+}} g\bigl(\theta _{i},x(\theta _{i}),x(\lambda \theta _{i}),{^{H}}D^{ \alpha,\beta;\psi}_{a^{+}}x( \lambda \theta _{i})\bigr) \\ &{} - I^{\phi _{1}+\phi _{2};\psi}_{a^{+}} g\bigl(b,x(b),x(\lambda b),{^{H}}D^{ \alpha,\beta;\psi}_{a^{+}}x( \lambda b)\bigr) - \sum_{i=1}^{m} \omega _{i} I^{\phi _{2};\psi}_{a^{+}} f\bigl(\theta _{i},x( \theta _{i})\bigr) \\ &{}+ I^{\phi _{2};\psi}_{a^{+}} f\bigl(b,x(b)\bigr) \Biggr], \end{aligned} \end{aligned}$$
(2)

where

$$\begin{aligned} \curlywedge = \frac{(\psi (b)-\psi (a))^{\gamma _{1}+\phi _{2}-1}}{\Gamma (\gamma _{1}+\phi _{2})} - \sum _{i=1}^{m} \omega _{i} \frac{(\psi (\theta _{i})-\psi (a))^{\gamma _{1}+\phi _{2}-1}}{\Gamma (\gamma _{1}+\phi _{2})}. \end{aligned}$$
(3)

Proof

Using Lemma 2 and applying operator \(I^{\phi _{1};\psi}_{a^{+}}\) on both sides of (1), we have

$$\begin{aligned} {^{H}}D^{\phi _{2},\eta _{2}:\psi}_{a^{+}} x(t) + f\bigl(t,x(t)\bigr)= c_{1} \frac{(\psi (t)-\psi (a))^{\gamma _{1}-1}}{\Gamma (\gamma _{1})} + I^{ \phi _{1};\psi}_{a^{+}} g \bigl(t,x(t),x(\lambda t),{^{H}}D^{\alpha,\beta; \psi}_{a^{+}}x(\lambda t)\bigr). \end{aligned}$$

Again applying operator \(I^{\phi _{2};\psi}_{a^{+}}\) on both sides of (1), we have

$$\begin{aligned} \begin{aligned} x(t)=& I^{\phi _{1}+\phi _{2};\psi}_{a^{+}} g\bigl(t,x(t),x( \lambda t),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x(\lambda t)\bigr) - I^{ \phi _{2};\psi}_{a^{+}} f\bigl(t,x(t)\bigr) \\ & + c_{1} \frac{(\psi (t)-\psi (a))^{\gamma _{1}+\phi _{2}-1}}{\Gamma (\gamma _{1}+\phi _{2})} + c_{2} \frac{(\psi (t)-\psi (a))^{\gamma _{2}-1}}{\Gamma (\gamma _{2})}. \end{aligned} \end{aligned}$$

When \(x(a)=0\), we get \(c_{2}=0\). Then the above equation reduces to

$$\begin{aligned} \begin{aligned} x(t)={}& I^{\phi _{1}+\phi _{2};\psi}_{a^{+}} g \bigl(t,x(t),x( \lambda t),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x(\lambda t)\bigr) - I^{ \phi _{2};\psi}_{a^{+}} f\bigl(t,x(t)\bigr) \\ &{} + c_{1} \frac{(\psi (t)-\psi (a))^{\gamma _{1}+\phi _{2}-1}}{\Gamma (\gamma _{1}+\phi _{2})}. \end{aligned} \end{aligned}$$
(4)

Applying the other boundary condition, we get

$$\begin{aligned} \begin{aligned} &I^{\phi _{1}+\phi _{2};\psi}_{a^{+}} g\bigl(b,x(b),{^{H}}D^{ \alpha,\beta;\psi}_{a^{+}}x(b) \bigr) - I^{\phi _{2};\psi}_{a^{+}} f\bigl(b,x(b)\bigr) + c_{1} \frac{(\psi (t)-\psi (a))^{\gamma _{1}+\phi _{2}-1}}{\Gamma (\gamma _{1}+\phi _{2})} \\ &\quad = \sum_{i=1}^{m} \omega _{i} I^{\phi _{1}+ \phi _{2};\psi}_{a^{+}} g\bigl(t,x(\theta _{i}),{^{H}}D^{\alpha,\beta; \psi}_{a^{+}}x( \theta _{i})\bigr) - \sum_{i=1}^{m} \omega _{i} I^{ \phi _{2};\psi}_{a^{+}} f\bigl(\theta _{i},x(\theta _{i})\bigr) \\ &\qquad{} + c_{1} \sum_{i=1}^{m} \omega _{i} \frac{(\psi (\theta _{i})-\psi (a))^{\gamma _{1}+\phi _{2}-1}}{\Gamma (\gamma _{1}+\phi _{2})}. \end{aligned} \end{aligned}$$

This implies

$$\begin{aligned} \begin{aligned} c_{1} = {}& \frac{1}{\curlywedge} \Biggl[ \sum _{i=1}^{m} \omega _{i} I^{\phi _{1}+\phi _{2};\psi}_{a^{+}} g\bigl(t,x(\theta _{i}),{^{H}}D^{ \alpha,\beta;\psi}_{a^{+}}x( \theta _{i})\bigr) - I^{\phi _{1}+\phi _{2}; \psi}_{a^{+}} g \bigl(b,x(b),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x(b)\bigr) \\ &{} - \sum_{i=1}^{m} \omega _{i} I^{\phi _{2};\psi}_{a^{+}} + I^{ \phi _{2};\psi}_{a^{+}} f\bigl(b,x(b) \bigr) f\bigl(\theta _{i},x(\theta _{i})\bigr) \Biggr]. \end{aligned} \end{aligned}$$

Thus, (2) is satisfied.

Conversely, by direct calculation, we verify that (2) satisfies (1). □

4 Existence and uniqueness results

To verify the existence and uniqueness results, we model our system (1) as a fixed point problem.

Let us define an operator \(\mathcal{U}:\mathcal{J} \longrightarrow \mathcal{J}\) by

$$\begin{aligned} \begin{aligned} \mathcal{U} x(t)={}&I^{\phi _{1}+\phi _{2};\psi}_{a^{+}} g\bigl(t,x(t),x( \lambda t),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x( \lambda t)\bigr)- I^{ \phi _{2};\psi}_{a^{+}} f\bigl(t,x(t)\bigr) \\ &{} + \frac{(\psi (t)-\psi (a))^{\gamma _{1}+\phi _{2}-1}}{\Gamma (\gamma _{1}+\phi _{2}) \cdot \curlywedge} \Biggl[ \sum_{i=1}^{m} \omega _{i} I^{\phi _{1}+\phi _{2}; \psi}_{a^{+}} g\bigl(\theta _{i},x(\theta _{i}),x(\lambda \theta _{i}),{^{H}}D^{ \alpha,\beta;\psi}_{a^{+}}x( \lambda \theta _{i})\bigr) \\ &{} - I^{\phi _{1}+\phi _{2};\psi}_{a^{+}} g\bigl(b,x(b),x(\lambda b),{^{H}}D^{ \alpha,\beta;\psi}_{a^{+}}x( \lambda b)\bigr) - \sum_{i=1}^{m} \omega _{i} I^{\phi _{2};\psi}_{a^{+}} f\bigl(\theta _{i},x( \theta _{i})\bigr) \\ &{} + I^{\phi _{2};\psi}_{a^{+}} f\bigl(b,x(b)\bigr) \Biggr]. \end{aligned} \end{aligned}$$
(5)

We state the following hypothesis:

\((\mathbf{H_{1}})\) Let \(g:\mathcal{S} \times \mathcal{J} \times \mathcal{J} \times \mathcal{J} \longrightarrow \mathcal{J}\) be a continuous function, and there exists a constant \(0< K_{g}<1\) such that, for all \(t \in \mathcal{S}\) and \(x_{1}, x_{2}, \bar{x_{1}}, \bar{x_{2}}, {x_{1}}^{\prime}, {x_{2}}^{ \prime }\in \mathcal{R}\),

$$\begin{aligned} \begin{aligned} \bigl\Vert g\bigl(t,x_{1}, \bar{x_{1}},{x_{1}}^{\prime}\bigr)- g \bigl(t,x_{2}, \bar{x_{2}},{x_{2}}^{\prime} \bigr) \bigr\Vert \leq {}& K_{g} \bigl( \bigl\Vert x_{1}(t) - x_{2}(t) \bigr\Vert + \bigl\Vert \bar{x_{1}}(t)-\bar{x_{2}}(t) \bigr\Vert \\ & {}+ \bigl\Vert {x_{1}}^{\prime}(t) - {x_{2}}^{\prime}(t) \bigr\Vert \bigr). \end{aligned} \end{aligned}$$

\((\mathbf{H_{2}})\) Let \(f:\mathcal{S} \times \mathcal{J} \longrightarrow \mathcal{J}\) be a continuous function, and there exists a constant \(0< K_{f}<1\) such that, for all \(t \in \mathcal{S}\) and \(x_{1}, x_{2} \in \mathcal{R}\),

$$\begin{aligned} \begin{aligned} \bigl\Vert f(t,x_{1})- f(t,x_{2}) \bigr\Vert &\leq K_{f} \bigl( \bigl\Vert x_{1}(t) - x_{2}(t) \bigr\Vert \bigr). \end{aligned} \end{aligned}$$

\((\mathbf{H_{3}})\) Let \(g:\mathcal{S} \times \mathcal{J} \times \mathcal{J} \times \mathcal{J} \longrightarrow \mathcal{J}\) and \(f:\mathcal{S} \times \mathcal{J} \longrightarrow \mathcal{J}\) be continuous functions, and there exist functions \(\sigma, \nu > 0\) such that, for all \(t \in \mathcal{S}\) and \(x, \bar{x}, {x}^{\prime}, \in \mathcal{R}\),

$$\begin{aligned} \begin{aligned} &\bigl\Vert g\bigl(t,x,\bar{x},{x}^{\prime} \bigr) \bigr\Vert \leq \sigma (t), \\ &\bigl\Vert f(t,x) \bigr\Vert \leq \nu (t). \end{aligned} \end{aligned}$$

To simplify the process, let us introduce some notations.

$$\begin{aligned} & \Upsilon (p,d) = \frac{(\psi (p)-\psi (a))^{d}}{\Gamma (d+1) }, \end{aligned}$$
(6)
$$\begin{aligned} &\mathcal{N} = 2K_{g} \mathcal{N}_{1} + K_{f} \mathcal{N}_{2}, \quad\text{where} \end{aligned}$$
(7)
$$\begin{aligned} &\mathcal{N}_{1} = \Upsilon (b,k) + \frac{\Upsilon (b,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, k) + \Upsilon (b,k) \Biggr], \end{aligned}$$
(8)
$$\begin{aligned} & \mathcal{N}_{2} = \Upsilon (b,\bar{k}) + \frac{\Upsilon (b,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \bar{k}) + \Upsilon (b, \bar{k}) \Biggr], \end{aligned}$$
(9)

where \(k= \phi _{1}+\phi _{2}\) or \(\phi _{1}+\phi _{2}-\alpha \), \(\bar{k}=\phi _{2}\) or \(\phi _{2}-\alpha \).

Uniqueness of solution.

Theorem 8

Assume that \((\mathbf{H_{1}})\) and \((\mathbf{H_{2}})\) are satisfied. Suppose that \(2K_{g} \mathcal{N}_{1} + K_{f} \mathcal{N}_{2} < 1\), where \(K_{f}\) and \(K_{g}\) are constants, \(\mathcal{N}_{1}\) and \(\mathcal{N}_{2}\) are given by (8) and (9) respectively. Then system (1) has a unique solution on \(\mathcal{S}\).

Proof

Consider the operator \(\mathcal{U}x(t)\) defined in (5).

Let \(\sup_{t\in \mathcal{S}} \Vert g(t,0,0,0) \Vert = M_{1} < \infty \), \(\sup_{t\in \mathcal{S}} \Vert f(t,0) \Vert = M_{2} < \infty \) and set

$$\begin{aligned} \mathcal{J}_{r}= \bigl\{ x \in \mathcal{J}: \Vert x \Vert _{\mathcal{J}} \leq r \bigr\} , \quad r \geq \frac{\mathcal{N}_{1} M_{1}+\mathcal{N}_{2} M_{2}}{1-\mathcal{N}}. \end{aligned}$$

\(\mathcal{J}_{r}\) is a bounded, closed and convex subset of \(\mathcal{J}\).

Step 1: \(\mathcal{U}\mathcal{J}_{r} \subset \mathcal{J}_{r}\).

For any \(x \in \mathcal{J}_{r}\), \(t \in \mathcal{S}\), using \((\mathbf{H_{1}}) \), we have

$$\begin{aligned} &\bigl\Vert g\bigl(t,x,\bar{x},x^{\prime}\bigr) \bigr\Vert \leq K_{g} \bigl( \bigl\Vert x(t) \bigr\Vert + \bigl\Vert \bar{x}(t) \bigr\Vert + \bigl\Vert x^{\prime}(t) \bigr\Vert \bigr) + M_{1},\\ &\bigl\Vert f(t,x) \bigr\Vert \leq K_{f} \bigl( \bigl\Vert x(t) \bigr\Vert \bigr) + M_{2}. \end{aligned}$$

Then, we obtain

$$\begin{aligned} &\bigl\Vert \mathcal{U}x(t) \bigr\Vert \\ &\quad\leq I^{\phi _{1}+\phi _{2};\psi}_{a^{+}} \bigl\Vert g\bigl(t,x(t),x( \lambda t),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x(\lambda t)\bigr) \bigr\Vert + I^{ \phi _{2};\psi}_{a^{+}} \bigl\Vert f\bigl(t,x(t)\bigr) \bigr\Vert \\ &\qquad{} + \frac{\Upsilon (t,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum_{i=1}^{m} \omega _{i} I^{\phi _{1}+\phi _{2}; \psi}_{a^{+}} \bigl\Vert g\bigl(\theta _{i},x(\theta _{i}),x(\lambda \theta _{i}),{^{H}}D^{ \alpha,\beta;\psi}_{a^{+}}x( \lambda \theta _{i})\bigr) \bigr\Vert \\ &\qquad{} + I^{\phi _{1}+\phi _{2};\psi}_{a^{+}} \bigl\Vert g\bigl(b,x(b),x(\lambda b),{^{H}}D^{ \alpha,\beta;\psi}_{a^{+}}x(\lambda b)\bigr) \bigr\Vert + \sum_{i=1}^{m} \omega _{i} I^{\phi _{2};\psi}_{a^{+}} \bigl\Vert f\bigl(\theta _{i},x( \theta _{i})\bigr) \bigr\Vert \\ &\qquad{} + I^{\phi _{2};\psi}_{a^{+}} \bigl\Vert f\bigl(b,x(b)\bigr) \bigr\Vert \Biggr] \\ &\quad\leq \Biggl\{ 2K_{g} \Biggl( \Upsilon (b,\phi _{1}+\phi _{2}) + \frac{\Upsilon (b,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{1}+ \phi _{2}) + \Upsilon (b,\phi _{1}+\phi _{2}) \Biggr] \Biggr) \\ &\qquad{} + K_{f} \Biggl( \Upsilon (b,\phi _{2}) + \frac{\Upsilon (b,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{2}) + \Upsilon (b,\phi _{2}) \Biggr] \Biggr) \Biggr\} \Vert x \Vert _{\mathcal{J}} \\ & \qquad{}+ \Biggl( \Upsilon (b,\phi _{1}+\phi _{2}) + \frac{\Upsilon (b,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{1}+\phi _{2}) + \Upsilon (b,\phi _{1}+\phi _{2}) \Biggr] \Biggr) M_{1} \\ &\qquad{} + \Biggl( \Upsilon (b,\phi _{2}) + \frac{\Upsilon (b,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum _{i=1}^{m} \omega _{i} \Upsilon ( \theta _{i}, \phi _{2}) + \Upsilon (b,\phi _{2}) \Biggr] \Biggr) M_{2} \end{aligned}$$

and

$$\begin{aligned} &\bigl\Vert {^{H}}D^{\alpha,\beta;\psi}_{a^{+}} \mathcal{U}x(t) \bigr\Vert \\ &\quad\leq I^{\phi _{1}+\phi _{2} - \alpha;\psi}_{a^{+}} \bigl\Vert g\bigl(t,x(t),x( \lambda t),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x(\lambda t)\bigr) \bigr\Vert + I^{ \phi _{2} - \alpha;\psi}_{a^{+}} \bigl\Vert f\bigl(t,x(t)\bigr) \bigr\Vert \\ & \qquad{}+ \frac{\Upsilon (t,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum_{i=1}^{m} \omega _{i} I^{\phi _{1}+\phi _{2} - \alpha;\psi}_{a^{+}} \bigl\Vert g\bigl(\theta _{i},x(\theta _{i}),x(\lambda \theta _{i}),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x( \lambda \theta _{i})\bigr) \bigr\Vert \\ &\qquad{} + I^{\phi _{1}+\phi _{2} - \alpha;\psi}_{a^{+}} \bigl\Vert g\bigl(b,x(b),x( \lambda b),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x(\lambda b)\bigr) \bigr\Vert + \sum_{i=1}^{m} \omega _{i} I^{\phi _{2} - \alpha;\psi}_{a^{+}} \bigl\Vert f\bigl(\theta _{i},x( \theta _{i})\bigr) \bigr\Vert \\ &\qquad{} + I^{\phi _{2} - \alpha;\psi}_{a^{+}} \bigl\Vert f\bigl(b,x(b)\bigr) \bigr\Vert \Biggr] \\ &\quad\leq \Biggl\{ 2K_{g} \Biggl( \Upsilon (b,\phi _{1}+\phi _{2} - \alpha ) + \frac{\Upsilon (b,\gamma _{1}+\phi _{2} -1)}{ \vert \curlywedge \vert } \Biggl[ \sum _{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{1}+\phi _{2} - \alpha ) \\ & \qquad{}+ \Upsilon (b,\phi _{1}+\phi _{2} - \alpha ) \Biggr] \Biggr) + K_{f} \Biggl( \Upsilon (b,\phi _{2} - \alpha ) + \frac{\Upsilon (b,\gamma _{1}+\phi _{2} -1)}{ \vert \curlywedge \vert } \\ & \qquad{}\times \Biggl[ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{2} - \alpha ) + \Upsilon (b,\phi _{2} - \alpha ) \Biggr] \Biggr) \Biggr\} \Vert x \Vert _{\mathcal{J}} + \Biggl( \Upsilon (b,\phi _{1}+ \phi _{2} - \alpha ) \\ & \qquad{}+ \frac{\Upsilon (b,\gamma _{1}+\phi _{2} -1)}{ \vert \curlywedge \vert } \Biggl[ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{1}+ \phi _{2} - \alpha )+ \Upsilon (b,\phi _{1}+\phi _{2} - \alpha ) \Biggr] \Biggr) M_{1} \\ &\qquad{} + \Biggl( \Upsilon (b,\phi _{2} - \alpha ) + \frac{\Upsilon (b,\gamma _{1}+\phi _{2} -1)}{ \vert \curlywedge \vert } \Biggl[ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{2} - \alpha ) + \Upsilon (b, \phi _{2} - \alpha ) \Biggr] \Biggr) M_{2}. \end{aligned}$$

Thus, \(\Vert \mathcal{U}x \Vert _{\mathcal{J}} \leq \mathcal{N} \Vert x \Vert _{\mathcal{J}} + \mathcal{N}_{1} M_{1} + \mathcal{N}_{2} M_{2} \leq r \).

This implies \(\mathcal{U}\mathcal{J}_{r} \subset \mathcal{J}_{r}\).

Step 2: \(\mathcal{U}\) is a contraction.

For any \(x, y \in \mathcal{J}_{r} \) and for each \(t \in \mathcal{S}\), using \((\mathbf{H_{1}})\), we have

$$\begin{aligned} & \bigl\Vert \mathcal{U}x(t)-\mathcal{U}y(t) \bigr\Vert \\ &\quad\leq I^{\phi _{1}+\phi _{2};\psi}_{a^{+}} \bigl\Vert g\bigl(t,x(t),x( \lambda t),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x(\lambda t)\bigr) - g \bigl(t,y(t),y( \lambda t),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}y(\lambda t)\bigr) \bigr\Vert \\ &\qquad{}+ I^{\phi _{2};\psi}_{a^{+}} \bigl\Vert f\bigl(t,x(t)\bigr) - f \bigl(t,y(t)\bigr) \bigr\Vert + \frac{\Upsilon (t,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum _{i=1}^{m} \omega _{i} I^{\phi _{1}+\phi _{2}; \psi}_{a^{+}} \\ &\qquad{}\times\bigl\Vert g\bigl(\theta _{i},x(\theta _{i}),x(\lambda \theta _{i}),{^{H}}D^{ \alpha,\beta;\psi}_{a^{+}}x(\lambda \theta _{i})\bigr) - g\bigl(\theta _{i},y( \theta _{i}),y(\lambda \theta _{i}),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}y( \lambda \theta _{i})\bigr) \bigr\Vert \\ &\qquad{} + I^{\phi _{1}+\phi _{2};\psi}_{a^{+}} \bigl\Vert g \bigl(b,x(b),x( \lambda b),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x(\lambda b)\bigr) - g\bigl(b,y(b),y( \lambda b),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}y( \lambda b)\bigr) \bigr\Vert \\ &\qquad{}+ \sum_{i=1}^{m} \omega _{i} I^{\phi _{2};\psi}_{a^{+}} \bigl\Vert f\bigl(\theta _{i},x( \theta _{i})\bigr) - f\bigl(\theta _{i},y(\theta _{i})\bigr) \bigr\Vert + I^{\phi _{2};\psi}_{a^{+}} \bigl\Vert f\bigl(b,x(b)\bigr) - f\bigl(b,y(b)\bigr) \bigr\Vert \Biggr] \\ &\quad\leq \Upsilon (b,\phi _{1}+\phi _{2}) 2 K_{g} \Vert x -y \Vert _{ \mathcal{J}} + \Upsilon (b,\phi _{2}) K_{f} \Vert x-y \Vert _{ \mathcal{J}} + \frac{\Upsilon (b,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \\ &\qquad{}\times \Biggl[ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{1}+\phi _{2})2 K_{g} \Vert x -y \Vert _{\mathcal{J}} + \Upsilon (b,\phi _{1}+\phi _{2}) 2 K_{g} \Vert x-y \Vert _{ \mathcal{J}} \\ &\qquad{}+ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i},\phi _{2})K_{f} \Vert x-y \Vert _{\mathcal{J}} + \Upsilon (b,\phi _{2}) K_{f} \Vert x-y \Vert _{\mathcal{J}} \Biggr] \\ &\quad\leq \Biggl\{ 2K_{g} \Biggl( \Upsilon (b,\phi _{1}+\phi _{2}) + \frac{\Upsilon (b,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{1}+ \phi _{2}) + \Upsilon (b,\phi _{1}+\phi _{2}) \Biggr] \Biggr) \\ &\qquad{}+ K_{f} \Biggl( \Upsilon (b,\phi _{2}) + \frac{\Upsilon (b,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{2}) + \Upsilon (b,\phi _{2}) \Biggr] \Biggr) \Biggr\} \Vert x-y \Vert _{\mathcal{J}} \end{aligned}$$

and

$$\begin{aligned} & \bigl\Vert {^{H}}D^{\alpha,\beta;\psi}_{a^{+}} \mathcal{U}x(t) - {^{H}}D^{\alpha,\beta;\psi}_{a^{+}} \mathcal{U}y(t) \bigr\Vert \\ &\quad\leq \Biggl\{ 2K_{g} \Biggl( \Upsilon (b,\phi _{1}+\phi _{2}- \alpha ) + \frac{\Upsilon (b,\gamma _{1}+\phi _{2} -1)}{ \vert \curlywedge \vert } \Biggl[ \sum _{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{1}+\phi _{2}-\alpha ) \\ &\qquad{}+ \Upsilon (b,\phi _{1}+\phi _{2}-\alpha ) \Biggr] \Biggr) + K_{f} \Biggl( \Upsilon (b,\phi _{2}-\alpha ) + \frac{\Upsilon (b,\gamma _{1}+\phi _{2} -1)}{ \vert \curlywedge \vert } \\ &\qquad{}\times \Biggl[ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{2}-\alpha ) + \Upsilon (b,\phi _{2}-\alpha ) \Biggr] \Biggr) \Biggr\} \Vert x-y \Vert _{\mathcal{J}}. \end{aligned}$$

Thus, \(\Vert \mathcal{U}x-\mathcal{U}y\Vert _{\mathcal{J}} \leq (2K_{g} \mathcal{N}_{1} + K_{f} \mathcal{N}_{2}) \Vert x-y \Vert _{ \mathcal{J}} \).

Since \(2K_{g} \mathcal{N}_{1} + K_{f} \mathcal{N}_{2} < 1\), the operator \(\mathcal{U}\) is a contraction.

Therefore, by Lemma 5, we conclude that \(\mathcal{U}\) has a unique fixed point, which is the unique solution of (1) on \(\mathcal{S}\). □

Existence of solution.

Theorem 9

Assume that \((\mathbf{H_{1}})\), \((\mathbf{H_{2}})\) and \((\mathbf{H_{3}})\) are satisfied. Suppose that \([2K_{g} (\mathcal{N}_{1}-\Upsilon (b,l)) + K_{f} (\mathcal{N}_{2}- \Upsilon (b,\bar{l})) ] < 1\), where \(l =\phi _{1}+\phi _{2}\) or \(\phi _{1}+\phi _{2}-\alpha \), \(\bar{l}=\phi _{2}\) or \(\phi _{2}-\alpha \), \(K_{f}\) and \(K_{g}\) are constants, \(\mathcal{N}_{1}\) and \(\mathcal{N}_{2}\) are given by (8) and (9) respectively. Then system (1) has at least one solution on \(\mathcal{S}\).

Proof

Let \(\sup_{t \in \mathcal{J}} \vert \sigma (t) \vert = \Vert \sigma \Vert, \sup_{t \in \mathcal{J}} \vert \nu (t) \vert = \Vert \nu \Vert \).

Also define a bounded subset \(\mathcal{J}_{\rho}\) of \(\mathcal{J} \), where \(\mathcal{J}_{\rho}= \{x \in \mathcal{J}: \Vert x \Vert \leq \rho \}\) with

$$\begin{aligned} \rho \geq \mathcal{N}_{1} \Vert \sigma \Vert + \mathcal{N}_{2} \Vert \nu \Vert . \end{aligned}$$

Let us define the operators \(\mathcal{U}_{1}\) and \(\mathcal{U}_{2} \) on \(\mathcal{J}_{\rho}\) for \(t \in \mathcal{S} \) as \(\mathcal{U} =\mathcal{U}_{1} + \mathcal{U}_{2} \), where

$$\begin{aligned} & \mathcal{U}_{1} x(t) = I^{\phi _{1}+\phi _{2};\psi}_{a^{+}} g\bigl(t,x(t),x(\lambda t),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x( \lambda t)\bigr)- I^{\phi _{2};\psi}_{a^{+}} f\bigl(t,x(t)\bigr), \\ &\mathcal{U}_{2} x(t) = \frac{\Upsilon (t,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum _{i=1}^{m} \omega _{i} I^{\phi _{1}+\phi _{2}; \psi}_{a^{+}} g\bigl(\theta _{i},x(\theta _{i}),x(\lambda \theta _{i}),{^{H}}D^{ \alpha,\beta;\psi}_{a^{+}}x(\lambda \theta _{i})\bigr) \\ & \phantom{\mathcal{U}_{2} x(t) =}{}- I^{\phi _{1}+\phi _{2};\psi}_{a^{+}} g\bigl(b,x(b),x(\lambda b),{^{H}}D^{ \alpha,\beta;\psi}_{a^{+}}x( \lambda b)\bigr) - \sum_{i=1}^{m} \omega _{i} I^{\phi _{2};\psi}_{a^{+}} f\bigl(\theta _{i},x( \theta _{i})\bigr) \\ &\phantom{\mathcal{U}_{2} x(t) =}{} + I^{\phi _{2};\psi}_{a^{+}} f\bigl(b,x(b)\bigr) \Biggr]. \end{aligned}$$

Step 1: \(\mathcal{U}_{1} x + \mathcal{U}_{2} y \in \mathcal{J}_{\rho} \).

For any \(x \in \mathcal{J}_{\rho}\), \(t \in \mathcal{S}\), we obtain

$$\begin{aligned} & \bigl\Vert \mathcal{U}_{1}x(t)+ \mathcal{U}_{2} y(t) \bigr\Vert \\ &\quad\leq \Upsilon (b,\phi _{1}+\phi _{2}) \Vert \sigma \Vert + \Upsilon (b,\phi _{2}) \Vert \nu \Vert + \frac{\Upsilon (b,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{1}+\phi _{2}) \Vert \sigma \Vert \\ &\qquad{}+ \Upsilon (b,\phi _{1}+\phi _{2}) \Vert \sigma \Vert + \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i},\phi _{2}) \Vert \nu \Vert + \Upsilon (b,\phi _{2}) \Vert \nu \Vert \Biggr] \\ &\quad\leq \Biggl\{ \Vert \sigma \Vert \Biggl( \Upsilon (b,\phi _{1}+ \phi _{2}) + \frac{\Upsilon (b,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum _{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{1}+\phi _{2}) + \Upsilon (b,\phi _{1}+\phi _{2}) \Biggr] \Biggr) \\ &\qquad{}+ \Vert \nu \Vert \Biggl( \Upsilon (b,\phi _{2}) + \frac{\Upsilon (b,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{2}) + \Upsilon (b,\phi _{2}) \Biggr] \Biggr) \Biggr\} \end{aligned}$$

and

$$\begin{aligned} & \bigl\Vert {^{H}}D^{\alpha,\beta;\psi}_{a^{+}} \mathcal{U}_{1}x(t) + {^{H}}D^{\alpha,\beta;\psi}_{a^{+}} \mathcal{U}_{2}y(t) \bigr\Vert \\ &\quad\leq \Upsilon (b,\phi _{1}+\phi _{2} - \alpha ) \Vert \sigma \Vert + \Upsilon (b,\phi _{2} - \alpha ) \Vert \nu \Vert + \frac{\Upsilon (b,\gamma _{1}+\phi _{2} -1)}{ \vert \curlywedge \vert } \\ &\qquad{}\times \Biggl[ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{1}+\phi _{2} - \alpha ) \Vert \sigma \Vert + \Upsilon (b,\phi _{1}+ \phi _{2} - \alpha ) \Vert \sigma \Vert + \sum _{i=1}^{m} \omega _{i} \Upsilon ( \theta _{i},\phi _{2} - \alpha ) \Vert \nu \Vert \\ &\qquad{}+ \Upsilon (b,\phi _{2} - \alpha ) \Vert \nu \Vert \Biggr] \\ &\quad\leq \Vert \sigma \Vert \Biggl( \Upsilon (b,\phi _{1}+\phi _{2} - \alpha ) + \frac{\Upsilon (b,\gamma _{1}+\phi _{2} -1)}{ \vert \curlywedge \vert } \Biggl[ \sum _{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{1}+\phi _{2} - \alpha ) \\ &\qquad{}+ \Upsilon (b,\phi _{1}+\phi _{2} - \alpha ) \Biggr] \Biggr)+ \Vert \nu \Vert \Biggl( \Upsilon (b,\phi _{2} - \alpha ) + \frac{\Upsilon (b,\gamma _{1}+\phi _{2} -1)}{ \vert \curlywedge \vert } \\ &\qquad{}\times \Biggl[ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{2} - \alpha ) + \Upsilon (b,\phi _{2} - \alpha ) \Biggr] \Biggr). \end{aligned}$$

Thus, \(\Vert \mathcal{U}_{1} x + \mathcal{U}_{2} y \Vert _{\mathcal{J}} \leq \mathcal{N}_{1} \Vert \sigma \Vert + \mathcal{N}_{2} \Vert \nu \Vert \leq \rho \).

Step 2: \(\mathcal{U}_{1}\) is completely continuous.

To prove \(\mathcal{U}_{1} \) is continuous and compact on \(\mathcal{J_{\rho}}\),

let \({x_{n}} \) be a sequence and \(x_{n} \longrightarrow x \) as \(n\longrightarrow \infty \) in \(\mathcal{J}_{\rho}\). Then, for \(t \in \mathcal{S}\), we have

$$\begin{aligned} & \bigl\Vert \mathcal{U}_{1} x_{n}(t) - \mathcal{U}_{1} x(t) \bigr\Vert \\ &\quad\leq I^{\phi _{1}+\phi _{2};\psi}_{a^{+}} \bigl\Vert g\bigl(t,x_{n}(t),x_{n}( \lambda t),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x_{n}(\lambda t)\bigr) - g\bigl(t,x(t),x( \lambda t),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x( \lambda t)\bigr) \bigr\Vert \\ &\qquad{}+ I^{\phi _{2};\psi}_{a^{+}} \bigl\Vert f\bigl(t,x_{n}(t) \bigr) - f\bigl(t,x(t)\bigr) \bigr\Vert \\ &\quad\leq \Upsilon (b,\phi _{1}+\phi _{2}) 2 K_{g} \Vert x_{n} - x \Vert _{\mathcal{J}} + \Upsilon (b,\phi _{2}) K_{f} \Vert x_{n}-x \Vert _{\mathcal{J}} \\ &\quad\longrightarrow 0\quad \text{as } n \longrightarrow \infty \end{aligned}$$

and

$$\begin{aligned} & \bigl\Vert {^{H}}D^{\alpha,\beta;\psi}_{a^{+}} \mathcal{U}_{1} x_{n}(t) - {^{H}}D^{\alpha,\beta;\psi}_{a^{+}} \mathcal{U}_{1} x(t) \bigr\Vert \\ &\quad\leq I^{\phi _{1}+\phi _{2}-\alpha;\psi}_{a^{+}} \bigl\Vert g\bigl(t,x_{n}(t),x_{n}(t \lambda ),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x_{n}(\lambda t)\bigr) - g\bigl(t,x(t),x( \lambda t),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x( \lambda t)\bigr) \bigr\Vert \\ &\qquad{}+ I^{\phi _{2}-\alpha;\psi}_{a^{+}} \bigl\Vert f\bigl(t,x_{n}(t) \bigr) - f\bigl(t,x(t)\bigr) \bigr\Vert \\ &\quad\leq \Upsilon (b,\phi _{1}+\phi _{2}-\alpha ) 2 K_{g} \Vert x_{n} - x \Vert _{\mathcal{J}} + \Upsilon (b,\phi _{2}-\alpha ) K_{f} \Vert x_{n}-x \Vert _{\mathcal{J}} \\ &\quad\longrightarrow 0\quad \text{as } n \longrightarrow \infty. \end{aligned}$$

Now, consider

$$\begin{aligned} & \bigl\Vert \mathcal{U}_{1}x(t_{2})- \mathcal{U}_{1}x(t_{1}) \bigr\Vert \\ &\quad= \Vert \int _{t_{1}}^{t_{2}} \biggl( \frac{1}{\Gamma (\phi _{1}+\phi _{2})} \psi ^{\prime}(s) \bigl(\psi (t_{2})- \psi (s)\bigr)^{\phi _{1}+\phi _{2}-1} g \bigl(s,x(s),{^{H}}D^{\alpha,\beta; \psi}_{a^{+}}x(s)\bigr) \\ &\qquad{}- \frac{1}{\Gamma (\phi _{2})} \psi ^{\prime}(s) \bigl(\psi (t_{2})- \psi (s)\bigr)^{\phi _{2}-1} f\bigl(s,x(s)\bigr) \biggr) \,ds + \int _{c}^{t_{2}} \biggl( \frac{1}{\Gamma (\phi _{1}+\phi _{2})} \psi ^{\prime}(s) \\ &\qquad{}\times \bigl[\bigl(\psi (t_{2})-\psi (s)\bigr)^{\phi _{1}+\phi _{2}-1} - \bigl(\psi (t_{1})- \psi (s)\bigr)^{\phi _{1}+\phi _{2}-1} \bigr] g\bigl(s,x(s),{^{H}}D^{\alpha, \beta;\psi}_{a^{+}}x(s) \bigr) \\ &\qquad{}- \frac{1}{\Gamma (\phi _{2})} \psi ^{\prime}(s) \bigl[\bigl(\psi (t_{2})- \psi (s)\bigr)^{\phi _{2}-1} - \bigl(\psi (t_{1})-\psi (s)\bigr)^{\phi _{2}-1} \bigr] f\bigl(s,x(s)\bigr) \biggr) \,ds \\ &\quad\leq \frac{1}{\Gamma (\phi _{1}+\phi _{2}+1)} \bigl[ 2\bigl(\psi (t_{2})- \psi (t_{1})\bigr)^{\phi _{1}+\phi _{2}}+\bigl(\psi (t_{2})-\psi (a) \bigr)^{\phi _{1}+ \phi _{2}} \\ &\qquad{}-\bigl(\psi (t_{1})-\psi (a)\bigr)^{\phi _{1}+\phi _{2}} \bigr] \bigl\Vert g\bigl(t,x(t),x( \lambda t),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x( \lambda t)\bigr) \bigr\Vert - \frac{1}{\Gamma (\phi _{2}+1)} \\ &\qquad{}\times \bigl[ 2\bigl(\psi (t_{2})-\psi (t_{1}) \bigr)^{\phi _{2}} +\bigl(\psi (t_{2})- \psi (a) \bigr)^{\phi _{2}} -\bigl(\psi (t_{1})-\psi (a)\bigr)^{\phi _{2}} \bigr] \bigl\Vert f\bigl(t,x(t)\bigr) \bigr\Vert \\ &\quad\longrightarrow 0 \quad\text{as } t_{2} \longrightarrow t_{1} \end{aligned}$$

and

$$\begin{aligned} & \bigl\Vert {^{H}}D^{\alpha,\beta;\psi}_{a^{+}} \mathcal{U}_{1}x(t_{2})-{^{H}}D^{ \alpha,\beta;\psi}_{a^{+}} \mathcal{U}_{1}x(t_{1}) \bigr\Vert \\ &\quad\leq \frac{1}{\Gamma (\phi _{1}+\phi _{2}-\alpha +1)} \bigl[ 2\bigl(\psi (t_{2})- \psi (t_{1})\bigr)^{\phi _{1}+\phi _{2}-\alpha}+\bigl(\psi (t_{2})-\psi (a) \bigr)^{ \phi _{1}+\phi _{2}-\alpha} \\ &\qquad{}-\bigl(\psi (t_{1})-\psi (a)\bigr)^{\phi _{1}+\phi _{2}-\alpha} \bigr] \bigl\Vert g\bigl(t,x(t),x(\lambda t),{^{H}}D^{\alpha,\beta;\psi}_{a^{+}}x( \lambda t)\bigr) \bigr\Vert \\ &\qquad{}- \frac{1}{\Gamma (\phi _{2}-\alpha +1)} \bigl[ 2\bigl(\psi (t_{2})- \psi (t_{1})\bigr)^{\phi _{2}}+\bigl(\psi (t_{2})-\psi (a) \bigr)^{\phi _{2}-\alpha} \\ &\qquad{}-\bigl(\psi (t_{1})-\psi (a)\bigr)^{\phi _{2}-\alpha} \bigr] \bigl\Vert f\bigl(t,x(t)\bigr) \bigr\Vert \\ &\quad\longrightarrow 0 \quad\text{as } t_{2} \longrightarrow t_{1}. \end{aligned}$$

Thus, \(\Vert \mathcal{U}_{1}x(t_{2})-\mathcal{U}_{1}x(t_{1}) \Vert _{ \mathcal{J}} \longrightarrow 0 \text{ as } t_{2} \longrightarrow t_{1} \), i.e. \(\mathcal{U}_{1}\mathcal{J}_{\rho}\) is equicontinuous.

Hence, \(\mathcal{U}_{1}\) is completely continuous on \(\mathcal{J}_{\rho}\) by the Arzela–Ascoli theorem [34].

Step 3: \(\mathcal{U}_{2}\) is a contraction.

For any \(x, y \in \mathcal{J}_{\rho }\) and for each \(t \in \mathcal{S}\), using \((\mathbf{H_{1}})\), we have

$$\begin{aligned} & \bigl\Vert \mathcal{U}_{2}x(t)- \mathcal{U}_{2}y(t) \bigr\Vert \\ &\quad\leq \frac{\Upsilon (b,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum_{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{1}+ \phi _{2})2 K_{g} \Vert x -y \Vert _{\mathcal{J}} + \Upsilon (b,\phi _{1}+\phi _{2}) \\ &\qquad{}\times 2 K_{g} \Vert x-y \Vert _{\mathcal{J}} + \sum _{i=1}^{m} \omega _{i} \Upsilon (\theta _{i},\phi _{2})K_{f} \Vert x-y \Vert _{ \mathcal{J}} + \Upsilon (b,\phi _{2}) K_{f} \Vert x-y \Vert _{ \mathcal{J}} \Biggr] \\ &\quad\leq \Biggl\{ 2K_{g} \frac{\Upsilon (b,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum _{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{1}+\phi _{2}) + \Upsilon (b,\phi _{1}+\phi _{2}) \Biggr] \\ &\qquad{}+ K_{f} \frac{\Upsilon (b,\gamma _{1}+\phi _{2}-1)}{ \vert \curlywedge \vert } \Biggl[ \sum _{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{2}) + \Upsilon (b,\phi _{2}) \Biggr] \Biggr\} \Vert x-y \Vert _{ \mathcal{J}} \end{aligned}$$

and

$$\begin{aligned} & \bigl\Vert {^{H}}D^{\alpha,\beta;\psi}_{a^{+}} \mathcal{U}_{2}x(t) - {^{H}}D^{\alpha,\beta;\psi}_{a^{+}} \mathcal{U}_{2}y(t) \bigr\Vert \\ &\quad\leq \Biggl\{ 2K_{g} \frac{\Upsilon (b,\gamma _{1}+\phi _{2} - 1)}{ \vert \curlywedge \vert } \Biggl[ \sum _{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{1}+\phi _{2} - \alpha ) + \Upsilon (b,\phi _{1}+\phi _{2} - \alpha ) \Biggr] \\ &\qquad{}+ K_{f} \frac{\Upsilon (b,\gamma _{1}+\phi _{2} -1)}{ \vert \curlywedge \vert } \Biggl[ \sum _{i=1}^{m} \omega _{i} \Upsilon (\theta _{i}, \phi _{2} - \alpha ) + \Upsilon (b,\phi _{2} - \alpha ) \Biggr] \Biggr\} \Vert x-y \Vert _{\mathcal{J}}. \end{aligned}$$

Thus, \(\Vert \mathcal{U}_{2}x-\mathcal{U}_{2}y\Vert _{\mathcal{J}} \leq [2K_{g} (\mathcal{N}_{1}-\Upsilon (b,l)) + K_{f} (\mathcal{N}_{2}- \Upsilon (b,\bar{l})) ] \Vert x-y \Vert _{\mathcal{J}} \).

Since \([2K_{g} (\mathcal{N}_{1}-\Upsilon (b,l)) + K_{f} (\mathcal{N}_{2}- \Upsilon (b,\bar{l})) ] < 1\), the operator \(\mathcal{U}_{2}\) is a contraction.

Therefore, by Theorem 6, we conclude that BVP (1) has at least one solution on \(\mathcal{S}\). □

5 Application

This section contains an example to demonstrate our results. Equation (1) can be found in various fields, including biology, physics and engineering, to model systems with memory effects and non-local dependencies; for instance, in describing the viscoelastic behaviour of the material that captures both internal dissipation and external influences. The linear viscoelastic Kelvin–Voigt model that describes the behaviour of materials exhibiting both elastic and viscous properties could be expressed using a sequential pantograph fractional differential equation.

Example 1

Consider the ψ-Hilfer sequential type pantograph fractional BVP

$$\begin{aligned} \textstyle\begin{cases} {^{H}}D^{\frac{1}{2},\frac{1}{10}:\sin t}_{0^{+}} ( {^{H}}D^{ \frac{7}{10},\frac{2}{5}:\sin t}_{0^{+}} x(t) + f(t,x(t)) )= g(t,x(t),x( \lambda t),{^{H}}D^{\frac{1}{5},\frac{1}{3};\sin t}_{0^{+}}x(\lambda t)) , \\ x(0)= 0, \qquad x(1) = \sum_{i=1}^{3} (\frac{-i}{i+3} )^{i+1} x(\frac{i}{5}),\quad t \in [0,1], \end{cases}\displaystyle \end{aligned}$$
(10)

where g and f are given by

$$\begin{aligned} &g\bigl(t,x(t),x(\lambda t),{^{H}}D^{\frac{1}{5},\frac{1}{3}; \sin t}_{0^{+}}x( \lambda t)\bigr) \\ &\quad= \frac{t^{2}}{5-\sin^{3} \pi t} \frac{ \vert x(t) \vert }{8 + \vert x(t) \vert } + \frac{t}{2(t+10)} \biggl\vert x \biggl(\frac{1}{4}t \biggr) \biggr\vert + \frac{ 2e^{-t} \vert {^{H}}D_{0^{+}}^{\frac{5}{4},\frac{1}{6};\sin t} x(\frac{1}{4}t) \vert }{ \vert {^{H}}D^{\frac{5}{4},\frac{1}{6};\sin t} x(\frac{1}{4}t) \vert + 24} , \\ & f\bigl(t,x(t)\bigr)= \frac{1}{(t+2)^{2}+9} \frac{ \vert x(t) \vert }{1 + \vert x(t) \vert }. \end{aligned}$$

Here \(\phi _{1}=\frac{1}{2}\), \(\phi _{2}=\frac{7}{10}\), \(\eta _{1}=\frac{1}{10}\), \(\eta _{2}=\frac{2}{5}\), \(\alpha =\frac{1}{5}\), \(\beta =\frac{1}{3}\), \(a=0\), \(b=1\), \(m=3\), \(\omega _{i}= (\frac{-i}{i+3} )^{i+1} \), \(\theta _{i}=\frac{i}{5}\), \(\psi (t)=\sin t\), \(\psi ^{\prime}(t)=\cos t\). Using the data, we evaluate \(\gamma _{1}=0.5500\), \(\gamma _{2}=0.8200\), \(\curlywedge \approx 1.0066\), \(\mathcal{N}_{1} \approx 3.5153 \) and \(\mathcal{N}_{2} \approx 4.3360\).

(i) Uniqueness of solution

For \(x_{1},\bar{x_{1}},x_{1}^{\prime},x_{2},\bar{x_{2}},x_{2}^{\prime}, \in \mathcal{J}\) and \(t \in [0,1]\), we have

$$\begin{aligned} &\bigl\Vert g\bigl(t,x_{1}, \bar{x_{1}},{x_{1}}^{\prime}\bigr)- g \bigl(t,x_{2}, \bar{x_{2}},{x_{2}}^{\prime} \bigr) \bigr\Vert \\ &\quad \leq \frac{1}{12} \bigl( \bigl\Vert x_{1}(t) - x_{2}(t) \bigr\Vert + \bigl\Vert \bar{x_{1}}(t)-\bar{x_{2}}(t) \bigr\Vert + \bigl\Vert {x_{1}}^{\prime}(t) - {x_{2}}^{\prime}(t) \bigr\Vert \bigr), \\ &\bigl\Vert f(t,x_{1})-f(t,x_{2}) \bigr\Vert \leq \frac{1}{13} \bigl( \bigl\Vert x_{1}(t) - x_{2}(t) \bigr\Vert \bigr). \end{aligned}$$

Comparing with \(\mathbf{(H_{1})}\) and \((\mathbf{H_{2}})\), we observe that \(K_{g}=\frac{1}{12}\) and \(K_{f}=\frac{1}{13} \).

We find that \(\Omega = 2K_{g} \mathcal{N}_{1} + K_{f} \mathcal{N}_{2} \approx 0.9194 < 1\).

Thus, the hypothesis of Theorem 8 is satisfied, and system (10) has a unique solution on \(\mathcal{S}\).

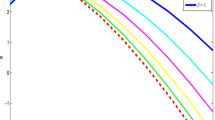
The numerical results of Ω for various values of \(t \in [0,1]\) and \(\phi _{1}\), \(\phi _{2} \in (0,1)\) are shown in Table 1.

Table 1 Ω for different values of \(\phi _{1}\) and \(\phi _{2}\)
Full size table

We observe that for an increase in time, Ω increases, and for an increase in order, Ω decreases. Clearly, Ω is less than 1. The results are graphically presented in Fig. 1.

Figure 1
figure 1

Representation of the impact of fractional order \(\phi _{1},\phi _{2}\) on Ω

Full size image

(ii) Existence of solution

For \(x,\bar{x},x^{\prime }\in \mathcal{J}\) and \(t \in [0,1]\), we have

$$\begin{aligned} &\bigl\Vert g\bigl(t,x,\bar{x},x^{\prime}\bigr) \bigr\Vert \leq \frac{t^{2}}{40} + \frac{t}{2(t+10)} + \frac{ e^{-t} }{12},\\ &\bigl\Vert f(t,x) \bigr\Vert \leq \frac{1}{(t+2)^{2}+9}. \end{aligned}$$

Hypothesis (\(\mathbf{H_{3}}\)) is satisfied.

We find that \(\Delta =\Omega -[2K_{g} \Upsilon (b,\phi _{1}+\phi _{2}-\alpha )+ K_{f} \Upsilon (b,\phi _{2}-\alpha )] \approx 0.6995 < 1\).

Thus, the hypothesis of Theorem 9 is satisfied, and system (10) has at least one solution on \(\mathcal{S}\).

The numerical results of Δ for various values of \(t \in [0,1]\) and \(\phi _{1}\), \(\phi _{2} \in (0,1)\) are shown in Table 2.

Table 2 Ω for different values of \(\phi _{1}\) and \(\phi _{2}\)
Full size table

We observe that for an increase in time, Δ increases, and for an increase in order, Δ decreases. Clearly, Δ is less than 1. The results are graphically presented in Fig. 2.

Figure 2
figure 2

Representation of the impact of fractional order \(\phi _{1},\phi _{2}\) on Δ

Full size image

6 Conclusion

In this research, the ψ-Hilfer sequential-type pantograph fractional BVP was identified. In a special working space, the existence and uniqueness of a solution to the BVP were investigated. The Krasnosel’skii’s fixed point theorem was used to analyse the existence result, and the Banach contraction principle was used to study the uniqueness result. We have developed an example to interpret our findings. To further illustrate, a graphical analysis was also performed. In the future, the study can be extended to investigate the coupled system of sequential FDEs, and the stability of the solution can be analysed.