1 Introduction

Classical unique continuation, which shows that the local information of the solution can uniquely determine the global information of the solution, is an important property of elliptic and parabolic equations. More specifically, the vanishment of the solution of the homogeneous problem in the open subset results in its vanishment in the entire domain, see Saut and Scheurer [1]. There are many important applications of the unique continuation properties. For the inverse source problem, we refer the readers to El Badia and Ha-Duong [2], Hu, Kian, and Zhao [3]. For approximate controllability, see Cannarsa, Tort, and Yamamoto [4], Dou and Lu [5].

Major advances have been made in fractional calculus in the last few decades. As a generalization of the classical diffusion equation, the fractional diffusion equation has become a research hotspot in mathematics. The extension of the unique continuation properties to fractional diffusion equations has attracted the attention of many researchers. Li and Yamamoto [6] investigated the lateral Cauchy problem for the one-dimensional time-fractional diffusion equation. As a direct conclusion of the uniqueness of the Cauchy problem, they proved that the classical unique continuation property is valid. Other researchers in recent years have investigated the unique continuation property for fractional differential equations via Carleman estimates, see Xu, Cheng, and Yamamoto [7], Cheng, Lin, and Nakamura [8]. Sakamoto and Yamamoto [9] indicated the weak unique continuation property of the time-fractional diffusion equations with the homogeneous Dirichlet boundary condition on the whole boundary. Jiang et al. [10] generalized the result in [9] to the multiterm case. The literature mentioned above focuses on the unique continuation properties in the inner open subset. However, as far as we know, there are few published results concerning the properties from sparse data. We wonder whether the global information of the solution can be determined from a small finite number N of measurement points. The primary goal of this paper is to investigate the unique continuation property of the following problem.

Let \(\Omega \subset \mathbb{R}^{2}\) be a unit disc and \(T>0\). Consider the following initial-boundary value problem of the time-fractional diffusion equation:

$$ \textstyle\begin{cases} ({}^{c}\partial _{t}^{\alpha}-\triangle ) u(x, t)=0, &\text{in } \Omega \times (0, T), \\ u(x, 0)=u_{0}, & \text{in } \Omega \times \{0\}, \\ u(x, t)=0, & \text{on } \partial \Omega \times (0, T). \end{cases} $$
(1)

\({}^{c} \partial _{t}^{\alpha} u\) denotes the Caputo derivative of u at time \(t>0\), which is defined by

$$ {}^{c} \partial _{t}^{\alpha} u(x,t)= \frac{1}{\Gamma (1-\alpha )} \int _{0}^{t}(t- \tau )^{-\alpha} u^{\prime}(x,\tau ) \,d\tau . $$
(2)

Here \(0<\alpha <1\). \(\Gamma (\cdot )\) denotes the gamma function. For the definition and properties of fractional derivatives, see Podlubny [11].

Problem 1.1

Let u be the solution of (1) and \(Z_{o b}= \{z_{1}, z_{2} \} \subset \partial \Omega \). Does \(\frac{\partial u}{\partial \nu}(z_{1},t)= \frac{\partial u}{\partial \nu}(z_{2},t)=0\) imply \(u \equiv 0\) in \(\Omega \times (0, T)\)? Here, the boundary flux data \(\frac{\partial u}{\partial \nu}\) are used, and ν is the unit outward normal vector of ∂Ω.

In practice, environmental authorities often need to determine the intensity and location of pollution sources based on monitoring data. The study of the inverse source problem has become popular due to the aforementioned issues. Anomalous transport poses significant challenges for accurate prediction and remediation of groundwater contamination. Fractional calculus has attracted more and more attention in anomalous diffusion due to its heritability and memorability. We refer the readers to Zhang, Meerschaert, and Baeumer [12], Sun et al. [13], and Yin et al. [14]. Furthermore, it is known that the fractional order is related to the inhomogeneity of the media, but it is not clear which physical law can relate the inhomogeneity to the fractional order. So we are also required to consider the inverse fractional order problem. There exists a large and rapidly growing number of publications related to the inverse problems in determining sources, fractional orders, and other unknown coefficients. For some early work on the determination of the source terms, we refer the readers to Zhang and Xu [15], Kirane and Malik [16], Chi, Li, and Jia [17], Liu, Rundell, and Yamamoto [18]; and for more recent works, we refer to Liu and Zhang [19], Rundell and Zhang [20], Li and Zhang [21], Phuong, Kumar, and Binh [22], Binh and Long [23], Phuong, Thi, and Luc [24] and the references therein. In particular, we mention the reference [10] by Jiang et al., where the uniqueness of an inverse problem in determining the spatial component in the source term by interior measurements utilizing the weak unique continuation property was proven. For the determination of the fractional orders and other unknown coefficients, refer to Cheng et al. [25], Li et al. [26], Li et al. [27], Kian et al. [28], Ozbilge and Demir [29], Jday and Mdimagh [30], Phuong et al. [31], Phuong et al. [32], Long and Saadati [33]. It is worth noting that some of the above inverse problems are studied in disc or rectangular domains mathematically. Inversion studies in these special domains have also received widespread attention in engineering defect identification (see [34–36] for instance). The study of inverse problems in these special regions can provide theoretical support for engineering numerical simulations.

This paper considers the inverse problem of simultaneously determining spatially dependent source terms and fractional orders from two point Neumann boundary data. More precisely, we consider an initial-boundary value problem:

$$ \textstyle\begin{cases} ({}^{c}\partial _{t}^{\alpha}-\triangle ) u(x, t)=g(t) f(x), &\text{in }\Omega \times (0, T), \\ u(x, 0)=0, & \text{in }\Omega \times \{0\}, \\ u(x, t)=0, &\text{on }\partial \Omega \times (0, T). \end{cases} $$
(3)

The above model explains the evolution of density \(u(x, t)\) at location x and time t of some substances, such as contaminants, where \(g(t) f(x)\) is a source term in Ω. The source term can often be assumed to be modeled in the form of the separation of variables. \(g(t)\) and \(f(x)\) describe the spatial distribution of the source and the time evolution pattern, respectively. We are dedicated to using sparse boundary data to simultaneously determine the spatially dependent source term \(f(x)\) and fractional order α.

A precise mathematical statement of this inverse problem is provided below.

Problem 1.2

Let Ω be the unit disc in \(\mathbb{R}^{2}\) and the fractional derivative be defined as above. Assume that the temporal component \(g(t)\) is known in equation (3). The boundary flux data are given at two points:

$$ \frac{\partial u}{\partial \nu}(z, t),\quad (z,t) \in Z_{\mathrm{ob}} \times (0, T). $$
(4)

Can we uniquely determine \(f(x)\) and α simultaneously? Here, \(Z_{\mathrm{ob}}\) is defined as in Problem 1.1.

It is worth noting that the observations required in this work are only for a limited period (i.e., \(t \in (0, T)\)), which is in contrast to Li and Zhang [21, Theorem 1.1]. Our aim is to find the connection between the above inverse problem and Problem 1.1, and to apply the conclusion of Problem 1.1 to prove the uniqueness of this inverse problem.

In the rest of this section, we first endeavor to answer the Problem 1.1. For this, we propose the following theorem.

Theorem 1.1

Let \(u_{0} \in L^{2}(\Omega )\) and \(u \in L^{2}(0,T; H_{0}^{1}(\Omega ))\) be the solution to (1). Set \(z_{\ell}= (\cos \theta _{\ell}, \sin \theta _{\ell} ) \in \partial \Omega \), \(\ell =1,2\) as the boundary points, and \(\theta _{\ell}\) satisfies \(\theta _{1}-\theta _{2} \notin \pi \mathbb{Q}, \mathbb{Q}\) as the set of rational numbers. Let \(\frac{\partial u}{\partial \nu}(z_{1},t)= \frac{\partial u}{\partial \nu}(z_{2},t)=0\). Then the following holds:

$$ u \equiv 0, \quad \textit{in } \Omega . $$

We give the following uniqueness theorem to answer Problem 1.2.

Theorem 1.2

Let \(u(x,t)\) satisfy (3). Suppose that the spatial component \(f\in L^{2}(\Omega )\neq 0\) in the source term is unknown and \(g\in C^{1}[0, T]\) with \(g(0) \neq 0\). Assume that \(1/2<\alpha _{1}, \alpha _{2}<1\). Then \(z_{\ell}= (\cos \theta _{\ell}, \sin \theta _{\ell} ) \in \partial \Omega \), \(\ell =1,2\), is set as the boundary observation points, and \(\theta _{\ell}\) satisfies \(\theta _{1}-\theta _{2} \notin \pi \mathbb{Q}, \mathbb{Q}\) as the set of rational numbers.

Denote the two sets of unknown solutions to equation (3) as \(u_{1}\) and \(u_{2}\). If

$$ \frac{\partial u_{1}}{\partial \nu} (z_{\ell}, t )= \frac{\partial u_{2}}{\partial \nu} (z_{\ell}, t ),\quad \ell =1,2, $$

then

$$ \alpha _{1}=\alpha _{2},\qquad f_{1}(x)=f_{2}(x), \quad x \in \Omega . $$

The rest of this paper is organized as follows. In Sect. 2, some prior knowledge is listed, such as the eigensystem of the Laplacian operator, the properties of Bessel functions, and the Mittag-Leffler function. In Sect. 3, we give the proof of Theorem 1.1. In Sect. 4, we present the proof of Theorem 1.2 as an application of Theorem 1.1. Finally, concluding remarks are provided in Sect. 5.

2 Preliminary information

In this section, we first set up notations and introduce the Dirichlet eigensystem of the Laplacian operator. Let \(L^{2}(\Omega )\) be a usual \(L^{2}\)-space with the inner product \(\langle \cdot , \cdot \rangle \), and let \(H_{0}^{1}(\Omega )\) denote the usual Sobolev spaces. We introduce the eigensystem \(\{ (\lambda _{n}, \varphi _{n} ) \}_{n=- \infty}^{\infty}\) of the Laplacian operator −Δ on Ω with the Dirichlet boundary condition, i.e.,

$$ \textstyle\begin{cases} -\Delta \varphi _{n}=\lambda _{n} \varphi _{n}, & \text{in } \Omega , \\ \varphi _{n}=0, & \text{on } \partial \Omega . \end{cases} $$
(5)

Since Ω is the unit disc in \(\mathbb{R}^{2}\) as mentioned above, we consider the eigensystem in polar coordinates for convenience. According to the Bessel function and its related properties, \(\{ \langle \lambda _{n}, \varphi _{n}\rangle \}_{n=0}^{\infty}\) is given as follows:

$$ 0 < \lambda _{0}< \lambda _{1} \leq \cdots , \lambda _{n} \rightarrow \infty ,\quad (n \rightarrow \infty ), $$

and \(\varphi _{n}\) denotes the corresponding eigenfunction

$$ \varphi _{n}(r, \theta )=\omega _{n} J_{\vert m(n)\vert} (\sqrt{ \lambda _{\vert n\vert}} r ) e^{i m(n) \theta}, \quad n \in \mathbb{Z}, $$
(6)

which forms a complete orthonormal basis of \(L^{2}(\Omega )\). Here, \((r, \theta )\) are the polar coordinates on Ω, \(J_{\vert m(n)\vert}(\cdot )\) is the Bessel function of order \(\vert m(n)\vert \) with \(\sqrt{\lambda _{\vert n \vert}}\) as its zero point, \(m(n)\) demonstrates the dependence of m on n such that \(m(n)=-m(-n)\), and \(\omega _{n}\) is the normalized coefficient and allows the form

$$ \omega _{n}=\pi ^{-1 / 2} \bigl[J_{\vert m(n)\vert +1} \bigl(\lambda _{ \vert n\vert}^{1 / 2} \bigr) \bigr]^{-1}, \quad n \in \mathbb{N}^{+} . $$
(7)

See [21, Sect. 2.2] for further details.

Sometimes, we also write \(\lambda _{n}=\lambda _{\vert n\vert}\) for simplicity. Therefore, for a given eigenvalue \(\lambda _{n_{0}}\), in the case of \(m (n_{0} ) \neq 0\), the corresponding eigenpairs are given as

$$ \bigl(\lambda _{n_{0}}, \omega _{n_{0}} J_{\lvert m (n_{0} )\rvert} \bigl(\lambda _{n_{0}}^{1 / 2} r \bigr) e^{i m (n_{0} ) \theta} \bigr), \qquad \bigl(\lambda _{n_{0}}, \omega _{n_{0}} J_{\lvert m (n_{0} )\rvert} \bigl(\lambda _{n_{0}}^{1 / 2} r \bigr) e^{-i m (n_{0} ) \theta} \bigr). $$

For the purpose of the latter proof, we list some properties of Bessel functions.

Lemma 2.1

[37] Bessel functions have the following differential relations and recurrence relations:

$$ \begin{aligned} &\frac{d}{d x} \bigl(x^{m} J_{m}(x) \bigr) =x^{m} J_{m-1}(x), \\ &\frac{d}{d x} \bigl(J_{m}(x) \bigr) =\frac{m}{x} J_{m}(x)-J_{m+1}(x), \\ &\frac{2 m}{x} J_{m}(x) =J_{m-1}(x)+J_{m+1}(x), \\ &x J_{m-1}(x) =x \frac{d}{d x} \bigl(J_{m}(x) \bigr)+m J_{m}(x). \end{aligned} $$
(8)

Next, we introduce the Mittag-Leffler function and some of its properties. The generalized Mittag-Leffler function plays an important role in fractional calculus [38]. The function is defined as follows:

$$ E_{\alpha , \beta}(z):=\sum_{k=0}^{\infty} \frac{z^{k}}{\Gamma (\alpha k+\beta )}, \quad (z \in \mathbb{C}, \alpha >0, \beta \in \mathbb{R}). $$

We provide the asymptotic property of the Mittag-Leffler function below.

Lemma 2.2

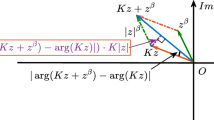
[11, Theorem 1.6] \(E_{\alpha , \beta}(z)\) is an analytic function. Assume \(\pi \alpha / 2<\rho <\min \{\pi , \pi \alpha \}\). Then there exists a constant \(C=C(\alpha , \beta ,\rho )>0\) such that

$$ \bigl\lvert E_{\alpha , \beta}(z)\bigr\rvert \leq \frac{C}{1+\lvert z \rvert}, \quad \bigl(0< \alpha < 2, \beta \in \mathbb{R},\rho \leq \bigl\lvert \arg (z) \bigr\rvert \leq \pi \bigr). $$

Then, we introduce the lemma for the Laplace transform of the Mittag-Leffler function. First, we define \(s \in \mathbb{C}^{+}:=\{s \in \mathbb{C}: \operatorname{Re}(s)>0\}\) to ensure analyticity. Here, s is the Laplace transform parameter.

Lemma 2.3

[39, Proposition 4] For \(\alpha \in (0,1)\), let \(\lambda \geq 0\), the Laplace transform \(\mathcal{L} \{t^{\alpha -1} E_{\alpha , \alpha} (-\lambda t^{ \alpha} ) \}\) exists at every point \(s \in \mathbb{C}^{+}\) and

$$ \mathcal{L} \bigl\{ t^{\alpha -1} E_{\alpha , \alpha} \bigl(-\lambda t^{ \alpha} \bigr) \bigr\} =\frac{1}{s^{\alpha}+\lambda}. $$

Lemma 2.4

[18, Lemma 4.1] Let u satisfy the initial-boundary value problem (3), where \(g\in C^{1}[0,T]\) and \(f \in L^{2}(\Omega )\). Then the weak solution u is denoted by

$$ u= \int _{0}^{t} \theta (t-\tau ) v(\tau ) \,d \tau , \quad 0< t< T, $$
(9)

where \(\theta \in L^{1}(0, T)\), \(J^{1-\alpha}\theta =g(t)\). v is the solution to the following problem:

$$ \textstyle\begin{cases} {}^{c}\partial _{t}^{\alpha}v-\Delta v =0, & \textit{in } \Omega \times (0, T), \\ v(x, 0)=f(x), & \textit{in } \Omega \times \{0\}, \\ v(x, t)=0, & \textit{on } \partial \Omega \times (0, T). \end{cases} $$
(10)

Here, \(J^{\alpha}\theta (t)\) is the Riemann–Liouville integral, which is defined as follows:

$$ J^{\alpha}\theta (t):=\frac{1}{\Gamma (\alpha )} \int _{0}^{t}(t-\eta )^{ \alpha -1}\theta ( \eta )\,d\eta . $$

3 A new type of unique continuation

In this section, we present the proof of Theorem 1.1. From the above lemma, we are ready to give the proof of the main result.

Proof of Theorem 1.1

We first obtain the eigenfunction expansions of the solution to (1) by the Fourier method. We multiply both sides of (1) by \(\varphi _{n}(x)\) and integrate the equation with respect to x. Using integration by parts for the second term and \(\varphi _{n}\vert _{\partial \Omega}=0\), we can derive

$$ \textstyle\begin{cases} {}^{c}\partial _{t}^{\alpha} u_{n}(t)+\lambda _{n} u_{n}(t) =0, \quad t \in (0, T), \\ u_{n}(0) = ( u_{0}, \varphi _{n} ), \end{cases} $$
(11)

where \(u_{n}(t)=\langle u(\cdot , t), \varphi _{n}\rangle \). By using the Mittag-Leffler function, we can formally obtain the expansion

$$ u_{n}(t)=E_{\alpha , 1} \bigl(-\lambda _{n} t^{\alpha} \bigr) \langle u_{0}, \varphi _{n} \rangle . $$

Together with (6), the following holds:

$$ \begin{aligned} u(r, \theta , t)&=\sum _{n=-\infty}^{\infty} E_{\alpha , 1} \bigl(- \lambda _{n} t^{\alpha} \bigr) \langle u_{0}, \varphi _{n}\rangle \varphi _{n}(r, \theta ) \\ &=\sum_{n=0}^{\infty} E_{\alpha , 1} \bigl(-\lambda _{n} t^{\alpha} \bigr)\langle u_{0}, \varphi _{n}\rangle \varphi _{n}(r, \theta )+\sum_{n=-\infty}^{-1} E_{\alpha , 1} \bigl(-\lambda _{n} t^{ \alpha} \bigr) \langle u_{0}, \varphi _{n}\rangle \varphi _{n}(r,\theta ). \end{aligned} $$
(12)

Next, we assert that \(u(r, \theta , t)\) is t-analytic. To validate this claim, since \(E_{\alpha , 1} (-\lambda _{n} t^{\alpha} )\) is analytic in \(\mathbb{C}\), we denote

$$\begin{aligned} \sum_{n=0}^{\infty} E_{\alpha , 1} \bigl(-\lambda _{n} z^{\alpha} \bigr)\langle u_{0}, \varphi _{n}\rangle \varphi _{n}(r, \theta )=:u^{+}, \end{aligned}$$

and

$$\begin{aligned} \sum_{n=-\infty}^{-1} E_{\alpha , 1} \bigl(-\lambda _{n} z^{\alpha} \bigr)\langle u_{0}, \varphi _{n}\rangle \varphi _{n}(r, \theta )=:u^{-}. \end{aligned}$$

Thus, for any \(K\subset \subset \{z \in \mathbb{C} ; \operatorname{Re} z>0 \}\),

$$ u_{N}^{+}(r, \theta , z):=\sum _{n=0}^{N}E_{\alpha , 1} \bigl(- \lambda _{n} z^{\alpha} \bigr) \langle u_{0}, \varphi _{n}\rangle \varphi (r,\theta ) $$

is analytic in K. According to Lemma 2.2 and Lemma 2.3, the following holds:

$$\begin{aligned} \bigl\Vert u^{+}(\cdot , z)-u^{+}_{N}( \cdot , z) \bigr\Vert _{L^{2}( \Omega )}^{2} &=\sum _{n=N+1}^{\infty} \bigl\vert \langle u_{0}, \varphi _{n}\rangle E_{\alpha , 1} \bigl(- \lambda _{n} z^{\alpha} \bigr) \bigr\vert ^{2} \\ &\leq C_{K} \sum_{n=N+1}^{\infty} \bigl\vert \langle u_{0}, \varphi _{n}\rangle \bigr\vert ^{2}, \quad z \in{K}. \end{aligned}$$

Thus, \(\lim_{n \rightarrow \infty}\| u^{+} -u^{+}_{N}\| _{L^{ \infty} (K ; L^{2}(\Omega ) )}=0\) so that \(u^{+}(r, \theta , t)\) is analytic in K. Analogously, we can obtain that \(u^{-}\) is also analytic in K. As a result of the arbitrariness of K, the above assertion is valid. A similar argument can be found in Sakamoto and Yamamoto [9].

From the analyticity of \(u(r, \theta , t)\), the solution u to the initial-boundary value problem (1) can be analytically extended from \((0, T)\) to \((0, \infty )\). For simplicity, we still denote the extension by u. Therefore, we arrive at the following initial-boundary value problem:

$$ \textstyle\begin{cases} {}^{c}\partial _{t}^{\alpha}u-\Delta u=0, & \text{in } \Omega \times (0, \infty ), \\ u=u_{0}, & \text{in } \Omega \times \{0\}, \\ u=0, & \text{on } \partial \Omega \times (0, \infty ) , \end{cases} $$
(13)

and the condition \(\frac{\partial u}{\partial \nu}(z_{1},t)= \frac{\partial u}{\partial \nu}(z_{2},t)=0\) on \(\partial \Omega \times (0, t)\) implies

$$ \frac{\partial u}{\partial \nu}(z_{1},t)= \frac{\partial u}{\partial \nu}(z_{2},t)=0, \quad \text{on } \partial \Omega \times (0, \infty ). $$
(14)

Next, we perform the Laplace transform in (13) and use the formula

$$ {}^{c}\widehat{\partial _{t}^{\alpha} g}(s)=s^{\alpha} \widehat{g}(s)-s^{ \alpha -1} g(0+), $$

to derive the transformed equation

$$ \textstyle\begin{cases} -\Delta \hat{u}(s)+s^{\alpha} \hat{u}(s)=s^{\alpha -1} u_{0}, \\ \hat{u}(s)=0, \quad \text{on } \partial \Omega . \end{cases} $$

From the eigensystem \(\{ \langle \lambda _{n}, \varphi _{n}\rangle \}_{n=-\infty}^{\infty}\) of −Δ on Ω with the Dirichlet boundary condition, the following holds:

$$ \hat{u}(r,\theta ;s)=\sum_{n=-\infty}^{\infty} \frac{s^{\alpha -1}}{s^{\alpha}+\lambda _{n}} \langle u_{0}, \varphi _{n}\rangle \varphi _{n}(r, \theta ), \quad \text{in } \Omega \times \{\operatorname{Re} s>0\}. $$

By using the formula \(\frac{\partial \hat{u}}{\partial \nu} (\cdot ; s )= \frac{\partial \hat{u}}{\partial r} (\cdot ; s )\) and Lemma 2.1, the following holds:

$$ \frac{\partial \hat{u}}{\partial r}(\cdot ;s)=\sum_{n=-\infty}^{ \infty} \frac{s^{\alpha -1}}{s^{\alpha}+\lambda _{n}} \langle u_{0}, \varphi _{n} \rangle \frac{\partial \varphi _{n}}{\partial r}(r,\theta ), $$
(15)

and together with (14), we have

$$ \frac{\partial \hat{u}}{\partial r} (z_{1}; s )= \frac{\partial \hat{u}}{\partial r} (z_{2}; s )=0. $$

Note that Ω is a unit disk, as mentioned in Sect. 1. Thus \(z_{1}\) and \(z_{2}\) are boundary observation points implying \(r=1\), there holds

$$ \frac{\partial \hat{u}}{\partial r} (z_{1}; s )=\sum_{n=- \infty}^{\infty} \frac{s^{\alpha -1}}{s^{\alpha}+\lambda _{n}} \langle u_{0}, \varphi _{n} \rangle \frac{\partial \varphi _{n}}{\partial r}(1,\theta _{1})=0, $$

and

$$ \frac{\partial \hat{u}}{\partial r} (z_{2}; s )=\sum_{n=- \infty}^{\infty} \frac{s^{\alpha -1}}{s^{\alpha}+\lambda _{n}} \langle u_{0}, \varphi _{n} \rangle \frac{\partial \varphi _{n}}{\partial r}(1,\theta _{2})=0. $$

We set \(\eta =s^{\alpha}\), which yields

$$ \begin{aligned} &\sum_{n=-\infty}^{\infty} \frac{1}{\eta +\lambda _{n}} \langle u_{0}, \varphi _{n} \rangle \frac{\partial \varphi _{n}}{\partial r}(1,\theta _{1}) \\ &\quad =\sum_{n=-\infty}^{\infty} \frac{1}{\eta +\lambda _{n}} \langle u_{0}, \varphi _{n}\rangle \frac{\partial \varphi _{n}}{\partial r}(1, \theta _{2})=0. \end{aligned} $$
(16)

It is readily seen that (16) holds for \(\eta \in \mathbb{C} \backslash \{-\lambda _{n} \}_{n=1}^{ \infty}\). Then, for any \(n=1,2, \ldots \) , we can take a sufficiently small circle centered at \(-\lambda _{n}\) that does not include distinct eigenvalues. Integrating (16) on this circle yields

$$ \langle u_{0}, \varphi _{n}\rangle \frac{\partial \varphi _{n}}{\partial r}(1,\theta _{\ell}) + \langle u_{0}, \varphi _{-n}\rangle \frac{\partial \varphi _{-n}}{\partial r}(1,\theta _{\ell})=0, \quad n \in \mathbb{N}^{+}, \ell =1,2. $$
(17)

Moreover, from the properties of Bessel functions in Lemma 2.1, it follows that

$$ \frac{\partial \varphi _{n}}{\partial r}(r,\theta ) = \omega _{n} \sqrt{\lambda _{\vert n\vert}} \biggl( \frac{1}{r\sqrt{\lambda _{\vert n\vert }}}J_{\vert m(n)\vert} (r \sqrt{ \lambda _{\vert n\vert}} ) - J_{\vert m(n)\vert +1}(r \sqrt{\lambda _{\vert n\vert}}) \biggr) e^{i m(n) \theta}. $$

Since \(J_{\vert m(n)\vert}(\cdot )\) is the Bessel function of order \(\vert m(n)\vert \) with \(\sqrt{\lambda _{n}}\) as its zero point, the above formula can be reduced to

$$ \frac{\partial \varphi _{n}}{\partial r}(1,\theta _{\ell}) = -\omega _{n} \sqrt{\lambda _{\vert n\vert}} J_{\vert m(n) \vert +1}(\sqrt{\lambda _{ \vert n\vert}}) e^{i m(n) \theta _{\ell}},\quad \ell =1,2. $$

By noting the definition of \(\omega _{n}\), we further see that

$$ \frac{\partial \varphi _{n}}{\partial r}(1,\theta _{\ell}) = - \frac{ \sqrt{\lambda _{\vert n \vert}}}{\sqrt{\pi}} e^{i m(n) \theta _{\ell}},\quad \ell =1,2. $$
(18)

By combining the above formulas, we finally get

$$ \langle u_{0}, \varphi _{n}\rangle e^{i m(n) \theta _{ \ell}} +\langle u_{0}, \varphi _{-n}\rangle e^{-i m(n) \theta _{\ell}}=0, \quad n\in \mathbb{N}^{+}, \ell =1,2. $$

We divide the next proofs into the following two cases.

Case 1. Provided that \(m(n)=0\), that is, \(n=0\), \(\langle u_{0}, \varphi _{0}\rangle = 0\) holds.

Case 2. Provided that \(m(n)\neq 0\), the following hold:

$$ \langle u_{0}, \varphi _{n}\rangle e^{i m(n) \theta _{1}}+ \langle u_{0}, \varphi _{-n}\rangle e^{-i m(n) \theta _{1}}=0, $$

and

$$ \langle u_{0}, \varphi _{n}\rangle e^{i m(n) \theta _{2}}+ \langle u_{0}, \varphi _{-n}\rangle e^{-i m(n) \theta _{2}}=0 . $$

We conclude that

[ e i m ( n ) θ 1 e − i m ( n ) θ 1 e i m ( n ) θ 2 e − i m ( n ) θ 2 ] [ 〈 u 0 , φ n 〉 〈 u 0 , φ − n 〉 ] = [ 0 0 ] .

From the matrix determinant and Euler’s formula, we conclude

$$ e^{im(n) (\theta _{1}-\theta _{2} )}-e^{-im(n) ( \theta _{1}-\theta _{2} )}=2 i \sin \bigl(m(n) (\theta _{1}- \theta _{2} ) \bigr). $$

Recalling Theorem 1.1, \(\theta _{1}\) and \(\theta _{2}\) are fulfilled

$$ \theta _{1}-\theta _{2} \notin \pi \mathbb{Q},\quad \mathbb{Q} \text{ is the set of rational numbers. } $$

Therefore, we have

$$ 2 i \sin \bigl(m(n) (\theta _{1}-\theta _{2} ) \bigr) \neq 0. $$

Hence, we conclude that \(\langle u_{0}, \varphi _{n}\rangle =\langle u_{0}, \varphi _{-n}\rangle =0\). Since n is chosen arbitrarily, we conclude \(\langle u_{0}, \varphi _{n}\rangle =0\) for all \(n\in \mathbb{Z}\), and thus \(u_{0}=u(\cdot , 0)=0\) in Ω, which indicates \(u=0\) in Ω. This completes the proof of Theorem 1.1. □

4 Fractional order and source term identification

In this section, our goal is to give the proof for the uniqueness of the inverse problem for the determination of the fractional order and source term.

Proof of Theorem 1.2

To prove Theorem 1.2, we first prove that the observation

$$ \frac{\partial u_{1}}{\partial \nu}(z_{1},t)= \frac{\partial u_{2}}{\partial \nu}(z_{1},t), $$

implies \(\alpha _{1}=\alpha _{2}\). To achieve this, we extend the function g from \((0,T)\) to \((0,\infty )\) by letting \(g=0\) outside of \((0,T)\). For simplicity, we still denote the extension by g and obtain the following initial-boundary value problem:

$$ \textstyle\begin{cases} {}^{c}\partial _{t}^{\alpha _{j}}u_{j} - \Delta u_{j}=g(t) f_{j}(x), & \text{in } \Omega \times (0, \infty ), \\ u=0, & \text{in } \Omega \times \{0\}, \\ u=0, & \text{on } \partial \Omega \times (0, \infty ). \end{cases} $$
(19)

The solution \(u_{j}\) to the initial-boundary value problem (19) is an extension of the solution u to problem (1.2). For simplicity, we still denote the extension as u.

By combining equation (18) and the series representation of the solution u (e.g., see Sakamoto and Yamamoto [9]), we have

$$ \begin{aligned} \frac{\partial u_{j}}{\partial r}(1,\theta ,t) &= \sum_{n=-\infty}^{ \infty} \int _{0}^{t} g(t-\tau ) \tau ^{\alpha _{j}-1} E_{\alpha _{j}, \alpha _{j}}\bigl(-\lambda _{\vert n \vert} \tau ^{\alpha _{j}}\bigr) \,d\tau \langle f_{j},\varphi _{n}\rangle \frac{\partial \varphi _{n}}{\partial r}(1,\theta ) \\ &= -\sum_{n=-\infty}^{\infty} \int _{0}^{t} g(t-\tau ) \tau ^{ \alpha _{j}-1} E_{\alpha _{j},\alpha _{j}}\bigl(-\lambda _{\vert n \vert} \tau ^{\alpha _{j}}\bigr) \,d\tau \langle f_{j},\varphi _{n}\rangle \frac{ \sqrt{\lambda _{\vert n \vert}}}{\sqrt{\pi}} e^{i m(n) \theta}, \\ &\quad j=1,2. \end{aligned} $$
(20)

We perform Laplace transform on both sides of the above formula to obtain

$$ \frac{\partial \hat{u}_{j}}{\partial r}(1,\theta ,t) = - \frac{\hat{g}(s)}{\sqrt{\pi}} \sum _{n=-\infty}^{\infty} \frac{\lambda _{\vert n\vert}^{\frac{3}{2}}}{s^{\alpha _{j}} + \lambda _{\vert n\vert}} \langle f_{j},\varphi _{n}\rangle e^{i m(n) \theta}, \quad \operatorname{Re} s>0, $$
(21)

which implies

$$\begin{aligned} &\frac{\partial \hat{u}_{1}}{\partial r}(1,\theta ;s) - \frac{\partial \hat{u}_{2}}{\partial r}(1,\theta ;s) \\ &\quad = -\frac{\hat{g}(s)}{\sqrt{\pi}} \sum_{n=-\infty}^{\infty} \lambda _{ \vert n\vert}^{\frac{3}{2}} \biggl[ \frac{ \langle f_{1},\varphi _{n}\rangle }{s^{\alpha _{1}} + \lambda _{\vert n\vert}} - \frac{ \langle f_{2},\varphi _{n}\rangle }{s^{\alpha _{2}} + \lambda _{\vert n\vert}} \biggr] e^{i m(n) \theta},\quad \operatorname{Re} s>0. \end{aligned}$$

Moreover, from the observation \(\frac{\partial u_{1}}{\partial r}(1,\theta _{1},t) = \frac{\partial u_{2}}{\partial r}(1,\theta _{1},t) \), \(t\in (0,T)\), it follows that

$$\begin{aligned} & \int _{T}^{\infty } \biggl[\frac{\partial u_{1}}{\partial r}(1, \theta _{1},t) - \frac{\partial u_{2}}{\partial r}(1,\theta _{1},t) \biggr]e^{-st} \,dt \\ &\quad = -\frac{\hat{g}(s)}{\sqrt{\pi}} \sum_{n=-\infty}^{\infty} \lambda _{ \vert n\vert}^{\frac{3}{2}} \biggl[ \frac{ \langle f_{1},\varphi _{n}\rangle }{s^{\alpha _{1}} + \lambda _{\vert n\vert}} - \frac{ \langle f_{2},\varphi _{n}\rangle }{s^{\alpha _{2}} + \lambda _{\vert n\vert}} \biggr] e^{i m(n) \theta _{1}},\quad \operatorname{Re} s>0. \end{aligned}$$

By choosing \(\varepsilon \in (0,T)\) and multiplying \(se^{s\varepsilon}\) on both sides of the above formula, we obtain

$$\begin{aligned} &\lim_{\operatorname{Re} s\to \infty ,\operatorname{Re} s>0}se^{ \varepsilon s} \int _{T}^{\infty } \biggl[ \frac{\partial u_{1}}{\partial r}(1, \theta _{1},t) - \frac{\partial u_{2}}{\partial r}(1,\theta _{1},t) \biggr]e^{-st} \,dt \\ &\quad = -\lim_{s\to \infty ,\operatorname{Re} s>0} \frac{s\hat{g}(s)}{\sqrt{\pi}} \sum _{n=-\infty}^{\infty} \lambda _{ \vert n\vert}^{\frac{3}{2}} \biggl[ \frac{ \langle f_{1},\varphi _{n}\rangle }{s^{\alpha _{1}} + \lambda _{\vert n\vert}} - \frac{ \langle f_{2},\varphi _{n}\rangle }{s^{\alpha _{2}} + \lambda _{\vert n\vert}} \biggr] e^{i m(n) \theta _{1}}. \end{aligned}$$

We note from the initial value theorem of the Laplace transforms that

$$ \lim_{\operatorname{Re} s\to \infty} s\hat{g}(s) = g(0)>0, $$

and then

$$\begin{aligned} \lim_{\operatorname{Re} s\to \infty ,\operatorname{Re} s>0} \sum_{n=- \infty}^{\infty} \lambda _{\vert n\vert}^{\frac{3}{2}} \biggl[ \frac{ \langle f_{1},\varphi _{n}\rangle }{s^{\alpha _{1}} + \lambda _{\vert n\vert}} - \frac{ \langle f_{2},\varphi _{n}\rangle }{s^{\alpha _{2}} + \lambda _{\vert n\vert}} \biggr] e^{i m(n) \theta _{1}} = 0. \end{aligned}$$

If \(\alpha _{1}\ne \alpha _{2}\), then from Lemma 3.7 in Li and Zhang [21], it follows that \(\langle f_{1},\varphi _{n}\rangle = \langle f_{2},\varphi _{n}\rangle =0\) for all \(n\in \mathbb{Z}\), which contradicts \(f\ne 0\). Therefore, we must have \(\alpha _{1}=\alpha _{2}\).

Now, it remains to prove that if \(\frac{\partial u}{\partial \nu}(z_{1},t)= \frac{\partial u}{\partial \nu}(z_{2},t)=0\) holds, then \(f(x)=0\) can be derived. Let u satisfy the initial-boundary value problem (3), where \(g \in C^{1}[0, T]\) and \(f \in L^{2}(\Omega )\). According to Lemma 2.4, u takes the form of (9). Therefore, the following holds:

$$ \frac{\partial u}{\partial \nu}(x,t)= \int _{0}^{t} \theta (t-\tau ) \frac{\partial v}{\partial \nu}(x,\tau ) \,d\tau , \quad (x,t)\in \Omega \times (0,T). $$

In particular,

$$ \frac{\partial u}{\partial \nu}(z_{1},t) = \frac{\partial u}{\partial \nu}(z_{2},t)=0, $$

then the following holds:

$$ \int _{0}^{t} \theta (t-\tau ) \frac{\partial v}{\partial \nu}(z_{\ell}, \tau ) \,d\tau =0, \quad \ell =1,2. $$

Applying the operator \(J^{1-\alpha}\) to both sides of the above formula yields

$$ \int _{0}^{t} g(t-\tau )\frac{\partial v}{\partial \nu}(z_{\ell}, \tau ) \,d\tau =0, \quad \ell =1,2. $$

Derivation of both sides of the above equation with respect to t, the following holds:

$$ g(0)\frac{\partial v}{\partial \nu}(z_{\ell},t) + \int _{0}^{t} g^{ \prime}(t-\tau ) \frac{\partial v}{\partial \nu}(z_{\ell},\tau ) \,d\tau =0, \quad \text{on } \partial \Omega , \ell =1,2. $$

Note that \(g(0) \neq 0\), and we estimate

$$ \begin{aligned} \biggl\vert \frac{\partial v}{\partial \nu}(z_{\ell}, t) \biggr\vert & \leq \frac{1}{ \vert g(0) \vert } \int _{0}^{t} \bigl\vert g^{\prime}(t- \tau ) \bigr\vert \cdot \biggl\vert \frac{\partial v}{\partial \nu}(z_{\ell}, \tau ) \biggr\vert \,d \tau \\ & \leq \frac{C_{g}}{ \vert g(0) \vert } \int _{0}^{t} \biggl\vert \frac{\partial v}{\partial \nu}(z_{\ell}, \tau ) \biggr\vert \,d \tau , \quad 0< t< T. \end{aligned} $$

According to Gronwall’s inequality, we obtain \(\frac{\partial v}{\partial \nu}(z_{\ell},t)=0\), \(z_{\ell} \in \partial \Omega \), and \(\ell =1,2\). Lastly, we apply Theorem 1.1 to the homogeneous problem (10) to derive \(v=0\) in \(\Omega \times (0,T)\), in which we can conclude \(f = 0\) in Ω. We therefore finish the proof of the Theorem 1.2. □

5 Concluding remarks and future work

In this paper, a new type of the unique continuation property for time-fractional diffusion equations is studied. The proof of this unique continuation principle was concerned, which leads to uniqueness of the corresponding inverse problems. We gave a representation formula for the solution in polar coordinates based on eigenfunction expansion and the Mittag-Leffler function. With the help of the Laplace transformation and the properties of the Bessel function, we proved the unique continuation property from two point Neumann boundary data. As an application, we considered the uniqueness of an inverse problem for simultaneously determining the spatial component in the source term and the fractional order from two point finite time observation data. The uniqueness result is slightly sensitive to the geometry of the domain. We will consider the case in other domains such as rectangular and elliptic in the future. Otherwise, it would be interesting to investigate the unique continuation properties of the solution in a high dimensional case.