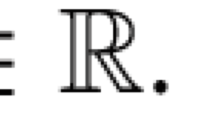Abstract
The Bénard problem consists in a system that couples the well-known Navier–Stokes equations and an advection-diffusion equation. In thin varying domains this leads to the g-Bénard problem, which turns out to be the classical Bénard problem when g is constant. The main goal of this paper is to, first of all, introduce the g-Bénard problem with time-fractional derivative of order \(\alpha \in (0,1)\). This formulation is new even in the classical Bénard problem, that is with constant g. The second goal of this paper is to prove the existence and uniqueness of a weak solution by means of the Faedo–Galerkin approximation method. Some recent works on time-fractional Navier–Stokes equations have opened new perspectives in studying variational aspects in problems involving time-fractional derivatives.
Similar content being viewed by others
1 Introduction
Fractional derivatives play a major role in modelling nonlocality, anomalous behaviour and memory effects, which are common characteristics of natural phenomena [15, 22] arising from complex systems. For instance, the memory effect results from the fact that fractional derivatives involve a convolution integral with a power-law memory kernel. This appears naturally when studying, for instance, viscoelastic materials and viscous fluid dynamics [22]. For more applications of fractional calculus, see, e.g. [14, 23–26, 30].
The introduction of time-fractional derivative in fluid dynamics goes back to Lions in [17], but for order less than \(1/4\) provided the space dimension is not further than 4. In recent works of Zhou and Peng [35], the question of weak solutions and an optimal control problem of time-fractional Navier–Stokes equations in fractal media were considered. Numerical results regarding such problems was treated firstly in [16] and constitute an emerging field of research.
More recently, a time-fractional g-Navier–Stokes problem has been introduced and results regarding the existence, uniqueness of solutions and optimal control have been proved [6]. This suggests, to the authors of the current paper, to consider various variations of g-Navier–Stokes equations that can be modelled by time-fractional derivatives instead of integer ones. It is, indeed, a general trend among researchers to try to find more applications where one can replace an integer derivative with various non-integer derivatives. In fluid dynamics the fact that fractal media exhibit memory-dependent behaviour justifies the use of time-fractional derivatives as suggested by Zhou and Peng [35].
It is worth mentioning that the theory of g-Navier–Stokes equations started with the works of Hale and Raugel [11, 12], Raugel and Sell [27] who studied 3D nonlinear equations and Navier–Stokes equations in thin domains. J. Roh [28], a student of Sell, generalised the previous works to thin domains of the form \(\Omega _{g}=\Omega \times (0,g)\), where g is some smooth scalar function. The derived equations are called the g-Navier–Stokes equations. This theory has interested many researchers in recent years, see [4, 5, 13] and the references therein.
On the other hand, heat conduction based on the classical Fourier law, which relates the heat flux vector and the temperature gradient, has shown its limits. The time-fractional heat conduction model can be seen as a good alternative (see [9, 18, 29] and the references therein). Boussinesq (or Bénard) model is a combination of the heat conduction model and Navier–Stokes equations and is a well-developed subject in modelling heat conducting fluids [7, 10, 33, 34]. The aim of this paper is to generalise the setting in [20, 21], where g-Bénard equations were considered, to time-fractional g-Bénard equations.
The novelty of this paper is, first of all, to introduce a new fractional model in fluid dynamics and then to prove the existence and uniqueness of its solutions. This is a starting point for more questions to answer, particularly related to numerical analysis, stability and long-term behaviour. More precisely, let \(\Omega _{g}=\Omega _{2}\times (0,g)\), where \(\Omega _{2}\) is a bounded domain in and g is some scalar nonnegative function. We introduce time-fractional g-Bénard equations of the following form:
where u is the fluid velocity, p is the pressure, θ is the temperature, \(f_{1}\) is the external force function, \(f_{2}\) is the heat source function, is a constant vector, ν is the kinematic viscosity and κ is the thermal diffusivity(ν and κ are positive constants). The derivative of order α is considered in the Caputo sense. The time-fractional g-Bénard problem consists in a system that couples time-fractional Navier–Stokes equations and time-fractional advection-diffusion heat equation in order to model a memory-dependent convection in a fluid considered in a fractal medium.
This paper is organised as follows: In Sect. 2, we recall some concepts and notations related to fractional calculus. Section 3 is devoted to the problem statement, and Sect. 4 is dedicated to the proof of the existence and uniqueness of weak solutions to time-fractional g-Bénard equations. In Sect. 5 we provide a conclusion.
2 Preliminaries on fractional calculus
In this section, we provide some notations and preliminary results concerning fractional calculus. For this purpose, assume X to be a Banach space. Let \(\alpha \in (0,1]\) and let \(k_{\alpha}\) denote the Riemann–Liouville kernel
For a function \(v:[0,T]\rightarrow X\), we give the following definitions of derivatives and integrals:
-
(1)
The left Riemann–Liouville integral of v is defined by
$$ I_{t}^{\alpha }v(t)= \int _{0}^{t} k_{\alpha}(t-s)v(s)\,ds, \quad t>0 ,$$provided the integral is point-wise defined on \([0,+\infty [\).
-
(2)
The right Riemann–Liouville integral of v is defined by
$$ I_{t,T}^{\alpha }v(t)= \int _{t}^{T} k_{\alpha}(t-s)v(s)\,ds,\quad t>0 ,$$provided the integral is point-wise defined on \([0,+\infty [\).
-
(3)
The left Caputo fractional derivative of order α of v is defined by
$$ D_{t}^{\alpha }v(t)= \int _{0}^{t} k_{1-\alpha}(t-s) \frac{d}{ds}v(s)\,ds .$$ -
(4)
The right Riemann–Liouville fractional derivative of order α of v is defined by
$$ D_{t,T}^{\alpha }v(t)=-\frac{d}{dt} \int _{t}^{T} k_{1-\alpha}(t-s)v(s)\,ds .$$ -
(5)
The Liouville–Weyl fractional integral on the real axis for functions is defined as follows:
$$ I_{-,t}^{\alpha }v(t)= \int _{-\infty}^{t} k_{\alpha}(t-s)v(s)\,ds .$$ -
(6)
The Caputo fractional derivative on the real axis for functions is defined as follows:
$$ D_{-,t}^{\alpha }v(t)= I_{-,t}^{1-\alpha} \frac{d}{dt} v(t) .$$
Note that the notation \(\partial _{t}^{\alpha}\) stands for Caputo fractional partial derivative, i.e. when functions have another argument than time. We have the following fractional integration by parts formula (see, e.g. [2]):
since for \(\psi \in C_{0}^{\infty}([0,T],X)\) one has \(\lim_{t\to T} I_{t,T}^{1-\alpha}\psi (t)=0\).
To pass from weak convergence to strong convergence, we will need a compactness result. Let \(X_{0}\), X, \(X_{1}\) be Hilbert spaces with \(X_{0} \hookrightarrow {} X \hookrightarrow {} X_{1}\) being continuous and \(X_{0}\hookrightarrow {} X\) being compact. Assume that and denote by v̂ its Fourier transform:
We have for \(\gamma >0\)
For given \(0<\gamma <1\), we introduce the following space:
Clearly, it is a Hilbert space for the norm
For any set , we associate with it the subspace \(W_{K}^{\gamma}\subset W^{\gamma}\) defined as
By similar discussion as in the proof of Theorem 2.2 in Temam [31], it is clear that is compact for any bounded set K and any \(\gamma >0\).
As a particular situation of the compactness result discussed above, let H, V be two Hilbert spaces endowed with the scalar product \((\cdot,\cdot )_{H}\) and \((\cdot,\cdot )_{V}\) and the norms \(|\cdot|_{H}\) and \(\|\cdot\|_{V}\), respectively. Denote by \(\langle \cdot,\cdot \rangle \) the dual pairing between V and \(V'\), the dual of V. Moreover assume that \(V \hookrightarrow {} H \hookrightarrow {} V'\) continuously and compactly and note that the space
is compactly embedded in \(L^{2}(0,T;H)\). It is then well known that
for \(u\in W^{\gamma}(0,T;V,V')\) and \(v\in H\). Moreover, for a derivable function \(v:[0,T]\rightarrow V\), we have from [3] that
We end this section by the following important result.
Lemma 2.1
Suppose that a nonnegative function satisfies
for \(c_{1}>0\) and \(c_{2}\) is a nonnegative integrable function for \(t\in [0,T]\). Then
For more details about fractional calculus, we refer to the monograph [14].
3 Problem statement
We introduce the usual notation used in the context of the mathematical theory of Navier–Stokes equations [31]. Let \(\Omega _{g} = \Omega _{2} \times (0, g) = (0, 1)\times (0, 1)\times (0, g)\), where \(g = g(y_{1}, y_{2})\) is a smooth function defined on \(\Omega _{2}\). In addition, we assume that
Let \(L^{2}(\Omega , g)\) denote the Hilbert space, of weighted Sobolev spaces type, with the inner product
and the induced norm \(|u|^{2}_{g} = \langle u, u\rangle _{g}\). Similarly, we can define the weighted Sobolev space \(H^{1}(\Omega , g)\) equipped with the norm
Moreover, we will need the following spaces:
where \(H_{g}\) is endowed with the inner product and the norm in \(L^{2}(\Omega g)\). In addition, the spaces \(V_{g}\) and Wg are endowed with the inner product and the norm in \(H^{1}(\Omega , g)\). Let us also remark that the inclusions
are dense and continuous [19, 28]. By the Riesz representation theorem, it is possible to write
Let us now define the orthogonal projection \(P_{g}\) as \(P_{g} : L^{2}_{ \mathrm{per}}(\Omega , g)\rightarrow H_{g}\). It is clear that \(Q \subseteq H^{\perp}_{g}\). Similarly, we define \(\widetilde{P}_{g}\) as \(\widetilde{P}_{g} :L^{2}_{ \mathrm{per}}(\Omega , g)\rightarrow W_{g}\). By taking into account the following equality [28]:
we define the g-Laplace operator and g-Stokes operator as follows:
and
respectively. We have the following result [28].
Proposition 3.1
For the g-Stokes operator \(A_{g}\), the following hold:
-
(1)
The g-Stokes operator \(A_{g}\) is a positive, self-adjoint operator with compact inverse, where the domain of \(A_{g}\) is \(D(A_{g}) = V_{g} \cap H^{2}(\Omega , g)\).
-
(2)
There exist countable eigenvalues of \(A_{g}\) satisfying
$$ 0< \frac{4\pi ^{2}m_{0}}{M_{0}}\leq \lambda _{1} \leq \lambda _{2} \leq \lambda _{3}\leq \cdot \cdot \cdot , $$where \(\lambda _{1}\) is the smallest eigenvalue of \(A_{g}\). In addition, there exists the corresponding collection of eigenfunctions that forms an orthonormal basis for \(H_{g}\).
The operators \(A_{g}\) and \(P_{g}\) are clearly self-adjoint, then by using integration by parts we have
It then follows that for \(u \in V_{g}\) we can write \(| A^{1/2}u|_{g}= | \nabla u |_{g}=\| u \|_{g} \). On the other hand, since the functional
is a continuous linear mapping on \(W_{g}\), we can define a continuous linear mapping \(\widetilde{A}_{g}\) on \(W'_{g}\) such that
for all \(\theta \in W_{g}\). For u, v and w laying in an appropriate subspaces of \(L^{2}_{\mathrm{per}}(\Omega , g)\), we can define the bilinear operator
and the trilinear form
As a consequence, one obtains \(b_{g}(u, v, w) = -b_{g}(u, w, v)\), which implies that \(b_{g}(u, v,v) = 0\). Moreover, we have the following inequality on \(b_{g}\)(see, e.g. [31, 32]):
Similarly, for \(u \in V_{g}\) and \(\theta , \tau \in W_{g}\), we define \(\widetilde{B}_{g}(u,\theta ) = \widetilde{P}_{g}[(u \cdot \nabla ) \theta ]\) and
We denote the operators \(C_{g}u = P_{g}[\frac{1}{g} (\nabla g \cdot \nabla )u]\) and \(\widetilde{C}_{g} \theta = \widetilde{P}_{g}[\frac{1}{g} (\nabla g \cdot \nabla )\theta ]\) such that
Finally, let \(\widetilde{D}_{g}\theta = \widetilde{P}_{g}[ \frac{\nabla g}{g}\theta ]\) such that
We can now rewrite the system of g-Bénard equations in the following abstract time-fractional evolutionary equations:
The proof of the following two lemmas can be found in [5].
Lemma 3.2
For \(n = 2\), there exists a positive constant c such that
Lemma 3.3
For \(u\in L^{2}( 0,T,V_{g})\), we have
4 Existence of weak solutions
In this section we prove the existence and uniqueness of the weak solution. The main technique is the Faedo–Galerkin approximation method, which allows to exhibit an approximating sequence that converges to the desired solution. The following gives the definition of weak solutions, that is, solutions in a variational sense.
Definition 4.1
A pair of functions \(\{ u,\theta \}\) is called a weak solution of system (3.3) if \(u\in L^{2}(0, T; V_{g})\) and \(\theta \in L^{2}(0, T; W_{g})\) satisfy the following equations:
for all \(v_{2} \in V_{g}\) and \(\tau \in W_{g}\).
The following theorem contains the main result of this paper.
Theorem 4.2
If \(f_{1}\in L^{\frac{2}{\alpha _{1}}}(0, T; L^{2}(\Omega , g))\) and \(f_{2}\in L^{\frac{2}{\alpha _{2}}}(0, T; L^{2}(\Omega , g))\) (\(\alpha _{1}, \alpha _{2}<\alpha \)), \(u_{0} \in H_{g}\), \(\theta _{0} \in L^{2}(\Omega , g)\) and g is a smooth function satisfying the conditions given in (3.1) defined on \(\Omega _{2}\), then there exists a unique weak solution \(\{ u,\theta \} \) of system (3.3) satisfying the periodic boundary conditions.
Proof
Since \(V_{g}\) is separable and \(\mathcal{V}_{1}\) is dense in \(V_{g}\), there exists a sequence forming a complete orthonormal system in \(H_{g}\) and a basis in \(V_{g}\). Similarly, there exists a sequence forming a complete orthonormal system in \(L^{2}(\Omega , g)\) and a basis in \(W_{g}\). Let m be an arbitrary but fixed nonnegative integer. For each m, we define the following approximate solution \(\{u^{(m)}(t), \theta ^{(m)}(t)\}\) of (3.3):
and we consider the following approximate problem (4.3)–(4.5):
and
This system forms a nonlinear fractional order system of ordinary differential equations for the functions \(f_{j}^{(m)}(t)\) and \(g_{j}^{(m)}(t)\) and has a maximal solution on some interval \([0, T ]\) (cf. [6]). We multiply (4.3) and (4.4) by \(f_{j}^{(m)}(t)\) and \(g_{j}^{(m)}(t)\), respectively, and add these equations for \(k = 1,\ldots , m\). Taking into account \(b_{g}(u^{(m)}, u^{(m)}, u^{(m)}) = 0\) and \(\widetilde{b}g(u^{(m)}, \theta ^{(m)},\theta ^{(m)}) =0\), we get
and
Using Schwarz and Young inequalities in (4.6) and (4.7),
By using the fact that \(|\nabla g |^{2}_{\infty}< \frac{\pi ^{2} m^{3}_{0}}{M_{0}}\) and noting \(\nu '=\nu (1- \frac{ M_{0}|\nabla g|^{2}_{\infty}}{2\pi ^{2} m^{3}_{0}} )\), \(\kappa '=\kappa (1- \frac{ M_{0}|\nabla g|^{2}_{\infty}}{2\pi ^{2} m^{3}_{0}} )\) and \(c'= \frac{ M^{2}_{0}\|\xi \|^{2}_{\infty}}{4\pi ^{4} m^{2}_{0}}\), we get the inequalities
and
Integrating (4.9) from 0 to T, in the fractional sense, we obtain
where \(b_{2}=\frac{\alpha -1}{1-\alpha _{2}}\) and \(C_{2}=\frac{2T^{1+b_{2}}}{\kappa (1+b_{2})\Gamma (\alpha )}\). It follows that
On the other hand, integrating (4.8) from 0 to T, in the fractional sense, we obtain
where \(b_{1}=\frac{\alpha -1}{1-\alpha _{1}}\) and \(C_{1}=\frac{c'}{\nu \kappa '}C_{2}+ \frac{4T^{1+b_{1}}}{\nu (1+b_{1})\Gamma (\alpha )}\). By using the fact that
and similarly
it follows that
Consequently,
which implies that the sequences \(\{u^{(m)}\}_{m}\) and \(\{\theta ^{(m)}\}_{m}\) remain in a bounded set of \(L^{\infty}(0, T ; H_{g})\) and \(L^{\infty}(0, T ; L^{2}(\Omega , g))\), respectively. Moreover, for \(t=T\), one obtains
which implies that the sequences \(\{u^{(m)}\}_{m}\) and \(\{\theta ^{(m)}\}_{m}\) remain in a bounded set of \(L^{2}(0, T ; V_{g})\) and \(L^{2}(0, T ; W_{g})\), respectively. Consequently, we can assert the existence of elements \(u \in L^{2}(0, T ; V_{g}) \cap L^{\infty}(0, T ; H_{g})\) and \(\theta \in L^{2}(0, T ; W_{g}) \cap L^{\infty}(0, T ; L^{2}(\Omega , g))\) and the subsequences \(\{u^{(m)}\}_{m}\) and \(\{\theta ^{(m)}\}_{m}\) such that \(u^{(m)} \rightarrow u \in L^{2}(0, T ; V_{g})\) and \(\theta ^{(m)} \rightarrow \theta \in L^{2}(0, T ; W_{g})\) weakly and \(u^{(m)}\rightarrow u \in L^{\infty}(0, T ; H_{g})\) and \(\theta ^{(m)} \rightarrow \theta \in L^{\infty}(0, T ; L^{2}(\Omega , g))\) weakly-star as \(m \rightarrow \infty \).
Let and be defined as
and their Fourier transforms be denoted by \(\widehat{u}^{(m)}\) and \(\widehat{\theta}^{(m)}\), respectively. We show that the sequence \(\{\tilde{u}^{(m)}\}_{m}\) remains bounded in and the sequence \(\{\tilde{\theta}^{(m)}\}_{m}\) remains bounded in . To do so, we need to verify that
and
In order to prove (4.19) and (4.20), we observe that
where \(\delta _{0}\), \(\delta _{T}\) are Dirac distributions at 0 and T and \(F_{m}^{u}\) and \(F_{m}^{\theta}\) are defined by
for \(k = 1,\ldots , m\). Here \(\widetilde{F}_{m}\) is defined as usual by
Indeed, it is classical that since \(\widetilde{u}^{(m)}\) and \(\widetilde{\theta}^{(m)}\) have two discontinuities at 0 and T, the Caputo derivative of \(\widetilde{u}^{(m)}\) is given by
and the one of \(\widetilde{\theta}^{(m)}\) is given by
By the Fourier transform, (4.21) and (4.22) yield
Here \(\widehat{u}^{(m)}\) and \(\widehat{F}_{m}\) denote the Fourier transforms of \(\tilde{u}^{(m)}\) and \(\widetilde{F}_{m}\), respectively. We multiply (4.28) and (4.30) by \(\widehat{f}_{j}^{(m)}\) and \(\widehat{g}_{j}^{(m)}\), respectively, and add these equations for \(k= 1,\dots , m\) to get
Since the integrals on the right-hand side of the inequalities
remain bounded, \(\|F_{1}(t) \|_{V'_{g}}\) and \(\|F_{2}(t) \|_{W'_{g}}\) are bounded in \(L^{1}(0, T ; V'_{g})\) and \(L^{1}(0, T ; W'_{g})\), respectively. Therefore, for all m,
Moreover, since \(u^{(m)}(0)\), \(u^{(m)}(T)\), \(\theta ^{(m)}(0)\) and \(\theta ^{(m)}(T )\) are bounded, we get
For γ fixed, \(\gamma <\alpha /4\), we observe that
Then we can write
By the Parseval inequality, the first integral is bounded as \(m\to \infty \). Applying the Schwarz inequality, the second integrals yield
The first integrals are finite due to \(\gamma <\alpha /4\). On the other hand, it follows from the Parseval equality that
which implies that (4.19) and (4.20) hold. We know that there exists a subsequence of \(\{u^{(m)}\}_{m}\) (which we will denote with the same symbols) that converges to some u weakly in \(L^{2}(0,T;V_{g})\) and weakly-star in \(L^{\infty}(0,T;H_{g})\) with \(u\in L^{2}(0,T;V_{g})\cap L^{\infty}(0,T;H_{g})\). Similarly, there exists a subsequence of \(\{\theta ^{(m)}\}_{m}\) (which we will denote with the same symbol) that converges to some θ weakly in \(L^{2}(0,T;W_{g})\) and weakly-star in \(L^{\infty}(0,T;L^{2}(\Omega ,g))\) with \(\theta \in L^{2}(0,T;W_{g})\cap L^{\infty}(0,T;L^{2}(\Omega ,g))\). As \(W^{\gamma}(0,T,V_{g};H_{g})\) is compactly embedded in \(L^{2}(0,T; H_{g})\) and in \(L^{2}(0, T ; L^{2}(\Omega , g))\), then \(\{u^{(m)}\}_{m}\) strongly converges in \(L^{2}(0,T;H_{g})\) and \(\{\theta ^{(m)}\}_{m}\) in \(L^{2}(0, T ; L^{2}(\Omega , g))\), respectively.
In order to pass to the limit, we consider scalar functions \(\Psi _{1}(t)\) and \(\Psi _{2}(t)\) that are continuously differentiable on \([0, T ]\) and such that \(\Psi _{1}(T)=\Psi _{2}(T)=0\). We multiply (4.3) and (4.4) by \(\Psi _{1}(t)\) and \(\Psi _{2}(t)\), respectively, and then integrate by parts. This leads to the equations
Following the same lines as in [8, 31], we obtain, as \(m \rightarrow \infty \),
These equations hold for v and τ that are finite linear combination of \(u_{k}\) and \(\theta _{k}\), respectively (\(k=1,\dots ,m\)), and by continuity the equations hold for any v in \(V_{g}\) and \(\tau \in H_{g}\). It then follows that \(\{u,\theta \}\) satisfies the two first equations of (3.3). To end the proof, we still need to check that \(\{u,\theta \}\) satisfies the initial conditions \(u(0)=u_{0}\) and \(\theta (0)=\theta _{0}\). To do so, it suffices to multiply the two first equations in (3.3) by \(\Psi _{1}\) and \(\Psi _{2}\), respectively, and then to integrate. By making use of the integration by part and comparing with (4.44) and (4.46), one can find that
which leads to the desired result by taking a particular choice of \(\Psi _{1}\) and \(\Psi _{2}\).
For the uniqueness of the weak solutions, let \((u_{1},\theta _{1})\) and \((u_{2},\theta _{2})\) be two weak solutions with the same initial condition. Let \(w = u_{1}- u_{2}\) and \(\widetilde{w} = \theta _{1} -\theta _{2}\). Then we have
Taking \(v = w(t)\) and \(\tau = \widetilde{ w}(t)\), one obtains
By applying the bounds on the terms \(b_{g}\), \(\widetilde{b}_{g}\), it then follows by the Cauchy–Schwarz inequality and Gronwall-like inequality that \(w(t) = 0\) and \(\widetilde{w}(t) = 0\) for all \(t \geq 0\), since we have \(w(0) = 0\) and \(\widetilde{w} (0) = 0\). Thus the theorem is proved. □
5 Conclusion
In this paper, we have introduced a new variation of Navier–Stokes equations. It consists in time-fractional Bénard equations in fractal thin media. The main technique to prove the existence of solutions to this problem is the Faedo–Galerkin approximation method. The deduced estimates allow us to get a (sub)sequence that converges to a solution. The uniqueness follows immediately from a Gronwall type inequality.
There is still a lot to do with this subject, namely a numerical study should be conducted in future works. Moreover, the analysis of the stochastic version, the attractors and the long-term behaviour should be of great interest.
Availability of data and materials
There is no data needed in our manuscript.
References
Aayadi, K., Akhlil, K., Ben Aadi, S., Mahdioui, H.: Weak solutions to the time-fractional g-Bénard equations. Preprint. arXiv:2011.01545v1
Agrawal, O.P.: Fractional variational calculus in terms of Riesz fractional derivatives. J. Phys. A 40, 6287–6303 (2007)
Alikhanov, A.A.: A priori estimates for solutions of boundary value problems for fractional-order equations. Differ. Equ. 46, 660–666 (2010)
Anh, C.T., Quyet, D.T.: g-Navier–Stokes equations with infinite delays. Vietnam J. Math. 40(1), 57–78 (2012)
Bae, H., Roh, J.: Existence of solutions of the g-Navier–Stokes equations. Taiwan. J. Math. 8(1), 85–102 (2004)
Ben Aadi, S., Akhlil, K., Aayadi, K.: Weak solutions to the time-fractional g-Navier–Stokes equations and optimal control. J. Appl. Anal. 28(1), 135–147 (2022)
Cannon, J.R., DiBenedetto, E.: The initial value problem for the Boussinesq equations with data in Lp. In: Approximation Methods for Navier–Stokes Problems, pp. 129–144. Springer, Berlin (1980)
Galdi, G.P.: Lectures in Mathematical Fluid Dynamics. Birkhäuser, Basel (2000)
Gorenflo, R., Iskenderov, A., Luchko, Y.: Mapping between solutions of fractional diffusion-wave equations. Fract. Calc. Appl. Anal. 3(1), 75–86 (2000)
Gresho, P.M., Lee, R.L., Chan, S.T., Sani, R.L.: Solution of the time-dependent incompressible Navier–Stokes and Boussinesq equations using the Galerkin finite element method. In: Approximation Methods for Navier–Stokes Problems, pp. 203–222. Springer, Berlin (1980)
Hale, J.K., Raugel, G.: Reaction-diffusion equation on thin domains. J. Math. Pures Appl. 71(1), 33–95 (1992)
Hale, J.K., Raugel, G.: A damped hyperbolic equation on thin domains. Trans. Am. Math. Soc. 329(1), 185–219 (1992)
Jiang, J.P., Hou, Y.R., Wang, X.X.: Pullback attractor of 2D nonautonomous g-Navier–Stokes equations with linear dampness. Appl. Math. Mech. 32(2), 151–166 (2011)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. North-Holland Math. Stud., vol. 204. Elsevier, Amsterdam (2006)
Kubica, A., Ryszewska, K., Yamamoto, M.: Time-Fractional Differential Equations: A Theoretical Introduction. Springer, Singapore (2020)
Kumar, S., Kumar, D., Abbasbandy, S., Rashidi, M.M.: Analytical solution of fractional Navier–Stokes equation by using modified Laplace decomposition method. Ain Shams Eng. J. 5(2), 569–574 (2014)
Lions, J.L.: Sur l’existence de solutions des équations de Navier–Stokes. C. R. Acad. Sci. Paris 248, 2847–2849 (1959)
Mainardi, F., Luchko, Y., Pagnini, G.: The fundamental solution of the space-time fractional diffusion equation. Fract. Calc. Appl. Anal. 4, 153–192 (2001)
Morimoto, H.: Non-stationary Boussinesq equations. J. Fac. Sci., Univ. Tokyo, Sect. 1A, Math. 39, 61–75 (1992)
Özlük, M., Kaya, M.: On the weak solutions and determining modes of the g-Bénard problem. Hacet. J. Math. Stat. (2016). https://doi.org/10.15672/HJMS.20174622762
Özlük, M., Kaya, M.: On the strong solutions and the structural stability of the g-Bénard problem. In: Numerical Functional Analysis and Optimization (2017). https://doi.org/10.1080/01630563.2017.1350975
Povstenko, Y.: Fractional Thermoelasticity. Springer, Switzerland (2015)
Rashid, S., Ashraf, R., Bonyah, E.: On analytical solution of time-fractional biological population model by means of generalized integral transform with their uniqueness and convergence analysis. J. Funct. Spaces 2022, Article ID 7021288 (2022)
Rashid, S., Ashraf, R., Jarad, F.: Strong interaction of Jafari decomposition method with nonlinear fractional-order partial differential equations arising in plasma via the singular and nonsingular kernels. AIMS Math. 7(5), 7936–7963 (2022)
Rashid, S., Jarad, F., Ahmad, A.G.: A novel fractal-fractional order model for the understanding of an oscillatory and complex behaviour of human liver with non-singular kernel. Results Phys. 35, 105292 (2022)
Rashid, S., Jarad, F., Ahmad, A.G., Abualnaja, K.M.: New numerical dynamics of the heroin epidemic model using a fractional derivative with Mittag-Leffler kernel and consequences for control mechanisms. Results Phys. 35, 105304 (2022)
Raugel, G., Sell, G.R.: Navier Stokes equations on thin 3D domains I. Global attractors and global regularity of solutions. J. Am. Math. Soc. 6(3), 503–568 (1993)
Roh, J.: g-Navier–Stokes equations. Thesis, University of Minnesota (2001)
Saichev, A.I., Zaslavsky, G.M.: Fractional kinetic equations: solutions and applications. Chaos, Interdiscip. J. Nonlinear Sci. 7(4), 753–764 (1997)
Singh, H., Srivastava, H.M., Nieto, J.J.: Handbook of Fractional Calculus for Engineering and Science. CRC Press, Boca Raton (2022)
Temam, R.: Navier–Stokes Equations, Theory and Numerical Analysis, 3rd edn. Studies in Mathematics and Its Applications, vol. 2. North-Holland, Amsterdam (1984)
Wu, D.: The finite-dimensional uniform attractors for the nonautonomous g-Navier–Stokes equations. J. Appl. Math. 2009, Article ID 150420 (2009)
Zeytounian, R.K.: The Bénard problem for deep convection: rigorous derivation of approximate equations. Int. J. Eng. Sci. 27(11), 1361–1366 (1989)
Zeytounian, R.K.: Joseph Boussinesq and his approximation: a contemporary view. C. R., Méc. 331(8), 575–586 (2003)
Zhou, Y., Peng, L.: On the time-fractional Navier–Stokes equations. Comput. Math. Appl. 73(6), 874–891 (2017)
Acknowledgements
A preprint of this paper has previously been published [1].
We would like to express our gratitude to the editor for taking time to handle the manuscript and to anonymous referees whose constructive comments were very helpful for improving the quality of our paper.
Funding
There is no institutional funding for this paper.
Author information
Authors and Affiliations
Contributions
The authors contributed to the manuscript equally. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Aayadi, K., Akhlil, K., Ben Aadi, S. et al. Weak solutions to the time-fractional g-Bénard equations. Bound Value Probl 2022, 70 (2022). https://doi.org/10.1186/s13661-022-01649-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-022-01649-3