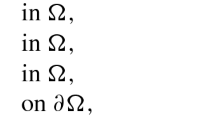1 Introduction

In this article, we are interested in establishing the existence of multiple solutions to the following Kirchhof-type systems in Orlicz–Sobolev spaces

$$ \textstyle\begin{cases} -M_{i} {(}\int _{\Omega }\Phi _{i}( \vert \nabla u_{i} \vert )\,dx {)} {(} \operatorname{div}(\alpha _{i}( \vert \nabla u_{i} \vert )\nabla u_{i}) {)}=\lambda F_{u_{i}}(x,u_{1}, \dots , u_{n}) \quad \text{in } \Omega , \\ u_{i}=0 \quad \text{on } \partial \Omega , \end{cases} $$
(1.1)

for \(1\leq i\leq n\), where Ω is a bounded domain in \(\mathbb{R}^{N}\) (\(N\geq 3\)), with smooth boundary ∂Ω and λ is a positive parameter, \(F:\Omega \times \mathbb{R}^{n}\rightarrow \mathbb{R}\) is a measurable function with respect to \(x\in \Omega \) for every \((t_{1}, \dots , t_{n})\in \mathbb{R}^{n}\) and is \(C^{1}\) with respect to \((t_{1}, t_{2}, \dots , t_{n})\in \mathbb{R}^{n}\) for a.e. \(x\in \Omega \); \(F_{t_{i}}\) denotes the partial derivative of F with respect to \(t_{i}\). Also \(M_{i}: \mathbb{R}\rightarrow \mathbb{R}\) (\(i=1, 2, \dots , n\)), are continuous and increasing functions satisfying the following boundedness condition:

(M):

There exist positive numbers \(m_{i}^{0}\), \(M_{i}^{0}\) such that

$$ m_{i}^{0}\leq M_{i}(t)\leq M_{i}^{0}, \quad \text{for all } t\geq 0\ (i=1, 2, \dots , n). $$

Throughout this article we assume that for \(i=1, \dots , n\), the functions \(\alpha _{i}: (0, +\infty )\rightarrow \mathbb{R}\) are such that the mappings \(\varphi _{i}:\mathbb{R}\rightarrow \mathbb{R}\) defined by

$$ \varphi _{i}(t)= \textstyle\begin{cases} \alpha _{i}( \vert t \vert )t& \text{for } t\neq 0, \\ 0& \text{for } t=0, \end{cases} $$

are odd, strictly increasing homeomorphisms from \(\mathbb{R}\) onto \(\mathbb{R}\). For the functions \(\varphi _{i}\) above, let us define \(\Phi _{i}(t)=\int _{0}^{t}\varphi _{i}(s)\,ds\) for all \(t\in \mathbb{R}\).

Notice that if \(i=1\), then problem (1.1) becomes

$$ \textstyle\begin{cases} -M {(}\int _{\Omega }\Phi ( \vert \nabla u \vert )\,dx {)} {(}\operatorname{div}( \alpha ( \vert \nabla u \vert )\nabla u) {)}=\lambda f(x,u) \quad \text{in } \Omega , \\ u=0 \quad \text{on } \partial \Omega . \end{cases} $$
(1.2)

It should be mentioned that if \(\varphi (t)=p|t|^{p-2}t\) for all \(t\in \mathbb{R}\), \(p>1\) then problem (1.2) becomes the well-known p-Kirchhoff-type equation

$$ \textstyle\begin{cases} -M(\int _{\Omega } \vert \nabla u \vert ^{p}\,dx)\Delta _{p}u=\lambda f(x, u)\quad \text{in } \Omega , \\ u=0\quad \text{on } \partial \Omega . \end{cases} $$
(1.3)

Problem (1.3) is related to the stationary problem

$$ \rho \frac{\partial ^{2}u}{\partial t^{2}}-\biggl(\frac{\rho _{0}}{h}+ \frac{E}{2L} \int ^{L}_{0} \biggl\vert \frac{\partial u}{\partial x} \biggr\vert ^{2}\,dx\biggr) \frac{\partial ^{2}u}{\partial x^{2}}=0, $$

where ρ, \(\rho _{0}\), h, E, L are constants, for \(0< x< L\), \(t \geq 0\), and where \(u=u(x,t)\) is the lateral displacement at the space coordinate x and time t, E the Young modulus, ρ the mass density, h the cross-section area, L the length, and \(\rho _{0}\) the initial axial tension, proposed by Kirchhoff [17] as an extension of the classical D’Alembert’s wave equation for free vibrations of elastic strings. This is an example of a nonlinear problem. One can refer to [3–5, 9, 13, 14, 20–23, 26–28, 30–32] for more relevant problems and techniques.

Now, we recall some basic facts about Orlicz and Orlicz–Sobolev spaces (see [2, 29] and the references therein). Let \(\varphi _{i}\) and \(\Phi _{i}\) be as introduced at the beginning of the paper. Set

$$ \Phi ^{*}_{i}(t)= \int _{0}^{t}\varphi ^{-1}_{i}(s) \,ds, \quad \text{for all } t\in \mathbb{R}. $$

We see that \(\Phi _{i}\), for \(1\leq i\leq n\), are Young functions, that is, \(\Phi _{i}(0)=0\), \(\Phi _{i}\) are convex, and \(\lim_{t\rightarrow \infty }\Phi _{i}(t)=+\infty \).

Also, since \(\Phi _{i}(t)=0\) if and only if \(t=0\),

$$ \lim_{t\rightarrow 0}\frac{\Phi _{i}(t)}{t}=0\quad \text{and}\quad \lim _{t\rightarrow \infty }\frac{\Phi _{i}(t)}{t}=+\infty , $$

then \(\Phi _{i}\) are called N-functions. The functions \(\Phi _{i}^{*}\), for \(1\leq i\leq n\) are called the complementary functions of \(\Phi _{i}\) and they satisfy

$$ \Phi _{i}^{*}(t)=\sup \bigl\{ st-\Phi _{i}(s); s\geq 0\bigr\} , \quad \text{for all } t \geq 0. $$

We observe that \(\Phi _{i}^{*}\) are also N-functions and the following Young’s inequality holds:

$$ st\leq \Phi _{i}(s)+\Phi _{i}^{*}(t),\quad \text{for all } s,t\geq 0. $$

We define the numbers

$$ (p_{i})_{0}:=\inf_{t>0} \frac{t\varphi (t)}{\Phi (t)}, \quad \text{and}\quad (p_{i})^{0}:=\sup _{t>0}\frac{t\varphi (t)}{\Phi (t)}. $$

Throughout this paper, we assume the following condition:

$$ N< (p_{i})_{0}\leq \frac{t\varphi _{i}(t)}{\Phi _{i}(t)} \leq (p_{i})^{0}< \infty , \quad \text{for all } t>0. $$
(1.4)

The Orlicz spaces \(L_{\Phi _{i}}(\Omega )\), for \(1\leq i\leq n\), defined by the N-functions \(\Phi _{i}\) are the spaces of measurable functions \(u:\Omega \rightarrow \mathbb{R}\) such that

$$ \Vert u \Vert _{L_{\Phi _{i}}}:=\sup \biggl\{ \biggl\vert \int _{\Omega } u(x)v(x)\,dx \biggr\vert : \int _{ \Omega } \Phi _{i}^{*}\bigl( \bigl\vert v(x) \bigr\vert \bigr)\,dx\leq 1\biggr\} < \infty . $$

Then \((L_{\Phi _{i}}(\Omega ),\|\cdot \|_{L_{\Phi _{i}}})\) are Banach spaces whose norms are equivalent to the Luxemburg norm

$$ \Vert u \Vert _{\Phi _{i}}:=\inf \biggl\{ k>0; \int _{\Omega }\Phi _{i}\biggl( \frac{u(x)}{k} \biggr)\,dx \leq 1 \biggr\} . $$

For Orlicz spaces, the Hölder’s inequality takes the form

$$ \int _{\Omega }uv \,dx \leq 2 \Vert u \Vert _{L_{\Phi _{i}}} \Vert v \Vert _{L_{\Phi _{i}^{*}}} \quad \text{for all } u\in L_{\Phi _{i}}( \Omega ) \text{ and } v\in L_{ \Phi _{i}^{*}}(\Omega ), 1\leq i\leq n. $$

The Orlicz–Sobolev spaces \(W^{1, \Phi _{i}}(\Omega )\), \(1\leq i\leq n\) are the spaces defined by

$$ W^{1,{\Phi _{i}}}(\Omega )=\biggl\{ u\in L_{\Phi _{i}}(\Omega ), \frac{\partial u}{\partial x_{j}}\in L_{\Phi _{i}}(\Omega ), j=1, \dots , N\biggr\} . $$

These are Banach spaces with respect to the norms:

$$ \Vert u \Vert _{1, \Phi _{i}}:= \Vert u \Vert _{\Phi _{i}}+\bigl\| | \nabla u|\bigr\| _{\Phi _{i}}, \quad 1\leq i\leq n. $$

Now, we introduce the Orlicz–Sobolev spaces \(W^{1,\Phi _{i}}_{0}(\Omega )\), for \(1\leq i\leq n\), as the closure of \(C^{\infty }_{0}(\Omega )\) in \(W^{1,\Phi _{i}}(\Omega )\) which can be renormed by equivalent norms:

$$ \Vert u \Vert _{{i}}:=\bigl\| |\nabla u|\bigr\| _{\Phi _{i}}. $$

The relation (1.4) implies that \(\Phi _{i}\) and \(\Phi _{i}^{*}\), for \(1\leq i\leq n\), both satisfy the \(\Delta _{2}\)-condition [1, 12], i.e.,

$$ \Phi _{i}(2t)\leq k\Phi _{i}(t) \quad \text{for all } t\geq 0, $$

where k is a positive constant. Furthermore, we assume that \(\Phi _{i}\) satisfy in the following conditions:

$$ \text{For each $x\in \bar{\Omega}$, the functions $t\rightarrow \Phi _{i}(x, \sqrt{t})$ are convex for all $t\in [0, \infty )$}. $$
(1.5)

Condition \(\Delta _{2}\) for \(\Phi _{i}\) assures that for each \(i\in \{1, \dots , n\}\) the Orlicz spaces \(L_{\Phi _{i}}(\Omega )\) are separable. Also the \(\Delta _{2}\) condition and (1.5) assure that \(L_{\Phi _{i}}(\Omega )\) are uniformly convex spaces, and thus reflexive Banach spaces (see [25, Proposition 2.2]), implying that Orlicz–Sobolev spaces \(W_{0}^{1,\Phi _{i}}(\Omega )\), \(i\in \{1, \dots , n\}\) are reflexive Banach spaces also [16].

We define the space \(X:=\prod_{i=1}^{n}W^{1,\Phi _{i}}_{0}(\Omega )\) for problem (1.1) which is a reflexive Banach space with respect to the norm

$$ \Vert u \Vert =\sum_{i=1}^{n} \Vert u_{i} \Vert _{i},\quad u=(u_{1}, \dots , u_{n})\in X. $$

Remark 1.1

In [12] we see that the Orlicz–Sobolev spaces \(W_{0}^{1,\Phi _{i}}(\Omega )\), \(i=1, \dots , n\), are continuously embedded in \(W_{0}^{1, (p_{i})_{0}}(\Omega )\). On the other hand, since we assume that \((p_{i})_{0}>N\), we conclude that \(W_{0}^{1, (p_{i})_{0}}(\Omega )\) are compactly embedded in \(C^{0}(\bar{\Omega })\), see [19]. Thus, we have that \(W_{0}^{1,\Phi _{i}}(\Omega )\) are compactly embedded in \(C^{0}(\bar{\Omega })\).

So, \(X\hookrightarrow C^{0}(\bar{\Omega })\times \cdots \times C^{0}( \bar{\Omega })\) is compact. We set a constant \(C>0\) such that

$$ C:=\max \biggl\{ \sup_{u_{i}\in W_{0}^{1,\Phi _{i}}\setminus \{0\}} \frac{\max_{x\in \bar{\Omega }} \vert u_{i}(x) \vert ^{(p_{i})^{0}}}{ \Vert u_{i} \Vert _{i}^{(p_{i})^{0}}} : \text{for } 1\leq i\leq n \biggr\} < +\infty . $$
(1.6)

Proposition 1.1

([24, Lemma 1])

Let \(u\in W_{0}^{1, \Phi _{i}}(\Omega )\), then the following relations hold:

  1. (I)

    \(\|u\|_{i}^{(p_{i})_{0}}\leq \int _{\Omega }\Phi _{i}(|\nabla u(x)|)\,dx \leq \|u\|_{i}^{(p_{i})^{0}}\) if \(\|u\|_{i}>1\), \(i=1, \dots , n\),

  2. (II)

    \(\|u\|_{i}^{(p_{i})^{0}}\leq \int _{\Omega }\Phi _{i}(|\nabla u(x)|)\,dx \leq \|u\|_{i}^{(p_{i})_{0}}\) if \(\|u\|_{i}<1\), \(i=1, \dots , n\).

Proposition 1.2

([21, Lemma 2.1])

Let \(u\in W_{0}^{1,\Phi _{i}}(\Omega ) \) and

$$ \int _{\Omega }\Phi _{i}\bigl( \bigl\vert \nabla u(x) \bigr\vert \bigr)\,dx \leq r $$

for some \(0< r<1\). Then one has \(\|u\|_{i}<1\).

Proposition 1.3

([7, Remark 2.1])

Let \(u\in W_{0}^{1,\Phi _{i}}(\Omega ) \) be such that \(\|u\|_{i}=1\). Then

$$ \int _{\Omega }\Phi _{i}\bigl( \bigl\vert \nabla u(x) \bigr\vert \bigr)\,dx=1. $$

Our aim is to prove the existence and multiplicity solutions for problem (1.1); so we study problem (1.1) by using the results as follows.

First, we recall the following three critical points theorem, obtained by G. Bonanno and S.A. Marano in [8].

Theorem 1.1

Let X be a reflexive real Banach space, \(J:X\rightarrow \mathbb{R}\) be a sequentially weakly lower semicontinuous and continuously Gâteaux differentiable functional that is bounded on bounded subsets of X and whose Gâteaux derivative admits a continuous inverse on \(X^{*}\), and let \(I:X\rightarrow \mathbb{R}\) be a continuously Gâteaux differentiable functional whose Gâteaux derivative is compact and satisfies \(J(0)=I(0)=0\). Assume that there exist \(r>0\) and \(\bar{v}\in X\), with \(r< J(\bar{v})\) such that:

  1. (a1)

    \(\frac{\sup_{J^{-1}(-\infty , r]}I(u)}{r}< \frac{I(\bar{v})}{J(\bar{v})}\);

  2. (a2)

    for each \(\lambda \in \Lambda _{r}:=\,]\frac{J(\bar{v})}{I(\bar{v})}, \frac{r}{\sup_{J^{-1}(-\infty , r]}I(u)}[\) the functional \(J-\lambda I\) is coercive.

Then, for each compact interval \([\alpha , \beta ]\subseteq \Lambda _{r}\), there exists \(\rho >0\) with the following property: for every \(\lambda \in [\alpha , \beta ]\), the equation

$$ J^{\prime }(u)-\lambda I^{\prime }(u)=0 $$

has at least three solutions in X whose norms are less than ρ.

Here, we recall a multiple critical points theorem of Bonanno et al. [6].

Theorem 1.2

Let X be a reflexive real Banach space, let \(J, I:X \rightarrow \mathbb{R}\) be two Gâteaux differentiable functionals such that J is strongly continuous, sequentially weakly lower semicontinuous and coercive, and I is sequentially weakly upper semicontinuous. For every \(r>\inf_{X} J\), let

$$\begin{aligned}& {\varphi }(r):=\inf_{u \in J^{-1}(-\infty ,r)} \frac{\sup_{v \in J^{-1}(-\infty ,r)} I(v)- I(u)}{r-J(u)}, \\& \gamma :=\liminf_{r\rightarrow +\infty }{\varphi }(r),\qquad \delta := \liminf _{r \rightarrow (\inf _{X} J)^{+}} {\varphi }(r). \end{aligned}$$

Then the following properties hold:

  1. (a)

    If \(\gamma <+\infty \), then for each \(\lambda \in\, ]0, \frac{1}{\gamma }[\), either

    1. (a1)

      \(h_{\lambda }:=J-\lambda I\) possesses a global minimum, or

    2. (a2)

      there is a sequence \(\{u_{n}\}\) of critical points (local minima) of \(h_{\lambda }\) such that

      $$ \lim_{n \rightarrow +\infty }J(u_{n})=+\infty ; $$
  2. (b)

    If \(\delta <+\infty \), then for each \(\lambda \in\, ]0, \frac{1}{\delta }[\), either

    1. (b1)

      there is a global minimum of J that is a local minimum of \(h_{\lambda }\), or

    2. (b2)

      there is a sequence \(\{u_{n}\}\) of pairwise distinct critical points (local minima) of \(h_{\lambda }\) that weakly converges to a global minimum of J with

      $$ \lim_{n \rightarrow +\infty }J(u_{n})=\inf_{u\in X }J(u). $$

2 Main results

Definition 2.1

We say that \(u=(u_{1}, u_{2}, \dots , u_{n})\) is a weak solution to the system (1.1) if \(u=(u_{1}, u_{2}, \dots , u_{n})\in X\) and

$$ \begin{aligned} &\sum_{i=1}^{n}M_{i} {\biggl(} \int _{\Omega }\Phi _{i}\bigl( \bigl\vert \nabla u_{i}(x) \bigr\vert \bigr)\,dx {\biggr)} \int _{\Omega }\alpha _{i}\bigl( \bigl\vert \nabla u_{i}(x) \bigr\vert \bigr) \nabla u_{i}(x)\nabla v_{i}(x) \,dx \\ &\quad {}-\lambda \int _{\Omega }\sum_{i=1}^{n}F_{u_{i}} \bigl(x, u_{1}(x), \dots , u_{n}(x)\bigr) v_{i}(x) \,dx=0, \end{aligned} $$

for every \(v=(v_{1}, v_{2}, \dots , v_{n}) \in X\).

Set \(\overline{p}:=\max \{(p_{i})^{0} : i=1, \dots , n\}\), \(m_{0}:=\min \{m_{i}^{0} : i=1, \dots , n\}\) and \(m_{1}:=\max \{M_{i}^{0} : i=1, \dots , n\}\). For all \(\sigma >0\), we define the set

$$ Q(\sigma ):=\Biggl\{ (t_{1}, \dots , t_{n})\in \mathbb{R}^{n}: \sum_{i=1}^{n} \vert t_{i} \vert \leq \sigma \Biggr\} . $$

We need the following proposition in the proof of the main results.

Proposition 2.1

Let \(T:X \rightarrow X^{*}\) be the operator defined by

$$ \begin{aligned} T(u_{1}, \dots , u_{n}) (v_{1}, \dots , v_{n})={}&\sum _{i=1}^{n}M_{i} {\biggl(} \int _{\Omega }\Phi _{i}\bigl( \bigl\vert \nabla u_{i}(x) \bigr\vert \bigr)\,dx {\biggr)} \\ &{}\times \int _{\Omega }\alpha _{i}\bigl( \bigl\vert \nabla u_{i}(x) \bigr\vert \bigr)\nabla u_{i}(x) \nabla v_{i}(x) \,dx, \end{aligned} $$

for every \(u=(u_{1}, \dots , u_{n})\), \(v=(v_{1}, \dots , v_{n})\in X\). Then T admits a continuous inverse on \(X^{*}\), where \(X^{*}\) denotes the dual of X.

Proof

By applying the Minty–Browder theorem [33, Theorem 26.A(d)], it is sufficient to verify that T is coercive, hemicontinuous, and uniformly monotone. Since

$$ (p_{i})_{0}\leq \frac{t\varphi _{i}(t)}{\Phi _{i}(t)}, \quad \text{for all } t>0, $$

by Proposition 1.1, for each \(u\in X\) with \(\|u_{i}\|_{i}>1\), we have

$$ \begin{aligned} &T(u_{1}, \dots , u_{n}) (u_{1}, \dots , u_{n}) \\ &\quad =\sum_{i=1}^{n}M_{i} { \biggl(} \int _{\Omega }\Phi _{i}\bigl( \bigl\vert \nabla u_{i}(x) \bigr\vert \bigr)\,dx {\biggr)} \int _{\Omega }\alpha _{i}\bigl( \bigl\vert \nabla u_{i}(x) \bigr\vert \bigr) \bigl\vert \nabla u_{i}(x) \bigr\vert ^{2} \,dx \\ &\quad \geq \sum_{i=1}^{n}M_{i} {\biggl(} \int _{\Omega }\Phi _{i}\bigl( \bigl\vert \nabla u_{i}(x) \bigr\vert \bigr)\,dx {\biggr)} \int _{\Omega }\Phi _{i}\bigl( \bigl\vert \nabla u_{i}(x) \bigr\vert \bigr) \,dx \\ &\quad \geq m_{0}\sum_{i=1}^{n} \Vert u_{i} \Vert _{i}^{2(p_{i})_{0}}, \end{aligned} $$

so if \((p_{i})_{0}>N\) then T is coercive. The fact that T is hemicontinuous can be verified using standard arguments. Similar to proof given in [18, Lemma 3.2], T is strictly monotone. Therefore, in view of Minty–Browder theorem, there exists \(T^{-1}:X^{*}\rightarrow X\), and, by a similar method as that given in [10], one has that \(T^{-1}\) is continuous. □

Now, we define the energy functional of problem (1.1) by \(h_{\lambda }:X\rightarrow \mathbb{R}\):

$$ h_{\lambda }(u)=J(u)-\lambda I(u), $$

for all \(u=(u_{1}, \dots , u_{n})\in X\), where

$$\begin{aligned}& J(u)=\sum_{i=1}^{n} \hat{M_{i}}\biggl( \int _{\Omega }\Phi _{i}\bigl( \bigl\vert \nabla u_{i}(x) \bigr\vert \bigr)\,dx\biggr), \qquad \hat{M_{i}}(t)= \int _{0}^{t}{M_{i}}(s) \,ds, \quad i=1, 2, \dots , n, \\& I(u)= \int _{\Omega }F\bigl(x, u_{1}(x), \dots , u_{n}(x)\bigr) \,dx. \end{aligned}$$

Note that the weak solutions of (1.1) are exactly the critical points of \(h_{\lambda }\). Similar arguments as in [25, Lemma 4.2] imply that J and I are continuously Gâteaux differentiable functionals and whose Gâteaux differentials at the point \(u=(u_{1}, \dots , u_{n})\in X\) are the functionals \(J^{\prime }(u)\) and \(I^{\prime }(u)\) given by

$$\begin{aligned}& J^{\prime }(u) (v)=\sum_{i=1}^{n}M_{i} {\biggl(} \int _{\Omega }\Phi _{i}\bigl( \bigl\vert \nabla u_{i}(x) \bigr\vert \bigr)\,dx {\biggr)} \int _{\Omega }\alpha _{i}\bigl( \bigl\vert \nabla u_{i}(x) \bigr\vert \bigr) \nabla u_{i}(x)\nabla v_{i}(x) \,dx, \\& I^{\prime }(u) (v)= \int _{\Omega }\sum_{i=1}^{n}F_{u_{i}} \bigl(x, u_{1}(x), \dots , u_{n}\bigr) v_{i}(x) \,dx. \end{aligned}$$

Moreover, \(I^{\prime }: X\rightarrow X^{*}\) is a compact derivative. For this purpose, it is enough to show that \(I^{\prime }\) is strongly continuous on X, so for a fixed \((u_{1}, u_{2}, \dots , u_{n})\in X\), let \((u_{1k}, u_{2k}, \dots , u_{nk})\rightharpoonup (u_{1}, u_{2}, \dots , u_{n})\) weakly in X as \(k\rightarrow +\infty \). Since X is compactly embedded in \(C^{0}(\bar{\Omega })\times \cdots \times C^{0}(\bar{\Omega })\), we have that \((u_{1k}, u_{2k}, \dots , u_{nk})\) converges uniformly to \((u_{1}, u_{2}, \dots , u_{n})\) on Ω as \(k\rightarrow +\infty \). Since \(F(x, \cdot , \dots , \cdot )\) is \(C^{1}\) in \(\mathbb{R}^{n}\) for every \(x\in \Omega \), and the partial derivatives of F are continuous in \(\mathbb{R}^{n}\) for every \(x\in \Omega \), \(F_{u_{i}}(x, u_{1k}, \dots , u_{nk})\rightarrow F_{u_{i}}(x, u_{1}, \dots , u_{n})\) strongly as \(k\rightarrow +\infty \), thus \(I^{\prime }(u_{1k}, \dots , u_{nk})\rightarrow I^{\prime }(u_{1}, \dots , u_{n})\) strongly as \(k\rightarrow +\infty \). So \(I^{\prime }\) is strongly continuous on X, which implies that \(I^{\prime }\) is a compact operator [33].

Lemma 2.1

J is coercive and sequentially weakly lower semicontinuous.

Proof

For all \(t\geq 0\), we have

$$ J(u)\geq \sum_{i=1}^{n}m^{0}_{i} \biggl( \int _{\Omega }\Phi _{i}\bigl( \bigl\vert \nabla u_{i}(x) \bigr\vert \bigr)\,dx\biggr), \quad i=1, 2, \dots , n, $$

and, by Proposition 1.1, for all \(u\in X\) with \(\|u_{i}\|_{i}>1\), we have

$$ J(u)\geq \sum_{i=1}^{n}m_{0} \Vert u_{i} \Vert _{i}^{(p_{i})_{0}}, $$

from which it follows that J is coercive. Moreover, since \(\Phi _{i}\) for \(1\leq i\leq n\) are convex, J is a convex functional, and thus it is sequentially weakly lower semicontinuous. □

Three weak solutions

Theorem 2.1

Assume that condition (M) holds and

  1. (h1)

    \(F(x, 0, \dots , 0)=0\), for a.e. \(x\in \Omega \).

  2. (h2)

    There exist \(\alpha (x)\in L^{1}(\Omega )\) and n positive constants \(\beta _{i}\), with \(\beta _{i}<(p_{i})_{0}\) for \(1\leq i\leq n\), such that

    $$ 0\leq F(x, t_{1}, \dots , t_{n})\leq \alpha (x) { \Biggl(}1+\sum_{i=1}^{n} \vert t_{i} \vert ^{ \beta _{i}} {\Biggr)}, $$

    for a.e. \(x\in \Omega \), \((t_{1}, \dots , t_{n})\in \mathbb{R}^{n}\).

  3. (h3)

    There exist \(x_{0}\in \Omega \), \(D>0\), \(\delta >0\), \(0< b_{i}<(\frac{C}{m_{0}})^{\frac{1}{(p_{i})^{0}}}\), and

    $$ m_{0}\frac{\pi ^{\frac{N}{2}}}{\Gamma (1+\frac{N}{2})}\biggl(\frac{D}{2} \biggr)^{N}\bigl(2^{N}-1\bigr) \sum _{i=1}^{n}\Phi _{i}\biggl( \frac{2\delta }{D}\biggr)>1 $$

    such that

    $$ \begin{aligned} \int _{\Omega }\sup_{|t_{1}|< b_{1}, \dots , |t_{n}|< b_{n}} F(x, t_{1}, \dots , t_{n})\,dx< {}&\frac{\min \{\frac{m_{0}}{C}(b_{i})^{(p_{i})^{0}}: 1\leq i\leq n\}}{m_{1}\frac{\pi ^{\frac{N}{2}}}{\Gamma (1+\frac{N}{2})}(\frac{D}{2})^{N}(2^{N}-1)\sum_{i=1}^{n}\Phi _{i}(\frac{2\delta }{D})} \\ &{}\times \int _{B(x_{0}, \frac{D}{2})} F(x, \delta , \dots , \delta ) \,dx. \end{aligned} $$

    Furthermore, set

    $$ \begin{aligned} &\underline{\lambda }:= \frac{m_{1}\frac{\pi ^{\frac{N}{2}}}{\Gamma (1+\frac{N}{2})}(\frac{D}{2})^{N}(2^{N}-1)\sum_{i=1}^{n}\Phi _{i}(\frac{2\delta }{D})}{\int _{B(x_{0}, \frac{D}{2})} F(x, \delta , \dots , \delta ) \,dx}, \\ &\overline{\lambda }:= \frac{\min \{\frac{m_{0}}{C}(b_{i})^{(p_{i})^{0}}: 1\leq i\leq n\}}{\int _{\Omega }\sup_{|t_{1}|< b_{1}, \dots , |t_{n}|< b_{n}} F(x, t_{1}, \dots , t_{n})\,dx}, \end{aligned} $$

then, for each \(\lambda \in \Lambda :=(\underline{\lambda }, \overline{\lambda })\), problem (1.1) possesses at least three distinct weak solutions in X.

Proof

Our aim is to apply Theorem 1.1 to our problem, so we check that the functionals J, I satisfy the conditions of Theorem 1.1. We set \(u_{0}=(0, \dots , 0)\). Then by the definitions of I, J and from (h1), we have \(J(u_{0})=I(u_{0})=0\). Let \(x_{0}\in \Omega \), \(D>0\), and take

$$ w(x)= \textstyle\begin{cases} 0 &x\in \Omega \setminus B(x_{0}, D), \\ \delta , &x\in B(x_{0}, \frac{D}{2}), \\ \frac{2\delta }{D}(D- \vert x-x_{0} \vert ) &x\in B(x_{0}, D)\setminus B(x_{0}, \frac{D}{2}). \end{cases} $$

Let \(\bar{u}=(w(x), \dots , w(x))\) and \(r=\min \{\frac{m_{0}}{C}(b_{i})^{(p_{i})^{0}}: 1\leq i\leq n\}\). Clearly, \(\bar{u}\in X\) and from (h3) we have

$$ \begin{aligned} J(\bar{u})&=\sum_{i=1}^{n} \hat{M_{i}}\biggl( \int _{\Omega } \Phi _{i}\bigl( \bigl\vert \nabla w(x) \bigr\vert \bigr)\,dx\biggr) \\ &\geq \sum_{i=1}^{n} m_{i}^{0} \int _{\Omega }\Phi _{i}\bigl( \bigl\vert \nabla w(x) \bigr\vert \bigr)\,dx \\ &\geq \sum_{i=1}^{n}m_{0} \Phi _{i}\biggl(\frac{2\delta }{D}\biggr) \frac{\pi ^{\frac{N}{2}}}{\Gamma (1+\frac{N}{2})} \biggl(\frac{D}{2}\biggr)^{N}\bigl(2^{N}-1\bigr) \\ & > r. \end{aligned} $$

On the other way, when \(J(u)\leq r\) for \(u=(u_{1}, \dots , u_{n})\in X\),

$$ \sum_{i=1}^{n}\hat{M_{i}} {\biggl(} \int _{\Omega }\Phi \bigl( \bigl\vert \nabla u_{i}(x) \bigr\vert \bigr)\,dx {\biggr)}\leq r. $$

Hence, since \(0< b_{i}<(\frac{C}{m_{0}})^{\frac{1}{(p_{i})^{0}}}\), using Propositions 1.1 and 1.2, we have

$$ m_{0} \Vert u_{i} \Vert ^{(p_{i})^{0}}_{i}< r, $$

and from (1.6) we obtain

$$ \bigl\vert u_{i}(x) \bigr\vert < \biggl(\frac{Cr}{m_{0}} \biggr)^{\frac{1}{(p_{i})^{0}}}=b_{i}, \quad \text{for } 1\leq i\leq n. $$

Therefore, for every \(u=(u_{1}, \dots , u_{n})\in X\),

$$ \begin{aligned} \sup_{u\in J^{-1}(-\infty , r)}I(u)&=\sup _{u\in J^{-1}(- \infty , r)} \int _{\Omega } F\bigl(x, u_{1}(x), \dots , u_{n}(x)\bigr) \,dx \\ &\leq \int _{\Omega }\sup_{|t_{1}|\leq b_{1}, \dots , |t_{n}|\leq b_{n}} F(x, t_{1}, \dots , t_{n}) \,dx. \end{aligned} $$

On the other hand, we have

$$ \begin{aligned} J(\bar{u})&=\sum_{i=1}^{n} \hat{M_{i}}\biggl( \int _{\Omega } \Phi _{i}\bigl( \bigl\vert \nabla w(x) \bigr\vert \bigr)\,dx\biggr) \\ &\leq m_{1}\frac{\pi ^{\frac{N}{2}}}{\Gamma (1+\frac{N}{2})}\biggl( \frac{D}{2} \biggr)^{N}\bigl(2^{N}-1\bigr)\sum _{i=1}^{n}\Phi _{i}\biggl( \frac{2\delta }{D}\biggr) \end{aligned} $$

and

$$ I(\bar{u})> \int _{B(x_{0}, \frac{D}{2})} F(x, \delta , \dots , \delta ) \,dx. $$

So, from (h3), we have

$$ \frac{\sup_{u\in J^{-1}(-\infty , r)}I(u)}{r}\leq \frac{\int _{\Omega }\sup_{|t_{1}|\leq b_{1}, \dots , |t_{n}|\leq b_{n}} F(x, t_{1}, \dots , t_{n}) \,dx}{\min \{\frac{m_{0}}{C}(b_{i})^{(p_{i})^{0}} :1\leq i\leq n\}}< \frac{I(\bar{u})}{J(\bar{u})}. $$

Hence, we observe that the condition (a1) of Theorem 1.1 is satisfied.

From (h2), it follows that the function \(J-\lambda I\) is coercive for every positive parameter λ, in particular for every

$$ \lambda \in \Lambda \subseteq \biggl(\frac{J(\bar{u})}{I(\bar{u})}, \frac{r}{\sup_{J(u)\leq r} I(u)}\biggr), $$

so the condition (a2) of Theorem 1.1 holds. Then all the assumptions of Theorem 1.1 are fulfilled. By Theorem 1.1, we know that there exist an open interval \(\Lambda \subseteq [0, \infty )\) and a positive constant ρ such that, for any \(\lambda \in \Lambda \), problem (1.1) has at least three weak solutions whose norms are less than ρ. □

Theorem 2.2

Assume that conditions (M) and (h1) hold and consider the following:

  1. (h4)

    \(F(x, t_{1}, \dots , t_{n})\geq 0\) for every \((x, t_{1}, \dots , t_{n})\in \Omega \times \mathbb{R}_{+}^{n}\).

  2. (h5)

    There exist \(x_{0}\in \Omega \) and values \(D, \varrho >0\) such that \(\overline{B(x_{0}, D)}\subseteq \Omega \),

    $$ \lim_{t\rightarrow 0^{+}}\frac{\Phi _{i}(t)}{t^{(p_{i})^{0}}}< \varrho , $$
    (2.1)

    and for

    $$ \begin{aligned} &A:=\liminf_{\sigma \rightarrow 0^{+}} \frac{\int _{\Omega }\sup_{(t_{1}, \dots , t_{n})\in Q(\sigma )}F(x, t_{1}, \dots , t_{n}) \,dx}{\sigma ^{\overline{p}}}, \\ &B:=\limsup_{(t_{1}, \dots , t_{n})\rightarrow (0^{+}, \dots , 0^{+})} \frac{\int _{B(x_{0}, \frac{D}{2})}F(x, t_{1}, \dots , t_{n}) \,dx}{\sum_{i=1}^{n}{t_{i}}^{(p_{i})^{0}}}, \end{aligned} $$

    one has

    $$ A < L B, $$

    where \(L=\min \{L_{(p_{i})^{0}}, i=1, 2, \dots , n\}\),

    $$ L_{(p_{i})^{0}}= \frac{\Gamma (1+\frac{N}{2})}{ {(}\sum_{i=1}^{n}(\frac{C}{m_{0}})^{\frac{1}{(p_{i})^{0}}} {)}^{\overline{p}}m_{1}\varrho \pi ^{\frac{N}{2}}(\frac{2}{D})^{(p_{i})^{0}-N}(2^{N}-1)}. $$
    (2.2)

Then for every

$$ \lambda \in \Lambda := \frac{1}{ {(}\sum_{i=1}^{n}(\frac{C}{m_{0}})^{\frac{1}{(p_{i})^{0}}} {)}^{\overline{p}}}\biggl( \frac{1}{LB}, \frac{1}{A}\biggr), $$

problem (1.1) admits a sequence of pairwise distinct weak solutions which strongly converges to zero in X.

Proof

We apply the part (b) of Theorem 1.2 and show that \(\delta <\infty \). Let \(\{\sigma _{k}\}\) be a sequence of positive numbers such that \(\lim_{k\rightarrow +\infty }\sigma _{k}=0\) then

$$ \begin{aligned} &\lim_{k\rightarrow +\infty } \frac{\int _{\Omega }\sup_{(t_{1}, \dots , t_{n})\in Q(\sigma _{k})} F(x, t_{1}, \dots , t_{n}) \,dx}{\sigma _{k}^{\overline{p}}} \\ &\quad =\liminf_{\sigma \rightarrow 0^{+}} \frac{\int _{\Omega }\sup_{(t_{1}, \dots , t_{n})\in Q(\sigma )} F(x, t_{1}, \dots , t_{n}) \,dx}{\sigma ^{\overline{p}}} \\ &\quad =A< +\infty . \end{aligned} $$
(2.3)

Putting

$$\begin{aligned}& r_{k}= \frac{\sigma _{k}^{\overline{p}}}{ {(}\sum_{i=1}^{n}(\frac{C}{m_{0}}) ^{\frac{1}{(p_{i})^{0}}} {)}^{\overline{p}}}\quad \text{for all } k\in \mathbb{N}, \\& \begin{aligned} J^{-1}\bigl(]-\infty , r_{k}[ \bigr)&:=\bigl\{ u=(u_{1}, u_{2}, \dots , u_{n}) \in X : J(u)< r_{k}\bigr\} \\ &\subseteq \Biggl\{ u\in X: \sum_{i=1}^{n} \hat{M_{i}}\biggl( \int _{\Omega }\Phi _{i}\bigl( \vert \nabla u_{i} \vert \bigr)\,dx\biggr)\leq {r_{k}}\Biggr\} , \end{aligned} \end{aligned}$$

by Propositions 1.1 and 1.2, for k large enough (\(0< r_{k}<1\)),

$$ m_{0} \Vert u_{i} \Vert _{i}^{(p_{i})^{0}}< r_{k}, $$

and from (1.6) we have \(\max_{x\in \bar{\Omega }}|u_{i}(x)|^{(p_{i})^{0}}\leq C\|u_{i}\|_{i}^{(p_{i})^{0}}\). Then we obtain for all \(x\in \Omega \),

$$ \bigl\vert u_{i}(x) \bigr\vert \leq \biggl( \frac{Cr_{k}}{m_{0}}\biggr)^{\frac{1}{(p_{i})^{0}}}. $$

Thus

$$ \sum_{i=1}^{n} \bigl\vert u_{i}(x) \bigr\vert \leq \sum_{i=1}^{n} \biggl(\frac{Cr_{k}}{m_{0}}\biggr)^{ \frac{1}{(p_{i})^{0}}}\leq r_{k}^{\frac{1}{\overline{p}}} \sum_{i=1}^{n}\biggl( \frac{C}{m_{0}}\biggr)^{\frac{1}{(p_{i})^{0}}}\leq \sigma _{k}. $$

Then we have

$$ J^{-1}(-\infty , r_{k})\subseteq \Biggl\{ u\in X: \sum _{i=1}^{n} \bigl\vert u_{i}(x) \bigr\vert \leq \sigma _{k}\Biggr\} . $$

From condition (h1), we have \(\min_{X}J=J(0, \dots , 0)=I(0, \dots , 0)=0\).

$$ \begin{aligned} \varphi (r_{k})&=\inf _{u\in J^{-1}(]-\infty , r_{k}[)} \frac{\sup_{v\in J^{-1}(]-\infty , r_{k}[)}I(v)- I(u) }{r_{k}- J(u)} \\ &\leq \frac{\sup_{v\in J^{-1}(]-\infty , r_{k}[)}I(v)}{r_{k}} \\ &\leq {\Biggl(}\sum_{i=1}^{n}\biggl( \frac{C}{m_{0}}\biggr)^{\frac{1}{(p_{i})^{0}}} {\Biggr)}^{\overline{p}} \frac{\int _{\Omega }\sup_{(t_{1}, t_{2}, \dots , t_{n})\in Q(\sigma _{k})}F(x, t_{1}, \dots , t_{n}) \,dx}{\sigma _{k}^{\overline{p}}}. \end{aligned} $$
(2.4)

Let \(\delta :=\liminf_{r\rightarrow 0^{+}}\varphi (r)\). It follows from (2.3) and (2.4) that

$$ \begin{aligned} \delta &\leq \liminf_{k\rightarrow +\infty } \varphi (r_{k}) \\ &\leq {\Biggl(}\sum_{i=1}^{n}\biggl( \frac{C}{m_{0}}\biggr)^{\frac{1}{(p_{i})^{0}}} {\Biggr)}^{\overline{p}}\lim _{k\rightarrow +\infty } \frac{\int _{\Omega }\sup_{ (t_{1}, t_{2}, \dots , t_{n})\in Q(\sigma _{k})}F(x, t_{1}, \dots , t_{n}) \,dx}{\sigma _{k}^{\overline{p}}} \\ &\leq {\Biggl(}\sum_{i=1}^{n}\biggl( \frac{C}{m_{0}}\biggr)^{\frac{1}{(p_{i})^{0}}} {\Biggr)}^{\overline{p}}A< +\infty . \end{aligned} $$

So \(\Lambda \subseteq\, ]0, \frac{1}{\delta }[\). For a fixed \(\lambda \in \Lambda \), we claim that the functional \(h_{\lambda }\) is unbounded from below. Indeed, since

$$ \frac{1}{\lambda }< {\Biggl(}\sum_{i=1}^{n} \biggl(\frac{C}{m_{0}}\biggr)^{ \frac{1}{(p_{i})^{0}}} {\Biggr)}^{\overline{p}}L B, $$

we can consider n positive real sequences \(\{d_{i, k}\}_{i=1}^{n}\) and \(\eta >0\) such that \(\sqrt{\sum_{i=1}^{n}d_{i, k}^{2}}\rightarrow 0\) as \(k\rightarrow +\infty \) and

$$ \frac{1}{\lambda }< \eta < L {\Biggl(}\sum _{i=1}^{n}\biggl(\frac{C}{m_{0}} \biggr)^{ \frac{1}{(p_{i})^{0}}} {\Biggr)}^{\overline{p}} \frac{\int _{B(x_{0}, \frac{D}{2})}F(x, d_{1, k}, \dots , d_{n, k}) \,dx}{\sum_{i=1}^{n}d_{i, k}^{(p_{i})^{0}}}. $$
(2.5)

Let \(\{u_{k}(x)=(u_{1k}, u_{2k}, \dots , u_{nk})\}\subseteq X\) be a sequence defined by

$$ u_{ik}(x)= \textstyle\begin{cases} 0,& x\in \bar{\Omega }\setminus B(x_{0}, D), \\ \frac{2d_{i, k}}{D} {(}D- \vert x-x_{0} \vert {)},& x\in B(x_{0}, D) \setminus B(x_{0}, \frac{D}{2}), \\ d_{i,k},& x\in B(x_{0}, \frac{D}{2}), \end{cases} $$

for \(1\leq i\leq n\). Then

$$ \begin{aligned} J(u_{k})&=\sum _{i=1}^{n}\hat{M_{i}}\biggl( \int _{\Omega }\Phi _{i}\bigl( \vert \nabla u_{ik} \vert \bigr)\,dx\biggr) \\ &< m_{1} \int _{B(x_{0}, D)\setminus B(x_{0}, \frac{D}{2})}\Phi _{i}\biggl( \frac{2d_{i, k}}{D} \biggr)\,dx. \end{aligned} $$

Moreover, from (2.1) and since \(\lim_{k\rightarrow \infty } \frac{2d_{i, k}}{D}=0\), there exist \(\zeta >0\) and \(n_{i}\in \mathbb{N}\) \(i=1, \dots , n\) such that \(\frac{2d_{i, k}}{D}\in (0, \zeta )\), and

$$\begin{aligned}& \Phi _{i}\biggl(\frac{2d_{i, k}}{D} \biggr)< \varrho \biggl(\frac{2}{D}\biggr) ^{(p_{i})^{0}} d_{i, k}^{(p_{i})^{0}} \quad \text{for all } n\geq n_{i}\ (i=1, \dots , n), \\& \int _{B(x_{0}, D)\setminus B(x_{0}, \frac{D}{2})}\Phi _{i}\biggl( \frac{2d_{i, k}}{D} \biggr)\,dx< \frac{\pi ^{\frac{N}{2}}}{\Gamma (1+{\frac{N}{2}})}\varrho \biggl( \frac{2}{D}\biggr) ^{(p_{i})^{0}-N} d_{i, k}^{(p_{i})^{0}}\bigl(2^{N}-1 \bigr). \end{aligned}$$

From (2.2), for all \(n\geq \max \{n_{1}, \dots , n_{2}\}\), we have

$$ \begin{aligned} J(u_{k})\leq \frac{1}{ {(}\sum_{i=1}^{n}(\frac{C}{m_{0}})^{\frac{1}{(p_{i})^{0}}} {)}^{\overline{p}}} \sum_{i=1}^{n} \frac{d_{i, k}^{(p_{i})^{0}}}{L_{{(p_{i})^{0}}}}. \end{aligned} $$
(2.6)

By (h4), we have

$$ I(u_{k})= \int _{\Omega } F(x, u_{1k}, \dots , u_{nk}) \,dx\geq \int _{B(x_{0}, \frac{D}{2})} F(x, d_{1, k}, \dots , d_{n, k}) \,dx. $$
(2.7)

By (2.5), (2.6), and (2.7), we have

$$\begin{aligned} h_{\lambda }(u_{k})&=J(u_{k})- \lambda I(u_{k}) \\ &\leq \frac{1}{ {(}\sum_{i=1}^{n}(\frac{C}{m_{0}})^{\frac{1}{(p_{i})^{0}}} {)}^{\overline{p}}} \sum_{i=1}^{n} \frac{d_{i, k}^{(p_{i})^{0}}}{L_{{(p_{i})^{0}}}}- \lambda \int _{B(x_{0}, \frac{D}{2})} F(x, d_{1, k}, \dots , d_{i, k}) \,dx \\ &< \frac{1-\lambda \eta }{L {(}\sum_{i=1}^{n}(\frac{C}{m_{0}})^{\frac{1}{(p_{i})^{0}}} {)}^{\overline{p}}} \sum_{i=1}^{n}{d_{i, k}^{(p_{i})^{0}}} \\ &< 0=h_{\lambda }(0, \dots , 0), \end{aligned}$$

for every \(n\in \mathbb{N}\) large enough. Then \((0, \dots , 0)\) is not a local minimum of \(h_{\lambda }\). Thus, owing to the fact that \((0, \dots , 0)\) is the unique global minimum of J, there exists a sequence \(\{u_{k}=(u_{1k}, \dots , u_{nk})\}\) of pairwise distinct critical points of \(h_{\lambda }\) such that \(\lim_{k\rightarrow +\infty }\|u_{k}\|=0\), and this completes the proof. □

We illustrate this abstract existence result with the following example.

Example 2.1

Let \(\Omega \subset \mathbb{R}^{3}\) be a bounded domain with \(|\Omega |=1\) and assume \(i=2\). Similar to [15, Remark 3.6], we have

$$ \varphi _{1}(t)= \textstyle\begin{cases} \frac{ \vert t \vert ^{4}t}{\log (1+ \vert t \vert )}&\text{if } t\neq 0, \\ 0&\text{if } t=0. \end{cases} $$

By [11, Example 3], one has \((p_{1})_{0}=5<(p_{1})^{0}=6\). Thus the condition (1.4) is satisfied. Moreover, owing to

$$ \lim_{t\rightarrow 0^{+}}\frac{1}{t^{5}} \int _{0}^{t} \frac{ \vert s \vert ^{4}s}{\log (1+|s|)}\,ds= \frac{1}{ 5}, $$

the condition (2.1) is also fulfilled (for example, take \(\varrho =\frac{1}{N}=\frac{1}{3}\)). Now let

$$ \varphi _{2}(t)=\log \bigl(1+ \vert t \vert ^{2} \bigr) \vert t \vert ^{2}t, \quad t\in \mathbb{R}. $$

Then by [11, Example 2], one has \((p_{2})_{0}=4<(p_{2})^{0}=6\). So the condition (1.4) is satisfied. Moreover, owing to

$$ \lim_{t\rightarrow 0^{+}}\frac{1}{t^{4}} \int _{0}^{t}\log \bigl(1+ \vert s \vert ^{2}\bigr) \vert s \vert ^{2}s\,ds=0, $$

the condition (2.1) is also fulfilled (here we take \(\varrho =\frac{1}{N}=\frac{1}{3}\), again). So we see that with the above choices, \(\varphi _{1}\) and \(\varphi _{2}\) satisfy the assumptions of Theorem 2.2. Let \(F:\mathbb{R}^{2}\rightarrow [0, \infty )\) be a continuous function defined by

$$\begin{aligned}& F(s, t)= \textstyle\begin{cases} s^{6}(1+\sin (\ln (1+ \vert t \vert ))), &(s, t)\neq (0, 0), \\ 0, &(s, t)=(0, 0), \end{cases}\displaystyle \\& A=\liminf_{\sigma \rightarrow 0^{+}} \frac{\int _{\Omega }\max_{ \vert s \vert + \vert t \vert \leq \sigma }F(s, t)\,dx }{\sigma ^{6}}= \vert \Omega \vert \liminf_{\sigma \rightarrow 0^{+}} \frac{\max_{ \vert s \vert + \vert t \vert \leq \sigma }F(s, t) }{\sigma ^{6}}=2, \\& B=\limsup_{s, t\rightarrow 0^{+}} \frac{\int _{B(x_{0}, \frac{D}{2})}F(s, t) \,dx}{s^{6}+t^{6}}= \biggl\vert B \biggl(x_{0}, \frac{D}{2}\biggr) \biggr\vert \limsup _{s, t\rightarrow 0^{+}} \frac{F(s, t)}{s^{6}+t^{6}}= \biggl\vert B \biggl(x_{0}, \frac{D}{2}\biggr) \biggr\vert . \end{aligned}$$

Then

$$ \lambda _{1}=\frac{7m_{1}}{3}\biggl(\frac{2}{D} \biggr)^{6}>0 \quad \text{and} \quad \lambda _{2}= \frac{m_{0}}{2^{7}C}>0, $$

with this condition \(2^{13}<\frac{3m_{0}D^{6}}{7m_{1}C}\). Then for \(\lambda \in\, ]\lambda _{1}, \lambda _{2}[\), the following system:

$$ \textstyle\begin{cases} -M_{1} {(}\int _{\Omega }\Phi _{1}( \vert \nabla u \vert )\,dx {)}\operatorname{div}( \frac{ \vert \nabla u \vert ^{4}}{\log (1+ \vert \nabla u \vert )}\nabla u)=\lambda F_{u}(x,u,v) \quad \text{in } \Omega , \\ -M_{2} {(}\int _{\Omega }\Phi _{2}( \vert \nabla v \vert )\,dx {)}\operatorname{div}( \log (1+ \vert \nabla v \vert ^{2}) \vert \nabla v \vert ^{2}\nabla v)=\lambda F_{v}(x,u,v) \quad \text{in } \Omega , \\ u=v=0\quad \text{on } \partial \Omega , \end{cases} $$

admits a sequence of pairwise distinct weak solutions which strongly converges to zero in \(W_{0}^{1, \Phi _{1}}(\Omega )\times W_{0}^{1, \Phi _{2}}(\Omega )\).