Cross-diffusion-driven Turing instability and weakly nonlinear analysis of Turing patterns in a uni-directional consumer-resource system

Abstract

Spatiotemporal patterns driven by cross-diffusion of a uni-directional consumer-resource (C-R) system with Holling-II type functional response are investigated in this paper. The existence of a unique positive steady state of the considered system is studied first. The linear stability analysis shows that the cross-diffusion is the key mechanism for the formation of spatiotemporal patterns through Turing bifurcation. We choose the cross-diffusion coefficient as bifurcation parameter and discuss three different types of Turing bifurcations, corresponding to simple, double non-resonant and double resonant cases. Based on weakly nonlinear analysis with the multiple scale method and the adjoint system theory, we derive the amplitude equations of the Turing patterns near the Turing bifurcation point and obtain the analytical approximation solutions of the patterns for each case. Specially, some qualitative results of amplitude equations of the resonant case are given in detail. Finally, numerical simulations are performed to illustrate the weakly nonlinear theoretical predictions and through these simulations some patterns (single mode pattern, mixed-mode pattern, super-squares pattern, roll pattern, hexagonal pattern) are found. Simultaneously, numerical simulations show that the resource supplying rate has an important impact on the direction of Turing bifurcation.

1 Introduction

The interaction of populations is one of the basic interspecies relations in biology and ecology [1]. The consumer-resource (C-R) system was originally incorporated into the study of interspecies interactions to describe the mechanisms or ways by which individuals of different species interact with one another [2]. A resource is considered to be a biotic or abiotic species that increases the population growth of its consumers, whereas a consumer exploits a resource and then reduces its growth rate. In this way, species interactions include bi-directional, uni-directional, and indirect C-R interactions. Bi-directional C-R interactions occur when each species functions as both a consumer and a resource of the other. Uni-directional C-R interactions occur when one species functions as a consumer and the other as a material and/or energy resource, but neither acts as both. Indirect C-R interactions occur when the effects of the two species on one another are mediated entirely by the density or traits of a third species that is a consumer or resource of one or both of them [3]. The general model of uni-directional C-R interactions proposed by Holland and DeAngelis [3] is

$$ \textstyle\begin{cases} \frac{du}{dt}=u[r_{1}+e_{1} f_{1}(u,v)-q_{1} g_{1}(u,v)-d_{1}u],\\ \frac{dv}{dt}=v[r_{2}+e_{2} f_{2}(u,v)-d_{2}v], \end{cases} $$

(1.1)

where u represents the population density of the resource, and v represents the population density of the consumer. $r_{1}$ and $r_{2}$ are intrinsic growth rates in the absence of the other species. The ratios $r_{1}/d_{1}$ and $r_{2}/d_{2}$ can be thought of as carrying capacities in the absence of the other species. The term $e_{i}f_{i}(u,v)$ represents the gain from the interaction, and the term $q_{1}g_{1}(u,v)$ represents the costs incurred by the interaction. In this case, there are positive effects occurring to both populations, but the species u has only one that incurs a loss due to the C-R interaction. In the uni-directional C-R interaction, the consumer provisions the resource species with a non-trophic beneficial service of dispersal or defense in the other direction [4]. As an example, consider an interaction between an insect pollinator species and the host plant species. The pollinator both pollinates the plant’s flowers and oviposits on them, so that the insect’s larvae can feed on the plant’s seeds.

Since the pioneering work of Holland and DeAngelis [3, 5], some articles on C-R interaction models have been published to illustrate the importance of this interaction. Previous studies of C-R interaction models mainly focused on the mechanisms that determine how interaction outcomes depend on the model parameters. Gross [6] considered positive interactions among competitors in two kinds of resource-competition models. Wang et al. [7] used uni-directional C-R theory to investigate the transitions of interaction outcomes for a kind of uni-directional C-R system. Based on the model (1.1), Wang and DeAngelis [8] considered a specific uni-directional C-R system as follows:

$$ \textstyle\begin{cases} \frac{du}{dt}=u[r_{1}+\frac{\alpha_{12}v}{c_{2}+v}-\beta _{1}v-d_{1}u],\\ \frac{dv}{dt}=v[r_{2}+\frac{\alpha_{21}u}{c_{1}+u}-d_{2}v], \end{cases} $$

(1.2)

where u, v, $r_{i}$ and $d_{i}$ have the same meanings as those in the general model (1.1), and the meanings of the other parameters in the system are referred to in Table 1. They studied the dynamical behavior of the system and demonstrated in this mechanism how and when interaction outcomes of this system vary with different conditions.

Table 1 Parameter definitions in systems ( 1.2 )-( 1.3 ) and their units, where $\pmb{[\mathrm{species}\ u]}$ indicates the species u density and $\pmb{[\mathrm{species}\ v]}$ indicates species v density

The aforementioned models only describe ideal populations and neglect spatial heterogeneity. In reality, according to Fick’s law, the species is spatially heterogeneous and hence individuals will tend to migrate towards regions of lower population density to increase the possibility of survival, and hence the species are distributed over space and interact with each other within their spatial domain [9]. Generally speaking, diffusion deals with transport from a region of higher concentration to one of lower concentration by random motion. The diffusion of individuals may be connected with other things, for example, the individuals look for food, the preys keep away from predators in order to not be caught, the individuals escape from high infection risks and so on (for example, see [10–16] and references therein). Considering the effects of spatial diffusion, Huang et al. [17] studied bifurcation and temporal periodic patterns in a delayed plant-pollinator model with a diffusion effect.

More generally, there exists a motional state of interaction as well, one that recognizes the possible bias, say, of the motion of one species toward or away from another species [18, 19]. This phenomenon is called cross-diffusion. The value of the cross-diffusion coefficient can be positive or negative. The term including positive cross-diffusion coefficients denotes the movement of the species in the direction of lower concentration of another species and negative cross-diffusion coefficients denote that one species tends to diffuse in the direction of a higher concentration. Since the pioneer work of [19], the concern on cross-diffusion in ecological models has attracted the attention of biologists, chemical experimenters and applied mathematicians and cross-diffusion has been one of the dominant topics in both ecology and mathematical ecology because of its universal existence and importance ([1, 9]). Shigesada et al. [20] investigated the effect of cross-diffusion in a competitive population system first. Then, many works have proposed to investigate the Turing instability driven by cross-diffusion and prove the existence of inhomogeneous steady states that induce the emergence of spatial patterns ([21–37] and [38–42]). Hence it is of great interest to explore the role of cross-diffusion in driving Turing instability and spatial pattern formation.

Based on the statements above, in this paper, we introduce the spatial diffusion with zero-flux boundary conditions into system (1.2), and further assume that species u is subject to self-diffusion, and that species v is subject to nonlinear positive cross-diffusion. We examine how the cross-diffusion induces the Turing instability and the spatial inhomogeneous distribution of the two species. Then the considered system appears as follows:

$$ \textstyle\begin{cases} \frac{\partial u(x,y,t)}{\partial t}=a_{1}\nabla ^{2}u+f_{1}(u,v),& (x,y)\in\Omega, t>0,\\ \frac{\partial v(x,y,t)}{\partial t}=\nabla\cdot\nabla ((a_{2}+bu)v)+f_{2}(u,v),& (x,y)\in\Omega, t>0,\\ \frac{\partial u(x,y,t)}{\partial\nu}=\frac{\partial v(x,y,t)}{\partial\nu}=0,& (x,y)\in\partial \Omega, t>0,\\ u(x,y,0)= u_{0}(x,y), \quad\quad v(x,y,0)=v_{0}(x,y),& (x,y)\in\Omega, \end{cases} $$

(1.3)

with

$$ \begin{aligned} &f_{1}(u,v)=u\biggl(r_{1}+ \frac{\alpha_{12}v}{c_{2}+v}-\beta _{1}v-d_{1}u\biggr), \\ &f_{2}(u,v)=v\biggl(r_{2}+\frac{\alpha_{21}u}{c_{1}+u}-d_{2}v \biggr). \end{aligned} $$

Here $u(x,y,t)$ and $v(x,y,t)$ represent the numbers of biomass density of the two species at any instant of time t and location $(x,y)$ subject to the non-negative initial condition $u_{0}(x,y)$ and $v_{0}(x,y)$ and Neumann boundary conditions ${\partial u}/{\partial\nu}={\partial v}/{\partial\nu}=0$; ∇ is the gradient operator in domain Ω and ν is the outward unit normal vector on ∂Ω. The homogeneous Neumann boundary conditions reflect the situation where the population cannot cross the boundary of Ω. Ω is a bounded open domain in $\mathbb{R}^{2}$ with smooth boundary ∂Ω. The parameters $a_{1}$, $a_{2}$ are the positive self-diffusion coefficients while b is the cross-diffusion coefficient. The meanings of other parameters in system (1.3) are the same as in system (1.2). Referring to [43], the units of parameters of system (1.3) are summarized in Table 1.

In our current work we first investigate the effect of cross-diffusion on the spatial inhomogeneous distribution of the two species in a uni-directional C-R system. Our results show that the resource supply rate has an important effect on the Turing bifurcation direction. We also show how the weakly nonlinear analysis of the C-R system (1.3) is able to point out some interesting phenomena like stable supercritical and subcritical Turing patterns and a hysteretic-type phenomenology due to the presence of a multiplicity of real stable equilibria for the amplitude equation in the subcritical case. The rest of the paper is organized as follows. Section 2 discusses the existence and unique positive spatially homogeneous steady state of system (1.3). The linear stability analysis of the proposed system and its corresponding non-spatial system are presented in Section 3. Weakly nonlinear pattern analysis and the related numerical simulations are given in Section 4. A brief conclusion and discussion are presented in Section 5. In the Appendix, we give the coefficient expressions of amplitude equations emerged in Section 4.

2 Existence of unique positive spatially homogeneous steady state

In this section, we shall prove the existence and uniqueness of a positive spatially homogeneous steady state for system (1.3) by analytical methods. Clearly system (1.3) admits one trivial steady state: $E_{0}:=(0,0)$ and two semi-trivial constant steady states: $E_{10}:=(\frac{r_{1}}{d_{1}},0)$ and $E_{01}:=(0,\frac {r_{2}}{d_{2}})$. In biology, we are interested in positive spatially homogeneous steady states. System (1.3) admits a positive spatially homogeneous steady state $E_{\ast}:= (u_{\ast}, v_{\ast})$ if $E_{\ast}$ is a positive constant solution to the following two equations:

$$\begin{aligned}& r_{1}+\frac{\alpha_{12}v}{c_{2}+v}-\beta_{1}v-d_{1}u=0, \end{aligned}$$

(2.1)

$$\begin{aligned}& r_{2}+\frac{\alpha_{21}u}{c_{1}+u}-d_{2}v=0. \end{aligned}$$

(2.2)

Assume that

$(H_{1})$::

$\frac{r_{2}}{d_{2}}<\frac{r_{1}+\alpha_{12}-c_{2}\beta _{1}+\sqrt{(r_{1}+\alpha_{12}-c_{2}\beta_{1})^{2}+4r_{1}\beta _{1}c_{2}}}{2\beta_{1}}$.

Then we have the following theorem.

Theorem 2.1

Under $(H_{1})$, system (1.3) has a unique positive spatially homogeneous steady state $E_{\ast}$.

Proof

It follows from (2.2) that $0< v<\frac{r_{2}+\alpha _{21}}{d_{2}}$. Define

$$ F_{1}(v)=\frac{1}{d_{1}}\biggl(r_{1}+\frac{\alpha _{12}v}{c_{2}+v}- \beta_{1}v\biggr),\quad\quad F_{2}(v)= \frac {c_{1}\alpha_{21}}{r_{2}+\alpha_{21}-d_{2}v}-c_{1}, $$

for $v\in(0,\frac{r_{2}+\alpha_{21}}{d_{2}})$. From (2.1) and (2.2), we know that the zero isoclines of system (1.3) are given by $u=F_{1}(v)$ and $u=F_{2}(v)$, respectively. Then the positive spatially homogeneous steady state $E_{\ast}=(u_{\ast },v_{\ast})$ of system (1.3) should satisfy $u_{\ast }=F_{1}(v_{\ast})=F_{2}(v_{\ast})$. Thus the question to look for a positive spatially homogeneous steady state is reduced to finding a positive constant solution v such that $F_{1}(v)=F_{2}(v)$. A direct calculation yields

$$\begin{aligned}& F_{1}(0)=\frac{r_{1}}{d_{1}}, \quad \quad F_{1} \bigl(v^{0}\bigr)=0,\quad \quad F_{1}^{\prime }(v)= \frac{1}{d_{1}} \biggl[ -\beta_{1}+\frac{\alpha _{12}c_{2}}{(c_{2}+v)^{2}} \biggr] , \\& F_{1}^{\prime\prime}(v)=-\frac{2\alpha _{12}c_{2}}{d_{1}(c_{2}+ v)^{3}}< 0, \end{aligned}$$

and

$$ F_{2}\biggl(\frac{r_{2}}{d_{2}}\biggr)=0,\quad \quad F_{2}'(v)= \frac{c_{1}\alpha _{21}d_{2}}{(r_{1}+\alpha_{21}-d_{2}v)^{2}}>0,\quad \quad F_{2}''(v)= \frac {2c_{1}\alpha_{21}d_{2}^{2}}{(r_{2}+\alpha_{21}-d_{2}v)^{3}}>0. $$

Denote by $(0,v^{0})$ the intersection of the zero isocline $u=F_{1}(v)$ and the v-axis. Then we get $v^{0}=\frac{r_{1}+\alpha _{12}-b_{2}\beta_{1}+\sqrt{(r_{1}+\alpha_{12}-b_{2}\beta _{1})^{2}+4r_{1}\beta_{1}b_{2}}}{2\beta_{1}}$. From the equalities above, we see that $u=F_{1}(v)$ is a continuous concave function on $(0, v^{0})$ satisfying $F_{1}(0)=\frac{r_{1}}{d_{1}}>0$ and $F_{1}(v^{0})=0$. Let $\hat{u}_{1}=F_{1}(\hat{v}_{1})=\frac{1}{d_{1}}(r_{1}+\frac {\alpha_{12}\hat{v}_{1}}{c_{2}+\hat{v}_{1}}-\beta_{1}\hat{v}_{1})$, $\hat{v}_{1}=\sqrt{\frac{\alpha_{12}c_{2}}{\beta_{1}}}-c_{2}$. Since ${\frac{dF_{1}}{dv}}|_{v=\hat{v}_{1}}=0$ and $F_{1}^{\prime \prime}(v)<0$, $(\hat{u}_{1}, \hat{v}_{1})$ is the maximum point of the function $u=F_{1}(v)$ and $F_{1}(v)$ is concave left as shown in Figure 1. Hence, when $v<\hat{v}_{1}$, $u=F_{1}(v)$ is monotonically increasing; when $v>\hat{v}_{1}$, $u=F_{1}(v)$ is monotonically decreasing.

Figure 1

Graphs of $\pmb{G_{1}(v)}$ and $\pmb{G_{2}(v)}$ . Figure 1 depicts that there exist parameters such that system (1.3) has a unique positive steady state. Here the parameter values of system (1.3) are chosen as ${r_{1}=0.6}$, $r_{2}=0.3$, $\alpha_{12}=0.1$, $\alpha _{21}=0.3$, $c_{1}=c_{2}=0.1$, ${d_{1}=d_{2}=0.01}$, $\beta_{1}=0.01$. A direct calculation yields the unique positive steady state $(u_{\ast}, v_{\ast})=(10.2725, 59.7108)$.

It is clear that $u=F_{2}(v)$ is a continuous and increasing concave down function on $(0,\frac{r_{2}+\alpha_{21}}{d_{2}})$ satisfying $F_{2}(0)=\frac{-c_{1}r_{2}}{r_{2}+\alpha_{21}}<0$, $F_{2}(\frac {r_{2}}{d_{2}})=0$ and $\lim_{v\rightarrow{\frac {r_{2}+\alpha_{21}}{d_{2}}}-0}F_{2}(v)=+\infty$.

Combining the above analysis and $(H_{1})$, we see that there is a unique constant solution $v_{\ast}\in(0,v^{0})$ such that $u_{\ast }=F_{1}(v_{\ast})=F_{2}(v_{\ast})$ and is positive. Therefore, system (1.3) has a unique positive spatially homogeneous steady state $E_{\ast}=(u_{\ast},v_{\ast})$. This completes the proof. □

3 Stability analysis

In this section, we shall investigate the impact of cross-diffusion on the stability of the unique positive spatially homogeneous steady state $E_{\ast}$ of the system (1.3). Specifically, we are interested in investigating the Turing instability of the system (1.3), which is induced by cross-diffusion, that is, the positive steady state $E_{\ast}$ of the model without cross-diffusion is stable, but it is unstable in the presence of the cross-diffusion term $buv$.

3.1 Stability analysis of the corresponding ODE system

First, we perform the stability analysis of the positive spatially homogeneous steady state $E_{\ast}$ in the absence of diffusion, that is, the system (1.3) degenerates to the corresponding ordinary differential equation (ODE) system (1.2) in this case. To study this, we linearize the system (1.2) along the positive steady state $E_{\ast}$ and the linear stability is determined by the eigenvalues of the following Jacobian matrix:

$$\begin{aligned} K=\left ( \begin{matrix} K_{11} & K_{12}\\ K_{21} & K_{22} \end{matrix} \right ) , \end{aligned}$$

(3.1)

where

$$ K_{11}=-d_{1}u_{\ast}, \quad\quad K_{12}= \frac{\alpha _{12}c_{2}u_{\ast}}{(c_{2}+v_{\ast})^{2}}-\beta_{1}u_{\ast}, \quad \quad K_{21}=\frac{\alpha_{21}c_{1}v_{\ast}}{(c_{1}+u_{\ast })^{2}},\quad\quad K_{22}=-d_{2}v_{\ast}. $$

The corresponding characteristic equation of K is

$$ \lambda^{2}-\operatorname {tr}(K)\lambda+\operatorname {det}(K)=0, $$

(3.2)

where

$$ \operatorname {tr}(K)=K_{11}+K_{22},\quad\quad \operatorname {det}(K)=K_{11}K_{22}-K_{12}K_{21}. $$

Theorem 3.1

Assume that $(H_{1})$ holds. Then we have

• (i) System (1.2) cannot undergo a Hopf bifurcation at the positive spatially homogeneous steady state $E_{\ast}$.

• (ii) Furthermore, if the parameters of the system (1.2) satisfy

  $$ (d_{1}u_{\ast}-\beta_{1}v_{\ast}) (c_{2}+v_{\ast})^{2}+\alpha _{12}c_{2}v_{\ast}< 0, $$

  (3.3)

  then the positive spatially homogeneous steady state $E_{\ast}$ is locally asymptotically stable.

Proof

Since $\operatorname {tr}(K)<0$ always holds, there is not any pair of imaginary roots in the characteristic equation (3.2), and the proof of (i) is completed.

(ii) Noting that

$$ \begin{aligned} \operatorname {det}(K)&=d_{1}d_{2}u_{\ast}v_{\ast}- \frac{\alpha _{21}c_{1}v_{\ast}}{(c_{1}+u_{\ast})^{2}} \biggl( \frac{\alpha _{12}c_{2}u_{\ast}}{(c_{2}+v_{\ast})^{2}}-\beta_{1}u_{\ast} \biggr) \\ &=d_{1}d_{2}u_{\ast}v_{\ast}+ \frac{\alpha_{21}c_{1}u_{\ast }}{(c_{1}+u_{\ast})^{2}} \biggl( \beta_{1}v_{\ast}-\frac{\alpha _{12}c_{2}v_{\ast}}{(c_{2}+v_{\ast})^{2}} \biggr) , \end{aligned} $$

it follows from the assumption (3.3) that $\operatorname {det}(K)>0$. Clearly $\operatorname {tr}(K)=-d_{1}u_{\ast}-d_{2}v_{\ast}<0$. Thus the positive steady state of system (1.2) is locally asymptotically stable, that is, system (1.3) is locally asymptotically stable in the absence of self-diffusion and cross-diffusion. This completes the proof of the theorem. □

3.2 No Turing instability without cross-diffusion

In this subsection, we shall prove system (1.3) still remains stable in the presence of self-diffusion but without cross-diffusion (i.e., $b=0$). Then the linearized form of system (1.3) with $b=0$ along the unique positive spatially homogeneous steady state $E_{\ast}=(u_{\ast}, v_{\ast})$ can be written as follows:

$$ {\dot{\mathbf{w}}}=K{\mathbf {w}}+\left ( \begin{matrix} a_{1} & 0\\ 0& a_{2} \end{matrix} \right ) \nabla^{2}{\mathbf {w}}, \quad\quad{\mathbf {w}}=\left ( \begin{matrix}u-u_{\ast}\\ v-v_{\ast} \end{matrix} \right ) , $$

(3.4)

with K given by (3.1).

Let us consider the solution of system (3.4) in the form

$$\begin{aligned} {\mathbf {w}}=\left ( \begin{matrix} c_{k}^{1}\\ c_{k}^{2} \end{matrix} \right ) e^{\lambda t+\mathrm{i}\mathbf{k}\cdot\mathbf{r}}, \end{aligned}$$

(3.5)

where $\mathbf{k}=(k_{x}, k_{y})$, $\mathbf{k}\cdot\mathbf{k}=k^{2}$, λ is the growth rate of perturbation in time t, $k_{x}$ and $k_{y}$ represent the wave numbers of the solutions, i is the imaginary unit, $\mathrm{i}^{2}=-1$ and $\mathbf{r}=(x,y)$ is the spatial vector in two-dimensional space. Substituting (3.5) into (3.4) leads to the following dispersion relation, which gives the eigenvalue ξ as a function of the wave number $k= \vert {\mathbf {k}} \vert$:

$$ \lambda^{2}-\operatorname {Tr}_{k}\lambda+\Delta_{k}=0, $$

(3.6)

where

$$ \operatorname {Tr}_{k}=\operatorname {tr}(K)-k^{2}(a_{1}+a_{2}), \quad\quad {\Delta}_{k}=a_{1}a_{2}k^{4}+(a_{1}d_{2}v_{\ast}+a_{2}d_{1}u_{\ast })k^{2}+ \operatorname {det}(K). $$

(3.7)

The following theorem shows that Turing instability does not occur in the uni-directional C-R system (1.3) without cross-diffusion.

Theorem 3.2

Assume that $(H_{1})$, (3.3) and $b=0$ in system (1.3). Then the unique positive spatially homogeneous steady state $E_{\ast}=(u_{\ast},v_{\ast})$ is locally asymptotically stable.

Proof

Since the assumption (3.3) holds, we get $\operatorname {det}(K)>0$. Clearly $\operatorname {tr}(K)<0$. Thus $\operatorname {Tr}_{k}<0$ and $\Delta_{k}>0$. This completes the proof. □

3.3 Turing instability induced by cross-diffusion

In this subsection, we shall prove that the only potential destabilizing mechanism in our system (1.3) is the presence of the cross-diffusion. Linearizing system (1.3) along the positive steady state $E_{\ast}=(u^{\ast}, v^{\ast})$ yields

$$ {\dot{\mathbf {w}}}=K{\mathbf {w}}+D^{b}\nabla^{2}{\mathbf {w}}, \quad\quad{\mathbf {w}}=\left ( \begin{matrix} u-u_{\ast}\\ v-v_{\ast} \end{matrix} \right ) , $$

(3.8)

where $D^{b}=\bigl( {\scriptsize\begin{matrix}{} a_{1} & 0\cr bv_{\ast}& a_{2}+bu_{\ast} \end{matrix}} \bigr)$ and K is given by (3.1).

Substituting (3.5) into (3.8) leads to the following dispersion relation, which gives the eigenvalue λ as a function of the wave number $k= \vert {\mathbf {k}} \vert$:

$$ \lambda^{2}+g\bigl(k^{2}\bigr)\lambda+h\bigl(k^{2} \bigr)=0, $$

(3.9)

where

$$ g\bigl(k^{2}\bigr)=k^{2}\operatorname {tr}\bigl(D^{b}\bigr)-\operatorname {tr}(K),\quad \quad h\bigl(k^{2}\bigr)=\operatorname {det}\bigl(D^{b} \bigr)k^{4}+qk^{2}+\operatorname {det}(K), $$

(3.10)

and

$$ q=a_{1}d_{2}v_{\ast}+a_{2}d_{1}u_{\ast}+bu_{\ast} \biggl( d_{1}u_{\ast}-\beta_{1}v_{\ast}+ \frac{\alpha_{12}c_{2}v_{\ast }}{(c_{2}+v_{\ast})^{2}} \biggr) . $$

(3.11)

Theorem 3.3

Cross-diffusion induced Turing instability

Assume that $(H_{1})$ and (3.3) hold. Then the unique positive spatially homogeneous steady state $E_{\ast }(u_{\ast},v_{\ast})$ of system (1.3) is spatially unstable when $b>b^{c}$, and the critical wave number is given by $k_{c}^{2}$, where $b^{c}$ and $k_{c}^{2}$ can be found in the proof of the theorem.

Proof

From Theorem 3.1 and Theorem 3.2, we know that system (1.3) still remains stable without diffusion or in the presence of self-diffusion alone. Therefore, it follows that the only potential destabilizing mechanism is the presence of the cross-diffusion terms. Then for the Turing instability to be realized and spatial patterns to form, there must be some $k\neq0$ such that the real part of at least one root of the characteristic equation (3.9) is greater than zero. Since $g(k^{2})>0$ for $\forall k\neq0$, instability can only be obtained in the case of $h(k^{2})<0$ for some $k\neq0$. Since $\operatorname {det}(D^{b})>0$, we get the condition for the marginal stability as follows:

$$ \min\bigl(h\bigl(k^{2}\bigr)\bigr)=h\bigl(k_{m}^{2} \bigr)=0, $$

(3.12)

where

$$ k_{m}^{2}=-\frac{q}{2\operatorname {det}(D^{b})}, $$

(3.13)

which requires that $q<0$. From $q<0$, we know that the necessary condition of Turing instability is as follows:

$$ d_{1}u_{\ast}-\beta_{1}v_{\ast}+ \frac{\alpha_{12}c_{2}v_{\ast }}{(c_{2}+v_{\ast})^{2}}< 0, $$

(3.14)

which is equivalent to the assumption (3.3).

In what follows, we shall choose the cross-diffusion coefficient b as bifurcation parameter. Let us now set $q=-\gamma b+\delta$, where the positive quantities γ and δ are defined as:

$$\begin{aligned} \begin{aligned} \gamma=-u_{\ast} \biggl( d_{1}u_{\ast}- \beta_{1}v_{\ast}+\frac {\alpha_{12}c_{2}v_{\ast}}{(c_{2}+v_{\ast})^{2}} \biggr) ,\quad \quad \delta=a_{1}d_{2}v_{\ast}+a_{2}d_{1}u_{\ast}. \end{aligned} \end{aligned}$$

Let $b=\frac{\delta}{\gamma}+\eta$. At bifurcation, $\min (h(k^{2}))=0$. Then substituting b into the second equality of (3.12) yields the following equation for η:

$$ \frac{\gamma^{2}\eta^{2}}{4\operatorname {det}(K)}-a_{1}u_{\ast}\eta - \biggl(a_{1}a_{2}+a_{1}u_{\ast} \frac{\delta}{\gamma}\biggr)=0. $$

(3.15)

Clearly, equation (3.15) has a unique positive root. Denote the unique positive root of equation (3.15) by $\eta^{+}$. Set

$$ b^{c}=\frac{\delta}{\gamma}+\eta^{+}. $$

(3.16)

Since

$$ q=0\quad \Leftrightarrow \quad b^{\ast}=\frac{\delta}{\gamma}, $$

we can see that $0< b^{\ast}< b^{c}$ and $q<0$, $\min(h(k^{2}))<0$ when $b>b^{c}$. Therefore, the unique steady state $E^{\ast}$ is unstable. This indicates that a Turing instability occurs and the critical value for bifurcation is $b=b^{c}$. The critical wave number $k_{c}$ is then given (using (3.13)) by

$$ k_{c}^{2}=\frac{\gamma\eta^{+}}{2\operatorname {det}(D^{b^{c}})}. $$

(3.17)

This completes the proof. □

Remark 1

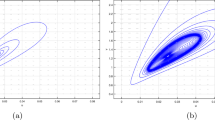
When $b>b^{c}$, there exists a range $(k_{1}^{2}, k_{2}^{2})$ of unstable wave numbers $k^{2}$ such that $h(k^{2})<0$, and correspondingly the real part of the eigenvalue of equation (3.9) $\operatorname {Re}(\lambda)>0$; see on the right of Figure 2.

Figure 2

Left: the growth rate $\pmb{\alpha_{12}}$ vs. the consumption rate $\pmb{\beta_{1}}$ ; Right: dispersion relation. In Figure 2, the bounded area Ω shows the parameter space where Turning instability may occur and the parameter values are chosen as $r_{1}=0.6$, $r_{2}=0.3$, $\alpha_{21}=0.3$, $c_{1}=c_{2}=0.1$, $d_{1}=d_{2}=0.01$. To the right of the figure, the parameter values are chosen as $r_{1}=0.6$, $r_{2}=0.3$, $c_{1}=c_{2}=0.1$, $d_{1}=d_{2}=0.01$, $\alpha_{21}=0.3$, $\alpha_{12}=0.6$, $\beta_{1}=0.02$, $a_{1}=0.1$, $a_{2}=0.2$ with $(\alpha_{12},\beta_{1})\in\Omega$.

In what follows, we shall consider only the case where there is one unstable eigenvalue, admissible for the Neumann boundary conditions, which falls within the band $(k_{1}^{2}, k_{2}^{2})$ in the sense of $k_{1}^{2}< k^{2}=\phi^{2}+\psi^{2}< k_{2}^{2}$ with $\phi=\frac{l\pi }{L_{x}}$ and $\psi=\frac{n\pi}{L_{y}}$, where l, n are integers. We denote by $\hat{k}_{c}^{2}$ the unstable admissible eigenvalue to distinguish it from the critical value $k_{c}^{2}$. As an example, we take the parameters of system (1.3) as $r_{1}=0.6$, $r_{2}=0.3$, $c_{1}=c_{2}=0.1$, $d_{1}=d_{2}=0.01$, $\alpha_{12}=0.4$, $\beta _{1}=0.02$, $\alpha_{21}=0.3$, $a_{1}=0.1$, $a_{2}=0.2$, $b=0.8$. The spatial domain is taken as $L_{x}=9\pi$, $L_{y}=8\pi$. Using Shengjin’s formula [44] and Matlab algorithm software, we can calculate that system (1.3) has a unique positive steady state $E_{\ast }=(0.1959, 49.8614)$. By (3.16), we compute that $b^{c}=0.7571< b=0.8$ and that $k_{1}^{2}=0.9430$, $k_{2}^{2}=2.0173$. Then there exists only a pair of $(l,n)=(9,8)$ such that the only unstable model allowed by the boundary condition is $\hat {k}_{c}^{2}=2$, which falls within the band of the unstable modes. According to Theorem 3.3, the unique positive spatially homogeneous steady state $E_{\ast}$ is spatially unstable and the spatial inhomogenous distribution of the two species are dipicted in Figure 3.

Figure 3

Snapshots of contour picture of spatial distribution of the species u (left) and species v (right). Figure 3 depicts the pattern formation of the two species when the cross-diffusion coefficient b is greater than its critical value $b^{c}$. The parameters of system (1.3) are chosen as $r_{1}=0.6$, $r_{2}=0.3$, $c_{1}=c_{2}=0.1$, $d_{1}=d_{2}=0.01$, $\alpha_{12}=0.4$, $\beta_{1}=0.02$, $\alpha_{21}=0.3$, $a_{1}=0.1$, $a_{2}=0.2$, $b=0.8$. The spatial domain is taken as $L_{x}=9\pi$, $L_{y}=8\pi$.

4 Weakly nonlinear analysis

In this section, we shall employ the multiple scale method to derive the amplitude equations describing the dynamics close to onset $b=b^{c}$ based on the weakly nonlinear analysis theory. For more details as regards the weakly nonlinear analysis, we refer the reader to [45, 46] and some articles which use similar techniques [47, 48]. In what follows, we will suppose that there exists only one unstable eigenvalue $\lambda(\hat {k}_{c}^{2})$, which lies in the instability band.

Now, we rewrite the linearized form of the original system (1.3) near the unique positive spatially homogeneous steady state $(u_{\ast}, v_{\ast})$ as follows:

$$\begin{aligned} \partial_{t}{\mathbf {w}}&= \mathcal{L}^{b}{\mathbf {w}}+\frac{1}{2}\Phi _{K}({ \mathbf {w}}, {\mathbf {w}})+\frac{1}{2}\nabla^{2} \Phi_{D}^{b}({\mathbf {w}}, {\mathbf {w}})+ \left ( \begin{matrix} f_{122}^{1}(u-u_{\ast})(v-v_{\ast })^{2}+{f_{222}^{1}}(v-v_{\ast})^{3} \\ f_{112}^{2}(u-u_{\ast})^{2}(v-v_{\ast})+f_{111}^{2}(u-u_{\ast})^{3} \end{matrix} \right ) \\ &\quad {}+\left ( \begin{matrix}f_{1222}^{1}(u-u_{\ast})(v-v_{\ast })^{3}+f_{2222}^{1}(v-v_{\ast})^{4} \\ f_{1112}^{2}(u-u_{\ast})^{3}(v-v_{\ast})+f_{1111}^{2}(u-u_{\ast})^{4} \end{matrix} \right ) \\ &\quad {}+\left ( \begin{matrix}f_{12222}^{1}(u-u_{\ast})(v-v_{\ast })^{4}+f_{22222}^{1}(v-v_{\ast})^{5} \\ f_{11112}^{2}(u-u_{\ast})^{4}(v-v_{\ast})+f_{11111}^{2}(u-u_{\ast})^{5} \end{matrix} \right ) + \cdots, \end{aligned}$$

(4.1)

where w is given by (3.8). The linear operator $\mathcal{L}^{b}$ is defined as follows:

$$ \mathcal{L}^{b}=K+D^{b}\nabla^{2},\quad K \text{ and } D^{b} \text{ are given by (3.1)} $$

(4.2)

and the bilinear operators $\Phi_{K}$ and $\Phi_{D}^{b}$ acting on $({\mathbf {x}}, {\mathbf {y}})$ with ${\mathbf {x}}=(x^{u}, x^{v})$ and ${\mathbf {y}}=(y^{u}, y^{v})$ are defined, respectively, as follows:

$$ {\Phi}_{K}({\mathbf {x}}, {\mathbf {y}})=\left ( \begin{matrix} -2d_{1}x^{u}y^{u}+(\frac{\alpha _{12}c_{2}}{(c_{2}+v_{\ast})^{2}}-\beta _{1})(x^{u}y^{v}+x^{v}y^{u})-\frac{2\alpha_{12}c_{2}u_{\ast }}{(c_{2}+v_{\ast})^{3}}x^{v}y^{v}\\ -2d_{2}x^{v}y^{v}+\frac{\alpha_{21}c_{1}}{(c_{1}+u_{\ast })^{2}}(x^{u}y^{v}+x^{v}y^{u})-\frac{2\alpha_{21}c_{1}v_{\ast }}{(c_{1}+u_{\ast})^{3}}x^{u}y^{u} \end{matrix} \right ) $$

(4.3)

and

$$\begin{aligned}& \Phi_{D}^{b}({\mathbf {x}}, {\mathbf {y}})=\left ( \begin{matrix} 0\\ b(x^{u}y^{v}+x^{v}y^{u}) \end{matrix} \right ) , \\& f_{122}^{1}=-\frac{\alpha_{12}c_{2}}{(c_{2}+v_{\ast})^{3}},\quad\quad f_{222}^{1}=\frac{\alpha_{12}c_{2}u_{\ast}}{(c_{2}+v_{\ast})^{4}},\quad\quad f_{112}^{2}=- \frac{\alpha_{21}c_{1}}{(c_{1}+u_{\ast})^{3}}, \quad\quad f_{111}^{2}=\frac{\alpha_{21}c_{1}v_{\ast}}{(c_{1}+u_{\ast})^{4}}, \\& f_{1222}^{1}=\frac{\alpha_{12}c_{2}}{(c_{2}+v_{\ast })^{4}},\quad\quad f_{2222}^{1}=- \frac{\alpha_{12}c_{2}u_{\ast}}{(c_{2}+v_{\ast})^{5}},\quad\quad f_{1112}^{2}=\frac{\alpha_{21}c_{1}}{(c_{1}+u_{\ast })^{4}},\\& f_{1111}^{2}=- \frac{\alpha_{21}c_{1}v_{\ast}}{(c_{1}+u_{\ast })^{5}}, \\& f_{12222}^{1}=-\frac{\alpha_{12}c_{2}}{(c_{2}+v_{\ast })^{5}},\quad\quad f_{22222}^{1}= \frac{\alpha_{12}c_{2}u_{\ast}}{(c_{2}+v_{\ast})^{6}}, \quad\quad f_{11112}^{2}=-\frac{\alpha_{21}c_{1}}{(c_{1}+u_{\ast})^{5}} ,\\& f_{11111}^{2}=\frac{\alpha_{21}c_{1}v_{\ast}}{(c_{1}+u_{\ast})^{6}}. \end{aligned}$$

(4.4)

We set

$$ \mathcal{L}^{b}=\mathcal{L}^{b^{c}}+\bigl(b-b^{c} \bigr)\left ( \begin{matrix}0&0\\ v_{\ast}\nabla^{2}&u_{\ast}\nabla^{2} \end{matrix} \right ) . $$

(4.5)

Next, let us introduce the multiple time scales:

$$ t=\frac{T_{1}}{\varepsilon}+\frac{T_{2}}{\varepsilon^{2}}+\frac {T_{3}}{\varepsilon^{3}}+\frac{T_{4}}{\varepsilon^{4}}+ \cdots, $$

(4.6)

and expand both the solution w and the bifurcation parameter b with respect to the small parameter ε as follows:

$$\begin{aligned}& {\mathbf {w}}=\varepsilon{\mathbf {w}}_{1}+\varepsilon^{2}{ \mathbf {w}}_{2}+\varepsilon ^{3}{\mathbf {w}}_{3}+ \varepsilon^{4}{\mathbf {w}}_{4}+O\bigl(\varepsilon^{5} \bigr), \end{aligned}$$

(4.7)

$$\begin{aligned}& b=b^{c}+\varepsilon b^{(1)}+\varepsilon^{2} b^{(2)}+\varepsilon^{3} b^{(3)}+\varepsilon^{4}b^{(4)}+O \bigl(\varepsilon^{5}\bigr). \end{aligned}$$

(4.8)

Substituting (4.2)-(4.8) into (4.1) and expanding the equation with respect to different orders of ε, we obtain the following sequence of linear equations for ${\mathbf {w}}_{i}=(u_{i}, v_{i})^{T}$:

$$\begin{aligned}& O(\varepsilon):\quad \mathcal{L}^{b^{c}}{\mathbf {w}}_{1}={\mathbf{0}}, \end{aligned}$$

(4.9)

$$\begin{aligned}& O\bigl(\varepsilon^{2}\bigr):\quad \mathcal{L}^{b^{c}}{\mathbf {w}}_{2}={\mathbf {G}}= \frac {\partial{\mathbf {w}}_{1}}{\partial T_{1}}-\frac{1}{2}\bigl(\Phi_{K}+\nabla ^{2}\Phi_{D}^{b^{c}}\bigr) ({\mathbf {w}}_{1}, {\mathbf {w}}_{1})-b^{(1)} \left ( \begin{matrix} 0&0\\ v_{\ast}&u_{\ast} \end{matrix} \right ) \nabla^{2}{\mathbf {w}}_{1}, \end{aligned}$$

(4.10)

$$\begin{aligned}& \begin{aligned}[b] O\bigl(\varepsilon^{3}\bigr):\quad \mathcal{L}^{b^{c}}{\mathbf {w}}_{3}&={\mathbf {H}} \\ &= \frac {\partial{\mathbf {w}}_{1}}{\partial T_{2}}+\frac{\partial{\mathbf {w}}_{2}}{\partial T_{1}}- \bigl(\Phi_{K}+ \nabla^{2}\Phi_{D}^{b^{c}}\bigr) ({\mathbf {w}}_{1}, {\mathbf {w}}_{2})-b^{(1)}\nabla^{2} \left ( \begin{matrix} 0\\ u_{1}v_{1} \end{matrix} \right ) \\ &\quad{}- \left ( \begin{matrix} 0&0\\ v_{\ast}&u_{\ast} \end{matrix} \right ) \bigl(b^{(1)}\nabla^{2}{\mathbf {w}}_{2}+b^{(2)}\nabla^{2}{\mathbf {w}}_{1} \bigr)-\left ( \begin{matrix} f_{122}^{1} u_{1}v_{1}^{2}+f_{222}^{1}v_{1}^{3}\\ f_{112}^{2} u_{1}^{2}v_{1}+f_{111}^{2} u_{1}^{3} \end{matrix} \right ) , \end{aligned} \end{aligned}$$

(4.11)

$$\begin{aligned}& \begin{aligned}[b] O\bigl(\varepsilon^{4}\bigr):\quad \mathcal{L}^{b^{c}}{\mathbf {w}}_{4}={\mathbf {P}}&= \frac {\partial{\mathbf {w}}_{1}}{\partial T_{3}}+\frac{\partial{\mathbf {w}}_{2}}{\partial T_{2}}+ \frac{\partial{\mathbf {w}}_{3}}{\partial T_{1}}-\bigl( \Phi_{K}+\nabla^{2}\Phi _{D}^{b^{c}}\bigr) ({\mathbf {w}}_{1}, {\mathbf {w}}_{3}) \\ &\quad{}- \frac{1}{2}\bigl(\Phi_{K}+\nabla^{2} \Phi_{D}^{b^{c}}\bigr) ({\mathbf {w}}_{2}, {\mathbf {w}}_{2})-b^{(1)}\nabla^{2}\left ( \begin{matrix} 0\\ u_{1}v_{2}+u_{2}v_{1} \end{matrix} \right ) \\ &\quad{}- \left ( \begin{matrix} 0&0\\ v_{\ast}&u_{\ast} \end{matrix} \right ) \bigl(b^{(1)}\nabla^{2}{\mathbf {w}}_{3}+b^{(2)}\nabla^{2}{\mathbf {w}}_{2}+b^{(3)}\nabla^{2}{\mathbf {w}}_{1} \bigr) \\ &\quad{}-\left ( \begin{matrix} f_{1222}^{1}u_{1}v_{1}^{3}+f_{2222}^{1}v_{1}^{4}\\ f_{1112}^{2}u_{1}^{3}v_{1}+f_{1111}^{2}u_{1}^{4} \end{matrix} \right ) - b^{(2)}\nabla^{2}\left ( \begin{matrix}0\\ u_{1}v_{1} \end{matrix} \right ) , \end{aligned} \end{aligned}$$

(4.12)

$$\begin{aligned}& O\bigl(\varepsilon^{5}\bigr):\quad \mathcal{L}^{b^{c}}{\mathbf {w}_{5}}={\mathbf {Q}} \\& \hphantom{O\bigl(\varepsilon^{5}\bigr):\quad \mathcal{L}^{b^{c}}{\mathbf {w}_{5}}}= \frac {\partial{\mathbf {w}}_{1}}{\partial T_{4}}+\frac{\partial{\mathbf {w}}_{2}}{\partial T_{3}}+ \frac{\partial{\mathbf {w}}_{3}}{\partial T_{2}}+\frac{\partial{\mathbf {w}}_{4}}{\partial T_{1}}- \bigl(\Phi_{K}+\nabla^{2}\Phi_{D}^{b^{c}} \bigr) ({\mathbf {w}}_{1}, {\mathbf {w}}_{4}) \\& \hphantom{O\bigl(\varepsilon^{5}\bigr):\quad \mathcal{L}^{b^{c}}{\mathbf {w}_{5}}}\quad {}- \bigl(\Phi_{K}+\nabla^{2}\Phi_{D}^{b^{c}} \bigr) ({\mathbf {w}}_{2}, {\mathbf {w}}_{3})-b^{(1)} \nabla^{2}\left ( \begin{matrix}0\\ u_{1}v_{3}+u_{2}v_{2}+u_{3}v_{1} \end{matrix} \right ) \\& \hphantom{O\bigl(\varepsilon^{5}\bigr):\quad \mathcal{L}^{b^{c}}{\mathbf {w}_{5}}}\quad {}- b^{(2)}\nabla^{2}\left ( \begin{matrix}0\\ u_{1}v_{2}+u_{2}v_{1} \end{matrix} \right ) -b^{(3)} \nabla^{2}\left ( \begin{matrix}0\\ u_{1}v_{1} \end{matrix} \right ) \\& \hphantom{O\bigl(\varepsilon^{5}\bigr):\quad \mathcal{L}^{b^{c}}{\mathbf {w}_{5}}}\quad{}-\left ( \begin{matrix}0&0\\ v_{\ast}&u_{\ast} \end{matrix} \right ) \bigl(b^{(1)}\nabla^{2}{\mathbf {w}}_{4}+b^{(2)} \nabla^{2}{\mathbf {w}}_{3}+b^{(3)} \nabla^{2}{\mathbf {w}}_{2} +b^{(4)} \nabla^{2}{\mathbf {w}}_{1}\bigr) \\& \hphantom{O\bigl(\varepsilon^{5}\bigr):\quad \mathcal{L}^{b^{c}}{\mathbf {w}_{5}}}\quad{}-\left ( \begin{matrix}f_{12222}^{1}u_{1}v_{1}^{4}+f_{22222}^{1}v_{1}^{5}\\ f_{11112}^{2}u_{1}^{4}v_{1}+f_{11111}^{2}u_{1}^{5} \end{matrix} \right ) . \end{aligned}$$

(4.13)

It is easy to see that the solution of linear problem (4.9) satisfying the Neumann boundary conditions is given by [1]

$$\begin{aligned}& {\mathbf {w}}_{1}=\sum _{i=1}^{m}A_{i}(T_{1},T_{2}){ \boldsymbol {\varrho}}\cos(\phi_{i} x)\cos(\psi_{i} y), \end{aligned}$$

(4.14)

$$\begin{aligned}& \hat{k}_{c}^{2}= \phi_{i}^{2}+\psi_{i}^{2}, \quad \text{where } \phi_{i}=\frac{l_{i}\pi}{L_{x}}, \psi_{i}= \frac{n_{i}\pi }{L_{y}}, l_{i}, n_{i}\in\mathbb{Z}, \end{aligned}$$

(4.15)

where $\mathbb{Z}$ represents the integer set, $A_{i}$ represents the varying amplitudes, m is the multiplicity of the eigenvalue λ of the characteristic equation (3.9) and

$$ {\boldsymbol{\varrho}}=\left ( \begin{matrix}1\\ M \end{matrix} \right ) \quad\text{with } M=-\frac{K_{21}-b^{c}v_{\ast }k_{c}^{2}}{K_{22}-(a_{2}+b^{c}u_{\ast})k_{c}^{2}}. $$

(4.16)

Clearly, ${\boldsymbol{\varphi}}=\sum_{i=1}^{m}\bigl( {\scriptsize\begin{matrix}{}1\cr M^{\ast} \end{matrix}} \bigr) \cos(\phi_{i} x)\cos(\psi_{i} y)$, with $M^{\ast}=-\frac{K_{12}}{K_{22}-(a_{2}+b^{c}u_{\ast})k_{c}^{2}}$ satisfying the following equality:

$$ \bigl(K-k_{c}^{2}D^{b^{c}}\bigr)^{\dagger}{ \boldsymbol{\varphi}}={\mathbf{0}}. $$

Here $(K-k_{c}^{2}D^{b^{c}})^{\dagger}$ is the adjoint operator of $(K-k_{c}^{2}D^{b^{c}})$ and φ will be later used to impose solvability conditions.

4.1 Simple eigenvalue case

In this case, $m=1$, that is, given $\hat{k}_{c}^{2}\in[k_{1}^{2},k_{2}^{2}]$, there exists only one pair of integers $(l,n)$ such that the following condition holds:

$$ \phi_{1}^{2}+\psi_{1}^{2}=\biggl( \frac{l\pi}{L_{x}}\biggr)^{2}+\biggl(\frac{n\pi }{L_{y}} \biggr)^{2}=\hat{k}_{c}^{2}. $$

(4.17)

Since the eigenvalue λ is simple, the solution of the linear problem (4.9) satisfying the Neumann boundary conditions is given by

$$ {\mathbf {w}}_{1}=A_{1}(T_{1},T_{2}){ \boldsymbol{\varrho}}\cos(\phi_{1} x)\cos(\psi_{1} y),\quad \text{with }\phi_{1}=\frac{l\pi }{L_{x}}, \psi_{1}= \frac{n\pi}{L_{y}}. $$

(4.18)

From (4.10), we get the following form of the vector G:

$$ \begin{aligned} {\mathbf {G}}&=\left ( \frac{\partial A_{1}}{\partial T_{1}} \boldsymbol {\varrho}+b^{(1)}\hat{k}_{c}^{2}A_{1} \left ( \begin{matrix}0\\ u_{\ast}M+v_{\ast} \end{matrix} \right ) \right ) \cos(\phi_{1}x)\cos(\psi_{1}y) \\ &\quad{}- \frac{1}{8}A_{1}^{2}\sum _{i,j=0,2}\mathcal {M}_{ij}^{1}(\boldsymbol{ \varrho},\boldsymbol{\varrho}) \cos(i\phi_{1}x)\cos(j \psi_{1}y), \end{aligned} $$

with $\mathcal{M}_{ij}^{l}==\Phi_{K}-(i^{2}\phi_{l}^{2}+j^{2}\psi _{l}^{2})\Phi_{D}^{b^{c}}$, $l=1,2$.

By imposing the solvability condition at $O(\varepsilon^{2})$ to equation (4.10), we obtain the quintic Stuart-Landau equations as follows:

$$ \frac{\partial A_{1}}{\partial T_{1}}=\alpha A_{1},\quad\quad\alpha =- \frac{b^{(1)}\hat{k}_{c}^{2}(u_{\ast}M+v_{\ast})}{1+MM^{\ast}}. $$

It follows from the above equation that $A_{1}\to0$ as $t\to\infty$, which implies that the pattern amplitude dies out at this order and there is no information that may be helpful at this stage and we should push the weakly nonlinear analysis to a higher order to obtain some qualitative results as regards the amplitude. Hence we impose $T_{1}=0$ and $b^{(1)}=0$ to suppress the secular terms at this order. Then the compatibility condition is automatically satisfied and the solution of linear problem (4.10) satisfying the Neumann boundary conditions is then calculated as follows:

$$ {\mathbf {w}}_{2}=A_{1}^{2}\sum _{i,j=0,2}{\mathbf {w}}_{2ij}\cos(i\phi _{1} x) \cos(j\psi_{1} y), $$

(4.19)

where the vectors ${\mathbf {w}}_{2ij}$ are the solutions to the following linear systems:

$$ \mathfrak{L}_{ij}^{l}{\mathbf {w}}_{2ij}=- \frac{1}{8}\mathcal {M}_{ij}^{l}({\boldsymbol{ \varrho}}, {\boldsymbol{\varrho}}),\quad i,j=0,2, $$

(4.20)

with $\mathfrak{L}_{ij}^{l}=K-(i^{2}\phi_{l}^{2}+j^{2}\psi _{l}^{2})D^{b^{c}}$, $l=1,2$.

According to (4.11), the vector H is given by

$$ {\mathbf {H}}=\biggl(\frac{dA_{1}}{dT_{2}}{\boldsymbol{\varrho}}+A_{1}{ \mathbf {H}}_{11}^{(1)}+A_{1}^{3}{\mathbf {H}}_{11}^{(3)}\biggr)\cos(\phi_{1} x)\cos(\psi _{1} y)+A_{1}^{3}{\mathbf {H}}^{\ast}, $$

(4.21)

where ${\mathbf {H}}_{11}^{(j)}$, $j=1,3$, and ${\mathbf {H}}^{\ast}$ depend on parameters of the original system (1.3), given in Appendix A.1.1. Applying the solvability condition $\langle {\mathbf {H}}, {\boldsymbol{\varphi}}\rangle=0$ to equation (4.11), we obtain the Stuart-Landau equation corresponding to the amplitude $A_{1}(T_{2})$ as follows:

$$ \frac{dA_{1}}{dT_{2}}=\sigma A_{1}-LA_{1}^{3}, $$

(4.22)

where σ and L are given by

$$ \sigma=-\frac{\langle{\mathbf {H}}_{11}^{(1)}\cos(\phi_{1} x)\cos(\psi _{1} y),{\boldsymbol{\varphi}}\rangle}{\langle{\boldsymbol{\varrho }}\cos(\phi_{1} x)\cos(\psi_{1} y),{\boldsymbol{\varphi}}\rangle }, \quad\quad L=\frac{\langle{\mathbf {H}}_{11}^{(3)}\cos(\phi_{1} x)\cos(\psi_{1} y),{\boldsymbol{\varphi}}\rangle}{\langle {\boldsymbol{\varrho}\cos(\phi_{1} x)\cos(\psi_{1} y)},{\boldsymbol{\varphi}}\rangle}. $$

Since the coefficient σ in equation (4.22) is always positive in the pattern-forming region, we distinguish two cases for the qualitative dynamics of the Stuart-Landau equation (4.22) according to the sign of the Landau constant L: (i) $L>0$, the supercritical bifurcation case; (ii) $L<0$, the subcritical bifurcation case.

In the following two subsections, we will concentrate ourselves to the discussion of the dynamics of the Stuart-Landau equation (4.22) according to the sign of Landau constant L.

4.1.1 The supercritical bifurcation case

In this case, since σ and L are both positive, for equation (4.22) there exists the stable stationary state $\sqrt{\frac {\sigma}{L}}$. Then summarizing the above analysis yields the following proposition.

Proposition 4.1

Assume that

• (i) $\varepsilon^{2}=\frac{b-b^{c}}{b^{c}}$ is small enough so that the positive constant steady state $(u_{\ast},v_{\ast})$ of system (1.3) is unstable to modes corresponding only to the eigenvalue $\hat{k}_{c}^{2}$, which is defined in (4.17);

• (ii) there exists only one pair of integers $(l,n)$ in (4.17);

• (iii) the Landau coefficient L in equation (4.22) is positive.

Then, according to (4.7), system (1.3) has a stationary pattern as follows:

$$ \begin{aligned}[b] \left ( \begin{matrix}u(x,y)\\ v(x,y) \end{matrix} \right ) &=\left ( \begin{matrix}u_{\ast}\\ v_{\ast} \end{matrix} \right ) +\varepsilon \sqrt{\frac{\sigma}{L}} {\boldsymbol{\varrho }}\cos(\phi_{1} x)\cos( \psi_{1} y) \\ &\quad{} +\varepsilon^{2} \frac{\sigma }{L}\sum _{i,j=0,2}{\mathbf {w}}_{2ij}\cos(i\phi_{1} x) \cos(j\psi _{1} y)+O\bigl(\varepsilon^{3}\bigr), \end{aligned} $$

(4.23)

where ϱ is given by (4.16), and ${\mathbf {w}}_{2ij}$ is given by (4.20).

As an illustrated example, from Figure 4, we calculate the band of the unstable modes is $[1.1849, 1.6372]$. Thus the most unstable model is chosen as $\hat{k}_{c}^{2}=1.25$, which falls within the band of the unstable modes. In this rectangular domain, there exists only the pair $(l,n)=(9,4)$ such that the equality (4.17) is satisfied. By calculation, we get $\sigma=0.2576$ and $L=1.3353>0$. In view of Proposition 4.1, a supercritical bifurcation occurs in this case. By (4.23), we get the approximation solution of the first order to the stationary pattern by weakly nonlinear analysis to read

$$ {\mathbf {w}}=0.4392\varepsilon{\boldsymbol{\rho}}\cos(0.5x)\cos (y)+O\bigl( \varepsilon^{2}\bigr), $$

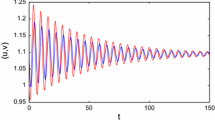
which shows a good qualitative agreement with the numerical solution of system (1.3). Through numerical computation we know that the error between the approximation solution and the simulation solution is $O(\varepsilon^{2})$ with $\varepsilon=0.1$.

Figure 4

Supercritical case. In Figure 4, we compare between the numerical solution of system (1.3) and the weakly nonlinear first order approximation of the solution under supercritical circumstance. Here the parameters are chosen as in Figure 3 except that $b=1.01b^{c}=0.7647$. The spatial domain is taken as $L_{x}=9\pi$, $L_{y}=8\pi$.

4.1.2 The subcritical bifurcation case

For certain values of the parameters appearing in system (1.3), the Landau coefficient L in equation (4.22) has a negative value. In this case equation (4.22) cannot capture the amplitude of the pattern. In order to predict the amplitude of the pattern, one needs to extend weakly nonlinear expansion to higher orders as suggested by [49] and references therein.

Pushing the weakly nonlinear analysis up to $O(\varepsilon^{5})$, one obtains the quintic Stuart-Landau equation for the amplitude $A_{1}$ at the time $T(T_{2}, T_{4})$ as follows:

$$ \frac{dA_{1}}{dT}=\overline{\sigma}A_{1}-\overline{L} A_{1}^{3}+\overline{R} A_{1}^{5}, $$

(4.24)

with

$$ \overline{\sigma}=\sigma+\varepsilon^{2}\widehat{\sigma},\quad \quad \overline{L}=L+\varepsilon^{2}\widehat{L},\quad \quad\overline {R}= \varepsilon^{2}\widehat{R}. $$

Here the details of the derivation and the explicit expression of the coefficients σ̂, L̂, R̂ are given in Appendix A.1.2.

Since $\sigma>0$, $L<0$, there exists $\vert \varepsilon \vert \ll1$ such that $\overline{\sigma}>0$, $\overline{L}<0$. Then when $\overline{R}<0$, there exists one stable stationary state

$$ A_{1\infty}=\sqrt{\frac{\overline{L}-\sqrt{\overline {L}^{2}-4\overline{\sigma}\overline{R}}}{2\overline{R}}}. $$

(4.25)

Then the above analysis implies the following proposition.

Proposition 4.2

Assume that the hypotheses (i) and (ii) of Proposition  4.1 hold and that

• (i) the control parameter ε is small enough so that the Landau coefficient L in (4.22) is negative;

• (ii) the coefficient R̅ or R̂ is negative.

Then the asymptotic solution of the reaction-diffusion system (1.3) can be expressed as

$$\begin{aligned} & \left ( \begin{matrix}u(x,y)\\ v(x,y) \end{matrix} \right ) \\ &\quad =\left ( \begin{matrix}u_{\ast}\\ v_{\ast} \end{matrix} \right ) +\varepsilon A_{1\infty}{\boldsymbol{\varrho}} \cos(\phi _{1} x)\cos(\psi_{1} y)+\varepsilon^{2} A_{1\infty}^{2}\sum_{i,j=0,2}{\mathbf {w}}_{2ij}\cos(i\phi_{1} x)\cos(j\psi_{1} y) \\ &\quad \quad{}+ \varepsilon^{3} \biggl( A_{1\infty}{\mathbf {w}}_{311}^{(1)} \cos(\phi_{1} x)\cos(\psi_{1} y)+A_{1\infty}^{3} \sum_{i,j=1,3}{\mathbf {w}}_{3ij}\cos(i \phi_{1} x)\cos(j\psi_{1} y) \biggr) \\ &\quad \quad{}+\varepsilon^{4} \biggl( \sum_{i,j=0,2}A_{1\infty}^{2}{ \mathbf {w}}_{4ij}^{(1)}\cos(i\phi_{1} x)\cos(j \psi_{1} y)+\sum_{i,j=0,2,4}A_{1\infty}^{4}{ \mathbf {w}}_{4ij}\cos(i\phi_{1} x)\cos(j\psi _{1} y) \biggr) \\ &\quad \quad{} +O\bigl(\varepsilon^{5}\bigr), \end{aligned}$$

(4.26)

where ϱ is given by (4.16), ${\mathbf {w}}_{2ij}$ ($i,j=0,2$) are given by (4.20), ${\mathbf {w}}_{311}^{(1)}$, ${\mathbf {w}}_{3ij}$ ($i,j=1,3$) are given by (A.1), ${\mathbf {w}}_{4ij}^{(1)}$ ($i,j=0,2$), ${\mathbf {w}}_{4ij}$ ($i,j=0,2,4$) are given by (A.2) and $A_{1\infty}$ is given by (4.25).

Figure 5 shows that the resource supply rate has an important effect on the Turing bifurcation direction.

Figure 5

Effect of the resource supplying rate $\pmb{\beta _{1}}$ on the bifurcation direction. In Figure 5, the parameters values are $r_{1}=0.6$, $r_{2}=0.3$, $c_{1}=c_{2}=0.1$, $\alpha_{21}=0.3$, $a_{1}=0.1$, $a_{2}=0.2$ and $\varepsilon=0.1$. The left one shows supercritical bifurcation and the right one shows subcritical bifurcation.

As an example, we take the parameters of system (1.3) as $r_{1}=0.6$, $r_{2}=0.3$, $c_{1}=c_{2}=0.1$, $d_{1}=d_{2}=0.01$, $\alpha _{12}=0.6$, $\beta_{1}=0.02$, $\alpha_{21}=0.3$, $a_{1}=0.1$, $a_{2}=0.2$. Here $b^{c}=0.045$, $\varepsilon=0.1$, $b=1.0101$, $b^{c}=0.0455$. Solving equations (2.1)-(2.2) yields a unique positive steady state $E_{\ast\ast}=(2.3485, 58.7748)$ and that the critical value of the cross-diffusion coefficient is $b^{c}=0.045$. Set $\varepsilon =0.1$, $b=(1+\varepsilon^{2}+\varepsilon^{4})$, $b^{c}=0.0455$. Then the band of the unstable modes is $[0.7748, 1.1615]$. The spatial domain is taken as $L_{x}=9\pi$, $L_{y}=5\pi$ and the only unstable model is chosen as $\hat{k}_{c}^{2}=1.04\in[0.7748,1.1645]$. In this rectangular domain, there exists only the pair $(l,n)=(9,1)$ such that equality (4.17) is satisfied. According to (4.22), we get the Landau coefficient $L=-0.0926$, which is less than zero. By a calculation, we obtain $\overline{\sigma}=0.2013$, $\overline {L}=-0.0214$ and $\overline{R}=-0.046$ for $\varepsilon=0.1$. Thus a subcritical bifurcation occurs according to Proposition 4.2 in this case. It can be seen from Figure 6 that both the approximation solution at $O(\varepsilon^{3})$ and the approximation at $O(\varepsilon^{5})$ have only a subtle difference with $\varepsilon=0.1$.

Figure 6

Subcritical case. In Figure 6, we give the comparison among the numerical solution of system (1.3) (left), the weakly nonlinear first order approximation of the solution (medium) and the weakly nonlinear fifth order approximation of the solution (right) under subcritical case. The parameters are chosen as $r_{1}=0.6$, $r_{2}=0.3$, $c_{1}=c_{2}=0.1$, $d_{1}=d_{2}=0.01$, $\alpha_{12}=0.6$, $\beta_{1}=0.02$, $\alpha_{21}=0.3$, $a_{1}=0.1$, $a_{2}=0.2$. Here $b^{c}=0.045$, $\varepsilon=0.1$, $b=1.0101b^{c}=0.0455$.

Figure 7 presents a complete bifurcation diagram for the bifurcation parameter b. It also shows that system (1.3) is a stable stationary pattern with a large amplitude branch which coexists in the range $b_{s}< b< b_{c}$, which is known as a hysteresis cycle. Varying the bifurcation parameter b following the direction of the arrows in Figure 7, the corresponding numerical solution of the full system shows the hysteresis phenomenon.

Figure 7

Bifurcation diagram of the quintic Stuart-Landau equation ( 4.24 ). In Figure 7, the values of the parameters are the same as in Figure 6. Here $b_{s}=0.0444$ and $b_{c}=0.045$. The solid line indicates the stable states and the dashed line indicates the unstable ones.

4.2 Double and non-resonant eigenvalue

When $m=2$, the two pairs of allowed spatial modes $(\phi_{1},\psi _{1})$ and $(\phi_{2}, \psi_{2})$ satisfy the following no-resonance condition [38]:

$$\begin{aligned}& \begin{aligned} &\phi_{i}+\phi_{j}\neq \phi_{j} \quad\text{or} \quad\psi_{i}-\psi_{j} \neq\psi_{j} \\ &\text{and} \\ &\phi_{i}-\phi_{j}\neq\phi_{j} \quad\text{or} \quad\psi_{i}+\psi_{j}\neq\psi_{j},\end{aligned} \end{aligned}$$

(4.27)

with $i,j=1,2$ and $i\neq j$.

Pushing weakly nonlinear analysis up to $O(\varepsilon^{3})$, we get the following Stuart-Landau equations for the amplitudes $A_{1}$ and $A_{2}$ at the time $T(T_{2})$:

$$ \begin{aligned} &\frac{dA_{1}}{dT}=\sigma A_{1}-L_{1}A_{1}^{3}+S_{1}A_{1}A_{2}^{2}, \\ &\frac{dA_{2}}{dT}=\sigma A_{2}-L_{2}A_{2}^{3}+S_{2}A_{1}^{2}A_{2}, \end{aligned} $$

(4.28)

where the coefficients σ, $L_{l}$, $S_{l}$, with $l=1,2$, are given in Appendix A.2.1. For the existence and stability of the equilibria of equations (4.28), we have the following propositions.

Proposition 4.3

• (i) The trivial equilibrium $E_{0}=(0,0)$ always exists.

• (ii) The boundary equilibria $E_{1}^{\pm}=(\pm\sqrt{\frac{\sigma }{L_{1}}},0)$ exist if and only if $L_{1}>0$.

• (iii) The boundary equilibria $E_{2}^{\pm}=(0,\pm\sqrt{\frac{\sigma }{L_{2}}})$ exist if and only if $L_{2}>0$.

• (iv) The interior equilibria $E_{3}^{\pm}= ( \pm\sqrt{\frac{\sigma (L_{2}+S_{1})}{L_{1}L_{2}-S_{1}S_{2}}},\pm\sqrt{\frac{\sigma (L_{1}+S_{2})}{L_{1}L_{2}-S_{1}S_{2}}} )$ exist if and only if either $L_{1}L_{2}-S_{1}S_{2}<0$, $L_{1}+S_{2}<0$, $L_{2}+S_{1}<0$ or $L_{1}L_{2}-S_{1}S_{2}>0$, $L_{1}+S_{2}>0$, $L_{2}+S_{1}>0$.

By a linear stability analysis, we have the following results.

Proposition 4.4

• (i) The trivial equilibrium $E_{0}$ is an unstable node.

• (ii) The boundary equilibria $E_{1}^{\pm}$ are stable nodes if $L_{1}+S_{2}<0$.

• (iii) The boundary equilibria $E_{2}^{\pm}$ are stable nodes if $L_{2}+S_{1}<0$.

• (iv) The interior equilibria $E_{3}^{\pm}$ are locally asymptotically stable if $L_{1}L_{2}-S_{1}S_{2}>0$, $L_{1}+S_{2}>0$, $L_{2}+S_{1}>0$ and $L_{1}S_{1}+L_{2}S_{2}+2L_{1}L_{2}>0$, while they are saddle points if $L_{1}L_{2}-S_{1}S_{2}<0$, $L_{1}+S_{2}<0$ and $L_{2}+S_{1}<0$.

Proof

(i), (ii) and (iii) are easily checked; here we omit their proofs. For (iv), we only give the proof for the positive equilibrium $E_{3}^{+}= ( \sqrt{\frac{\sigma (L_{2}+S_{1})}{L_{1}L_{2}-S_{1}S_{2}}},\sqrt{\frac{\sigma (L_{1}+S_{2})}{L_{1}L_{2}-S_{1}S_{2}}} )$ as the other cases can be proved similarly. Linearizing system (4.28) about $E_{3}^{+}$ yields the Jacobian matrix as follows:

$$ J=\left ( \begin{matrix}{} \frac{-2\sigma L_{1}L_{2}-2\sigma L_{1}S_{1}}{L_{1}L_{2}-S_{1}S_{2}} & 2S_{1}\sqrt{\frac{\sigma (L_{2}+S_{1})}{L_{1}L_{2}-S_{1}S_{2}}}\sqrt{\frac{\sigma (L_{1}+S_{2})}{L_{1}L_{2}-S_{1}S_{2}}}\\ 2S_{2}\sqrt{\frac{\sigma(L_{2}+S_{1})}{L_{1}L_{2}-S_{1}S_{2}}}\sqrt {\frac{\sigma(L_{1}+S_{2})}{L_{1}L_{2}-S_{1}S_{2}}}&\frac{-2\sigma L_{1}L_{2}-2\sigma L_{2}S_{2}}{L_{1}L_{2}-S_{1}S_{2}} \end{matrix} \right ) . $$

Then the characteristic equation of the linearized system can be calculated as follows:

$$ \lambda^{2}+\frac{2\sigma (L_{1}S_{1}+L_{2}S_{2}+2L_{1}L_{2})}{L_{1}L_{2}-S_{1}S_{2}}\lambda +\frac{4\sigma^{2}(L_{1}+S_{2})(L_{2}+S_{1})}{L_{1}L_{2}-S_{1}S_{2}}=0. $$

(4.29)

When $L_{1}L_{2}-S_{1}S_{2}>0$, $L_{1}+S_{2}>0$, $L_{2}+S_{1}>0$ and $L_{1}S_{1}+L_{2}S_{2}+2L_{1}L_{2}>0$, it is easy to know that all the zeros of the characteristic equation (4.29) have negative real parts. However, the characteristic equation (4.29) has at least one positive real zero when $L_{1}L_{2}-S_{1}S_{2}<0$, $L_{1}+S_{2}<0$ and $L_{2}+S_{1}<0$. This completes the proof. □

Remark 2

From the above analysis, we see that the boundary equilibria $E_{1}^{\pm}$ and $E_{2}^{\pm}$ are unstable when any equilibrium in $E_{3}^{\pm}$ exists and is stable. When one of the two boundary equilibria $E_{1}$, $E_{2}$ is stable, the interior equilibria $E_{3}^{\pm}$ are all unstable. Thus, we shall distinguish two kinds of stationary patterns: (i): a single mode stationary pattern when any of the equilibria $E_{1}^{\pm}$ or $E_{2}^{\pm}$ is stable; (ii): a mixed-mode stationary pattern when any of the equilibria $E_{3}^{\pm}$ is stable.

Remark 3

It should be pointed out that the stability condition of the interior equilibria $E_{3}^{\pm}$ requires that $L_{1}S_{1}+L_{2}S_{2}+2L_{1}L_{2}>0$ but not $L_{1}S_{1}+L_{2}S_{2}+2L_{1}L_{2}<0$, emerging in [38]. Here we give a detailed analysis and the corrected proof.

Suppose that system (4.28) admits at least one stable equilibrium $(A_{1\infty}, A_{2\infty})$. Then we have the following conclusion.

Proposition 4.5

Assume that the hypothesis (i) of Proposition  4.1 and the no-resonance condition (4.27) hold. Then system (1.3) has an asymptotic solution,

$$ \left ( \begin{matrix}u(x,y)\\ v(x,y) \end{matrix} \right ) =\left ( \begin{matrix}u_{\ast}\\ v_{\ast} \end{matrix} \right ) +\varepsilon{\boldsymbol{\varrho}} \sum _{i=1}^{2}A_{i\infty}\cos(\phi_{i} x) \cos(\psi_{i} y)+O\bigl(\varepsilon^{2}\bigr), $$

(4.30)

where $(A_{1\infty}, A_{2\infty})$ is a stable equilibrium of system (4.28).

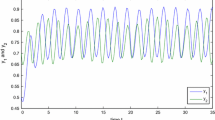
In Figure 8, we show the pattern formation, starting from initial conditions, which reveals random periodic perturbations about the equilibrium $(0.167, 4.8763)$. Here we consider the rectangular domain with $L_{x}=8\pi$ and $L_{y}=4\pi$. With these parameter values the only admitted unstable mode is chosen as $\hat{k}_{c}^{2}=0.8125\in [0.8021,2.4506]$, which is the band of the unstable modes. Then there exist two mode pairs $(4,3)$ and $(6,2)$ which satisfy the condition (4.17) and the non-resonant condition (4.27). By a calculation, we have $L_{1}=L_{2}=3.6765$, $S_{1}=S_{2}=-51.6425$. Then we get $L_{1}+S_{2}=L_{2}+S_{1}=-47.9662<0$, $L_{1}L_{2}-S_{1}S_{2}=-2653.4<0$. Therefore, the equilibria $E_{1}^{\pm }$ and $E_{2}^{\pm}$ are all stable and $E_{3}^{\pm}$ are all unstable. Therefore, the predicted asymptotic solution is the following single mode pattern:

$$ {\mathbf {w}}=\varepsilon{\boldsymbol{\varrho}} \bigl( A_{1\infty}\cos (0.5x) \cos(0.75y) \bigr) +O\bigl(\epsilon^{2}\bigr) $$

(4.31)

or

$$ {\mathbf {w}}=\varepsilon{\boldsymbol{\varrho}} \bigl( A_{2\infty}\cos (0.75x)\cos(0.5y) \bigr) +O\bigl(\epsilon^{2}\bigr), $$

(4.32)

where $A_{1\infty}$ and $A_{2\infty}$ are the coordinates of the equilibria $E_{1}^{\pm}$ and $E_{2}^{\pm}$, respectively. In Figure 8, we see a good qualitative agreement of the approximation (4.31) or (4.32) with the numerical solution of the full system (1.3).

Figure 8

Single mode pattern. Figure 8 gives the comparison among the numerical solution of system (1.3) (left), the weakly nonlinear first order approximation of the solution with stable equilibrium $(A_{1\infty},0)$ (medium) and the weakly nonlinear first order approximation of the solution with stable equilibrium $(0, A_{2\infty})$ (right) under double and non-resonant eigenvalue case. The parameters are $r_{1}=0.6$, $r_{2}=0.3$, $c_{1}=c_{2}=0.1$, $d_{1}=d_{2}=0.1$, $\alpha_{21}=0.3$, $a_{1}=0.1$, $a_{2}=0.2$, $\alpha_{12}=0.4$, $\beta_{1}=0.2$. Here $b^{c}=0.993$, $\varepsilon=0.36$ and $b=(1+\epsilon^{2})b^{c}$.

According to the parameter values of Figure 9, the only admitted unstable mode is chosen as $\hat{k}_{c}^{2}=1.25$, which belongs to the band of unstable modes allowed by the boundary conditions. Then the two mode pairs $(8,2)$ and $(4,4)$ satisfy the conditions (4.17) and (4.27). From (4.28), we obtain $\sigma _{1}=\sigma_{2}=0.2324$, $L_{1}=L_{2}=0.6442$, $S_{1}=S_{2}=-0.1545$. Thus the only stable positive equilibrium is $E_{3}^{+}$ according to Proposition 4.4. Therefore, the predicted asymptotic solution given by the positive equilibrium $E_{3}^{+}$ is the following mixed-mode pattern:

$$ {\mathbf {w}}=\varepsilon{\boldsymbol{\varrho}} \bigl( A_{1\infty}\cos (x)\cos(0.5y)+A_{2\infty}\cos(0.5x)\cos(y) \bigr) +O \bigl(\epsilon^{2}\bigr), $$

(4.33)

where $A_{1\infty}$ and $A_{2\infty}$ are the coordinates of the positive equilibrium $E_{3}^{+}$. Figure 9 provides the comparison between the numerical solution of system (1.3) and the weakly nonlinear approximation solution with $L_{x}=8\pi$ and $L_{y}=4\pi$ at the first order.

Figure 9

Mixed-mode pattern. Figure 9 gives the comparison between the numerical solution of system (1.3) (left) and the weakly nonlinear first order approximation of the solution (right) in the double and non-resonant eigenvalue case. The parameters are the same as in Figure 6 except that $\alpha_{12}=0.5$ and $\beta_{1}=0.02$. Here $b^{c}=0.2676$, $\varepsilon=0.1$ and $b=(1+\varepsilon^{2})b^{c}$.

According to the parameter values of Figure 10, the only unstable model is chosen as $\hat{k}_{c}^{2}=1.25$, which falls within the band of admitted unstable modes. Then there exist the two mode pairs $(8,4)$ and $(4,8)$ satisfying the conditions (4.17) and (4.27). The predicted asymptotic solution has the same form as (4.33). From Figures 9 and 10, we see a significant quantitative discrepancy between the numerical solution of the original system and the approximated solution. The fact that the weakly nonlinear analysis has poorer performances in predicting the mixed-mode pattern was also reported in [38].

Figure 10

Mixed-mode super-squares pattern. Figure 10 gives the comparison between the numerical solution of system (1.3) (left) and the weakly nonlinear first order approximation of the solution (right) under double and non-resonant eigenvalue case. The parameter values are chosen the same as in Figure 9. Here a square domain with $L_{x}=L_{y}=8\pi$ is chosen.

4.3 Double and resonant eigenvalue

When $m=2$, the two pairs of allowed spatial modes $(\phi_{1},\psi _{1})$ and $(\phi_{2}, \psi_{2})$ satisfy the following resonance condition [38]:

$$\begin{aligned} \begin{aligned} &\phi_{i}+\phi_{j}= \phi_{j} \quad\text{and}\quad \psi_{i}-\psi_{j}= \psi_{j} \\ &\text{or} \\ &\phi_{i}-\phi_{j}= \phi_{j} \quad\text{and} \quad \psi_{i}+\psi_{j}= \psi_{j}, \end{aligned} \end{aligned}$$

(4.34)

with $i,j=1,2$ and $i\neq j$. In what follows, without of loss generality, we shall assume that the first conditions in (4.34) hold with $i=2$, $j=1$. Thus it follows that $\phi_{2}=0$, $\psi _{2}=\hat{k}_{c}$, $\psi_{1}=\frac{\hat{k}_{c}}{2}$, $\phi_{1}=\sqrt {3}\psi_{1}$ and $\psi_{2}=2\psi_{1}$.

When the resonance condition (4.34) holds, the solution (4.14) at the order ε reads

$$ {\mathbf {w}}_{1}=A_{1}\boldsymbol{\varrho}\cos(\sqrt{3} \psi_{1} x)\cos (\psi_{1} y)+A_{2}\boldsymbol{ \varrho}\cos(2\psi_{1} y). $$

(4.35)

By imposing the solvability condition at $O(\varepsilon^{2})$ to equation (4.10), we obtain the Stuart-Landau equations as follows:

$$ \begin{aligned} &\frac{\partial A_{1}}{\partial T_{1}}=\tilde{\sigma}A_{1}- \tilde {L}A_{1}A_{2}, \\ &\frac{\partial A_{2}}{\partial T_{1}}=\tilde{\sigma}A_{2}- \frac {\tilde{L}}{4}A_{1}^{2}. \end{aligned} $$

(4.36)

Here the coefficients σ̃ and L̃ are given in Appendix A.3.1.

It is easy to see that the steady states of equation (4.36) are the trivial equilibrium $(0,0)$ and $E^{\pm}=(\pm\frac{2\tilde {\sigma}}{\tilde{L}}, \frac{\tilde{\sigma}}{\tilde{L}})$. By computing the eigenvalues of the Jacobian matrix evaluated at $E^{\pm }$, we obtain the stationary solutions $E^{\pm}$ are always unstable, and it is not possible to predict the amplitude of the pattern at this order. Therefore the weakly nonlinear analysis as regards the amplitude has to be pushed to a higher order to obtain some qualitatively results. Pushing the weakly nonlinear analysis to $O(\varepsilon ^{3})$, we obtain the following Stuart-Landau equations for the amplitudes $A_{1}$ and $A_{2}$ at the time $T(T_{1},T_{2})$:

$$ \begin{aligned} &\frac{dA_{1}}{dT}=\bar{\sigma}_{1}A_{1}- \bar{L}_{1} A_{1}A_{2}+\bar{\gamma}_{1} A_{1}^{3}+\bar{\delta }_{1}A_{1}A_{2}^{2}, \\ &\frac{dA_{2}}{dT}=\bar{\sigma}_{2}A_{2}- \bar{L}_{2} A_{1}^{2}+\bar {\gamma}_{2} A_{2}^{3}+\bar{\delta}_{2}A_{1}^{2}A_{2}, \end{aligned} $$

(4.37)

where the coefficients in (4.37) are given in Appendix A.3.2. Then we can draw a conclusion from the weakly nonlinear analysis about the resonant case as follows.

Proposition 4.6

Assume that the hypothesis (i) of Proposition  4.1 and the resonance condition (4.34) hold. Then system (1.3) has an asymptotic solution

$$ \left ( \begin{matrix}u(x,y)\\ v(x,y) \end{matrix} \right ) =\left ( \begin{matrix}u_{\ast}\\ v_{\ast} \end{matrix} \right ) +\varepsilon{\boldsymbol{\varrho}} \sum _{i=1}^{2}A_{i\infty}\cos(\phi_{i} x) \cos(\psi_{i} y)+O\bigl(\varepsilon^{2}\bigr), $$

(4.38)

where $(A_{1\infty}, A_{2\infty})$ is a stable equilibrium of system (4.37).

Clearly, system (4.37) has a trivial equilibrium $E_{0}=(0,0)$. The boundary equilibrium $R^{\pm}=(0,\pm\sqrt{\frac {-\bar{\sigma}_{2}}{\bar{\gamma}_{2}}})$ exists if and only if $\bar{\gamma}_{2}<0$. System (4.37) admits an interior equilibrium $H=(A_{1}, A_{2})$ if H is a solution to the following two equations:

$$\begin{aligned} \textstyle\begin{cases} A_{2}^{3}(\bar{\gamma}_{1}\bar{\gamma}_{2}-\bar{\delta}_{1}\bar {\delta}_{2})+A_{2}^{2}(\bar{L}_{1}\bar{\delta}_{2}+\bar {L}_{2}\bar{\delta}_{1})+A_{2}(\bar{\gamma}_{1}\bar{\sigma }_{2}-\bar{L}_{1}\bar{L}_{2}-\bar{\sigma}_{1}\bar{\delta }_{2})+\bar{\sigma}_{1}\bar{L}_{2}=0,\\ A_{1}^{2}=\frac{-\bar{\sigma}_{1}+\bar{L}_{1}A_{2}-\bar{\delta }_{1}A_{2}^{2}}{\bar{\gamma}_{1}}. \end{cases}\displaystyle \end{aligned}$$

(4.39)

Without loss of generality, we assume the first equation of (4.39) has three real roots, denoted by $A_{2i}$, $i=1,2,3$. Substituting it into the second equation of (4.39) yields the existence of interior equilibria as follows.

Proposition 4.7

System (4.37) has six interior equilibria $H_{i}^{\pm}= ( \pm\sqrt{\frac{-\bar{\sigma}_{1}+\bar{L}_{1}A_{2i}-\bar{\delta }_{1}A_{2i}^{2}}{\bar{\gamma}_{1}}}, A_{2i} )$ if and only if $\bar{\gamma}_{1}(-\bar{\sigma}_{1}+\bar{L}_{1}A_{2i}-\bar{\delta }_{1}A_{2i}^{2})>0$ for $i=1,2,3$.

To investigate the stability of the interior equilibrium $(A_{1i}, A_{2i})$, linearizing system (4.37) yields the Jacobian matrix about it as follows:

$$ \bar{J}=\left ( \begin{matrix}{} \bar{\sigma}_{1}-\bar{L}_{1}A_{2i}+3\bar{\gamma }_{1} A_{1i}^{2}+\bar{\delta}_{1}A_{2i}^{2}& -\bar {L}_{1}A_{1i}+2\bar{\delta}_{1}A_{1i}A_{2i}\\ -2\bar{L}_{2}A_{1i}+2\bar{\delta}_{2}A_{1i}A_{2i}&\bar{\sigma }_{2}+3\bar{\gamma}_{2}A_{2i}^{2}+\bar{\delta}_{2}A_{1i}^{2} \end{matrix} \right ) . $$

Denote

$$\begin{aligned} &\operatorname {tr}(\bar{J}_{i})=\bar{\sigma}_{1}+\bar{\sigma }_{2}+(3\bar{\gamma}_{1}+\bar{\delta}_{2})A_{1i}^{2}+(3 \bar{\gamma }_{2}+\bar{\delta}_{1})A_{2i}^{2}- \bar{L}_{1}A_{2i}, \\ &\begin{aligned} \operatorname {det}(\bar{J}_{i})&=3\bar{\gamma}_{1}\bar{\delta }_{2}A_{1i}^{4}+3\bar{\delta}_{1}\bar{ \gamma}_{2}A_{2i}^{4}+ (9\bar{\gamma}_{1} \bar{\gamma}_{2}-3\bar{\delta}_{1}\bar{\delta }_{2})A_{1i}^{2}A_{2i}^{2}-3 \bar{L}_{1}\bar{\gamma }_{2}A_{2i}^{3}+( \bar{L}_{1}\bar{\delta}_{2}+4\bar{L}_{2}\bar { \delta}_{1})A_{1i}^{2}A_{2i} \\ &\quad{}+(\bar{\sigma}_{1}\bar{\delta}_{2}-2\bar {L}_{1}\bar{L}_{2}+3\bar{\sigma}_{2}\bar{\gamma }_{1})A_{1i}^{2}+(3\bar{\sigma}_{1}\bar{ \gamma}_{2}+\bar{\sigma }_{2}\bar{\delta}_{1})A_{2i}^{2} -\bar{\sigma}_{2}\bar{L}_{1}A_{2i}+\bar{ \sigma}_{1}\bar{\sigma}_{2}, \end{aligned} \end{aligned}$$

where $A_{1i}^{2}=\frac{-\bar{\sigma}_{1}+\bar{L}_{1}A_{2i}-\bar {\delta}_{1}A_{2i}^{2}}{\bar{\gamma}_{1}}$.

Then we have the following stability results about the equilibria of system (4.37).

Proposition 4.8

• (i) The trivial equilibrium $E_{0}$ is an unstable node.

• (ii) The boundary equilibrium $R^{+}$ is a stable node if $\bar {\sigma}_{1}<\bar{L}_{1}\sqrt{\frac{-\bar{\sigma}_{2}}{\bar {\gamma}_{2}}}+\frac{\bar{\delta}_{1}\bar{\sigma}_{2}}{\bar {\gamma}_{2}}$, while unstable if $\bar{\sigma}_{1}>\bar {L}_{1}\sqrt{\frac{-\bar{\sigma}_{2}}{\bar{\gamma}_{2}}}+\frac {\bar{\delta}_{1}\bar{\sigma}_{2}}{\bar{\gamma}_{2}}$. The boundary equilibrium $R^{-}$ is a stable node if $\bar{\sigma }_{1}<-\bar{L}_{1}\sqrt{\frac{-\bar{\sigma}_{2}}{\bar{\gamma }_{2}}}+\frac{\bar{\delta}_{1}\bar{\sigma}_{2}}{\bar{\gamma }_{2}}$, while unstable if $\bar{\sigma}_{1}>-\bar{L}_{1}\sqrt {\frac{-\bar{\sigma}_{2}}{\bar{\gamma}_{2}}}+\frac{\bar{\delta }_{1}\bar{\sigma}_{2}}{\bar{\gamma}_{2}}$.

• (iii) The equilibria $H_{i}^{\pm}$ are locally asymptotically stable if $\operatorname {tr}(\bar{J}_{i})<0$ and $\operatorname {det}(\bar{J}_{i})>0$, while unstable if $\operatorname {det}(\bar{J}_{i})<0$.

Proof

The proof is trivial, we omit it. □

According to the parameter values of Figure 11, we get the critical value $b^{c}=1.0769$, letting $\varepsilon=0.03$ be a very small positive constant. The only admitted discrete unstable mode is chosen as $\hat{k}_{c}^{2}=2.25\in[0.8428, 2.9863]$, which is the band of unstable modes allowed by the boundary conditions. Then there exist two mode pairs $(18,3)$ and $(0,6)$ satisfying the conditions (4.15) and (4.34). By (A.8), we get $\bar{\sigma }_{1}=\bar{\sigma}_{2}=0.8156$, $\bar{L}_{1}=0.8037$, $\bar {L}_{2}=0.2009$, $\bar{\gamma}_{1}=0.0808$, $\bar{\gamma}_{2}=-0.2169$, $\bar{\delta}_{1}=0.1631$, $\bar{\delta}_{2}=0.0816$. Thus according to Proposition 4.8, the only stable equilibrium of system (4.37) is $R^{+}=(0, 1.9391)$. Therefore the predicted asymptotic solution of system (1.3) via the weakly nonlinear analysis is the following single mode pattern:

$$ {\mathbf {w}}=1.9391\varepsilon{\boldsymbol{\varrho}}\cos (1.5y)+O\bigl( \varepsilon^{2}\bigr). $$

(4.40)

By performing 20 thousand simulations, which start from a random periodic perturbation of the equilibrium of $(0.3236,5.2918)$, we observe that the solution eventually evolves to the hexagonal pattern on the left of Figure 11. However, by equation (4.40), we obtain the roll pattern on the right of Figure 11.

Figure 11

Double and resonant eigenvalue case with the only stable state $\pmb{R^{+}=(0,1.9391)}$ . In Figure 11, the parameters are chosen as $r_{1}=0.6\ r_{2}=0.3$, $c_{1}=c_{2}=0.1$, $d_{1}=d_{2}=0.1$, $\alpha_{12}=0.5$, $\beta_{1}=0.2$, $\alpha_{21}=0.3$, $a_{1}=0.1$, $a_{2}=0.2$. Here $b^{c}=0.9947$, $\varepsilon=0.03$ and $b=1.0254$. We give the comparison between the numerical solution of system (1.3) (left) and the weakly nonlinear first order approximation of the solution (right) with the only stable state $R^{+}=(0, 1.9391)$ under double and resonant eigenvalue case. The spatial domain is confined to a rectangular domain with $L_{x}=8\sqrt{3}\pi$ and $L_{y}=4\pi$.

According to the parameter values of Figure 12, the only admitted allowed unstable mode is chosen as $\hat{k}_{c}^{2}=1$, which falls within the band of unstable modes allowed by the boundary conditions. Then the two pair modes $(12,2)$ and $(0,4)$ satisfy the conditions (4.15) and the resonance conditions (4.34). By (A.8), we get $\bar{\sigma}_{1}=\bar{\sigma}_{2}=0.2642$, $\bar {L}_{1}=0.083$, $\bar{L}_{2}=0.0207$, $\bar{\gamma}_{1}=-0.0517$, $\bar {\gamma}_{2}=0.4712$, $\bar{\delta}_{1}=-0.8454$, $\bar{\delta }_{2}=-0.4712$. Since $\bar{\gamma}_{2}>0$, the boundary equilibria $R^{\pm}$ do not exist. By a calculation, we have two interior equilibria $H_{1}^{\pm}=(\pm2.2682, -0.0559)$ and $\operatorname {tr}(\bar {J}_{1})=-2.4383<0$ and $\operatorname {det}(\bar{J}_{1})=1.0144>0$. Thus the two interior equilibria are stable according to Proposition 4.8. Then the predicted asymptotic solution by the two stable states $H_{1}^{\pm}$ can be expressed as

$$ {\mathbf {w}}=\varepsilon{\boldsymbol{\varrho}}\bigl(2.2682\cos(\sqrt {3}x/{2}) \cos(0.5y)-0.0559\cos(y)\bigr)+O\bigl(\epsilon^{2}\bigr) $$

or

$$ {\mathbf {w}}=\varepsilon{\boldsymbol{\varrho}}\bigl(-2.2682\cos(\sqrt {3}x/{2}) \cos(0.5y)-0.0559\cos(y)\bigr)+O\bigl(\epsilon^{2}\bigr). $$

From Figure 12, we also observe a qualitative agreement of the approximation with the numerical solution of the original system.

Figure 12

Double and resonant eigenvalue case with the stable state $\pmb{H_{1}^{+}=(2.2682,-0.0559)}$ . In Figure 12, the parameters are $r_{1}=0.6$, $r_{2}=0.3$, $c_{1}=c_{2}=0.1$, $d_{1}=d_{2}=0.1$, $\alpha_{12}=0.6$, $\beta_{1}=0.25$, $\alpha_{21}=0.3$, $a_{1}=0.1$, $a_{2}=0.1$. Here $b^{c}=1.0769$, $\varepsilon=0.15$ and $b=1.2627$. The rectangular domain is chosen the same as in Figure 11. We give the comparison between the numerical solution of system (1.3) (left) and the weakly nonlinear first order approximation of the solution (right) with the stable state $H_{1}^{+}=(2.2682, -0.0559)$ in the double and resonant eigenvalue case.

5 Details of numerical simulations

In all numerical simulations, for the choice of the parameter values in our system (1.3), we refer to [3, 8] and Table 1 for their units. The numerical simulations presented in this paper have been performed utilizing a Chebyshev spectral method according to the following steps [50]:

Step 1::

According to the Euler method, discretize $\frac {\partial u}{\partial t}$ and $\frac{\partial v}{\partial t}$ as follows:

$$ \frac{\partial u}{\partial t}\rightarrow\frac {u(t+\Delta t)-u(t)}{\Delta t},\quad\quad\frac{\partial v}{\partial t} \rightarrow\frac{v(t+\Delta t)-v(t)}{\Delta t}. $$

Step 2::

Calculate the Chebyshev differentiation matrices at Chebyshev points $(x_{0}, x_{1}, \ldots, x_{N})^{T}$, which we shall denote by $D_{N}$. Discretize the functions u, v at the Chebyshev points as $u_{(N+1)\times(N+1)}$ and $v_{(N+1)\times(N+1)}$. Utilizing the Chebyshev differentiation matrices to deal with the diffusive term $\frac{\partial^{2}u}{\partial x^{2}}+\frac{\partial^{2}u}{\partial y^{2}}$, we have

$$ \frac{\partial^{2}u}{\partial y^{2}}\rightarrow D_{N}^{2}u_{(N+1)\times(N+1)}, \quad\quad\frac{\partial ^{2}u}{\partial x^{2}}\rightarrow u_{(N+1)\times(N+1)}\bigl(D_{N}^{2} \bigr)^{T}. $$

Step 3::

By the relation $(u^{\prime}(x_{0}), u^{\prime }(x_{1}), \ldots, u^{\prime}(x_{N}))=D_{N}(u_{0}, u_{1}, \ldots, u_{N})^{T}$, we deal with the Neumann boundary conditions, where $(u_{0}, u_{1}, \ldots, u_{N})^{T}$ is the vector value of the function u at Chebyshev points $(x_{0}, x_{1}, \ldots, x_{N})^{T}$.

To show the pattern formation around the unique positive spatially homogeneous steady state $E_{\ast}$, we choose the initial condition to be a small perturbation around the unique steady state $E_{\ast}$:

$$u(x,y,0)=u_{\ast}+\varepsilon\cos x\sin y,\quad\quad v(x,y,0)=v_{\ast}+\varepsilon\cos x\sin y \quad \text{with } \varepsilon=0.001. $$

In addition, in our 2D numerical experiments, the time step is always chosen as 0.001, which was always small enough to ensure the numerical stability of the method, and we have always used the same spatial step for the two spatial directions and the number of Chebyshey points was always chosen as $N=64$ to ensure the spectral method accuracy.

6 Conclusions

In this paper, we have investigated the Turing mechanism and the phenomena of pattern formation induced by nonlinear cross-diffusion in a uni-directional C-R system. We discuss in detail the asymptotic behavior of patterns by virtue of amplitude equation in three cases: simple eigenvalue, double and non-resonant eigenvalue, double and resonant eigenvalue. In every case, we give a detailed analysis and make a comparison between a numerical solution of system (1.3) and its weakly nonlinear approximation solution by numerical simulations. In our numerical simulations, we show that the system exhibits patterns like rhombic pattern, mixed-mode pattern, super-squares pattern, roll, and hexagonal pattern. We also tested the influence of the resource supply rate $\beta_{1}$ on the bifurcation direction (see Figure 5), and found that the bifurcation direction varied when we changed the parameter $\beta_{1}$. We have also found that there exists a hysteresis cycle as the bifurcation parameter b starts from the value larger that its critical value $b^{c}$, then decreases to become less than another threshold value, $b^{s}$, and next increases to become larger than $b^{c}$ (see Figure 7). Clearly, comparing our results with those in [8], the effect caused by the nonlinear cross-diffusion was presented.

Appendix:  The weakly nonlinear analysis

1.1 A.1 Simple eigenvalue case

1.1.1 A.1.1 The coefficients of system (4.21)

Once we have defined ${\boldsymbol{\Gamma}}=\bigl( {\scriptsize\begin{matrix}{}f_{122}^{1}M^{2}+f_{222}^{1}M^{3}\cr f_{112}^{2}M+f_{111}^{2} \end{matrix}} \bigr)$, the coefficients ${\mathbf {H}}_{11}^{(j)}$, $j=1,3$ and ${\mathbf {H}}^{\ast}$ in (4.21) are given here:

$$ \begin{aligned} &{\mathbf {H}}_{11}^{(1)}=b^{(2)}{ \hat{k}}_{c}^{2}\left ( \begin{matrix} 0 \\ u_{\ast}M+v_{\ast} \end{matrix} \right ) , \\ &{\mathbf {H}}_{11}^{(3)}=-\mathcal{M}_{11}^{1} \biggl( \boldsymbol{\varrho }, {\mathbf {w}}_{200}+\frac{1}{2}{ \mathbf {w}}_{202}+\frac{1}{2}{\mathbf {w}}_{220}+ \frac{1}{4}{\mathbf {w}}_{222} \biggr) -\frac{9}{16}{ \boldsymbol {\Gamma}}, \end{aligned} $$

and

$${\mathbf {H}}^{\ast}={\mathbf {H}}_{1}^{\ast}\cos(3 \phi_{1} x)\cos(\psi_{1} y)+{\mathbf {H}}_{2}^{\ast} \cos(\phi_{1} x)\cos(3\psi_{1} y)+{\mathbf {H}}_{3}^{\ast}\cos(3\phi_{1} x)\cos(3 \psi_{1} y), $$

with

$$ \begin{aligned} &{\mathbf {H}}_{1}^{\ast}=- \frac{1}{2}\mathcal{M}_{31}^{1} \biggl( {\boldsymbol{ \varrho}},{\mathbf {w}}_{220}+\frac{1}{2}{\mathbf {w}}_{222} \biggr) -\frac{3}{16} {\boldsymbol{\Gamma}}, \\ &{\mathbf {H}}_{2}^{\ast}=-\frac{1}{2} \mathcal{M}_{13}^{1} \biggl( {\boldsymbol{\varrho}},{\mathbf {w}}_{202}+\frac{1}{2}{\mathbf {w}}_{222} \biggr) - \frac{3}{16} {\boldsymbol{\Gamma}}, \\ &{\mathbf {H}}_{3}^{\ast}=-\frac{1}{4} \mathcal{M}_{33}^{1} ( {\boldsymbol{\varrho}},{\mathbf {w}}_{222} ) -\frac{1}{16} {\boldsymbol{\Gamma}}. \end{aligned} $$

1.1.2 A.1.2 The coefficients of system (4.24)

Substituting (4.2)-(4.8) into (4.1), we obtain the same equations as presented in (4.9)-(4.11). Obviously (4.22) still holds for the amplitude $A_{1}$, except now it is a partial derivative with respect to $T_{2}$. Noticing the solvability condition $\langle{\mathbf {H}}, {\boldsymbol{\varphi}}\rangle =0$ to equation (4.12) is satisfied, the solution of (4.12) satisfying the Neumann boundary conditions is given by

$$ {\mathbf {w}}_{3}=A_{1}{\mathbf {w}}_{311}^{(1)} \cos(\phi_{1} x)\cos(\psi_{1} y)+A_{1}^{3} \sum_{i,j=1,3}{\mathbf {w}}_{3ij}\cos(i \phi_{1} x)\cos (j\psi_{1} y), $$

where the vectors ${\mathbf {w}}_{3ij}$, $i,j=1,3$ are determined by the following linear equations, respectively:

$$\begin{aligned}& \begin{aligned} &\mathfrak{L}_{11}^{1}{\mathbf {w}}_{311}^{(1)}={\mathbf {H}}_{11}^{(1)}+\sigma {\boldsymbol{\varrho}}, \quad \quad \mathfrak{L}_{11}^{1}{ \mathbf {w}}_{311}={\mathbf {H}}_{11}^{(3)}-L{\boldsymbol {\varrho}}, \\ &\mathfrak{L}_{31}^{1}{\mathbf {w}}_{331}={\mathbf {H}}_{1}^{\ast},\quad\quad \mathfrak{L}_{13}^{1}{ \mathbf {w}}_{313}={\mathbf {H}}_{2}^{\ast}, \quad\quad \mathfrak{L}_{33}^{1}{\mathbf {w}}_{333}={\mathbf {H}}_{3}^{\ast}. \end{aligned} \end{aligned}$$

(A.1)

Once we have defined ${\boldsymbol{\Theta}}=\bigl( {\scriptsize\begin{matrix}{}f_{1222}^{1}M^{3}+f_{2222}^{1}M^{4}\cr f_{1112}^{2}M+f_{1111}^{2} \end{matrix}} \bigr)$, according to (4.12), the vector P is given by

$$ \begin{aligned} {\mathbf {P}}&=\sum_{i,j=0,2}A_{1}^{2}{ \mathbf {P}}_{ij}^{(1)}\cos(i\phi _{1} x)\cos(j \psi_{1} y)+\sum_{i,j=0,2,4}A_{1}^{4}{ \mathbf {P}}_{ij}\cos(i\phi_{1} x)\cos(j\psi_{1} y) \\ &\quad{} +{ \mathbf {P}}_{11}\cos(\phi _{1} x)\cos(\psi_{1} y), \end{aligned} $$

where

$$\begin{aligned} &{\mathbf {P}}_{00}^{(1)}=2\sigma{\mathbf {w}}_{200}- \frac{1}{4}\mathcal {M}_{00}^{1}\bigl(\boldsymbol{ \varrho},{\mathbf {w}}_{311}^{(1)}\bigr), \\ & \begin{aligned} {\mathbf {P}}_{00}&=-2L{\mathbf {w}}_{200}-\frac{1}{4} \mathcal {M}_{00}^{1}(\boldsymbol{\varrho},{\mathbf {w}}_{311})-\frac{1}{2}\mathcal {M}_{00}^{1}({ \mathbf {w}}_{200}, {\mathbf {w}}_{200})-\frac{1}{4}\mathcal {M}_{00}^{1}({\mathbf {w}}_{220}, {\mathbf {w}}_{220})- \\ &\quad{} -\frac{1}{4}\mathcal{M}_{00}^{1}({ \mathbf {w}}_{202}, {\mathbf {w}}_{202})-\frac{1}{8} \mathcal{M}_{00}^{1}({\mathbf {w}}_{222}, {\mathbf {w}}_{222})- \frac{9}{64}{\boldsymbol{\Theta}}, \end{aligned} \\ &{\mathbf {P}}_{11}=\frac{\partial A_{1}}{\partial T_{3}}{\boldsymbol { \varrho}}+b^{(3)}A_{1}\hat{k}_{c}^{2} \left ( \begin{matrix}0\\ u_{\ast}M+v_{\ast} \end{matrix} \right ) , \\ &{\mathbf {P}}_{20}^{(1)}=-\frac{1}{4} \mathcal{M}_{20}^{1}\bigl(\boldsymbol {\varrho},{\mathbf {w}}_{311}^{(1)}\bigr)+2\sigma{\mathbf {w}}_{220}+b^{(2)} \phi _{1}^{2}\left ( \begin{matrix}0\\ M \end{matrix} \right ) + 4b^{(2)}\phi_{1}^{2} \left ( \begin{matrix}0&0\\ v_{\ast}&u_{\ast} \end{matrix} \right ) {\mathbf {w}}_{220}, \\ & \begin{aligned} {\mathbf {P}}_{20}&=-2L{\mathbf {w}}_{220}-\frac{1}{4} \mathcal {M}_{20}^{1}(\boldsymbol{\varrho},{\mathbf {w}}_{311}+{\mathbf {w}}_{331})-\mathcal{M}_{20}^{1}({ \mathbf {w}}_{200},{\mathbf {w}}_{220})-\frac {1}{2} \mathcal{M}_{20}^{1}({\mathbf {w}}_{202},{\mathbf {w}}_{222}) \\ &\quad{}- \frac{3}{16}{\boldsymbol{\Theta}}, \end{aligned} \\ &{\mathbf {P}}_{02}^{(1)}=-\frac{1}{4} \mathcal{M}_{02}^{1}\bigl(\boldsymbol {\varrho},{\mathbf {w}}_{311}^{(1)}\bigr)+2\sigma{\mathbf {w}}_{202}+b^{(2)} \psi _{1}^{2}\left ( \begin{matrix}0\\ M \end{matrix} \right ) + 4b^{(2)}\psi_{1}^{2} \left ( \begin{matrix}0&0\\ v_{\ast}&u_{\ast} \end{matrix} \right ) {\mathbf {w}}_{202}, \\ &\begin{aligned} {\mathbf {P}}_{02}&=-2L{\mathbf {w}}_{202}-\frac{1}{4} \mathcal {M}_{02}^{1}(\boldsymbol{\varrho},{\mathbf {w}}_{311}+{\mathbf {w}}_{313})-\mathcal{M}_{02}^{1}({ \mathbf {w}}_{200},{\mathbf {w}}_{202})-\frac {1}{2} \mathcal{M}_{02}^{1}({\mathbf {w}}_{220},{\mathbf {w}}_{222}) \\ &\quad{}-\frac{3}{16}{\boldsymbol{\Theta}}, \end{aligned} \\ &{\mathbf {P}}_{22}^{(1)}=-\frac{1}{4} \mathcal{M}_{22}^{1}\bigl(\boldsymbol {\varrho},{\mathbf {w}}_{311}^{(1)}\bigr)+2\sigma{\mathbf {w}}_{222}+b^{(2)} \hat {k}_{c}^{2}\left ( \begin{matrix}0\\ M \end{matrix} \right ) + 4b^{(2)}\hat{k}_{c}^{2} \left ( \begin{matrix}0&0\\ v_{\ast}&u_{\ast} \end{matrix} \right ) {\mathbf {w}}_{222}, \\ &{\mathbf {P}}_{22}=-2L{\mathbf {w}}_{222}-\frac{1}{4} \mathcal {M}_{22}^{1}\biggl(\boldsymbol{\varrho},\sum _{i,j=1,3}{\mathbf {w}}_{3ij}\biggr)-\mathcal{M}_{22}^{1}({ \mathbf {w}}_{200}, {\mathbf {w}}_{222})-\mathcal {M}_{22}^{1}({\mathbf {w}}_{202}, {\mathbf {w}}_{220})-\frac{1}{4}{\boldsymbol {\Theta}}, \\ &{\mathbf {P}}_{40}=-\frac{1}{4}\mathcal{M}_{40}^{1}( \boldsymbol{\varrho }, {\mathbf {w}}_{331})-\frac{1}{4} \mathcal{M}_{40}^{1}({\mathbf {w}}_{220},{\mathbf {w}}_{220})-\frac{1}{8}\mathcal{M}_{40}^{1}({ \mathbf {w}}_{222}, {\mathbf {w}}_{222})-\frac{3}{64}{ \boldsymbol{\Theta}}, \\ &{\mathbf {P}}_{04}=-\frac{1}{4}\mathcal{M}_{04}^{1}( \boldsymbol{\varrho }, {\mathbf {w}}_{313})-\frac{1}{4} \mathcal{M}_{04}^{1}({\mathbf {w}}_{202},{\mathbf {w}}_{202})-\frac{1}{8}\mathcal{M}_{04}^{1}({ \mathbf {w}}_{222}, {\mathbf {w}}_{222})-\frac{3}{64}{ \boldsymbol{\Theta}}, \\ &{\mathbf {P}}_{42}=-\frac{1}{4}\mathcal{M}_{42}^{1}( \boldsymbol{\varrho }, {\mathbf {w}}_{331}+{\mathbf {w}}_{333})- \frac{1}{2}\mathcal{M}_{42}^{1}({\mathbf {w}}_{220}, {\mathbf {w}}_{222})-\frac{1}{16}{\boldsymbol{ \Theta}}, \\ &{\mathbf {P}}_{24}=-\frac{1}{4}\mathcal{M}_{24}^{1}( \boldsymbol{\varrho }, {\mathbf {w}}_{313}+{\mathbf {w}}_{333})- \frac{1}{2}\mathcal{M}_{24}^{1}({\mathbf {w}}_{202}, {\mathbf {w}}_{222})-\frac{1}{16}{\boldsymbol{ \Theta}}, \\ &{\mathbf {P}}_{44}=-\frac{1}{4}\mathcal{M}_{44}^{1}( \boldsymbol{\varrho }, {\mathbf {w}}_{333})-\frac{1}{8} \mathcal{M}_{44}^{1}({\mathbf {w}}_{222}, {\mathbf {w}}_{222})-\frac{1}{64}{\boldsymbol{\Theta}}. \end{aligned}$$

One imposes $T_{3}=0$ and $b^{(3)}=0$ and the compatibility condition for (4.12) is satisfied, then the solution satisfying the Neumann boundary conditions is

$$ {\mathbf {w}}_{4}=\sum_{i,j=0,2}A_{1}^{2}{ \mathbf {w}}_{4ij}^{(1)}\cos (i\phi_{1} x)\cos(j \psi_{1} y)+\sum_{i,j=0,2,4}A_{1}^{4}{ \mathbf {w}}_{4ij}\cos(i\phi_{1} x)\cos(j\psi_{1} y), $$

where ${\mathbf {w}}_{4ij}^{(1)}$, $i,j=0,2$ and ${\mathbf {w}}_{4ij}$, $i,j=0,2,4$ are the solutions of the following linear equations:

$$ \mathfrak{L}_{ij}^{1}{\mathbf {w}}_{4ij}^{(1)}={ \mathbf {P}}_{ij}^{(1)},\quad \quad\mathfrak{L}_{ij}^{1}{ \mathbf {w}}_{4ij}={\mathbf {P}}_{ij}. $$

(A.2)

According to (4.13), the vector Q is given by

$$ {\mathbf {Q}}= \biggl( \frac{\partial A_{1}}{\partial T_{4}} \boldsymbol {\varrho}+{\mathbf {Q}}_{11}^{(1)}A_{1}+{\mathbf {Q}}_{11}^{(3)}A_{1}^{3}+{ \mathbf {Q}}_{11}^{(5)}A_{1}^{5} \biggr) \cos(\phi_{1} x)\cos(\psi_{1} y)+{\mathbf {Q}}^{\ast}. $$

Here $Q^{\ast}$ contains terms which automatically satisfy the compatibility condition and

$$\begin{aligned} &{\mathbf {Q}}_{11}^{(1)}=\sigma{ \mathbf {w}}_{311}^{(1)}+\hat{k}_{c}^{2} \left ( \begin{matrix}0&0\\ v_{\ast}&u_{\ast} \end{matrix} \right ) \bigl(b^{(2)}{\mathbf {w}}_{311}^{(1)}+b^{(4)} \boldsymbol{\varrho}\bigr), \\ &\begin{aligned} {\mathbf {Q}}_{11}^{(3)}&=3\sigma{\mathbf {w}}_{311}-L{ \mathbf {w}}_{311}^{(1)}-\mathcal {M}_{11}^{1} \biggl(\boldsymbol{\varrho},{\mathbf {w}}_{400}^{(1)}+ \frac {1}{2}{\mathbf {w}}_{420}^{(1)}+\frac{1}{2}{ \mathbf {w}}_{402}^{(1)}+\frac {1}{4}{\mathbf {w}}_{422}^{(1)}\biggr) \\ &\quad{}- \mathcal{M}_{11}^{1}\biggl({\mathbf {w}}_{200}+\frac{1}{2}{\mathbf {w}}_{220}+ \frac{1}{2}{\mathbf {w}}_{202}+\frac{1}{4}{\mathbf {w}}_{222},{\mathbf {w}}_{311}^{(1)}\biggr)+b^{(2)} \hat{k}_{c}^{2}\left ( \begin{matrix}0&0\\ v_{\ast}&u_{\ast} \end{matrix} \right ) {\mathbf {w}}_{311} \\ &\quad{}+ b^{(2)}\hat{k}_{c}^{2}\left ( \begin{matrix}0\\ v_{200}+\frac{1}{2}v_{220}+\frac{1}{2}v_{202}+\frac {1}{4}v_{222}+M( u_{200}+\frac{1}{2}u_{220}+\frac{1}{2}u_{202}+\frac {1}{4}u_{222}) \end{matrix} \right ) , \end{aligned} \\ &\begin{aligned} {\mathbf {Q}}_{11}^{(5)}&=-3L{\mathbf {w}}_{311}-\mathcal{M}_{11}^{1}\biggl(\boldsymbol { \varrho}, {\mathbf {w}}_{400}+\frac{1}{2}{\mathbf {w}}_{420}+\frac{1}{2}{\mathbf {w}}_{402}+ \frac{1}{4}{\mathbf {w}}_{422}\biggr)-\frac{1}{2}\mathcal {M}_{11}^{1}({\mathbf {w}}_{220}, {\mathbf {w}}_{331}) \\ &\quad{} -\mathcal{M}_{11}^{1}\biggl({\mathbf {w}}_{311},{\mathbf {w}}_{200}+\frac{1}{2}{\mathbf {w}}_{220}+\frac{1}{2}{\mathbf {w}}_{202}+ \frac {1}{4}{\mathbf {w}}_{222}\biggr)-\frac{1}{2} \mathcal{M}_{11}^{1}({\mathbf {w}}_{202}, {\mathbf {w}}_{313}) \\ &\quad{} -\frac{1}{4}\mathcal{M}_{11}^{1}({ \mathbf {w}}_{222}, {\mathbf {w}}_{313}+{\mathbf {w}}_{331}+{\mathbf {w}}_{333})-\frac{25}{64}\left ( \begin{matrix}f_{12222}^{1}M^{4}+f_{22222}^{1}M^{5}\\ f_{11112}^{2}M+f_{11111}^{2} \end{matrix} \right ) , \end{aligned} \end{aligned}$$

where $\bigl( {\scriptsize\begin{matrix}{}u_{200}\cr v_{200} \end{matrix}} \bigr) ={\mathbf {w}}_{200}$, $\bigl( {\scriptsize\begin{matrix}{}u_{220}\cr v_{220} \end{matrix}} \bigr) ={\mathbf {w}}_{220}$, $\bigl( {\scriptsize\begin{matrix}{}u_{202}\cr v_{202} \end{matrix}} \bigr) ={\mathbf {w}}_{202}$, $\bigl( {\scriptsize\begin{matrix}{}u_{222}\cr v_{222} \end{matrix}} \bigr) ={\mathbf {w}}_{222}$.

The solvability condition for (4.13) yields

$$ \frac{\partial A_{1}}{\partial T_{4}}=\widehat{\sigma}A_{1}-\widehat {L}A_{1}^{3}+\widehat{R}A_{1}^{5}, $$

(A.3)

where the coefficients are

$$ \begin{aligned} &\widehat{\sigma}=-\frac{\langle{\mathbf {Q}}_{11}^{(1)}\cos(\phi_{1} x)\cos(\psi_{1} y),\boldsymbol{\varphi}\rangle}{\langle \boldsymbol{\varrho}\cos(\phi_{1} x)\cos(\psi_{1} y),\boldsymbol {\varphi}\rangle}, \quad\quad \widehat{L}= \frac{\langle{\mathbf {Q}}_{11}^{(3)}\cos (\phi_{1} x)\cos(\psi_{1} y),\boldsymbol{\varphi}\rangle}{\langle \boldsymbol{\varrho}\cos(\phi_{1} x)\cos(\psi_{1} y),\boldsymbol {\varphi}\rangle}, \\ &\widehat{R}=-\frac{\langle{\mathbf {Q}}_{11}^{(5)}\cos(\phi_{1} x)\cos (\psi_{1} y),\boldsymbol{\varphi}\rangle}{\langle\boldsymbol {\varrho}\cos(\phi_{1} x)\cos(\psi_{1} y),\boldsymbol{\varphi }\rangle}. \end{aligned} $$

Combining (4.6), (4.22) and (A.3), we get the quintic Stuart-Landau equation (4.24).

1.2 A.2 Double and non-resonant eigenvalue case

1.2.1 A.2.1 The coefficients of system (4.28)

When $m=2$, the solution of linear equation (4.9) is expressed as follows:

$$ {\mathbf {w}}_{1}=\boldsymbol{\varrho}A_{1}\cos( \phi_{1} x)\cos(\psi _{1} y)+\boldsymbol{\varrho}A_{2} \cos(\phi_{2} x)\cos(\psi_{2} y). $$

(A.4)

Using the same analysis as simple eigenvalue case, we impose $b^{(1)}=0$ and $T_{1}=0$ to equation (4.10) so that the information as regards the amplitude of the pattern can be predicted. The solution of linear problem (4.10) is then calculated as follows:

$$ \begin{aligned}[b] {\mathbf {w}}_{2}&=\sum _{l=1}^{2}A_{l}^{2}\sum _{i,j=0,2}{\mathbf {w}}_{2ij}^{l}\cos(i \phi_{l} x)\cos(j\psi_{l} y) \\ &\quad{} +A_{1}A_{2}\sum_{m,n=-1,1}{ \mathbf {w}}_{2mn}\cos\bigl((\phi _{1}+m\phi_{2})x \bigr)\cos\bigl((\psi_{1}+n\psi_{2})y\bigr), \end{aligned} $$

(A.5)

where ${\mathbf {w}}_{2ij}^{l}$ and ${\mathbf {w}}_{2mn}$ are defined as follows:

$$ \mathfrak{L}_{ij}^{l}{\mathbf {w}}_{2ij}^{l}=-\frac{1}{8}\mathcal {M}_{ij}^{l}(\boldsymbol{\varrho},\boldsymbol{\varrho}), \quad \quad\mathfrak{L}_{mn}{\mathbf {w}}_{2mn}=- \frac{1}{4}\mathcal {M}_{mn}(\boldsymbol{\varrho},\boldsymbol{ \varrho}) $$

with

$$ \begin{aligned} &\mathfrak{L}_{mn}=K-\bigl(( \phi_{1}+m\phi_{2})^{2}+(\psi_{1}+n\psi _{2})^{2}\bigr)D^{b^{c}}, \\ &\mathcal{M}_{mn}=\Phi_{K}-\bigl((\phi_{1}+m \phi_{2})^{2}+(\psi _{1}+n\psi_{2})^{2} \bigr)\Phi_{D}^{b^{c}}. \end{aligned} $$

When the no-resonance condition holds, the expression of the vector H appearing in equation (4.11) at order $\varepsilon ^{3}$ reads

$$ {\mathbf {H}}=\sum_{l=1}^{2} \biggl( \frac {dA_{l}}{dT_{2}}\boldsymbol{\varrho}+A_{l}{\mathbf {H}}_{11}^{(1l)}+A_{l}^{3}{\mathbf {H}}_{11}^{(3l)}+\frac {A_{1}^{2}A_{2}^{2}}{A_{l}}{\mathbf {H}}_{11}^{l} \biggr) \cos(\phi_{l} x)\cos(\psi_{l} y)+\widehat{\mathbf {H}}, $$

where

$$ \begin{aligned} &{\mathbf {H}}_{11}^{(1l)}=b^{(2)}{ \hat{k}}_{c}^{2}\left ( \begin{matrix} 0 \\ u_{\ast}M+v_{\ast} \end{matrix} \right ) , \\ &{\mathbf {H}}_{11}^{(3l)}=-\mathcal{M}_{11}^{l} \biggl( {\boldsymbol {\varrho}}, {\mathbf {w}}_{200}^{l}+ \frac{1}{2}{\mathbf {w}}_{220}^{l}+\frac {1}{2}{ \mathbf {w}}_{202}^{l}+\frac{1}{4}{\mathbf {w}}_{222}^{l} \biggr) -\frac {9}{16}{\boldsymbol{ \Gamma}}, \\ &{\mathbf {H}}_{11}^{l}=-\mathcal{M}_{11}^{l} \biggl( \boldsymbol{\varrho}, {\mathbf {w}}_{200}^{2/l}+ \frac{1}{4}\sum_{m,n=-1,1}{\mathbf {w}}_{2mn} \biggr) -\frac{3}{4}{\boldsymbol{\Gamma}}, \end{aligned} $$

and the expression of vector ${\widehat{\mathbf {H}}}$ depends on the following three different cases according to equation (4.27):

(i) only one of the relations $\phi_{1}=\psi_{2}=0$ and $\phi _{2}=\psi_{1}=0$ holds (without loss of generality, we shall assume $\phi_{1}=\psi_{2}=0$.) Then the expression for ${\widehat{\mathbf {H}}}$ is

$$ {\widehat{\mathbf {H}}}=\sum_{l=1}^{2} \biggl(A_{l}^{3}{\widehat {\mathbf {H}}}_{11}^{(3l)}+ \frac{A_{1}^{2}A_{2}^{2}}{A_{l}}{\widehat {\mathbf {H}}}_{11}^{l}\biggr) \cos(\phi_{l} x)\cos(\psi_{l}y)+{\widehat {\mathbf {H}}}^{\ast}, $$

where

$$\begin{aligned}& {\widehat{\mathbf {H}}}_{11}^{(31)}=- \mathcal{M}_{11}^{1}\biggl(\boldsymbol {\varrho}, \frac{1}{2}{\mathbf {w}}_{220}^{1}+\frac{1}{4}{ \mathbf {w}}_{222}^{1}\biggr)-\frac{3}{16}{\boldsymbol{ \Gamma}}, \\& {\widehat {\mathbf {H}}}_{11}^{(32)}=- \mathcal{M}_{11}^{1}\biggl(\boldsymbol{\varrho}, \frac {1}{2}{\mathbf {w}}_{220}^{2}+\frac{1}{4}{ \mathbf {w}}_{222}^{2}\biggr)-\frac {3}{16}{\boldsymbol{ \Gamma}}, \\& {\widehat{\mathbf {H}}}_{11}^{1}=-\mathcal{M}_{11}^{1} \biggl(\boldsymbol {\varrho}, {\mathbf {w}}_{202}^{2}+ \frac{1}{4}\sum_{m,n=-1,1}{\mathbf {w}}_{2mn}\biggr)-\frac{3}{4}{\boldsymbol{\Gamma}}, \\& {\widehat{ \mathbf {H}}}_{11}^{2}=-\mathcal{M}_{11}^{1} \biggl(\boldsymbol{\varrho }, {\mathbf {w}}_{220}^{1}+ \frac{1}{4}\sum_{m,n=-1,1}{\mathbf {w}}_{2mn}\biggr)-\frac{3}{4}{\boldsymbol{\Gamma}}, \end{aligned}$$

and ${\widehat{\mathbf {H}}}^{\ast}$ contains only terms orthogonal to φ. By applying the solvability condition to equation (4.11), we get the coefficients in (4.28) given here:

$$\begin{aligned}& \sigma=\sigma_{l}=-\frac{\langle{\mathbf {H}}_{11}^{(1l)}\cos(\phi _{l}x)\cos(\psi_{l}y),\boldsymbol{\varphi}\rangle}{\langle \boldsymbol{\varrho}\cos(\phi_{l}x)\cos(\psi_{l}y),\boldsymbol {\varphi}\rangle}, \\& L_{l}=\frac{\langle{\mathbf {H}}_{11}^{(3l)}\cos(\phi_{l}x)\cos(\psi _{l}y),\boldsymbol{\varphi}\rangle}{\langle\boldsymbol{\varrho }\cos(\phi_{l}x)\cos(\psi_{l}y),\boldsymbol{\varphi}\rangle }+L_{l}^{\star}, \quad \quad S_{l}=-\frac{\langle{\mathbf {H}}_{11}^{l}\cos(\phi _{l}x)\cos(\psi_{l}y),\boldsymbol{\varphi}\rangle}{\langle \boldsymbol{\varrho}\cos(\phi_{l}x)\cos(\psi_{l}y),\boldsymbol {\varphi}\rangle}+S_{l}^{\star}, \end{aligned}$$

and

$$ L_{l}^{\star}=\frac{\langle{\widehat{\mathbf {H}}}_{11}^{(3l)}\cos(\phi _{l}x)\cos(\psi_{l}y),\boldsymbol{\varphi}\rangle}{\langle \boldsymbol{\varrho}\cos(\phi_{l}x)\cos(\psi_{l}y),\boldsymbol {\varphi}\rangle},\quad \quad S_{l}^{\star}=- \frac{\langle{\widehat {\mathbf {H}}}_{11}^{l}\cos(\phi_{l}x)\cos(\psi_{l}y),\boldsymbol{\varphi }\rangle}{\langle\boldsymbol{\varrho}\cos(\phi_{l}x)\cos(\psi _{l}y),\boldsymbol{\varphi}\rangle}. $$

(ii) $\phi_{1}=0$, $\phi_{2}\neq0$, $\psi_{l}\neq0$ or $\phi _{1}\neq0$, $\phi_{2}=0$, $\psi_{l}\neq0$ or $\phi_{l}\neq0$, $\psi _{1}=0$, $\psi_{2}\neq0$ or $\phi_{l}\neq0$, $\psi_{1}\neq0$, $\psi _{2}=0$ for $l=1,2$ (without loss of generality, we shall assume $\phi _{1}=0$, $\phi_{2}\neq0$, $\psi_{l}\neq0$ for $l=1,2$). In this case, we have ${\widehat{\mathbf {H}}}_{11}^{(32)}={\widehat{\mathbf {H}}}_{11}^{1}={\mathbf {0}}$. Then it follows that $L_{2}^{\star}=S_{1}^{\star}=0$ and $L_{1}^{\star}$, $S_{2}^{\star}$ are the same as in case (i).

(iii) $\phi_{l}\neq0$ and $\psi_{l}\neq0$ for $l=1,2$. In this case, $L_{l}^{\star}$ and $S_{l}^{\star}$ are all zero for $l=1,2$.

1.3 A.3 Double and resonant eigenvalue case

1.3.1 A.3.1 The coefficients of system (4.36)

Since $\phi_{1}=\sqrt{3}\psi_{1}$, $\phi_{2}=0$, $\psi_{2}=2\psi _{1}$, substituting (4.28) into equation (4.10) yields

$$ \begin{aligned} {\mathbf {G}}&=\biggl(\frac{dA_{1}}{dT_{1}}\boldsymbol{ \varrho}+A_{1}{\mathbf {F}}_{11}^{(11)}+A_{1}A_{2}{ \mathbf {F}}_{11}^{(21)}\biggr)\cos(\phi_{1} x)\cos ( \psi_{1} y) \\ &\quad{} +\biggl(\frac{dA_{2}}{dT_{1}}\boldsymbol{\varrho}+A_{2}{ \mathbf {F}}_{11}^{(12)}+A_{1}^{2}{\mathbf {F}}_{11}^{(22)}\biggr)\cos(\psi_{2} y) \\ &\quad{} +{\mathbf {F}}^{\ast}, \end{aligned} $$

where

$$\begin{aligned}& {\mathbf {F}}_{11}^{(11)}={\mathbf {F}}_{11}^{(12)}=b^{(1)} \hat{k}_{c}^{2}\left ( \begin{matrix}0\\ u_{\ast}M+v_{\ast} \end{matrix} \right ) , \quad\quad {\mathbf {F}}_{11}^{(21)}=- \frac{1}{2}\mathcal{M}_{11}^{1}(\boldsymbol {\varrho}, \boldsymbol{\varrho}), \\& {\mathbf {F}}_{11}^{(22)}=- \frac {1}{8}\mathcal{M}_{11}^{2}(\boldsymbol{\varrho}, \boldsymbol{\varrho })=\frac{1}{4}{\mathbf {F}}_{11}^{(21)}, \end{aligned}$$

and the vector ${\mathbf {F}}^{\ast}$ contains terms which automatically satisfy the solvability condition given here:

$$ {\mathbf {F}}^{\ast}={\mathbf {F}}_{1}^{\ast}+{\mathbf {F}}_{2}^{\ast}+{\mathbf {F}}_{3}^{\ast}, $$

with

$$ \begin{aligned} &{\mathbf {F}}_{1}^{\ast}=- \frac{1}{8}A_{1}^{2} \bigl( \mathcal {M}_{00}^{1}(\boldsymbol{\varrho},\boldsymbol{\varrho})+ \mathcal {M}_{20}^{1}(\boldsymbol{\varrho},\boldsymbol{ \varrho})\cos(2\phi _{1} x)+ \mathcal{M}_{22}^{1}( \boldsymbol{\varrho},\boldsymbol{\varrho })\cos(2\phi_{1} x)\cos(2 \psi_{1} y) \bigr) , \\ &{\mathbf {F}}_{2}^{\ast}=-\frac{1}{4}A_{2}^{2} \bigl( \mathcal {M}_{00}^{2}(\boldsymbol{\varrho}, \boldsymbol{\varrho})+\mathcal {M}_{02}^{2}\cos(2 \psi_{2}y) \bigr) , \\ &{\mathbf {F}}_{3}^{\ast}=- \frac{1}{2}A_{1}A_{2}\mathcal {M}_{13}^{1}( \boldsymbol{\varrho},\boldsymbol{\varrho})\cos(\phi _{1} x)\cos(3 \psi_{1} y). \end{aligned} $$

By imposing the Fredholm solvability condition to equation (4.10), we obtain the quintic Stuart-Landau equations (4.36). The coefficients σ̃ and L̃ are given below:

$$ \tilde{\sigma}=\tilde{\sigma}_{l}=-\frac{\langle{\mathbf {F}}_{11}^{(1l)} \cos(\phi_{l} x)\cos(\psi_{l} y),\boldsymbol{\varphi }\rangle}{\langle{\boldsymbol{\varrho}}\cos(\phi_{l} x)\cos(\psi _{l} y),\boldsymbol{\varphi}\rangle},\quad\quad \tilde{L}=\frac{\langle {\mathbf {F}}_{11}^{(21)}\cos(\phi_{1} x)\cos(\psi_{1} y),\boldsymbol {\varphi}\rangle}{\langle{\boldsymbol{\varrho}}\cos(\phi_{1} x)\cos(\psi_{1} y),\boldsymbol{\varphi}\rangle}. $$

1.3.2 A.3.2 The coefficients of system (4.37)

From A.3.1, we know that equation (4.10) can be solved and its solution has the following form:

$$\begin{aligned} {\mathbf {w}}_{2}&=\sum_{l=1}^{2} \biggl( A_{l}{\mathbf {w}}_{211}^{(l1)}+ \frac{A_{1}^{2}A_{2}}{A_{l}}{\mathbf {w}}_{211}^{(l2)} \biggr) \cos( \phi_{l}x)\cos(\psi_{l}y)+A_{1}^{2} \bigl({\mathbf {w}}_{200}^{1}+{\mathbf {w}}_{220}^{1} \cos(2\phi_{1}x) \\ &\quad{}+ {\mathbf {w}}_{222}^{1}\cos(2\phi_{1}x) \cos(2\psi _{1}y)\bigr)+A_{2}^{2}\sum _{i=0,2}{\mathbf {w}}_{20i}^{2}\cos(i\psi _{2}y) \\ &\quad{} +A_{1}A_{2}{\mathbf {w}}_{213}^{1} \cos(\phi_{1}x)\cos(3\psi_{1}y), \end{aligned}$$

(A.6)

where

$$ \begin{aligned} &\mathfrak{L}_{11}^{l}{\mathbf {w}}_{211}^{(l1)}=\tilde{\sigma}\boldsymbol { \varrho}+b^{(1)}\hat{k}_{c}^{2}\left ( \begin{matrix}0\\ u_{\ast}M+v_{\ast} \end{matrix} \right ) ,\quad\quad \mathfrak{L}_{11}^{1}{\mathbf {w}}_{211}^{(12)}=- \tilde {L}\boldsymbol{\varrho}-\frac{1}{2}\mathcal{M}_{11}^{1}( \boldsymbol {\varrho},\boldsymbol{\varrho}), \\ &\mathfrak{L}_{11}^{2}{\mathbf {w}}_{211}^{(22)}=- \frac{\tilde {L}}{4}\boldsymbol{\varrho}-\frac{1}{8}\mathcal {M}_{11}^{2}(\boldsymbol{\varrho},\boldsymbol{\varrho}),\quad \quad \mathfrak{L}_{00}^{1}{\mathbf {w}}_{200}^{1}=- \frac{1}{8}\mathcal {M}_{00}^{1}(\boldsymbol{ \varrho},\boldsymbol{\varrho}), \\ & \mathfrak{L}_{20}^{1}{ \mathbf {w}}_{220}^{1}=-\frac{1}{8}\mathcal {M}_{20}^{1}(\boldsymbol{\varrho},\boldsymbol{\varrho}), \quad\quad \mathfrak{L}_{22}^{1}{\mathbf {w}}_{222}^{1}=- \frac{1}{8}\mathcal {M}_{22}^{1}(\boldsymbol{\varrho}, \boldsymbol{\varrho}), \\ & \mathfrak{L}_{i0}^{2}{\mathbf {w}}_{20i}^{2}=-\frac{1}{4}\mathcal {M}_{0i}^{2}(\boldsymbol{\varrho},\boldsymbol{\varrho}), \quad \quad \mathfrak{L}_{13}^{1}{\mathbf {w}}_{213}^{1}=- \frac{1}{2}\mathcal {M}_{13}^{1}(\boldsymbol{\varrho}, \boldsymbol{\varrho}). \end{aligned} $$

At $O(\varepsilon^{3})$, the expression of the vector H appearing in equation (4.11) is given by

$$ \begin{aligned} {\mathbf {H}}=\sum_{l=1}^{2} \biggl( \frac{dA_{l}}{dT_{2}}\boldsymbol {\varrho}+A_{l}{\mathbf {H}}_{11}^{(l1)}+\frac{A_{1}^{2}A_{2}}{A_{l}}{\mathbf {H}}_{11}^{(l2)}+A_{l}^{3}{ \mathbf {H}}_{11}^{(l3)}+\frac {A_{1}^{2}A_{2}^{2}}{A_{l}}{\mathbf {H}}_{11}^{l} \biggr) \cos(\phi_{l} x)\cos( \psi_{l} y)+\widetilde{\mathbf {H}}^{\ast}, \end{aligned} $$

where

$$\begin{aligned} &{\mathbf {H}}_{11}^{(l1)}=\tilde{\sigma} {\mathbf {w}}_{211}^{(l1)}+b^{(1)}\hat {k}_{c}^{2} \left ( \begin{matrix}0&0\\ v_{\ast}&u_{\ast} \end{matrix} \right ) {\mathbf {w}}_{211}^{(l1)}+b^{(2)}\hat{k}_{c}^{2} \left ( \begin{matrix}0&0\\ v_{\ast}&u_{\ast} \end{matrix} \right ) \boldsymbol{\varrho}, \\ &{\mathbf {H}}_{11}^{(12)}=2\tilde{\sigma} {\mathbf {w}}_{211}^{(12)}-\tilde {L} {\mathbf {w}}_{211}^{(11)}+b^{(1)} \hat{k}_{c}^{2}\left ( \begin{matrix}0\\ M \end{matrix} \right ) +b^{(1)}\hat{k}_{c}^{2} \left ( \begin{matrix}0&0\\ v_{\ast}&u_{\ast} \end{matrix} \right ) {\mathbf {w}}_{211}^{(12)}-\frac{1}{2}\mathcal{M}_{11}^{1} \Biggl( \boldsymbol{\varrho}, \sum_{l=1}^{2}{ \mathbf {w}}_{211}^{(l1)} \Biggr) , \\ &{\mathbf {H}}_{11}^{(22)}=2\tilde{\sigma} {\mathbf {w}}_{211}^{(22)}-\frac {\tilde{L}}{4}{\mathbf {w}}_{211}^{(21)}+\frac{b^{(1)}}{4}\hat {k}_{c}^{2} \left ( \begin{matrix}0\\ M \end{matrix} \right ) +b^{(1)}\hat{k}_{c}^{2}\left ( \begin{matrix}0&0\\ v_{\ast}&u_{\ast} \end{matrix} \right ) {\mathbf {w}}_{211}^{(22)}- \frac{1}{4}\mathcal{M}_{11}^{1} \bigl( \boldsymbol{ \varrho}, {\mathbf {w}}_{211}^{(11)} \bigr) , \\ &{\mathbf {H}}_{11}^{(13)}=-\frac{\tilde{L}}{4}{\mathbf {w}}_{211}^{(12)}-\mathcal{M}_{11}^{1} \biggl( \boldsymbol{\varrho}, {\mathbf {w}}_{200}^{1}+ \frac{1}{2}{\mathbf {w}}_{211}^{(22)}+\frac{1}{2}{ \mathbf {w}}_{220}^{1}+\frac{1}{4}{\mathbf {w}}_{222}^{1} \biggr) -\frac {9}{16}{\boldsymbol{ \Gamma}}, \\ &{\mathbf {H}}_{11}^{(23)}=-\mathcal{M}_{11}^{2} \biggl(\boldsymbol{\varrho},{\mathbf {w}}_{200}^{2}+ \frac{1}{2}{\mathbf {w}}_{202}^{2}\biggr)- \frac{3}{4}{\boldsymbol {\Gamma}}, \\ &{\mathbf {H}}_{11}^{1}=-\tilde{L} {\mathbf {w}}_{211}^{(12)}-\mathcal {M}_{11}^{1} \biggl( \boldsymbol{\varrho}, {\mathbf {w}}_{200}^{2}+ \frac {1}{2}{\mathbf {w}}_{211}^{(12)}+\frac{1}{2}{ \mathbf {w}}_{213}^{1} \biggr) -\frac {3}{2}{\boldsymbol{ \Gamma}}, \\ &{\mathbf {H}}_{11}^{2}=-2\tilde{L} {\mathbf {w}}_{211}^{(22)}-\mathcal {M}_{11}^{2} \biggl( \boldsymbol{\varrho},{\mathbf {w}}_{200}^{1}+ \frac {1}{4} {\mathbf {w}}_{211}^{(12)}+\frac{1}{4} {\mathbf {w}}_{213}^{1} \biggr) -\frac{3}{4}{ \boldsymbol{\Gamma}}, \end{aligned}$$

and $\widetilde{\mathbf {H}}^{\ast}$ contains terms which automatically satisfy the Fredholm solvability condition. By applying the solvability condition to equation (4.11), we obtain the following two coupled Stuart-Landau equations:

$$ \frac{\partial A_{1}}{\partial T_{2}}=\hat{\sigma}_{1} A_{1}-\hat {L}_{1}A_{1}A_{2}+\hat{\gamma}_{1}A_{1}^{3}+ \hat{\delta }_{1}A_{1}A_{2}^{2},\quad\quad \frac{\partial A_{2}}{\partial T_{2}}=\hat{\sigma}_{2} A_{2}-\hat {L}_{2}A_{1}^{2}+\hat{\gamma}_{2}A_{2}^{3}+ \hat{\delta}_{2}A_{1}^{2}A_{2}, $$

(A.7)

where

$$ \begin{aligned} &\hat{\sigma}_{l}=-\frac{\langle{\mathbf {H}}_{11}^{(l1)}\cos(\phi_{l} x)\cos(\psi_{l} y),\boldsymbol{\varphi}\rangle}{\langle \boldsymbol{\varrho}\cos(\phi_{l} x)\cos(\psi_{l} y),\boldsymbol {\varphi}\rangle},\quad\quad \hat{L}_{l}=\frac{\langle{\mathbf {H}}_{11}^{(l2)}\cos(\phi_{l} x)\cos(\psi_{l} y),\boldsymbol{\varphi }\rangle}{\langle\boldsymbol{\varrho}\cos(\phi_{l} x)\cos(\psi _{l} y),\boldsymbol{\varphi}\rangle}, \\ &\hat{\gamma}_{l}=-\frac{\langle{\mathbf {H}}_{11}^{(l3)}\cos(\phi_{l} x)\cos(\psi_{l} y),\boldsymbol{\varphi}\rangle}{\langle \boldsymbol{\varrho}\cos(\phi_{l} x)\cos(\psi_{l} y),\boldsymbol {\varphi}\rangle},\quad\quad \hat{ \delta}_{l}=-\frac{\langle{\mathbf {H}}_{11}^{l}\cos(\phi_{l} x)\cos(\psi_{l} y),\boldsymbol{\varphi }\rangle}{\langle\boldsymbol{\varrho}\cos(\phi_{l} x)\cos(\psi _{l} y),\boldsymbol{\varphi}\rangle}. \end{aligned} $$

Combining (4.6), (4.36) and (A.7) yields the coefficients in equation (4.37) as follows:

$$ \bar{\sigma}_{l}=\tilde{\sigma}+\varepsilon\hat{\sigma}_{l},\quad \quad\bar{L}_{1}=\tilde{L}+\varepsilon\hat{L}_{1}, \quad \quad\bar {L}_{2}=\frac{\tilde{L}}{4}+\varepsilon\hat{L}_{2},\quad \quad\bar {\gamma}_{l}=\varepsilon\hat{\gamma}_{l},\quad \quad\bar{\delta }_{l}=\varepsilon\hat{\delta}_{l}. $$

(A.8)