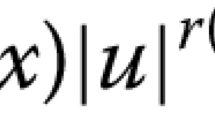Existence,multiplicity, and nonexistence of solutions for a p-Kirchhoff elliptic equation on $\mathbb{R}^{N}$

Abstract

In this paper, we study the multiplicity of solutions for the following nonhomogeneous p-Kirchhoff elliptic equation:

$$ \biggl(a+\lambda \biggl( \int_{\mathbb{R}^{N}} \bigl(|\nabla{u}|^{p}+|u|^{p} \bigr)\,dx \biggr)^{m} \biggr) \bigl(-\Delta_{p}u+|u|^{p-2}u \bigr) =f(u)+h(x),\quad x\in\mathbb{R}^{N}, $$

(0.1)

with $a,\lambda,m>0$ and $1< p< N$. By variational methods we prove that problem (0.1) admits at least two solutions under appropriate assumptions on $f(u)$ and $h(x)$. The main difficulty to overcome is the lack of an a priori bound for Palais-Smale sequence. Motivated by Jeanjean (Proc. R. Soc. Edinb., Sect. A 129:787-809, 1999), we use a cut-off functional to obtain a bounded (PS) sequence. Also, if $f(u)=|u|^{q-2}u$, $p< q<\min\{p(m+1), p^{*}=\frac{pN}{N-p}\}$, and $h(x)=0$, then we prove that problem (0.1) has at least one nontrivial solution for any $\lambda\in(0, \lambda^{*}]$ and has no nontrivial weak solutions for any $\lambda\in(\lambda^{*}, +\infty)$.

1 Introduction

In this paper, we are interested in the multiplicity of solutions to the following nonhomogeneous p-Kirchhoff elliptic problem:

$$ \biggl(a+\lambda \biggl( \int_{\mathbb{R}^{N}} \bigl(\vert \nabla{u} \vert ^{p}+\vert u \vert ^{p} \bigr)\,dx \biggr)^{m} \biggr) \bigl(- \Delta_{p}u+\vert u\vert ^{p-2}u \bigr) =f(u)+h(x),\quad x\in \mathbb{R}^{N}, $$

(1.1)

where $\Delta_{p}u=\operatorname {div}(\vert \nabla{u} \vert ^{p-2}\nabla{u})$ is the p-Laplacian operator, and the nontrivial function $h(x)$ can be seen as a perturbation term. Problem (1.1) is a generalization of the model introduced by Kirchhoff [2]. More precisely, Kirchhoff proposed the model given by the equation

$$ \rho_{tt}- \biggl(\frac{P_{0}}{h}+\frac{E}{2L} \int^{L}_{0}u^{2}_{x}\,dx \biggr)u_{xx}=0,\quad 0< x< L, t>0, $$

(1.2)

which takes into account the changes in length of string produced by transverse vibration. The parameters in (1.2) have the following meaning: L is the length of the string, h is the area of cross-section, E is the Young modulus of material, ρ is the mass density, and $P_{0}$ is the initial tension.

The equation

$$ \rho_{tt}-M \bigl(\Vert \nabla u\Vert ^{2}_{2} \bigr)\Delta u=f(x,u), \quad x\in\Omega, t>0, $$

(1.3)

generalizes equation (1.2), where $M: \mathbb{R}^{+}\to\mathbb{R}$ is a given function, Ω is a domain of $\mathbb{R}^{N}$. The stationary counterpart of (1.3) is the Kirchhoff-type elliptic equation

$$ -M \bigl(\Vert \nabla u\Vert ^{2}_{2} \bigr) \Delta u=f(x,u), \quad x\in\Omega, t>0. $$

(1.4)

Some classical and interesting results on Kirchhoff-type elliptic equations can be found, for example, in [3–9].

Particularly, Li et al. [10] considered the Kirchhoff-type problem

$$ \biggl(a+\lambda \biggl( \int_{\mathbb{R}^{N}} \bigl(\vert \nabla{u} \vert ^{2}+b \vert u\vert ^{2} \bigr)\,dx \biggr) \biggr) (-\Delta u+bu) =f(u),\quad x \in \mathbb{R}^{N}, $$

(1.5)

where $N \geq3$, with constants $a, b > 0$ and $\lambda\geq0$ under the following assumptions:

$(H_{1})$ :

$f\in C(\mathbb{R}^{+},\mathbb{R}^{+})$, $\vert f(t)\vert \leq C(1+t^{q-1})$ for all $t\in\mathbb{R}^{+}=[0,+\infty)$ and some $q\in(2,2^{*})$, where $2^{*}=\frac{2N}{N-2}$ for $N\geq3$;

$(H_{2})$ :

$\lim_{t\rightarrow0}\frac{f(t)}{t}=0$; $\lim_{t\rightarrow+\infty}\frac{f(t)}{t}=+\infty$.

It is easy to see that $f(u)=\vert u\vert ^{q-2}u$, $2< q<4$, and $N=3$ satisfy these conditions. They obtained that there exists $\lambda _{0} > 0$ such that, for any $\lambda\in[0, \lambda_{0})$, problem (1.5) has at least one positive solution in $W^{1,2}({\mathbb {R}}^{N})$. The $\lambda_{0}$ depends on f, a, b, the Sobolev constant, and several test functions in [10]; it is not very clear whether the the existence of solutions for (1.5) still holds for large $\lambda >0$. Recently, Chen et al. [11] studied the existence of positive solutions to the p-Kirchhoff problem

$$ \textstyle\begin{cases} (a+\lambda( \int_{\mathbb{R}^{N}} (\vert \nabla u\vert ^{p}+b \vert u\vert ^{p} )\,dx )^{\tau} ) (- \Delta_{p}u+b\vert u\vert ^{p-2}u ) \\ \quad =\vert u\vert ^{m-2}u+\mu \vert u\vert ^{q-2}u, \quad x\in \mathbb{R}^{N}, \\ u(x)>0, \quad x\in\mathbb{R}^{N},\quad \quad u(x)\in W^{1,p} ( \mathbb{R}^{N} ), \end{cases} $$

(1.6)

where $a,b>0$, $\tau,\lambda\ge0$, $\mu\in\mathbb{R}$, and $1< p< N$. By the Nehari manifold method, they proved that problem (1.6) admits at least a positive ground state solution for any $\lambda>0$ when $p(\tau +1)< q< m< p^{*}=\frac{pN}{N-p}$. However, does the existence of solutions for (1.5) still hold for any $\lambda>0$ when $p< q< p(\tau+1)$ and $\mu=0$? This is a interesting problem. In this paper, we answer positively this question. More interesting results for Kirchhoff-type problems can be found in [1, 2, 5–7, 10–14].

In the present paper, we are ready to extend the analysis to the nonhomogeneous p-Kirchhoff-type equation of (1.1) in $\mathbb{R}^{N}$ with the nonlinearity $f(u)$ satisfying the following conditions:

$(F_{1})$ :

$f\in C(\mathbb{R}^{+},\mathbb{R}^{+})$, $\vert f(t)\vert \leq C(t^{p-1}+t^{q-1})$ for all $t\in\mathbb{R}^{+}$ and some $q\in(p,p^{*})$, where $p^{*}={pN}/({N-p})$, $1< p< N$;

$(F_{2})$ :

$\lim_{t\rightarrow0^{+}}\frac{f(t)}{t^{p-1}}=0$;

$(F_{3})$ :

$\lim_{t\rightarrow+\infty}\frac{f(t)}{t^{p-1}}=+\infty$.

In addition, we suppose that the nontrivial and nonnegative function $h(x)\equiv h(\vert x\vert )\in C^{1}(\mathbb{R}^{N})\cap L^{p'}(\mathbb{R}^{N})$ satisfies

$(H)$ :

there exists $\xi(x)\in L^{p'}(\mathbb{R}^{N})\cap W^{1,\infty}(\mathbb{R}^{N})$ such that

$$ \bigl\vert \nabla h(x)\cdot x \bigr\vert \leq\xi^{p'}(x), \quad \forall x \in\mathbb{R}^{N}, $$

(1.7)

with $p'=\frac{p}{p-1}$.

We will use the Ekeland variational principle [15] and a version of the mountain pass theorem in [1] to study the existence of multiple solutions of problem (1.1) in ${\mathbb {R}}^{N}$. It is well known that an important technical condition to get a bounded (PS) sequence is the following Ambrosetti-Rabinowitz-type condition (AR): there exists $\theta>p$ such that $0<\theta F(s)\le sf(s)$ for $s>0$. The loss of (AR) condition renders variational techniques more delicate. Inspired by [1, 10], we use a cut-off functional and obtain a bounded (PS) sequence.

In order to state our main result, we introduce some Sobolev spaces and norms. Let $W^{1,p}(\mathbb{R}^{N})$ be the usual Sobolev space with the norm

$$ \Vert u\Vert = \biggl( \int_{\mathbb{R}^{N}}\vert \nabla u\vert ^{p}+\vert u \vert ^{p}\,dx \biggr)^{\frac{1}{p}}, \quad 1< p< \infty. $$

(1.8)

We denote by $\Vert \cdot \Vert _{q}$ the usual $L^{q}({\mathbb {R}}^{N})$ norm. Then it well known that the embedding $W^{1,p}(\mathbb {R}^{N})\hookrightarrow L^{q}(\mathbb{R}^{N})$ is continuous for $q\in (p,p^{*}]$ and there exists a constant $S_{q}$ such that

$$ \Vert u\Vert _{q}\leq S_{q}\Vert u \Vert , \quad \forall u\in W^{1,p} \bigl(\mathbb{R}^{N} \bigr). $$

(1.9)

Let $X=W_{r}^{1,p}(\mathbb{R}^{N})$ be the subspace of $W^{1,p}(\mathbb {R}^{N})$ containing only the radial functional. Then by the Lemma 2.2 in [11] we have that the embedding $X\hookrightarrow L^{q}(\mathbb {R}^{N})$ is compact for $q\in(p,p^{*})$.

A function $u\in X$ is said to be a weak solution of (1.1) if for all $v \in X$,

$$ \bigl(a+\lambda \Vert u\Vert ^{pm} \bigr) \int_{\mathbb{R}^{N}} \bigl(\vert \nabla u\vert ^{p-2}\nabla u \nabla v+\vert u\vert ^{p-2}uv \bigr) \,dx= \int_{\mathbb{R}^{N}} \bigl(f(u)+h \bigr)v \,dx. $$

(1.10)

Let $I(u):X\rightarrow\mathbb{R}$ be the energy functional associated with problem (1.1) defined by

$$ I(u)=\frac{a}{p}\Vert u\Vert ^{p}+\frac{\lambda}{p(m+1)}\Vert u \Vert ^{p(m+1)}- \int_{\mathbb{R}^{N}} \bigl(F(u)+hu \bigr)\,dx, $$

(1.11)

where $F(u)=\int_{0}^{u}f(s)\,ds$. It is easy to see that the functional $I\in C^{1}(X,\mathbb{R})$ and its Gateaux derivative is given by

$$ \begin{aligned}[b] I'(u)v&= \bigl(a+\lambda \Vert u\Vert ^{pm} \bigr) \int_{\mathbb{R}^{N}} \bigl(\vert \nabla u\vert ^{p-2} \nabla u \nabla v+\vert u\vert ^{p-2}uv \bigr)\,dx \\ &\quad{} - \int_{\mathbb{R}^{N}} \bigl(f(u)+h \bigr)v\,dx, \quad \forall v\in X. \end{aligned} $$

(1.12)

Clearly, we see that a weak solution of (1.1) corresponds to a critical point of the functional.

The main result in this paper is as follows.

Theorem 1.1

Let $(F_{1})$-$(F_{3})$ and $(H)$ hold. Then, there exist $\lambda_{0}, \widetilde{{m}}_{0}>0$ such that, for any $\lambda\in[0,\lambda_{0})$, (1.1) has at least two nontrivial solutions in X when $\Vert h\Vert _{p'}<\widetilde{{m}}_{0}$.

Furthermore, consider $h(x)=0$ and $f(x,u)=\vert u\vert ^{q-2}u$, $p< q<\min\{p(m+1),p^{*}\}$, that is,

$$ \biggl(a+\lambda \biggl( \int_{\mathbb{R}^{N}} \bigl(\vert \nabla{u} \vert ^{p}+\vert u \vert ^{p} \bigr)\,dx \biggr)^{m} \biggr) \bigl(- \Delta_{p}u+\vert u\vert ^{p-2}u \bigr) =\vert u\vert ^{q-2}u, \quad x\in\mathbb{R}^{N}. $$

(1.13)

We can now state the second main result.

Theorem 1.2

Let $a>0$ and $p< q<\min\{p(m+1),p^{*}\}$. Then there exists $\lambda ^{*}>0$ such that problem (1.13) has at least one nontrivial solution for any $\lambda\in(0, \lambda^{*}]$ and has no nontrivial weak solutions for any $\lambda\in(\lambda^{*}, +\infty)$.

Remark 1.3

In [11], Chen and Zhu considered the case $p< p(m+1)< q<p^{*}$. They proved that problem (1.1) admits at least one positive solution for any $\lambda>0$.

2 Proof of Theorem 1.1

In this section, we first establish some properties of the functional I and then prove Theorem 1.1. Throughout the paper, we denote by C or $C_{i}$ s positive constants that may vary from line to line and are not essential to the problem.

Lemma 2.1

If assumptions $(F_{1})$-$(F_{3})$ hold and $h(x)\in L^{p'}(\mathbb{R}^{N})$, then there exist $\rho, \alpha, m_{0}>0$ such that $I(u)\geq\alpha>0$ with $\Vert u\Vert =\rho$ and $\Vert h\Vert _{p'}< m_{0}$.

Proof

It follows from $(F_{1})$-$(F_{2})$ that

$$ F(s)\leq\varepsilon \vert s\vert ^{p}+C_{\varepsilon} \vert s \vert ^{q}, \quad \forall s\in\mathbb{R}, $$

(2.1)

with $\varepsilon>0$. By the Hölder inequality we have

$$ \biggl\vert \int_{\mathbb{R}^{N}}hu\,dx \biggr\vert \leq S_{q}^{-1} \Vert h\Vert _{p'}\Vert u\Vert \leq\epsilon \Vert u\Vert ^{p}+C_{\epsilon} \Vert h\Vert _{p'}^{p'}. $$

(2.2)

Thus,

$$ \begin{aligned}[b] I(u)&\geq\frac{a}{p}\Vert u\Vert ^{p}- \varepsilon \Vert u\Vert ^{p}-C_{\varepsilon} \Vert u\Vert ^{q}-\epsilon \Vert u\Vert ^{p}-C_{\epsilon} \Vert h \Vert _{p'}^{p'} \\ &\geq\frac{a}{2p}\Vert u\Vert ^{p}-C_{1}\Vert u\Vert ^{q}-C_{2} \Vert h\Vert ^{p'}_{p'}, \end{aligned} $$

(2.3)

where $\varepsilon=\epsilon=\frac{a}{4p}$, $C_{1}$, $C_{2}$ are some positive constants. Let

$$ z(t)=\frac{a}{2p}t^{p}-C_{1}t^{q}, \quad t\geq0. $$

(2.4)

We see that there exists $\rho>0$ such that $\max_{t\geq0}z(t)=z(\rho)\equiv m_{0}>0$. Then it follows from (2.3) that there exists $\alpha>0$ such that $I(u)\geq\alpha$ with $\Vert u\Vert =\rho$ and $\Vert h\Vert _{p'}< m_{0}$. This ends the proof of Lemma 2.1. □

We denote by $B_{r}$ the open ball in X centered at the origin with radius r. By Ekland’s variational principle [15] we get the following lemma, which implies that there exists a function $u_{0}$ such that $I'(u_{0})=0$ and $I(u_{0})<0$ if $\Vert h\Vert _{p'}$ is small.

Lemma 2.2

Let assumptions $(F_{1})$-$(F_{3})$ hold, and $h(x)\in L^{p'}(\mathbb{R}^{N})$, $h(x)\not\equiv0$, with $\Vert h\Vert _{p'}< m_{0}$. Then there exists a function $u_{0}\in X$ such that

$$ I(u_{0})=\inf \bigl\{ I(u):u\in{\overline{B}_{\rho}} \bigr\} < 0, $$

(2.5)

and $u_{0}$ is a nontrivial weak solution of problem (1.1).

Proof

Choose a function $\phi\in C_{0}^{1}(\mathbb{R}^{N})$ such that $\int_{\mathbb{R}^{N}}h(x)\phi(x)\,dx>0$. Then

$$ I(t\phi)\leq\frac{a}{p}t^{p}\Vert \phi \Vert ^{p}+ \frac{\lambda}{p(m+1)}t^{p(m+1)}\Vert \phi \Vert ^{p(m+1)}-t \int_{\mathbb{R}^{N}}h(x)\phi \,dx< 0 $$

(2.6)

for small $t>0$ and thus for any open ball ${B}_{\kappa}\subset X$ such that $-\infty< c_{\kappa}=\inf_{\overline{B}_{\kappa}}I(u)<0$. Thus,

$$ c_{\rho}=\inf_{u\in\overline{B}_{\rho}}I(u)< 0 \quad \mbox{and}\quad \inf _{u\in\partial B_{\rho}}I(u)>0, $$

(2.7)

where ρ is given in Lemma 2.1. Let $\varepsilon_{n}\downarrow0$ be such that

$$ 0< \varepsilon_{n}< \inf_{u\in\partial B_{\rho}}I(u)- \inf_{u\in B_{\rho}}I(u). $$

(2.8)

Then, by Ekland’s variational principle [15] there exists $\{u_{n}\} \subset\overline{B}_{\rho}$ such that

$$ c_{\rho}\leq I(u_{n})< c_{\rho}+ \varepsilon_{n} $$

(2.9)

and

$$ I(u_{n})< I(u)+\varepsilon_{n}\Vert u_{n}-u\Vert \qquad\mbox{for all } u\in\overline{B_{\rho}}, u_{n}\neq u. $$

(2.10)

Then, it follows from (2.8)-(2.10) that

$$ I(u_{n})< c_{\rho}+\varepsilon_{n}\leq\inf _{u\in B_{\rho}}I(u)+ \varepsilon_{n}< \inf_{u\in\partial B_{\rho}}I(u). $$

(2.11)

So $u_{n}\in B_{\rho}$, and we now consider the function $F: \overline {B}_{\rho}\to {\mathbb {R}}$ given by

$$ F(u)=I(u)+\varepsilon_{n}\Vert u_{n}-u\Vert , \quad u\in \overline{B}_{\rho}. $$

(2.12)

Then (2.10) shows that $F(u_{n})< F(u)$, $u\in\overline{{B}}_{\rho}$, $u_{n}\neq u$, and thus $u_{n}$ is a strict local minimum of F. Moreover,

$$ t^{-1} \bigl(F(u_{n}+tv)-F(u_{n}) \bigr)\geq0 \quad\mbox{for small } t>0, \forall v\in B_{1}. $$

(2.13)

Hence,

$$ t^{-1} \bigl(I(u_{n}+tv)-I(u_{n}) \bigr)+ \varepsilon_{n}\Vert v\Vert \geq0. $$

(2.14)

Passing to the limit as $t\to0^{+}$, it follows that

$$ I'(u_{n})v+\varepsilon_{n} \Vert v\Vert \geq0,\quad\forall v\in B_{1}. $$

(2.15)

Replacing v in (2.15) by −v, we get

$$ -I'(u_{n})v+\varepsilon_{n}\Vert v\Vert \geq0,\quad\forall v\in B_{1}, $$

(2.16)

so that $\Vert I'(u_{n})\Vert \leq\varepsilon_{n}$. Therefore, there is a sequence $\{u_{n}\}\in B\rho$ such that $I(u_{n})\to c_{\rho}<0$ and $I'(u_{n})\to0$ in $X^{*}$ as $n\to\infty$. In the following, we will prove that $\{u_{n}\}$ has a convergent subsequence in X. Indeed, since $\Vert u_{n}\Vert <\rho$, by the reflexivity of X and compact embedding $X\hookrightarrow L^{q}$ for all $q\in(p,p^{*})$, passing to a subsequence, we can assume that

$$ u_{n}\rightharpoonup u_{0}, \quad \text{in } X; \quad\quad u_{n} \rightarrow u_{0},\quad L^{q} \bigl( \mathbb{R}^{N} \bigr); \quad\quad u_{n}\rightarrow u_{0}, \quad \mbox{a.e. in } \mathbb{R}^{N}. $$

(2.17)

By (1.12) we can get

$$ \bigl(I(u_{n})-I(u_{0}) \bigr)'(u_{n}-u_{0})=P_{n}+Q_{n}+K_{n}, $$

(2.18)

where

$$ \begin{gathered} P_{n} = \bigl(a+\lambda \Vert u_{n}\Vert ^{pm} \bigr) \int_{\mathbb{R}^{N}} \bigl(\vert \nabla u_{n}\vert ^{p-2}\nabla u_{n}-\vert \nabla u\vert ^{p-2} \nabla u \bigr)\nabla(u_{n}-u_{0}) \\ \hphantom{P_{n} =}{} + \bigl(\vert u_{n}\vert ^{p-2}u_{n}-u_{0}^{p-2}u_{0} \bigr) (u_{n}-u_{0})\,dx, \\ Q_{n}= \lambda \bigl( \bigl(\Vert u_{n}\Vert ^{pm}-\Vert u_{0}\Vert ^{pm} \bigr) \bigr) \int_{\mathbb{R}^{N}}\vert \nabla u_{0}\vert ^{p-2} \nabla{u_{0}}\nabla(u_{n}-u_{0}) \\ \hphantom{Q_{n}=}{}+\vert u_{0}\vert ^{p-2}u_{0}(u_{n}-u_{0})\,dx, \\ K_{n}= \int_{\mathbb{R}^{N}} \bigl(f(u_{n})-f(u_{0}) \bigr) (u_{n}-u_{0})\,dx. \end{gathered} $$

(2.19)

It is clear that

$$ \bigl(I(u_{n})-I(u_{0}) \bigr)'(u_{n}-u_{0}) \rightarrow0 \quad\text{as } n\rightarrow\infty. $$

(2.20)

By $(F_{1})$ and $(F_{2})$, for any $\varepsilon>0$, there exists $C_{\varepsilon}>0$ such that

$$ \bigl\vert f(t) \bigr\vert \leq\varepsilon \vert t\vert ^{p-1}+C_{\varepsilon} \vert t\vert ^{q-1},\quad t\in \mathbb{R}. $$

(2.21)

Hence,

$$\begin{aligned} \begin{aligned}[b] \vert K_{n}\vert &= \biggl\vert \int_{\mathbb{R}^{N}} \bigl(f(u_{n})-f(u_{0}) \bigr) (u_{n}-u_{0})\,dx \biggr\vert \\ &\leq\varepsilon \bigl(\Vert u_{n}\Vert ^{p-1}+\Vert u_{0}\Vert ^{p-1} \bigr)\Vert u_{n}-u_{0} \Vert +C_{\varepsilon}\bigl(\Vert u_{n}\Vert ^{q-1}_{q}+\Vert u_{0}\Vert ^{q-1}_{q} \bigr)\Vert u_{n}-u_{0} \Vert _{q} \\ &\to0 \quad \mbox{as } n\to\infty. \end{aligned} \end{aligned}$$

(2.22)

Define the linear function $g:X\rightarrow\mathbb{R}$ by

$$ g(\omega)= \int_{\mathbb{R}^{N}}\vert \nabla u_{0}\vert ^{p-2} \nabla u_{0}\nabla\omega+\vert u_{0}\vert ^{p-2}u_{0}\omega \,dx. $$

(2.23)

Noticing that $\vert g(\omega)\vert \leq2\Vert u_{0}\Vert ^{p-1}\Vert \omega \Vert$, we can deduce that g is continuous on X. Using $u_{n}\rightharpoonup u_{0}$ in X, we have

$$ \begin{aligned}[b] g(u_{n}-u_{0})&= \int_{\mathbb{R}^{N}}\vert \nabla u_{0}\vert ^{p-2} \nabla u_{0}\nabla(u_{n}-u_{0})+\vert u_{0}\vert ^{p-2}u_{0}(u_{n}-u_{0})\,dx \\ & \rightarrow0 \quad \mbox{as } n\rightarrow\infty. \end{aligned} $$

(2.24)

Since $\Vert u_{n}\Vert <\rho$, we deduce that $\vert Q_{n}\vert \rightarrow0$ as $n\rightarrow\infty$.

Combining the above results, we have $\vert P_{n}\vert \to0$ as $n\to\infty$, Then, using the standard inequalities in $\mathbb{R}^{N}$

$$\begin{aligned} \begin{aligned} &\bigl\langle \vert x\vert ^{p-2}x- \vert y\vert ^{p-2}y,x-y \bigr\rangle \geq{C_{p}}\vert x-y\vert ^{p}, \quad p\geq2, \\ &\bigl\langle \vert x\vert ^{p-2}x-\vert y\vert ^{p-2}y,x-y \bigr\rangle \geq\frac{C_{p}\vert x-y\vert ^{p}}{{\vert x\vert +\vert y\vert }^{2-p}},\quad 2>p>1, \end{aligned} \end{aligned}$$

(2.25)

where $\langle\cdot,\cdot\rangle$ denotes the scalar product in $\mathbb{R}^{N}$, we can show that $u_{n} \rightarrow u_{0}$ in X. Thus, $u_{0}$ is a nontrivial weak solution of problem (1.1). The proof is completed. □

Next, we prove that problem (1.1) has a mountain-pass-type solution. To overcome the difficulty of finding a bounded (PS) sequence for the associated functional I, motivated by [1, 10], we use a cut-off function $\psi\in C_{0}^{1}(\mathbb{R}^{+})$ that satisfies

$$ \begin{aligned} &\psi(t)=1, \quad \forall t\in[0,1]; \quad\quad 0\leq\psi\leq1, \quad \forall t\in(1,2); \\& \psi(t)\equiv0,\quad \forall t \in[2,+\infty); \quad\quad \bigl\Vert \psi' \bigr\Vert _{\infty}\leq2, \end{aligned} $$

(2.26)

and study the following modified functional $I^{T}$ defined by

$$ I^{T}(u)=\frac{a}{p}\Vert u\Vert ^{p}+ \frac{\lambda}{p(m+1)}\eta_{T}(u)\Vert u\Vert ^{p(m+1)}- \int_{\mathbb{R}^{N}} \bigl(F(u)+hu \bigr)\,dx, \quad u\in X, $$

(2.27)

where $T>0$ and $\eta_{T}(u)=\psi(\frac{\Vert u\Vert ^{p}}{T^{p}})$. For $T>0$ sufficiently large and λ sufficiently small, we will prove that there exists a critical point $\tilde{u}_{0}$ of $I_{T}$ such that $\Vert \tilde{u}_{0}\Vert \leq T$, and so $\tilde{u}_{0}$ is also a critical point of I. For this purpose, we use the following theorem given in [1].

Lemma 2.3

see[1]

Let X be a Banach space with norm $\Vert \cdot \Vert _{X}$, and $K\subset\mathbb{R}^{+}$ be an interval. Consider the family of $C^{1}$ functionals on X

$$ I_{\mu}(u)=A(u)-\mu B(u),\quad \mu\in K, $$

(2.28)

with B nonnegative and either $A(u)\rightarrow\infty$ or $B(u)\rightarrow\infty$ as $\Vert u\Vert _{X}\rightarrow\infty$ and $I_{\mu}(0)=0$. For any $\mu\in K$, we set

$$ \Gamma_{\mu}= \bigl\{ \gamma\in \bigl( C[0,1], X \bigr): \gamma(0)=0,I_{\mu}\bigl(\gamma(1) \bigr)< 0 \bigr\} . $$

(2.29)

If for any $\mu\in K$, the set $\Gamma_{\mu}$ is nonempty, and

$$ c_{\mu}=\inf_{\gamma\in \Gamma_{\mu}}\max_{t\in[0,1]}I_{\mu}\bigl(\gamma(t) \bigr)>0, $$

(2.30)

then, for almost every $\mu\in K$, there is a sequence $\{u_{n}\}\subset X$ such that (i) $\{u_{n}\}$ is bounded; (ii) $I_{\mu}(u_{n})\rightarrow c_{\mu}$; (iii) $I'_{\mu}(u_{n})\rightarrow0$ in $X^{-1}$.

In our case,

$$ A(u)=\frac{a}{p}\Vert u\Vert ^{p}+\frac{\lambda}{p(m+1)} \eta_{T}(u)\Vert u\Vert ^{p(m+1)}, \quad\quad B(u)= \int_{\mathbb{R}^{N}} \bigl(F(u)+hu \bigr)\,dx. $$

(2.31)

So the perturbed functional we study is

$$ I^{T}_{\mu}(u)=\frac{a}{p}\Vert u\Vert ^{p}+\frac{\lambda}{p(m+1)}\eta_{T}(u)\Vert u\Vert ^{p(m+1)}-\mu \int_{\mathbb{R}^{N}} \bigl(F(u)+hu \bigr)\,dx, $$

(2.32)

and

$$ \bigl(I^{T}_{\mu}(u) \bigr)'v={\widehat{M}} \bigl(\Vert u\Vert \bigr) \int_{\mathbb{R}^{N}} \bigl(\vert \nabla{u} \vert ^{p - 2} \nabla{u}\nabla{v} + \vert u\vert ^{p - 2}uv \bigr)\,dx -\mu \int_{\mathbb{R}^{N}} \bigl(f(u)+h \bigr)v\,dx, $$

(2.33)

where ${\widehat{M}}(\Vert u\Vert )=(a + \lambda\eta_{T}(u)\Vert u\Vert ^{pm} + \frac{\lambda}{(m + 1)T^{p}}\eta'_{T}(u)\Vert u\Vert ^{p(m + 1)})$. The following lemmas, Lemma 2.4 and Lemma 2.5, imply that $I^{T}_{\mu}$ satisfies the conditions of Lemma 2.3.

Lemma 2.4

Let $(F_{1})$-$(F_{3})$ hold, Then $\Gamma_{\mu}\neq\emptyset$ for all $\mu\in[\frac{1}{2},1]$.

Proof

Choose $\beta(x)\in C_{0}^{1}(\mathbb{R}^{N})$ with $\beta(x)\geq0$ in $\mathbb{R}^{N}$, $\Vert \beta \Vert =1$, and $\operatorname{supp}(\beta)\subset B_{R}$ for some $R>0$. By $(F_{3})$ we have that, for any $C_{3}>0$ with ${C_{3}}/{2}\int_{B_{R}}\beta^{p}\,dx>{a}/{p}$, there exists $C_{4}>0$ such that

$$ F(t)\geq C_{3}\vert t\vert ^{p}-C_{4}, \quad t\in \mathbb{R}^{+}. $$

(2.34)

Then, for $t^{p}>2T^{p}$,

$$ \begin{aligned}[b] I^{T}_{\mu}(t\beta)&= \frac{a}{p}\Vert t\beta \Vert ^{p}+\frac{\lambda}{p(m+1)}\psi \biggl( \frac{\Vert t\beta \Vert ^{p}}{T^{p}} \biggr)\Vert t\beta \Vert ^{p(m+1)}-\mu \int_{\mathbb{R}^{N}} \bigl(F(t\beta)+ht\beta \bigr)\,dx \\ &=\frac{a}{p}\Vert t\beta \Vert ^{p}-\mu \int_{\mathbb{R}^{N}} \bigl(F(t\beta)+ht\beta \bigr)\,dx\leq \biggl( \frac{a}{p} -\frac{C_{3}}{2} \int_{B_{R}}\beta^{p}\,dx \biggr)t^{p}+C_{5}. \end{aligned} $$

(2.35)

It follows that we can choose $t>0$ large enough such that $I^{T}_{\mu}(t\beta)<0$. The proof is completed. □

Lemma 2.5

Let $(F_{1})$-$(F_{3})$ hold. Then there exists a constant $c>0$ such that $c_{\mu}\geq c>0$ for all $\mu\in[\frac{1}{2},1]$ if $\Vert h\Vert _{p'}< m_{1}$.

Proof

Similarly as in the proof of Lemma 2.1, we can show that, for every $\mu\in[\frac{1}{2},1]$, there exists $c>0$ such that $I^{T}_{\mu}(u)\geq c$ with $\Vert u\Vert =\tilde{\rho}$ and $\Vert h\Vert _{p'}< m_{1}$. Fix $\mu\in[\frac{1}{2},1]$ and $\gamma\in\Gamma_{\mu}$. By the definition of $\Gamma_{\mu}$, $\Vert \gamma({1})\Vert >\tilde{\rho }$. By the continuity we deduce that there exists $t_{\gamma}\in(0,1)$ such that $\Vert \gamma({t_{\gamma}})\Vert _{E}=\tilde{\rho}$. Therefore, for any $\mu\in[\frac{1}{2},1]$,

$$ c_{\mu}=\inf_{\gamma\in\Gamma_{\mu}}\max_{t\in[0,1]}I^{T}_{\mu}\bigl( \gamma(t) \bigr)\geq\inf_{\gamma\in\Gamma_{\mu}} I^{T}_{\mu}\bigl( \gamma(t_{\gamma}) \bigr)\geq c>0, $$

(2.36)

which completes the proof. □

Lemma 2.6

For any $\mu\in[\frac{1}{2},1]$ and $a>2^{m+1}(\frac{m+3}{m+1})\lambda T^{pm}$, each bounded (PS) sequence of the functional $I^{T}_{\mu}$ admits a convergent subsequence.

Proof

By Lemmas 2.3-2.5, we obtain that, for a.e. $\mu\in [1/2,1]$, there is a bounded sequence $\{u_{n}\}$ in X that satisfies

$$ I^{T}_{\mu}(u_{n})\rightarrow c_{\mu},\quad\quad \bigl(I^{T}_{\mu}(u_{n}) \bigr)' \rightarrow0 \quad \text{in } X^{*},\quad \text{and} \quad\sup_{n} \Vert u_{n}\Vert < T. $$

(2.37)

Since the embedding $X\hookrightarrow L^{q}(\mathbb{R}^{N})$ is compact for $q\in(p,p^{*})$, passing to a subsequence, we can assume that

$$ u_{n}\rightharpoonup u, \quad\text{in } X; \quad\quad u_{n} \rightarrow u, \quad L^{q} \bigl(\mathbb{R}^{N} \bigr);\quad\quad u_{n} \rightarrow u, \quad \text{a.e. in } \mathbb{R}^{N}. $$

(2.38)

By (2.16) we can get

$$ \bigl(I^{T}_{\mu}(u_{n})-I^{T}_{\mu}(u) \bigr)'(u_{n}-u)=A_{n}+B_{n}+\mu C_{n}, $$

(2.39)

where

$$ \begin{gathered} A_{n}= \widehat{M}(u_{n}) \int_{\mathbb{R}^{N}} \bigl(\vert \nabla u_{n}\vert ^{p-2}\nabla u_{n} -\vert \nabla u\vert ^{p-2} \nabla u \bigr)\nabla(u_{n}-u) \\ \hphantom{A_{n}=}{}+ \bigl(\vert u_{n}\vert ^{p-2}u_{n}-u^{p-2}u \bigr) (u_{n}-u)\,dx, \\ B_{n}= \bigl(\widehat{M}(u_{n})-\widehat{M}(u) \bigr) \int_{\mathbb{R}^{N}}\vert \nabla u\vert ^{p-2}\nabla{u} \nabla(u_{n}-u)+\vert u\vert ^{p-2}u(u_{n}-u)\,dx, \\ C_{n}= \int_{\mathbb{R}^{N}} \bigl(f(u_{n})-f(u) \bigr) (u_{n}-u)\,dx. \end{gathered} $$

(2.40)

It is clear that

$$ \bigl(I^{T}_{\mu}(u_{n})-I^{T}_{\mu}(u) \bigr)'(u_{n}-u)\rightarrow0 \quad\text{as } n \rightarrow \infty. $$

(2.41)

An analogous argument as in (2.22) and (2.25) gives us that

$$ B_{n}\to0 \quad \mbox{and}\quad C_{n}\to0 \quad\text{as } n\to\infty. $$

(2.42)

Combining the above results and $a>2^{m+1}(\frac{m+3}{m+1})\lambda T^{pm}$, we have that $\vert A_{n}\vert \to0$ as $n\to\infty$. Then, using a standard equality ([3], Lemma 2.1), we can show that $u_{n} \rightarrow u$ in X. The proof is completed. □

Lemma 2.7

Assume $(F_{1})$-$(F_{3})$ and $a>2^{m+1}(\frac{m+3}{m+1})\lambda T^{pm}$. Then, for almost every $\mu\in[\frac{1}{2},1]$, there exist $u^{\mu}\in X\setminus\{0\}$ such that $(I^{T}_{\mu})'(u^{\mu})=0$ and $I^{T}_{\mu}(u^{\mu})=c_{\mu}$ with $\Vert h\Vert _{p'}< m_{1}$.

Proof

It follows from Lemmas 2.3-2.5 that, for every $\mu \in[\frac{1}{2},1]$, there exists a bounded sequence $\{u_{n}^{\mu}\} \subset X$ such that

$$ I^{T}_{\mu}\bigl(u^{\mu}_{n} \bigr)\rightarrow c_{\mu}\quad \mbox{and} \quad \bigl(I^{T}_{\mu}\bigr)' \bigl(u^{\mu}_{n} \bigr)\rightarrow0\quad \mbox{as } n\rightarrow\infty. $$

By Lemma 2.6 we can suppose that $u^{\mu}\in X$ and $u^{\mu}_{n}\rightarrow u^{\mu}$ in X. The proof is completed. □

According to Lemma 2.6, there exists a sequence $\{\mu_{n}\}\subset[\frac{1}{2},1]$ with $\mu_{n}\rightarrow1$ and $\{u_{n}\}\subset X$ as $n\rightarrow\infty$ such that $I^{T}_{\mu_{n}}(u_{n})=c_{\mu_{n}}$, $(I^{T}_{\mu_{n}})'(u_{n})=0$, and $u_{n}$ is a positive solution of

$$\begin{aligned} {\widehat{M}} \bigl(\Vert u\Vert \bigr) \bigl(-\Delta_{p} u+ \vert u\vert ^{p-2}u \bigr)=\mu_{n} \bigl(f(u)+h(x) \bigr). \end{aligned}$$

(2.43)

In the following, to obtain $\Vert u_{n}\Vert < T$, we establish an identity that extends the Kazin-Pohozav identity in ([13], Thm. 29.4) with $p=2$.

Lemma 2.8

Assume that $f(x,u):\mathbb{R}^{N}\times\mathbb{R}^{1}\rightarrow\mathbb{R}^{1}$ is a Carethéodary function, $u\in C^{2}_{\mathrm {loc}}(\mathbb{R}^{N})$ is a solution of

$$ \textstyle\begin{cases} -\Delta_{p} u+f(x,u)=0\quad \textit{in } \mathbb{R}^{N}, \\ u(x)\rightarrow0 \quad\textit{as } \rightarrow0, \end{cases} $$

(2.44)

$\frac{\partial u}{\partial x_{i}}\in L^{p}({\mathbb{R}^{N}})$, $i=1,2,\ldots$ , and $F(x,u), F_{1}(x,u)\in L^{1}(\mathbb{R}^{N})$. Then

$$ \frac{N-p}{p} \int_{\mathbb{R}^{N}}\vert \nabla u\vert ^{p}\,dx+ \int_{\mathbb{R}^{N}} \bigl(NF(x,u)+F_{1}(x,u) \bigr)\,dx=0, $$

(2.45)

where $F(x,u)=\int^{u}_{0}f(x,s)\,ds$ and $F_{1}(x,u)=\sum^{N}_{i=1}x_{i}\frac{\partial F(x,u)}{\partial x_{i}}$.

Proof

Multiplying equation (2.44) by $x\cdot\nabla u$ and integrating over the ball $B_{R}$, we obtain

$$\begin{aligned} \int_{B_{R}}f(x,u)x\cdot\nabla u\,dx= \int_{B_{R}}\operatorname {div}\bigl(\vert \nabla u\vert ^{p-2} \nabla u \bigr)x\cdot\nabla u\,dx. \end{aligned}$$

(2.46)

Then

$$ \begin{aligned}[b] \int_{B_{R}}f(x,u)x\cdot\nabla u\,dx&=\sum ^{N}_{i=1} \int_{B_{R}}x_{i} f(x,u)\frac{\partial u}{\partial x_{i}}\,dx \\ &=\sum^{N}_{i=1} \int_{B_{R}} \biggl(\frac{\partial}{\partial x_{i}} \bigl(x_{i}F(x,u) \bigr)- \biggl(F(x,u)+x_{i}\frac{\partial F(x,u)}{\partial x_{i}} \biggr) \biggr)\,dx \\ &=\sum^{N}_{i=1} \int_{\partial B_{R}}F(x,u) x_{i}n_{i}\,ds- \int_{B_{R}} \bigl(NF(x,u)+F_{1}(x,u) \bigr)\,dx \\ &=R \int_{\partial B_{R}}F(x,u)\,ds- \int_{B_{R}} \bigl(NF(x,u)+F_{1}(x,u) \bigr)\,dx, \end{aligned} $$

(2.47)

where $n_{i}$ are the components of the unit outward normal to $\partial B_{R}$, and ds is an area element. On the other hand, integrating by parts, we obtain

$$ \begin{aligned}[b] & \int_{B_{R}}\operatorname {div}\bigl(\vert \nabla u\vert ^{p-2} \nabla u \bigr)x\cdot\nabla u\,dx \\ &\quad =\sum^{N}_{j=1} \int_{B_{R}}\frac{\partial}{\partial x_{j}} \biggl(\vert \nabla u\vert ^{p-2}\frac{\partial u}{\partial x_{j}} \biggr)\sum^{N}_{i=1}x_{i} \frac{\partial u}{\partial x_{i}}\,dx \\ &\quad =\sum^{N}_{j=1} \int_{B_{R}} \Biggl(\frac{\partial}{\partial x_{j}} \Biggl(\vert \nabla u \vert ^{p-2}\frac{\partial u}{\partial x_{j}}\sum^{N}_{i=1}x_{i} \frac{\partial u}{\partial x_{i}} \Biggr)-\vert \nabla u\vert ^{p-2} \frac{\partial u}{\partial x_{j}} \Biggl(\frac{\partial}{\partial x_{j}}\sum^{N}_{i=1}x_{i} \frac{\partial u}{\partial x_{i}} \Biggr) \Biggr)\,dx \\ &\quad = \int_{\partial B_{R}} \vert \nabla u\vert ^{p-2} \frac{\partial u}{\partial n}x\cdot\nabla u\,ds- \int_{B_{R}}\vert \nabla u\vert ^{p}\,dx \\ &\quad\quad{} - \int_{B_{R}}\sum^{N}_{j=1} \vert \nabla u\vert ^{p-2} \Biggl(\sum^{N}_{i=1}x_{i} \frac{\partial^{2} u}{\partial x_{i}\,\partial x_{j}}\frac{\partial u}{\partial x_{j}} \Biggr)\,dx. \end{aligned} $$

(2.48)

On $B_{R}$, we have $\nabla u=\frac{\partial u}{n}\cdot\vec{n}=\frac {\partial u}{\partial n}\frac{x}{R}$ and

$$ \int_{\partial B_{R}}\vert \nabla u\vert ^{p-2} \frac{\partial u}{\partial n}x\cdot\nabla u\,dx=R \int_{\partial B_{R}}\vert \nabla u\vert ^{p}\,ds. $$

(2.49)

Further, we have

$$ \begin{aligned}[b] & \int_{B_{R}}\sum^{N}_{j=1} \vert \nabla u\vert ^{p-2} \Biggl(\sum^{N}_{i=1}x_{i} \frac{\partial^{2} u}{\partial x_{i}\,\partial x_{j}}\frac{\partial u}{\partial x_{j}} \Biggr)\,dx \\ &\quad =\frac{1}{p}\sum^{N}_{i=1} \int_{B_{R}} \biggl(\frac{\partial}{\partial x_{i}} \bigl(x_{i} \vert \nabla u\vert ^{p} \bigr)-\vert \nabla u\vert ^{p} \biggr) \,dx \\ &\quad =\frac{R}{p} \int_{\partial B_{R}}\vert \nabla u\vert ^{p}\,ds- \frac{N}{p} \int_{B_{R}}\vert \nabla u\vert ^{p}\,dx. \end{aligned} $$

(2.50)

Therefore, we obtain

$$ R \int_{\partial B_{R}} \biggl(F- \biggl(1-\frac{1}{p} \biggr)\vert \nabla u\vert ^{p} \biggr)\,ds+ \biggl(1-\frac{N}{p} \biggr) \int_{B_{R}}\vert \nabla u\vert ^{p}\,dx- \int_{B_{R}}(NF+F_{1})\,dx=0. $$

(2.51)

Since $F(x,u)\in L^{1}({\mathbb {R}}^{N})$ and $u\in X$, we claim that

$$ \liminf_{n\to\infty}R \int_{\partial B_{R}} \bigl( \bigl\vert F(x,u) \bigr\vert +\vert \nabla u\vert ^{p} \bigr)\,dS=0. $$

(2.52)

Indeed, otherwise,

$$ \liminf_{n\to\infty}R \int_{\partial B_{R}} \bigl( \bigl\vert F(x,u) \bigr\vert +\vert \nabla u\vert ^{p} \bigr)\,dS=a_{0}>0. $$

(2.53)

Then, there exists $R_{0}>0$ such that, for $R\geq R_{0}$,

$$ R \int_{\partial B_{R}} \bigl( \bigl\vert F(x,u) \bigr\vert +\vert \nabla u\vert ^{p} \bigr)\,dS\geq\frac{a_{0}}{2}. $$

(2.54)

Let $R_{n}=R_{0}+n$, $n=1,2,\dots$. Then $R_{n}\to\infty$ as $n\to\infty$. It follows from the integral mean theorem that there is $\xi_{n}\in (R_{n-1},R_{n})$ and $\xi_{n}\geq R_{0}$ such that, for $R\geq R_{0}$,

$$ \int^{R_{n}}_{R_{n-1}} \int_{\partial B_{R}} \bigl(\vert F\vert +\vert \nabla u\vert ^{p} \bigr)\,ds\,dR=\xi_{n} \int_{\partial B_{\xi_{n}}} \bigl(\vert F\vert +\vert \nabla u\vert ^{p} \bigr)\,ds\geq\frac{a_{0}}{2}, $$

(2.55)

and thus

$$ \int^{\infty}_{R_{0}} \int_{\partial B_{R}} \bigl(\vert F\vert +\vert \nabla u\vert ^{p} \bigr)\,ds\,dR\geq\sum^{\infty}_{n=2} \int^{R_{n}}_{R_{n-1}} \int_{\partial B_{R}} \bigl(\vert F\vert +\vert \nabla u\vert ^{p} \bigr)\,ds\,dR=\infty. $$

(2.56)

This contradicts the fact

$$ \int_{{\mathbb {R}}^{N}} \bigl(\vert F\vert +\vert \nabla u\vert ^{p} \bigr)\,dx= \int^{\infty}_{0} \int_{\partial B_{R}} \bigl(\vert F\vert +\vert \nabla u\vert ^{p} \bigr)\,ds\,dR< \infty. $$

(2.57)

Therefore, (2.52) is true. Thus, letting $R\to\infty$ in (2.51), we have

$$ \frac{N-p}{p} \int_{\mathbb{R}^{N}}\vert \nabla u\vert ^{p}\,dx+ \int_{\mathbb{R}^{N}} \bigl(NF(x,u)+F_{1}(x,u) \bigr)\,dx=0. $$

(2.58)

Then, we finish the proof of Lemma 2.8. □

Lemma 2.9

Let $a>2^{m+1}(\frac{m+3}{m+1})\lambda T^{pm}$, and let $u\in X$ be a weak solution of

$$ {\widehat{M}} \bigl(\Vert u\Vert \bigr) \bigl(- \Delta_{p} u+\vert u\vert ^{p-2}u \bigr)=\mu \bigl(f(u)+h(x) \bigr), $$

(2.59)

where ${\widehat{M}}(\Vert u\Vert )=(a + \lambda\eta_{T}(u)\Vert u\Vert ^{pm} + \frac{\lambda}{(m + 1)T^{p}}\eta'_{T}(u)\Vert u\Vert ^{p(m + 1)})$. Then the following identity holds:

$$ \begin{aligned}[b] &{\widehat{M}} \bigl(\Vert u\Vert \bigr) \biggl( \frac{N-p}{p} \int_{\mathbb{R}^{N}} \vert \nabla u\vert ^{p}\,dx + \frac{N}{p} \int_{\mathbb{R}^{N}}\vert u\vert ^{p}\,dx \biggr) \\ &\quad = N\mu \int_{\mathbb{R}^{N}} \bigl(F(u)+hu \bigr)\,dx + \mu \int_{\mathbb{R}^{N}}\nabla h\cdot xu\,dx. \end{aligned} $$

(2.60)

Proof

Since $u\in X$ is a weak solution of (2.59), by standard regularity results, $u\in C^{2}_{\mathrm {loc}}(\mathbb{R}^{N})\cap W^{1,p}(\mathbb {R}^{N})$. Let

$$ g(x,u)=\frac{\mu(f(u)+h(x))}{{\widehat{M}}(\Vert u\Vert )}-\vert u\vert ^{p-2}u. $$

(2.61)

Then $u\in X$ is also a solution of

$$ -\Delta_{p} u=g(x,u). $$

(2.62)

By Lemma 2.8,

$$ \frac{N-p}{p} \int_{\mathbb{R}^{N}}\vert \nabla u\vert ^{p}\,dx= \int_{\mathbb{R}^{N}} \bigl(NG(u)+ G_{1}(x, u) \bigr)\,dx, $$

(2.63)

where $G(x,u)=\int^{u}_{0}g(x,s)\,ds$ and $G_{1}(x,u)=\sum^{N}_{i=1}x_{i}\frac {\partial G(x,u)}{\partial x_{i}}$. Then the conclusion holds. □

Lemma 2.10

Assume that $(F_{1})$-$(F_{3})$ and $(H)$ hold and that $\Vert h\Vert _{p'}< m_{1}$ for $m_{1}$ given in Lemma  2.6. Let $u_{n}$ be a critical point of $I^{T}_{\mu_{n}}$ at level $c_{\mu_{n}}$. Then for T sufficiently large, there exists $\lambda_{0}=\lambda_{0}(T)$ with $\lambda_{0}< a(\frac{m+1}{m+3})T^{-pm}$ such that, for any $\lambda\in[0,\lambda_{0})$, subject to a subsequence, $\Vert u_{n}\Vert < T$ for all $n\in\mathbb{N}$.

Proof

Since $(I^{T}_{\mu_{n}})'(u_{n})=0$, by Lemma 2.9 $u_{n}$ satisfies

$$ \begin{aligned}[b] & {\widehat{M}} \bigl( \Vert u\Vert \bigr) \biggl( \frac{N}{p}\Vert u\Vert ^{p}+ \int_{{\mathbb {R}}^{N}}\vert \nabla u\vert ^{p}\,dx \biggr) \\ &= N \mu_{n} \int_{\mathbb{R}^{N}} \bigl(F(u_{n}) + hu_{n} \bigr)\,dx + \mu_{n} \int_{\mathbb{R}^{N}} \nabla h\cdot xu_{n}\,dx. \end{aligned} $$

(2.64)

Using $I^{T}_{\mu_{n}}(u_{n})=c_{\mu_{n}}$, we have

$$ \frac{aN}{p}\Vert u_{n}\Vert ^{p}+ \frac{\lambda N}{p(m+1)}\eta_{T}(u_{n})\Vert u_{n} \Vert ^{p(m+1)}=N\mu_{n} \int_{\mathbb{R}^{N}} \bigl(F(u_{n})+h u_{n} \bigr)\,dx+Nc_{\mu_{n}}. $$

(2.65)

Therefore, by (2.64), (2.65) and $a>2^{m+1}(\frac {m+3}{m+1})\lambda T^{pm}$ we deduce that

$$\begin{aligned}& \frac{a}{2} \int_{\mathbb{R}^{N}}\vert \nabla u_{n}\vert ^{p}\,dx \\& \quad \leq{\widehat{M}} \bigl( \Vert u_{n}\Vert \bigr) \int_{\mathbb{R}^{N}}\vert \nabla u_{n}\vert ^{p}\,dx \\& \quad =N c_{\mu_{n}}+N \biggl(\widehat{M} \bigl( \Vert u_{n} \Vert \bigr)-\frac{a}{p} \biggr)\Vert u\Vert ^{p}- \frac{\lambda N}{p(m+1)}\eta_{T}(u_{n})\Vert u_{n} \Vert ^{p(m+1)} - \mu_{n} \int_{\mathbb{R}^{N}}\nabla hx\cdot u_{n}\,dx \\& \quad \leq N c_{\mu_{n}} + \frac{\lambda Nm}{p(m+1)}\eta_{T}(u_{n}) \Vert u_{n}\Vert ^{p(m+1)} + \frac{\lambda N}{p(m+1)T^{p}} \eta'_{T}(u_{n})\Vert u_{n}\Vert ^{p(m+2)} \\& \quad{} - \mu_{n} \int_{\mathbb{R}^{N}}\nabla hx\cdot u_{n}\,dx. \end{aligned}$$

(2.66)

By the min-max definition of the mountain pass level, Lemma 2.5, and (2.35) we have

$$ \begin{aligned}[b] c_{\mu_{n}}&\leq\max_{t} I^{T}_{\mu_{n}}(t \beta) \\ &\leq\max_{t} \biggl\{ \biggl(\frac{a}{p}- \frac{C_{3}}{2} \int_{B_{R}}\vert \beta \vert ^{p}\,dx \biggr)t^{p}+C_{5} \biggr\} +\max_{t} \frac{\lambda}{p(m+1)} \psi \biggl(\frac{t^{p}}{T^{p}} \biggr)t^{p(m+1)} \\ &\leq\frac{\lambda2^{m+1}}{p(m+1)}T^{p(m+1)}+C_{5}. \end{aligned} $$

(2.67)

Using $(H)$ and the Young equality, we have

$$ \begin{aligned}[b] \int_{\mathbb{R}^{N}}\nabla h\cdot xu_{n} \,dx &\leq\frac{ 1}{p'} \int_{\mathbb{R}^{N}}\vert \xi \vert ^{p'}\,dx+ \frac{1}{p} \int_{\mathbb{R}^{N}}\vert \xi \vert ^{p'}\vert u_{n}\vert ^{p}\,dx \\ & \leq\frac{1}{p} \int_{\mathbb{R}^{N}}\vert \xi \vert ^{p'}\vert u_{n}\vert ^{p}\,dx+C_{6}. \end{aligned} $$

(2.68)

We can easily calculate that

$$ \eta_{T}(u_{n})\Vert u_{n} \Vert ^{p(m+1)}\leq2^{m+1}T^{p(m+1)}, \quad\quad \eta'(u_{n}) \Vert u_{n}\Vert ^{p(m+2)}\leq2^{m+2}T^{p(m+2)}. $$

(2.69)

Combining the above estimates, we see that

$$ \frac{a}{2} \int_{\mathbb{R}^{N}}\vert \nabla u_{n}\vert ^{p}\,dx \leq\frac{\lambda N(m+5)}{p(m+1)}2^{m+1}T^{p(m+1)}+ \frac{1}{p} \int_{\mathbb{R}^{N}}\vert \xi \vert ^{p'}\vert u_{n}\vert ^{p}\,dx+C_{7}. $$

(2.70)

Since $\xi(x)\in L^{p'}(\mathbb{R}^{N})\cap W^{1,\infty}$, we see that $\xi^{p'}u_{n}\in X$. It follows from $(I^{T}_{\mu_{n}}(u_{n}))'(\xi^{p'}u_{n})=0$ that

$$ \begin{aligned}[b] & \widehat{M} \bigl( \bigl\Vert \xi^{p'}u_{n} \bigr\Vert \bigr) \int_{\mathbb{R}^{N}}\vert \nabla u_{n}\vert ^{p-2} \nabla u_{n}\nabla \bigl(\xi^{p'}u_{n} \bigr) + \vert u_{n}\vert ^{p-2}u \bigl(\xi^{p'}u_{n} \bigr)\,dx \\ &\quad = \mu_{n} \int_{\mathbb{R}^{N}} \bigl(f(u_{n})+h \bigr) \xi^{p'}u_{n}\,dx. \end{aligned} $$

(2.71)

Since $a>2^{m+1}(\frac{m+3}{m+1})\lambda T^{pm}$, we have $({3a}/2)\geq \widehat{M}( \Vert \xi^{p'}u_{n}\Vert )$, and it follows from (2.69) and (2.71) that

$$ ({3a}/2) \int_{\mathbb{R}^{N}}\vert \nabla u_{n}\vert ^{p-2} \nabla u_{n}\nabla \bigl(\xi^{p'}u_{n} \bigr) +\vert u_{n}\vert ^{p}\xi^{p'}\,dx\geq(1/ {2}) \int_{\mathbb{R}^{N}}f(u_{n})u_{n} \xi^{p'}\,dx. $$

(2.72)

From (2.70) by the Hölder inequality we deduce that

$$ \begin{aligned}[b] &{3a} \int_{\mathbb{R}^{N}}\vert \nabla u_{n}\vert ^{p-2} \nabla u_{n}\nabla \bigl(\xi^{p'}u_{n} \bigr)\,dx \\ &\quad \leq{3a} \int_{\mathbb{R}^{N}}\vert \nabla u_{n}\vert ^{p-2} \nabla u_{n} \bigl(p'\xi^{p'-1}u_{n} \nabla\xi+\xi^{p'}\nabla u_{n} \bigr)\,dx \\ &\quad \leq3 \bigl(\Vert \xi \Vert ^{\infty}_{p'}+\Vert \nabla \xi \Vert ^{\infty}_{p'} \bigr) \biggl({a} \int_{\mathbb{R}^{N}}\vert \nabla u_{n}\vert ^{p}\,dx \biggr)+{3a} {(p-1)^{-1}} \int_{\mathbb{R}^{N}}\xi^{p'}\vert u_{n}\vert ^{p}\,dx \\ &\quad \leq C\lambda T^{p(m+1)}+C \int_{\mathbb{R}^{N}}\xi^{p'}\vert u_{n}\vert ^{p}\,dx+C, \end{aligned} $$

(2.73)

where C is a constant independent of λ and T.

By $(F_{3})$, for any $L>0$, there exists $C(L)>0$ such that

$$ f(s)s\geq Ls^{p}-C(L) \quad\text{for all } s>0. $$

(2.74)

Combining (2.72)-(2.74), we get

$$ \biggl(\frac{1}{2}L-C \biggr) \int_{\mathbb{R}^{N}}\xi^{p'}\vert u_{n}\vert ^{p}\,dx\leq C\lambda T^{p(m+1)}+C. $$

(2.75)

For $L>0$ large enough, we obtain

$$ \int_{\mathbb{R}^{N}}\xi^{p'}\vert u_{n}\vert ^{p}\,dx\leq C\lambda T^{p(m+1)}+C. $$

(2.76)

It follows from (2.70) and (2.76) that

$$ \int_{\mathbb{R}^{N}}\vert \nabla u_{n}\vert ^{p}\,dx \leq C\lambda T^{p(m+1)}+C. $$

(2.77)

On the other hand,

$$ \begin{aligned}[b] &a\Vert u_{n}\Vert ^{p} + \eta_{T}(u_{n})\Vert u_{n} \Vert ^{p(m+1)} + \frac{\lambda}{m+1}\eta'_{T}(u_{n}) \Vert u_{n}\Vert ^{p(m+2)} \\ &\quad = \mu_{n} \int_{\mathbb{R}^{N}} \bigl(f(u_{n})u_{n}+hu_{n} \bigr)\,dx \\ &\quad \leq\varepsilon \Vert u_{n}\Vert ^{p} + C_{\varepsilon} \Vert u_{n}\Vert _{p^{*}}^{p^{*}} + \frac{1}{p'} \Vert h\Vert ^{p'}_{p'} + \frac{1}{p}\Vert u \Vert ^{p}. \end{aligned} $$

(2.78)

By (2.77) and (2.78) we have

$$ \begin{aligned}[b] (a-\varepsilon-{1}/{p})\Vert u_{n}\Vert ^{p}&\leq C_{\varepsilon} \Vert u_{n}\Vert ^{p*}_{p*}-{\lambda}/ \bigl({(m+1)T^{p}} \bigr) \eta'_{T}(u_{n})\Vert u_{n}\Vert ^{p(m+2)}+C \\ &\leq C\Vert \nabla u_{n}\Vert ^{p*}_{p}+{ \lambda2^{m+2}} {(m+1)}^{-1}T^{p(m+1)}+C \\ &\leq C\lambda T^{p^{*}(m+1)}+C\lambda T^{p(m+1)}+C. \end{aligned} $$

(2.79)

Suppose that $\Vert u_{n}\Vert >T$ for $n\in {\mathbb {N}}$ and T large enough. Then

$$ T^{p}< \Vert u_{n}\Vert ^{p}\leq C\lambda T^{p^{*}(m+1)}+C\lambda T^{p(m+1)}+C, $$

(2.80)

which is not true if we choose T large and λ small enough. So by setting $\lambda(T)$ small we obtain that the sequence $\{u_{n}\}$ is bounded for any $\lambda\in[0,\lambda_{0})$, and the conclusion holds. □

Lemma 2.11

Let T, $\lambda_{0}$ be defined by Lemma  2.10, and $u_{n}$ be the critical point of $I^{T}_{\mu_{n}}$ at level $c_{\mu_{n}}$. Then the sequence $\{u_{n}\}$ is also a (PS) sequence for I.

Proof

From the proof of Lemma 2.10 we may assume that $\Vert u_{n}\Vert \leq T$. So

$$ I(u_{n})=I^{T}_{\mu_{n}}(u_{n})+( \mu_{n}-1) \int_{\mathbb{R}^{N}} \bigl(F(u_{n})+hu_{n} \bigr)\,dx. $$

(2.81)

Since $\mu_{n}\rightarrow1$, we can show that $\{u_{n}\}$ is a (PS) sequence of I. Indeed, the boundedness of $\{u_{n}\}$ implies that $\{I^{T}_{\mu_{n}}\}$ is bounded. Also,

$$ I'(u_{n})v= \bigl(I^{T}_{\mu_{n}} \bigr)'(u_{n},v)+(\mu_{n}-1) \int_{\mathbb{R}^{N}} \bigl(f(u_{n})+h(u_{n}) \bigr)v\,dx, \quad v\in X. $$

(2.82)

Thus, $I'(u_{n})\rightarrow0$, and $\{u_{n}\}$ is a bounded (PS) sequence of I. By Lemma 2.5, $\{u_{n}\}$ has a convergent subsequence. We may assume that $u_{n}\rightarrow\tilde{u}_{0}$. Consequently, $I'(\tilde{u}_{0})=0$. According to Lemma 2.4, we have that $I(\tilde{u}_{0})=\lim_{n\rightarrow\infty} I(u_{n})=\lim_{n\rightarrow\infty}I^{T}_{\mu_{n}}(u_{n})\geq c>0$ and $\tilde{u}_{0}$ is a solution of problem (1.1). Thus, we completed the proof. □

Proof of Theorem 1.1

By Lemma 2.2 the problem has a solution $u_{0}\in X$ with $I(u_{0})<0$. From Lemma 2.9 we know that problem (1.1) possesses a second solution $\tilde{u}_{0}\in X$ with $I(\tilde{u}_{0})\geq c>0$. Hence, $u_{0}\neq\tilde{u}_{0}$, and we complete the proof of Theorem 1.1. □

3 Proof of Theorem 1.2

Let $I_{\lambda}(u):X\rightarrow\mathbb{R}$ be the energy functional associated with problem (1.13) defined by

$$ I_{\lambda}(u)=\frac{a}{p}\Vert u\Vert ^{p}+ \frac{\lambda}{p(m+1)}\Vert u\Vert ^{p(m+1)}-\frac{1}{q}\Vert u \Vert ^{q}_{q}, $$

(3.1)

where $F(u)=\int_{0}^{u}f(s)\,ds$. It is easy to see that the functional $I\in C^{1}(E,\mathbb{R})$ and its Gateaux derivative is given by

$$ \begin{aligned}[b] I_{\lambda}'(u)v&= \bigl(a+\lambda \Vert u\Vert ^{pm} \bigr) \int_{\mathbb{R}^{N}} \bigl(\vert \nabla u\vert ^{p-2} \nabla u \nabla v+\vert u\vert ^{p-2}uv \bigr)\,dx \\ &\quad{} - \int_{\mathbb{R}^{N}} \vert u\vert ^{q-2}uv\,dx,\quad \forall v \in E. \end{aligned} $$

(3.2)

Clearly, we see that a weak solution of (1.13) corresponds to a critical point of the functional.

In this part, we first proof the nonexistence for problem (1.13) for large $\lambda>\lambda^{*}$. which means that if a solution exists, then λ must sufficiently small. Secondly, we obtain that there exists $\lambda^{**}$ such that problem (1.1) has at least one solution for any $0<\lambda<\lambda^{**}$. Finally, by the properties of $\lambda^{*}$ and $\lambda^{**}$ we deduce that $\lambda^{*}=\lambda ^{**}$. We will break the proof into six steps.

Proof of Theorem 1.2

Step 1. Nonexistence for large $\lambda>0$ . It is sufficient to show that if u is a nontrivial solution of problem (1.13), then $\lambda>0$ must be small. Assume that u is a nontrivial solution of problem (1.1). Then we get $I'_{\lambda}(u)u=0$, that is,

$$ a\Vert u\Vert ^{p}+\lambda \Vert u\Vert ^{p(m+1)}=\Vert u\Vert _{q}^{q}. $$

(3.3)

Since $p< q<\min\{p(m+1),p^{*}\}$, applying the Young inequality and (1.9), we deduce that

$$ a\Vert u\Vert ^{p}+\lambda \Vert u\Vert ^{p(m+1)}=\Vert u\Vert _{q}^{q}\leq S_{q}^{q}\Vert u\Vert ^{q}_{E}\leq a \Vert u\Vert ^{p}_{E}+\lambda_{1}\Vert u \Vert ^{p(m+1)}_{E}, $$

(3.4)

which implies that $\lambda\leq\lambda_{1}=(S^{q}_{q})^{\frac {pm}{q-p}}a^{-\frac{p(m+1)-q}{q-p}}$. On the other hand, if $\lambda ^{*}\geq\lambda_{1}$, then we conclude that problem (1.1) has no solution for any $\lambda\in(\lambda^{*}, +\infty)$.

Step 2. Coercivity of $I_{\lambda}(u)$ . Indeed, for any $u\in E$ and all $\lambda>0$,

$$ \begin{aligned}[b] I_{\lambda}(u)&=\frac{a}{p}\Vert u \Vert ^{p}+\frac{\lambda}{p(m+1)}\Vert u\Vert ^{p(m+1)}- \frac{1}{q}\Vert u\Vert ^{q}_{q} \\ &\geq\frac{a}{p}\Vert u\Vert ^{p}+\frac{\lambda}{2p(m+1)} \Vert u\Vert ^{p(m+1)}+\frac{\lambda}{2p(m+1)}\Vert u\Vert ^{p(m+1)}- \frac{S^{q}_{q}}{q}\Vert u\Vert ^{q}. \end{aligned} $$

(3.5)

Since $q< p(m+1)$, there exists $C_{1}=C_{1}(\lambda,q,m,S_{q})$ such that

$$ \frac{S^{q}_{q}}{q}\Vert u\Vert ^{q}\leq\frac{\lambda}{2p(m+1)}\Vert u \Vert ^{p(m+1)}+C_{1}. $$

(3.6)

It follows that

$$ I_{\lambda}(u)\geq\frac{a}{p}\Vert u\Vert ^{p}+ \frac{\lambda}{2p(m+1)}\Vert u\Vert ^{p(m+1)}-C_{1}. $$

(3.7)

This implies that $I_{\lambda}(u)$ is coercive.

Step 3. The infimum of $I_{\lambda}$ is attained. Let $\{u_{n}\}$ be a minimizing sequence of $I_{\lambda}$. Then from Step 2 we immediately see that $\{u_{n}\}$ is bounded in X. Therefore, without loss of generality, we may assume that $\{u_{n}\}$ is nonnegative and converges weakly and pointwise to some u in X.

Using the compact embedding $X\hookrightarrow L^{q}(\mathbb{R}^{N})$, we have

$$ \Vert u\Vert _{q}=\lim_{n\to\infty} \Vert u_{n}\Vert _{q} \quad\text{and} \quad \Vert u\Vert \leq \liminf_{n\to\infty} \Vert u_{n}\Vert $$

(3.8)

by the weak lower semicontinuity of the norm $\Vert \cdot \Vert$. Thus,

$$\begin{aligned} \begin{aligned}[b] I_{\lambda}(u)&=\frac{a}{p}\Vert u \Vert ^{p}+\frac{\lambda}{p(m+1)}\Vert u\Vert ^{p(m+1)}- \frac{1}{q}\Vert u\Vert ^{q}_{q} \\ &\leq\liminf_{n\to\infty} \biggl(\frac{a}{p}\Vert u_{n}\Vert ^{p}+\frac{\lambda}{p(m+1)}\Vert u_{n} \Vert ^{p(m+1)} \biggr)-\frac{1}{q}\lim_{n\to\infty} \Vert u_{n}\Vert ^{q}_{q} \\ &\leq\liminf_{n\to\infty} \biggl(\frac{a}{p}\Vert u_{n}\Vert ^{p}+\frac{\lambda}{p(m+1)}\Vert u_{n} \Vert ^{p(m+1)}- \frac{1}{q}\Vert u_{n} \Vert ^{q}_{q} \biggr)=\liminf_{n\to\infty}I_{\lambda}(u_{n}). \end{aligned} \end{aligned}$$

(3.9)

Therefore, u is a global minimum for $I_{\lambda}$, and hence it is a critical point, namely a weak solution to problem (1.1).

Step 4. The weak solution u is nontrivial if $\lambda>0$ is sufficiently small. Clearly, $I_{\lambda}(0)=0$. Therefore, it is sufficient to show that there exists $\lambda_{0}>0$ such that

$$ \inf_{u\in E}I_{\lambda}(u)< 0, \quad \mbox{for any } \lambda\in(0, \lambda_{0}). $$

(3.10)

Choose $u_{0}\in C^{\infty}_{0}({\mathbb {R}}^{N})$, $u_{0}\not\equiv0$, such that $\Vert u_{0}\Vert _{E}=1$. Denote

$$ I_{\lambda}(tu_{0})=t^{p}s(t), \quad\quad s(t)=B_{1}+ \lambda B_{2}t^{pm}-B_{3}t^{q-p}, \quad t\geq0, $$

(3.11)

where

$$B_{1}=\frac{a}{p}, \quad\quad B_{2}=\frac{1}{p(m+1)}>0,\quad\quad B_{3}=\frac{1}{q} \int_{{\mathbb {R}}^{N}}\vert u_{0}\vert ^{q}\,dx>0. $$

Then there exist $\lambda_{0}>0$ and large $t_{\lambda}>0$ such that $I_{\lambda}(t_{\lambda}u_{0})<0$ for $\lambda\in(0,\lambda_{0}]$. Let $e=t_{\lambda}u_{0}$. Then $\Vert e\Vert =t_{\lambda}$ and $I_{\lambda}(e)<0$. This implies that (3.10) is true. So the weak solution u is nontrivial if $\lambda>0$ is sufficiently small.

Now, we define

$$\begin{aligned}& \lambda^{**}=\sup \bigl\{ \lambda>0, \mbox{problem (1.13) admits a nontrival weak solution} \bigr\} , \\& \lambda^{*}=\inf \bigl\{ \lambda>0, \mbox{problem (1.13) does not admit any nontrival weak solution} \bigr\} . \end{aligned}$$

Clearly, $\lambda^{**}\geq\lambda^{*}$. To complete the proof of Theorem 1.2, it suffices to prove the following facts: (a) problem (1.13) has a weak solution for any $\lambda<\lambda^{**}$; (b) $\lambda ^{**}=\lambda^{*}$, and problem (1.13) admits a weak solution when $\lambda=\lambda^{*}$.

Step 5. Problem ( 1.13 ) has a solution for any $\lambda <\lambda^{**}$ and $\lambda^{*}=\lambda^{**}$ . Fix $\lambda<\lambda ^{**}$. By the definition of $\lambda^{**}$, there exists $\mu\in (\lambda,\lambda^{**})$ such that $I_{\lambda}$ has a nontrivial critical point $u_{\mu}\in E$. Clearly, we have

$$ \biggl(a+\lambda \biggl( \int_{\mathbb{R}^{N}} \bigl(\vert \nabla{u_{m}u}\vert ^{p}+\vert u_{\mu} \vert ^{p} \bigr)\,dx \biggr)^{m} \biggr) \bigl(-\Delta_{p}u_{\mu}+\vert u_{\mu} \vert ^{p-2}u_{\mu}\bigr)\leq \vert u_{\mu} \vert ^{q-2}u_{\mu}. $$

(3.12)

This implies that $u_{\mu}$ is a subsolution of problem (1.13). In order to find a supsolution of (1.13) that dominates $u_{\mu}$, we consider the constrained minimization problem

$$ \inf \biggl\{ \frac{a}{p}\Vert \omega \Vert ^{p}+ \frac{\lambda}{p(m+1)}\Vert \omega \Vert ^{p(m+1)}-\frac{1}{q}\Vert \omega \Vert ^{q}_{q}:\omega\in E,\Vert \omega \Vert ^{q}_{q}=q \mbox{ and } \omega\geq u_{\mu}\biggr\} . $$

(3.13)

Arguments similar to those used in Step 3 and Step 4 show that the above minimization has a solution $u_{\lambda}\geq u_{\mu}$, which is also a weak solution of problem (1.13). Hence, problem (1.13) admits a weak solution for any $\lambda\in[0,\lambda^{**})$, This means that $\lambda^{*}\geq\lambda^{**}$ by the definition of $\lambda^{*}$. But we already know that $\lambda^{**}\geq\lambda^{*}$, and therefore $\lambda^{**}=\lambda^{*}$.

Step 6. Problem ( 1.13 ) admits a nontrivial solution when $\lambda=\lambda^{*}$ . Let $\{\lambda_{n}\}$ be a increasing sequence converging to $\lambda ^{*}$, and $\{u_{n}\}$ be a sequence of solutions of (1.1) corresponding to $\lambda_{n}$. By Step 2, $\{u_{n}\}$ is bounded in X, and without loss of generality we may assume that $u_{n}\rightharpoonup u$ in X, $u_{n}\rightarrow u$ in $L^{q}({\mathbb {R}}^{N})$, and $u_{n}\rightarrow u^{*}$ a.e. in X. It follows from $I_{\lambda}(u_{n})v=0$ that, for any $v\in X$,

$$ \bigl(a+\lambda_{n}\Vert u_{n}\Vert ^{pm} \bigr) \int_{\mathbb{R}^{N}} \bigl(\vert \nabla u_{n}\vert ^{p-2}\nabla u_{n} \nabla v+\vert u_{n}\vert ^{p-2}u_{n}v \bigr) \,dx= \int_{\mathbb{R}^{N}}\vert u_{n}\vert ^{q-2}u_{n}v \,dx. $$

(3.14)

Then, passing to the limit as $n\to\infty$, we deduce that $u^{*}$ satisfies $I_{\lambda}(u^{*})v=0$ when $\lambda=\lambda^{*}$. Now, it remains to prove that $u^{*}$ is a nontrivial critical point for $I_{\lambda^{*}}$. From $I'_{\lambda}(u_{n})u_{n}=0$ it is easy to deduce that $\Vert u_{n}\Vert \geq(\lambda_{n} S_{q}^{-q})^{1/(q-p(m+1))}$, which implies that $u_{n}$ has a lower bound. Next, since $\lambda_{n}\nearrow\lambda^{*}$ as $n\to\infty$, it suffices to show that $\Vert u_{n}-u^{*}\Vert \to 0$ as $n\to\infty$.

Since $u_{n}$ and $u^{*}$ are the solutions of (1.1) corresponding to $\lambda_{n}$ and $\lambda^{*}$, we see that

$$ 0= \bigl(I_{\lambda_{n}}'(u_{n})-I_{\lambda^{*}}' \bigl(u^{*} \bigr) \bigr) (u_{n}-u)=X_{n}+Y_{n}-Z_{n}, $$

(3.15)

where

$$\begin{aligned}& X_{n}= \bigl(a+\lambda_{n}\Vert u_{n}\Vert ^{pm} \bigr) \int_{\mathbb{R}^{N}} \bigl(\vert \nabla{u_{n}}\vert ^{p-2}\nabla{u_{n}}- \bigl\vert \nabla{u^{*}} \bigr\vert ^{p-2}\nabla{u^{*}} \bigr)\nabla \bigl(u_{n}-u^{*} \bigr)\,dx \\& \hphantom{X_{n}=} {}+ \bigl(\vert u_{n}\vert ^{p-2}u_{n}- \bigl\vert u^{*} \bigr\vert ^{p-2}u^{*} \bigr) \bigl(u_{n}-u^{*} \bigr)\,dx; \\& Y_{n}= \bigl(\lambda_{n}\Vert u_{n}\Vert ^{pm} - \lambda^{*} \bigl\Vert u^{*} \bigr\Vert ^{pm} \bigr) \int_{\mathbb{R}^{N}} \bigl\vert \nabla{u^{*}} \bigr\vert ^{p-2} \nabla{u^{*}}\nabla \bigl(u_{n}-u^{*} \bigr) \\& \hphantom{Y_{n}=} {}+ \bigl\vert u^{*} \bigr\vert ^{p-2}u^{*} \bigl(u_{n}-u^{*} \bigr)\,dx; \\& Z_{n}= \int_{\mathbb{R}^{N}} \bigl(\vert u_{n}\vert ^{q-2}u_{n}- \bigl\vert u^{*} \bigr\vert ^{q-2}u^{*} \bigr) \bigl(u_{n}-u^{*} \bigr)\,dx. \end{aligned}$$

By the Hölder inequality and compact embedding $u_{n}\to u$ in $L^{q}(\mathbb{R}^{N},H)$ we have

$$ \begin{aligned}[b] \vert X_{n}\vert &= \biggl\vert \int_{\mathbb{R}^{N}} \bigl(\vert u_{n}\vert ^{q-2}u_{n}- \bigl\vert u^{*} \bigr\vert ^{q-2}u^{*} \bigr) \bigl(u_{n}-u^{*} \bigr)\,dx \biggr\vert \\ &\leq \int_{\mathbb{R}^{N}} \bigl(\vert u_{n}\vert ^{q-1}+ \bigl\vert u^{*} \bigr\vert ^{q-1} \bigr) \bigl\vert u_{n}-u^{*} \bigr\vert \,dx \\ &\leq C \bigl(\Vert u_{n}\Vert ^{q-1}+ \bigl\Vert u^{*} \bigr\Vert ^{q-1} \bigr) \bigl\Vert u_{n}-u^{*} \bigr\Vert _{q}\to{0} \quad \mbox{as } n\to\infty. \end{aligned} $$

(3.16)

Next, consider the functional $j:X\to\mathbb{R}$ defined by

$$ j(\omega)= \int_{\mathbb{R}^{N}} \bigl\vert \nabla{u^{*}} \bigr\vert ^{p-2} \nabla{u^{*}}\nabla{\omega}+ \bigl\vert u^{*} \bigr\vert ^{p-2}u^{*}\omega \,dx. $$

(3.17)

Since $\vert j(\omega)\vert \leq2\Vert u^{*}\Vert ^{p-1}\Vert \omega \Vert$, j is continuous on X. Using $u_{n}\rightharpoonup{u^{*}}$ and the boundedness of $u_{n}$ and $u^{*}$ in X, we have that

$$ \vert Y_{n}\vert \le \bigl(\Vert u_{n} \Vert ^{pm}+ \bigl\Vert u^{*} \bigr\Vert ^{pm} \bigr) \bigl\vert g \bigl(u_{n}-u^{*} \bigr) \bigr\vert \to{0} \quad \mbox{as } n\to \infty. $$

(3.18)

Combining (3.15), (3.16), and (3.18), this forces $X_{n}\to{0}$ as $n\to\infty$. Then, using the standard inequality (2.25) in $\mathbb{R}^{N}$, we have that $\Vert u_{n}-u^{*}\Vert \to{0}$ as $n\to\infty$, and thus $u^{*}$ is a nontrivial weak solution of problem (1.13) corresponding to $\lambda=\lambda^{*}$. This completes the proof of Theorem 1.2. □