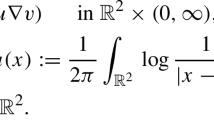Global existence and exponential stability for the strong solutions in $H^{2}$ to the 3-D chemotaxis model

Abstract

We prove the global existence of a unique strong solution to the initial boundary value problem for the 3-D chemotaxis model on a bounded domain with slip boundary condition when the initial perturbation is small in $H^{2}$. Moreover, based on energy methods, we also prove that the strong solution converges to a steady state exponentially fast in time.

1 Introduction

In this paper, we investigate global existence and exponential stability of strong solutions to the following 3-D chemotaxis model:

$$ \left \{ \textstyle\begin{array}{@{}l} \mathbf{v}_{t}-\nabla f(u)=0,\\ u_{t}-\nabla\cdot(u\mathbf{v})=D\Delta u, \end{array}\displaystyle \right . $$

(1.1)

which is one of the models describing the chemotaxis phenomenon in biology and is closely related to the following system:

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} \frac{\partial p}{\partial t}=D\nabla \cdot (p\nabla (\ln\frac{p}{\Phi(w)} ) ),\\ \frac{\partial w}{\partial t}=\Psi(p, w), \end{array}\displaystyle \right . \end{aligned}$$

(1.2)

which is motivated by biological considerations and numerical computations carried out by Othmer and Stevens in [1] and Levine and Sleeman in [2]. Here $p(x, t)$ denotes the particle density and $w(x, t)$ is the concentration of chemicals. $D>0$ is the diffusion rate of particles. The function Φ is commonly referred to as the chemotactic potential and Ψ denotes the chemical kinetics. Depending on the specific modeling goals, the kinetic function $\Psi(p, w)$ has a wide variability. In this paper, we consider a class of nonlinear kinetic functions $\Psi(p, w)$

$$ \Psi(p, w)=\beta f(p)w, $$

(1.3)

where β is a positive constant and f is a smooth function satisfying

$$ f'(u)>0 $$

(1.4)

for all $u>0$.

Direct applications of (1.2) include two aspects: (1) the modeling of haptotaxis, where cells move toward an increasing concentration of immobilized signals such as surface or matrix-bound adhesive molecules; (2) the initiation of angiogenesis, which is a vital process in the growth and development of granulation tissue and wound healing and is a fundamental step in the transition of tumors from a dormant to a malignant state. A comprehensive qualitative and numerical analysis of (1.2) was provided in [2]. In particular, explicit solutions describing and predicting aggregation, blowup, and collapse were constructed in one-dimensional space, based on special choices of initial data and the method of matched asymptotic expansion. The results were generalized by Yang et al. [3]. More discussions on model (1.2) can be found in [4, 5].

In fact, as in [6, 7], let $\Phi(w)=w^{-\alpha}$ with α being a positive constant and let $\Psi(p, w)$ be defined in (1.3). System (1.2) can be rewritten as the following form:

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} p_{t}=D\Delta p+D\alpha\nabla\cdot (p\frac{\nabla w}{w} ),\\ w_{t}=\beta f(p)w. \end{array}\displaystyle \right . \end{aligned}$$

(1.5)

Furthermore, by setting

$$\mathbf{q}=\nabla(\ln w)=\frac{\nabla w}{w}, $$

we can rewrite system (1.5) as

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} p_{t}=D\Delta p+D\alpha\nabla\cdot (p\mathbf{q} ),\\ \mathbf{q}_{t}=\beta\nabla f(p). \end{array}\displaystyle \right . \end{aligned}$$

(1.6)

Finally, for positive constants A, B, and $c_{1}$ to be determined below, if taking $\tau=At$, $\xi=Bx$, $u=p$, $\mathbf{v}=c_{1}\mathbf{q}$, then system (1.6) becomes

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} \mathbf{v}_{\tau}=\frac{\beta Bc_{1}}{A} \nabla_{\xi}f(u),\\ u_{\tau}=\frac{DB^{2}}{A}\Delta_{\xi} u+\frac{D\alpha B}{Ac_{1}} \nabla_{\xi}\cdot(u\mathbf{v}). \end{array}\displaystyle \right . \end{aligned}$$

(1.7)

If we choose

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} \frac{\beta Bc_{1}}{A}=1,\\ \frac{B^{2}}{A}=1,\\ \frac{D\alpha B}{Ac_{1}}=1, \end{array}\displaystyle \right . \end{aligned}$$

(1.8)

i.e.,

$$A=D\alpha\beta>0,\qquad B=\sqrt{D\alpha\beta}>0,\qquad c_{1}=\sqrt{ \frac {D\alpha}{\beta}}>0, $$

then it is easy to see that u and v satisfy

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} \mathbf{v}_{\tau}-\nabla_{\xi}f(u)=0,\\ u_{\tau}-\nabla_{\xi}\cdot(u\mathbf{v})=D\Delta_{\xi} u. \end{array}\displaystyle \right . \end{aligned}$$

(1.9)

If we replace the variables $(\tau, \xi)$ by $(x, t)$, (1.9) is exactly (1.1).

In this paper, we are concerned with the initial boundary value problem to system (1.1). The system is supplemented by the following initial and boundary conditions:

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} (\mathbf{v}, u)(\mathbf{x},0)=(\mathbf{v}_{0}, u_{0})(\mathbf {x}), \quad \mathbf{x}\in\Omega,\\ \mathbf{v}\cdot \mathbf{n}|_{\partial\Omega}=\frac{\partial u}{\partial\mathbf{n}}|_{\partial\Omega}=0, \quad t\geq0,\\ \frac{1}{|\Omega|}\int_{\Omega}u_{0}(\mathbf{x})\,d\mathbf{x}=\bar{u}>0, \end{array}\displaystyle \right . \end{aligned}$$

(1.10)

where $\Omega\subset\mathbb{R}^{3}$ is a bounded domain with smooth boundary ∂Ω, n is the unit outward normal vector on the boundary of Ω, and the last condition is imposed to avoid the trivial case, $u\equiv0$.

To go directly to the theme of this paper, we now only review some former results closely related. For the one-dimensional version of the chemotaxis model (1.1), the existence and asymptotic behavior of smooth solutions have been studied by several authors. When the function f is linear, i.e., $f(u)=\lambda u-\mu$ with λ (>0) and μ (≥0) being given constants, the corresponding system reads as follows:

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} v_{t}-u_{x}=0,\\ u_{t}-(uv)_{x}=u_{xx}. \end{array}\displaystyle \right . \end{aligned}$$

(1.11)

The initial boundary value problem and the Cauchy problem for system (1.11) was considered by [6] and [7], respectively. In [6], they considered the initial boundary value problem for system (1.11). When $\|u_{0}-1\|_{H^{2}}^{2}+\|v_{0}\|_{H^{2}}^{2}$ is sufficiently small, they proved the global existence of smooth solutions to system (1.11). In [7], the authors obtained the global existence of smooth solutions to the Cauchy problem for system (1.11) with large initial data. Recently, the authors in [8–10] extended the results of [6, 7] to the case that f is a nonlinear function of u, respectively. For high dimensions, the global well-posedness of a smooth small solution to (1.1) with $f(u)=u$ was investigated in [11, 12] for the Cauchy problem and the initial-boundary value problem, respectively. In [12], they obtained global existence and optimal decay rates of strong solutions when the $H^{3}$-norm of the initial perturbation is sufficiently small and the $L^{1}$-norm of the initial perturbation is bounded. In [11], they obtained global existence and exponential decay rates of strong solutions when the initial perturbation is small in $H^{3}$. Recently, the authors in [13] considered the Cauchy problem to system (1.1) and proved global existence and optimal decay rates of strong solutions when the $H^{2}$-norm of the initial perturbation is sufficiently small and the $L^{1}$-norm of the initial perturbation is bounded. For other related results, such as nonlinear stability of waves in one dimension and so on, please refer to [8–10, 14–34] and the references therein.

However, to our knowledge, so far there has been no result on global existence and asymptotic behavior of the strong solutions to the initial boundary value problem (1.1), (1.10). The main motivation of this paper is to give a positive answer to this question. In particular, we prove the global existence and exponential stability of a strong solution when the initial perturbation is small in $H^{2}$. The proofs are based on energy methods which have been developed in [35–39] and the references therein.

Before stating our main results, we explain the notations and conventions used throughout this paper. We denote positive constants by C. Moreover, the character ‘C’ may differ in different places. $L^{p}=L^{p}(\Omega)$ ($1\leq p\leq\infty$) denotes the usual Lebesgue space with the norm

$$\begin{aligned}& \|g\|_{L^{p}}= \biggl(\int_{\Omega }\bigl|g(x)\bigr|^{p} \,dx \biggr)^{\frac{1}{p}},\quad 1\leq p< \infty, \\& \|g\|_{L^{\infty}}= \sup_{\Omega}\bigl|g(x)\bigr|. \end{aligned}$$

$H^{l}(\Omega)$ ($l\geq0$) denotes the usual lth-order Sobolev space with the norm

$$\|g\|_{l}= \Biggl( \sum_{j=0}^{l} \bigl\| \nabla^{j}g\bigr\| ^{2} \Biggr)^{\frac{1}{2}}, $$

where $\|\cdot\|=\|\cdot\|_{0}=\|\cdot\|_{L^{2}}$. $\langle\cdot, \cdot\rangle$ denotes the inner-product in $L^{2}(\Omega)$.

Now, we are in a position to state the main results.

Theorem 1.1

Assume $\nabla\times\mathbf{v}_{0}=0$ and $\|(\mathbf{v}_{0}, u_{0}-\bar{u})\|_{2}$ is sufficiently small. Then the initial boundary value problem (1.1), (1.10) admits a unique strong solution $(\mathbf{v}, u)$ globally in time, satisfying

$$ \begin{aligned} &\mathbf{v}\in C^{0} \bigl(0, \infty;H^{2}(\Omega) \bigr)\cap C^{1} \bigl(0, \infty;H^{1} (\Omega) \bigr), \\ &u-\bar{u}\in C^{0} \bigl(0,\infty;H^{2}(\Omega) \bigr)\cap C^{1} \bigl(0,\infty;L^{2} (\Omega) \bigr) \end{aligned} $$

(1.12)

and

$$\begin{aligned} &\bigl\| (\mathbf{v},u-\bar{u}) (t)\bigr\| _{2}^{2}+\int _{0}^{t} \bigl(\bigl\| \nabla \cdot\mathbf{v}(\tau) \bigr\| _{1}^{2}+\bigl\| \nabla u(\tau)\bigr\| _{2}^{2} \bigr)\,d\tau\leq C_{1}\bigl\| (\mathbf{v}_{0},u_{0}- \bar{u})\bigr\| _{2}^{2}, \\ &\quad\forall t\in[0, +\infty], \end{aligned}$$

(1.13)

where $C_{1}$ is a positive constant independent of t. Moreover, there exist positive constants $C_{2}$, ϑ independent of t such that for any $t\geq0$, the solution $(\mathbf{v}, u)$ has the following exponential decay bound:

$$ \bigl\| (\mathbf{v}, u-\bar{u}) (\cdot, t)\bigr\| _{2}\leq C_{2}e^{-\vartheta t}. $$

(1.14)

Remark 1.2

As compared to the classic results in [8, 17, 30, 36], where smallness conditions on the $H^{3}$-norm of the initial data were proposed, we are able to prove the global existence and exponential stability for the strong solutions to the initial boundary problem under only the $H^{2}$-norm of the initial data is sufficiently small.

Finally, let us explain on some of the main difficulties and techniques involved in the process. First, by noting that we consider the $H^{2}$ case, it is nontrivial to follow the framework of [11] directly, where the global existence and exponential decay rates of strong solutions in $H^{3}$ for system (1.1) with $f(u)=u$ are obtained. In fact, the main idea in [11] is to reduce the total energy of the solution to those of the lower order spatial derivatives and temporal derivatives of u, together with the div and curl of v. However, this method does not work in our $H^{2}$ case. One main observation in this paper is that the total energy of the solution is equivalent to the sum of $H^{1}$-norm of $\nabla\cdot\mathbf{v}$ and $L^{2}$-norm of Δu. With this in hand, we can make full use of the dissipation structure of the system and deal with nonlinear terms and boundary terms carefully to close the energy estimates of solutions. Second, compared to [11], we need to make careful energy estimates on nonlinear terms arising from the nonlinearity of $f(u)$ (see (3.16), (3.19), (3.24), (3.30), and (3.35)).

The rest of this paper is devoted to proving Theorem 1.1. In Section 2, we reformulate the problem. In Section 3, we deduce the a priori estimate of the solutions and complete the proof of Theorem 1.1.

2 Reformulated system

In this section, we will first reformulate the problem. Set

$$ \lambda=\sqrt{\frac{f'(\bar{u})}{\bar{u}}},\qquad \lambda _{1}=\sqrt{ \bar{u}f'(\bar{u})}, \qquad\lambda_{2}=\sqrt{ \frac{\bar{u}}{f'(\bar {u})}}. $$

Taking change of variables $(\mathbf{v}, u)\rightarrow(\lambda\mathbf {v}, u+\bar{u})$ and linearizing the system around $(0, \bar{u})$, we can reformulate the initial boundary value problem (1.1), (1.10) as

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} \mathbf{v}_{t}-\lambda_{1}\nabla u=F_{1},\\ u_{t}-\lambda_{1}\nabla\cdot\mathbf{v}-D\Delta u=F_{2},\\ (\mathbf{v}, u)(\mathbf{x},0)=(\mathbf{v}_{0}, u_{0})(\mathbf {x}), \quad \mathbf{x}\in\Omega,\\ \mathbf{v}\cdot \mathbf{n}|_{\partial\Omega}=\frac{\partial u}{\partial\mathbf{n}}|_{\partial\Omega}=0, \quad t\geq0,\\ \frac{1}{|\Omega|}\int_{\Omega}u_{0}(\mathbf{x})\,d\mathbf{x}=0, \end{array}\displaystyle \right . \end{aligned}$$

(2.1)

where

$$ \begin{aligned} &F_{1}=\lambda_{2} \bigl(f'(u+\bar{u})-f'(\bar{u}) \bigr)\nabla u, \\ &F_{2}=\lambda\nabla\cdot(u\mathbf{v}). \end{aligned} $$

(2.2)

Here and in the sequel, for the notational simplicity, we still denote the reformulated variables by $(\mathbf{v}, u)$.

To prove the global existence of a solution to (2.1), we will combine the local existence result together with a priori estimates. To begin with, we state the following local existence, the proof of which can be found in [40].

Proposition 2.1

(Local existence)

Assume that $(\mathbf{v}_{0}, u_{0})\in H^{2}(\Omega)$. Then there exists a sufficiently small positive constant $t_{0}$ depending only on $\|(\mathbf{v}_{0}, u_{0})\|_{2}$ such that the initial boundary value problem (2.1) admits a unique solution $(\mathbf{v}, u)(\mathbf{x}, t)\in C([0, t_{0}], H^{2}(\Omega))$ satisfying

$$\sup_{t\in[0, t_{0}]}\bigl\| (\mathbf{v}, u) (\cdot, t)\bigr\| _{2}\leq2\bigl\| (\mathbf{v}_{0}, u_{0})\bigr\| _{2}. $$

Proposition 2.2

(A priori estimate)

Let $\nabla\times\mathbf{v}_{0}=0$ and $(\mathbf{v}_{0},{u}_{0})\in H^{2}(\Omega)$. Assume that the initial boundary value problem (2.1) has a solution $(\mathbf{v},u)(\mathbf{x}, t)$ on $\Omega\times[0, T]$ for some $T>0$ in the same function class as in Proposition  2.1. Then there exist a small constant $\delta>0$ and a constant $C_{3}$, which are independent of T, such that if

$$ \sup_{0\leq t\leq T}\bigl\| (\mathbf{v},u) (t)\bigr\| _{2}\leq \delta, $$

then for any $t\in[0,T]$, it holds that

$$\begin{aligned} \bigl\| (\mathbf{v},u) (t)\bigr\| _{2}^{2}+\int _{0}^{t} \bigl(\bigl\| \nabla\cdot \mathbf{v}(\tau) \bigr\| _{1}^{2}+\bigl\| \nabla u(\tau)\bigr\| _{2}^{2} \bigr)\,d\tau\leq C_{3}\bigl\| (\mathbf{v}_{0},u_{0}- \bar{u})\bigr\| _{2}^{2}. \end{aligned}$$

(2.3)

Moreover, there exist positive constants $C_{4}$, ϑ independent of t such that for any $t\in[0, T]$, the solution $(\mathbf{v}, u)$ has the following exponential decay bound:

$$ \bigl\| (\mathbf{v}, u) (t)\bigr\| _{2}\leq C_{4}e^{-\vartheta t}. $$

(2.4)

Theorem 1.1 follows from Propositions 2.1-2.2 and standard continuity arguments. The proof of Proposition 2.2 will be given in Section 3.

3 Proof of Proposition 2.2

Throughout this section and the next section, we assume that all conditions of Proposition 2.2 are satisfied. Moreover, we make the a priori assumption

$$ \sup_{0\leq t\leq T}\bigl\| (\mathbf{v}, u) (t)\bigr\| _{2} \leq \delta, $$

(3.1)

where δ is a sufficiently small positive constant.

The proof of Proposition 2.2 is based on several steps of careful energy estimates which are stated as a sequence of lemmas. First we recall some inequalities of Sobolev type (see [41]).

Lemma 3.1

Let Ω be any bounded domain in $\mathbb{R}^{3}$ with smooth boundary. Then it holds

$$\begin{aligned}& (\mathrm{i})\quad \|f\|_{L^{\infty}(\Omega)}\leq C\| f\|_{H^{2}(\Omega)}, \\& (\mathrm{ii})\quad \|f\|_{L^{q}(\Omega)}\leq C\|f\|_{H^{1}(\Omega)},\ 2\leq q \leq6, \end{aligned}$$

for some constant $C>0$ depending only on Ω.

As in [11], the following lemma (see [42]) plays an important role in our proofs, which gives the estimate of ∇v by $\nabla\cdot\mathbf{v}$ and $\nabla\times \mathbf{v}$.

Lemma 3.2

Let $\mathbf{V}\in H^{k}(\Omega)$ be a vector-valued function satisfying $\mathbf{V}\cdot n|_{\Omega}=0$, where n is the unit outer normal vector of ∂Ω. Then

$$ \|\mathbf{V}\|_{k}\leq C\bigl(\|\nabla\cdot\mathbf {V} \|_{k-1}+\|\nabla\times\mathbf{V}\|_{k-1}+\|\mathbf{V} \|_{k-1}\bigr) $$

(3.2)

for $k\geq1$, and the constant C depends only on k and Ω.

The next lemma is an application of Lemma 3.2, which is crucial to complete the proof of Proposition 2.2. Indeed, the lemma states that the total energy of the solution is equivalent to the sum of $H^{1}$-norm of $\nabla\cdot v$ and $L^{2}$-norm of Δu. Define

$$ \mathbb{E}(t)=\bigl\| (\mathbf{v}, u)\bigr\| _{2}^{2}, \quad\mbox{and} \quad \mathbb{G}(t)=\|\nabla\cdot\mathbf{v}\|_{1}^{2}+\|\Delta u\|^{2}. $$

(3.3)

Lemma 3.3

Under the assumptions of Proposition  2.2, there exist positive constants $C_{5}$, $C_{6}$ which are independent of δ and t such that

$$ C_{5}\mathbb{G}(t)\leq\mathbb{E}(t)\leq C_{6} \mathbb{G}(t). $$

(3.4)

Proof

First, by virtue of (2.1)₂, (2.1)₄-(2.1)₅, and (2.2), we have

$$ \int_{\Omega}u(\mathbf{x}, t)\,d\mathbf{x}=0, $$

(3.5)

which together with the Poincaré inequality gives

$$ \|u\|\leq C\|\nabla u\|. $$

(3.6)

Due to the boundary condition $\frac{\partial u}{\partial \mathbf{n}}|_{\partial\Omega}=0$, we can use integration by parts, the Hölder inequality, and (3.6) to get

$$ \|\nabla u\|\leq C\|\Delta u\|. $$

(3.7)

Applying Lemma 3.2 with $k=1$ and using (3.7), we have

$$\begin{aligned} \|\nabla u\|_{1}&\leq C \bigl(\bigl\| \nabla\cdot(\nabla u) \bigr\| + \bigl\| \nabla \times(\nabla u)\bigr\| +\|\nabla u\| \bigr) \\ &\leq C\bigl(\|\Delta u\|+\|\nabla u\|\bigr) \\ &\leq C\|\Delta u\|. \end{aligned}$$

(3.8)

Combining (3.6)-(3.8) yields

$$ \|u\|_{2}\leq C\|\Delta u\|. $$

(3.9)

Next, we deal with the case for v. Taking the curl for (2.1)₁ and noting that $\nabla\times\mathbf{v}_{0}=0$, we have

$$ \nabla\times\mathbf{v}\equiv0. $$

(3.10)

Since $\Delta\mathbf{v}=\nabla(\nabla\cdot \mathbf{v})-\nabla\times(\nabla\times\mathbf{v})$, we have from (2.1)₄ and (3.10) that

$$ \|\nabla\mathbf{v}\|\leq\|\nabla\cdot\mathbf{v}\|, $$

(3.11)

which together with the Poincaré inequality implies

$$ \|\mathbf{v}\|\leq C\|\nabla\mathbf{v}\|\leq C\|\nabla \cdot \mathbf{v}\|, $$

(3.12)

where we have used the boundary condition $\mathbf{v}\cdot \mathbf{n}|_{\partial\Omega}=0$.

Applying Lemma 3.2 with $k=1,2$, and using (3.10) and (3.12), we conclude that

$$\begin{aligned} \|\mathbf{v}\|_{2}\leq C\bigl(\|\nabla\cdot\mathbf{v}\|+\| \nabla \times\mathbf{v}\|+\|\mathbf{v}\|_{1}\bigr) \leq C\bigl(\|\nabla\cdot\mathbf{v}\|_{1}+\|\mathbf{v}\|\bigr) \leq C\|\nabla\cdot\mathbf{v}\|_{1}. \end{aligned}$$

(3.13)

Therefore, (3.9) and (3.13) yield

$$ \mathbb{E}(t)\leq C\mathbb{G}(t). $$

(3.14)

The proof of the first inequality in (3.4) is trivial. Therefore, we have completed the proof of Lemma 3.2. □

Lemma 3.2 reduced the estimates of $\mathbb{E}(t)$ to those for $\mathbb{G}(t)$. Our next goal is to deduce the estimates of $\mathbb{G}(t)$.

Lemma 3.4

Under the assumptions of Proposition  2.2, there exists a positive constant $C_{7}$ which is independent of δ and t such that

$$ \mathbb{E}(t)+\int_{0}^{t} \bigl(\bigl\| \nabla\cdot\mathbf {v}(\tau)\bigr\| _{1}^{2}+\bigl\| \Delta u(\tau) \bigr\| _{1}^{2} \bigr)\leq C_{7} \mathbb {E}(0) \quad \textit{for any } t\geq0. $$

(3.15)

Proof

We will prove Lemma 3.3 in five steps.

Step 1 (Zero order estimate): Multiplying (2.1)₁-(2.1)₂ by v, u respectively, then summing up and integrating, we have

$$ \frac{1}{2}\frac{d}{dt}\bigl\| (\mathbf{v},u) \bigr\| ^{2}+D\|\nabla {u}\|^{2}=\langle\mathbf{v},F_{1} \rangle+\langle u,F_{2} \rangle, $$

(3.16)

where we have used the boundary condition (2.1)₄.

Applying the mean value theorem, the Hölder inequality, Lemma 3.1, and (2.1)₄, it is clear that the two terms on the right-hand side of (3.16) can be estimated as follows:

$$\begin{aligned} \bigl|\langle v,F_{1} \rangle\bigr|+\bigl|\langle u,F_{2} \rangle\bigr|&\leq C\int_{\Omega}|\mathbf{v}u\nabla u|\,dx \\ &\leq C\|\mathbf{v}\|_{L^{3}}\|u\|_{L^{6}}\|\nabla u\| \\ &\leq C\|\mathbf{v}\|_{1}\|\nabla u\|^{2} \\ &\leq C\delta\|\nabla u\|^{2}. \end{aligned}$$

(3.17)

Combining (3.16) with (3.17) and using the fact that δ is sufficiently small, we have

$$ \frac{d}{dt}\bigl\| (\mathbf{v},u)\bigr\| ^{2}+C\|\nabla {u} \|^{2}\leq0. $$

(3.18)

Step 2 (First order estimate): Applying ∇⋅ and ∇ to (2.1)₁ and (2.1)₂, respectively, and multiplying them by $\nabla\cdot\mathbf{v}$, ∇u, respectively, and then integrating them over Ω, we obtain

$$ \begin{aligned}[b] &\frac{1}{2}\frac{d}{dt} \bigl(\|\nabla\cdot\mathbf{v} \| ^{2}+\|\nabla u\|^{2} \bigr)+D\|\Delta u\|^{2}\\ &\quad =\langle\nabla\cdot\mathbf{v},\nabla\cdot F_{1}\rangle-\langle \Delta u, F_{2}\rangle+\int_{\Omega}\nabla\cdot \bigl\{ \bigl[\lambda_{1}\nabla\cdot \mathbf{v}+D\Delta u+\lambda\nabla\cdot(u \mathbf{v}) \bigr]\nabla u \bigr\} \,d\mathbf{x}\\ &\quad:=J_{1}+J_{2}+J_{3}. \end{aligned} $$

(3.19)

Next, we estimate the terms $J_{1}$-$J_{3}$ one by one. To begin with, by using (2.2), the Hölder inequality, the Cauchy inequality, and Lemma 3.1, we can estimate the term $J_{1}$ as follows:

$$\begin{aligned} J_{1}&\leq C \int_{\Omega}\bigl(|u\Delta u \nabla\cdot \mathbf{v}|+|\nabla u\nabla u \nabla\cdot\mathbf{ v}|\bigr)\,d\mathbf{x} \\ &\leq C\bigl(\|u\|_{L^{\infty}}\|\Delta u\|\|\nabla\cdot \mathbf{v}\|+\|\nabla u \|_{L^{3}}\|\nabla u\|_{L^{6}}\|\nabla\cdot\mathbf{v}\|\bigr) \\ &\leq C\delta \bigl(\|\nabla\cdot\mathbf{v}\|^{2}+\|\Delta{u} \|^{2} \bigr). \end{aligned}$$

(3.20)

Using similar arguments, we also have the following estimate for the term $J_{2}$:

$$ J_{2} \leq C\delta \bigl(\|\nabla\cdot\mathbf{v} \|^{2}+\|\Delta{u}\|^{2} \bigr). $$

(3.21)

Noting the boundary condition (2.1)₄, it is clear that

$$ J_{3}=0. $$

(3.22)

Substituting (3.20)-(3.22) into (3.19) and noting that δ is sufficiently small, we have

$$ \frac{d}{dt} \bigl(\|\nabla\cdot\mathbf{v}\|^{2}+ \| \nabla u\|^{2} \bigr)+C\|\Delta u\|^{2}\leq C\delta\|\nabla \cdot\mathbf{v}\|^{2}. $$

(3.23)

Step 3 (Second order estimate): Applying $\nabla\nabla\cdot$ and Δ to (2.1)₁ and (2.1)₂, respectively, and multiplying them by $\nabla\nabla\cdot\mathbf{v}$, Δu, respectively, and then integrating them over Ω, we obtain

$$\begin{aligned} &\frac{1}{2}\frac{d}{dt} \bigl(\|\nabla\nabla\cdot \mathbf {v}\|^{2}+\|\Delta u\|^{2} \bigr)+D\|\nabla\Delta u \|^{2} \\ &\quad =\langle\nabla\nabla\cdot \mathbf{v},\nabla\nabla\cdot F_{1} \rangle-\langle\nabla\Delta u, \nabla F_{2}\rangle \\ &\qquad{}+\int _{\Omega}\nabla\cdot \bigl\{ \bigl[\lambda_{1}\nabla \nabla \cdot \mathbf{v}+D\nabla\Delta u+\lambda\nabla\nabla\cdot (u\mathbf{v}) \bigr] \Delta u \bigr\} \,d\mathbf{x} \\ &\quad :=K_{1}+K_{2}+K_{3}. \end{aligned}$$

(3.24)

Next, we estimate the terms $K_{1}$-$K_{3}$ respectively. Applying (2.2), (3.9), the Hölder inequality, the Cauchy inequality, and Lemma 3.1, the term $K_{1}$ can be estimated as follows:

$$\begin{aligned} K_{1}&\leq C \int_{\Omega}\bigl(|u \nabla \Delta u|+|\Delta u\nabla u|+|\nabla^{2} u\nabla u|+|\nabla u|^{3} \bigr)|\nabla\nabla \cdot\mathbf{v}|\,d\mathbf{x} \\ &\leq C \bigl(\|u\|_{L^{\infty}}\|\nabla\Delta u\|+\|\Delta u \|_{L^{6}} \|\nabla u\|_{L^{3}}+\|\nabla^{2} u \|_{L^{6}}\|\nabla u \|_{L^{3}}+\|\nabla u\|_{L^{6}}^{3} \bigr)\|\nabla\nabla \cdot\mathbf{v}\| \\ &\leq C\delta \bigl(\|\nabla\nabla\cdot\mathbf{v}\|^{2}+\|\Delta{u} \|_{1}^{2} \bigr). \end{aligned}$$

(3.25)

Using similar arguments, we also have the following estimate for the term $K_{2}$:

$$ K_{2} \leq C\delta \bigl(\|\nabla\nabla\cdot \mathbf{v} \|^{2}+\|\Delta{u}\|_{1}^{2} \bigr). $$

(3.26)

Noting the boundary condition (2.1)₄ and equation (2.1)₂, we have

$$ \bigl[\lambda_{1}\nabla\nabla\cdot \mathbf{v}+D\nabla \Delta u+\lambda\nabla\nabla\cdot (u\mathbf{v}) \bigr]\cdot\mathbf{n}|_{\partial\Omega}=( \nabla u)_{t}\cdot \mathbf{n}|_{\partial\Omega}=0, $$

(3.27)

which implies

$$ K_{3}=0. $$

(3.28)

Combining (3.24)-(3.26) and (3.28) gives

$$ \frac{d}{dt} \bigl(\|\nabla\nabla\cdot \mathbf{v} \|^{2}+\|\Delta u\|^{2} \bigr)+C\|\nabla\Delta u \|^{2} \leq C\delta \bigl(\|\nabla\nabla\cdot \mathbf{v} \|^{2}+ \|\Delta{u}\|_{1}^{2} \bigr). $$

(3.29)

Step 4 (Estimate for $\|\nabla\cdot\mathbf{v}\|_{1}$): To begin with, multiplying (2.1)₂ by $\nabla\cdot\mathbf{v}$ and integrating the resulting equation over Ω, we have

$$ \lambda_{1}\|\nabla\cdot\mathbf{v}\|^{2}= \langle {u}_{t},\nabla \cdot\mathbf{v} \rangle+\langle-D\Delta u, \nabla \cdot \mathbf{v}\rangle+\langle-F_{2},\nabla\cdot v \rangle, $$

(3.30)

where from (2.1)₁ and (2.1)₄ the first term on the right-hand side can be written as

$$\begin{aligned} \langle{u}_{t}, \nabla\cdot\mathbf{v} \rangle&= \frac{d}{dt}\langle u,\nabla\cdot\mathbf{v} \rangle-\langle u,\nabla\cdot \mathbf{v}_{t}\rangle \\ &=-\frac{d}{dt}\langle\nabla u, \mathbf{v} \rangle+\langle \nabla u, \mathbf{v}_{t} \rangle \\ &=-\frac{d}{dt}\langle\nabla u, \mathbf{v} \rangle+\langle \nabla u, \lambda_{1}\nabla u+F_{1} \rangle. \end{aligned}$$

(3.31)

Then it follows from (3.30)-(3.31), (2.2), the Hölder inequality, and the Young inequality that

$$\begin{aligned} &\lambda_{1}\|\nabla\cdot\mathbf{v}\|^{2} + {\mathrm{d}\over \mathrm{d}t}\langle\nabla u, \mathbf{v}\rangle \\ &\quad=\langle \nabla u,\lambda_{1}\nabla u+F_{1} \rangle+ \langle-D\Delta u, \nabla\cdot \mathbf{v}\rangle+\langle F_{2},\nabla \cdot\mathbf{v} \rangle \\ &\quad\leq C\|\Delta {u}\|^{2}+{\lambda_{1}\over 4}\|\nabla\cdot \mathbf{v}\|^{2}+C\delta\|\nabla\cdot{\mathbf{v}}\|^{2}+C\| \nabla {u}\|^{2}. \end{aligned}$$

(3.32)

This together with the fact that δ is sufficiently small implies

$$ \frac{d}{dt}\langle\nabla u,\mathbf{v}\rangle + \frac{\lambda_{1}}{2}\|\nabla\cdot\mathbf{v}\|^{2}\leq C \bigl(\|\nabla {u} \|^{2}+\|\Delta{u}\|^{2} \bigr). $$

(3.33)

Next, we deal with the estimate of $\|\nabla\nabla\cdot\mathbf{v}\|$. Applying ∇ to (2.1)₂ and then multiplying by $\nabla(\nabla\cdot \mathbf{v})$, we have from the Cauchy inequality that

$$ \frac{\lambda_{1}}{2}\|\nabla\nabla\cdot\mathbf{v}\| ^{2} \leq\langle\nabla{u}_{t}, \nabla\nabla\cdot\mathbf{v}\rangle+C\|\nabla \Delta u\|^{2}+C\|\nabla F_{2}\|^{2}. $$

(3.34)

By integrating by parts several times, we estimate the first term on the right-hand side of (3.34) as follows:

$$ \begin{aligned}[b] \langle\nabla{u}_{t}, \nabla\nabla\cdot\mathbf{v} \rangle&=-{\mathrm{d}\over \mathrm{d}t}\langle\Delta u,\nabla\cdot\mathbf{v}\rangle + \langle\Delta u, \nabla\cdot\mathbf{v}_{t}\rangle \\ &=-{\mathrm{d}\over \mathrm{d}t}\langle\Delta u,\nabla\cdot \mathbf{v}\rangle+\langle \Delta u, \lambda_{1}\Delta u+\nabla\cdot F_{1}\rangle \\ &\leq-{\mathrm{d}\over \mathrm{d}t}\langle\Delta u,\nabla\cdot \mathbf{v}\rangle+C\| \Delta u\|^{2}. \end{aligned} $$

(3.35)

From (2.2), (3.9), (3.1), the Hölder inequality, the Cauchy inequality, and Lemma 3.1, we have

$$\begin{aligned} \|\nabla F_{2}\|&\leq C \bigl\{ \|\nabla \mathbf{v} \|_{L^{3}}\|\nabla u\|_{L^{6}} +\|\mathbf{ v}\|_{L^{\infty}}\bigl\| \nabla^{2} u\bigr\| +\| u\|_{L^{\infty}}\|\nabla\nabla\cdot\mathbf{v}\| \bigr\} \\ &\leq C\delta\bigl(\|\nabla\nabla\cdot\mathbf{v}\|+\|\Delta u\|\bigr). \end{aligned}$$

(3.36)

Substituting (3.35)-(3.36) into (3.34) and using the fact that δ is sufficiently small, we have

$$ {\mathrm{d}\over \mathrm{d}t}\langle\Delta u,\nabla \cdot\mathbf{v} \rangle(t)+\frac{\lambda_{1}}{2}\|\nabla\nabla\cdot \mathbf{v}\|^{2} \leq C \|\Delta u\|^{2}_{1}. $$

(3.37)

Combining (3.33) and (3.37) gives

$$ {\mathrm{d}\over \mathrm{d}t} \bigl(\langle\nabla u,\mathbf{v}\rangle+ \langle\Delta u,\nabla\cdot\mathbf{v}\rangle \bigr) (t) +\frac{\lambda_{1}}{2}\|\nabla \cdot\mathbf{v}\|_{1}^{2} \leq C \bigl(\|\nabla u \|^{2}+\|\Delta u\|^{2}_{1} \bigr). $$

(3.38)

Step 5 (Closure the energy estimate): Since δ is sufficiently small, multiplying ((3.18) + (3.23) + (3.29)) by a suitably large positive constant $D_{1}$ and adding it to (3.38) give

$$ \frac{d}{dt}\mathbb{H}(t)+\mathbb{G}(t)\leq0, $$

(3.39)

where

$$ \mathbb{H}(t)=D_{1} \bigl(\bigl\| (\mathbf{v}, u) \bigr\| ^{2}+\|\nabla u\| ^{2}+\mathbb{G}(t) \bigr)+\langle\nabla u, \mathbf{v}\rangle+\langle\Delta u,\nabla\cdot\mathbf{v}\rangle. $$

(3.40)

Applying Lemma 3.3 and noting that $D_{1}$ is sufficiently large, it is clear that $\mathbb{H}(t)$ is equivalent to $\mathbb{G}(t)$. This implies

$$ \frac{d}{dt}\mathbb{H}(t)+\mathbb{H}(t)\leq0. $$

(3.41)

Integrating the above equation over $[0, t]\times\Omega$ gives (3.15), and thus we complete the proof of Lemma 3.4. □

Proof of Proposition 2.2

First, by virtue of Lemma 3.4 and the Poincaré inequality, we can obtain (2.3). Applying (2.3) and Lemma 3.3, we can use the Gronwall inequality to get the exponential decay rate (2.4). Therefore, we have completed the proof of Proposition 2.2. □