Dynamics analysis and optimal control of delayed SEIR model in COVID-19 epidemic

Abstract

The coronavirus disease 2019 (COVID-19) remains serious around the world and causes huge deaths and economic losses. Understanding the transmission dynamics of diseases and providing effective control strategies play important roles in the prevention of epidemic diseases. In this paper, to investigate the effect of delays on the transmission of COVID-19, we propose a delayed SEIR model to describe COVID-19 virus transmission, where two delays indicating the incubation and recovery periods are introduced. For this system, we prove its solutions are nonnegative and ultimately bounded with the nonnegative initial conditions. Furthermore, we calculate the disease-free and endemic equilibrium points and analyze the asymptotical stability and the existence of Hopf bifurcations at these equilibrium points. Then, by taking the weighted sum of the opposite number of recovered individuals at the terminal time, the number of exposed and infected individuals during the time horizon, and the system cost of control measures as the cost function, we present a delay optimal control problem, where two controls represent the social contact and the pharmaceutical intervention. Necessary optimality conditions of this optimal control problem are exploited to characterize the optimal control strategies. Finally, numerical simulations are performed to verify the theoretical analysis of the stability and Hopf bifurcations at the equilibrium points and to illustrate the effectiveness of the obtained optimal strategies in controlling the COVID-19 epidemic.

1 Introduction

The coronavirus disease 2019 (COVID-19) is an epidemic caused by the SARS-CoV-2 virus, which affects mostly the human respiratory system. Due to the strong infectivity, fast transmission speed, and long incubation period, it has brought significant losses to human life and the global economy [1, 2]. Although many prevention and control measures have been taken to mitigate the disease spread, the world is still suffering from the infection and death cases of COVID-19. According to the World Health Organization report, as of 2 November 2023, the total number of infections caused by the COVID-19 epidemic has reached 697,318,367, with more than 6,934,066 deaths [3]. Thus, there is an urgent need to study the COVID-19 virus transmission behavior and provide effective control measures to prevent the spread of the disease.

Mathematical models have been proven effective means in describing and understanding the complex transmission dynamics of epidemics [4–6]. In this regard, several mathematical models have been investigated to formulate and control COVID-19 spread [7–9]. SIR (Susceptible, Infectious, Removed) models have been proposed to simulate and predict the COVID-19 pandemic in [10, 11]. The stability of the SEIR (Susceptible, Exposed, Infectious, Removed) model is analyzed in [12]. Stability analysis of a spatial extension of the SEIR model is carried out in [13]. Optimal control of both non-pharmacological and pharmacological interventions for a modified SEIR epidemiological model is studied in [14]. Optimal control of COVID-19 spread considering quarantine effect on people with diabetes is investigated in [15]. Stability analysis and optimal control of a COVID-19 system, including susceptible, exposed, symptomatically infected, asymptomatically infected, hospitalized, and recovered individuals, are discussed in [16]. Bifurcation analysis and optimal control of a discrete SIR system are studied in [17]. Optimal control of the Omicron and Delta strains in COVID-19 is investigated in [18]. Although the aforementioned results are certainly valid and interesting, time delays are ignored in the dynamics analysis and optimal control problems. In fact, time delays exist in COVID-19 virus transmission since there is an incubation period for the exposed individual to manifest COVID-19 symptoms and signs, and a recovery period is required for the infected individual to become a recovered individual [19, 20].

Motivated by the above issue, in the current paper, we propose a delayed SEIR model to describe COVID-19 virus transmission in which two delays representing the incubation period and the recovery period are introduced. For this delayed SEIR system, we prove that its solutions with the nonnegative initial conditions are nonnegative and ultimately bounded. Furthermore, we calculate the disease-free and endemic equilibrium points and analyze the locally asymptotical stability and Hopf bifurcations of these two equilibrium points. Then, by taking the weighted sum of the opposite number of recovered individuals at the terminal time, the number of exposed and infected individuals during the time horizon, and the system cost of control measures as the cost function, we present a delay optimal control problem, where two controls denote the social contact and the pharmaceutical intervention. We also derive the necessary optimality conditions to characterize the optimal controls. Based on the necessary optimality conditions, we develop a numerical approach for solving the delay optimal control problem, which is different from the reported methods in [21–26]. Finally, numerical simulations are performed to verify the theoretical analysis of the stability and the existence of Hopf bifurcations at equilibrium points and demonstrate the effectiveness of computed optimal strategies in controlling the COVID-19 epidemic. Compared with the existing literature, the main contributions and innovations of this paper include: (i) a novel SEIR system with incubation and recovery delays is proposed for COVID-19 virus transmission; (ii) the stability and Hopf bifurcation of the equilibria in the delayed SEIR model are thoroughly analyzed; and (iii) an effective solution approach is developed for solving the delayed optimal control problem with both the terminal and integral costs.

The paper is organized as follows: In Sect. 2, the delayed SEIR system is proposed, and some important properties are proved. In Sect. 3, the stability and existence of Hopf bifurcations at the disease-free and endemic equilibrium points are analyzed. In Sect. 4, we present the delay optimal control problem and derive the corresponding necessary optimality conditions. In Sect. 5, we illustrate the numerical simulation results. In Sect. 6, we provide conclusions.

2 Delayed SEIR model

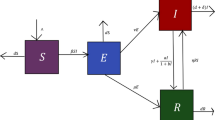
In the COVID-19 virus transmission process, the primary source of transmission is social contact between susceptible and exposed individuals who are usually asymptomatic. Another transmission source is direct contact between frontline workers and infected individuals. Some exposed individuals usually recover due to their strong natural immune systems or use over-the-counter medications, while others require hospitalization after a certain incubation period. Many infected individuals recover from the disease after extensive treatment, but unfortunately, for some, the infection costs their lives. As is well-known, a susceptible individual does not show the corresponding symptoms quickly after infection with the virus; that is, there is an incubation period for the exposed individual to be an infective individual. Besides, it is required for the infected individual to spend some time to be a recovered individual. Thus, time delays must be incorporated into the COVID-19 virus transmission process. Based on SEIR system [14], we propose the following delayed SEIR system to describe the COVID-19 virus transmission:

$$\begin{aligned} \textstyle\begin{cases} \dot{S}(t) = \Lambda - \frac{\beta _{1} S(t)E(t)}{N(t)} - \frac{\beta _{2} S(t)I(t)}{N(t)} -dS(t) , \\ \dot{E}(t) = \frac{\beta _{1} S(t)E(t)}{N(t)} + \frac{\beta _{2} S(t) I(t)}{N(t)} - \varepsilon E(t-\tau _{1}) - (\gamma _{2}+d) E(t), \\ \dot{I}(t) = \varepsilon E(t-\tau _{1}) - \gamma _{1} I(t-\tau _{2})- (\mu +d) I(t) , & t\geq 0, \\ \dot{R}(t) = \gamma _{1} I(t-\tau _{2}) + \gamma _{2} E(t) - dR(t), \end{cases}\displaystyle \end{aligned}$$

(1)

where t is the time of process; $S(t)$, $E(t)$, $I(t)$, and $R(t)$ are, respectively, the susceptible, exposed, infected, and recovered individuals; $N(t)=S(t)+E(t)+I(t)+R(t)$ is the total number of individuals affected by the outbreak; Λ is the recruitment in the human population; d is the natural mortality rate; ${\beta _{1}}$ is the transmission rate due to social contact; ${\beta _{2}}$ is the transmission rate due to frontline contact; ε is the infection rate; ${\gamma _{1}}$ is the recovery rate of infectious individuals; ${\gamma _{2}}$ is the immune recovery rate; μ is the probability of death due to COVID-19; $\tau _{1}$ and $\tau _{2}$ are two delay arguments that indicate the incubation and recovery periods, respectively. A flow chart of the delayed SEIR system (1) is shown in Fig. 1.

Figure 1

Flow chart of delayed SEIR model

For system (1), the initial conditions are given by

$$\begin{aligned} S(t)=\varphi _{1}(t),\qquad E(t)=\varphi _{2}(t),\qquad I(t)=\varphi _{3}(t),\qquad R(t)=\varphi _{4}(t), \end{aligned}$$

(2)

where $t \in [-\tau ,0]$ with $\tau =\max \{\tau _{1},\tau _{2}\}$; and $\varphi _{i}$, $i=1,2,3,4$, are given functions. For system (1) with the initial conditions (2), we have the following theorem:

Theorem 1

If the initial conditions are as follows $\varphi _{i} \geq 0$, $i=1,2,3,4$, then the solutions of system (1) are nonnegative and ultimately bounded.

Proof

It is easy to show by Theorem 5.2.1 [27] that $S(t)\geq 0$, $E(t)\geq 0$, $I(t)\geq 0$ and $R(t)\geq 0$ for $t\geq 0$. Hence, the nonnegative cone $\mathbb{R}^{4}_{+}$ is invariant for system (1) with nonnegative initial conditions $\varphi _{i} \geq 0$, $i=1,2,3,4$. Furthermore, from (1), we have

$$ \Lambda -(d+\mu )N(t) \leq \frac{dN(t)}{dt}=\Lambda -dN(t)-\mu I(t) \leq \Lambda -dN(t), $$

which gives

$$ \frac{\Lambda }{d+\mu } \leq \liminf_{t \to \infty} N(t) \leq \limsup _{t \to \infty} N(t) \leq \frac{\Lambda }{d}. $$

Then, the delayed SEIR system (1) has a biologically feasible range as indicated below:

$$ \biggl\{ \bigl(S(t),E(t),I(t),R(t)\bigr) \in \mathbb{R}^{4}_{+} : \frac{\Lambda }{d+\mu } \leq S(t)+E(t)+I(t)+R(t) \leq \frac{\Lambda }{d}, t \geq 0 \biggr\} , $$

which implies the ultimate boundedness of the solutions. □

3 Equilibrium points, stability and Hopf bifurcation

In this section, we will analyze the local stability of system (1) at the equilibrium points and establish the existence of Hopf bifurcations at the equilibrium points.

3.1 Equilibrium points

For system (1), the disease-free and the endemic equilibrium points are defined as

$$ E_{0}= \biggl(\frac{\Lambda }{d}, 0, 0, 0 \biggr) \quad \text{and}\quad E_{1}=\bigl(S^{*},E^{*},I^{*},R^{*} \bigr), $$

(3)

where

$$\begin{aligned} \textstyle\begin{cases} S^{*}= \frac{\Lambda (\varepsilon +\gamma _{2}+d)(\mu + \gamma _{1} +d)}{d[\beta _{1}(\mu + \gamma _{1}+d)+ \varepsilon \beta _{2}]}, \\ {E^{*}} = \frac{-\Lambda (\varepsilon +\gamma _{2}+d)(\mu + \gamma _{1} +d)+\Lambda \beta _{1}(\mu + \gamma _{1} +d)+\Lambda \varepsilon \beta _{2}}{\varepsilon \beta _{2}(\varepsilon +\gamma _{2}+d)+\beta _{1}(\varepsilon +\gamma _{2}+d)(\mu + \gamma _{1} +d)}, \\ {I^{*}} = \frac{\varepsilon [\Lambda \beta _{1}(\mu + \gamma _{1} +d)+\Lambda \varepsilon \beta _{2}-\Lambda (\varepsilon +\gamma _{2}+d)(\mu + \gamma _{1} +d)]}{\beta _{1}(\mu + \gamma _{1} +d)^{2}(\varepsilon +\gamma _{2}+d)+\varepsilon \beta _{2}(\mu + \gamma _{1} +d)(\varepsilon +\gamma _{2}+d)}, \\ {R^{*}} =\frac{\gamma _{1} I^{*} + \gamma _{2} E^{*}}{d}. \end{cases}\displaystyle \end{aligned}$$

(4)

Now, we consider the basic reproduction number $R_{0}$ [28], which can be used to determine whether a disease is an epidemic. To begin with, we rewrite system (1) as $\dot{x} = f - v$, where

$$x=\left(\begin{array}{c}S\\ E\\ I\\ R\end{array}\right),f=\left(\begin{array}{c}0\\ \frac{{\beta }_{1}SE}{N}+\frac{{\beta }_{2}SI}{N}\\ 0\\ 0\end{array}\right),v=\left(\begin{array}{c}-\mathrm{\Lambda }+\frac{{\beta }_{1}SE}{N}+\frac{{\beta }_{2}SI}{N}+dS\\ \epsilon E(t-{\tau }_1)+({\gamma }_2+d)E\\ -\epsilon E(t-{\tau }_1)+\mu I+{\gamma }_{1}I(t-{\tau }_2)+dI\\ -{\gamma }_{1}I(t-{\tau }_2)-{\gamma }_{2}E+dR\end{array}\right).$$

Then, by taking E and I as the infection compartments, we obtain the following Jacobian matrices F and V at the disease-free equilibrium point $E_{0}$:

$$ \begin{aligned} {F}& = \begin{pmatrix} \beta _{1} & \beta _{2} \\ 0 & 0 \end{pmatrix}, \qquad {V} = \begin{pmatrix} {\varepsilon + \gamma _{2}+d} & 0 \\ {-\varepsilon } & {{\mu} + {\gamma _{1}}+d } \end{pmatrix}. \end{aligned} $$

Thus, $R_{0}$ can be defined as

$$ R_{0}=\rho \bigl(FV^{-1}\bigr)= \frac{\beta _{1}}{\varepsilon + \gamma _{2} + d} + \frac{\beta _{2} \varepsilon }{(\varepsilon + \gamma _{2} + d)(\mu + \gamma _{1} + d)}. $$

(5)

Furthermore, the endemic equilibrium point $E_{1}$ defined in (3) can be rewritten as

$$ \biggl(\frac{\Lambda }{dR_{0}}, \frac{\Lambda }{\varepsilon +\gamma _{2}+d}\biggl(1- \frac{1}{R_{0}} \biggr), \frac{\Lambda \varepsilon }{(\mu +\gamma _{1}+d)(\varepsilon +\gamma _{2}+d)}\biggl(1- \frac{1}{R_{0}}\biggr), \frac{\gamma _{1} I^{*} + \gamma _{2} E^{*}}{d} \biggr). $$

Therefore, system (1) has a positive endemic equilibrium point when $R_{0} > 1$.

3.2 Stability and Hopf bifurcation of disease-free equilibrium point

The Jacobian matrix of system (1) at ${E_{0}}$ is given by

$$ { J_{E_{0}}} = \begin{pmatrix} {- d} & {-\beta _{1}} & {-\beta _{2}} & {0} \\ {0} & {- (\varepsilon e^{-\lambda \tau _{1}} +\gamma _{2} + d) + \beta _{1}} & {\beta _{2}} & {0} \\ {0} & {\varepsilon e^{-\lambda \tau _{1}}} & {- (\mu + d + \gamma _{1} e^{-\lambda \tau _{2}})} & {0} \\ {0} & {\gamma _{2}} & {\gamma _{1} e^{-\lambda \tau _{2}}} & {- d} \end{pmatrix} . $$

(6)

For (6), two negative eigenvalues are given by $\lambda _{1}=\lambda _{2}=-d$. The other two eigenvalues are determined by the following characteristic equation:

$$ \lambda ^{2} + A_{1}^{1}\lambda + A_{2}^{1} + \bigl(B_{0}^{1}\lambda + B_{1}^{1}\bigr)e^{- \lambda \tau _{1}}+ \bigl(C_{0}^{1} \lambda + C_{1}^{1}\bigr)e^{-\lambda \tau _{2}} + D_{0}^{1} e^{-\lambda (\tau _{1}+\tau _{2})}=0, $$

(7)

where $A_{1}^{1} =\gamma _{2} + d - \beta _{1} + \mu + d$; $A_{2}^{1} =(\gamma _{2} + d - \beta _{1})(\mu + d)$; $B_{0}^{1} =\varepsilon$; $B_{1}^{1} =\varepsilon (\mu + d - \beta _{2})$; $C_{0}^{1} =\gamma _{1}$; $C_{1}^{1} = \gamma _{1}(\gamma _{2} + d - \beta _{1})$; and $D_{0}^{1} =\varepsilon \gamma _{1}$.

Now, we study the following cases for delay arguments $\tau _{1}$ and $\tau _{2}$ at $E_{0}$.

Case 3.2.1 If $\tau _{1}=\tau _{2}=0$, then equation (7) becomes

$$ \lambda ^{2} + \bigl(A_{1}^{1} + B_{0}^{1} + C_{0}^{1}\bigr)\lambda + A_{2}^{1} + B_{1}^{1} + C_{1}^{1} + D_{0}^{1} = 0. $$

(8)

It follows from (5) that

$$ R_{0}=R_{1}+R_{2}, $$

(9)

where $R_{1}= \frac{\beta _{1} }{\varepsilon + \gamma _{2} + d}$; and $R_{2}= \frac{\beta _{2} \varepsilon }{(\varepsilon + \gamma _{2} + d)(\mu + \gamma _{1} +d)}$. Obviously, $R_{1}>0$, and $R_{2}>0$. Let

$$ \textstyle\begin{cases} {a_{0}^{1}}=1, \\ {a_{1}^{1}} =A_{1}^{1} + B_{0}^{1} + C_{0}^{1} =\mu + \gamma _{1} + \varepsilon + \gamma _{2} + 2d - \beta _{1} \\ \hphantom{{a_{1}^{1}}} =(1-R_{1})(\varepsilon + \gamma _{2} +d)+\mu + \gamma _{1} + d, \\ {a_{2}^{1}} =A_{2}^{1} + B_{1}^{1} + C_{1}^{1} + D_{0}^{1}=( \varepsilon +\gamma _{2} + d - \beta _{1}) (\mu + \gamma _{1} + d) - { \beta _{2} \varepsilon} \\ \hphantom{{a_{2}^{1}} } =(1-{R_{0}})(\varepsilon +\gamma _{2} + d) (\mu + \gamma _{1} + d), \\ {a_{3}^{1}}=0. \end{cases} $$

Then, we have

$$ a_{1}^{1}a_{2}^{1}>a_{0}^{1}a_{3}^{1}, \quad \text{and}\quad a_{i}^{1}>0, \quad i=0,1,2, \text{for } R_{0}< 1, $$

and

$$ a^{1}_{2}< 0\quad \text{for } R_{0}>1. $$

By the Routh-Hurwitz theorem [29], we obtain the following theorem:

Theorem 2

Suppose that ${\tau _{1}=\tau _{2}=0}$.

(i) If ${R_{0}<1}$, then ${E_{0}}$ is locally asymptotically stable;

(ii) If ${R_{0}>1}$, then $E_{0}$ is unstable.

Case 3.2.2 If $\tau _{1}=0$, and $\tau _{2}>0$, then equation (7) turns to

$$ \lambda ^{2} + \bigl(A_{1}^{1} + B_{0}^{1}\bigr)\lambda + A_{2}^{1} + B_{1}^{1} + \bigl[C_{0}^{1}\lambda + \bigl(C_{1}^{1} + D_{0}^{1}\bigr) \bigr]e^{-\lambda \tau _{2}}=0. $$

(10)

Next, we will discuss the Hopf bifurcation of (10). Obviously, $\lambda =i\omega$ ($\omega >0$) is a pure imaginary root of the equation (10) if and only if

$$ -\omega ^{2} + \bigl(A_{1}^{1} + B_{0}^{1}\bigr)i\omega + A_{2}^{1} + B_{1}^{1} + \bigl[C_{0}^{1} i\omega + \bigl(C_{1}^{1} + D_{0}^{1}\bigr)\bigr] \bigl[\cos (\omega \tau _{2}) - i\sin (\omega \tau _{2}) \bigr]=0. $$

(11)

Separating the real part from the imaginary part in (11) gives

$$ \textstyle\begin{cases} {\omega ^{2} - (A_{2}^{1} + B_{1}^{1})}=C_{0}^{1}\omega \sin (\omega \tau _{2}) + (C_{1}^{1} + D_{0}^{1})\cos (\omega \tau _{2}), \\ {-(A_{1}^{1} + B_{0}^{1})\omega}=C_{0}^{1}\omega \cos (\omega \tau _{2}) - (C_{1}^{1} + D_{0}^{1})\sin (\omega \tau _{2}). \end{cases} $$

(12)

By adding the squares of two equations in (12), we obtain

$$ \omega ^{4} + \bigl[\bigl(A_{1}^{1} + B_{0}^{1}\bigr)^{2} - 2\bigl(A_{2}^{1} + B_{1}^{1}\bigr) - \bigl(C_{0}^{1} \bigr)^{2}\bigr]\omega ^{2} + \bigl(A_{2}^{1} + B_{1}^{1}\bigr)^{2} - \bigl(C_{1}^{1} + D_{0}^{1}\bigr)^{2} = 0 . $$

(13)

Let $z=\omega ^{2}$, $h_{01}=(A_{2}^{1} + B_{1}^{1})^{2} - (C_{1}^{1} + D_{0}^{1})^{2}$ and $h_{11}=(A_{1}^{1} + B_{0}^{1})^{2} - 2(A_{2}^{1} + B_{1}^{1}) - (C_{0}^{1})^{2}$. Then, equation (13) can be rewritten as

$$ \begin{aligned} z^{2} + h_{11}z + h_{01} = 0 . \end{aligned} $$

(14)

Without loss of generality, we assume that equation (14) has two positive roots, denoted by $z_{1}$ and $z_{2}$. Then, two positive roots of equation (13) are

$$ \omega _{2}^{1}=\sqrt{z_{1}}\quad \text{and}\quad \omega _{2}^{2}=\sqrt{z_{2}}. $$

(15)

Furthermore, substituting (15) into (12) and solving the resulting equations, we have

$$ \tau _{2}^{j,k}= \frac{1}{\omega _{2}^{j}} \biggl(\arccos \biggl[ \frac{M_{1}M_{3}(\omega _{2}^{j}) + M_{2}M_{4}(\omega _{2}^{j})}{M_{1}^{2} +M_{2}^{2}} \biggr] + 2k\pi \biggr),\quad j=1,2; k=0,1,\ldots , $$

where $M_{1} =C_{1}^{1} + D_{0}^{1}$; $M_{2} =C_{0}^{1}$; $M_{3}(\omega _{2}^{j}) = ({\omega _{2}^{j}} )^{2} - (A_{2}^{1} + B_{1}^{1})$; and $M_{4}(\omega _{2}^{j}) =-(A_{1}^{1} + B_{0}^{1})\omega _{2}^{j}$. Clearly,

$$ \lim_{k \to \infty} \tau _{2}^{j,k} = \infty ,\quad j=1,2. $$

Thus, we can define

$$ \tau _{2}^{0} =\min_{j\in \{1,2\}} \bigl\{ \tau _{2}^{j,0}\bigr\} ,\quad \text{and}\quad \omega _{2}^{0} = \arg \min_{j\in \{1,2\}} \bigl\{ \tau _{2}^{j,0}\bigr\} . $$

(16)

Now, we consider the roots of equation (10) as a function of $\tau _{2}$ and the root $\lambda _{1}(\tau _{2})=\xi _{1}(\tau _{2})+i \omega _{1}(\tau _{2})$ of equation (10) such that

$$ \xi _{1}\bigl(\tau _{2}^{0}\bigr)=0, \quad \text{and}\quad \omega _{1}\bigl(\tau _{2}^{0}\bigr)= \omega _{2}^{0}, $$

where $\tau _{2}^{0}$ and $\omega _{2}^{0}$ are as defined in (16). Substituting $\lambda _{1}(\tau _{2})$ into equation (10) and taking the derivative with respect to $\tau _{2}$, we have

$$ \begin{aligned} \biggl(&{\frac{d\lambda _{1}}{d\tau _{2}}} \biggr)^{-1}= \frac{2\lambda _{1} + A_{1}^{1} + B_{0}^{1} }{-\lambda _{1} [(\lambda _{1})^{2} + (A_{1}^{1} + B_{0}^{1})\lambda _{1} + A_{2}^{1} + B_{1}^{1}]} + \frac{C_{0}^{1}}{\lambda _{1}(C_{0}^{1}\lambda _{1} + C_{1}^{1} + D_{0}^{1})}- \frac{\tau _{2}}{\lambda _{1}}. \end{aligned} $$

Then,

$$ \begin{aligned} \operatorname{Re} \biggl[& \biggl( \frac{d\lambda _{1}}{d\tau _{2}}\bigg|_{ \tau _{2} = \tau _{2}^{0}} \biggr)^{-1} \biggr]= \frac{(M_{1}^{1} N_{1}^{1} + S_{1}^{1} T_{1}^{1})[{(P_{1}^{1})}^{2} + {(O_{1}^{1})}^{2}] + (Q_{1}^{1} P_{1}^{1} )[{(N_{1}^{1})}^{2} + {(T_{1}^{1})}^{2}]}{[{(N_{1}^{1})}^{2} + {(T_{1}^{1})}^{2}][{(P_{1}^{1})}^{2} + {(O_{1}^{1})}^{2}]}, \end{aligned} $$

where $M_{1}^{1}= A_{1}^{1} + B_{0}^{1}$; $S_{1}^{1}= 2\omega _{2}^{0}$; $N_{1}^{1}= (A_{1}^{1} + B_{0}^{1}) ({\omega _{2}^{0}} )^{2}$; $T_{1}^{1}= ({\omega _{2}^{0}} )^{3} - (A_{2}^{1} + B_{1}^{1})\omega _{2}^{0}$; $Q_{1}^{1}= C_{0}^{1}$; $P_{1}^{1} = -C_{0}^{1} ({\omega _{2}^{0}} )^{2}$; and $O_{1}^{1} = (C_{1}^{1}+D_{0}^{1})\omega _{2}^{0}$. It follows that if the condition

$$ {\bigl(M_{1}^{1} N_{1}^{1} + S_{1}^{1} T_{1}^{1}\bigr)\bigl[{ \bigl(P_{1}^{1}\bigr)}^{2} + {\bigl(O_{1}^{1} \bigr)}^{2}\bigr] + \bigl(Q_{1}^{1} P_{1}^{1} \bigr)\bigl[{\bigl(N_{1}^{1} \bigr)}^{2} + {\bigl(T_{1}^{1}\bigr)}^{2} \bigr]} \neq 0 $$

(17)

is satisfied, then

$$ \operatorname{Re} \biggl[ \biggl( \frac{d\lambda _{1}}{d\tau _{2}} \bigg|_{ \tau _{2} = \tau _{2}^{0}} \biggr)^{-1} \biggr] \neq 0. $$

Therefore, by Lemma 2.2 in [30] and Hopf bifurcation theory [31], we obtain the following theorem:

Theorem 3

Suppose that $\tau _{1} = 0$, and $\tau _{2} > 0$. If equation (14) has positive roots and condition (17) is met, then

(i) when $\tau _{2} \in (0,\tau _{2}^{0})$, $E_{0}$ is locally asymptotically stable;

(ii) when $\tau _{2}>\tau _{2}^{0}$, $E_{0}$ is unstable;

(iii) when $\tau _{2}=\tau _{2}^{0}$, system (1) has a Hopf bifurcation at $E_{0}$.

Case 3.2.3 If $\tau _{1}>0$, and $\tau _{2}=0$, then equations (7) and (13) become

$$ \lambda ^{2} + \bigl(A_{1}^{1} + C_{0}^{1}\bigr)\lambda + A_{2}^{1} + C_{1}^{1} + \bigl[B_{0}^{1}\lambda + \bigl(B_{1}^{1} + D_{0}^{1}\bigr) \bigr]e^{-\lambda \tau _{1}}=0, $$

(18)

and

$$ \omega ^{4} + \bigl[\bigl(A_{1}^{1} + C_{0}^{1}\bigr)^{2} - 2\bigl(A_{2}^{1} + C_{1}^{1}\bigr) - \bigl(B_{0}^{1} \bigr)^{2}\bigr]\omega ^{2} + \bigl(A_{2}^{1} + C_{1}^{1}\bigr)^{2} - \bigl(B_{1}^{1} + D_{0}^{1}\bigr)^{2} =0, $$

(19)

respectively, where $A_{1}^{1}$, $A_{2}^{1}$, $B_{0}^{1}$, $B_{1}^{1}$, $C_{0}^{1}$, $C_{1}^{1}$, and $D_{0}^{1}$ are as defined in (7). Using similar argument as for Case 3.2.2, we have

$$ \begin{aligned} \tau _{1}^{j}&={ \frac{1}{\omega _{1}^{j}} \biggl(\arccos \biggl[ \frac{\bar{M}_{1} \bar{M}_{3}(\omega _{1}^{j}) + \bar{M}_{2} \bar{M}_{4}(\omega _{1}^{j})}{\bar{M}_{1}^{2} +\bar{M}_{2}^{2}} \biggr] \biggr)},\quad j=1,2, \\ \tau _{1}^{0}&=\min_{j\in \{1,2\}} \bigl\{ \tau _{1}^{j}\bigr\} , \qquad \omega _{1}^{0} = \arg \min_{j\in \{1,2\}} \bigl\{ \tau _{1}^{j} \bigr\} , \end{aligned} $$

where $\omega _{1}^{1}$ and $\omega _{1}^{2}$ are two positive roots of (19); $\bar{M}_{1} =B_{1}^{1} + D_{0}^{1}$; $\bar{M}_{2} =B_{0}^{1}$; $\bar{M}_{3}(\omega _{1}^{j}) = ({\omega _{1}^{j}} )^{2} - (A_{2}^{1} + C_{1}^{1})$; and $\bar{M}_{4}(\omega _{1}^{j}) =-(A_{1}^{1} + C_{0}^{1})\omega _{1}^{j}$. Moreover, we consider the root of equation (18) as $\lambda _{2}(\tau _{1})=\xi _{2}(\tau _{1})+i\omega _{2}(\tau _{1})$ with $\xi _{2}(\tau ^{0}_{1})=0$ and $\omega _{2}(\tau _{1}^{0})=\omega _{1}^{0}$. Then, we have

$$ \begin{aligned} \operatorname{Re} \biggl[& \biggl( \frac{d\lambda _{2}}{d\tau _{1}}\bigg|_{ \tau _{1} = \tau _{1}^{0}} \biggr)^{-1} \biggr]= \frac{(\bar{M}_{1}^{1} \bar{N}_{1}^{1} + \bar{S}_{1}^{1} \bar{T}_{1}^{1})[{(\bar{P}_{1}^{1})}^{2} + {(\bar{O}_{1}^{1})}^{2}] + (\bar{Q}_{1}^{1} \bar{P}_{1}^{1} )[{(\bar{N}_{1}^{1})}^{2} + {(\bar{T}_{1}^{1})}^{2}]}{[{(\bar{N}_{1}^{1})}^{2} + {(\bar{T}_{1}^{1})}^{2}][{(\bar{P}_{1}^{1})}^{2} + {(\bar{O}_{1}^{1})}^{2}]}, \end{aligned} $$

where $\bar{M}_{1}^{1}= A_{1}^{1} + C_{0}^{1}$; $\bar{S}_{1}^{1}= 2\omega _{1}^{0}$; $\bar{N}_{1}^{1}= (A_{1}^{1} + C_{0}^{1}) ({\omega _{1}^{0}} )^{2}$; $\bar{T}_{1}^{1}= ({\omega _{1}^{0}} )^{3} - (A_{2}^{1} + C_{1}^{1}) \omega _{1}^{0}$; $\bar{Q}_{1}^{1}= B_{0}^{1}$; $\bar{P}_{1}^{1} = -B_{0}^{1} ({\omega _{1}^{0}} )^{2}$; and $\bar{O}_{1}^{1} = (B_{1}^{1}+D_{0}^{1})\omega _{1}^{0}$. Obviously, if condition

$$ {\bigl(\bar{M}_{1}^{1} \bar{N}_{1}^{1} + \bar{S}_{1}^{1} \bar{T}_{1}^{1}\bigr)\bigl[{\bigl( \bar{P}_{1}^{1} \bigr)}^{2} + {\bigl(\bar{O}_{1}^{1} \bigr)}^{2}\bigr] + \bigl(\bar{Q}_{1}^{1} \bar{P}_{1}^{1} \bigr)\bigl[{\bigl(\bar{N}_{1}^{1} \bigr)}^{2} + {\bigl(\bar{T}_{1}^{1} \bigr)}^{2}\bigr]} \neq 0 $$

(20)

is satisfied, then

$$ \operatorname{Re} \biggl[ \biggl( \frac{d\lambda _{2}}{d\tau _{1}} \bigg|_{ \tau _{1} = \tau _{1}^{0}} \biggr)^{-1} \biggr] \neq 0. $$

Thus, we have the following theorem:

Theorem 4

Suppose that $\tau _{2} = 0$, and $\tau _{1} > 0$. If equation (19) has positive roots and condition (20) is met, then

(i) when $\tau _{1} \in (0,\tau _{1}^{0})$, $E_{0}$ is locally asymptotically stable;

(ii) when $\tau _{1}>\tau _{1}^{0}$, $E_{0}$ is unstable;

(iii) when $\tau _{1}=\tau _{1}^{0}$, system (1) has a Hopf bifurcation at $E_{0}$.

Case 3.2.4 If $\tau _{1}>0$, and $\tau _{2}>0$, then as shown in [32], it is difficult to directly analyze the Hopf bifurcation with two delays. Thus, further, we only discuss the Hopf bifurcation of equilibrium point for system (1) with one delay and the other delay lying in its stability region. Without loss of generality, we investigate the Hopf bifurcation at $E_{0}$ for system (1) with $\tau _{1}>0$ and $\tau _{2} \in (0, \tau _{2}^{0})$, where $\tau _{2}^{0}$ is as given in Case 3.2.2. Let $\tau _{2}\in (0, \tau _{2}^{0})$ be arbitrary but fixed. Then, $\lambda =i\omega$ ($\omega >0$) is a pure imaginary root of equation (7) if and only if

$$ \begin{aligned} &-\omega ^{2} + A_{1}^{1} i\omega + A_{2}^{1} + \bigl(B_{0}^{1} i\omega + B_{1}^{1}\bigr) \bigl(\cos (\omega \tau _{1}) - i\sin (\omega \tau _{1}) \bigr) + \bigl(C_{0}^{1} i\omega + C_{1}^{1} \bigr) \\ &\quad {}\times \bigl[\cos (\omega \tau _{2}) - i\sin (\omega \tau _{2}) \bigr] + D_{0}^{1}\bigl[ \cos \bigl(\omega (\tau _{1}+\tau _{2})\bigr) - i\sin \bigl(\omega (\tau _{1}+\tau _{2})\bigr)\bigr] = 0. \end{aligned} $$

(21)

Separating the real part from the imaginary part in (21) gives

$$ \textstyle\begin{cases} (B_{0}^{1}\omega - D_{0}^{1}\sin ({\omega \tau _{2}}))\sin ({\omega \tau _{1}}) + (B_{1}^{1} + D_{0}^{1} \cos ({\omega \tau _{2}})) \cos ({ \omega \tau _{1}}) \\ \quad = -[(-\omega ^{2} + A_{2}^{1})+ C_{0}^{1}\omega \sin ({\omega \tau _{2}}) + C_{1}^{1} \cos ({\omega \tau _{2}})] , \\ (B_{0}^{1}\omega - D_{0}^{1}\sin ({\omega \tau _{2}}))\cos ({\omega \tau _{1}}) - (B_{1}^{1} + D_{0}^{1} \cos ({\omega \tau _{2}})) \sin ({ \omega \tau _{1}}) \\ \quad =-(A_{1}^{1}\omega + C_{0}^{1}\omega \cos ({\omega \tau _{2}}) - C_{1}^{1} \sin ({\omega \tau _{2}})) . \end{cases} $$

(22)

By adding the squares of two equations in (22), we obtain

$$ \omega ^{4} + l_{1}(\omega )\omega ^{3} + l_{2}(\omega )\omega ^{2} + l_{3}( \omega )\omega + l_{4}(\omega )=0, $$

(23)

where $l_{1}(\omega )=-2C_{0}^{1}\sin ({\omega \tau _{2}})$; $l_{2}(\omega )=(A_{1}^{1})^{2} - 2A_{2}^{1} + (C_{0}^{1})^{2} - (B_{0}^{1})^{2} + 2(-C_{1}^{1} + A_{1}^{1}C_{0}^{1})\cos{\omega \tau _{2}}$; $l_{3}(\omega )=2(A_{2}^{1}C_{0}^{1} + B_{0}^{1}D_{0}^{1} - A_{1}^{1}C_{1}^{1}) \sin ({\omega \tau _{2}})$; and $l_{4}(\omega )=(A_{2}^{1})^{2} + (C_{1}^{1})^{2} - (B_{1}^{1})^{2} - (D_{0}^{1})^{2} + 2(A_{2}^{1}C_{1}^{1} - B_{1}^{1}D_{0}^{1})\cos{\omega \tau _{2}}$. Let

$$ G_{1}(\omega )=\omega ^{4} + l_{1}( \omega )\omega ^{3} + l_{2}( \omega )\omega ^{2} + l_{3}(\omega )\omega + l_{4}(\omega ). $$

(24)

Clearly, if $l_{4}(0)<0$, then $G_{1}(0)<0$. Besides, $\lim_{\omega \to +\infty} G_{1}(\omega )=+\infty$. Hence, equation (23) has at least one positive root denoted by $\tilde{\omega}_{1}$. Furthermore, substituting $\tilde{\omega}_{1}$ into (22) and solving the resulting equations, we have

$$ \tilde{\tau}_{1}^{k}= \frac{1}{\tilde{\omega}_{1}} \biggl(\arccos \biggl[ \frac {M_{5}(\tilde{\omega}_{1})M_{7}(\tilde{\omega}_{1}) + M_{6} (\tilde{\omega}_{1})M_{8}(\tilde{\omega}_{1})}{{M_{5}}^{2}(\tilde{\omega}_{1}) +{M_{6}}^{2}(\tilde{\omega}_{1})} \biggr]+ 2k\pi \biggr),\quad k=0,1,2,\ldots , $$

where $M_{5}(\tilde{\omega}_{1})=(B_{1}^{1} + D_{0}^{1} \cos ({ \tilde{\omega}_{1} \tau _{2}}))$; $M_{6}(\tilde{\omega}_{1})=(B_{0}^{1}\tilde{\omega}_{1} - D_{0}^{1} \sin ({\tilde{\omega}_{1} \tau _{2}}))$; $M_{7}(\tilde{\omega}_{1}) = -[(-{\tilde{\omega}_{1}}^{2} + A_{2}^{1}) + C_{0}^{1} \tilde{\omega}_{1} \sin ({\tilde{\omega}_{1} \tau _{2}}) + C_{1}^{1} \cos ({\tilde{\omega}_{1} \tau _{2}})]$; and $M_{8}(\tilde{\omega}_{1})=-(A_{1}^{1}\tilde{\omega}_{1} + C_{0}^{1} \tilde{\omega}_{1} \cos ({\tilde{\omega}_{1} \tau _{2}}) - C_{1}^{1} \sin ({ \tilde{\omega}_{1} \tau _{2}}))$. Obviously,

$$ \lim_{k \to \infty} \tilde{\tau}_{1}^{k} = \infty . $$

Thus, we can define

$$ \tilde{\omega}^{0}_{1} =\arg \min \bigl\{ \tilde{\tau}^{0}_{1}\bigr\} . $$

(25)

As discussed in Case 3.2.3, we consider the roots of equation (7) as a function of $\tau _{1}$ and the root $\lambda _{3}(\tau _{1})= \xi _{3}(\tau _{1})+i\omega _{3}(\tau _{1})$ of equation (7) such that

$$ \xi _{3}\bigl(\tilde{\tau}^{0}_{1}\bigr)=0, \quad \text{and}\quad \omega _{3}\bigl( \tilde{\tau}^{0}_{1} \bigr)= \tilde{\omega}^{0}_{1}. $$

Substituting $\lambda _{3}(\tau _{1})$ into equation (7) and taking the derivative with respect to $\tau _{1}$, we have

$$ \begin{aligned} \biggl({\frac{d\lambda _{3}}{d\tau _{1}}} \biggr)^{-1} &={} \frac{2\lambda _{3} + A_{1}^{1} + C_{0}^{1}e^{-\lambda _{3} \tau _{2}} + (C_{0}^{1}\lambda _{3} + C_{1}^{1})e^{-\lambda _{3} \tau _{2}}(-\tau _{2})}{-\lambda _{3} [(\lambda _{3})^{2} + A_{1}^{1}\lambda _{3} + A_{2}^{1} + (C_{0}^{1}\lambda _{3} + C_{1}^{1})e^{-\lambda _{3} \tau _{2}}]} + \frac{B_{0}^{1} + D_{0}^{1}e^{-\lambda _{3} \tau _{2}}(- \tau _{2})}{\lambda _{3} [(B_{0}^{1}\lambda _{3} + B_{1}^{1}) + D_{0}^{1}e^{-\lambda _{3} \tau _{2}}]} \\&\quad - \frac{\tau _{1}}{\lambda _{3}}. \end{aligned} $$

Then,

$$ \begin{aligned} &\operatorname{Re} \biggl[ \biggl(\frac{d\lambda _{3}}{d\tau _{1}} \bigg|_{ \tau = \tilde{\tau}^{0}_{1}} \biggr)^{-1} \biggr] =\frac{(M_{3}^{1} N_{3}^{1} + S_{3}^{1} T_{3}^{1})[{(P_{3}^{1})}^{2} + {(O_{3}^{1})}^{2}] + (Q_{3}^{1} P_{3}^{1} + R_{3}^{1} O_{3}^{1})[{(N_{3}^{1})}^{2} + {(T_{3}^{1})}^{2}]}{[{(N_{3}^{1})}^{2} + {(T_{3}^{1})}^{2}][{(P_{3}^{1})}^{2} + {(O_{3}^{1})}^{2}]}, \end{aligned} $$

where $M_{3}^{1}= A_{1}^{1} + C_{0}^{1} \cos (\tilde{\omega}^{0}_{1} \tau _{2}) - \tau _{2} C_{0}^{1} \tilde{\omega}^{0}_{1} \sin (\tilde{\omega}^{0}_{1} \tau _{2}) - \tau _{2} C_{1}^{1} \cos (\tilde{\omega}^{0}_{1} \tau _{2})$; $S_{3}^{1}= 2\tilde{\omega}^{0}_{1} - C_{0}^{1} \sin (\tilde{\omega}^{0}_{1} \tau _{2}) - \tau _{2} C_{0}^{1} \tilde{\omega}^{0}_{1} \cos ( \tilde{\omega}^{0}_{1} \tau _{2}) + \tau _{2} C_{1}^{1} \sin ( \tilde{\omega}^{0}_{1} \tau _{2})$; $N_{3}^{1}= -A_{1}^{1} (\tilde{\omega}^{0}_{1})^{2} - C_{0}^{1}( \tilde{\omega}^{0}_{1})^{2}\cos (\tilde{\omega}^{0}_{1} \tau _{2}) + C_{1}^{1} \tilde{\omega}^{0}_{1}\sin (\tilde{\omega}^{0}_{1} \tau _{2})$; $T_{3}^{1}= - (\tilde{\omega}^{0}_{1})^{3} + A_{2}^{1} \tilde{\omega}^{0}_{1} + C_{0}^{1}(\tilde{\omega}^{0}_{1})^{2}\sin (\tilde{\omega}^{0}_{1} \tau _{2}) + C_{1}^{1}\tilde{\omega}^{0}_{1}\cos (\tilde{\omega}^{0}_{1} \tau _{2})$; $Q_{3}^{1}= B_{0}^{1} - \tau _{2}^{0} D_{0}^{1} \cos (\tilde{\omega}^{0}_{1} \tau _{2}^{0})$; $R_{3}^{1}= \tau _{2}^{0} D_{0}^{1} \sin (\tilde{\omega}^{0}_{1} \tau _{2}^{0})$; $P_{3}^{1} = -B_{0}^{1} (\tilde{\omega}^{0}_{1})^{2}+ D_{0}^{1} \cos (\tilde{\omega}^{0}_{1} \tau _{2}^{0})$; and $O_{3}^{1} = B_{1}^{1} \tilde{\omega}^{0}_{1} - D_{0}^{1} \sin ( \tilde{\omega}^{0}_{1} \tau _{2}^{0})$. It follows that if the condition

$$ {\bigl(M_{3}^{1} N_{3}^{1} + S_{3}^{1} T_{3}^{1}\bigr)\bigl[{ \bigl(P_{3}^{1}\bigr)}^{2} + {\bigl(O_{3}^{1} \bigr)}^{2}\bigr] + \bigl(Q_{3}^{1} P_{3}^{1}+ R_{3}^{1} O_{3}^{1}\bigr)\bigl[{\bigl(N_{3}^{1} \bigr)}^{2} + {\bigl(T_{3}^{1}\bigr)}^{2} \bigr]} \neq 0 $$

(26)

is satisfied, then

$$ \operatorname{Re} \biggl[ \biggl( \frac{d\lambda _{3}}{d\tau _{1}} \bigg|_{ \tau _{1} = \tilde{\tau}^{0}_{1}} \biggr)^{-1} \biggr]\neq 0. $$

As a result, by the Hopf bifurcation theory [31], we obtain the following theorem:

Theorem 5

Suppose that $\tau _{1} > 0$, and $\tau _{2} \in (0,\tau _{2}^{0})$ with $\tau ^{0}_{2}$ as defined in Case 3.2.2. If equation (23) has positive roots and condition (26) is met, then

(i) when $\tau _{1} \in (0,\tilde{\tau}^{0}_{1})$, $E_{0}$ is locally asymptotically stable;

(ii) when $\tau _{1}>\tilde{\tau}^{0}_{1}$, $E_{0}$ is unstable;

(iii) when $\tau _{1}=\tilde{\tau}^{0}_{1}$, system (1) has a Hopf bifurcation at $E_{0}$.

3.3 Stability and Hopf bifurcation of endemic equilibrium point

The Jacobian matrix of the system (1) at ${E_{1}}$ is given by

$$ J_{E_{1}} = \begin{pmatrix} {-( Y + d)} & {-Y_{1}} & {-Y_{2}} & {-\frac{- \beta _{1} S^{*}E^{*} - \beta _{2} S^{*} I^{*} }{(N^{*}) ^{2}}} \\ {Y} & {-( Y_{3} - Y_{1})} & {Y_{2}} & {-\frac{\beta _{1} S^{*} E^{*} + \beta _{2} S^{*} I^{*} }{(N^{*})^{2}}} \\ {0} & {\varepsilon e^{-\lambda \tau _{1}}} & {Y_{4}} & {0} \\ {0} & {\gamma _{2}} & {\gamma _{1} e^{-\lambda \tau _{2}}} & {- d} \end{pmatrix}, $$

(27)

where $N^{*}=S^{*}+E^{*}+I^{*}+R^{*}$; $Y= \frac{\beta _{1} (N^{*}-S^{*})E^{*}}{(N^{*})^{2}} + \frac{\beta _{2} (N^{*} -S^{*})I^{*}}{(N^{*})^{2}}$; $Y_{1}=\frac{\beta _{1} S^{*}N^{*} - \beta _{1} S^{*}E^{*} - \beta _{2} S^{*}I^{*}}{(N^{*})^{2}}$; $Y_{2}=\frac{\beta _{2} S^{*}N^{*} - \beta _{2} S^{*}I^{*} - \beta _{1} S^{*}E^{*}}{(N^{*})^{2}}$; $Y_{3}= \varepsilon e^{-\lambda \tau _{1}} +\gamma _{2} + d$; and $Y_{4} =-(\mu + d + \gamma _{1} e^{-\lambda \tau _{2}})$. For (27), one negative eigenvalue is given by $\lambda _{1}=-d$. The other eigenvalues are determined by the following characteristic equation:

$$ \begin{aligned} &\lambda ^{3} + A_{1}^{2}\lambda ^{2} + A_{2}^{2} \lambda + A_{3}^{2} + \bigl(B_{0}^{2} \lambda ^{2} + B_{1}^{2}\lambda + B_{2}^{2}\bigr)e^{- \lambda \tau _{1}} +\bigl(C_{0}^{2} \lambda ^{2} + C_{1}^{2}\lambda \\ &\quad {}+ C_{2}^{2}\bigr)e^{-\lambda \tau _{2}} + \bigl(D_{0}^{2} \lambda + D_{1}^{2}\bigr)e^{- \lambda (\tau _{1} + \tau _{2})}=0, \end{aligned} $$

(28)

where $A_{1}^{2}=(Y + d)+(\gamma _{2} + d)+(\mu + d) - Y_{1}$; $A_{2}^{2}=(Y + d)(\gamma _{2} + d) +(Y + d)(\mu + d) + (\gamma _{2} + d)(\mu + d) - (\mu + 2d)Y_{1} + \gamma _{2} {\frac{\beta _{1} S^{*}E^{*} + \beta _{2} S^{*}I^{*}}{(N^{*})^{2}}}$; $A_{3}^{2}=(Y + d)(\gamma _{2} + d) (\mu + d) -Y_{1}(\mu + d)d + { \frac{\beta _{1} S^{*}E^{*} + \beta _{2} S^{*}I^{*}}{(N^{*})^{2}}} (\mu + d) \gamma _{2}$; $B_{0}^{2}=\varepsilon$; $B_{1}^{2}=(Y + d)\varepsilon + (\mu + d)\varepsilon - Y_{2} \varepsilon$; $B_{2}^{2}=(Y + d)(\mu + d)\varepsilon - \varepsilon d Y_{2}$; $C_{0}^{2}=\gamma _{1}$; $C_{1}^{2}=(Y + d)\gamma _{1} + (\gamma _{2} + d)\gamma _{1} - Y_{1} \gamma _{1}$; $C_{2}^{2}=(Y + d)(\gamma _{2} + d)\gamma _{1} + \gamma _{1} \gamma _{2} {\frac{\beta _{1} S^{*}E^{*} + \beta _{2} S^{*}I^{*}}{(N^{*})^{2}}} - \gamma _{1}\,dY_{1}$; $D_{0}^{2}=\varepsilon \gamma _{1}$; and $D_{1}^{2}={\frac{\beta _{1} S^{*}E^{*} + \beta _{2} S^{*}I^{*}}{(N^{*})^{2}}} \varepsilon \gamma _{1} + (Y + d)\varepsilon \gamma _{1}$.

Now, we investigate the following cases for $\tau _{1}$ and $\tau _{2}$ at the endemic equilibrium point $E_{1}$.

Case 3.3.1 If $\tau _{1}= \tau _{2}= 0$, then equation (28) turns to

$$ \lambda ^{3}+ \bigl(A_{1}^{2} + B_{0}^{2} + C_{0}^{2}\bigr)\lambda ^{2} + \bigl(A_{2}^{2} + B_{1}^{2} + C_{1}^{2} + D_{0}^{2}\bigr)\lambda + A_{3}^{2} + B_{2}^{2} + C_{2}^{2} + D_{1}^{2} = 0. $$

(29)

Let

$$ \textstyle\begin{cases} {a_{0}^{2}} =1, \\ {a_{1}^{2}} =A_{1}^{2} + B_{0}^{2} + C_{0}^{2} \\ \hphantom{{a_{1}^{2}}} =Y + \gamma _{2} +\mu + 3d + \varepsilon + \gamma _{1} + \frac{\beta _{1} S^{*}E^{*} + \beta _{2} S^{*}I^{*}}{(N^{*})^{2}} -\frac{\beta _{1} S^{*}N^{*}}{(N^{*})^{2}}, \\ {a_{2}^{2}}=A_{2}^{2} + B_{1}^{2} + C_{1}^{2} + D_{0}^{2} =(Y+d)( \varepsilon +\gamma _{2} + d)+(Y + d) (\mu + \gamma _{1} +d) \\ \hphantom{{a_{2}^{2}}=}{} +(\varepsilon +\gamma _{2} + d ) (\mu + \gamma _{1} +d)+ ( \varepsilon +\gamma _{2} + \mu + \gamma _{1} + 2d) \\ \hphantom{{a_{2}^{2}}=}{} +(\varepsilon +\gamma _{2}+\gamma _{1} + \mu + 2d) \frac{\beta _{1} S^{*}E^{*} + \beta _{2} S^{*}I^{*}}{(N^{*})^{2}}- (\gamma _{1} + \mu +2d) \\ \hphantom{{a_{2}^{2}}=}{}\times \frac{\beta _{1} S^{*}N^{*}}{(N^{*})^{2}} - \varepsilon \frac{\beta _{2} S^{*}N^{*}}{(N^{*})^{2}}, \\ {a_{3}^{2}} = A_{3}^{2} + B_{2}^{2} + C_{2}^{2} + D_{1}^{2} = Y( \varepsilon +\gamma _{2} + d)(\mu + \gamma _{1} +d) + [d(\varepsilon + \mu \\ \hphantom{{a_{3}^{2}} =}{} +\gamma _{1} +d) + \varepsilon \gamma _{1} + (\mu + \gamma _{1} +d)\gamma _{2}]\frac{\beta _{1} S^{*}E^{*} + \beta _{2} S^{*}I^{*}}{(N^{*})^{2}}. \end{cases} $$

Obviously,

$$ a_{1}^{2}>Y+ d + \mu + \gamma _{1} +d + \frac{\beta _{1} S^{*}E^{*} + \beta _{2} S^{*}I^{*}}{(N^{*})^{2}}, $$

and

$$ \begin{aligned}a_{2}^{2}>{}&Y(\varepsilon +\gamma _{2} + d) + (Y + d) ( \mu + \gamma _{1} +d) + (\varepsilon + \gamma _{2} + d + \mu + \gamma _{1} +d) \\ &{}\times \frac{\beta _{1} S^{*}E^{*} + \beta _{2} S^{*}I^{*}}{(N^{*})^{2}}. \end{aligned} $$

Then, we have

$$ a_{1}^{2}a_{2}^{2}>a_{0}^{2}a_{3}^{2}, \quad \text{and}\quad a_{i}^{2}>0,\quad i=0,1,2,3. $$

Recall that the positive endemic equilibrium point $E_{1}$ exists if and only if $R_{0}> 1$. Thus, by the Routh-Hurwitz theorem [29], we have the following theorem:

Theorem 6

Suppose that $\tau _{1} =\tau _{2}= 0$. If $R_{0}>1$, then $E_{1}$ is locally asymptotically stable.

Case 3.3.2 If $\tau _{1}=0$, and $\tau _{2} > 0$, then equation (28) turns to

$$ \begin{aligned} &\lambda ^{3} + \bigl(A_{1}^{2} + B_{0}^{2}\bigr)\lambda ^{2} + \bigl(A_{2}^{2} + B_{1}^{2} \bigr)\lambda + A_{3}^{2} + B_{2}^{2} \\ &\quad {}+ \bigl[C_{0}^{2}\lambda ^{2} + \bigl(C_{1}^{2} + D_{0}^{2}\bigr)\lambda + C_{2}^{2} + D_{1}^{2} \bigr]e^{-\lambda \tau _{2}}=0. \end{aligned} $$

(30)

To discuss the Hopf bifurcation of (30), we observe that $\lambda =i\omega$ ($\omega >0$) is a pure imaginary root of the equation (30) if and only if

$$ \begin{aligned} &-i\omega ^{3} - \bigl(A_{1}^{2} + B_{0}^{2}\bigr)\omega ^{2} + \bigl(A_{2}^{2} + B_{1}^{2} \bigr)i\omega + A_{3}^{2} + B_{2}^{2} \\ &\quad {} +\bigl[-C_{0}^{2}\omega ^{2} + \bigl(C_{1}^{2} + D_{0}^{2}\bigr)i\omega + C_{2}^{2} + D_{1}^{2}\bigr]\bigl(\cos ( \omega \tau _{2}) - i\sin (\omega \tau _{2})\bigr)=0 . \end{aligned} $$

(31)

Separating the real part from the imaginary part in (31) gives

$$ \textstyle\begin{cases} {(A_{1}^{2} + B_{0}^{2})\omega ^{2} - (A_{3}^{2} + B_{2}^{2})}=(-C_{0}^{2} \omega ^{2} + C_{2}^{2} + D_{1}^{2})\cos (\omega \tau _{2}) + (C_{1}^{2} + D_{0}^{2}) \omega \sin (\omega \tau _{2}),\\ {\omega ^{3} - (A_{2}^{2} + B_{1}^{2})\omega}=-(-C_{0}^{2} \omega ^{2} + C_{2}^{2} + D_{1}^{2})\sin (\omega \tau _{2}) + (C_{1}^{2} + D_{0}^{2}) \omega \cos (\omega \tau _{2}). \end{cases}$$

(32)

By adding the squares of two equations in (32), we obtain

$$ \begin{aligned} & \omega ^{6} + \bigl[ \bigl(A_{1}^{2} + B_{0}^{2} \bigr)^{2} - 2\bigl(A_{2}^{2} + B_{1}^{2} \bigr) - \bigl(C_{0}^{2}\bigr)^{2}\bigr]\omega ^{4} + \bigl[\bigl(A_{2}^{2} + B_{1}^{2} \bigr)^{2} - 2\bigl(A_{1}^{2} + B_{0}^{2} \bigr) \bigl(A_{3}^{2} \\ &\quad {}+ B_{2}^{2}\bigr)- \bigl(C_{1}^{2} + D_{0}^{2}\bigr)^{2} + 2C_{0}^{2} \bigl(C_{2}^{2} + D_{1}^{2}\bigr)\bigr] \omega ^{2} + \bigl(A_{3}^{2} + B_{2}^{2}\bigr)^{2} - \bigl(C_{2}^{2} + D_{1}^{2}\bigr)^{2} = 0. \end{aligned} $$

(33)

Let $z = \omega ^{2}$, $h_{03}=(A_{3}^{2} + B_{2}^{2})^{2} - (C_{2}^{2} + D_{1}^{2})^{2}$, $h_{13}=(A_{2}^{2} + B_{1}^{2})^{2} - 2(A_{1}^{2} + B_{0}^{2})(A_{3}^{2} + B_{2}^{2}) - (C_{1}^{2} + D_{0}^{2})^{2} + 2C_{0}^{2}(C_{2}^{2} + D_{1}^{2})$ and $h_{23}=(A_{1}^{2} + B_{0}^{2})^{2} - 2(A_{2}^{2} + B_{1}^{2}) - (C_{0}^{2})^{2}$. Then, (33) can be rewritten as

$$ z^{3} + h_{23} z^{2} + h_{13} z + h_{03} = 0. $$

(34)

Without loss of generality, we assume that equation (34) has three positive roots denoted by $\bar{z}_{j}$, $j = 1,2,3$. Then, three positive roots of equation (33) are

$$ \bar{\omega}_{2}^{j}=\sqrt { \bar{z}_{j}},\quad j = 1,2,3. $$

(35)

Furthermore, substituting (35) into (32) and solving the resulting equations, we have

$$ \begin{aligned} &\bar{\tau}_{2}^{j,k}= \frac{1}{\bar{\omega }_{2}^{j}} \biggl( \arccos \biggl[ \frac{(\hat{J}-\hat{F}C_{0}^{2})(\bar{\omega }_{2}^{j})^{4} + (C_{0}^{2}\hat{I} + \hat{F}\hat{K} - \hat{H}\hat{J})(\bar{\omega }_{2}^{j})^{2} - \hat{I}\hat{K}}{\hat{J}^{2}(\bar{\omega }_{2}^{j})^{2} + (\hat{K}-C_{0}^{2}(\bar{\omega }_{2}^{j})^{2})^{2}} \biggr]+ 2k\pi \biggr), \\ & j=1,2,3;\quad k=0,1,\ldots , \end{aligned} $$

where $\hat{F}={A_{1}^{2} + B_{0}^{2}}$; $\hat{H}={A_{2}^{2} + B_{1}^{2}}$; $\hat{I}={A_{3}^{2} + B_{2}^{2}}$; $\hat{J}={C_{1}^{2} + D_{0}^{2}}$; and $\hat{K}={C_{2}^{2} + D_{1}^{2}}$. Clearly,

$$ \lim_{k \to \infty} \bar{\tau}_{2}^{j,k} = \infty ,\quad j=1,2,3. $$

Thus, we can define

$$ \bar{\tau}_{2}^{0} = \min _{j\in \{1,2,3\}} \bigl\{ \bar{\tau}_{2}^{j,0} \bigr\} , \quad \text{and}\quad \bar{\omega}_{2}^{0} = \arg \min _{j\in \{1,2,3 \}} \bigl\{ \bar{\tau}_{2}^{j,0}\bigr\} . $$

(36)

Now, we consider the roots of equation (30) as a function of $\tau _{2}$ and the root $\tilde{\lambda}_{1}(\tau _{2})=\alpha _{1}( \tau _{2})+i\tilde{\omega}_{1}(\tau _{2})$ of equation (30) such that

$$ \alpha _{1}\bigl(\bar{\tau}_{2}^{0}\bigr)=0, \quad \text{and}\quad \tilde{\omega}_{1}\bigl( \bar{\tau}_{2}^{0} \bigr)=\bar{\omega}_{2}^{0}, $$

where $\bar{\tau}_{2}^{0}$ and $\bar{\omega}_{2}^{0}$ are as defined in (36). Substituting $\tilde{\lambda}_{1}(\tau _{2})$ into equation (30) and taking the derivative with respect to $\tau _{2}$, we have

$$ \begin{aligned} \biggl({\frac{d\tilde{\lambda }_{1}}{d\tau _{2}}} \biggr)^{-1} ={}& \frac{3\tilde{\lambda }_{1}^{2} + 2(A_{1}^{2} + B_{0}^{2})\tilde{\lambda }_{1} + (A_{2}^{2} + B_{1}^{2})}{-\tilde{\lambda }_{1} [\tilde{\lambda }_{1}^{3} + (A_{1}^{2} + B_{0}^{2})\tilde{\lambda }_{1}^{2} + (A_{2}^{2} + B_{1}^{2})\tilde{\lambda }_{1} + A_{3}^{2} + B_{2}^{2}]} \\ &{} + \frac{2C_{0}^{2} \tilde{\lambda }_{1} + C_{1}^{2} + D_{0}^{2}}{\tilde{\lambda }_{1} [C_{0}^{2}\tilde{\lambda }_{1}^{2} + (C_{1}^{2} + D_{0}^{2})\tilde{\lambda }_{1} + C_{2}^{2} + D_{1}^{2}]} - \frac{\tau _{2}}{\tilde{\lambda }_{1}}. \end{aligned} $$

Then,

$$ \begin{aligned} &\operatorname{Re} \biggl[ \biggl(\frac{d\tilde{\lambda }_{1}}{d\tau _{2}} \bigg|_{\tau _{2} = \bar{\tau}_{2}^{0}} \biggr)^{-1} \biggr] =\frac{(M_{1}^{2} N_{1}^{2} + S_{1}^{2} T_{1}^{2})[{(P_{1}^{2})}^{2} + {(O_{1}^{2})}^{2}] + (Q_{1}^{2} P_{1}^{2} + R_{1}^{2} O_{1}^{2})[{(N_{1}^{2})}^{2} + {(T_{1}^{2})}^{2}]}{[{(N_{1}^{2})}^{2} + {(T_{1}^{2})}^{2}][{(P_{1}^{2})}^{2} + {(O_{1}^{2})}^{2}]}, \end{aligned} $$

where $M_{1}^{2}= -3(\bar{\omega}_{2}^{0})^{2} + (A_{2}^{2} + B_{1}^{2})$, $S_{1}^{2}= 2(A_{1}^{2} + B_{0}^{2})\bar{\omega}_{2}^{0}$, $N_{1}^{2}= -(\bar{\omega}_{2}^{0})^{4} + (A_{2}^{2} + B_{1}^{2})(\bar{\omega}_{2}^{0})^{2}$, $T_{1}^{2}= (A_{1}^{2} + B_{0}^{2})(\bar{\omega}_{2}^{0})^{3} - (A_{3}^{2} + B_{2}^{2}) \bar{\omega}_{2}^{0}$, $Q_{1}^{2}= C_{1}^{2} + D_{0}^{2}$, $R_{1}^{2}= 2C_{0}^{2} \bar{\omega}_{2}^{0}$, $P_{1}^{2} = -(C_{1}^{2} + D_{0}^{2})(\bar{\omega}_{2}^{0})^{2}$, and $O_{1}^{2} = -C_{0}^{2}(\bar{\omega}_{2}^{0})^{3} + (C_{2}^{2} + D_{1}^{2})\bar{\omega}_{2}^{0}$. It follows that if the condition

$$ {\bigl(M_{1}^{2} N_{1}^{2} + S_{1}^{2} T_{1}^{2}\bigr)\bigl[{ \bigl(P_{1}^{2}\bigr)}^{2} + {\bigl(O_{1}^{2} \bigr)}^{2}\bigr] + \bigl(Q_{1}^{2} P_{1}^{2} + R_{1}^{2} O_{1}^{2}\bigr)\bigl[{\bigl(N_{1}^{2} \bigr)}^{2} + {\bigl(T_{1}^{2}\bigr)}^{2} \bigr]} \neq 0 $$

(37)

is satisfied, then

$$ \operatorname{Re} \biggl[ \biggl( \frac{d\tilde{\lambda }_{1}}{d\tau _{2}} \bigg|_{\tau _{2} = \bar{\tau}_{2}^{0}} \biggr)^{-1} \biggr] \neq 0. $$

Hence, by the Hopf bifurcation theory [31] and Lemma 2.1 in [33], we can obtain the following theorem:

Theorem 7

Suppose that $\tau _{1} = 0$, and $\tau _{2} > 0$. If equation (34) has positive roots and condition (37) is met, then

(i) when $\tau _{2} \in (0,\bar{\tau}_{2}^{0})$, $E_{1}$ is locally asymptotically stable;

(ii) when $\tau _{2}>\bar{\tau}_{2}^{0}$, $E_{1}$ is unstable;

(iii) when $\tau _{2}=\bar{\tau}_{2}^{0}$, system (1) has a Hopf bifurcation at $E_{1}$.

Case 3.3.3 If $\tau _{1}>0$, and $\tau _{2}=0$, then equations (28) and (33) become

$$ \begin{aligned} &\lambda ^{3} + \bigl(A_{1}^{2} + C_{0}^{2}\bigr)\lambda ^{2} + \bigl(A_{2}^{2} + C_{1}^{2} \bigr)\lambda + A_{3}^{2} + C_{2}^{2} \\ & \quad {}+ \bigl[B_{0}^{2}\lambda ^{2} + \bigl(B_{1}^{2} + D_{0}^{2}\bigr)\lambda + B_{2}^{2}+ D_{1}^{2} \bigr]e^{-\lambda \tau _{1}}=0. \end{aligned} $$

(38)

and

$$\begin{aligned} &\omega ^{6} + \bigl[\bigl(A_{1}^{2} + C_{0}^{2}\bigr)^{2} - 2\bigl(A_{2}^{2} + C_{1}^{2}\bigr) - \bigl(B_{0}^{2} \bigr)^{2}\bigr]\omega ^{4} + \bigl[\bigl(A_{2}^{2} + C_{1}^{2}\bigr)^{2} - 2\bigl(A_{1}^{2} + C_{0}^{2}\bigr) \bigl(A_{3}^{2} \\ &\quad {}+C_{2}^{2}\bigr)- \bigl(B_{1}^{2} + D_{0}^{2}\bigr)^{2} + 2B_{0}^{2} \bigl(B_{2}^{2} + D_{1}^{2}\bigr)\bigr] \omega ^{2}+ \bigl(A_{3}^{2} + C_{2}^{2} \bigr)^{2} - \bigl(B_{2}^{2} + D_{1}^{2} \bigr)^{2} = 0, \end{aligned}$$

(39)

respectively, where $A_{1}^{2}$, $A_{2}^{2}$, $A_{3}^{2}$, $B_{0}^{2}$, $B_{1}^{2}$, $B_{2}^{2}$, $C_{0}^{2}$, $C_{1}^{2}$, $C_{2}^{2}$, $D_{0}^{2}$, and $D_{1}^{2}$ are as defined in (28). Using similar argument as given for Case 2.2.3, we have

$$ \begin{aligned} &\bar{\tau}_{1}^{j} = \frac{1}{\bar{\omega }_{2}^{j}} \biggl( \arccos \biggl[ \frac{(\bar{J}-\bar{F}B_{0}^{2})(\bar{\omega }_{1}^{j})^{4} + (B_{0}^{2}\bar{I} + \bar{F}\bar{K} - \bar{H}\bar{J})(\bar{\omega }_{1}^{j})^{2} - \bar{I}\bar{K}}{\bar{J}^{2}(\bar{\omega }_{1}^{j})^{2} + (\bar{K}-B_{0}^{2}(\bar{\omega }_{1}^{j})^{2})^{2}} \biggr] \biggr), \\ & j=1,2,3, \\ &\bar{\tau}_{1}^{0} = \min_{j\in \{1,2,3\}} \bigl\{ \bar{\tau}_{1}^{j} \bigr\} , \qquad \bar{\omega}_{1}^{0} = \arg \min_{j\in \{1,2,3\}} \bigl\{ \bar{\tau}_{1}^{j} \bigr\} , \end{aligned} $$

where $\bar{\omega}_{1}^{1}$, $\bar{\omega}_{1}^{2}$, and $\bar{\omega}_{1}^{3}$ are three positive roots of (39); $\bar{F}={A_{1}^{2} + C_{0}^{2}}$; $\bar{H}={A_{2}^{2} + C_{1}^{2}}$; $\bar{I}={A_{3}^{2} + C_{2}^{2}}$; $\bar{J}={B_{1}^{2} + D_{0}^{2}}$; and $\bar{K}={B_{2}^{2} + D_{1}^{2}}$. Furthermore, we consider the root of equation (38) as $\tilde{\lambda}_{2}(\tau _{1})=\alpha _{2}(\tau _{1})+i \tilde{\omega}_{2}(\tau _{1})$ with $\alpha _{2}(\bar{\tau}_{1}^{0})=0$ and $\tilde{\omega}_{2}(\bar{\tau}_{1}^{0})=\bar{\omega}_{1}^{0}$. Then, we have

$$ \begin{aligned} &\operatorname{Re} \biggl[ \biggl(\frac{d\tilde{\lambda }_{2}}{d\tau _{1}} \bigg|_{\tau _{1} = \bar{\tau}_{1}^{0}} \biggr)^{-1} \biggr] \\ &\quad =\frac{(\bar{M}_{1}^{2} \bar{N}_{1}^{2} + \bar{S}_{1}^{2} \bar{T}_{1}^{2})[{(\bar{P}_{1}^{2})}^{2} + {(\bar{O}_{1}^{2})}^{2}] + (\bar{Q}_{1}^{2} \bar{P}_{1}^{2} + \bar{R}_{1}^{2} \bar{O}_{1}^{2})[{(\bar{N}_{1}^{2})}^{2} + {(\bar{T}_{1}^{2})}^{2}]}{[{(\bar{N}_{1}^{2})}^{2} + {(\bar{T}_{1}^{2})}^{2}][{(\bar{P}_{1}^{2})}^{2} + {(\bar{O}_{1}^{2})}^{2}]}, \end{aligned} $$

where $\bar{M}_{1}^{2}= -3(\bar{\omega}_{1}^{0})^{2} + (A_{2}^{2} + C_{1}^{2})$, $\bar{S}_{1}^{2}= 2(A_{1}^{2} + C_{0}^{2})\bar{\omega}_{1}^{0}$, $\bar{N}_{1}^{2}= -(\bar{\omega}_{1}^{0})^{4} + (A_{2}^{2} + C_{1}^{2})( \bar{\omega}_{1}^{0})^{2}$, $\bar{T}_{1}^{2}= (A_{1}^{2} + C_{0}^{2})(\bar{\omega}_{1}^{0})^{3} - (A_{3}^{2} + C_{2}^{2}) \bar{\omega}_{1}^{0}$, $\bar{Q}_{1}^{2}= B_{1}^{2} + D_{0}^{2}$, $\bar{R}_{1}^{2}= 2B_{0}^{2} \bar{\omega}_{1}^{0}$, $\bar{P}_{1}^{2} = -(B_{1}^{2} + D_{0}^{2})(\bar{\omega}_{1}^{0})^{2}$, and $\bar{O}_{1}^{2} = -B_{0}^{2}(\bar{\omega}_{1}^{0})^{3} + (B_{2}^{2} + D_{1}^{2}) \bar{\omega}_{1}^{0}$. Clearly, if condition

$$ {\bigl(\bar{M}_{1}^{2} \bar{N}_{1}^{2} + \bar{S}_{1}^{2} \bar{T}_{1}^{2}\bigr)\bigl[{\bigl( \bar{P}_{1}^{2} \bigr)}^{2} + {\bigl(\bar{O}_{1}^{2} \bigr)}^{2}\bigr] + \bigl(\bar{Q}_{1}^{2} \bar{P}_{1}^{2} + \bar{R}_{1}^{2} \bar{O}_{1}^{2}\bigr)\bigl[{\bigl(\bar{N}_{1}^{2} \bigr)}^{2} + {\bigl(\bar{T}_{1}^{2} \bigr)}^{2}\bigr]} \neq 0 $$

(40)

is satisfied, then

$$ \operatorname{Re} \biggl[ \biggl( \frac{d\tilde{\lambda }_{2}}{d\tau _{1}} \bigg|_{\tau _{1} = \bar{\tau}_{1}^{0}} \biggr)^{-1} \biggr] \neq 0. $$

Thus, we have the following theorem:

Theorem 8

Suppose that $\tau _{1} > 0$, and $\tau _{2} = 0$. If equation (39) has positive roots and condition (40) is met, then

(i) when $\tau _{1} \in (0,\bar{\tau}_{1}^{0})$, $E_{1}$ is locally asymptotically stable;

(ii) when $\tau _{1}>\bar{\tau}_{1}^{0}$, $E_{1}$ is unstable;

(iii) when $\tau _{1}=\bar{\tau}_{1}^{0}$, system (1) has a Hopf bifurcation at $E_{1}$.

Case 3.3.4 If $\tau _{1}>0$, and $\tau _{2}>0$, then using the similar discussion as for Case 3.2.4, we consider the Hopf bifurcation of $E_{1}$ for the system (1) with $\tau _{1}>0$ and $\tau _{2} \in (0, \bar{\tau}_{2}^{0})$, where $\bar{\tau}_{2}^{0}$ as given in Case 3.3.2. Let $\tau _{2} \in (0,\bar{\tau}_{2}^{0})$ be arbitrary but fixed. Then, $\lambda =i\omega$ ($\omega >0$) is a pure imaginary root of the equation (28) if and only if

$$ \begin{aligned} &-i\omega ^{3} - A_{1}^{2}\omega ^{2} + A_{2}^{2} i \omega + A_{3}^{2} + \bigl(-B_{0}^{2} \omega ^{2} + B_{1}^{2} i\omega + B_{2}^{2}\bigr) \bigl[\cos (\omega \tau _{1}) \\ &\quad {}- i\sin (\omega \tau _{1})\bigr] + \bigl(-C_{0}^{2} \omega ^{2} + C_{1}^{2} i \omega + C_{2}^{2}\bigr)\bigl[\cos (\omega \tau _{2}) - i \sin (\omega \tau _{2})\bigr] \\ &\quad {}+ \bigl(D_{0}^{2} i\omega + D_{1}^{2} \bigr)\bigl[\cos \bigl(\omega (\tau _{1}+\tau _{2})\bigr) - i \sin \bigl(\omega (\tau _{1}+\tau _{2})\bigr)\bigr] = 0. \end{aligned} $$

(41)

Separating the real part from the imaginary part in (41) gives

$$ \textstyle\begin{cases} A_{1}^{2} \omega ^{2} - A_{3}^{2} -(-C_{0}^{2}\omega ^{2} + C_{2}^{2}) \cos ({\omega \tau _{2}}) - C_{1}^{2}\omega \sin ({\omega \tau _{2}}) \\ \quad = (- B_{0}^{2}\omega ^{2} +B_{2}^{2}+ D_{1}^{2}\cos ({\omega \tau _{2}}) + D_{0}^{2}\omega \sin ({ \omega \tau _{2}}))\cos ({\omega \tau _{1}}) \\ \qquad {} + (B_{1}^{2} \omega - D_{1}^{2} \sin ({\omega \tau _{2}}) +D_{0}^{2} \omega \cos ({\omega \tau _{2}})) \sin ({\omega \tau _{1}}), \\ \omega ^{3} - A_{2}^{2}\omega +(-C_{0}^{2}\omega ^{2} + C_{2}^{2}) \sin ({\omega \tau _{2}}) - C_{1}^{2}\omega \cos ({\omega \tau _{2}}) \\ \quad = -(- B_{0}^{2}\omega ^{2}+B_{2}^{2} + D_{1}^{2}\cos ({\omega \tau _{2}}) + D_{0}^{2}\omega \sin ({\omega \tau _{2}}))\sin ({\omega \tau _{1}}) \\ \qquad {} + (B_{1}^{2} \omega - D_{1}^{2}\sin ({\omega \tau _{2}}) +D_{0}^{2} \omega \cos ({\omega \tau _{2}})) \cos ({\omega \tau _{1}}). \end{cases} $$

(42)

By adding the squares of two equations in (42), we obtain

$$ \omega ^{6} + \bar{l}_{1}(\omega )\omega ^{5} + \bar{l}_{2}(\omega ) \omega ^{4} + \bar{l}_{3}(\omega )\omega ^{3} + \bar{l}_{4}(\omega ) \omega ^{2} + \bar{l}_{5}(\omega )\omega + \bar{l}_{6}(\omega )=0, $$

(43)

where $\bar{l}_{1}(\omega ) = -2C_{0}^{2}\sin ({\omega \tau _{2}})$; $\bar{l}_{2}(\omega ) = (A_{1}^{2})^{2} - 2A_{2}^{2} + (C_{0}^{2})^{2} - (B_{0}^{2})^{2} + 2(A_{1}^{2}C_{0}^{2} - C_{1}^{2})\cos ({\omega \tau _{2}})$; $\bar{l}_{3}(\omega ) = 2(C_{2}^{2} + A_{2}^{2}C_{0}^{2} -A_{1}^{2}C_{1}^{2} + B_{0}^{2}D_{0}^{2})\sin ({\omega \tau _{2}})$; $\bar{l}_{4}(\omega ) = (A_{2}^{2})^{2} + (C_{1}^{2})^{2} + 2B_{0}^{2}B_{2}^{2} - 2A_{1}^{2}A_{3}^{2} - 2C_{0}^{2}C_{2}^{2} - (B_{1}^{2})^{2} - (D_{0}^{2})^{2} - 2(A_{1}^{2}C_{2}^{2} - A_{2}^{2}C_{1}^{2} +A_{3}^{2}C_{0}^{2} + B_{1}^{2}D_{0}^{2} - B_{0}^{2}D_{1}^{2})\cos ({\omega \tau _{2}})$; $\bar{l}_{5}(\omega ) = 2(A_{3}^{2}C_{1}^{2} -A_{2}^{2}C_{2}^{2} -B_{2}^{2}D_{0}^{2} + B_{1}^{2}D_{1}^{2})\sin ({\omega \tau _{2}})$; and $\bar{l}_{6}(\omega ) = (C_{2}^{2})^{2} + (A_{3}^{2})^{2} - (B_{2}^{2})^{2} - (D_{1}^{2})^{2} + ( 2A_{3}^{2}C_{2}^{2} -2B_{2}^{2}D_{1}^{2})\cos ({ \omega \tau _{2}})$. Let

$$ G_{2}(\omega )=\omega ^{6} + \bar{l}_{1}(\omega )\omega ^{5} + \bar{l}_{2}( \omega ) \omega ^{4} + \bar{l}_{3}(\omega )\omega ^{3} + \bar{l}_{4}( \omega )\omega ^{2} + \bar{l}_{5}(\omega )\omega + \bar{l}_{6}(\omega ). $$

(44)

Obviously, if $\bar{l}_{6}(0)<0$, then $G_{2}(0)<0$. In addition, $\lim_{\omega \to +\infty} G_{2}(\omega )=+\infty$. Hence, equation (43) has at least one positive root denoted by $\hat{\omega}_{1}$. Furthermore, substituting $\hat{\omega}_{1}$ into (43) and solving the resulting equations, we have

$$ \hat{\tau}_{1}^{k} = \frac{1}{\hat{\omega}_{1}} \biggl(\arccos \biggl[ \frac {M_{9}(\hat{\omega}_{1})M_{11}(\hat{\omega}_{1}) + M_{10}(\hat{\omega}_{1}) M_{12}(\hat{\omega}_{1})}{{M_{9}}^{2}(\hat{\omega}_{1}) +{M_{10}}^{2}(\hat{\omega}_{1})} \biggr] + 2k\pi \biggr),\quad k=0,1,\ldots , $$

where $M_{9}(\hat{\omega}_{1})=- B_{0}^{2}(\hat{\omega}_{1})^{2} + B_{2}^{2} + D_{1}^{2}\cos ({\hat{\omega}_{1} \tau _{2}}) + D_{0}^{2} \hat{\omega}_{1} \sin ({\hat{\omega}_{1} \tau _{2}})$; $M_{10}( \hat{\omega}_{1})= B_{1}^{2} \hat{\omega}_{1} - D_{1}^{2}\sin ({ \hat{\omega}_{1} \tau _{2}}) + D_{0}^{2} \hat{\omega}_{1} \cos ({ \hat{\omega}_{1} \tau _{2}})$; $M_{11}(\hat{\omega}_{1})= A_{1}^{2} ( \hat{\omega}_{1})^{2} - A_{3}^{2} -(-C_{0}^{2}(\hat{\omega}_{1})^{2} + C_{2}^{2})\cos ({\hat{\omega}_{1} \tau _{2}}) - C_{1}^{2}\hat{\omega}_{1} \sin ({\hat{\omega}_{1} \tau _{2}})$; and $M_{12}(\hat{\omega}_{1})=( \hat{\omega}_{1})^{3} - A_{2}^{2}\hat{\omega}_{1} +(-C_{0}^{2}( \hat{\omega}_{1})^{2} + C_{2}^{2})\sin ({\hat{\omega}_{1} \tau _{2}}) - C_{1}^{2}\hat{\omega}_{1} \cos ({\hat{\omega}_{1} \tau _{2}})$. Clearly,

$$ \lim_{k \to \infty} \hat{\tau}_{1}^{k} = \infty . $$

Thus, we can define

$$ \hat{\omega}^{0}_{1} =\arg \min \bigl\{ \hat{ \tau}^{0}_{1}\bigr\} . $$

(45)

Next, we consider the roots of equation (28) as a function of $\tau _{1}$ and the root $\tilde{\lambda}_{3}(\tau _{1})=\alpha _{3}( \tau _{1})+i\tilde{\omega}_{3}(\tau _{1})$ of equation (28) such that

$$ \alpha _{3}\bigl(\hat{\tau}_{1}^{0}\bigr)=0, \quad \text{and} \quad \tilde{\omega}_{3}\bigl( \hat{\tau}_{1}^{0} \bigr)=\hat{\omega}^{0}_{1}. $$

Substituting $\tilde{\lambda}_{3}(\tau _{1})$ into equation (28) and taking the derivative with respect to $\tau _{1}$, we have

$$\begin{aligned} & \biggl({\frac {d\tilde{\lambda}_{3}}{d\tau _{1}}} \biggr)^{-1} \\ & \quad =\frac{3(\tilde{\lambda }_{3})^{2} + 2A_{1}^{2}\tilde{\lambda }_{3} + A_{2}^{2} + (2C_{0}^{2}\tilde{\lambda }_{3} + C_{1}^{2})e^{-\tilde{\lambda }_{3} \tau _{2}} - \tau _{2} (C_{0}^{2}(\tilde{\lambda }_{3})^{2} + C_{1}^{2}\tilde{\lambda }_{3} + C_{2}^{2})e^{-\tilde{\lambda }_{3} \tau _{2}}}{-\tilde{\lambda }_{3} [(\tilde{\lambda }_{3})^{3} + A_{1}^{2}(\tilde{\lambda }_{3})^{2} + A_{2}^{2}\tilde{\lambda }_{3} + A_{3}^{2} + (C_{0}^{2}(\tilde{\lambda }_{3})^{2} + C_{1}^{2}\tilde{\lambda }_{3} + C_{2}^{2})e^{-\tilde{\lambda }_{3} \tau _{2}}]} \\ & \qquad {}+ \frac{2B_{0}^{2}\tilde{\lambda }_{3} + B_{1}^{2} + D_{0}^{2}e^{-\tilde{\lambda }_{3} \tau _{2}} - \tau _{2}(D_{0}^{2}\tilde{\lambda }_{3} + D_{1}^{2})e^{-\tilde{\lambda }_{3} \tau _{2}}}{\tilde{\lambda }_{3}[B_{0}^{2}(\tilde{\lambda }_{3})^{2} + B_{1}^{2}\tilde{\lambda }_{3} + B_{2}^{2} + (D_{0}^{2}\tilde{\lambda }_{3} + D_{1}^{2})e^{-\tilde{\lambda }_{3} \tau _{2}}]} - \frac{\tau _{1}}{\tilde{\lambda }_{3}}. \end{aligned}$$

Then,

$$ \begin{aligned} &\operatorname{Re} \biggl[ \biggl(\frac{d\tilde{\lambda }_{3}}{d\tau _{1}} \bigg|_{\tau _{1} = \hat{\tau}_{1}^{0}} \biggr)^{-1} \biggr] =\frac{(M_{3}^{2} N_{3}^{2} + S_{3}^{2} T_{3}^{2})[{(P_{3}^{2})}^{2} + {(O_{3}^{2})}^{2}] + (Q_{3}^{2} P_{3}^{2} + R_{3}^{2} O_{3}^{2})[{(N_{3}^{2})}^{2} + {(T_{3}^{2})}^{2}]}{[{(N_{3}^{2})}^{2} + {(T_{3}^{2})}^{2}][{(P_{3}^{2})}^{2} + {(O_{3}^{2})}^{2}]}, \end{aligned} $$

where $M_{3}^{2}= -3 (\hat{\omega}^{0}_{1})^{2} + A_{2}^{2} + 2C_{0}^{2} \hat{\omega}^{0}_{1}\sin (\hat{\omega}^{0}_{1} \tau _{2}) + C_{1}^{2} \cos (\hat{\omega}^{0}_{1} \tau _{2}) - \tau _{2}(-C_{0}^{2}( \hat{\omega}^{0}_{1})^{2} + C_{2}^{2})\cos (\hat{\omega}^{0}_{1} \tau _{2}) - \tau _{2} C_{1}^{2}\hat{\omega}^{0}_{1} \sin ( \hat{\omega}^{0}_{1} \tau _{2})$; $S_{3}^{2}= 2 A_{1}^{2}\hat{\omega}^{0}_{1} + 2C_{0}^{2}\hat{\omega}^{0}_{1} \cos (\hat{\omega}^{0}_{1} \tau _{2}) - C_{1}^{2}\sin (\hat{\omega}^{0}_{1} \tau _{2}) + \tau _{2}(-C_{0}^{2}(\hat{\omega}^{0}_{1})^{2} + C_{2}^{2}) \sin (\hat{\omega}^{0}_{1} \tau _{2}) - \tau _{2} C_{1}^{2} \hat{\omega}^{0}_{1} \cos (\hat{\omega}^{0}_{1} \tau _{2})$; $N_{3}^{2}= -(\hat{\omega}^{0}_{1})^{4} + A_{2}^{2}(\hat{\omega}^{0}_{1})^{2} + (C_{0}^{2}(\hat{\omega}^{0}_{1})^{3} - C_{2}^{2}\hat{\omega}^{0}_{1}) \sin (\hat{\omega}^{0}_{1} \tau _{2}) + C_{1}^{2}(\hat{\omega}^{0}_{1})^{2} \cos (\hat{\omega}^{0}_{1} \tau _{2})$; $T_{3}^{2}= A_{1}^{2}(\hat{\omega}^{0}_{1})^{3} - A_{3}^{2} \hat{\omega}^{0}_{1} + (C_{0}^{2}(\hat{\omega}^{0}_{1})^{3} - C_{2}^{2}\hat{\omega}^{0}_{1})\cos (\hat{\omega}^{0}_{1} \tau _{2}) - C_{1}^{2}(\hat{\omega}^{0}_{1})^{2}\sin (\hat{\omega}^{0}_{1} \tau _{2})$; $Q_{3}^{2}= B_{1}^{2} + D_{0}^{2}\cos (\hat{\omega}^{0}_{1} \tau _{2}) -\tau _{2}D_{0}^{2}\hat{\omega}^{0}_{1} \sin (\hat{\omega}^{0}_{1} \tau _{2})- \tau _{2}D_{1}^{2}\cos (\hat{\omega}^{0}_{1} \tau _{2})$; $R_{3}^{2}= 2B_{0}^{2}\hat{\omega}^{0}_{1} - D_{0}^{2}\sin ( \hat{\omega}^{0}_{1} \tau _{2})- \tau _{2}D_{0}^{2}\hat{\omega}^{0}_{1} \cos (\hat{\omega}^{0}_{1} \tau _{2}) + \tau _{2}D_{1}^{2} \sin (\hat{\omega}^{0}_{1} \tau _{2})$; $P_{3}^{2} = - B_{1}^{2}(\hat{\omega}^{0}_{1})^{2} - D_{0}^{2}( \hat{\omega}^{0}_{1})^{2} \cos (\hat{\omega}^{0}_{1} \tau _{2})+ D_{1}^{2} \hat{\omega}^{0}_{1}\sin (\hat{\omega}^{0}_{1} \tau _{2})$; and $O_{3}^{2} = -B_{0}^{2}(\hat{\omega}^{0}_{1})^{3} + B_{2}^{2} \hat{\omega}^{0}_{1}+ D_{0}^{2}(\hat{\omega}^{0}_{1})^{2} \sin ( \hat{\omega}^{0}_{1} \tau _{2})+ D_{1}^{2}\hat{\omega}^{0}_{1}\cos ( \hat{\omega}^{0}_{1} \tau _{2})$. Furthermore, if condition

$$ {\bigl(M_{3}^{2} N_{3}^{2} + S_{3}^{2} T_{3}^{2}\bigr)\bigl[{ \bigl(P_{3}^{2}\bigr)}^{2} + {\bigl(O_{3}^{2} \bigr)}^{2}\bigr] + \bigl(Q_{3}^{2} P_{3}^{2} + R_{3}^{2} O_{3}^{2}\bigr)\bigl[{\bigl(N_{3}^{2} \bigr)}^{2} + {\bigl(T_{3}^{2}\bigr)}^{2} \bigr]} \neq 0 $$

(46)

is satisfied, then

$$ \operatorname{Re} \biggl[ \biggl( \frac{d\tilde{\lambda }_{3}}{d\tau _{1}} \bigg|_{\tau _{1} = \hat{\tau}_{1}^{0}} \biggr)^{-1} \biggr] \neq 0. $$

Thus, by the Hopf bifurcation theory [31], we can obtain the following theorem:

Theorem 9

Suppose that $\tau _{1} > 0$, and $\tau _{2} \in (0,\bar{\tau}_{2}^{0})$ with $\bar{\tau}^{0}_{2}$ as defined in Case 3.3.2. If equation (43) has positive roots and condition (46) is met, then

(i) when $\tau _{1} \in (0,\hat{\tau}_{1}^{0})$, $E_{1}$ is locally asymptotically stable;

(ii) when $\tau _{1}>\hat{\tau}_{1}^{0}$, $E_{1}$ is unstable;

(iii) when $\tau _{1}=\hat{\tau}_{1}^{0}$, system (1) has a Hopf bifurcation at $E_{1}$.

4 Delay optimal control problem

In this section, we will consider the delay optimal control problem in the COVID-19 epidemic and will derive the corresponding necessary optimality conditions.

The outbreak of the COVID-19 epidemic can be controlled by two interventions: (i) reduction and suppression of social contact through masking, home isolation, etc. and (ii) pharmacological interventions, leading to the use of novel treatments that minimize mortality and shorten hospital stays. Let $u_{1}(t)$ and $u_{2}(t)$ be the social contact and the pharmaceutical intervention, respectively. Then, the controlled SEIR model in the COVID-19 virus transmission can be formulated as:

$$\begin{aligned} \textstyle\begin{cases} \dot{S}(t) = \Lambda - \frac{\beta _{1}(1-u_{1}(t)) S(t)E(t)}{N(t)} - \frac{\beta _{2}(1-u_{1}(t)) S(t)I(t)}{N(t)} -dS(t) , \\ \dot{E}(t) = \frac{\beta _{1} (1-u_{1}(t)) S(t)E(t)}{N(t)} + \frac{\beta _{2} (1-u_{1}(t))S(t) I(t)}{N(t)} - \varepsilon E(t-\tau _{1}) \\ \hphantom{\dot{E}(t) =}{} - (\gamma _{2}+d) E(t), & t\in [0,T], \\ \dot{I}(t) = \varepsilon E(t-\tau _{1}) - \gamma _{1}(1+u_{2}(t)) I(t- \tau _{2})- (\mu +d) I(t) , \\ \dot{R}(t) = \gamma _{1} (1+u_{2}(t)) I(t-\tau _{2}) + \gamma _{2} E(t) - dR(t), \end{cases}\displaystyle \end{aligned}$$

(47)

where $T>0$ is a given terminal time. It should be noted that the suppression of social contacts is generally costly, and it will result in economy recession. Pharmacological intervention is also expensive because it requires extensive clinical trials prior to experimental treatment. Therefore, we assume that

$$ 0\leq u_{i}(t)\leq u_{i}^{\max},\quad i=1,2, t\geq 0, $$

(48)

where $u_{i}^{\max}$ (≤1), $i=1,2$, are the upper bounds for controls $u_{i}(t)$. Let $\mathcal{U}$ be the set of all Borel measurable functions $u_{i}: [0,T]\rightarrow \mathbb{R}$, $i=1,2$, satisfying constraint (48).

Let $x(t)= (S(t), E(t), I(t), R(t))^{\top}$, $u(t)=(u_{1}(t), u_{2}(t))^{\top}$, and the right-hand side of system (47) be $\tilde{f}(x(t),x(t-\tau _{1}),x(t-\tau _{2}),u(t))$. Then, system (47) with the condition (2) in a finite time horizon $[-\tau ,T]$ can be rewritten as

$$ \textstyle\begin{cases} \dot{x}(t)=\tilde{f}(x(t),x(t-\tau _{1}),x(t-\tau _{2}),u(t)), & t \in [0,T], \\ x(t)=\varphi (t), &t\in [-\tau ,0], \end{cases} $$

(49)

where $\varphi (t)=(\varphi _{1}(t),\varphi _{2}(t),\varphi _{3}(t), \varphi _{4}(t))^{\top}$ is the initial condition.

During the COVID-19 spread, social contacts can be mitigated and suppressed by non-pharmacological interventions, such as wearing masks, maintaining social distancing, testing and isolation, and closing businesses, while the length of hospital stay can be minimized by pharmacological interventions and using new treatment modalities. Thus, using both non-pharmacological and pharmacological interventions as the control strategies, our goal is to maximize the number of recovered individuals at the terminal time, as well as to minimize the number of exposed and infected individuals during the time horizon, and the system cost of control measures. Therefore, the cost function in controlling the COVID-19 epidemic can be stated as

$$ J(u)= - q_{1}x_{4}(T) + \frac{1}{2} \int _{0}^{T} \bigl[ {q_{2}} x_{2}^{2}(t)+q_{3}x_{3}^{2}(t)+r_{1} u_{1}^{2}(t)+r_{2}u_{2}^{2}(t) \bigr]\,dt, $$

(50)

where $q_{i}>0$, $i = 1,2,3$, $r_{1}>0$ and $r_{2}>0$ are weighting coefficients. As a result, we propose the following delay optimal control problem:

$$ \begin{aligned} \text{(DOCP)} \quad\min&\quad J(u) \\ \text{s.t.}&\quad \textstyle\begin{cases} \dot{x}(t)=\tilde{f}(x(t),x(t-\tau _{1}),x(t-\tau _{2}),u(t)), & t \in [0,T], \\ x(t)=\varphi (t), &t\in [-\tau ,0], \end{cases}\displaystyle \\ &\quad u\in \mathcal{U} . \end{aligned} $$

To solve Problem (DOCP), we establish the following necessary optimality conditions.

Theorem 10

Let $u^{*} \in \mathcal{U}$ be the optimal control of Problem (DOCP), and let $x^{*}=x(\cdot |u^{*})$ be the corresponding solution of system (49). Then, there exists a costate vector $\lambda ^{*}(t)=(\lambda _{1}^{*}(t),\lambda _{2}^{*}(t),\ldots , \lambda _{4}^{*}(t))^{\top}$ satisfying

$$ \textstyle\begin{cases} \dot{\lambda}_{1}^{*}(t) = {\lambda _{1}^{*}}(t)(W_{1} + W_{2} + d ) - {\lambda _{2}^{*}}(t) (W_{1} + W_{2} ), \\ \dot{\lambda}_{2}^{*}(t)= - q_{2} x_{2}^{*}(t) + {\lambda _{1}^{*}}(t) ( W_{3} - W_{5} ) - {\lambda _{2}^{*}}(t) (W_{3} - W_{5} - \gamma _{2} - d ) \\ \hphantom{\dot{\lambda}_{2}^{*}(t)=}{}+ {\lambda _{2}^{*}}(t+\tau _{1}) \varepsilon -{\lambda _{3}^{*}}(t+ \tau _{1}) \varepsilon - \lambda _{4}^{*} \gamma _{2}, & t\in [0,T], \\ \dot{\lambda}_{3}^{*}(t)= - q_{3} x_{3}^{*}(t) + {\lambda _{1}^{*}}(t) ( W_{4}-W_{6}) - {\lambda _{2}^{*}}(t)(W_{4} -W_{6}) \\ \hphantom{\dot{\lambda}_{3}^{*}(t)=}{} + {\lambda _{3}^{*}}(t+\tau _{2}) \gamma _{1}(1+ {u}_{2}^{*}(t)) + { \lambda _{3}^{*}}(t) (\mu + d) -{\lambda _{4}^{*}}(t+\tau _{2}) \gamma _{1} (1+{u}_{2}^{*}(t)), \\ \dot{\lambda}_{4}^{*}(t)= - \lambda _{1}^{*}(W_{5} + W_{6}) + \lambda _{2}^{*}(W_{5} + W_{6}) + \lambda _{4}^{*} d,\end{cases} $$

with the conditions

$$\begin{aligned}& \lambda (T) =(0,0,0,-q_{1})^{\top}, \\& \lambda (t) =(0,0,0,0)^{\top}, \quad t>T, \end{aligned}$$

where $\bar{x}^{*}(t)=x_{1}^{*}(t) + x_{2}^{*}(t) + x_{3}^{*}(t) + x_{4}^{*}(t)$; $W_{1} =\frac{\beta _{1} x_{2}^{*}(t)(1-{u}_{1}^{*}(t))(\bar{x}^{*}(t)-x_{1}^{*}(t))}{(\bar{x}^{*}(t))^{2}}$; $W_{2} = \frac{\beta _{2} x_{3}^{*}(t)(1-{u}_{1}^{*}(t))(\bar{x}^{*}(t) - x_{1}^{*}(t))}{(\bar{x}^{*}(t))^{2}}$; $W_{3} =\frac{\beta _{1} x_{1}^{*}(t) (1-{u}_{1}^{*}(t))(\bar{x}^{*}(t) - x_{2}^{*}(t))}{(\bar{x}^{*}(t))^{2}}$; $W_{4} =\frac{\beta _{2} x_{1}^{*}(t)(1-{u}_{1}^{*}(t))(\bar{x}^{*}(t)-x_{3}^{*}(t))}{(\bar{x}^{*}(t))^{2}}$; $W_{5} =\frac{\beta _{2} (1-{u}_{1}^{*}(t)) x_{1}^{*}(t) x_{3}^{*}(t)}{(\bar{x}^{*}(t))^{2}}$; and $W_{6} =\frac{\beta _{1} (1-{u}_{1}^{*}(t)) x_{1}^{*}(t) x_{2}^{*}(t)}{(\bar{x}^{*}(t))^{2}}$. Furthermore, the optimal control $u^{*}$ can be expressed as

$$ \textstyle\begin{cases} {u^{*}_{1}}(t) = \min (\max (\frac{(\lambda ^{*}_{2}(t)-\lambda ^{*}_{1}(t))( x_{1}^{*}(t) x_{2}^{*}(t) + x_{1}^{*}(t) x_{3}^{*}(t))}{\bar{x}^{*}(t) r_{1}},0 ),u_{1}^{\max} ), \\ {u^{*}_{2}}(t) = \min (\max (\frac{(\lambda ^{*}_{3}(t)-\lambda ^{*}_{4}(t)) x_{3}^{*}(t-\tau _{2})}{r_{2}},0 ),u_{2}^{\max} ). \end{cases} $$

Proof

Using proof similar to Theorem 1 in [34], we can complete the proof. □

5 Numerical simulations

In this section, we will carry out some numerical simulations to verify the stability and the Hopf bifurcation of equilibrium points in Sect. 3. Moreover, Problem (DOCP) will be solved based on the derived necessary optimality conditions in Sect. 4.

5.1 Numerical simulations of stability and Hopf bifurcation

In numerical simulations, two sets of parameter values for system (1) are chosen (Table 1). In addition, the initial condition is chosen as $\varphi (t)=(99999, 1, 0, 0)^{\top}$ for $t \in [-\tau ,0]$. For the first set of parameter values (i.e., the second row in Table 1), we obtain $R_{0}=0.7037(<1)$. In this case, system (1) has a unique disease-free equilibrium point $E_{0}=(30,0,0,0)$. For $\tau _{1}=\tau _{2}=0$, we have $a_{0}^{1}= 1$, $a_{1}^{1}=1.65$, $a_{2}^{1}=0.32$ and $a_{3}^{1}=0$. Obviously, $a_{1}^{1} a_{2}^{1} > a_{0}^{1} a_{3}^{1}$ and $E_{0}$ is locally stable from Theorem 2 (Fig. 2). For $\tau _{1}=0$ and $\tau _{2}>0$, we obtain $\omega _{2}^{0}=0.3820$ and $\tau _{2}^{0}=3.8658$. As shown in Theorem 3, $E_{0}$ is asymptotically stable when $\tau _{2} \in (0,3.8658)$, and the Hopf bifurcation occurs when $\tau _{2}=3.8658$, which are illustrated in Figs. 3 and 4. For $\tau _{1}>0$ and $\tau _{2}=0$, we obtain $\omega _{1}^{0}=0.9840$ and $\tau _{1}^{0}=1.4683$. The corresponding asymptotic stability and the Hopf bifurcation of $E_{0}$ are shown in Figs. 5 and 6. For $\tau _{1}>0$ and $\tau _{2}=2 \in (0,3.8658)$, we get $\tilde{\omega}_{1}^{0}=1.2902$ and $\tilde{\tau}_{1}^{0}=1.2340$. The corresponding asymptotic stability and the Hopf bifurcation of $E_{0}$ are plotted in Figs. 7 and 8.

Figure 2

When $\tau _{1}=\tau _{2}=0$, $E_{0}$ is asymptotically stable

Figure 3

When $\tau _{1}=0$, $E_{0}$ is asymptotically stable for $\tau _{2}=2.5<\tau _{2}^{0}=3.8658$

Figure 4

When $\tau _{1}=0$, $E_{0}$ is unstable for $\tau _{2}=3.87>\tau _{2}^{0}=3.8658$

Figure 5

When $\tau _{2}=0$, $E_{0}$ is asymptotically stable for $\tau _{1}=0.9<\tau _{1}^{0}=1.4683$

Figure 6

When $\tau _{2}=0$, $E_{0}$ is unstable for $\tau _{1}=1.4684>\tau _{1}^{0}=1.4683$

Figure 7

When $\tau _{2}=2$, $E_{0}$ is asymptotically stable for $\tau _{1}=0.5<\tilde{\tau}_{1}^{0}=1.2340$

Figure 8

When $\tau _{2}=2$, $E_{0}$ is unstable for $\tau _{1}=1.235>\tau _{1}^{0}=1.2340$

Table 1 Two sets parameter values in the simulations

For the second set of parameter values (i.e., the third row in Table 1), we obtain $R_{0}=1.1746(>1)$. In this case, system (1) has a unique endemic equilibrium point $E_{1}=(8.5135, 0.0787, 0.0708, 0.7236)$. For $\tau _{1}=\tau _{2}=0$, we have $a_{0}^{2}=1$, $a_{1}^{2}=1.16365$, $a_{2}^{2}=0.4634$ and $a_{3}^{2}=0.0047$. Obviously, $a_{1}^{2} a_{2}^{2} > a_{0}^{2} a_{3}^{2}$ and $E_{1}$ is asymptotically stable from Theorem 6 (Fig. 9). For $\tau _{1}=0$, $\tau _{2}>0$, we get $\bar{\omega}_{2}^{0}=0.2881$ and $\bar{\tau}_{2}^{0}=4.1563$. Using Theorem 7, we conclude that $E_{1}$ is asymptotically stable when $\tau _{2} \in (0,4.1563)$ and that the Hopf bifurcation occurs when $\tau _{2}=4.1563$ (Figs. 10 and 11). For $\tau _{1}>0$ and $\tau _{2}=0$, we obtain $\bar{\omega}_{1}^{0}=1.0086$ and $\bar{\tau}_{1}^{0}=1.2326$. The corresponding asymptotic stability and the Hopf bifurcation are plotted in Figs. 12 and 13. For $\tau _{1}>0$ and $\tau _{2}=3.5 \in (0,4.1563)$, we obtain $\hat{\omega}_{1}^{0}=1.8961$ and $\hat{\tau}_{1}^{0}=0.5437$. The corresponding asymptotic stability and the Hopf bifurcation are shown in Figs. 14 and 15.

Figure 9

When $\tau _{1}=\tau _{2}=0$, $E_{1}$ is asymptotically stable

Figure 10

When $\tau _{1}=0$, $E_{1}$ is asymptotically stable for $\tau _{2}=3.1<\bar{\tau}_{2}^{0}=4.1563$

Figure 11

When $\tau _{1}=0$, $E_{1}$ is unstable for $\tau _{2}=4.16>\bar{\tau}_{2}^{0}=4.1563$

Figure 12

When $\tau _{2}=0$, $E_{1}$ is asymptotically stable for $\tau _{1}=1.1<\bar{\tau}_{1}^{0}=1.2326$

Figure 13

When $\tau _{2}=0$, $E_{1}$ is unstable for $\tau _{1}=1.24>\bar{\tau}_{1}^{0}=1.2326$

Figure 14

When $\tau _{2}=3.5$, $E_{1}$ is asymptotically stable for $\tau _{1}=0.05<\hat{\tau}_{1}^{0}=0.5437$

Figure 15

When $\tau _{2}=3.5$, $E_{1}$ is unstable for $\tau _{1}=0.55>\hat{\tau}_{1}^{0}=0.5437$

5.2 Numerical results of optimal control problem

In this section, we will present numerical results for solving Problem (DOCP). Here, the delayed SEIR system (49) was solved using software package DDE23 in Matlab with delay arguments $\tau _{1}=0.5$ and $\tau _{2}=0.7$ and the initial condition $\varphi (t) = (99999, 1, 0, 0)^{\top}$ [14]. The weight coefficients in the cost functional (50) are chosen as $q_{1} = 10^{-8}$, $q_{2} = q_{3} = 10^{-4}$, $r_{1} = 50$ and $r_{2} = 1$ [14]. In addition, we choose two sets of parameter values listed in Table 1 for calculating the optimal control strategies. As for the control boundaries, we assume that $u^{\max}_{1} = 0.07$ and $u^{\max}_{2} = 0.1$. Note that Problem (DOCP) was solved using forward-backward sweep method [35] in conjunction with the necessary optimality conditions in Theorem 10.

To explore the effects of each control means, we set up the following control scheme.

(i) Strategy A: Social contact only ($u_{1}$).

(ii) Strategy B: Pharmaceutical intervention only ($u_{2}$).

(iii) Strategy C: Social contact + Pharmaceutical intervention ($u_{1}$, $u_{2}$).

For the first set of parameters (i.e., the second row in Table 1), we solve Problem (DOCP) and obtain the optimal control strategies $u_{1}^{*}$ and $u^{*}_{2}$ shown in Fig. 16. The state trajectories corresponding to different control strategies, i.e., $u_{1}=u_{2}=0$, $u_{1}=u_{1}^{*}$ and $u_{2}=0$, $u_{1}=0$ and $u_{2}=u_{2}^{*}$, and $u_{1}=u_{1}^{*}$ and $u_{2}=u_{2}^{*}$, are plotted in Fig. 17. Similarly, for the second set of parameters (i.e., the third row in Table 1), we also solve Problem (DOCP) and obtain the optimal control strategies $\bar{u}^{*}_{1}$ and $\bar{u}_{2}^{*}$ depicted in Fig. 18. The state trajectories corresponding to different control strategies, i.e., $u_{1}=u_{2}=0$, $u_{1}=\bar{u}_{1}^{*}$ and $u_{2}=0$, $u_{1}=0$ and $u_{2}=\bar{u}_{2}^{*}$, and $u_{1}=\bar{u}_{1}^{*}$ and $u_{2}=\bar{u}_{2}^{*}$, are plotted in Fig. 19.

Figure 16

The optimal control strategies under the first set of parameter values

Figure 17

State trajectories with different control strategies under the first set of parameter values

Figure 18

The optimal control strategies under the second set of parameter values

Figure 19

State trajectories with different control strategies under the second set of parameter values

From Figs. 16 and 18, we can see that, for the social contact $u_{1}$, it begins with the maximal value of 0.07, keeps the maximal value for a period of time, and then decreases to zero. This is mainly because, in the case of a sudden outbreak of COVID-19, quarantine measures are effective in stopping the spread of the disease by cutting off the route of transmission in the real world. As for the pharmacological intervention $u_{2}$, since the pharmacological intervention for the infected individuals is not immediately administered, it starts from the minimal value of zero, rapidly increases to the maximal value of 0.1, maintains at this maximal value for a period of time, and ultimately reduces to zero.

From Figs. 17(b), 17(c), 19(b), and 19(c), it can be seen that the number of exposed and infected individuals under no control is the highest, while the lowest number of exposed and infected individuals is under strategy C. Moreover, the implementation of $u_{1}$ can decrease the number of both exposed and infectious individuals, while the implementation of $u_{2}$ is particularly effective in reducing the number of infected individuals. Nevertheless, relying solely on one control measure (strategies A and B) or not implementing any control measures at all is less effective than the optimal control strategy C.

For strategy C, we also solved the optimal control problem without delay. The computed optimal control strategies under two sets of parameter values are also illustrated in Figs. 16 and 18, respectively. Under the optimal control strategies in Figs. 16 and 18, the corresponding optimal state trajectories are depicted in Figs. 20 and 21. From Figs. 20 and 21, we observe that the peaks of infected individuals for the cases with $\tau _{1}=0.5$ and $\tau _{2}=0.7$ are higher than those without delay. This implies that time delays could aggravate the transmission of COVID-19. As a result, to minimize the number of infections, effective control strategies should be implemented as soon as possible.

Figure 20

Optimal state trajectories under the first set of parameter values

Figure 21

Optimal state trajectories under the second set of parameter values

6 Conclusion

In this paper, we have studied the dynamics analysis and optimal control of the delayed SEIR model in the COVID-19 epidemic. Two delays representing the incubation and recovery periods in COVID-19 virus transmission have been introduced. A key issue with delays describing the incubation and recovery periods is whether they cause sustained oscillations. This was investigated through Hopf bifurcation analysis. By using the characteristic equations of delay differential equations, the existence of Hopf bifurcations at the disease-free and endemic equilibrium points was established. It has been shown that under some conditions, delays representing the incubation and recovery periods may destabilize the disease-free and endemic equilibrium points and cause the population to fluctuate. From Theorems 3, 4, 5, 7, 8, and 9, we see that thresholds for two delays were identified to characterize the existence of Hopf bifurcations at the disease-free and endemic equilibrium points. In addition, two controls representing the social contact and pharmaceutical intervention have also been introduced. The delay optimal control problem was formulated, and its necessary optimality conditions were exploited to solve the optimal controls. Numerical simulation results indicate that the pharmacological intervention was more effective for hospitalized patients, whereas suppression of social contact reduced the number of exposed individuals. More importantly, the obtained optimal strategies are effective in preventing and controlling the spread of COVID-19 infection.

We note that the effect of vaccination is ignored in systems (1) and (47). Vaccination has played a major role in preventing the spread of COVID-19 [36–38]. Moreover, the fractional derivative can be regarded as the generalization of the traditional integer derivative, which shows many important properties that the integer derivative does not have [39–44]. Many scholars have applied fractional derivative differential equations to study the spread of COVID-19 [45–47]. As a result, it is worthwhile to investigate the fractional optimal control of the COVID-19 epidemic by incorporating vaccination. This will be left for future research work.