Abstract
In this paper, we study the generalized multiple-set split feasibility problem including the common fixed-point problem for a finite family of generalized demimetric mappings and the monotone inclusion problem in 2-uniformly convex and uniformly smooth Banach spaces. We propose an inertial Halpern-type iterative algorithm for obtaining a solution of the problem and derive a strong convergence theorem for the algorithm. Then, we apply our convergence results to the convex minimization problem, the variational inequality problem, the multiple-set split feasibility problem and the split common null-point problem in Banach spaces.
Similar content being viewed by others
1 Introduction
Let E be a real Banach space with a dual space \(E^{*}\). We consider the monotone inclusion problem, which involves a single-valued monotone operator \(A: E \to E^{*}\) and a multivalued monotone operator \(B: E \to 2^{E^{*}}\). The problem aims to find a solution \(x^{*} \in E\) such that \(0 \in (A+B)x^{*}\). The set of solutions to this problem is denoted by \((A + B)^{-1}0\). This problem has practical applications in various fields such as image recovery, signal processing, and machine learning. It also encompasses several mathematical problems as special cases, including variational inequalities, split feasibility problems, minimization problems, and Nash equilibrium problems in noncooperative games, see, for instance, [1–4] and the references therein. The forward–backward splitting algorithm, introduced in [1, 2], is a well-known method for approximating solutions to the monotone inclusion problem. In this method, defined in a Hilbert space \(\mathcal{H}\), we start with an initial iterate \(x_{1} \in \mathcal{H}\) and update subsequent iterates as follows:
where \(n \geq 1\) and λ is a step-size parameter. Over the past few decades, the convergence properties and modified versions of the forward–backward splitting algorithm have been extensively studied in the literature. In [5] (see also [6]), Takahashi et al. introduced and analyzed a Halpern-type modification of the forward–backward splitting algorithm in real Hilbert spaces. They established the strong convergence of the sequence generated by their algorithm to a solution of the monotone inclusion problem. In 2019, Kimura and Nakajo [7] proposed a modified forward–backward splitting method and proved a strong convergence theorem for solutions of the monotone inclusion problem in a real 2-uniformly convex and uniformly smooth Banach space. Their convergence result is as follows:
Theorem 1.1
Let C be a nonempty, closed, and convex subset of a real 2-uniformly convex and uniformly smooth Banach space E. Let \(A: C\to E^{*}\) be an α-inverse strongly monotone and \(B: E\to 2^{ E^{*}}\) be a maximal monotone. Suppose that \(\Omega = (A+B)^{-1}0 \neq \emptyset \). Let \(\{x_{n}\}\) be a sequence generated by \(x_{0}\in C\), \(u\in E\) and by:
where \(\Pi _{C}\) is the generalized projection of E onto C, \(J_{\lambda _{n}}^{B}\) is the resolvent of B, \(J_{E}\) is the normalized duality mapping of E, \(\{\lambda _{n}\} \subset (0,\infty )\) and \(\{\gamma _{n}\} \subset (0,1)\) such that \(\lim_{n\to \infty}\gamma _{n}=0\) and \(\sum_{n=1}^{\infty}\gamma _{n}=\infty \). Then, if \(0<\inf_{n\in \mathbb{N}}\lambda _{n}\leq \sup_{n\in \mathbb{N}} \lambda _{n}< 2\alpha c\), (where c is the constant in Lemma 2.2), the sequence \(\{x_{n}\}\) converges strongly to \(\Pi _{\Omega}u\).
The inertial technique has gained significant interest among researchers due to its favorable convergence characteristics and the ability to improve algorithm performance. It was first considered in [8] for solving smooth, convex minimization problems. The key idea behind these methods is to utilize two previous iterates to update the next iterate, resulting in accelerated convergence. In [9], Lorenz and Pock proposed an inertial forward–backward splitting algorithm in real Hilbert spaces, formulated as follows:
where \(\theta _{n} \in [0, 1)\) is an extrapolation factor, \(\lambda _{n}\) is a step-size parameter, and \(\mathcal{H}\) represents the Hilbert space. They proved that the sequence \({x_{n}}\) generated by this algorithm converges weakly to a zero of \(A+B\).
In addition to the monotone inclusion problem, we consider the fixed-point problem for a nonlinear mapping \(U: E \to E\). A point \(x \in E\) such that \(Ux = x\) is called a fixed point of U. The set of fixed points of the nonlinear mapping U is denoted by \(\operatorname{Fix}(U)\).
Let E and F be Banach spaces and \(T:E\to F\) be a bounded linear operator. Let \(\{C_{i}\}_{i=1}^{p}\) be a family of nonempty, closed, and convex subsets in E and \(\{Q_{j}\}_{j=1}^{r}\) be a family of nonempty, closed, and convex subsets in F. The multiple-set split feasibility problem (MSSFP) is formulated as finding a point \(x^{\star}\) with the property:
The multiple-set split feasibility problem with \(p=r=1\) is known as the split feasibility problem (SFP). The MSSFP was first introduced by Censor et al. [10] in the framework of Hilbert spaces for modeling inverse problems that arise from phase retrievals and medical image reconstruction. Such models were successfully developed, for instance, in radiation-therapy treatment planning, sensor networks, resolution enhancement, and so on [11, 12]. Initiated by SFP, several split-type problems have been investigated and studied. For example, the split common fixed-point problem [13], the split monotone variational inclusions problem [14], and the split common null-point problem [15]. Algorithms for solving these problems have received great attention, (see, e.g., [16–31] and some of the references therein).
In 2018, Kawasaki and Takahashi [32], introduced a new general class of mappings, called generalized demimetric mappings as follows:
Definition 1.2
Let E be a smooth, strictly convex, and reflexive Banach space. Let ζ be a real number with \(\zeta \neq 0\). A mapping \(U:E\to E\) with \(\operatorname{Fix}(U)\neq \emptyset \) is called generalized demimetric, if
for all \(x\in E\) and \(x^{\star}\in \operatorname{Fix}(U)\). This mapping U is called ζ-generalized demimetric.
Such a class of mappings is fundamental because it includes many types of nonlinear mappings arising in applied mathematics and optimization, see [32–34] for details.
In this paper, we study the following generalized multiple-set split feasibility problem: let E be a 2-uniformly convex and uniformly smooth Banach space and let F be a smooth, strictly convex, and reflexive Banach space. Let for \(i=1,2,\ldots,m\), \(U_{i}: F\to F \) be a finite family of generalized demimetric mappings, \(A_{i}: E\to E^{*}\) be an inverse strongly monotone and \(B_{i}: E\to 2^{ E^{*}}\) be maximal monotone mappings. Let for each \(i=1,2,\ldots,m\), \(T_{i}: E\to F\) be a bounded linear operator such that \(T_{i}\neq 0\). Consider the following problem:
By combining the concepts and techniques from the inertial algorithm, forward–backward splitting algorithm, and the Halpern method, we introduce a new and efficient iterative method for solving the generalized multiple-set split feasibility problem. We establish strong convergence theorems for the proposed method under standard and mild conditions. The iterative scheme does not require prior knowledge of the operator norm. Finally, we apply our convergence results to the convex minimization problem, variational inequality problem, multiple-set split feasibility problem, and split common null-point problem in Banach spaces. The main results presented in this paper improve and generalize the previous results obtained by Kimura and Nakajo [7], Takahashi et al. [17] and others.
2 Preliminaries
Let E be a real Banach space with norm \(\|.\|\) and let \(E^{*}\) be the dual space of E. We denote the value of \(y^{*}\in E^{*}\) at \(x\in E\) by \(\langle x, y^{*}\rangle \). Let \(S(E) =\{x\in E: \|x\|=1\}\) denote the unit sphere of E. A Banach space E is said to be strictly convex if \(\|\frac{x+y}{2}\|<1\) for all \(x,y\in S(E)\) with \(x\neq y\). The Banach space E is said to be smooth provided
exists for each \(x,y\in S(E)\). The modulus of convexity of E is defined by
The space E is called uniformly convex if \(\delta _{E}(\epsilon )>0\) for any \(\epsilon \in (0,2]\), and 2-uniformly convex if there is a \(c>0\) so that \(\delta _{E}(\epsilon )\geq c\epsilon ^{2} \) for any \(\epsilon \in (0,2]\). We know that a uniformly convex Banach space is strictly convex and reflexive. The modulus of smoothness of E is defined by
The space E is called uniformly smooth if \(\lim_{\tau \rightarrow 0}\frac {\rho _{E}(\tau )}{\tau}=0\), and 2-uniformly smooth if there exists a \(C>0\) so that \(\rho _{E}(\tau )\leq C\tau ^{2}\) for any \(\tau >0\). It is observed that every 2-uniformly convex (2-uniformly smooth) space is a uniformly convex (uniformly smooth) space. It is known that E is 2-uniformly convex (2-uniformly smooth) if and only if its dual \(E^{*}\) is 2-uniformly smooth (2-uniformly convex). It is known that all Hilbert spaces and Lebesgue spaces \(L_{p}\) for \(1 < p \leq 2\) are uniformly smooth and 2-uniformly convex. See [35, 36] for more details.
The normalized duality mapping of E into \(2^{E^{*}}\) is defined by
for all \(x\in E\). The normalized duality mapping \(J_{E}\) has the following properties (see, e.g., [36]):
• if E is a smooth, strictly convex, and reflexive Banach space, then \(J_{E}\) is a single-valued bijection and in this case, the inverse mapping \(J_{E}^{-1}\) coincides with the duality mapping \(J_{E^{*}}\);
• if E is uniformly smooth, then \(J_{E}\) is uniformly norm-to-norm continuous on each bounded subset of E.
The following lemma was proved by Xu [37].
Lemma 2.1
Let E be a 2-uniformly smooth Banach space. Then, there exists a constant \(\gamma > 0\) such that for every \(x,y\in E\) there holds the following inequality:
Lemma 2.2
([37]) Let E be a smooth Banach space. Then, E is 2-uniformly convex if and only if there exists a constant \(c> 0\) such that for each \(x,y\in E\), \(\|x+ y\|^{2}\geq \|x\|^{2 }+2\langle y,J_{E}(x)\rangle + c\|y\|^{2}\) holds.
Lemma 2.3
([38]) If E is a 2-uniformly convex Banach space, then there exists a constant \(d > 0\) such that for all \(x,y\in E\),
Let E be a smooth Banach space. The function \(\phi : E\times E\to \mathbb{R}\) is defined by
Observe that, in Hilbert spaces, \(\phi (x,y)\) reduces to \(\|x-y\|^{2}\). It is obvious from the definition of function ϕ that
We also know that if E is strictly convex and smooth, then, for \(x,y\in E\), \(\phi (x,y)=0\) if and only if \(x = y\); see [39, 40]. We will use the following mapping \(V:E\times E^{\star} \to \mathbb{R}\) studied in [39]
for all \(x\in E\) and \(x^{*}\in E^{*}\). Obviously, \(V(x, x^{*}) =\phi (x,J_{E}^{-1}(x^{*}))\) for all \(x\in E\) and \(x^{*}\in E^{*}\).
Lemma 2.4
[39] Let E be a reflexive, strictly convex, and smooth Banach space with \(E^{*}\) as its dual. Then,
for all \(x\in E\) and \(x^{*},y^{*}\in E^{*}\).
Lemma 2.5
([41]) Let E be a uniformly convex and smooth real Banach space, and let \(\{x_{n}\}\) and \(\{y_{n}\}\) be two sequences of E. If either \(\{x_{n}\}\) or \(\{y_{n}\}\) is bounded and \(\lim_{n\to \infty}\phi (x_{n},y_{n})=0\) then \(\lim_{n\to \infty}\|x_{n}-y_{n}\|=0\).
Let C be a nonempty, closed, and convex subset of a strictly convex, reflexive, and smooth Banach space E and let \(x\in E\). Then, there exists a unique element \(\overline{x}\in C\) such that
We denote x̅ by \(\Pi _{C}x\) and call \(\Pi _{C}\) the generalized projection of E onto C; see [39, 41]. We have the following well-known result [39, 41] for the generalized projection.
Lemma 2.6
Let C be a nonempty, convex subset of a smooth Banach space E, \(x\in E\) and \(\overline{x}\in C\). Then, \(\phi (\overline{x},x)=\inf_{y\in C}\phi (y,x)\) if and only if \(\langle \overline{x}-y,J_{E}x-J_{E}\overline{x}\rangle \geq 0\) for every \(y\in C\), or equivalently \(\phi (y,\overline{x})+\phi (\overline{x},x)\leq \phi (y,x)\) for all \(y\in C\).
Definition 2.7
Let E be a Banach space and \(T: E\to E\) be a nonlinear mapping with \(\operatorname{Fix}(T )\neq \emptyset \). Then, \(I-T\) is said to be demiclosed at zero if \(\{x_{n}\}\) is a sequence in E converges weakly to x and \((I-T)x_{n}\) converges strongly to zero, then \((I-T)x=0\).
Lemma 2.8
([32]) Let E be a smooth, strictly convex, and reflexive Banach space and let ζ be a real number with \(\zeta \neq 0\). Let \(T:E\to E\) be a ζ-generalized demimetric mapping. Then, the fixed point set \(\operatorname{Fix}(T)\) of T is closed and convex.
Definition 2.9
An operator \(A:E\to E^{*}\) is called an inverse, strongly monotone operator, if there exist \(\alpha >0\) such that
In this case, we say that A is an α-inverse strongly monotone.
Let B be a mapping of E into \(2^{E^{*}}\). The effective domain of B is denoted by \(D(B)\), that is, \(D(B)=\{x\in E: Bx\neq \emptyset \}\). A multivalued mapping B on E is said to be monotone if \(\langle x-y,u-v\rangle \geq 0\) for all x, \(y\in D(B)\), \(u\in Bx\) and \(v\in By\). A monotone mapping B on E is said to be maximal if its graph is not properly contained in the graph of any other monotone mapping on E. The set of null points of B is denoted by \(B^{-1}0=\{x\in E: 0\in Bx\}\). Let E be a reflexive, strictly convex, and smooth real Banach space and let \(B: E\to 2^{E^{*}}\) be a maximal monotone operator. Then, for any \(\lambda >0\) and \(u\in E\), there exists a unique element \(u_{\lambda}\in D(B)\) such that \(J_{E}(u)\in J_{E}(u_{\lambda})+\lambda B(u_{\lambda})\). We define \(J_{\lambda}^{B}\) by \(J_{\lambda}^{B}u=u_{\lambda}\) for every \(u\in E\) and \(\lambda >0\) and such \(J_{\lambda}^{B}\) is called the resolvent of B. Alternatively, \(J_{\lambda}^{B}=(J_{E}+\lambda B)^{-1} J_{E}\). Let E be a uniformly convex and smooth Banach space and B be a maximal monotone operator. Then, \(B^{-1}0=\operatorname{Fix}(J_{\lambda}^{B})\) for all \(\lambda >0\). See [36, 42] for more details.
The lemma that follows is stated and proven in [[7], Lemma 3.1].
Lemma 2.10
Let E be a 2-uniformly convex and uniformly smooth real Banach space. Let \(A:E\to E^{*}\) be an α-inverse strongly monotone and \(B: E\to 2^{ E^{*}}\) be a maximal monotone. Let \(T_{\lambda} (x)=J_{\lambda}^{B}J_{E}^{-1}( J_{E}x-\lambda A x)\) for all \(\lambda >0\) and \(x\in E\). Then, the following hold:
(i) \(\operatorname{Fix}(T_{\lambda})=(A + B)^{-1}0\) and \((A + B)^{-1}0\) is closed and convex;
(ii) \(\phi (x^{*},T_{\lambda} (x))\leq \phi (x^{*},x)-(c-\lambda \beta ) \|x-T_{\lambda} (x)\|^{2} - \lambda ( 2\alpha -\frac{1}{\beta} )\|Ax-Ax^{*} \|^{2}\) for every \(\beta > 0\) and \(x^{*}\in (A + B)^{-1}0\), where c is the constant in Lemma 2.2.
The following lemmas are very helpful for the convergence analysis of the algorithm.
Lemma 2.11
([43]) Let \(\{\gamma _{n}\}\) be a sequence in (0,1) and \(\{\delta _{n}\}\) be a sequence in \(\mathbb{R}\) satisfying
-
(i)
\(\sum_{n=1}^{\infty}\gamma _{n}=\infty \);
-
(ii)
\(\limsup_{n\to \infty}\delta _{n}\leq 0\) or \(\sum_{n=1}^{\infty}|\gamma _{n}\delta _{n}|<\infty \).
If \(\{a_{n}\}\) is a sequence of nonnegative real numbers such that
for each \(n\geq 0\), then \(\lim_{n\to \infty}a_{n}=0\).
Lemma 2.12
([44]) Let \(\{s_{n}\}\) be a sequence of real numbers that does not decrease at infinity, in the sense that there exists a subsequence \(\{s_{n_{i}}\}\) of \(\{s_{n}\}\) such that \(s_{n_{i}}\leq s_{n_{i}+1}\) for all \(i\geq 0\). For every \(n\in \mathbb{N}\), (sufficiently large) define an integer sequence \(\{\tau (n)\}\) as
Then, \(\tau (n)\to \infty \) as \(n\to \infty \) and
3 Main results
We first prove the following lemma.
Lemma 3.1
Let E be a Banach space and F be a smooth, strictly convex, and reflexive Banach space. Let \(J_{F}\) be the duality mappings on F. Let \(A: E\to F\) be a bounded linear operator such that \(A\neq 0\) and let \({A}^{*}\) be the adjoint operator of A. Let \(\zeta \neq 0\) and \(U: F\to F\) be a ζ-generalized demimetric mapping. If \(A^{-1}(\operatorname{Fix}(U))\neq \emptyset \), then
Proof
It is clear that for each \(x\in E\), \(Ax-UAx=0\) implies that \(A^{*}J_{F}(Ax-UAx)=0\). To see the converse, let \(x\in E\) such that \(A^{*}J_{F}(Ax-UAx)=0\). Taking \(x^{*}\in A^{-1}(\operatorname{Fix}(U))\) we have
which implies that \(Ax-UAx=0\). □
Now, in this position, we give our algorithm and its convergence analysis for the generalized multiple-set split feasibility problem in Banach spaces.
Theorem 3.2
Let E be a 2-uniformly convex and uniformly smooth Banach space and let F be a smooth, strictly convex, and reflexive Banach space. Let \(J_{E}\) and \(J_{F}\) be the duality mappings on E and F, respectively. Let for \(i=1,2,\ldots,m\), \(\zeta _{i}\neq 0\) and \(U_{i}: F\to F \) be a finite family of \(\zeta _{i}\)-generalized demimetric mappings such that \(U_{i}- I\) is demiclosed at 0. Let for each \(i=1,2,\ldots,m\), \(A_{i}: E\to E^{*}\) be an \(\eta _{i}\)-inverse strongly monotone and \(B_{i}: E\to 2^{ E^{*}}\) be a maximal monotone. Let for each \(i=1,2,\ldots,m\), \(T_{i}: E\to F\) be a bounded linear operator such that \(T_{i}\neq 0\) and let \({T_{i}}^{*}:F^{*}\rightarrow E^{*}\) be the adjoint of \(T_{i}\). Suppose that \(\Omega =\{ x^{\ast}\in \bigcap_{i=1}^{m} (A_{i}+B_{i})^{-1}0 : T_{i}x^{\ast}\in \operatorname{Fix}( U_{i}), i=1,2,\ldots,m\}\neq \emptyset \). Let \(\{x_{n}\}\) be a sequence generated by \(v,x_{0},x_{1}\in E\) and by:
where \(l_{i}= \frac{\zeta _{i}}{|\zeta _{i}|}\), \(0\leq \theta _{n}\leq \overline{\theta}_{n}\) and \(\theta ^{*} \in (0,1)\) such that
Suppose the stepsizes are chosen in such a way that for small enough \(\epsilon > 0\),
otherwise \(r_{n,i}=r_{i}\) is any nonnegative real number (where γ is the constant in Lemma 2.1). Suppose that the following conditions are satisfied:
(i) \(\alpha _{n}\in (0,1)\), \(\lim_{n\rightarrow \infty}\alpha _{n}=0\) and \(\sum_{n=1}^{\infty}\alpha _{n}=\infty \);
(ii) \(0<\inf_{n\in N}\lambda _{n,i}\leq \sup_{n\in N}\lambda _{n,i}< 2\eta _{i}c\), (c is the constant in Lemma 2.2);
(iii) \(\gamma _{n,i}\in (0,1)\), \(\alpha _{n}+\sum_{i=1}^{m} \gamma _{n,i}=1\) and \(\liminf_{n\to \infty}\gamma _{n,i}>0\);
(iv) \(\varepsilon _{n}>0\) and \(\lim_{n\to \infty}\frac {\varepsilon _{n}}{\alpha _{n}}=0\).
Then, \(\{x_{n}\}\) converges strongly to \(\Pi _{\Omega}v\), where \(\Pi _{\Omega}\) is the generalized projection of E onto Ω.
Proof
From Lemma 3.1, we have that the stepsizes \(r_{n,i}\) are well defined. We show that \(\{x_{n}\}\) is bounded. Indeed, let \(x^{\star}\in \Omega \), since for each \(i=1,2,\ldots,m\), \(U_{i}\) is a \(\zeta _{i}\)-generalized demimetric mapping and by Lemma 2.1 we have
For \(n\in \Lambda \), from the condition of \(r_{n,i}\) we have
hence
This implies that
Utilizing Lemma 2.10 we have
for each \(\beta >0\) and \(n\in \mathbb{N}\). Since \(0<\inf_{n\in \mathbb{N}}\lambda _{n,i} \leq \sup_{n\in \mathbb{N}} \lambda _{n,i}<2c\eta _{i}\), for each \(i\in \{1,2,\ldots,m\}\) there exists \(\beta _{i} > 0\) such that \(\inf_{n\in \mathbb{N}} (c-\lambda _{n,i}\beta _{i})>0\) and \(\inf_{n\in \mathbb{N}}\lambda _{n,i}( 2\eta _{i}- \frac{1}{\beta _{i}} )>0\). From inequalities (5), (6), and (7), we obtain
From the definition of \(w_{n}\), we obtain
From inequalities (8) and (9) we obtain
Therefore, \(\phi (x^{*},x_{n})\) is bounded and by inequality (3), the sequence \(\{x_{n}\}\) is also bounded. Consequently, \(\{w_{n}\}\), \(\{y_{n,i}\}\), \(\{z_{n,i}\}\), and \(\{T_{i}w_{n}\}\) are all bounded. We have \(\theta _{n}\|J_{E}(x_{n})- J_{E}(x_{n-1})\|\leq \varepsilon _{n}\) for all n, which together with \(\lim_{n\to \infty} \frac{\varepsilon _{n}}{\alpha _{n}}=0\) implies that
Utilizing Lemma 2.3 we obtain that
Since the sequence \(\{x_{n}\}\) is bounded, there exists a constant \(M>0\) such that
Hence, from (11) and (10) we obtain
From inequalities (5), (6), (7), and (8) we obtain
This implies that
where \(K_{1}=\sup_{n\in \mathbb{N}} \{|\phi (x^{*},v)- \phi (x^{*},x_{n})| \}\) and \(K_{2}=\sup_{n\in \mathbb{N}} \{|\frac{\theta _{n}}{\alpha _{n}} [ \phi (x^{*},x_{n-1})- \phi (x^{*},x_{n})]|\}\).
Utilizing Lemma 2.4, we have
Therefore,
where
From Lemma 2.10 and Lemma 2.8, we have that Ω is closed and convex. Therefore, the generalized projection \(\Pi _{\Omega}\) from E onto Ω is well defined. Suppose \(x^{*}=\Pi _{\Omega}v\). The next task is to prove that the sequence \(\{x_{n}\}\) converges to the point \(x^{*}\). In order to prove this, we consider two possible cases.
Case 1. Suppose that there exists \(n_{0} \in \mathbb{N}\) such that \(\{\phi (x^{*},x_{n})\}_{n=n_{0}}^{\infty}\) is nonincreasing. By the boundedness of \(\{\phi (x^{*},x_{n})\}\), we have \(\{\phi (x^{*},x_{n})\}\) is convergent. Furthermore, we have \(\phi (x^{*},x_{n})- \phi (x^{*},x_{n+1})\rightarrow 0\) as \(n\rightarrow \infty \). Therefore, from (13), for each \(i\in \{1,2,\ldots,m\}\) we obtain
This implies that
From Lemma 3.1 we obtain
In a similar way we obtain that
By our assumption we obtain
Since \(J_{E}\) is uniformly continuous on bounded subsets of E, we obtain
Also, we have
Furthermore, for \(i=1,2,\ldots,m\), we obtain that
Therefore, we obtain
This implies that
By uniform continuity of \(J_{E}^{-1}\) on bounded subset of \(E^{*}\), we conclude that
Since \(\{x_{n}\}\) is bounded and E is a reflexive Banach space, there exits a subsequence \(\{x_{n_{k}}\}\) of \(\{x_{n}\}\) such that \(x_{n_{k}}\rightharpoonup z\). Since \(\|y_{n,i}-x_{n}\|\rightarrow 0\), we have \(y_{n_{k},i}\rightharpoonup z\), (\(i=1,2,\ldots,m\)). Thus, we obtain \(z\in \bigcap_{i=1}^{m}(A_{i}+B_{i})^{-1}0\) (see, e.g., [7] for this proof). Since \(\|w_{n}-x_{n}\|\rightarrow 0\), we have \(w_{n_{k}}\rightharpoonup z\). From the continuity of \(T_{i}\), we have that \(T_{i}w_{n_{k}}\rightharpoonup T_{i}z\). Now, from (16) and the demiclosedness of \(I-U_{i}\), we obtain \(T_{i} z\in \operatorname{Fix}(U_{i})\). This implies that \(z\in \Omega \). Next, we show that \(\limsup_{n\rightarrow \infty}\langle x_{n+1}-x^{*},J_{E}v- J_{E}x^{*} \rangle \leq 0\). We can choose a subsequence \(\{x_{n_{k}}\}\) of \(\{x_{n}\}\) such that
Since \(x^{*}=\Pi _{\Omega}v\), applying Lemma 2.6 we obtain
This, together with \(\lim_{n\rightarrow \infty}\|x_{n+1}-x_{n}\|=0\), implies that
Applying inequality (14) and Lemma 2.11, we deduce that \(\lim_{n\rightarrow \infty} \phi (x^{*},x_{n})=0\). Now, from Lemma 2.5 we obtain, \(\lim_{n\rightarrow \infty}\|x_{n}-x^{*}\|=0\).
Case 2: Put \(\Gamma _{n}= \phi (x^{*},x_{n})\) for all \(n\in \mathbb{N}\). Suppose there exists a subsequence \(\{\Gamma _{n_{j}}\}\) of \(\{\Gamma _{n}\}\) such that \(\Gamma _{n_{j}}\leq \Gamma _{{n_{j}}+1}\) for all \(j\in \mathbb{N}\). Define a mapping \(\tau :\mathbb{N}\to \mathbb{N}\) by \(\tau (n)= \max \{k\leq n: \Gamma _{k}<\Gamma _{k+1}\}\) for all \(n\geq n_{0}\) (for some \(n_{0}\) large enough). Thus, by Lemma 2.12 we have \(\tau (n)\to \infty \) and \(0\leq \Gamma _{\tau (n)}\leq \Gamma _{\tau (n)+1}\) for all \(n\geq n_{0}\). Following the proof line in Case 1, we can show that
and
Further, we can show that
It follows from (14) that
Since \(\phi (x^{*},x_{\tau (n)})<\phi (x^{*},x_{\tau (n)+1})\), we have
Since \(\alpha _{\tau (n)}>0\) and \(\limsup_{n\rightarrow \infty}\chi _{\tau (n)}\leq 0\), we deduce that
Using this and inequality (24), we conclude that \(\lim_{n\rightarrow \infty}\phi (x^{*},x_{\tau (n)+1})=0\). Now, from Lemma 2.12, we have that \(\lim_{n\rightarrow \infty}\phi (x^{*},x_{n})=0\). Hence, \(\lim_{n\rightarrow \infty}\|x^{*}-x_{n}\|=0\). This completes the proof. □
We know that every Hilbert space \(\mathcal{H}\), is a 2-uniformly convex and uniformly smooth Banach space and the normalized duality mapping is \(J_{\mathcal{H}}=I\). Also, we have the following relation in Hilbert space \(\mathcal{H}\):
Therefore, in Lemma 2.2 and Lemma 2.1 the constant \(c=\gamma =1\). Theorem 3.2 now yields the following result regarding an algorithm for solving the generalized multiple-set split feasibility problem in Hilbert spaces.
Theorem 3.3
Let E and F be Hilbert spaces. Let for \(i=1,2,\ldots,m\), \(\zeta _{i}\neq 0\) and \(U_{i}: F\to F \) be a finite family of \(\zeta _{i}\)-generalized demimetric mappings such that \(U_{i}- I\) is demiclosed at 0. Let for \(i=1,2,\ldots,m\), \(A_{i}: E\to E\) be an \(\eta _{i}\)-inverse strongly monotone and \(B_{i}: E\to 2^{ E}\) be a maximal monotone. Let for each \(i=1,2,\ldots,m\), \(T_{i}: E\to F\) be a bounded linear operator such that \(T_{i}\neq 0\) and let \({T_{i}}^{*}:F\rightarrow E\) be the adjoint operator of \(T_{i}\). Suppose that \(\Omega =\{ x^{\ast}\in \bigcap_{i=1}^{m} (A_{i}+B_{i})^{-1}0 : T_{i}x^{\ast}\in \operatorname{Fix}( U_{i}), i=1,2,\ldots,m\}\neq \emptyset \). Let \(\{x_{n}\}\) be a sequence generated by \(v,x_{0},x_{1}\in E\) and by:
where \(l_{i}= \frac{\zeta _{i}}{|\zeta _{i}|}\), \(0\leq \theta _{n}\leq \overline{\theta}_{n}\) and \(\theta ^{*} \in (0,1)\) such that
Suppose the stepsizes are chosen in such a way that for small enough \(\epsilon > 0\),
otherwise \(r_{n,i}=r_{i}\) is any nonnegative real number. Suppose that the following conditions are satisfied:
(i) \(\alpha _{n}\in (0,1)\), \(\lim_{n\rightarrow \infty}\alpha _{n}=0\) and \(\sum_{n=1}^{\infty}\alpha _{n}=\infty \);
(ii) \(0<\inf_{n\in N}\lambda _{n,i}\leq \sup_{n\in N}\lambda _{n,i}< 2\eta _{i}\);
(iii) \(\gamma _{n,i}\in (0,1)\), \(\alpha _{n}+\sum_{i=1}^{m} \gamma _{n,i}=1\) and \(\liminf_{n\to \infty}\gamma _{n,i}>0\);
(iv) \(\varepsilon _{n}>0\) and \(\lim_{n\to \infty}\frac {\varepsilon _{n}}{\alpha _{n}}=0\).
Then, \(\{x_{n}\}\) converges strongly to \(P_{\Omega}v\).
4 Applications
In this section we present some applications of our main result.
4.1 Common solutions to variational inequality problems
Let C be a nonempty, closed, and convex subset of a Banach space E and \(A:E\to E^{*}\) be an operator. The variational inequality problem (VIP) is formulated as follows:
The set of solutions of this problem is denoted by \(VI(C,A )\). It is well known that the VIP is a fundamental problem in optimization theory and nonlinear analysis (see [45]).
Let \(f:E\to (-\infty ,+\infty ]\) be a proper, lower semicontinuous, and convex function. Then, it is known that the subdifferential ∂f of f defined by
for \(x\in E\) is a maximal monotone operator; see [46].
Let \(i_{C}:E\to (-\infty ,+\infty ]\) be the indicator function of C. We know that \(i_{C}\) is proper lower semicontinuous and convex, and hence its subdifferential \(\partial i_{C}\) is a maximal monotone operator. Let \(B=\partial i_{C}\). Then, it is easy to see that \(J_{\lambda}^{B}x = \Pi _{C} x\) for every \(\lambda >0\) and \(x\in E\). Further, we also obtain \((A+B)^{-1}(0)= VI(C,A)\).
Now, as an application of our main result, we obtain the following theorem for finding a common element of the set of common solutions of a system of a variational inequality problem and the set of common fixed points of a finite family of generalized demimetric mappings in 2-uniformly convex and uniformly smooth Banach spaces.
Theorem 4.1
Let E be a 2-uniformly convex and uniformly smooth Banach space. Let \(\{C_{i}\}_{i=1}^{m}\) be a finite family of nonempty, closed, and convex subsets of E. Let for \(i=1,2,\ldots,m\), \(\zeta _{i}\neq 0\) and \(U_{i}: E\to E \) be a finite family of \(\zeta _{i}\)-generalized demimetric mappings such that \(U_{i}- I\) is demiclosed at 0. Let for \(i=1,2,\ldots,m\), \(A_{i}: E\to E^{*}\) be an \(\eta _{i}\)-inverse strongly monotone. Suppose that \(\Omega =\{ x^{\ast}\in \bigcap_{i=1}^{m} (VI( C_{i},A_{i}) \cap \operatorname{Fix}( U_{i}))\}\neq \emptyset \). Let \(\{x_{n}\}\) be a sequence generated by \(v,x_{0},x_{1}\in E\) and by:
where \(l_{i}= \frac{\zeta _{i}}{|\zeta _{i}|}\), \(0\leq \theta _{n}\leq \overline{\theta}_{n}\) and \(\theta ^{*} \in (0,1)\) such that
Suppose that the following conditions are satisfied:
(i) \(\alpha _{n}\in (0,1)\), \(\lim_{n\rightarrow \infty}\alpha _{n}=0\) and \(\sum_{n=1}^{\infty}\alpha _{n}=\infty \);
(ii) \(0<\inf_{n\in N}\lambda _{n,i}\leq \sup_{n\in N}\lambda _{n,i}< 2\eta _{i}c\), (c is the constant in Lemma 2.2);
(iii) \(\gamma _{n,i}\in (0,1)\), \(\alpha _{n}+\sum_{i=1}^{m} \gamma _{n,i}=1\) and \(\liminf_{n\to \infty}\gamma _{n,i}>0\);
(iv) \(r_{n,i}\in (\epsilon , \frac{2l_{i}}{\gamma \zeta _{i}}- \epsilon )\) for some \(\epsilon >0\), (γ is the constant in Lemma 2.1);
(v) \(\varepsilon _{n}>0\) and \(\lim_{n\to \infty}\frac {\varepsilon _{n}}{\alpha _{n}}=0\).
Then, \(\{x_{n}\}\) converges strongly to \(\Pi _{\Omega}v\).
Proof
Setting \(F=E\), \(T_{i}=I\), and \(B_{i}=\partial i_{C_{i}}\), we obtain the desired result from Theorem 3.2. □
Remark 4.2
Setting \(U_{i}=I\) in Theorem 4.1, our result generalizes the result of [47] from the problem of finding common solutions to unrelated variational inequalities in a Hilbert space to a 2-uniformly smooth and uniformly convex Banach space.
Remark 4.3
We extend the main results of Kimura and Nakajo [7] from the problem of finding a solution of the variational inequality problem to the problem of finding a common element of the set of common solutions of a system of a variational inequality problem and a common fixed-point problem.
4.2 Convex minimization problem
For a convex differentiable function \(\Phi : E\to \mathbb{R}\) and a proper convex lower semicontinuous function \(\Psi :E\to (-\infty ,+\infty ]\), the convex minimization problem is to find a point \(x^{\star}\in E\) such that
If ∇Φ and ∂Ψ represent the gradient of Φ and subdifferential of Ψ, respectively, then Fermat’s rule ensures the equivalence of problem (26) to the problem of finding a point \(x^{\star}\in E\) such that
Many optimization problems from image processing, statistical regression, and machine learning (see, e.g., [48, 49]) can be adapted into the form of (26). In this setting, we assume that Φ is Gâteaux-differentiable with derivative ∇Φ that is an inverse strongly monotone.
Now, as an application of our main result we obtain the following theorem.
Theorem 4.4
Let E be a 2-uniformly convex and uniformly smooth Banach space. Let \(\zeta \neq 0\) and \(U: E\to E \) be a ζ-generalized demimetric mapping such that \(U- I\) is demiclosed at 0. Let \(\Phi : E\to \mathbb{R}\) be a convex differentiable function such that its gradient ∇Φ is an η-inverse strongly monotone and let \(\Psi :E\to (-\infty ,+\infty ]\) be a proper function with convexity and lower semicontinuity. Suppose that \(\Omega = \{x\in \operatorname{Fix}(U): x= \operatorname{argmin}_{z\in E} \Phi (z)+\Psi (z)\}\neq \emptyset \). Let \(\{x_{n}\}\) be a sequence generated by \(v,x_{0},x_{1}\in E\) and by:
where \(l= \frac{\zeta}{|\zeta |}\), \(0\leq \theta _{n}\leq \overline{\theta}_{n}\) and \(\theta ^{*} \in (0,1)\) such that
Suppose that the following conditions are satisfied:
(i) \(\alpha _{n}\in (0,1)\), \(\lim_{n\rightarrow \infty}\alpha _{n}=0\) and \(\sum_{n=1}^{\infty}\alpha _{n}=\infty \);
(ii) \(0<\inf_{n\in N}\lambda _{n}\leq \sup_{n\in N}\lambda _{n}< 2\eta c\), (c is the constant in Lemma 2.2);
(iii) \(\gamma _{n}\in (0,1)\), \(\alpha _{n}+\gamma _{n}=1\) and \(\liminf_{n\to \infty}\gamma _{n}>0\);
(iv) \(r_{n}\in (\epsilon , \frac{2l}{\gamma \zeta}- \epsilon )\) for some \(\epsilon >0\), (γ is the constant in Lemma 2.1);
(v) \(\varepsilon _{n}>0\) and \(\lim_{n\to \infty}\frac {\varepsilon _{n}}{\alpha _{n}}=0\).
Then, \(\{x_{n}\}\) converges strongly to \(\Pi _{\Omega}v\).
Proof
We know that the subdifferential mapping ∂Ψ of a proper, convex, and lower semicontinuous function Ψ is a maximal monotone. Also, we have (see [50]):
Now, setting \(F=E\), \(m=1\), \(T_{i}=I\) and \(A=\nabla \Phi \), we obtain the desired result from Theorem 3.2. □
4.3 The multiple-set split feasibility problem
Let C be a nonempty, closed, and convex subset of a strictly convex and reflexive Banach space E. Then, we know that for any \(x\in E\), there exists a unique element \(z\in C\) such that \(\|x-z\|\leq \|x-y\|\) for all \(y\in C\). Putting \(z=P_{C}x\), we call \(P_{C}\) the metric projection of E onto C. Let E be a uniformly convex and smooth Banach space and let C be a nonempty, closed, and convex subset of E. Then, \(P_{C}\) is 1-generalized demimetric and \(I-P_{C}\) is demiclosed at zero (see [33] for details).
As another application of our main result, we obtain the following strong convergence theorem for the multiple-set split feasibility problem.
Theorem 4.5
Let E be a 2-uniformly convex and uniformly smooth Banach space and let F be a uniformly convex and smooth Banach space. Let \(\{C_{i}\}_{i=1}^{m}\) and \(\{Q_{i}\}_{i=1}^{m}\) be two finite families of nonempty, closed, and convex subsets of E and F, respectively. Let for each \(i=1,2,\ldots,m\), \(T_{i}: E\to F\) be a bounded linear operator such that \(T_{i}\neq 0\). Suppose that \(\Omega =\{ x^{\ast}\in \bigcap_{i=1}^{m} C_{i} : T_{i}x^{\ast} \in Q_{i}, i=1,2,\ldots,m\}\neq \emptyset \). Let \(\{x_{n}\}\) be a sequence generated by \(v,x_{0},x_{1}\in E\) and by:
where \(0\leq \theta _{n}\leq \overline{\theta}_{n}\) and \(\theta ^{*} \in (0,1)\) such that
Suppose the stepsizes are chosen in such a way that for small enough \(\epsilon > 0\),
otherwise \(r_{n,i}=r_{i}\) is any nonnegative real number (where γ is the constant in Lemma 2.1). Suppose that the following conditions are satisfied:
(i) \(\alpha _{n}\in (0,1)\), \(\lim_{n\rightarrow \infty}\alpha _{n}=0\) and \(\sum_{n=1}^{\infty}\alpha _{n}=\infty \);
(ii) \(\gamma _{n,i}\in (0,1)\), \(\alpha _{n}+\sum_{i=1}^{m}\gamma _{n,i}=1\) and \(\liminf_{n\to \infty}\gamma _{n,i}>0\);
(iii) \(\varepsilon _{n}>0\) and \(\lim_{n\to \infty}\frac {\varepsilon _{n}}{\alpha _{n}}=0\).
Then, \(\{x_{n}\}\) converges strongly to \(\Pi _{\Omega}v\).
4.4 Split common null-point problem
Let E be a uniformly convex and smooth Banach space and let \(G: E\to 2^{ E^{*}}\) be a maximal monotone operator. For each \(x\in E\) and \(\mu >0\), we define the metric resolvent of G for \(\mu >0\) by
It is observed that \(0\in J_{E}(Q_{\mu}^{G}(x)-x)+\mu G Q_{\mu}^{G}(x)\) and \(G^{-1}0= \operatorname{Fix}( Q_{\mu}^{G})\), (see [51]). It is known that \(Q_{\mu}^{G}\) is 1-generalized demimetric. Also, we know that \(I-Q_{\mu}^{G}\) is demiclosed at zero (see [33] for details).
We obtain the following strong convergence result for split common null-point problem.
Theorem 4.6
Let E be a 2-uniformly convex and uniformly smooth Banach space and let F be a uniformly convex and smooth Banach space. Let for \(i=1,2,\ldots,m\), \(B_{i}: E\to 2^{ E^{*}}\) and \(G_{i}: F\to 2^{ F^{*}}\) be maximal monotone operators. Let for \(i=1,2,\ldots,m\), \(J_{r_{i}}^{B_{i}}\), be resolvent operators of \(B_{i}\) for \(r_{i} > 0\) and \(Q_{\mu _{i}}^{G_{i}}\), be metric resolvent operators of \(G_{i}\) for \(\mu _{i} > 0\). Let for each \(i=1,2,\ldots,m\), \(T_{i}: E\to F\) be a bounded linear operator such that \(T_{i}\neq 0\). Suppose that \(\Omega =\{ x^{\ast}\in \bigcap_{i=1}^{m} {B_{i}}^{-1}0 : T_{i}x^{ \ast}\in {G_{i}}^{-1}0 , i=1,2,\ldots,m\}\neq \emptyset \). Let \(\{x_{n}\}\) be a sequence generated by \(v,x_{0},x_{1}\in E\) and by:
where \(0\leq \theta _{n}\leq \overline{\theta}_{n}\) and \(\theta ^{*} \in (0,1)\) such that
Suppose the stepsizes are chosen in such a way that for small enough \(\epsilon > 0\),
otherwise \(r_{n,i}=r_{i}\) is any nonnegative real number (where γ is the constant in Lemma 2.1). Suppose that the following conditions are satisfied:
(i) \(\alpha _{n}\in (0,1)\), \(\lim_{n\rightarrow \infty}\alpha _{n}=0\) and \(\sum_{n=1}^{\infty}\alpha _{n}=\infty \);
(ii) \(0<\inf_{n\in N}\lambda _{n,i}\);
(iii) \(\gamma _{n,i}\in (0,1)\), \(\alpha _{n}+\sum_{i=1}^{m} \gamma _{n,i}=1\) and \(\liminf_{n\to \infty}\gamma _{n,i}>0\);
(iv) \(\varepsilon _{n}>0\) and \(\lim_{n\to \infty}\frac {\varepsilon _{n}}{\alpha _{n}}=0\).
Then, \(\{x_{n}\}\) converges strongly to \(\Pi _{\Omega}v\).
4.5 Split common fixed point
Let \(\mathcal{H}\) be a Hilbert space. The mapping \(T:\mathcal{H}\to \mathcal{H}\) is called:
• A strict pseudocontraction, if there exists a constant \(\beta \in [0,1)\) such that
We obtain the following strong convergence result for the split common fixed-point problem.
Theorem 4.7
Let E and F be Hilbert spaces. Let for each \(i=1,2,\ldots,m\), \(U_{i}: F\to F \) be a \(\varsigma _{i}\)-strict pseudocontraction mapping and let \(S_{i}:E\to E\) be a \(\kappa _{i}\)-strict pseudocontraction mapping. Let for each \(i=1,2,\ldots,m\), \(T_{i}: E\to F\) be a bounded linear operator such that \(T_{i}\neq 0\). Suppose that \(\Omega =\{ x^{\ast}\in \bigcap_{i=1}^{m} \operatorname{Fix}(S_{i}) : T_{i}x^{ \ast}\in \operatorname{Fix}( U_{i}), i=1,2,\ldots,m\}\neq \emptyset \). Let \(\{x_{n}\}\) be a sequence generated by \(v,x_{0},x_{1}\in E\) and by:
where \(0\leq \theta _{n}\leq \overline{\theta}_{n}\) and \(\theta ^{*} \in (0,1)\) such that
Suppose the stepsizes are chosen in such a way that for small enough \(\epsilon > 0\),
otherwise \(r_{n,i}=r_{i}\) is any nonnegative real number. Suppose that the following conditions are satisfied:
(i) \(\alpha _{n}\in (0,1)\), \(\lim_{n\rightarrow \infty}\alpha _{n}=0\) and \(\sum_{n=1}^{\infty}\alpha _{n}=\infty \);
(ii) \(0<\inf_{n\in N}\lambda _{n,i}\leq \sup_{n\in N}\lambda _{n,i}< (1-\kappa _{i})\);
(iii) \(\gamma _{n,i}\in (0,1)\), \(\alpha _{n}+\sum_{i=1}^{m} \gamma _{n,i}=1\) and \(\liminf_{n\to \infty}\gamma _{n,i}>0\);
(iv) \(\varepsilon _{n}>0\) and \(\lim_{n\to \infty}\frac {\varepsilon _{n}}{\alpha _{n}}=0\).
Then, \(\{x_{n}\}\) converges strongly to \(P_{\Omega}v\).
Proof
Put \(A_{i}= I- S_{i}\) and \(B_{i}=0\), for each \(i=1,2,\ldots,m\). Then, \(A_{i}\) is \(\frac{1-\kappa _{i}}{2}\)-inverse strongly monotone and \(\operatorname{Fix}( S_{i} )={A_{i}}^{-1}(0)\). Since for each \(i\in \{1,2,\ldots,m\}\), \(S_{i}\) is a \(\varsigma _{i}\)-strict pseudocontraction, we have \(S_{i}\) is a \(\frac{2}{1-\varsigma _{i}}\)-generalized demimetric mapping and \(I-S_{i}\) is demiclosed at zero. Hence, by Theorem 3.2, we obtain the desired result. □
5 Numerical experiments
Example 5.1
We consider the following multiple-set split feasibility problem: Find an element \(x^{\star}\in \Omega \) with
where \(C_{i}\subset {\mathbb{R}}^{10}\) and \(Q_{i}\subset {\mathbb{R}}^{20}\) that are defined by
and \(T_{i}: {\mathbb{R}}^{10}\to {\mathbb{R}}^{20}\), are bounded linear operators with the elements of the representing matrix that are randomly generated in the closed interval \([-2,2]\). We examine the convergence of the sequences \(\{x_{n}\}\), which are defined in Theorem 4.5, where the coordinates of the points \(a_{i}\), \(i=1,2,3\), are randomly generated in the closed interval \([1,4]\) and the numbers \(b_{i}\), \(i=1,2,3\), are randomly generated in the closed interval \([1,2]\), and the numbers \(d_{i}\), \(i=1,2,3\), are randomly generated in the closed interval \([0,1]\). The coordinates of the point u and the initial points \(x_{0}\) and \(x_{1}\) are randomly generated in the interval \([0,1]\). The stopping criterion is \(E_{n} = \|x_{n}-x_{n-1}\|< 10^{-5}\). In this case, \(x^{*}=0\), is a solution of this problem. We know that for \(i=1,2,3\),
and
The numerical results that we have obtained are presented in Table 1.
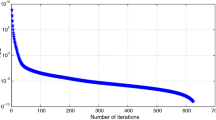
The behavior of \(E_{n}\) in Table 1 with \(\theta ^{*}=0.7\) is depicted in Fig. 1.
Example 5.2
In Theorem 4.7, set \(E=F=\ell _{2}(\mathbb{R}):=\{ x=(x_{1},x_{2},\ldots,x_{n},\ldots), x_{i} \in \mathbb{R}: \sum_{i=1}^{\infty}|x_{i}|^{2}<\infty \}\), with inner product \(\langle ., .\rangle \) and norm \(\|.\|\) defined by
Let \(S:E\to E\), \(U:F\to F\), and \(T:E\to F\) be defined by
It is easy to verify that S is a \(\frac{1}{5}\)-strict pseudocontraction mapping, U is nonexpansive (a 0-strict pseudocontraction mapping) and T is a bounded linear operator. Furthermore, \(\Omega = \operatorname{Fix}(U)\cap \operatorname{Fix}(S)=\{0\}\). We take \(\theta _{n}=0\), \(r_{n}=\frac{2}{3}\), \(\lambda _{n}=\frac{1}{2}\), \(v=0\), and \(\alpha _{n}=\frac{1}{n+1}\). Then, the sequence \(\{x_{n}\}\) induced by our algorithm, reduces to
Now, for \(x_{0}= (1,1,1,0,0,\ldots)\), we obtain the following numerical results:
6 Conclusions
In this paper, a new iterative scheme with inertial effect is proposed for solving the generalized multiple-set split feasibility problem in a 2-uniformly convex and uniformly smooth Banach space E and a smooth, strictly convex, and reflexive Banach space F. The strong convergence of the iterative sequences generated by the presented algorithm is established without requiring the prior knowledge of operator norm. Finally, we applied our result to study and approximate the solutions of certain classes of optimization problems. The results obtained in this paper improved and extended many others known in the field. As part of our future research, we would like to extend the results in this paper to a more general space, such as the p-uniformly convex Banach space. Furthermore, we would consider the generalized multiple-set split feasibility problem involving a sum of maximal monotone and Lipschitz continuous monotone mappings. It would be interesting if the algorithm proposed in this paper could be applied to some practical optimization problems.
Data availability
Not applicable.
References
Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16, 964–979 (1979)
Passty, G.B.: Ergodic convergence to a zero of the sum of monotone operators in Hilbert spaces. J. Math. Anal. Appl. 72, 383–390 (1979)
Chen, G.H.-G., Rockafellar, R.T.: Convergence rates in forward-backward splitting. SIAM J. Optim. 7, 421–444 (1997)
Combettes, P.L., Wajs, V.R.: Signal recovery by proximal forward–backward splitting. Multiscale Model. Simul. 4, 1168–1200 (2005)
Takahashi, W., Wong, N.-C., Yao, J.-C.: Two generalized strong convergence theorems of Halpern’s type in Hilbert spaces and applications. Taiwan. J. Math. 16, 1151–1172 (2012)
Nakajo, K., Shimoji, K., Takahashi, W.: Strong convergence theorems of Halpern’s type for families of nonexpansive mappings in Hilbert spaces. Thai J. Math. 7, 49–67 (2009)
Kimura, Y., Nakajo, K.: Strong convergence for a modified forward–backward splitting method in Banach spaces. J. Nonlinear Var. Anal. 3(1), 5–18 (2019)
Polyak, B.T.: Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 4, 1–17 (1964)
Lorenz, D.A., Pock, T.: An inertial forward-backward algorithm for monotone inclusions. J. Math. Imaging Vis. 51, 311–325 (2015)
Censor, Y., Elfving, T., Kopf, N., Bortfeld, T.: The multiple-sets split feasibility problem and its application. Inverse Probl. 21, 2071–2084 (2005)
Byrne, C.: A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Probl. 20, 103–120 (2004)
Censor, Y., Bortfeld, T., Martin, B., Trofimov, A.: A unified approach for inversion problems in intensity-modulated radiation therapy. Phys. Med. Biol. 51, 2353–2365 (2006)
Censor, Y., Segal, A.: The split common fixed point problem for directed operators. J. Convex Anal. 16, 587–600 (2009)
Moudafi, A.: Split monotone variational inclusions. J. Optim. Theory Appl. 150, 275–283 (2011)
Byrne, C., Censor, Y., Gibali, A., Reich, S.: The split common null point problem. J. Nonlinear Convex Anal. 13, 759–775 (2012)
Dong, Q.L., He, S., Zhao, J.: Solving the split equality problem without prior knowledge of operator norms. Optimization 64, 1887–1906 (2015)
Takahashi, W., Xu, H.K., Yao, J.-C.: Iterative methods for generalized split feasibility problems in Hilbert spaces. Set-Valued Var. Anal. 23, 205–221 (2015)
Eslamian, M., Vahidi, J.: Split common fixed point problem of nonexpansive semigroup. Mediterr. J. Math. 13, 1177–1195 (2016). https://doi.org/10.1007/s00009-015-0541-3
Eslamian, M.: Split common fixed point and common null point problem. Math. Methods Appl. Sci. 40, 7410–7424 (2017)
Reich, S., Tuyen, T.M.: Iterative methods for solving the generalized split common null point problem in Hilbert spaces. Optimization 69, 1013–1038 (2020)
Taiwo, A., Jolaoso, L.O., Mewomo, O.T.: Viscosity approximation method for solving the multiple-set split equality common fixed point problems for quasi-pseudocontractive mappings in Hilbert spaces. J. Ind. Manag. Optim. 17(5), 2733–2759 (2021)
Taiwo, A., Jolaoso, L.O., Mewomo, O.T.: Inertial-type algorithm for solving split common fixed point problems in Banach spaces. J. Sci. Comput. 86, 12 (2021)
Yao, Y., Shehu, Y., Li, X.-H., Dong, Q.-L.: A method with inertial extrapolation step for split monotone inclusion problems. Optimization 70, 741–761 (2021)
Eslamian, M.: Split common fixed point problem for demimetric mappings and Bregman relatively nonexpansive mappings. Optimization (2022). https://doi.org/10.1080/02331934.2022.2094266
Alakoya, T.O., Uzor, V.A., Mewomo, O.T., Yao, J.C.: On a system of monotone variational inclusion problems with fixed-point constraint. J. Inequal. Appl. 2022, 47 (2022)
Alakoya, T.O., Uzor, V.A., Mewomo, O.T.: A new projection and contraction method for solving split monotone variational inclusion, pseudomonotone variational inequality, and common fixed point problems. Comput. Appl. Math. 42(1), 3 (2023)
Dong, Q.L., Liu, L., Qin, X., Yao, J.C.: An alternated inertial general splitting method with linearization for the split feasibility problem. Optimization 72, 2585–2607 (2023)
Godwin, E.C., Izuchukwu, C., Mewomo, O.T.: Image restoration using a modified relaxed inertial method for generalized split feasibility problems. Math. Methods Appl. Sci. 46(5), 5521–5544 (2023)
Godwin, E.C., Mewomo, O.T., Alakoya, T.O.: A strongly convergent algorithm for solving multiple set split equality equilibrium and fixed point problems in Banach spaces. Proc. Edinb. Math. Soc. 66, 475–515 (2023)
Izuchukwu, C., Reich, S., Shehu, Y.: Relaxed inertial methods for solving the split monotone variational inclusion problem beyond co-coerciveness. Optimization 72, 607–646 (2023)
Uzor, V.A., Alakoya, T.O., Mewomo, O.T.: On split monotone variational inclusion problem with multiple output sets with fixed points constraints. Comput. Methods Appl. Math. 23(3), 729–949 (2023)
Kawasaki, T., Takahashi, W.: A strong convergence theorem for countable families of nonlinear nonself mappings in Hilbert spaces and applications. J. Nonlinear Convex Anal. 19, 543–560 (2018)
Takahashi, W.: The split common fixed point problem for generalized demimetric mappings in two Banach spaces. Optimization 68, 411–427 (2019)
Eslamian, M.: Strong convergence theorem for common zero points of inverse strongly monotone mappings and common fixed points of generalized demimetric mappings. Optimization 71, 4265–4287 (2022)
Beauzamy, B.: Introduction to Banach Spaces and Their Geometry, 2nd edn. North-Holland Mathematics Studies, vol. 68. North-Holland, Amsterdam (1985)
Takahashi, W.: Nonlinear Functional Analysis. Yokohama Publishers, Yokohama (2000)
Xu, H.K.: Inequalities in Banach spaces with applications. Nonlinear Anal. 16, 1127–1138 (1991)
Cheng, Q., Su, Y., Zhang, J.: Duality fixed point and zero point theorem and application. Abstr. Appl. Anal. 2012, Article ID 391301 (2012)
Alber, Y.I.: Metric and generalized projection operators in Banach spaces: properties and applications. In: Theory and Applications of Nonlinear Operators of Accretive and Monotone Type. Lecture Notes in Pure and Appl. Math., vol. 178, pp. 15–50. Dekker, New York (1996)
Matsushita, S., Takahashi, W.: A strong convergence theorem for relatively nonexpansive mappings in a Banach space. J. Approx. Theory 134, 257–266 (2005)
Kamimura, S., Takahashi, W.: Strong convergence of a proximal-type algorithm in a Banach space. SIAM J. Optim. 13, 938–945 (2002)
Barbu, V.: Nonlinear Semigroups and Differential Equations in Banach Spaces. Editura Academiei R.S.R., Bucharest (1976)
Xu, H.K.: Iterative methods for the split feasibility problem in infinite-dimensional Hilbert spaces. Inverse Probl. 26(10), Article ID 105018 (2010)
Maingé, P.E.: Strong convergence of projected subgradient methods for nonsmooth and nonstrictly convex minimization. Set-Valued Anal. 16, 899–912 (2008)
Kinderlehrer, D., Stampacchia, G.: An Introduction to Variational Inequalities and Their Applications. Academic Press, New York (1980)
Rockafellar, R.T.: On the maximal monotonicity of subdifferential mappings. Pac. J. Math. 33, 209–216 (1970)
Censor, Y., Gibali, A., Reich, S.: A von Neumann alternating method for finding common solutions to variational inequalities. Nonlinear Anal. 75, 4596–4603 (2012)
Bredies, K.: A forward-backward splitting algorithm for the minimization of non-smooth convex functionals in Banach space. Inverse Probl. 25(1), 015005 (2009)
Wang, Y., Xu, H.-K.: Strong convergence for the proximal-gradient method. J. Nonlinear Convex Anal. 15, 581–593 (2014)
Shehu, Y.: Convergence results of forward-backward algorithms for sum of monotone operators in Banach spaces. Results Math. 74, 1–24 (2019)
Aoyama, K., Kohsaka, F., Takahashi, W.: Three generalizations of firmly nonexpansive mappings: their relations and continuity properties. J. Nonlinear Convex Anal. 10, 131–147 (2009)
Acknowledgements
The author is thankful to the editor and anonymous referees for their valuable comments and suggestions.
Funding
There was no funding for this research article.
Author information
Authors and Affiliations
Contributions
M. Eslamian wrote and reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Eslamian, M. Inertial Halpern-type iterative algorithm for the generalized multiple-set split feasibility problem in Banach spaces. J Inequal Appl 2024, 7 (2024). https://doi.org/10.1186/s13660-024-03082-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-024-03082-9