1 Introduction

As can be seen in the literature, retarded differential or integral inequalities play a crucial role in the study of the qualitative behavior of delay differential equations. The first result in this direction was given in the earlier work of Hanalay [1] (see also [2, pp. 378]), which is now called Halanay’s inequality. This inequality can be seen as a retarded version of the classical Gronwall inequality. Since then, there have appeared various retarded inequalities, generalizing Halanay’s inequality to different cases; see, e.g., [3–11].

Very recently, Li et al. [6] established a new integral inequality involving finite (bounded) time delay, which can be seen as a more general extension of the Gronwall–Bellman inequality. It allows us to obtain necessary estimates for solutions of retarded differential equations in the same manner as in the situation of nonretarded equations; see [6, 12].

In applications, many problems from different areas such as sampled-data control, neural networks, economics, and biology are described by difference equations [13–18]. (The numerical computation of continuous-time systems also give rise to numerous difference equations.) As in the case of continuous-time systems, in many cases we have to fall back on difference inequalities while studying the dynamical behavior of difference equations. The interested reader is referred to [8, 13, 19, 20] etc., where one can find many nice results in this area.

In this note, we are basically interested in delay difference inequalities. As far as we know, the first result concerning this topic was given in Liz [21], which is actually a discretization of Hanalay’s inequality. Later, there appeared many such inequalities, most of which were focused on finite time delay [3, 4, 7, 18, 20–24]. In contrast to that of finite delay, the situation in the case of unbounded or infinite time delay seems to be much more complicated, in fact, even if the phase space for dealing with a problem involving infinite delay needs to be carefully constructed. Inspired by the work in [6], we establish a difference inequality parallel to the one in [6] in a more general setting of infinite delay, which is one of our main innovations. As the argument involved in the proof of the corresponding result in [6] depends heavily on the continuity of the inequality, such an extension is not trivial even in the special case of finite delay. We also mention that [6] only concerns finite time delay. Since the inequalities in this present work involve infinite delay, we need to put them into suitable phase spaces that are different from the usual ones used in [6] and overcome some new technical difficulties brought about by the delay, although the basic ideas used here are borrowed directly from [6].

As an application, we consider the asymptotic stability of the zero solution for the nonlinear Volterra difference system

$$ {y(n+1)-y(n)=A(n)}y(n)+\sum^{n}_{s=-\infty}G \bigl(n,s,y(s)\bigr), \quad y(n)\in \mathbb{R}^{N}, n\in \mathbb{Z}, $$
(1.1)

where \(A(n)\) is an \(N\times N\) matrix for each \(n\in \mathbb{Z}\), and \(G\in C (\mathbb{Z}\times \mathbb{Z}\times \mathbb{R}^{N}; \mathbb{R}^{N} )\). Equation (1.1) is actually the discretization of the Volterra integrodifferential equation

$$ \frac{d}{dt}x(t)=A(t)x(t)+ \int ^{t}_{-\infty }G\bigl(t,s,x(s)\bigr)\,ds. $$

(This type of equation arise in various fields such as the viscoelasticity theory and the processes of biomechanics; see, e.g., [25, 26] and references therein.) In the past two decades, there have appeared many nice works on the asymptotic behavior of such equations; see [16, 27–31], etc. In particular, in [31] Ngoc and Hieu studied the asymptotic stability of difference equations like (1.1) extensively by using the Perron–Frobenius theory and some comparison principles. Here, we give a new criteria for the asymptotic stability of the null solution of the equation by applying the delay difference inequality established here, which is not covered by the general results in [31].

This paper is organized as follows. Section 2 consists of some preliminary work. Specifically, we recall the notions of some suitable Banach spaces introduced in Matsunage and Murakami [32] and the notion of asymptotic stability. Section 3 is devoted to the main results mentioned above. In Sect. 4 we discuss the asymptotic stability of the Volterra difference equation (1.1). A concrete example will also be presented.

2 Preliminaries

This section consists of some preliminary work.

  • Notations and notions

Let \({\mathbb{Z}}\) and \({\mathbb{R}}\) denote the sets of integers and real numbers, respectively.

A subset \({\mathcal {I}}\) of \({\mathbb{Z}}\) is called an interval in \({\mathbb{Z}}\), if there is an interval \(J\subset {\mathbb{R}}\) such that \({\mathcal {I}}=J\cap {\mathbb{Z}}\). Clearly, both the sets \({\mathbb{Z}}^{+}\) of nonnegative integers and \({\mathbb{Z}}^{-}\) of non-positive integers are intervals in \({\mathbb{Z}}\). For an interval \(J\subset {\mathbb{R}}\), we denote by \(J_{{\mathbb{Z}}}\) the interval \(J\cap {\mathbb{Z}}\) in \({\mathbb{Z}}\).

A mapping y from an interval \({\mathcal {I}}\) in \({\mathbb{Z}}\) to a set X will be referred to as a sequence in X, usually written as \(y=y(n)\) or \(y=y_{n}\) (\(n\in {\mathcal {I}}\)).

Given an interval \({\mathcal {I}}\) in \({\mathbb{Z}}\), denote by \({\mathcal {S}} ({\mathcal {I}}; {\mathbb{R}}^{N} )\) the set of sequences \(y=y(n)\) (\(n\in {\mathcal {I}}\)) taking values in \({\mathbb{R}}^{N}\). If \(N=1\), we will simply write \({\mathcal {S}} ({\mathcal {I}}; {\mathbb{R}} )={\mathcal {S}} ({\mathcal {I}} )\).

Let \({\mathcal {S}}_{0}:={\mathcal {S}} ({\mathbb{Z}}^{-}; {\mathbb{R}}^{N} )\).

Definition 2.1

Let \({\mathcal {I}}^{-}=(-\infty ,a]_{{\mathbb{Z}}}\), where \(-\infty < a\leq \infty \). (Here, we identify \((-\infty ,a]_{{\mathbb{Z}}}\) with \({\mathbb{Z}}\) if \(a=\infty \).) For each sequence \(y\in {\mathcal {S}} ({\mathcal {I}}^{-}; {\mathbb{R}}^{N} )\), define the lift of y in \({\mathcal {S}}_{0}\) to be the sequence \(\hat{y}=y_{n}\) (\({n\in {\mathcal {I}}^{-}}\)) given by

$$ y_{n}(k)=y(n+k), \quad k\in {\mathbb{Z}}^{-}. $$

  • Admissible spaces

To deal with problems with infinite delay, we need to introduce the notion of an admissible space.

Definition 2.2

An admissible space \(\mathfrak{B}=(\mathfrak{B}, \|\cdot \|)\) is a Banach space consisting of sequences in \({\mathcal {S}}_{0}\) satisfying the following axiom (see [32]):

  1. (A0)

    There exists \(N_{0}>0\) and \(K,M\in {\mathcal {S}} ({\mathbb{Z}}^{+};{\mathbb{R}}^{+} )\) such that if \(x\in {\mathcal {S}} ({\mathbb{Z}}; {\mathbb{R}}^{N} )\) and \(x_{m}\in \mathfrak{B}\) for some \(m\in {\mathbb{Z}}\), then we have \(x_{n}\in \mathfrak{B}\) for all \(n\geq m\); furthermore,

    $$ N_{0} \bigl\vert x(n) \bigr\vert \leq \Vert x_{n} \Vert \leq K(n-m)\sup_{k\in [m,n]_{{\mathbb{Z}}}} \bigl\vert x(k) \bigr\vert +M(n-m) \Vert x_{m} \Vert .$$
    (2.1)

As in the continuous case (see Hale and Kato [33, §3]), for an admissible space \(\mathfrak{B}\), we also assume that the functions \(K(n)\) and \(M(n)\) in axiom (A0) satisfy

  1. (A1)

    there exist constants \(K^{*}\) and \(M^{*}\) such that

    $$ {K(n)\leq K^{*}}, \qquad M(n)\leq M^{*}, \quad n\in {\mathbb{Z}}^{+} $$
    (2.2)

    and

    $$ M(n)\rightarrow 0 \ \text{as } n\rightarrow \infty . $$
    (2.3)

Remark 2.3

The requirement “if \(x\in {\mathcal {S}} ({\mathbb{Z}}; {\mathbb{R}}^{N} )\) and \(x_{m}\in \mathfrak{B}\) for some \(m\in {\mathbb{Z}}\), then we have \(x_{n}\in \mathfrak{B}\) for all \(n\geq m\)” in axiom (A0) is actually an expression of a fundamental completeness requirement on \(\mathfrak{B}\): if \(y\in \mathfrak{B}\), then the “expansion” ỹ of y by adding in y a finite number of elements \(a_{1},a_{2},\ldots ,a_{k}\in {\mathbb{R}}^{N}\) as below belongs to \(\mathfrak{B}\):

$$ \tilde{y}(n)=\textstyle\begin{cases} y(n+k),&n\leq -k; \\ a_{n+k},&-k+1\leq n\leq 0.\end{cases} $$

In fact, in the definition of \(\mathfrak{B}\), it is also natural to ask that if \(y\in \mathfrak{B}\), then the sequence obtained by simply deleting a finite number of elements from y belongs to \(\mathfrak{B}\). However, this latter requirement does not seem to be quite necessary in applications, hence, it is removed.

By (2.3) we see that if \(n-m\) is large enough then the term \(M(n-m)\|x_{m}\|\) in (2.1) can be very small. Hence, the second inequality in (2.1) indicates that the norm \(\|x\|\) of a sequence \(x\in \mathfrak{B}\) mainly concentrates on a finite segment of x. In applications, this corresponds to the principle of fading memory in areas such as continuum mechanics, etc.

  • Asymptotic stability

Let \(\mathfrak{B}\) be an admissible space. Given \(\phi \in \mathfrak{B}\), denote by \(y(n;m,\phi )\) the solution \(y = y(n)\) of equation (1.1) with initial data \(y_{m}=\phi \).

Suppose \(G(n,s,0)=0\) for all \(n\in {\mathbb{Z}}\) and \(s\leq n\), and hence \(y(n)\equiv 0\) is a trivial solution of equation (1.1).

The null solution 0 is called stable, if for every \(m\in { \mathbb{Z}}\) and \(\varepsilon >0\), there is \(\delta >0\) such that for every solution \(y=y(n;m,\phi )\) with \(\|\phi \| \leq \delta \),

$$ \Vert y_{n} \Vert < \varepsilon , \quad \forall n\geq m. $$

The null solution is said to be globally asymptotically stable (GAS in brief), if it is stable; furthermore, for every solution \(y=y(n;m,\phi )\) of (1.1), we have

$$ \Vert y_{n} \Vert \rightarrow 0 \ \text{as }n\rightarrow \infty . $$

It is said to be globally exponentially asymptotically stable (GEAS in brief), if for every \(m\in {\mathbb{Z}}\), there exist \(K,\sigma >0\) with \(\sigma <1\) such that

$$ \Vert y_{n} \Vert \leq K \Vert \phi \Vert \sigma ^{n-m}, \quad \forall n>m $$

for every solution \(y=y(n;m,\phi )\).

Remark 2.4

By definition it is obvious that GEAS automatically implies GAS.

Remark 2.5

For a nonautonomous dynamical system, one can actually introduce different notions to describe the asymptotic behavior of the system, according to different stability and attracting properties. For instance, if we require the constants K and σ in the definition of GEAS to be independent of the initial time \(m\in {\mathbb{Z}}\), then we give a stronger notion of asymptotic stability, called the uniform global asymptotic stability.

  • Convention

Throughout this paper, we always assign the values of an empty sum and an empty product to be 0 and 1, respectively. For instance, if \(\{x(n)\}_{n\in {\mathbb{Z}}}\) is a sequence and \(n>m\), then we put

$$ \sum_{k=n}^{m}x(k)=0, \qquad \prod _{k=n}^{m}x(k)=1. $$

3 A discrete Gronwall–Halanay-type inequality with infinite delay

Denote by \(\mathscr{S}^{+}(Q)\) the family of nonnegative functions on \(Q:=({\mathbb{Z}}^{+})^{2}\), and define the families \(\mathscr{F}\) and \(\mathscr{G}\) of functions on Q as follows:

$$\begin{aligned}& \mathscr{F}= \bigl\{ f\in \mathscr{S}^{+}(Q) : \lim _{n \to \infty } {f(n+m,m)} = 0 \text{ uniformly w.r.t. } m \in {\mathbb{Z}}^{+} \bigr\} ,\\& \mathscr{G}= \Biggl\{ g \in \mathscr{S}^{+}(Q) : \sum _{k=0}^{n}g(n,k) < \infty \text{ for all } n \in { \mathbb{Z}}^{+} \Biggr\} . \end{aligned}$$

For every \(f\in {\mathscr{F}}\) and \(g\in \mathscr{G}\), we write

$$ \vartheta (f):=\sup_{n \geq m \geq 0} f(n,m),\qquad \kappa (g):= \sup _{n \geq m \geq 0} \Biggl(\sum_{k =m}^{n}{g(n,k)} \Biggr). $$

Let \((\mathfrak{B},\|\cdot \|)\) be an admissible space consisting of sequences in \({\mathcal {S}}({\mathbb{Z}}^{-})\), and let

$$ {{\mathcal {S}}^{+}_{\mathfrak{B}}({\mathbb{Z}}):= \bigl\{ y\in { \mathcal {S}}({\mathbb{Z}}): y(n)\geq 0\text{ for all }n\in {\mathbb{Z}}, y_{0}\in \mathfrak{B} \bigr\} .} $$

Given \(f\in {\mathscr{F}}\), \(g\in \mathscr{G}\) and \(\rho \geq 0\), consider the following inequality:

$$\begin{aligned} y(n)&\leq f(n,m) \Vert y_{m} \Vert +\sum _{k = m }^{n}g(n,k) \Vert y_{k} \Vert + \rho , \quad \forall n \geq m\geq 0, \end{aligned}$$
(3.1)

where \(y\in {\mathcal {S}}^{+}_{\mathfrak{B}}({\mathbb{Z}})\). For convenience in statement, set

$$ {\mathscr{L}}(f; g; \rho )= \bigl\{ y\in {\mathcal {S}}^{+}_{ \mathfrak{B}} ({\mathbb{Z}} ):y\text{ satisfies (3.1)} \bigr\} . $$

Our main result is summarized in the following theorem.

Theorem 3.1

Let \(K^{*}\) and \(M^{*}\) be the constants in axiom (A1). Then, the following assertions hold:

  1. (1)

    If \(\kappa (g) K^{*}<1\), then for every \(y\in {\mathscr{L}}(f; g; \rho )\),

    $$ \limsup_{n\rightarrow \infty} \Vert y_{n} \Vert \leq \mu \rho , \quad \textit{where } \mu =\frac{K^{*}}{1-\kappa (g) K^{*}}. $$
    (3.2)
  2. (2)

    If \(\kappa (g) K^{*}<1/(1+M^{*}+\vartheta (f)K^{*})\), then there exist \(B,\sigma >0\) with \(\sigma <1\) such that

    $$ \Vert y_{n} \Vert \leq B \Vert y_{0} \Vert \sigma ^{n}+\gamma \rho , \quad n \in {\mathbb{Z}}^{+} $$
    (3.3)

    for all \(y\in {\mathscr{L}}(f; g; \rho )\), where

    $$ \gamma =\frac{1+\mu }{1-\kappa (g) K^{*}c},\qquad c=\max \biggl\{ \frac{K^{*}\vartheta (f)+M^{*}}{1-\kappa (g) K^{*}},1 \biggr\} . $$
    (3.4)

Remark 3.2

Under the hypothesis in assertion (2), one trivially verifies that \(\kappa (g) K^{*}c <1\). Hence, the constant γ in (3.4) is well defined.

Note also that the definition of μ in (3.2) implies that

$$ K^{*}\bigl(\kappa (g) \mu +1\bigr)=\mu . $$
(3.5)

Remark 3.3

Theorem 3.1 can be seen as a generalization of the inequalities in [32, Lemma A.3] and [20, Theorem 3]. We mention that [32, Lemma A.3] only concerns finite delay, and [20, Theorem 3] focuses on unbounded delay. Note also that our inequality given here takes a quite different form from the two in the literature mentioned above. It is in fact a discrete version of some integral Halanay-type inequalities with infinite delay in the literature.

To simplify the notation, in what follows we will write

$$ \vartheta (f)=\vartheta , \qquad \kappa (g)=\kappa . $$

To prove Theorem 3.1, let us first give an estimate for \(\|y_{n}\|\):

Lemma 3.4

Suppose that \(\kappa K^{*}< 1\). Let \(y\in {\mathscr{L}}(f; g; \rho )\), then

$$ \Vert y_{n} \Vert \leq c \Vert y_{0} \Vert +\mu \rho , \quad n \in {\mathbb{Z}}^{+}, $$
(3.6)

where μ and c are the constants defined in (3.2) and (3.4), respectively.

Proof

To prove (3.6), it suffices to check that for any \(\varepsilon >0\),

$$ \Vert y_{n} \Vert \leq c\bigl( \Vert y_{0} \Vert +\varepsilon \bigr)+\mu \rho , \quad n \in {\mathbb{Z}}^{+}. $$
(3.7)

For clarity, we write \(A_{\varepsilon }:=\|y_{0}\|+\varepsilon \). We argue by contradiction and suppose that (3.7) was false. Then, there would exist \(\ell \in {\mathbb{Z}}\) with \(\ell \geq 1\) such that

$$\begin{aligned} &\Vert y_{\ell} \Vert > cA_{\varepsilon }+\mu \rho , \end{aligned}$$
(3.8)
$$\begin{aligned} &\Vert y_{n} \Vert \leq cA_{\varepsilon }+\mu \rho , \quad n\in [0,\ell )_{{\mathbb{Z}}}. \end{aligned}$$
(3.9)

Combining (2.1), (3.1), and (3.9) we derive that

$$ \begin{aligned} \Vert y_{\ell} \Vert &\leq K(\ell )\sup _{k\in [0,\ell ]_{{\mathbb{Z}}}} \bigl\vert y(k) \bigr\vert +M( \ell ) \Vert y_{0} \Vert \\ &\leq K^{*}\sup_{k\in [0,\ell ]_{{\mathbb{Z}}}} \Biggl\{ f(k,0) \Vert y_{0} \Vert +\sum_{i=0}^{k}{g(k,i) \Vert y_{i} \Vert }+\rho \Biggr\} +M^{*} \Vert y_{0} \Vert \\ &\leq K^{*} \bigl\{ \vartheta A_{\varepsilon }+G(j) (cA_{\varepsilon }+ \mu \rho )+g(\ell ,\ell )\delta _{j\ell} \Vert y_{\ell} \Vert +\rho \bigr\} +M^{*} A_{\varepsilon }, \end{aligned} $$

where

$$ G(j)=\max \Biggl\{ \sup_{k\in [0,\ell -1]_{{\mathbb{Z}}}}\sum_{i=0}^{k}g(k,i), \sum_{i=0}^{\ell -1}g(\ell ,i) \Biggr\} $$

and j is the nonnegative integer such that the following equality is fulfilled:

$$ G(j)=\sum_{i=0}^{j-\delta _{j\ell}}g(j,i), $$

\(\delta _{j\ell}\) is the Kronecker symbol, i.e., \(\delta _{\ell \ell}=1\) and \(\delta _{j\ell}=0\) with \(j\neq \ell \). Hence,

$$ \bigl(1-K^{*}g(\ell ,\ell )\delta _{j\ell}\bigr) \Vert y_{\ell} \Vert \leq \bigl(K^{*} \vartheta +K^{*}G(j)c+M^{*}\bigr)A_{\varepsilon }+K^{*} \bigl(G(j)\mu +1\bigr)\rho . $$

Noting that \(1-K^{*}g(\ell ,\ell )\delta _{j\ell}\geq 1-\kappa K^{*}>0\), it follows from (3.8) that

$$ \begin{aligned} &\quad \bigl(1-K^{*}g(\ell ,\ell ) \delta _{j\ell} \bigr) (cA_{ \varepsilon }+\mu \rho ) \\ &< \bigl(1-K^{*}g(\ell ,\ell )\delta _{j\ell} \bigr) \Vert y_{\ell} \Vert \\ & \leq \bigl(K^{*}\vartheta +K^{*}G(j)c+M^{*} \bigr)A_{\varepsilon }+ \bigl(K^{*}G(j)\mu +K^{*} \bigr)\rho . \end{aligned} $$
(3.10)

Observing that

$$ \sup_{k\in [0,\ell ]_{{\mathbb{Z}}}}\sum_{i = 0}^{k}{g(k,i)}=G(j)+g( \ell ,\ell )\delta _{j\ell}, $$

by (3.10) and the assumption \(\sup_{k\in [0,\ell ]_{{\mathbb{Z}}}}\sum_{i = 0}^{k}{g(k,i)}\leq \kappa \), we deduce that

$$ \begin{aligned} cA_{\varepsilon }< {}& \Biggl(K^{*}\vartheta +\sup_{k\in [0,\ell ]_{{ \mathbb{Z}}}}\sum _{i = 0}^{k}{g(k,i)}K^{*}c+M^{*} \Biggr)A_{ \varepsilon } \\ & {}+ \Biggl(\sup_{k\in [0,\ell ]_{{\mathbb{Z}}}}\sum_{i = 0}^{k}{g(k,i)}K^{*} \mu +K^{*}-\mu \Biggr)\rho \\ \leq{}& \bigl(K^{*}\vartheta +\kappa K^{*}c+M^{*} \bigr)A_{ \varepsilon }+\bigl(\kappa K^{*}\mu +K^{*}-\mu \bigr) \rho \\ ={}&(\text{by (3.5)})= \bigl(K^{*}\vartheta +\kappa K^{*}c+M^{*} \bigr)A_{\varepsilon }. \end{aligned} $$
(3.11)

Since \(A_{\varepsilon }>0\), (3.11) implies \(c < (K^{*}\vartheta +M^{*})/(1-\kappa K^{*}) \leq c\), which is a contradiction. □

Remark 3.5

Let \(y \in {\mathscr{L}}(f;g;\rho )\). For \(\ell \in {\mathbb{Z}}^{+}\), if we set \(\tilde{y}(n)=y(n+\ell )\), and define

$$ \tilde{f}(n,m)=f(n+\ell ,m+\ell ), \qquad \tilde{g}(n,m)=g(n+\ell ,m+\ell ) $$

for \(n,m \in {\mathbb{Z}}^{+}\), then one easily checks that \(\tilde{y} \in {\mathscr{L}}(f;g;\rho )\) with

$$ \kappa (\tilde{g})K^{*} \leq \kappa (g)K^{*} \leq \kappa K^{*} < 1. $$

Thus, by Lemma 3.4 we see that

$$ \Vert y_{n+\ell} \Vert \leq c \Vert y_{n} \Vert +\mu \rho , \quad n,\ell \in {\mathbb{Z}}^{+}. $$
(3.12)

Proof of Theorem 3.1.

(1) We check the validity of the conclusion in (3.2).

Suppose the contrary. Then, since y is bounded (see Lemma 3.4), we would have

$$ \limsup_{n\rightarrow \infty} \Vert y_{n} \Vert = \mu \rho + \delta $$

for some \(\delta >0\). Take a nondecreasing sequence \(\tau _{n}\in {\mathbb{Z}}^{+}\) with \(\tau _{n}\rightarrow \infty \) such that \(\lim_{n\rightarrow \infty} \|y_{\tau _{n}}\|=\mu \rho +\delta \).

Let \(\varepsilon >0\) be arbitrary. Take a \(T>0\) sufficiently large such that

$$ \Vert y_{n} \Vert \leq \mu \rho +\delta +\varepsilon , \quad n\geq T. $$

Then, for each \(\tau _{n}>T\) and \(j\in {\mathbb{Z}}^{+}\) sufficiently large, by axiom (A0), we deduce that \(y_{\tau _{n}}, y_{\tau _{n+j}}\in \mathfrak{B}\), and

$$\begin{aligned} \Vert y_{\tau _{n+j}} \Vert \leq{}& K(\tau _{n+j}-\tau _{n})\sup_{k\in [\tau _{n}, \tau _{n+j}]_{{\mathbb{Z}}}} \bigl\vert y(k) \bigr\vert +M( \tau _{n+j}-\tau _{n}) \Vert y_{\tau _{n}} \Vert \\ \leq{}& (\text{by (3.1)})\leq K^{*}\sup _{k\in [\tau _{n}, \tau _{n+j}]_{{\mathbb{Z}}}} \Biggl\{ f(k,T) \Vert y_{T} \Vert +\sum _{i=T}^{k}g(k,i) \Vert y_{i} \Vert +\rho \Biggr\} \\ & {}\qquad\quad\qquad{}+ M(\tau _{n+j}-\tau _{n}) \Vert y_{\tau _{n}} \Vert \\ \leq{}& K^{*} \Bigl\{ \Bigl(\sup_{k\in [\tau _{n},\tau _{n+j}]_{{ \mathbb{Z}}}}f(k,T)+\kappa \Bigr) (\mu \rho +\delta +\varepsilon )+ \rho \Bigr\} + M(\tau _{n+j}-\tau _{n}) \Vert y_{\tau _{n}} \Vert . \end{aligned}$$

Setting \(j\rightarrow \infty \) in the above inequality, it follows from (2.3) that

$$ \mu \rho +\delta \leq K^{*} \Bigl\{ \Bigl(\sup_{k\in [\tau _{n}, \infty )_{{\mathbb{Z}}}}f(k,T)+ \kappa \Bigr) (\mu \rho +\delta + \varepsilon )+\rho \Bigr\} . $$

Since \(f\in \mathscr{F}\) and therefore \(\sup_{k\in [\tau _{n},\infty )_{{\mathbb{Z}}}}f(k,T)\rightarrow 0\) as \(\tau _{n}\rightarrow \infty \), setting \(n\rightarrow \infty \) in the above inequality this yields

$$ \mu \rho +\delta \leq K^{*} \bigl(\kappa (\mu \rho +\delta + \varepsilon )+\rho \bigr). $$

As ε is arbitrary, we finally obtain that

$$ \mu \rho +\delta \leq K^{*}(\kappa \mu +1)\rho +K^{*}\kappa \delta . $$

This and (3.5) imply that \(\delta \leq \kappa K^{*}\delta \), i.e., \(\kappa K^{*}\geq 1\), which leads to a contradiction and completes the proof of (3.2).

(2) Now, we assume that \(\kappa K^{*}<1/(1+M^{*}+K^{*}\vartheta )\). To derive the exponential decay estimate in (3.3), let us first prove a temporary result:

There exists a positive number \(\sigma < 1\) and an integer \(N>0\) such that if \(\|y_{0}\| \leq C+\gamma \rho \) with \(C>0\), then

$$ \Vert y_{n} \Vert \leq C \sigma ^{n}+ \gamma \rho , \quad n \geq N. $$
(3.13)

For this purpose, we take a real number λ as

$$ \lambda =\frac{1+(2r-1)\kappa K^{*}c}{2r}, \quad r=[\mu ]+2,$$
(3.14)

where μ is the number given in (3.2). (Here and below \([p]\) denotes the integer part of a real number p.) By Remark 3.2, it is easy to see that \(\lambda < 1\). Define

$$ \eta =\min \bigl\{ m \in [1,\infty )_{{\mathbb{Z}}}: \Vert y_{n} \Vert \leq \lambda C+\gamma \rho \text{ for all } n \geq m+1 \bigr\} . $$
(3.15)

Since \(\gamma > \mu \) (see (3.4)) and \(C >0\), by (3.2) it is clear that \(\eta < \infty \). Therefore, we necessarily have

$$ \Vert y_{\eta} \Vert >\lambda C +\gamma \rho . $$
(3.16)

In what follows let us give an estimate for the upper bound of η.

By (2.3), there exists a positive integer \(n_{0}\) such that

$$ M(n)c< \frac{1-\kappa K^{*}c}{4r}, \qquad M(n)\mu < \frac{1}{4}, \quad n\geq n_{0}. $$
(3.17)

As \(f\in {\mathscr{F}}\), we can also take a number \(n_{1}\in [0, \infty )_{{\mathbb{Z}}}\) with \(n_{0}< n_{1}\) such that

$$ f(m+n,m) < \min \biggl\{ \frac{1}{2K^{*}\gamma}, \frac{1-\kappa K^{*}c}{4rK^{*}} \biggr\} , \quad \forall n\geq n_{1}, m \in \mathbb{Z^{+}}. $$
(3.18)

Let \(\tau =[\eta /2]\), and set

$$ b(\eta ):=\sup_{k\in [\tau , \eta ]_{{\mathbb{Z}}}}f(k,0). $$

In what follows we show that

$$ \tau \leq n_{1}. $$

It then follows that

$$ \eta \leq 2(n_{1}+1), $$

which is precisely what we desired.

We argue by contradiction and suppose \(\tau >n_{1}\). Then, by (3.18) it can be easily seen that

$$ b(\eta )< \min \biggl\{ \frac{1}{2K^{*}\gamma}, \frac{1-\kappa K^{*}c}{4rK^{*}} \biggr\} . $$
(3.19)

On the other hand, by (2.1) we have

$$\begin{aligned} \Vert y_{\eta} \Vert \leq{}& K(\eta -\tau )\sup_{k\in [\tau ,\eta ]_{{\mathbb{Z}}}} \bigl\vert y(k) \bigr\vert +M( \eta -\tau ) \Vert y_{\tau} \Vert \\ \leq{}& (\text{by (3.1)})\leq K^{*}\sup _{k\in [\tau ,\eta ]_{{ \mathbb{Z}}}} \Biggl\{ f(k,0) \Vert y_{0} \Vert +\sum _{i=0}^{k}g(k,i) \Vert y_{i} \Vert + \rho \Biggr\} \\ &{}\qquad \quad \qquad{} + M(\eta -\tau ) \Vert y_{\tau} \Vert \\ \leq{}& (\text{by (3.12)})\leq K^{*} \bigl\{ b(\eta ) \Vert y_{0} \Vert + \kappa \bigl(c \Vert y_{0} \Vert +\mu \rho \bigr)+\rho \bigr\} + M(\eta -\tau ) \Vert y_{\tau} \Vert \\ \leq{}& \bigl( K^{*}b(\eta )+\kappa K^{*}c\bigr) \Vert y_{0} \Vert +K^{*}(\kappa \mu +1) \rho +M(\eta -\tau ) \bigl(c \Vert y_{0} \Vert +\mu \rho \bigr) \\ \leq{}& (\text{by (3.5)})\leq \bigl( K^{*}b(\eta )+\kappa K^{*}c\bigr) \Vert y_{0} \Vert +\mu \rho +M(\eta -\tau ) \bigl(c \Vert y_{0} \Vert +\mu \rho \bigr). \end{aligned}$$

Noting that \(\eta -\tau \geq \tau >n_{1}>n_{0}\), it follows from (3.17) that

$$ \Vert y_{\eta} \Vert \leq \biggl( K^{*}b(\eta )+\kappa K^{*}c+ \frac{1-\kappa K^{*}c}{4r} \biggr) \Vert y_{0} \Vert + \biggl(\mu +\frac{1}{4} \biggr)\rho . $$

Since \(\|y_{0}\| \leq C+\gamma \rho \), we infer from the above estimate that

$$ \begin{aligned} \Vert y_{\eta} \Vert \leq{}& \biggl( K^{*}b(\eta )+\kappa K^{*}c+ \frac{1-\kappa K^{*}c}{4r} \biggr)C \\ &{} + \biggl(K^{*}b(\eta )\gamma +\kappa K^{*}c\gamma + \frac{(1-\kappa K^{*}c)\gamma }{4r}+\mu +\frac{1}{4} \biggr)\rho .\end{aligned} $$
(3.20)

By the definitions of γ and r (see (3.4) and (3.14)) one easily verifies that

$$ \frac{(1-\kappa K^{*}c)\gamma }{4r}=\frac{1+\mu}{4r}< \frac{1}{4}. $$

Therefore, by (3.16) and (3.20), we deduce that

$$ \begin{aligned} \lambda C+\gamma \rho < {}& \Vert y_{\eta} \Vert \leq{} \biggl( K^{*}b(\eta )+ \kappa K^{*}c+\frac{1-\kappa K^{*}c}{4r} \biggr)C \\ &{}\qquad \qquad {} + \biggl(K^{*}b(\eta )\gamma +\kappa K^{*}c\gamma +\mu + \frac{1}{2} \biggr)\rho . \end{aligned} $$
(3.21)

The definition of γ and (3.19) also imply that

$$ \gamma =1+\kappa K^{*}c\gamma +\mu > K^{*}b(\eta )\gamma + \kappa K^{*}c \gamma +\mu +\frac{1}{2}, $$

by which we find that the second term in the right-hand side in (3.21) is less than γρ. Combining this with (3.21) yields

$$ \lambda C < \biggl( K^{*}b(\eta )+\kappa K^{*}c+ \frac{1-\kappa K^{*}c}{4r} \biggr)C. $$

Hence,

$$ b(\eta ) > \frac{4r(\lambda -\kappa K^{*}c)-(1-\kappa K^{*}c)}{4rK^{*}}= \frac{1-\kappa K^{*}c}{4rK^{*}}, $$

which contradicts (3.19).

By the definition of η in (3.15), we have proved that if \(\|y_{0}\|\leq C+\gamma \rho \) then

$$ \Vert y_{n} \Vert \leq \lambda C+\gamma \rho , \quad \forall n\geq \eta +1 =: N. $$

Note that the constants λ, γ, and η are independent of C.

Define

$$ \tilde{y}(n)=y(n+N), \quad n\in {\mathbb{Z}}. $$

Then, ỹ satisfies a similar inequality as y does. Since \(\|\tilde{y}_{0}\| \leq \lambda C+\gamma \rho \), the same argument as above applies to show that

$$ \Vert \tilde{y}_{n} \Vert \leq \lambda (\lambda C)+\gamma \rho , \quad \forall n\geq N, $$

i.e.,

$$ \Vert y_{n} \Vert \leq {\lambda}^{2} C+\gamma \rho , \quad \forall n\geq 2N. $$

Repeating the above procedure we finally obtain that

$$ \Vert y_{n} \Vert \leq {\lambda}^{k} C+ \gamma \rho ,\quad n \geq k N, k=1,2,\cdots . $$
(3.22)

Setting \(\sigma =\exp \{\ln \lambda /(2N)\}\), one has

$$ {\lambda}^{k} \leq \sigma ^{n}, \quad n \in \bigl[kN,(k+1)N \bigr]_{{\mathbb{Z}}}, k=1,2,\cdots . $$

The estimate (3.13) then follows from (3.22).

We are now in a position to accomplish the proof of the theorem.

Note that (3.12) implies that if \(\|y_{0}\|=0\), then

$$ \Vert y_{n} \Vert \leq \mu \rho \leq \gamma \rho , \quad n \in { \mathbb{Z}}^{+}, $$

and therefore the conclusion trivially holds true. Thus, we assume \(\|y_{0}\|>0\).

Take \(C=\|y_{0}\|\). Clearly \(\|y_{0}\|=C \leq C+\gamma \rho \). Therefore, by (3.13) we have

$$ \Vert y_{n} \Vert \leq \Vert y_{0} \Vert \sigma ^{n}+\gamma \rho , \quad n \in [N,\infty )_{{\mathbb{Z}}}. $$
(3.23)

On the other hand, by (3.6) we deduce that

$$ \Vert y_{n} \Vert \leq c \Vert y_{0} \Vert +\mu \rho \leq c \Vert y_{0} \Vert +\gamma \rho , \quad n \in [0,N]_{{\mathbb{Z}}}. $$

Set \(B=c\sigma ^{-N}\). Then,

$$ \Vert y_{n} \Vert \leq c \Vert y_{0} \Vert +\gamma \rho \leq B\sigma ^{n} \Vert y_{0} \Vert + \gamma \rho , \quad n \in [0,N]_{{\mathbb{Z}}}. $$

Combining this with (3.23) we immediately arrive at the estimate (3.3). □

4 Asymptotic stability of nonautonomous difference equations with infinite delay

As an application for Theorem 3.1, we now consider the asymptotic stability of the null solution of system (1.1). Assume that the mapping G in (1.1) satisfies the following hypotheses:

  1. (G1)

    There is a mapping \(c:{{\mathbb{Z}}}\times {\mathbb{Z}}\rightarrow {\mathbb{R}}^{+}\) such that

    $$ \bigl\vert G(n,s,y) \bigr\vert \leq c(n,s) \vert y \vert , \quad (n,s,y)\in {{\mathbb{Z}}}\times {\mathbb{Z}}\times {\mathbb{R}}^{N}, {s \leq n}.$$
    (4.1)
  2. (G2)

    There is \(p>0\) such that

    $$ \beta (n):=\sum^{n}_{s=-\infty }c(n,s)e^{p(n- s)}< \infty , \quad \forall n\in {{\mathbb{Z}}}. $$

Note that (4.1) implies \(G(n,s,0)=0\) for all \(n,s\in { \mathbb{Z}}\), \(s\leq n\), hence \(y(n)\equiv 0\) is a solution of (1.1).

Define

$$ \mathfrak{B}^{p} := \Bigl\{ \phi \in {\mathcal {S}} \bigl({\mathbb{Z}}^{-}; {\mathbb{R}}^{N} \bigr): \Vert \phi \Vert :=\sup _{k\in {\mathbb{Z}}^{-}} \bigl( \bigl\vert \phi (k) \bigr\vert e^{p k} \bigr)< \infty \Bigr\} . $$

It is easy to check that \((\mathfrak{B}^{p} ,\|\cdot \|)\) is an admissible phase space for equation (1.1) with the corresponding constants in axioms (A0) and (A1) to be taken as

$$ N_{0}=K^{*}=M^{*}=1, \qquad M(n)=e^{-p n}. $$

(In what follows we will also use the notation \(\|\cdot \|\) to denote the operator norm of a matrix, hoping that this will cause no confusion.)

Given \(m\in {\mathbb{Z}}\), denote by \(y(n;m,\phi )\) the solution \(y = y(n)\) of equation (1.1) with initial value \(y_{m}=\phi \in \mathfrak{B}^{p}\). Write

$$ {E(n,m):=\prod^{n-1}_{k=m} \bigl\Vert I+A(k) \bigr\Vert }, \quad n, m\in {\mathbb{Z}}, $$

where I denotes the identity matrix. (By the convention in Sect. 2, if \(n-1< m\) then we assign \(E(n,m)=1\).) Set

$$ \vartheta = \sup_{n \geq m }{E(n,m)}, \qquad \kappa = \sup _{n \geq m } \Biggl(\sum_{k =m}^{n}{E(n,k+1)} \beta (k) \Biggr). $$

Theorem 4.1

Suppose that \(\|I+A(n)\|\neq 0\) for all \(n\in {\mathbb{Z}}\), and that

$$ E(m+n,m)\rightarrow 0\ \textit{as }n\rightarrow +\infty \textit{ uniformly with respect to }m\in {\mathbb{Z}}. $$
  1. (1)

    If \(\kappa < 1\), then the null solution 0 of equation (1.1) is GAS.

  2. (2)

    If \(\kappa <1/(2+\vartheta )\), then it is GEAS.

Proof

We first show that for any solution \(y=y(n,m;\phi )\) of equation (1.1),

$$ \Vert y_{n} \Vert \leq c \Vert \phi \Vert , \quad n\geq m, $$
(4.2)

where \(c>0\) is a constant that is defined as in (3.4) and is therefore independent of \(m\in {\mathbb{Z}}\). Hence, the zero solution is stable.

For simplicity, we may put \(m=0\). Solving (1.1) by variation of constants formula for difference equations (see, e.g., [13, §2.5.]) we find that

$$ y(n)= \prod_{k=\tau}^{n-1} \bigl(I+A(k) \bigr)y(\tau )+\sum_{k = \tau }^{n-1}\prod _{j=k+1}^{n-1} \bigl(I+A(j) \bigr)h(k,y_{k}), \quad n\geq \tau \geq 0, $$

where \(h(n,y_{n})=\sum^{n}_{s=-\infty }G(n,s,y(s))\). By (G1) and (G2) we have

$$ \begin{aligned} \bigl\vert h(n,y_{n}) \bigr\vert &\leq \sum^{n}_{s=-\infty }c(n,s) \bigl\vert y(s) \bigr\vert \\ &\leq \sum^{n}_{s=- \infty } \bigl(c(n,s)e^{p (n-s)} \bigr) \bigl(e^{-p(n-s)} \bigl\vert y(s) \bigr\vert \bigr) \\ &= \sum^{n}_{s=-\infty } \bigl(c(n,s)e^{p (n-s)} \bigr) \bigl(e^{-p(n-s)} \bigl\vert y_{n}(s-n) \bigr\vert \bigr) \\ &\leq \sum^{n}_{s=-\infty } \bigl(c(n,s)e^{p (n-s)} \bigr) \Vert y_{n} \Vert = \beta (n) \Vert y_{n} \Vert . \end{aligned} $$

Making use of the property of the norm \(\|\cdot \|\) of \(\mathfrak{B}^{p}\) as stated in (2.1) and the above estimate, we easily derive that

$$ \bigl\vert y(n) \bigr\vert \leq E(n,\tau ) \Vert y_{\tau} \Vert +\sum^{n-1}_{k=\tau}E(n,k+1) \beta (k) \Vert y_{k} \Vert , \quad \forall n \geq \tau \geq 0. $$
(4.3)

Since \(\kappa < 1\), by Lemma 3.4 one immediately concludes the validity of (4.2).

To prove assertion (1), it remains to check that for any solution \(y=y(n,m;\phi )\) of equation (1.1),

$$ y(n)\rightarrow 0\ \text{as }n\rightarrow +\infty .$$
(4.4)

As above, once again we can put \(m=0\). Then, y satisfies the inequality (4.3). The asymptotic property in (4.4) then directly follows from Theorem 3.1(1).

Assertion (2) can be obtained by making use of the inequality in (4.3) and applying Theorem 3.1(2). We omit the details. □

Remark 4.2

The global exponential stability of the null solution for difference equations like (1.1) was extensively studied in Ngoc and Hieu [31] by using the Perron–Frobenius theory. We mention that our result and method here are different from those in [31] in some aspects.

Example 4.3

Consider the difference equation:

$$ \Delta y(n)= - \biggl(\sin \frac{2\pi n}{3} \biggr) y(n)+\sum ^{n}_{s=- \infty }\frac{1}{3^{n-s}}g\bigl(y(s) \bigr),$$
(4.5)

where \(\Delta y(n)=y(n+1)-y(n)\), g is a globally Lipschitz continuous function with Lipschitz constant L and \(g(0)=0\).

We observe that \(G(n,s,y)=\frac{1}{3^{n-s}}g(y)\) satisfies (G1) and (G2) with \(p=\ln 2\) and \(\beta (n)\equiv 3L\). Since \(\sin \frac{2\pi n}{3}\) is a periodic function with period 3, for each \(k\in {\mathbb{Z}}^{+}\), we have

$$\begin{aligned} E(m+3k+1,m) :=&\prod^{m+3k}_{j=m} \biggl\vert 1-\sin \frac{2\pi j}{3} \biggr\vert \\ =& \biggl(1-\sin \frac{2\pi m}{3} \biggr) \biggl(\frac{1}{4} \biggr)^{k} \\ \leq& \biggl(1+\frac{\sqrt{3}}{2} \biggr) \biggl(\frac{1}{4} \biggr)^{k}. \end{aligned}$$

Thus, \(E(m+n,m)\rightarrow 0\) as \(n\rightarrow +\infty \) uniformly with respect to \(m\in {\mathbb{Z}}\). It is also easy to check that \({\vartheta }=1+\frac{\sqrt{3}}{2}\), and

$$ \kappa =3L\sup_{n \geq m \geq 0} \Biggl(\sum_{k =m}^{n-1}{E(n-1,k+1)} \Biggr) \leq (12+2\sqrt{3} )L. $$

According to Theorem 4.1, we deduce the following results.

Proposition 4.4

If \(L <1/ (12+2\sqrt{3} ) {\approx 0.064665}\), then the null solution of equation (4.5) is GAS in \(\mathfrak{B}^{\ln 2}\); and if \(L <1/ (39+12\sqrt{3} ) {\approx 0.016726}\), then it is GEAS in \(\mathfrak{B}^{\ln 2}\).

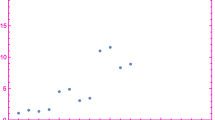
We now give the numerical simulation of equation (4.5) via Matlab to verify the correctness of our results. For simplicity, we assume that \(g(x)=Lx\) and

$$ y(n)=1, \quad \forall n\in {\mathbb{Z}}^{-}. $$

Thus, \(y_{0}\in \mathfrak{B}^{\ln 2}\). Indeed,

$$ \Vert y_{0} \Vert :=\sup_{k\in {\mathbb{Z}}^{-}} \bigl( \bigl\vert y(k) \bigr\vert e^{ ( \ln 2 ) k} \bigr)=\sup_{k\in {\mathbb{Z}}^{-}}2^{k}=1< \infty . $$

Taking \(L=0.0645\) and \(L=0.0165\), our PC produces Fig. 1 and Fig. 2 as follows.

Figure 1
figure 1

\(L=0.0645\)

Full size image
Figure 2
figure 2

\(L=0.0165\)

Full size image

Remark 4.5

We remark that the global exponential stability of the null solution of equation (4.5) can not be derived by applying [31, Theorem 3.2 or Corollary 3.5]. Indeed, if we take \(n=3k-1\) (\(k=0,1,\cdots \)) in this example, then

$$ 1- \biggl(\sin \frac{2\pi (3k-1)}{3} \biggr)=1+\frac{\sqrt{3}}{2}>1, $$

which indicates that the conditions required in [31, Theorem 3.2 or Corollary 3.5] are not satisfied.