Hyers–Ulam stability of non-autonomous and nonsingular delay difference equations

Abstract

In this paper, we study the uniqueness and existence of the solution of a non-autonomous and nonsingular delay difference equation using the well-known principle of contraction from fixed point theory. Furthermore, we study the Hyers–Ulam stability of the given system on a bounded discrete interval and then on an unbounded interval. An example is also given at the end to illustrate the theoretical work.

1 Introduction

In most of the fields of science like mathematics, statistics, economics, and engineering, people take the number of samples as a discrete form, not in a continuous form. In real life, some model such as [1–4] are used to analyze the real life problems from mechanics and biomathematics by means of partial differential equations, but some models like cobweb [5] and national income model [6] can be described by difference equations. People study difference equations because of their many applications in population models and information transmission. S.A. Kuruklis [7] and J.S. Yu [8] studied the asymptotic behavior of the variable type delay difference equation. W. Kosmala [9] provided a good insight and discussed the behavior of solution of the difference equation of the type $U_{k+1}=(A+U_{k-1})/(BU_{k}+U_{k-1})$. Zheng-Fan Liu [10] designed the exponential behavior of switch discrete-time delay system. Marwen Kermani [11] discussed the stability techniques about the switched nonlinear time-delay difference equations. Yuanyuan Liu [12] described the stability techniques of a higher-order difference system. The stability of higher-order rational difference systems was studied by A. Khaliq [13].

A difference system has a lot of qualitative properties, among them stability is a very useful property. It is a vital part for a system to work appropriately. There are many types of stability, but today’s general interest that leads people to want to know more is about Hyers–Ulam stability. Ulam [14], in 1940, initially studied the theory of Hyers–Ulam stability. When he lectured a seminar, he put out some problems related to the group homomorphisms stability. A year later, Hyers [15] answered brightly to the problem by considering that groups are Banach spaces, specified by Hyers–Ulam stability. Rassias [16], in 1978, gave an outstanding general approach of the Hyers–Ulam stability, specified by Hyers–Ulam–Rassias stability. In particular, he also extended the same concept to Cauchy difference equation. This idea was then extended to differential equations by Obloza [17]. Later on, this stability of difference equations was proved by Jung [18] and Khan et al. [19].

Delay systems can have a lot of uses in the characterization of the evolution process in automatic engine, physiology system, and control theory. Khusainov and Shuklin [20] solved the linear autonomous delay-time system with commutable matrices. Diblik and Khusainov [21] gave the description about the solutions of a discrete delayed system using the idea [20]. Then Wang et al. [22] studied relative controllability and exponential stability of nonsingular systems. The consequences about Ulam stability of nonsingular delay differential equation having first order were shown by A. Zada et al. [23]. Recently, some results on Ulam type stability of a first-order nonlinear impulsive time varying delay dynamic system was discussed by S.O. Shah et al. in [24, 25].

In this study, we discuss the Hyers–Ulam stability of nonsingular delay difference system of the form:

$$ \textstyle\begin{cases} \mathbb{A}\mathbf{G}_{n+1}=\mathbf{M}\mathbf{G}_{n}+\mathcal{N} \mathbf{G}_{n-k}+\mathbb{F}(n,\mathbf{G}_{n-k}), \quad n\geq 0, k\geq 0, \\ \mathbf{G}_{n}=\phi _{n}, \quad -k\leq n\leq 0, \end{cases} $$

(1.1)

where the constant matrices $\mathbb{A}$, M, and $\mathcal{N}$ are commutable having order $n\times n$. The matrix A is invertible and $\phi \in \mathcal{B}(\mathbb{Z}_{+},X)$, where $\mathcal{B}(\mathbb{Z}_{+},X)$ is the space of bounded sequences, also $\mathbb{F}\in \mathcal{CS}(\mathbb{Z}_{+}\times X,X)$, the space of all convergent sequences, where $I=\{-k,-k+1,\ldots,0\}$, $\mathbb{Z}_{+}=\{0,1,2,\ldots \}$ and $X=\mathcal{R}^{n}$. Such work in the continuous case is given in [26].

2 Preliminaries

In this portion, we discuss some definitions and basic concepts which are useful for establishing the main work. We will use the notation $\mathcal{R}$, $\mathcal{R}^{+}$, $\mathcal{Z}_{+}$ for the real numbers, non-native real numbers, all nonnegative integers, and the space of all n-tuples of $\mathcal{R}$ is denoted by $\mathcal{R}^{n}$. The set $J=\{0,1,\ldots,k\}$ is the subset of $\mathcal{Z}$ and $X=\mathcal{R}^{n}$, the space of all bounded and convergent sequences from J to X is represented by $\mathcal{CS}(J,X)$ with the norm

$$ \Vert \mathbf{G} \Vert _{cs}= \Bigl\{ \sup_{n\in J} \bigl\Vert \mathbf{G}(n) \bigr\Vert \text{ for all } \mathbf{G}\in \mathcal{CS}(J,X) \Bigr\} . $$

Besides, we define $\mathcal{C}^{1}(J,X)=\{\mathbf{G}\in \mathcal{C}(J,X) ; \mathbf{G}'\in \mathcal{C}^{1}(J,X)\}$.

Lemma 2.1

The nonsingular delay difference system

$$ \textstyle\begin{cases} A\mathbf{G}_{n+1}=M\mathbf{G}_{n}+N\mathbf{G}_{n-k}+\mathbb{F}(n, \mathbf{G}_{n-k}), \quad n\geq 0, k\geq 0, \\ \mathbf{G}_{n}=\Phi _{n}, \quad -k\leq n\leq 0, \end{cases} $$

has the solution

$$\begin{aligned} \mathbf{G}_{n} =& M^{n}A^{-n }\Phi _{0}+M^{n-1}A^{-n}\sum_{i=0}^{k}M^{-i}A^{i} { \bigl(}N\Phi _{i-k}+\mathbb{F}(i,\Phi _{i-k}) { \bigr)} \\ &{}+ M^{n-1}A^{-n}\sum_{i=k+1}^{n}M^{-i}A^{i} { \bigl(}N\mathbf{G}_{i-k}+ \mathbb{F}(i,\mathbf{G}_{i-k}) { \bigr)}, \end{aligned}$$

where $MN=NM$, $NA=AN$, and $MA=AM$.

The proof can be easily obtained by successively putting the values of $n \in \{-k,-k+1,\ldots\}$.

Definition 2.1

The solution of system (1.1) will be exponentially stable if there exist positive real numbers $\lambda _{1}$ and $\lambda _{2}$ such that

$$ \Vert \mathbf{G}_{n} \Vert \leq \lambda _{1}e^{-\lambda _{2}n}, \quad \forall n \geq 0. $$

Definition 2.2

For a positive real number ϵ, the sequence $\boldsymbol{\psi}_{n}$ is said to be an ϵ-approximate solution of (1.1) if

$$ \textstyle\begin{cases} \Vert A\boldsymbol{\psi}_{n+1}-M\boldsymbol{\psi}_{n}-N\boldsymbol{\psi}_{n-k}- \mathbb{F}(n,\boldsymbol{\psi}_{n-k}) \Vert \leq \epsilon , \quad n\geq 0, k\geq 0, \\ \Vert \boldsymbol{\psi}_{n}-\phi _{n} \Vert \leq \epsilon , \quad -k\leq n\leq 0. \end{cases} $$

(2.1)

Definition 2.3

System (1.1) will be Hyers–Ulam stable if, for every ϵ-approximate solution $\boldsymbol{\psi}_{n}$ of system (1.1), there will be an exact solution $\mathbf{Y}_{n}$ of (1.1) and a nonnegative real number K such that

$$ \Vert \mathbf{Y}_{n}-\boldsymbol{\psi}_{n} \Vert \leq \mathbf{K}\epsilon , \quad n\in J. $$

Definition 2.4

A function $\Vert \cdot \Vert _{\beta }:\mathbb{V}\rightarrow [0,\infty )$ is called β-norm, with $0<\beta \leq 1$, where $\mathbb{V}$ is a vector space over field K, if the function satisfies the following properties:

• (1) $\Vert \mathcal{H} \Vert _{\beta }=0$ if and only if $\mathcal{G}=0$;

• (2) $\Vert \kappa \mathcal{H} \Vert _{\beta }= \vert \kappa \vert ^{\beta } \Vert \mathcal{H} \Vert _{ \beta }$ for each $\kappa \in \mathbf{K}$ and $\mathcal{H}\in \mathbb{V}$;

• (3) $\Vert \mathcal{H}+\mathcal{H}_{1} \Vert _{\beta }\leq \Vert \mathcal{H} \Vert _{\beta }+ \Vert \mathcal{H}_{1} \Vert _{\beta }$ for all $\mathcal{H}, \mathcal{H}\in \mathbb{V}$.

And $(\mathbb{V}, \Vert \cdot \Vert _{\beta })$ is said to be a β-norm space.

Lemma 2.2

If $z_{n}$ and $g_{n}$ are nonnegative sequences and $a\geq 0$, which satisfies the inequality

$$ \Vert z_{n} \Vert \leq a+\sum_{i=0}^{n} \Vert g_{i} \Vert \Vert z_{i} \Vert , \quad n\geq 0, $$

then

$$ \Vert z_{n} \Vert \leq a \exp { \Biggl(} \sum _{i=0}^{n} \Vert z_{i} \Vert { \Biggr)}. $$

Remark 2.1

It is clear from (2.1) that $\mathbf{Y}\in \mathcal{C}^{1}(J,X)$ satisfies (2.1) if and only if there exists $f\in \mathcal{CS}(J,X)$ satisfying

$$ \textstyle\begin{cases} \Vert f_{n} \Vert \leq \epsilon , \quad n \in J, \\ \mathbb{A}\mathcal{Y}_{n+1}=\mathbf{M}\mathcal{Y}_{n}+\mathcal{N} \mathcal{Y}_{n-k}+\mathbb{F}(n,\mathcal{Y}_{n-k})+{f}_{n}, \quad n\in \mathbb{Z}_{+} , \\ \mathcal{Y}_{n}=\phi _{n},\quad -k\leq n \leq 0. \end{cases} $$

3 Existence result

To describe the existence result of the system given by (1.1), we have the following assumptions which will be needed:

$\Lambda _{1}$::

The linear system $A\mathbf{G}_{n+1}=M\mathbf{G}_{n}+N\mathbf{G}_{n-k}$ is well modeled.

$\Lambda _{2}$::

The continuous function $\mathcal{H}:J\times X \rightarrow X$ satisfies the Caratheodory condition

$$ \bigl\Vert \mathcal{H}(n,f)-\mathcal{H} \bigl(n,f^{\prime } \bigr) \bigr\Vert \leq \mathcal{K} \bigl\Vert f-f^{\prime } \bigr\Vert , \quad \mathcal{K}\geq 0, $$

for every $f, f^{\prime }\in X$.

$\Lambda _{3}$::

$\mathcal{M}^{n-1}\mathcal{A}^{-n}(N+\mathcal{K})L<1$.

Theorem 1

If assumptions $\Lambda _{1}$–$\Lambda _{3}$ hold, then system (1.1) has the unique solution $\mathbf{G}\in \mathcal{B}(J,X)$.

Proof

Define $T:\mathcal{B}(J,X)\rightarrow \mathcal{B}(J,X)$ by

$$\begin{aligned} (T\mathbf{G})_{n} =&\mathbf{M}^{n}\mathbb{A}^{-n } \phi _{0}+ \mathbf{M}^{n-1}\mathbb{A}^{-n}\sum _{i=0}^{k}\mathbf{M}^{-i} \mathbb{A}^{i} { \bigl(}\mathcal{N}\phi _{j-k}+\mathbb{F}(i, \phi _{i-k}) { \bigr)} \\ &{}+ \mathbf{M}^{n-1}\mathbb{A}^{-n}\sum _{i=k+1}^{n}\mathbf{M}^{-i} \mathbb{A}^{i} { \bigl(}\mathcal{N}\mathbf{G}_{i-k}+ \mathbb{F}(i, \mathbf{G}_{i-k}) { \bigr)}. \end{aligned}$$

Now, for any $\mathbf{G}, \mathbf{G}^{\prime }\in \mathcal{B}(J,X)$, we have

$$\begin{aligned} \bigl\Vert (T\mathbf{G})_{n}- \bigl(T\mathbf{G}' \bigr)_{n} \bigr\Vert =& { \Biggl\Vert }\mathbf{M}^{n} \mathbb{A}^{-n }\phi _{0}+\mathbf{M}^{n-1} \mathbb{A}^{-n}\sum_{i=0}^{k} \mathbf{M}^{-i}\mathbb{A}^{i} { \bigl(}\mathcal{N}\phi _{i-k}+ \mathbb{F}(i,\phi _{i-k}) { \bigr)} \\ &{}+ \mathbf{M}^{n-1}\mathbb{A}^{-n}\sum _{i=k+1}^{n}\mathbf{M}^{-i} \mathbb{A}^{i} { \bigl(}\mathcal{N}\mathbf{G}_{i-k}+ \mathbb{F}(i, \mathbf{G}_{i-k}) { \bigr)} \\ &{}- \mathbf{M}^{n-1}\mathbb{A}^{-n}\phi _{0}- \mathbf{M}^{n-1} \mathbb{A}^{-n}\sum _{i=k+1}^{n}\mathbf{M}^{-i} \mathbb{A}^{i} { \bigl(} \mathcal{N}\phi _{i-k}+\mathbb{F}(i, \phi _{i-k}) { \bigr)} \\ &{}- \mathbf{M}^{n-1}\mathbb{A}^{-n}\sum _{i=k+1}^{n}\mathbf{M}^{-i} \mathbb{A}^{i} { \bigl(}\mathcal{N}\mathbf{G'}_{i-k}+ \mathbb{F} \bigl(i, \mathbf{G'}_{i-k} \bigr) { \bigr)} { \Biggr\Vert }. \end{aligned}$$

This implies that

$$\begin{aligned} \bigl\Vert (T\mathbf{G})_{n}- \bigl(T\mathbf{G}^{\prime } \bigr)_{n} \bigr\Vert \leq & \bigl\Vert \mathbf{M}^{n-1} \bigr\Vert \bigl\Vert \mathbb{A}^{-n} \bigr\Vert \sum _{i=k+1}^{n} \bigl\Vert \mathbf{M}^{-i} \bigr\Vert \bigl\Vert \mathbb{A}^{i} \bigr\Vert { \bigl(} \bigl\Vert \mathcal{N}\mathbf{G}_{i-k}-\mathcal{N} \mathbf{G^{\prime }}_{i-k} \bigr\Vert \\ &{}+ \bigl\Vert \mathbb{F}(i,\mathbf{G}_{i-k})-\mathbb{F} \bigl(i, \mathbf{G^{\prime }}_{i-k} \bigr) \bigr\Vert { \bigr)} \\ \leq & \bigl\Vert \mathbf{M}^{n-1} \bigr\Vert \bigl\Vert \mathbb{A}^{-n } \bigr\Vert \sum_{i=k+1}^{n} \mathbf{M}^{-i}\mathbb{A}^{i} { \bigl(} \bigl\Vert \mathcal{N}\mathbf{G}_{i-k}- \mathcal{N}\mathbf{G^{\prime }}_{i-k} \bigr\Vert \\ &{}+ \mathcal{K} \bigl\Vert \mathbf{G}_{i-k}-\mathbf{G'}_{i-k} \bigr\Vert { \bigr)} \\ =& \bigl\Vert \mathbf{M}^{n-1} \bigr\Vert \bigl\Vert \mathbb{A}^{-n} \bigr\Vert (\mathcal{N}+\mathcal{K}) \sum _{i=k+1}^{n}\mathbf{M}^{-i} \mathbb{A}^{i} \bigl\Vert \mathbf{G}_{i-k}- \mathbf{G^{\prime }}_{i-k} \bigr\Vert \\ \leq & \bigl\Vert \mathbf{M}^{n-1} \bigr\Vert \bigl\Vert \mathcal{A}^{-n} \bigr\Vert (\mathcal{N}+ \mathcal{K})L \bigl\Vert \mathbf{G}-\mathbf{G^{\prime }} \bigr\Vert _{\mathcal{B}}. \end{aligned}$$

Thus, T is a contraction if $\Vert \mathbf{M}^{n} \Vert \Vert \mathbb{A}^{-n} \Vert (\mathcal{N}+\mathcal{K})L < 1$, so (by BCP) it has a unique fixed point and will be the solution of system(1.1). □

4 Hyers–Ulam stability on bounded discrete interval

To describe the Hyers–Ulam stability of system (1.1) over a bounded discrete interval, we have to put some assumptions:

$\Lambda _{1}$::

The linear system $A\mathbf{G}_{n+1}=M\mathbf{G}_{n}+N\mathbf{G}_{n-k}$ is well posed.

$\Lambda _{2}$::

The map $F:J\times X \rightarrow X$ satisfies the Caratheodory condition

$$ \bigl\Vert F(n,\vartheta )-F \bigl(n,\vartheta ^{\prime } \bigr) \bigr\Vert \leq \mathrm{K} \bigl\Vert \vartheta - \vartheta ^{\prime } \bigr\Vert $$

for some $\mathrm{K}\geq 0$ and for all $\vartheta , \vartheta ^{\prime }\in \mathcal{B}(J,X)$.

$\Lambda _{3}$::

There exists nondecreasing $\varphi _{n} \in \mathcal{B}(J,X)$ with a constant η such that

$$ \sum_{r=1}^{n-k}\phi _{r}\leq \eta \varphi _{n} \quad \text{for each } n \in J. $$

Theorem 2

If $\Lambda _{1}$, $\Lambda _{2}$, and $\Lambda _{3}$ along with (2.1) and Remark 2.1hold, then system (1.1) is Hyers–Ulam stable.

Proof

The solution of delay difference equation

$$ \textstyle\begin{cases} A\mathbf{G}_{n+1}=M\mathbf{G}_{n}+N\mathbf{G}_{n-k}+\mathbb{F}(n, \mathbf{G}_{n-k}), \quad n\geq 0, k\geq 0, \\ \mathbf{G}_{n}=\Psi _{n}, \quad -k\leq n\leq 0, \end{cases} $$

is

$$\begin{aligned} \mathbf{G}_{n} =& M^{n}A^{-n }\Psi _{0}+M^{n-1}A^{-n}\sum_{i=0}^{k}M^{-i}A^{i} { \bigl(}N\Psi _{i-k}+\mathbb{F}(i,\Psi _{i-k}) { \bigr)} \\ &{}+ M^{n-1}A^{-n}\sum_{i=k+1}^{n}M^{-i}A^{i} { \bigl(}N\mathbf{G}_{i-k}+ \mathbb{F}(i,\mathbf{G}_{i-k}) { \bigr)}. \end{aligned}$$

From Remark 2.1 the solution of

$$ \textstyle\begin{cases} A\mathbb{Y}_{n+1}=M\mathbb{Y}_{n}+N\mathbb{Y}_{n-k}+\mathbb{F}(n, \mathbb{Y}_{n-k})+\mathbf{f}_{n}, \quad n\geq 0, k\geq 0, \\ \mathbb{Y}_{n}=\Psi _{n}, \quad -k\leq n\leq 0, \end{cases} $$

is

$$\begin{aligned} \mathbb{Y}_{n} =& M^{n}A^{-n }\Psi _{0}+M^{n-1}A^{-n}\sum_{i=0}^{k}M^{-i}A^{i} { \bigl(}N\Psi _{i-k}+\mathbb{F}(i,\Psi _{i-k}) { \bigr)} \\ &{}+ M^{n-1}A^{-n}\sum_{i=k+1}^{n}M^{-i}A^{i} { \bigl(}N\mathbb{Y}_{i-k}+ \mathbb{F}(i,\mathbb{Y}_{i-k})+ \mathbf{f}_{i-k} { \bigr)}. \end{aligned}$$

Now, we have

$$\begin{aligned}& \begin{aligned} \Vert \mathbb{Y}_{n}-\mathbf{G}_{n} \Vert ={}& { \Biggl\Vert }M^{n}A^{-n }\Psi _{0}+M^{n-1}A^{-n} \sum_{i=0}^{k}M^{-i}A^{i} { \bigl(}N\Psi _{i-k}+\mathbb{F}(i,\Psi _{i-k}) { \bigr)} \\ &{}+ M^{n-1}A^{-n}\sum_{i=k+1}^{n}M^{-i}A^{i} { \bigl(}N\mathbb{Y}_{i-k}+ \mathbb{F}(i,\mathbb{Y}_{i-k})+ \mathbf{f}_{i-k} { \bigr)} \\ &{}- M^{n}A^{-n }\Psi _{0}-M^{n-1}A^{-n} \sum_{i=0}^{k}M^{-i}A^{i} { \bigl(}N\Psi _{i-k}+\mathbb{F}(i,\Psi _{i-k}) { \bigr)} \\ &{}- M^{n-1}A^{-n}\sum_{i=k+1}^{n}M^{-i}A^{i} { \bigl(}N\mathbf{G}_{i-k}+ \mathbb{F}(i,\mathbf{G}_{i-k}) { \bigr)} { \Biggr\Vert }, \end{aligned} \\& \begin{aligned} \Vert \mathbb{Y}_{n}-\mathbf{G}_{n} \Vert ={}& { \Biggl\Vert } M^{n-1}A^{-n}\sum_{i=k+1}^{n}M^{-i}A^{i} { \bigl(}N\mathbb{Y}_{i-k}+\mathbb{F}(i,\mathbb{Y}_{i-k})+ \mathbf{f}_{i-k} { \bigr)} \\ &{}- M^{n-1}A^{-n}\sum_{i=k+1}^{n}M^{-i}A^{i} { \bigl(}N\mathbf{G}_{i-k}+ \mathbb{F}(i,\mathbf{G}_{i-k}) { \bigr)} { \Biggr\Vert }, \end{aligned} \\& \begin{aligned} \Vert \mathbb{Y}_{n}-\mathbf{G}_{n} \Vert \leq{}& \Vert M \Vert ^{n-1} \Vert A \Vert ^{-n}\sum _{i=k+1}^{n} \Vert M \Vert ^{-i} \Vert A \Vert ^{i} { \bigl(} \Vert N\mathbb{Y}_{i-k}-N \mathbf{G}_{i-k} \Vert \\ &{}+ \bigl\Vert \mathbb{F}(i,\mathbb{Y}_{i-k})-\mathbb{F}(i, \mathbf{G}_{i-k}) \bigr\Vert + \Vert \mathbf{f}_{i-k} \Vert { \bigr)}, \end{aligned} \\& \begin{aligned} \Vert \mathbb{Y}_{n}-\mathbf{G}_{n} \Vert \leq{}& \Vert M \Vert ^{n-1} \Vert A \Vert ^{-n}\sum _{i=k+1}^{n} \Vert M \Vert ^{-i} \Vert A \Vert ^{i} { \bigl(} \Vert N\mathbb{Y}_{i-k}-N \mathbf{G}_{i-k} \Vert \\ &{}+ \mathrm{K} \Vert \mathbb{Y}_{i-k}-\mathbf{G}_{i-k} \Vert + \Vert \mathbf{f}_{i-k} \Vert { \bigr)} \\ ={}& \Vert M \Vert ^{n-1} \Vert A \Vert ^{-n}\sum _{j=k+1}^{n} \Vert M \Vert ^{-i} \Vert A \Vert ^{i} { \bigl(} \bigl\Vert (N+\mathrm{K}) \mathbb{Y}_{i-k} \\ &{}-(N+\mathrm{K})\mathbf{G}_{i-k} \bigr\Vert + \Vert \mathbf{f}_{i-k} \Vert { \bigr)} \\ \leq{}& \Vert M \Vert ^{n-1} \Vert A \Vert ^{-n}\sum _{i=k+1}^{n} \Vert M \Vert ^{-i} \Vert A \Vert ^{i} \Vert \mathbf{f}_{i-k} \Vert \\ \leq{}& \Vert M \Vert ^{n-1} \Vert A \Vert ^{-n}\sum _{i=k+1}^{n} \Vert M \Vert ^{-i} \Vert A \Vert ^{i} \epsilon \phi _{i-k} \\ ={}& \epsilon \Vert M \Vert ^{n-1} \Vert A \Vert ^{-n} \sum_{r=1}^{n-k} \Vert M \Vert ^{-k-r} \Vert A \Vert ^{k+r} \phi _{r} \\ ={}& \epsilon L^{4}\sum_{r=1}^{n-k} \phi _{r} \\ \leq{}& \epsilon L^{4} \eta _{\varphi }\varphi _{n} \\ ={}& \mathbf{K}\epsilon . \end{aligned} \end{aligned}$$

Therefore, system (1.1) is Hyers–Ulam stable over a bounded discrete interval. □

5 Hyers–Ulam stability on unbounded discrete interval

To discuss the Hyers–Ulam stability over an unbounded discrete interval, we have the following assumptions:

$A_{1}$::

The operator family $\Vert L^{4} \Vert \leq Ne^{-\nu n}$, $n\geq 0$, $\nu \geq 0$, $N\geq 1$.

$A_{2}$::

The linear system $A\mathbf{G}_{n+1}=M\mathbf{G}_{n}+N\mathbf{G}_{n-k}$ is well posed.

$A_{3}$::

The continuous function $\mathbb{H}:\mathbb{Z}_{+}\times X\rightarrow X$ satisfies the Caratheodory condition

$$ \bigl\Vert \mathbb{H}(n,\omega )-\mathbb{H} \bigl(n,\omega ^{\prime } \bigr) \bigr\Vert \leq K \bigl\Vert \omega - \omega ^{\prime } \bigr\Vert , \quad K\geq 0, $$

for every $n\in \mathbb{Z}_{+}$ $\omega ,\omega ^{\prime }\in X$.

$A_{4}$::

Also, assume that

$$ \sum_{r=1}^{n-1}\phi _{r}\leq \eta \varphi _{n} $$

for each $n\in \mathbb{Z}_{+}$, $\eta \geq 0$ and $\varphi _{n}$ is a convergent sequence.

Theorem 3

If $A_{1}$–$A_{4}$ along with (2.1) and Remark 2.1are satisfied, then system (1.1) is Hyers–Ulam stable over an unbounded interval.

Proof

Since the exact solution of the non-autonomous and nonsingular delay difference equation

$$ \textstyle\begin{cases} \mathbf{A}U_{n+1}=\mathcal{M}U_{n}+\mathbb{N}U_{n-k}+\mathrm{F}(n,U_{n-k}), \quad n\geq 0, k\geq 0, \\ U_{n}=\psi _{n}, \quad -k\leq n\leq 0, \end{cases} $$

is

$$\begin{aligned} U_{n} =& \mathcal{M}^{n}\mathbf{A}^{-n }\psi _{0}+\mathcal{M}^{n-1} \mathbf{A}^{-n}\sum _{i=0}^{k}\mathcal{M}^{-i} \mathbf{A}^{i} { \bigl(} \mathbb{N}\psi _{i-k}+\mathrm{F}(i, \psi _{i-k}) { \bigr)} \\ &{}+ \mathcal{M}^{n-1}\mathbf{A}^{-n}\sum _{i=k+1}^{n}\mathcal{M}^{-i} \mathbf{A}^{i} { \bigl(}\mathbb{N}U_{i-k}+ \mathrm{F}(i,U_{i-k}) { \bigr)}. \end{aligned}$$

Letting Y be the approximate solution of the above system, then clearly for a sequence $f_{n}$ with $\Vert f_{n} \Vert \leq \epsilon$ we have

$$ \textstyle\begin{cases} \mathbf{A}Y_{n+1}=\mathcal{M}Y_{n}+\mathbb{N}Y_{n-k}+\mathrm{F}(n,Y_{n-k})+ \mathrm{f}_{n}, \quad n\geq 0, k\geq 0, \\ Y_{n}=\psi _{n}, \quad -k\leq n\leq 0, \end{cases} $$

and

$$\begin{aligned} Y_{n} =& \mathcal{M}^{n}\mathbf{A}^{-n }\psi _{0}+\mathcal{M}^{n-1} \mathbf{A}^{-n}\sum _{i=0}^{k}\mathcal{M}^{-i} \mathbf{A}^{i} { \bigl(} \mathbb{N}\psi _{i-k}+\mathrm{F}(i, \psi _{i-k}) { \bigr)} \\ &{}+ \mathcal{M}^{n-1}\mathbf{A}^{-n}\sum _{i=k+1}^{n}\mathcal{M}^{-i} \mathbf{A}^{i} { \bigl(}\mathbb{N}Y_{i-k}+ \mathrm{F}(i,Y_{i-k})+ \mathrm{f}_{i-k} { \bigr)}. \end{aligned}$$

Now, consider

$$\begin{aligned} \Vert Y_{n}-U_{n} \Vert =& { \Biggl\Vert } \mathcal{M}^{n}\mathbf{A}^{-n }\psi _{0}+ \mathcal{M}^{n-1}\mathbf{A}^{-n}\sum _{i=0}^{k}\mathcal{M}^{-i} \mathbf{A}^{i} { \bigl(}\mathbb{N}\psi _{i-k}+\mathrm{F}(i, \psi _{i-k}) { \bigr)} \\ &{}+ \mathcal{M}^{n-1}\mathbf{A}^{-n}\sum _{i=k+1}^{n}\mathcal{M}^{-i} \mathbf{A}^{i} { \bigl(}\mathbb{N}Y_{i-k}+ \mathrm{F}(i,Y_{i-k})+ \mathrm{f}_{i-k} { \bigr)} \\ &{}- \mathcal{M}^{n}\mathbf{A}^{-n }\psi _{0}- \mathcal{M}^{n-1} \mathbf{A}^{-n}\sum _{i=0}^{k}\mathcal{M}^{-i} \mathbf{A}^{i} { \bigl(} \mathbb{N}\psi _{i-k}+\mathrm{F}(i, \psi _{i-k}) { \bigr)} \\ &{}- \mathcal{M}^{n-1}\mathbf{A}^{-n}\sum _{i=k+1}^{n}\mathcal{M}^{-i} \mathbf{A}^{i} { \bigl(}\mathbb{N}U_{i-k}+ \mathrm{F}(i,U_{i-k}) { \bigr)} { \Biggr\Vert }. \end{aligned}$$

That is,

$$\begin{aligned} \Vert Y_{n}-U_{n} \Vert =& \Vert \mathcal{M} \Vert ^{n-1} \Vert \mathbf{A} \Vert ^{-n} { \Biggl\Vert } \sum _{i=k+1}^{n}\mathcal{M}^{-i} \mathbf{A}^{i} { \bigl(}\mathbb{N}Y_{i-k}+ \mathrm{F}(i,Y_{i-k})-\mathbb{N}U_{i-k}-\mathrm{F}(i,U_{i-k}) { \bigr)} \\ &{}+ \sum_{i=k+1}^{n}\mathcal{M}^{-i} \mathbf{A}^{i}\mathrm{f}_{i-k} { \Biggr\Vert } \\ \leq & \Vert \mathcal{M} \Vert ^{n-1} \Vert \mathbf{A} \Vert ^{-n}\sum_{i=k+1}^{n} \Vert \mathcal{M} \Vert ^{-i} \Vert \mathbf{A} \Vert ^{i} { \bigl(} \Vert \mathbb{N}Y_{i-k}- \mathbb{N}U_{i-k} \Vert \\ &{}+ \bigl\Vert \mathrm{F}(i,Y_{i-k})-\mathrm{F}(i,U_{i-k}) \bigr\Vert + \Vert \mathrm{f}_{i-k} \Vert { \bigr)} \\ \leq & \Vert \mathcal{M} \Vert ^{n-1} \Vert \mathbf{A} \Vert ^{-n}\sum_{i=k+1}^{n} \Vert \mathcal{M} \Vert ^{-i} \Vert \mathbf{A} \Vert ^{i} { \bigl(} \Vert \mathbb{N}Y_{i-k}- \mathbb{N}U_{i-k} \Vert +K \Vert Y_{i-k}-U_{i-k} \Vert \\ &{}+ \Vert \mathrm{f}_{i-k} \Vert { \bigr)} \\ =& \Vert \mathcal{M} \Vert ^{n-1} \Vert \mathbf{A} \Vert ^{-n}\sum_{i=k+1}^{n} \Vert \mathcal{M} \Vert ^{-i} \Vert \mathbf{A} \Vert ^{i} { \bigl(} \bigl\Vert (\mathbb{N}+K)Y_{i-k} \\ &{}- (\mathbb{N}+K)U_{i-k} \bigr\Vert + \Vert \mathrm{f}_{i-k} \Vert { \bigr)} \\ =& \Vert \mathcal{M} \Vert ^{n-1} \Vert \mathbf{A} \Vert ^{-n}\sum_{i=k+1}^{n} \Vert \mathcal{M} \Vert ^{-i} \Vert \mathbf{A} \Vert ^{i} \Vert \mathrm{f}_{i-k} \Vert . \end{aligned}$$

That is,

$$\begin{aligned} \Vert Y_{n}-U_{n} \Vert \leq & \Vert \mathcal{M} \Vert ^{n-1} \Vert \mathbf{A} \Vert ^{-n}\sum _{i=k+1}^{n} \Vert \mathcal{M} \Vert ^{-i} \Vert \mathbf{A} \Vert ^{i}\epsilon \phi _{i-k} \\ =& \epsilon \Vert \mathcal{M} \Vert ^{n-1} \Vert \mathbf{A} \Vert ^{-n}\sum_{r=1}^{n-k} \Vert \mathcal{M} \Vert ^{-k-r} \Vert \mathbf{A} \Vert ^{k+r} \phi _{r} \\ =& \epsilon L^{4}\sum_{r=1}^{n-k} \phi _{r} \\ \leq & \epsilon L^{4}\eta \varphi _{n} \\ \leq & Ne^{-\nu n}\eta K \epsilon \\ \leq & N\eta K \epsilon \\ =& \mathbf{K}\epsilon , \end{aligned}$$

where $\mathbf{K}= N\eta K$. Thus, system (1.1) is Hyers–Ulam stable over an unbounded discrete interval. □

6 β-Hyers–Ulam stability

To describe β-Hyers–Ulam stability over an unbounded interval, we needed some assumptions:

$A_{0}$::

The operator family $\Vert L^{4} \Vert \leq \mathbb{N}e^{k n}$, $n\geq 0$, $k \leq 0$, $N\geq 1$.

$A_{1}$::

The linear system $A\mathbf{G}_{n+1}=M\mathbf{G}_{n}+N\mathbf{G}_{n-k}$ is well posed.

$A_{2}$::

The continuous function $\mathbf{H}:\mathbb{Z}_{+}\times X\rightarrow X$ satisfies the Caratheodory condition

$$ \bigl\Vert \mathbf{H}(n,\rho )-\mathbf{H} \bigl(n,\rho ^{\prime } \bigr) \bigr\Vert \leq K_{n} \bigl\Vert \rho - \rho ^{\prime } \bigr\Vert , \quad K\geq 0, $$

for every $n\in \mathbb{Z}_{+}$ $\rho ,\rho ^{\prime }\in X$.

$A_{3}$::

Also, assume that

$$ \sum_{i=k+1}^{n}e^{kn}(N+K_{n}) \leq \eta _{\varphi }\varphi _{n}, \quad k\leq 0, $$

for each $n\in \mathbb{Z}_{+}$, $\eta _{\varphi } \geq 0$, and $\varphi _{n}$ is a convergent sequence.

By considering inequality (2.1) and the above mentioned assumptions, we are able to prove the following theorem.

Theorem 4

If $A_{0}$–$A_{3}$ are satisfied, then system (6.1) is β-Hyers–Ulam stable over an unbounded interval.

Proof

The only one solution of nonsingular delay difference equation

$$ \textstyle\begin{cases} \mathcal{AU}_{n+1}=\mathcal{MU}_{n}+\mathcal{NU}_{n-k}+F(n, \mathcal{U}_{n-k}), \quad n\geq 0, k\geq 0, \\ \mathcal{U}_{n}=\Phi _{n}, \quad -k\leq n \leq 0, \end{cases} $$

(6.1)

is

$$\begin{aligned} \mathcal{U}_{n} =& \mathcal{M}^{n}\mathcal{A}^{-n } \Phi _{0}+ \mathcal{M}^{n-1}\mathcal{A}^{-n}\sum _{l=0}^{k}\mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\Phi _{l-k}+\mathrm{F}(l, \Phi _{l-k}) { \bigr)} \\ &{}+ \mathcal{M}^{n-1}\mathcal{A}^{-n}\sum _{l=k+1}^{n}\mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\mathcal{U}_{l-k}+ \mathrm{F}(l, \mathcal{U}_{l-k}) { \bigr)}. \end{aligned}$$

Let $\mathcal{Y}$ satisfy (2.1), then for every $n\in \mathcal{Z}_{+}$ we have

$$\begin{aligned}& \Biggl\Vert \mathcal{Y}_{n}-\mathcal{M}^{n} \mathcal{A}^{-n }\Phi _{0}- \mathcal{M}^{n-1} \mathcal{A}^{-n}\sum_{l=0}^{k} \mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\Phi _{l-k}+\mathrm{F}(l,\Phi _{l-k}) { \bigr)} \\& \quad\quad{} - \mathcal{M}^{n-1}\mathcal{A}^{-n}\sum _{l=k+1}^{n} \mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\mathcal{Y}_{l-k}+ \mathrm{F}(l,\mathcal{Y}_{l-k}) { \bigr)} { \Biggr\Vert } \\& \quad = \Biggl\Vert \mathcal{M}^{n-1}\mathcal{A}^{-n} \sum_{l=k+1}^{n}\mathcal{M}^{-l} \mathcal{A}^{l}f_{l-k} \Biggr\Vert \\& \quad = \bigl\Vert \mathcal{M}^{n-1} \bigr\Vert \bigl\Vert \mathcal{A}^{-n} \bigr\Vert \sum_{l=k+1}^{n} \bigl\Vert \mathcal{M}^{-l} \bigr\Vert \bigl\Vert \mathcal{A}^{l} \bigr\Vert \Vert f_{l-k} \Vert \\& \quad = \sum_{l=k+1}^{n}L^{4} \epsilon \phi _{n} \\& \quad = \sum_{l=k+1}^{n}\mathbb{N}e^{kn} \epsilon \phi _{n}. \end{aligned}$$

Now,

$$\begin{aligned}& \begin{aligned} \Vert \mathcal{Y}_{n}-\mathcal{U}_{n} \Vert ^{\beta } ={}& { \Biggl\Vert }\mathcal{Y}_{n}- \mathcal{M}^{n}\mathcal{A}^{-n }\Phi _{0}- \mathcal{M}^{n-1} \mathcal{A}^{-n}\sum _{i=0}^{k}\mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\Phi _{l-k}+\mathrm{F}(l, \Phi _{l-k}) { \bigr)} \\ &{}- \mathcal{M}^{n-1}\mathcal{A}^{-n}\sum _{l=k+1}^{n}\mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\mathcal{U}_{l-k}+ \mathrm{F}(l, \mathcal{U}_{l-k}) { \bigr)} { \Biggr\Vert }^{\beta }, \end{aligned} \\& \begin{aligned} \Vert \mathcal{Y}_{n}-\mathcal{U}_{n} \Vert ^{\beta } ={}& { \Biggl\Vert }\mathcal{Y}_{n}- \mathcal{M}^{n}\mathcal{A}^{-n }\Phi _{0}- \mathcal{M}^{n-1} \mathcal{A}^{-n}\sum _{l=0}^{k}\mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\Phi _{l-k}+\mathrm{F}(l, \Phi _{l-k}) { \bigr)} \\ &{}- \mathcal{M}^{n-1}\mathcal{A}^{-n}\sum _{l=k+1}^{n}\mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\mathcal{U}_{l-k}+ \mathrm{F}(l, \mathcal{U}_{l-k}) { \bigr)} \\ &{}+ \mathcal{M}^{n-1}\mathcal{A}^{-n}\sum _{l=k+1}^{n}\mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\mathcal{Y}_{l-k}+ \mathrm{F}(l, \mathcal{Y}_{l-k}) { \bigr)} \\ &{}- \mathcal{M}^{n-1}\mathcal{A}^{-n}\sum _{l=k+1}^{n}\mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\mathcal{Y}_{l-k}+ \mathrm{F}(l, \mathcal{Y}_{l-k}) { \bigr)} { \Biggr\Vert }^{\beta } \\ ={}& { \Biggl\Vert }\mathcal{Y}_{n}-\mathcal{M}^{n} \mathcal{A}^{-n }\Phi _{0}- \mathcal{M}^{n-1} \mathcal{A}^{-n}\sum_{l=0}^{k} \mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\Phi _{l-k}+\mathrm{F}(l,\Phi _{l-k}) { \bigr)} \\ &{}- \mathcal{M}^{n-1}\mathcal{A}^{-n}\sum _{l=k+1}^{n}\mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\mathcal{Y}_{l-k}+ \mathrm{F}(l, \mathcal{Y}_{l-k}) { \bigr)} \\ &{}+ \mathcal{M}^{n-1}\mathcal{A}^{-n}\sum _{l=k+1}^{n}\mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\mathcal{Y}_{l-k}+ \mathrm{F}(l, \mathcal{Y}_{l-k}) { \bigr)} \\ &{}- \mathcal{M}^{n-1}\mathcal{A}^{-n}\sum _{l=k+1}^{n}\mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\mathcal{U}_{l-k}+ \mathrm{F}(l, \mathcal{U}_{l-k}) { \bigr)} { \Biggr\Vert }^{\beta }, \end{aligned} \\& \Vert \mathcal{Y}_{n}-\mathcal{U}_{n} \Vert ^{\beta } \leq { \Biggl\Vert } \mathcal{Y}_{n}- \mathcal{M}^{n}\mathcal{A}^{-n }\Phi _{0}- \mathcal{M}^{n-1} \mathcal{A}^{-n}\sum _{l=0}^{k}\mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\Phi _{l-k}+\mathrm{F}(l, \Phi _{l-k}) { \bigr)} \\& \hphantom{\Vert \mathcal{Y}_{n}-\mathcal{U}_{n} \Vert ^{\beta } }\quad {}- \mathcal{M}^{n-1}\mathcal{A}^{-n}\sum _{l=k+1}^{n}\mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\mathcal{Y}_{l-k}+ \mathrm{F}(l, \mathcal{Y}_{l-k}) { \bigr)} { \Biggr\Vert }^{\beta } \\& \hphantom{\Vert \mathcal{Y}_{n}-\mathcal{U}_{n} \Vert ^{\beta } }\quad{}+ { \Biggl\Vert } \mathcal{M}^{n-1}\mathcal{A}^{-n}\sum _{l=k+1}^{n} \mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\mathcal{Y}_{l-k}+ \mathrm{F}(l,\mathcal{Y}_{l-k}) { \bigr)} \\& \hphantom{\Vert \mathcal{Y}_{n}-\mathcal{U}_{n} \Vert ^{\beta } }\quad{}- \mathcal{M}^{n-1}\mathcal{A}^{-n}\sum _{l=k+1}^{n}\mathcal{M}^{-l} \mathcal{A}^{l} { \bigl(}\mathcal{N}\mathcal{U}_{l-k}+ \mathrm{F}(l, \mathcal{U}_{l-k}) { \bigr)} { \Biggr\Vert }^{\beta } \\& \hphantom{\Vert \mathcal{Y}_{n}-\mathcal{U}_{n} \Vert ^{\beta } }\leq { \Biggl(}\sum_{l=k+1}^{n} \mathbb{N}e^{kn}\epsilon \phi _{n} { \Biggr)}^{\beta }+ { \Biggl(} \bigl\Vert \mathcal{M}^{n-1} \bigr\Vert \bigl\Vert \mathcal{A}^{-n} \bigr\Vert \sum_{l=k+1}^{n} \bigl\Vert \mathcal{M}^{-l} \bigr\Vert \bigl\Vert \mathcal{A}^{l} \bigr\Vert { \bigl\Vert } \mathcal{N} \mathcal{Y}_{l-k} \\& \hphantom{\Vert \mathcal{Y}_{n}-\mathcal{U}_{n} \Vert ^{\beta } }\quad{}+\mathrm{F}(l,\mathcal{Y}_{l-k})-\mathcal{N}\mathcal{U}_{l-k}- \mathrm{F}(l,\mathcal{U}_{l-k}) { \bigr\Vert } { \Biggr)}^{\beta }, \\& \begin{aligned} \Vert \mathcal{Y}_{n}-\mathcal{U}_{n} \Vert ^{\beta } ={}& { \Biggl(}\sum_{l=k+1}^{n} \mathbb{N}e^{kn}\epsilon \phi _{n} { \Biggr)}^{\beta } \\ &{}+ { \Biggl(} \bigl\Vert \mathcal{M}^{n-1} \bigr\Vert \bigl\Vert \mathcal{A}^{-n} \bigr\Vert \sum_{l=k+1}^{n} \bigl\Vert \mathcal{M}^{-l} \bigr\Vert \bigl\Vert \mathcal{A}^{l} \bigr\Vert { \bigl(} \Vert \mathcal{N} \mathcal{Y}_{l-k} - \mathcal{N}\mathcal{U}_{l-k} \Vert \\ &{}+ \bigl\Vert \mathrm{F}(l,\mathcal{Y}_{l-k})-\mathrm{F}(l, \mathcal{U}_{l-k}) \bigr\Vert { \bigr)} { \Biggr)}^{\beta } \\ \leq{}& { \Biggl(}\sum_{l=k+1}^{n} \mathbb{N}e^{kn}\epsilon \phi _{n} { \Biggr)}^{\beta } \\ &{}+ { \Biggl(} \bigl\Vert \mathcal{M}^{n-1} \bigr\Vert \bigl\Vert \mathcal{A}^{-n} \bigr\Vert \sum_{l=k+1}^{n} \bigl\Vert \mathcal{M}^{-l} \bigr\Vert \bigl\Vert \mathcal{A}^{l} \bigr\Vert { \bigl(} \Vert \mathcal{N} \mathcal{Y}_{l-k} -\mathcal{N}\mathcal{U}_{l-k} \Vert \\ &{}+ K_{n} \Vert \mathcal{Y}_{l-k}-\mathcal{U}_{l-k} \Vert { \bigr)} { \Biggr)}^{ \beta } \\ ={}& { \Biggl(}\sum_{l=k+1}^{n} \mathbb{N}e^{kn}\epsilon \phi _{n} { \Biggr)}^{\beta }+ { \Biggl(}\sum_{l=k+1}^{n}L^{4} (N+K_{n}) \Vert \mathcal{Y}_{l-k}-\mathcal{U}_{l-k} \Vert { \Biggr)}^{\beta } \\ \leq{}& { \Biggl(}\sum_{l=k+1}^{n} \mathbb{N}e^{kn}\epsilon \phi _{n} { \Biggr)}^{\beta }+ { \Biggl(}\sum_{l=k+1}^{n} \mathbb{N}e^{kn} (N+K_{n}) \Vert \mathcal{Y}_{l-k}- \mathcal{U}_{l-k} \Vert { \Biggr)}^{\beta }, \end{aligned} \\& \Vert \mathcal{Y}_{n}-\mathcal{U}_{n} \Vert = { \Biggl[} { \Biggl(}\sum_{l=k+1}^{n} \mathbb{N}e^{kn}\epsilon \phi _{n} { \Biggr)}^{\beta }+ { \Biggl(}\sum_{l=k+1}^{n} \mathbb{N}e^{kn}(N+K_{n}) \Vert \mathcal{Y}_{l-k}- \mathcal{U}_{l-k} \Vert { \Biggr)}^{\beta } { \Biggr]}^{\frac{1}{\beta }}. \end{aligned}$$

Now, using

$$ (\varrho +\xi )^{\alpha }\leq 3^{\alpha -1} \bigl(\varrho ^{\alpha }+\xi ^{ \alpha } \bigr), \quad \varrho ,\xi \geq 0 \text{ and } \alpha >1, $$

we obtain

$$\begin{aligned} \Vert \mathcal{Y}_{n}-\mathcal{U}_{n} \Vert \leq & 3^{\frac{1}{\beta }-1} \sum_{l=k+1}^{n} \mathbb{N}e^{kn}\epsilon \phi _{n}+ 3^{ \frac{1}{\beta }-1}(N+K_{n}) \sum_{l=k+1}^{n}\mathbb{N}e^{kn} \Vert \mathcal{Y}_{l-k}-\mathcal{U}_{l-k} \Vert , \end{aligned}$$

with the help of Lemma(2.2), we get

$$\begin{aligned}& \Vert \mathcal{Y}_{n}-\mathcal{U}_{n} \Vert \leq 3^{\frac{1}{\beta }-1} \sum_{l=k+1}^{n} \mathbb{N}e^{kn}\epsilon \phi _{n}\exp { \Biggl(} 3^{ \frac{1}{\beta }-1} \sum_{l=k+1}^{n} \mathbb{N}e^{kn}(N+K_{n}) { \Biggr)}, \\& \begin{aligned} \Vert \mathcal{Y}_{n}-\mathcal{U}_{n} \Vert \leq{}& \epsilon { \Biggl(} 3^{ \frac{1}{\beta }-1}\sum_{l=k+1}^{n} \mathbb{N}e^{kn} { \Biggr)}\exp { \Biggl(}3^{\frac{1}{\beta }-1}\sum _{l=k+1}^{n}\mathbb{N}e^{kn}(N+K_{n}) { \Biggr)} \\ ={}& \epsilon { \Biggl(} 3^{\frac{1}{\beta }-1}\sum_{l=k+1}^{n} \mathbb{N}e^{kn} { \Biggr)}\exp { \bigl(}3^{\frac{1}{\beta }-1} \mathbb{N}e^{kn} \eta _{\varphi } \varphi _{n} { \bigr)}, \end{aligned} \\& \begin{aligned} \Vert \mathcal{Y}_{n}-\mathcal{U}_{n} \Vert ^{\beta } ={}& \epsilon ^{\beta } { \Biggl(}3^{\frac{1}{\beta }-1}\sum _{l=k+1}^{n}\mathbb{N}e^{kn} { \Biggr)}^{\beta } \exp { \bigl(}3^{\frac{1}{\beta }-1}\mathbb{N}e^{kn} \eta _{\varphi }\varphi _{n} { \bigr)}^{\beta } \\ ={}& \epsilon ^{\beta } { \Biggl(}3^{\frac{1}{\beta }-1}\sum _{l=k+1}^{n} \mathbb{N}e^{kn} { \Biggr)}^{\beta } { \bigl(}\exp \bigl(\mathbb{N}3^{ \frac{1}{\beta }-1} \bigr) { \bigr)}^{\beta } { \bigl(}\exp (\eta _{\varphi } \varphi _{n}) { \bigr)}^{\beta } \\ ={}& L_{\mathrm{F}, \mathbb{N}, \phi , \beta }\epsilon ^{\beta }\eta _{ \varphi }^{\beta } \varphi _{n}^{\beta }, \end{aligned} \end{aligned}$$

where

$$ L_{\mathrm{F}, \mathbb{N}, \phi , \beta }= { \Biggl(}3^{\frac{1}{\beta }-1} \sum_{l=k+1}^{n} \mathbb{N}e^{kn} { \Biggr)}^{\beta } { \bigl(}\exp \bigl( \mathbb{N}3^{\frac{1}{\beta }-1} \bigr) { \bigr)}^{\beta }. $$

So, system (6.1) is β-Hyers–Ulam stable over an unbounded interval. □

7 An example

Consider we have the following nonsingular delay difference equation:

$$ \textstyle\begin{cases} \mathcal{AG}_{n+1}=\mathcal{MG}_{n}+\mathcal{NG}_{n-3}+F(n, \mathcal{G}_{n-3}), \quad \mathcal{G}_{0}=1, n\in \{0,1,2,3\}, \\ \mathcal{G}_{n}=\Phi _{n}, \quad -3\leq n \leq 0, \end{cases} $$

(7.1)

with inequality

$$ \textstyle\begin{cases} \Vert \mathcal{AG}_{n+1}-\mathcal{MG}_{n}-\mathcal{NG}_{n-3}-F(n, \mathcal{G}_{n-3}) \Vert \leq 0.7, \quad n\in \{0,1,2,3\}, \\ \Vert \mathcal{G}_{n}-\Phi _{n} \Vert \leq 1, \quad -3\leq n \leq 0, \end{cases} $$

(7.2)

here $k=3$. If we fix

$$\begin{aligned}& \mathcal{M}= \begin{pmatrix} -3.5 & 1.4 \\ 3.2 & 1.6 \end{pmatrix} ,\quad \quad \mathcal{N}= \begin{pmatrix} 3.6 & 1.4 \\ -3.2 & 1.7 \end{pmatrix} , \quad\quad \mathcal{A}= \begin{pmatrix} 1.3 & 0 \\ 0 & 1.3 \end{pmatrix} , \end{aligned}$$

$F(n,G_{n-3})=G_{n-3}[\begin{array}{cc}0.3sin(n)& 0.15sin(n)\end{array}]$ and ${\varphi }_n={[\begin{array}{cc}cos(n+\frac{\pi }{2})& cos(n+\frac{\pi }{2})\end{array}]}^t$ (obviously, ${\varphi }_n={[\begin{array}{cc}0& 0\end{array}]}^t$, when $n=0$), hence, we get

$$\begin{aligned}& \mathcal{NM}= \begin{pmatrix} 8.12 & 7.28 \\ -16.64 & -1.76 \end{pmatrix} = \mathcal{MN}, \quad\quad \mathcal{AN}= \begin{pmatrix} 4.68 & 1.28 \\ -4.16 & 2.12 \end{pmatrix} =\mathcal{NA}, \\& \mathcal{AM}= \begin{pmatrix} 4.55 & 1.82 \\ -4.16 & 2.08 \end{pmatrix} = \mathcal{MA}, \quad\quad \mathcal{A}^{-1}= \begin{pmatrix} 0.769231 & 0 \\ 0 & 0.769231 \end{pmatrix} , \\& \mathcal{A}^{-1}\mathcal{N}= \begin{pmatrix} 2.762316 & 1.0769234 \\ -2.4615392 & 1.3076927 \end{pmatrix} =\mathcal{N}\mathcal{A}^{-1}, \\& \mathcal{A}^{-1}\mathcal{M}= \begin{pmatrix} 2.6923085 & 1.0769234 \\ -2.4615392 & 1.2307696 \end{pmatrix} =\mathcal{M}\mathcal{A}^{-1}. \end{aligned}$$

Moreover, if G satisfies (7.2), then there exists $f_{n}$ such that $\Vert f_{n} \Vert \leq 0.7$, and

$$ \textstyle\begin{cases} \mathcal{AG}_{n+1}=\mathcal{MG}_{n}+\mathcal{NG}_{n-3}+F(n, \mathcal{G}_{n-3})+f_{n}, \quad \mathcal{G}_{0}=1, n\in \{0,1,2,3\}, \\ \mathcal{G}_{n}=\Phi _{n}, \quad -3\leq n \leq 0, \end{cases} $$

also the solution of (7.1) is

$$\begin{aligned} \mathcal{G}_{n} = &\mathcal{M}^{n} \mathcal{A}^{-n }\Phi _{0}+ \mathcal{M}^{n-1} \mathcal{A}^{-n}\sum_{i=0}^{k} \mathcal{M}^{-i} \mathcal{A}^{i} { \bigl(}\mathcal{N}\Phi _{i-k}+F(i,\Phi _{i-k}) { \bigr)} \\ &{}+ \mathcal{M}^{n-1}\mathcal{A}^{-n}\sum _{i=k+1}^{n}\mathcal{M}^{-i} \mathcal{A}^{i} { \bigl(}\mathcal{N}\mathcal{G}_{i-k}+F(i, \mathcal{G}_{i-k}) { \bigr)}, \end{aligned}$$

(7.3)

where $\mathcal{MA}=\mathcal{AM}$, $\mathcal{NA}=\mathcal{AN}$, and $\mathcal{MN}=\mathcal{NM}$.

Let $\epsilon =0.7$, and $f:\mathcal{Z}_{+}\rightarrow \mathcal{R}^{2}$ be as given below

$$\begin{aligned}& f_{n}= \begin{bmatrix} 0.6 \cos (n+\frac{\pi }{2}) & 0.6\sin (n+\frac{\pi }{2}) \end{bmatrix} ^{t}, \end{aligned}$$

then clearly

$$\begin{aligned} \Vert f_{n} \Vert =&\sqrt{ { \biggl(}0.6\cos \biggl(n+ \frac{\pi }{2} \biggr) { \biggr)}^{2}+ { \biggl(}0.6\sin \biggl(n+ \frac{\pi }{2} \biggr) { \biggr)}^{2}} \\ =& { \biggl[}(0.6)^{2}\cos ^{2} \biggl(n+ \frac{\pi }{2} \biggr)+(0.6)^{2}\sin ^{2} \biggl(n+ \frac{\pi }{2} \biggr) { \biggr]}^{\frac{1}{2}} \\ =& \sqrt{0.6^{2}}=0.6 \\ \leq & \epsilon =0.7. \end{aligned}$$

Now the perturbed delay difference system (7.3) has the solution

$$\begin{aligned} H_{n} =& \mathcal{M}^{n}\mathbf{A}^{-n }\psi _{0}+\mathcal{M}^{n-1} \mathbf{A}^{-n}\sum _{i=0}^{k}\mathcal{M}^{-i} \mathbf{A}^{i} { \bigl(} \mathbb{N}\psi _{i-k}+\mathrm{F}(i, \psi _{i-k}) { \bigr)} \\ &{}+ \mathcal{M}^{n-1}\mathbf{A}^{-n}\sum _{i=k+1}^{n}\mathcal{M}^{-i} \mathbf{A}^{i} { \bigl(}\mathbb{N}H_{i-k}+ \mathrm{F}(i,H_{i-k})+ \mathrm{f}_{i-k} { \bigr)}. \end{aligned}$$

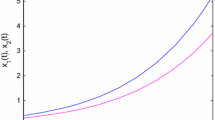
Using Mathematica, we get the values given in Table 1.

Table 1 Table for $G_{n}$ and $H_{n}$

Plotting these values, we have the following graphs.

Hence, we have a solution within a multiple of $\epsilon =0.7$ and a constant, so system (1.1) has a unique solution in $B(\mathcal{Z}_{+},\mathcal{R}^{2})$, which is Hyers–Ulam stable on $\mathcal{Z}_{+}$.