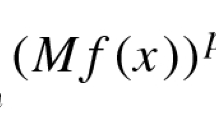Structure of a generalized class of weights satisfy weighted reverse Hölder’s inequality

Abstract

In this paper, we will prove some fundamental properties of the power mean operator

$$ \mathcal{M}_{p}g(t)= \biggl( \frac{1}{\Upsilon(t)} \int _{0}^{t} \lambda (s)g^{p} ( s ) \,ds \biggr) ^{1/p},\quad\text{for }t\in \mathbb{I}\subseteq \mathbb{R}_{+}, $$

of order p and establish some lower and upper bounds of the compositions of operators of different powers, where g, λ are a nonnegative real valued functions defined on $\mathbb{I}$ and $\Upsilon(t)=\int _{0}^{t}\lambda ( s ) \,ds$. Next, we will study the structure of the generalized class $\mathcal{U}_{p}^{q}(B)$ of weights that satisfy the reverse Hölder inequality

$$ \mathcal{M}_{q}u\leq B\mathcal{M}_{p}u, $$

for some $p< q$, $p.q\neq 0$, and $B>1$ is a constant. For applications, we will prove some self-improving properties of weights in the class $\mathcal{U}_{p}^{q}(B)$ and derive the self improving properties of the weighted Muckenhoupt and Gehring classes.

1 Introduction

In [20], Muckenhoupt introduced a full characterization of Muckenhoupt $A^{p}$-class of weights in connection with the boundedness of the Hardy-Littlewood maximal operator in the space $L_{u}^{p}(\mathbb{R}_{+})$ with a weight u. Another important class of weights, the Gehring class $G^{q}$, for $1< q<\infty$, was introduced by Gehring [11, 12] in connection with local integrability properties of the gradient of quasiconformal mappings. Due to the importance of these two classes in mathematical and harmonic analysis, their structure has been studied by several authors, and various results regarding the relationship between them and their applications have been established. We refer the reader to the papers [1, 2, 4–10, 13, 14, 16–19, 26–30, 32] and the references cited therein.

In the following, for the sake of completeness, we present the background and the basic definitions that will be used in this paper. We fix an interval $\mathbb{I}\subset \mathbb{R}_{+}=[0,\infty )$ and consider subintervals I of $\mathbb{I}$ of the form $[0,t]$, for $0< t<\infty$ and denote by $\vert I \vert$ the Lebesgue measure of I. Throughout the paper, we assume that $1< p<\infty$. A weight u is a nonnegative locally integrable function defined on $\mathbb{R}_{+}$. Most often u, which is a positive function of real numbers defined on $\mathbb{R}_{+}$, will appear in the role of the weight in $L_{u}^{p}(\mathbb{R}_{+})$-estimates, i.e. we shall consider the norm

$$ \Vert g \Vert _{L_{u}^{p}(\mathbb{R}_{+})}:= \biggl( \int _{0}^{\infty } \bigl\vert g(t) \bigr\vert ^{p}u(t)\,dt \biggr) ^{1/p}< \infty . $$

In the literature, a nonnegative measurable weight function u defined on a bounded interval $\mathbb{I}$ is called an $A^{p}(\mathcal{C})$-Muckenhoupt weight for $1< p<\infty$ if there exists a constant $\mathcal{C}<\infty$ such that

$$ \biggl( \frac{1}{ \vert I \vert } \int _{I}u(t)\,dt \biggr) \biggl( \frac{1}{ \vert I \vert } \int _{I}u^{-\frac{1}{p-1}}(t)\,dt \biggr) ^{p-1} \leq \mathcal{C}, $$

(1)

for every subinterval $I\subset \mathbb{I}$. Muckenhoupt [20] proved the following result. If $1< p<\infty$ and u satisfies the $A^{p}$-condition (1) on the interval $\mathbb{I}$, with constant $\mathcal{C}$, then there exist constants q and $\mathcal{C}_{1}$ depending on p and $\mathcal{C}$ such that $1< q< p$, and u satisfies the $A^{q}$-condition

$$ \biggl( \frac{1}{ \vert I \vert } \int _{I}u(t)\,dt \biggr) \biggl( \frac{1}{ \vert I \vert } \int _{I}u^{-\frac{1}{q-1}}(t)\,dt \biggr) ^{q-1} \leq \mathcal{C}_{1}, $$

(2)

for every subinterval $I\subset \mathbb{I}$. In other words, Muckenhoupt’s result (see also Coifman and Fefferman [3]) for self-improving property states that: if $u\in A^{p}(\mathcal{C})$ then there exists a constant $\epsilon >0$ and a positive constant $\mathcal{C}_{1}$ such that $u\in A^{p-\epsilon }(\mathcal{C}_{1})$, and then

$$ A^{p}(\mathcal{C})\subset A^{p-\epsilon }(\mathcal{C}_{1}). $$

(3)

In [20], Muckenhoupt introduced the characterizations of $A^{p}$-class of weights in connection with the boundedness of the Hardy-Littlewood maximal operator

$$ Mg(x):=\sup_{y\neq x, y\in \mathbb{I}}\frac{1}{y-x} \int _{x}^{y}g(s)\,ds, $$

(4)

in the space $L_{u}^{p}(\mathbb{R}_{+})$ with a weight u. In particular, Muckenhoupt proved the following result: If $g(x)$ is nonnegative weight on an interval $\mathbb{I}$ and $1< p<\infty$, then the inequality

$$ \int _{\mathbb{R}_{+}} \bigl( Mg(x) \bigr) ^{p}u(x)\,dx\leq K \int _{\mathbb{R}_{+}} \bigl( \bigl\vert g(x) \bigr\vert \bigr) ^{p}u(x)\,dx, $$

holds if and only if the inequality (1) holds, where the constant K independent of g. Another important class of weights, which is related to the Muckenhoupt class, is the $G^{q}$-class for $1< q<\infty$ of weights that satisfy the reverse Hölder inequality. This class has been introduced by Gehring [11, 12] in connection with local integrability properties of the gradient of quasiconformal mappings. A weight u satisfies the $G^{q}$-condition (or is said to belong to the Gehring class $G^{q}(\mathcal{K})$) if there exists $\mathcal{K>}1$ such that the inequality

$$ \biggl( \frac{1}{ \vert I \vert } \int _{I}u^{q}(x)\,dx \biggr) ^{1/q}\leq \mathcal{K} \biggl( \frac{1}{ \vert I \vert }\int _{I}u(x)\,dx \biggr) ,\quad\text{for all }I\subset \mathbb{I}. $$

(5)

holds. Gehring result says that if a weight satisfies a reverse Hölder inequality for some exponent, then it satisfies a reverse Hölder inequality for a slightly larger exponent. In particular, Gehring proved that there exists $\epsilon =\epsilon (n,q,\mathcal{K})>0$ such that $u\in L^{p}(I)$ for $p< q+\epsilon$, while for each p, there exists a new constant $\mathcal{K}_{p}=\mathcal{K}_{p}(n,q,\mathcal{K},p)$ such that

$$ \frac{1}{ \vert I \vert } \int _{I}u^{p}(x)\,dx\leq \mathcal{K}_{p} \biggl( \frac{1}{ \vert I \vert } \int _{I}u(x)\,dx \biggr) ^{p}. $$

(6)

In other words, Gehring’s result for self-improving property states that:

$$ u\in G^{q}(\mathcal{K})\quad \Rightarrow \quad \exists \epsilon >0 \quad\text{such that }u\in G^{{q+\epsilon }}(\mathcal{K}_{p}). $$

The proof of Gehring’s inequality has been obtained using the Calderón-Zygmund Decomposition Theorem and the scale structure of $L^{p}$-spaces. In [25], Popoli established the sharp results for the self-improving and the transition properties of Gehring $G^{q}$ and Muckenhoupt $A^{p}$ weights by unifying the corresponding sharp results for weights satisfying a general reverse Hölder inequality in a general space named $B_{q}^{p}$. We say that u belongs to the class $B_{q}^{p}(K)$ if u satisfies the reverse Hölder inequality

$$ \biggl[ \int _{I}u^{p}(t)\,dt \biggr] ^{\frac{1}{p}}\leq K \biggl[ \int _{I}u^{q}(t)\,dt \biggr] ^{\frac{1}{q}},\quad K>0, $$

for some constants $p>q$ and for every subinterval $I\subseteq \mathbb{I}$. Popoli showed that the optimal exponents of integrability as well as the best constants in the integral inequalities could be obtained by means of the function

$$ \omega (p,q,x)= \biggl( \frac{x}{x-p} \biggr) ^{-\frac{1}{p}} \biggl( \frac{x}{x-q} \biggr) ^{\frac{1}{q}}, $$

(7)

provided the appropriate setting of variables. Actually, by observing that the function ω is strictly increasing for x in $(-\infty ,0)$ and strictly decreasing in $(0,+\infty )$, we have that the equation $\omega (p,q,x)=B$, $B>1$ admits only one negative solution $\nu _{-}=\nu _{-}(p,q,B)$ and one positive solution $\nu _{+}=\nu _{+}(p,q,B)$. One way of establishing Gehring’s Lemma involves exploiting the correspondence between a weighted Muckenhoupt class and a reverse Hölder class. In fact from (5), we get that

$$ \biggl( \frac{1}{ \vert I \vert } \int _{I}u^{q- \frac{1}{p-1}}(x) \biggl( \frac{1}{u(x)} \biggr) ^{\frac{-1}{p-1}}\,dx \biggr) ^{p-1} \leq \mathcal{K}^{q(p-1)} \biggl( \frac{1}{ \vert I \vert }\int _{I}u(x)\,dx \biggr) ^{q(p-1)}. $$

(8)

By taking $q=p/ ( p-1 )$, we have from (8) that (here $U(I)=\int _{I}u(t)\,dt$)

$$\begin{aligned} & \biggl( \frac{1}{U(I)} \int _{I}u(x) \biggl( \frac{1}{u(x)} \biggr) \,dx \biggr) \biggl( \frac{1}{U(I)} \int _{I}u(x) \biggl( \frac{1}{u(x)} \biggr) ^{\frac{-1}{p-1}}\,dx \biggr) ^{p-1} \\ &\quad \leq \mathcal{K}^{q(p-1)} \frac{ \vert I \vert ^{p}}{U^{p}(I)} \biggl( \frac{U(I)}{ \vert I \vert } \biggr) ^{p}=\mathcal{K}^{p}, \quad \text{for all }I\subset \mathbb{I}, \end{aligned}$$

which is a weighted $A_{u}^{p}(\mathcal{K}^{p}\mathcal{)}$ condition for $u^{-1}$ with respect the weight u and $p=q/(q-1)$. This shows that if $u\in G^{q}(\mathcal{K})$ then $u^{-1}\in A_{u}^{p}(\mathcal{C)}$ with $\mathcal{C}=\mathcal{K}^{1/p}$ where $p=q/(q-1)$. On the other hand, in considering mean convergence problems for various series in [21–23], it was natural to consider the weighted Hardy-Littlewood maximal operator

$$ \mathcal{M}g(x):=\sup_{y\neq x, x,y\in \mathbb{I}} \frac{1}{\int _{x}^{y}\,dm(t)} \int _{x}^{y}g(t)\,dm(t), $$

(9)

where $m(t)$ was a suitable measure, and the quotient is to taken as zero if the numerator and the denominator are both zero or both infinity. In [20], the author proved that if m is a Borel measure on an interval $\mathbb{I}$, which is 0 on sets consisting of single points, $1< p<\infty$ and $g(x)$ be a nonnegative weight on $\mathbb{I}$, then $\mathcal{M}g$ is bounded on $L_{u}^{p}(\mathbb{R}_{+})$ if and only if

$$ \biggl( \frac{1}{m(I)} \int _{I}u(t)\,dm(t) \biggr) \biggl( \frac{1}{m(I)}\int _{I}u^{-\frac{1}{p-1}}(t)\,dm(t) \biggr) ^{p-1}\leq \mathcal{C}, $$

(10)

for every subinterval $I\subset \mathbb{I}$, where $\mathcal{C}$ is a positive constant independent of g. So, it was natural to study the structure of the Muckenhoput class $A_{\lambda }^{p}(\mathcal{C})$ with a weight λ and the Gehring $G_{\lambda }^{q}$ with a weight λ. A nonnegative measurable weight function u defined on a bounded interval $\mathbb{I}$ is called an $A_{\lambda}^{p}(\mathcal{C})$-Muckenhoupt weight for $p>1$ if there exists a constant $\mathcal{C}<\infty$ such that

$$ \biggl( \frac{1}{\Upsilon (I)} \int _{I}\lambda(t)u(t)\,dt \biggr) \biggl( \frac{1}{\Upsilon (I)} \int _{I}\lambda(t)u^{-\frac{1}{p-1}}(t)\,dt \biggr) ^{p-1} \leq \mathcal{C}, $$

(11)

for every subinterval $I\subset \mathbb{I}$, where $\Upsilon (I)=\int _{I}\lambda (t)\,dt$. In [24], Popoli extended the results established in [15] and proved that the self-improving property holds and gave explicit and sharp values of exponents. We say that the nonnegative measurable function u satisfies the weighted Gehring $G_{\lambda}^{q}$-condition if there exists a constant $\mathcal{K}\geq 1$ such that

$$ \biggl( \frac{1}{\Upsilon (I)} \int _{I}u^{q}(x)\lambda (x)\,dx \biggr) ^{1/q} \leq \mathcal{K} \biggl( \frac{1}{\Upsilon (I)} \int _{I}\lambda (x)u(x)\,dx \biggr) , $$

(12)

for all $I\subset \mathbb{I}$, where $\Upsilon (I)=\int _{I}\lambda (x)\,dx$. For a given exponent $q>1$, we define the $G^{q}$-norm of u as

$$ G_{\lambda }^{q}(u):=\sup_{\mathbb{I}\subset \mathbb{I}} \biggl[ \biggl( \frac{1}{\Upsilon (I)} \int _{I}\lambda (t)u(t)\,dt \biggr) ^{-1} \biggl( \frac{1}{\Upsilon (I)} \int _{I}\lambda (t)u^{q}(t)\,dt \biggr) ^{\frac{1}{q}} \biggr] ^{\frac{q}{q-1}}, $$

(13)

where the supremum is taken over all intervals $I\subseteq \mathbb{I}$ and represents the best constant for which the $G_{\lambda }^{q}$-condition holds true independently on the interval $I\subseteq \mathbb{I}$. In [31, Theorem 4.1], Sbordone proved that if (12) holds and $\lambda(x)\,dx$ is a doubling measure, i.e. there exists a constant $d>0$ such that $\Upsilon (2I)\leq d\Upsilon (I)$, then there exists a $p>q$ such that

$$ \biggl( \frac{1}{\Upsilon (I)} \int _{I}u^{p}(x)\lambda (x)\,dx \biggr) ^{1/p} \leq \mathcal{K}_{1} \biggl( \frac{1}{\Upsilon (I)} \int _{I}\lambda (x)u(x)\,dx \biggr) . $$

(14)

By the weighted power mean operator $\mathcal{M}_{q}g$ of order $q\neq 0$ and nonnegative weight g defined on $\mathbb{I}$, we call the operator

$$ \mathcal{M}_{q}g:= \biggl( \frac{1}{\Upsilon (I)} \int _{I}\lambda (s)g^{q}(s)\,ds \biggr) ^{1/q},\quad\text{for }I\subset \mathbb{I}. $$

(15)

In the present paper, we consider the class $\mathcal{U}_{p}^{q}(B)$ of all nonnegative weights g satisfying the reverse Hölder inequality

$$ \mathcal{M}_{q}g\leq B\mathcal{M}_{p}g, $$

(16)

where the constant $B>1$ is independent of $\mathbb{I}$ and p, q such that $q>p$. The smallest constant, independent of the interval $\mathbb{I}$ and satisfying the inequality (16), is called the $\mathcal{U}_{p}^{q}$-norm of the weight g and will be denoted by $\mathcal{U}_{p}^{q}(g)$ and given by

$$ \mathcal{U}_{p}^{q}(g):=\sup_{I\subset \mathbb{I}} ( \mathcal{M}_{p}g ) ^{-\frac{1}{p}} ( \mathcal{M}_{q}g ) ^{ \frac{1}{q}},\quad \text{for }I\subset \mathbb{I}. $$

(17)

We say that g is a $\mathcal{U}_{p}^{q}$-weight if its $\mathcal{U}_{p}^{q}$-norm is finite, i.e.

$$ g\in \mathcal{U}_{p}^{q}\quad \iff\quad \mathcal{U}_{p}^{q}(g)< + \infty . $$

When we fix a constant $\mathcal{C}>1$, the triple of real numbers $(p,q,\mathcal{C})$ defines the $\mathcal{U}_{p}^{q}$ class:

$$ g\in \mathcal{U}_{p}^{q}(\mathcal{C})\quad \iff\quad \mathcal{U}_{p}^{q}(g)\leq \mathcal{C}, $$

and we will refer to $\mathcal{C}$ as the $\mathcal{U}_{p}^{q}$-constant of the class. It is immediate to observe that the classes $A_{\lambda }^{p}$ and $G_{\lambda }^{q}$ are special cases of the class $\mathcal{U}_{p}^{q}$ of weights as follows:

$$ A_{\lambda }^{p}:=\mathcal{U}_{\frac{1}{1-p}}^{1},\quad \text{and}\quad G_{ \lambda }^{q}:=\mathcal{U}_{1}^{q}. $$

The paper is organized as follows: In Sect. 2, we state and prove some basic lemmas concerning the bounds of power mean operator $\mathcal{M}_{p}g$. In Sect. 3, we establish some lower and upper bounds of the compositions using two special functions $\rho _{p}$ and $\rho _{q}$ defined later and prove some inclusion properties. For example, we prove that if $g\in \mathcal{U}_{p}^{q}(B)$ then $\mathcal{M}_{q}g\in \mathcal{U}_{p}^{\eta } ( B_{1} )$ with exact values of η and $B_{1}$. In Sect. 4, we present some applications of the main results and prove the self-improving properties of a monotone weights from $\mathcal{U}_{p}^{q}$, i.e. we will prove that if $g\in \mathcal{U}_{p}^{q}(B)$ then $g\in \mathcal{U}_{p}^{\eta } ( B_{1} )$ with exact values of η and $B_{1}$. For illustrations, we will derive the self-improving properties of the Muckenhoupt and Gehring weights as special cases. The results in this paper improve the results in [24, 31] in the sense that the results are valid for arbitrary parameters $p< q$, $p.q\neq 0$ and can be considered the natural extension of the results in [7].

2 Basic lemmas and some fundamental properties

In this section, we state and prove the basic lemmas that will give some properties of the power mean operator that will be used to prove the main results later. We will assume that $\mathbb{I}$ is a fixed finite subset of $\mathbb{R}_{+}$, and we recall the power mean operator $\mathcal{M}_{p}g$ that we will consider in this paper is given by

$$ \mathcal{M}_{p}g(t)= \biggl( \frac{1}{\Upsilon (t)} \int _{0}^{t} \lambda (s)g^{p}(s)\,ds \biggr) ^{1/p}, \quad\text{for all }t\in \mathbb{I}, $$

(18)

for any nonnegative weight $g:\mathbb{I}\rightarrow \mathbb{R}^{+}$ and $p\in \mathbb{R}\backslash \{0\}$ and $\Upsilon (t)=\int _{0}^{t}\lambda (s)\,ds$. For the sake of conventions, we assume that $0\cdot \infty =0$ and $0/0=0$.

Lemma 1

Assume that $g:\mathbb{I}\rightarrow \mathbb{R}^{+}$ is any nonnegative weight and $p\in \mathbb{R}\backslash \{0\}$. Then the following properties hold:

$(1)$. If g is nonincreasing, then $\mathcal{M}_{p}g$ is nonincreasing and $\mathcal{M}_{p}g(t)\geq g(t)$, for all $t \in \mathbb{I}$.

$(2)$. If g is nondecreasing, then $\mathcal{M}_{p}g$ is nondecreasing and $\mathcal{M}_{p}g(t)\leq g(t)$, for all $t \in \mathbb{I}$.

Proof

1). From the definition of $\mathcal{M}_{p}g$ and the fact that g is nonincreasing, we get for $p=1$ that

$$ \mathcal{M}_{1}g(t)= \biggl( \frac{1}{\Upsilon (t)} \int _{0}^{t} \lambda (s)g(s)\,ds \biggr) \geq \biggl( \frac{1}{\Upsilon (t)} \int _{0}^{t} \lambda (s)g(t)\,ds \biggr) =g(t). $$

For the general case when $p\neq 1$, we also have for all $t\in \mathbb{I}$ that

$$ \mathcal{M}_{p}g(t)= \biggl( \frac{1}{\Upsilon (t)} \int _{0}^{t} \lambda (s)g^{p}(s)\,ds \biggr) ^{1/p}\geq \biggl( \frac{1}{\Upsilon (t)}\int _{0}^{t}\lambda (s)g^{p}(t)\,ds \biggr) ^{1/p}=g(t). $$

From this inequality, we get that

$$ \Upsilon (t)g^{p}(t)\leq \int _{0}^{t}\lambda (s)g^{p}(s)\,ds, \quad\text{for all }t\in \mathbb{I}. $$

(19)

Now, using (19) and the fact that g is nonincreasing, we obtain that

$$\begin{aligned} \bigl( \mathcal{M}_{p}g(t) \bigr) ^{{\prime }} =& \frac{1}{p} \biggl( \frac{1}{\Upsilon (t)} \int _{0}^{t}\lambda (s)g^{p}(s)\,ds \biggr) ^{(1/p)-1} \frac{\Upsilon (t)\lambda (t)g^{p}(t)-\lambda (t)\int _{0}^{t}\lambda (s)g^{p}(s)\,ds}{\Upsilon ^{2}(t)} \\ \leq &\frac{1}{p}\lambda (t) \biggl( \frac{1}{\Upsilon (t)}\int _{0}^{t}\lambda (s)g^{p}(s)\,ds \biggr) ^{(1/p)-1} \frac{\int _{0}^{t}\lambda (s)g^{p}(s)\,ds-\int _{0}^{t}\lambda (s)g^{p}(s)\,ds}{\Upsilon ^{2}(t)} \\ =&0, \end{aligned}$$

that is $( \mathcal{M}_{p}g(t) ) ^{{\prime }}\leq 0$ for all $t\in \mathbb{I}$, and thus $\mathcal{M}_{p}g(t)$ is nonincreasing.

2). From the definition of $\mathcal{M}_{p}g(t)$ and the fact that $g(t)$ is nondecreasing, we have for $p=1$ that

$$ \mathcal{M}_{1}g(t)=\frac{1}{\Upsilon (t)} \int _{0}^{t}\lambda (s)g(s)\,ds \leq \frac{1}{\Upsilon (t)} \int _{0}^{t}\lambda (s)g(t)\,ds=g(t). $$

(20)

For the general case when $p\neq 1$, we also have for all $t\in \mathbb{I}$ that

$$ \mathcal{M}_{p}g(t)= \biggl( \frac{1}{\Upsilon (t)} \int _{0}^{t} \lambda (s)g^{p}(s)\,ds \biggr) ^{1/p}\leq \biggl( \frac{1}{\Upsilon (t)}\int _{0}^{t}\lambda (s)g^{p}(t)\,ds \biggr) ^{1/p}=g(t). $$

From this inequality, we see that

$$ \Upsilon (t)g^{p}(t)\geq \int _{0}^{t}\lambda (s)g^{p}(s)\,ds, \quad\text{for all }t\in \mathbb{I}. $$

(21)

Then, using inequality (21) and the fact that g is nondecreasing and proceeding as in the first case, we obtain that

$$\begin{aligned} & \bigl( \mathcal{M}_{p}g(t) \bigr) ^{{\prime }} \\ &\quad =\frac{1}{p} \biggl( \frac{1}{\Upsilon (t)} \int _{0}^{t}\lambda (s)g^{p}(s)\,ds \biggr) ^{(1/p)-1} \frac{\Upsilon (t)\lambda (t)g^{p}(t)-\lambda (t)\int _{0}^{t}\lambda (s)g^{p}(s)\,ds}{\Upsilon ^{2}(t)} \\ &\quad \geq \frac{1}{p}\lambda (t) \biggl( \frac{1}{\Upsilon (t)}\int _{0}^{t}\lambda (s)g^{p}(s)\,ds \biggr) ^{(1/p)-1} \frac{\int _{0}^{t}\lambda (s)g^{p}(s)\,ds-\int _{0}^{t}\lambda (s)g^{p}(s)\,ds}{\Upsilon ^{2}(t)} \\ &\quad =0, \end{aligned}$$

which implies that $( \mathcal{M}_{p}g(t) ) ^{{\prime }}\geq 0$ for all $t\in \mathbb{I}$, and thus $\mathcal{M}_{p}g(t)$ is nondecreasing. The proof is complete. □

As in the proof of Lemma 1, we can also prove the following results.

Lemma 2

Assume that $g:\mathbb{I}\rightarrow \mathbb{R}^{+}$ is any nonnegative weight and $q\in \mathbb{R}\backslash \{0\}$. Then the following properties hold:

$(1)$. If g is nonincreasing, then $\mathcal{M}_{q}g$ is nonincreasing and $\mathcal{M}_{q}g(t)\geq g(t)$, for all $t \in \mathbb{I}$.

$(2)$. If g is nondecreasing, then $\mathcal{M}_{q}g$ is nondecreasing and $\mathcal{M}_{q}g(t)\leq g(t)$, for all $t \in \mathbb{I}$.

To prove the main results in this section, we will use the properties of the function

$$ \rho _{p}(\eta )= \biggl( 1-\frac{p}{\eta } \biggr) ^{1/p}, $$

of the variable for $\eta \in (-\infty ,\min (0,p))\cup (\max (0,p),\infty )$. It is clear that the function $\rho _{p}(\eta )$ is continuous and increases from 1 to +∞ on $(-\infty ,\min (0,p))$ and from 0 to 1 on $(\max (0,p),\infty )$ and

$$\begin{aligned} \rho _{p}(\eta )\rho _{p}(p-\eta ) =& \biggl( 1- \frac{p}{\eta } \biggr) ^{1/p} \biggl( 1-\frac{p}{p-\eta } \biggr) ^{1/p} \\ =& \biggl( \frac{\eta -p}{\eta } \biggr) ^{1/p} \biggl( \frac{\eta }{\eta -p} \biggr) ^{1/p}=1. \end{aligned}$$

We set

$$ S_{p,q}(\eta )=\frac{\rho _{p}(\eta )}{\rho _{q}(\eta )},\quad\text{for } \eta \in \bigl(- \infty ,\min (0,p)\bigr)\cup \bigl(\max (0,q),\infty \bigr). $$

The function $S_{p,q}(\eta )$ is continuous and increases from 1 to +∞ on $(-\infty ,\min (0,p))$ and decreases from +∞ to 1 on $(\max (0,q),\infty )$. Therefore, for any $B>1$, the equation

$$ S_{p,q}(\eta )=\frac{(1-p/\eta )^{1/p}}{(1-q/\eta )^{1/q}}=B, $$

(22)

has two roots: a positive root $\eta ^{+}$ and a negative root $\eta ^{-}$.

Theorem 3

Let $p< q$, $p.q\neq 0$, and $g:\mathbb{I\rightarrow R}^{+}$ be any nonnegative weight. If $g\in \mathcal{U}_{p}^{q}(B)$ for $B>1$, then

$$ \rho _{p}\bigl(\eta ^{+}\bigr)\leq \frac{\mathcal{M}_{q}g(t)}{\mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t)}\leq \rho _{p}\bigl(\eta ^{-}\bigr), \quad\textit{for all }t\in \mathbb{I}, $$

(23)

where $\eta ^{+}$ and $\eta ^{-}$ are the roots of (22).

Proof

From the definition of $\mathcal{M}_{p}g(t)$, we have that

$$\begin{aligned} \bigl[ \Upsilon (s)\mathcal{M}_{q}^{p}g(s) \bigr] ^{{\prime }} =& \biggl[ \Upsilon (s) \biggl( \frac{1}{\Upsilon (s)} \int _{0}^{s} \lambda (u)g^{q}(u)\,du \biggr) ^{p/q} \biggr] ^{{\prime }} \\ =&\lambda (s) \biggl( \frac{1}{\Upsilon (s)} \int _{0}^{s}\lambda (u)g^{q}(u)\,du \biggr) ^{p/q} \\ &{}+\Upsilon (s) \biggl( \biggl( \frac{1}{\Upsilon (s)} \int _{0}^{s} \lambda (u)g^{q}(u)\,du \biggr) ^{p/q} \biggr) ^{{\prime }}. \end{aligned}$$

(24)

The second term in (24) is given by

$$\begin{aligned} &\Upsilon (s) \biggl( \biggl( \frac{1}{\Upsilon (s)} \int _{0}^{s} \lambda (u)g^{q}(u)\,du \biggr) ^{p/q} \biggr) ^{{\prime }} \\ &\quad =\frac{p}{q}\Upsilon (s) \biggl( \frac{\int _{0}^{s}\lambda (u)g^{q}(u)\,du}{\Upsilon (s)} \biggr) ^{(p/q)-1} \biggl( \frac{\Upsilon (s)\lambda (s)g^{q}(s)-\lambda (s)\int _{0}^{s}\lambda (u)g^{q}(u)\,du}{\Upsilon ^{2}(s)} \biggr) \\ &\quad =\frac{p}{q} \biggl( \frac{\int _{0}^{s}\lambda (u)g^{q}(u)\,du}{\Upsilon (s)} \biggr) ^{(p/q)-1}\lambda (s)g^{q}(s)-\frac{p}{q}\lambda (s) \biggl( \frac{\int _{0}^{s}\lambda (u)g^{q}(u)\,du}{\Upsilon (s)} \biggr) ^{p/q}. \end{aligned}$$

(25)

By combining (25) and (24), we obtain

$$\begin{aligned} \bigl[ \Upsilon (s)\mathcal{M}_{q}^{p}g(s) \bigr] ^{{\prime }} =& \biggl( \frac{q-p}{q} \biggr) \biggl( \frac{1}{\Upsilon (s)} \int _{0}^{s} \lambda (u)g^{q}(u)\,du \biggr) ^{p/q}\lambda (s) \\ &{}+\frac{p}{q} \biggl( \frac{1}{\Upsilon (s)} \int _{0}^{s}\lambda (u)g^{q}(u)\,du \biggr) ^{(p/q)-1}\lambda (s)g^{q}(s). \end{aligned}$$

(26)

Integrating (26) from 0 to t and dividing by $\Upsilon (t)$, we have that

$$\begin{aligned} \mathcal{M}_{q}^{p}g(t) =& \biggl( \frac{q-p}{q} \biggr) \frac{1}{\Upsilon (t)}\int _{0}^{t}\lambda (s) \biggl( \frac{1}{\Upsilon (s)} \int _{0}^{s} \lambda (u)g^{q}(u)\,du \biggr) ^{p/q}\,ds \\ &{}+\frac{p}{q}\frac{1}{\Upsilon (t)} \int _{0}^{t} \biggl( \frac{1}{\Upsilon (s)}\int _{0}^{s}\lambda (u)g^{q}(u)\,du \biggr) ^{(p/q)-1}\lambda (s)g^{q}(s)\,ds. \end{aligned}$$

(27)

From the definition of $\mathcal{M}_{q}g$, we see that the first term in (27) is given by

$$ \frac{1}{\Upsilon (t)} \int _{0}^{t}\lambda (s) \biggl( \frac{1}{\Upsilon (s)}\int _{0}^{s}\lambda (u)g^{q}(u)\,du \biggr) ^{p/q}\,ds= \bigl[ \mathcal{M}_{p}(\mathcal{M}_{q}g) ( t ) \bigr] ^{p}. $$

(28)

Now, we have the term

$$ \frac{1}{\Upsilon (t)} \int _{0}^{t} \biggl( \frac{1}{\Upsilon (s)}\int _{0}^{s}\lambda (u)g^{q}(u)\,du \biggr) ^{(p/q)-1}\lambda (s)g^{q}(s)\,ds. $$

By applying reverse Hölder’s inequality for $p/q<1$ and $p/(p-q)$, we obtain that

$$\begin{aligned} &\frac{1}{\Upsilon (t)} \int _{0}^{t} \biggl( \frac{1}{\Upsilon (s)}\int _{0}^{s}\lambda (u)g^{q}(u)\,du \biggr) ^{(p/q)-1}\lambda (s)g^{q}(s)\,ds \\ &\quad \geq \biggl( \frac{1}{\Upsilon (t)} \int _{0}^{t}\lambda (s) \biggl( \frac{1}{\Upsilon (s)} \int _{0}^{s}\lambda (u)g^{q}(u)\,du \biggr) ^{p/q}\,ds \biggr) ^{ ( p-q ) /p} \\ &\qquad {}\times \biggl( \frac{1}{\Upsilon (t)} \int _{0}^{t}\lambda (s)g^{p}(s)\,ds \biggr) ^{q/p} \\ &\quad = \bigl[ \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) \bigr] ^{p-q} \bigl[ \mathcal{M}_{p}g(t) \bigr] ^{q}. \end{aligned}$$

(29)

By substituting (29) and (28) into (27), dividing by $p [ \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) ] ^{p}$, and then applying (16), we obtain that

$$\begin{aligned} \frac{1}{p} \frac{ [ \mathcal{M}_{q}g(t) ] ^{p}}{ [ \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) ] ^{p}} \geq & \biggl( \frac{1}{p}- \frac{1}{q} \biggr) +\frac{1}{q} \frac{ [ \mathcal{M}_{p}g(t) ] ^{q}}{ [ \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) ] ^{q}} \\ \geq & \biggl( \frac{1}{p}-\frac{1}{q} \biggr) +B^{-q} \frac{1}{q} \frac{ [ \mathcal{M}_{q}g(t) ] ^{q}}{ [ \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) ] ^{q}}. \end{aligned}$$

(30)

By setting

$$ \eta :=p \frac{ [ \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) ] ^{p}}{ [ \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) ] ^{p}- [ \mathcal{M}_{q}g(t) ] ^{p}}, $$

(31)

we see that inequality (30) can be written in the form

$$\begin{aligned} &B^{-q} \biggl[ 1- \frac{ [ \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) ] ^{p}- [ \mathcal{M}_{q}g(t) ] ^{p}}{ [ \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) ] ^{p}} \biggr] ^{q/p} \\ &\quad =B^{-q} \biggl[ \frac{ [ \mathcal{M}_{q}g(t) ] ^{p}}{ [ \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) ] ^{p}} \biggr] ^{q/p}\leq 1-\frac{q}{p}+\frac{q}{p} \frac{ [ \mathcal{M}_{q}g(t) ] ^{p}}{ [ \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) ] ^{p}} \\ &\quad \leq 1-\frac{q}{p} \biggl( 1- \frac{ [ \mathcal{M}_{q}g(t) ] ^{p}}{ [ \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) ] ^{p}} \biggr) \\ &\quad =1-\frac{q}{p} \biggl( \frac{ [ \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) ] ^{p}- [ \mathcal{M}_{q}g(t) ] ^{p}}{ [ \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) ] ^{p}} \biggr) . \end{aligned}$$

(32)

This inequality can be written now as

$$ \biggl( 1-\frac{p}{\eta } \biggr) ^{1/p}\leq B \biggl( 1- \frac{q}{\eta } \biggr) ^{1/q}, $$

or equivalently

$$ S_{p,q}(\eta )= \frac{ ( 1-\frac{p}{\eta } ) ^{1/p}}{ ( 1-\frac{q}{\eta } ) ^{1/q}}\leq B,\quad\text{for all }p< q. $$

This means that $\eta \in (-\infty ,\eta ^{-}]\cup {}[ \eta ^{+},+\infty )$. The properties of the weight $\rho _{p}$ imply that $\rho _{p}(\eta ^{+})\leq \rho _{p}(\eta )\leq \rho _{p}(\eta ^{-})$, and since

$$\begin{aligned} \rho _{p}(\eta ) =& \biggl( 1-\frac{p}{\eta } \biggr) ^{1/p}= \biggl( 1- \frac{ [ \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) ] ^{p}- [ \mathcal{M}_{q}g(t) ] ^{p}}{ [ \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) ] ^{p}} \biggr) ^{1/p} \\ =& \biggl( 1-1+ \frac{ [ \mathcal{M}_{q}g(t) ] ^{p}}{ [ \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) ] ^{p}} \biggr) ^{1/p}= \frac{ [ \mathcal{M}_{q}g(t) ] }{\mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t)}, \end{aligned}$$

we obtain that

$$ \rho _{p}\bigl(\eta ^{+}\bigr)\leq \frac{ [ \mathcal{M}_{q}g(t) ] }{\mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t)}\leq \rho _{p}\bigl(\eta ^{-}\bigr), $$

(33)

which is the desired inequality (23). The proof is complete. □

Theorem 4

Let $p< q$, $p.q\neq 0$, and $g:\mathbb{I\rightarrow R}^{+}$ be any nonnegative weight. If $g\in \mathcal{U}_{p}^{q}(B)$ for $B>1$, then

$$ \rho _{q}\bigl(\eta ^{+}\bigr)\leq \frac{\mathcal{M}_{p}g(t)}{\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t)}\leq \rho _{q}\bigl(\eta ^{-}\bigr), \quad\textit{for all }t\in \mathbb{I}, $$

(34)

where $\eta ^{+}$ and $\eta ^{-}$ are the roots of (22).

Proof

From the definition of $\mathcal{M}_{p}g(t)$, we obtain that

$$\begin{aligned} &\bigl[ \Upsilon (s)\mathcal{M}_{p}^{q}g(s) \bigr] ^{{\prime }} \\ &\quad = \biggl[ \Upsilon (s) \biggl( \frac{1}{\Upsilon (s)} \int _{0}^{s} \lambda (u)g^{p}(u)\,du \biggr) ^{q/p} \biggr] ^{{\prime }} \\ &\quad =\lambda (s) \biggl( \frac{1}{\Upsilon (s)} \int _{0}^{s}\lambda (u)g^{p}(u)\,du \biggr) ^{q/p}+\Upsilon (s) \biggl[ \biggl( \frac{1}{\Upsilon (s)}\int _{0}^{s}\lambda (u)g^{p}(u)\,du \biggr) ^{q/p} \biggr] ^{{\prime }}. \end{aligned}$$

(35)

Proceeding as in the proof of Theorem 3, we get that

$$\begin{aligned} \bigl[ \mathcal{M}_{p}g(s) \bigr] ^{q} \leq & \biggl( 1- \frac{q}{p} \biggr) \frac{1}{\Upsilon (t)} \int _{0}^{t}\lambda (s) \biggl( \frac{1}{\Upsilon (s)}\int _{0}^{s}\lambda (u)g^{p}(u)\,du \biggr) ^{q/p}\,ds \\ &{}+\frac{q}{p}\frac{1}{\Upsilon (t)} \int _{0}^{t} \biggl( \frac{1}{\Upsilon (s)}\int _{0}^{s}\lambda (u)g^{p}(u)\,du \biggr) ^{(q/p)-1}\lambda (s)g^{p}(s)\,ds. \end{aligned}$$

(36)

From the definition of $\mathcal{M}_{p}g$, we see that the first term in (36) is given by

$$ \frac{1}{\Upsilon (t)} \int _{0}^{t}\lambda (s) \biggl( \frac{1}{\Upsilon (s)}\int _{0}^{s}\lambda (u)g^{p}(u)\,du \biggr) ^{q/p}\,ds= \bigl[ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \bigr] ^{q}. $$

(37)

Now, we simplify the term

$$ \frac{1}{\Upsilon (t)} \int _{0}^{t} \biggl( \frac{1}{\Upsilon (s)}\int _{0}^{s}\lambda (u)g^{p}(u)\,du \biggr) ^{(q/p)-1}\lambda (s)g^{p}(s)\,ds. $$

By applying Hölder’s inequality for $q/p>1$ and $q/(q-p)$, we obtain

$$\begin{aligned} &\frac{1}{\Upsilon (t)} \int _{0}^{t} \biggl( \frac{1}{\Upsilon (s)}\int _{0}^{s}\lambda (u)g^{p}(u)\,du \biggr) ^{(q/p)-1}\lambda (s)g^{p}(s)\,ds \\ &\quad \leq \biggl( \frac{1}{\Upsilon (t)} \int _{0}^{t}\lambda (s) \biggl( \frac{1}{\Upsilon (s)} \int _{0}^{s}\lambda (u)g^{p}(u)\,du \biggr) ^{q/p}\,ds \biggr) ^{ ( q-p ) /q} \biggl( \frac{\int _{0}^{t}\lambda (s)g^{q}(s)\,ds}{\Upsilon (t)} \biggr) ^{p/q} \\ &\quad = \bigl[ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \bigr] ^{q-p} \bigl[ \mathcal{M}_{q}g(t) \bigr] ^{p}. \end{aligned}$$

(38)

By substituting (37) and (38) into (36), dividing by $q [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{q}$, and applying (16), we obtain

$$\begin{aligned} \frac{ [ \mathcal{M}_{p}g(t) ] ^{q}}{q [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{q}} \leq & \biggl( \frac{1}{q}- \frac{1}{p} \biggr) +\frac{1}{p} \frac{ [ \mathcal{M}_{p}g(t) ] ^{p}}{ [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{p}} \\ \leq & \biggl( \frac{1}{q}-\frac{1}{p} \biggr) + \frac{B^{p}}{p} \frac{ [ \mathcal{M}_{p}g(t) ] ^{p}}{ [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{p}}. \end{aligned}$$

(39)

This inequality now takes the form

$$\begin{aligned} & \biggl[ B \biggl( 1- \frac{ [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{q}- [ \mathcal{M}_{p}g(t) ] ^{q}}{ [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{q}} \biggr) ^{1/q} \biggr] ^{p} \\ &\quad = \biggl[ B \biggl( \frac{ [ \mathcal{M}_{p}g(t) ] ^{q}}{ [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{q}} \biggr) ^{1/q} \biggr] ^{p}=B^{p} \frac{ [ \mathcal{M}_{p}g(t) ] ^{p}}{ [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{p}} \\ &\quad \geq 1-\frac{p}{q}+\frac{p}{q} \frac{ [ \mathcal{M}_{p}g(t) ] ^{q}}{ [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{q}}=1-\frac{p}{q} \biggl( 1- \frac{ [ \mathcal{M}_{p}g(t) ] ^{q}}{ [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{q}} \biggr) \\ &\quad =1-\frac{p}{q} \frac{ [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{q}- [ \mathcal{M}_{p}g(t) ] ^{q}}{ [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{q}}. \end{aligned}$$

(40)

By setting

$$ \eta :=q \frac{ [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{q}}{ [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{q}- [ \mathcal{M}_{p}g(t) ] ^{q}}, $$

(41)

we see that the inequality (40) takes the form

$$ \biggl( 1-\frac{p}{\eta } \biggr) ^{1/p}\leq B \biggl( 1- \frac{q}{\eta } \biggr) ^{1/q}, $$

or equivalently,

$$ S_{p,q}(\eta )= \frac{ ( 1-\frac{p}{\eta } ) ^{1/p}}{ ( 1-\frac{q}{\eta } ) ^{1/q}}\leq B. $$

This means that $\eta \in (-\infty ,\eta ^{-}]\cup {}[ \eta ^{+},+\infty )$. The properties of the weight $\rho _{q}$ imply that $\rho _{q}(\eta ^{+})\leq \rho _{q}(\eta )\leq \rho _{q}(\eta ^{-})$, and since

$$\begin{aligned} \rho _{q}(\eta ) =& \biggl( 1-\frac{q}{\eta } \biggr) ^{1/q}= \biggl( 1- \frac{ [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{q}- [ \mathcal{M}_{p}g(t) ] ^{q}}{ [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{q}} \biggr) ^{1/q} \\ =& \biggl( 1-1+ \frac{ [ \mathcal{M}_{p}g(t) ] ^{q}}{ [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{q}} \biggr) ^{1/q}= \frac{ [ \mathcal{M}_{p}g(t) ] }{ [ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] }, \end{aligned}$$

we obtain that

$$ \rho _{q}\bigl(\eta ^{+}\bigr)\leq \frac{\mathcal{M}_{p}g(t)}{\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t)}\leq \rho _{q}\bigl(\eta ^{-}\bigr), $$

which is the required inequality (34). The proof is complete. □

The assumptions and the conclusions of Theorems 3 and 4 will be used in proving the following theorems.

Theorem 5

Assume that the conditions in Theorems 3and 4hold. Then the compositions

$$ \bigl( \Upsilon (t) \bigr) ^{1/\eta ^{-}}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t),\quad\textit{and}\quad \bigl( \Upsilon (t) \bigr) ^{1/\eta ^{-}}\mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t), $$

(42)

are nonincreasing

$$ \bigl( \Upsilon (t) \bigr) ^{1/\eta ^{+}}\mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t),\quad\textit{and}\quad \bigl( \Upsilon (t) \bigr) ^{1/\eta ^{+}}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t), $$

(43)

are nondecreasing.

Proof

Using the definition of $\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t)$, we see that

$$\begin{aligned} & \bigl( \bigl( \Upsilon (t) \bigr) ^{1/\eta ^{\pm }}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \bigr) ^{{\prime }} \\ &\quad = \bigl( \bigl( \Upsilon (t) \bigr) ^{1/\eta ^{\pm }} \bigr) ^{{ \prime }}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t)+\bigl(\Upsilon (t)\bigr)^{1/ \eta ^{\pm }} \bigl( \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \bigr) ^{{\prime }} \\ &\quad =\frac{1}{\eta ^{\pm }}\bigl(\Upsilon (t)\bigr)^{(1/\eta ^{\pm })-1}\lambda (t)\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t)+\bigl( \Upsilon (t)\bigr)^{1/ \eta ^{\pm }} \bigl( \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \bigr) ^{{\prime }}. \end{aligned}$$

(44)

From the definition of $\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t)$, we see that

$$\begin{aligned} & \bigl( \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \bigr) ^{{ \prime }} \\ &\quad = \biggl( \biggl( \frac{1}{\Upsilon (t)} \int _{0}^{t}\lambda (s) \biggl( \frac{1}{\Upsilon (s)} \int _{0}^{s}\lambda (u)g^{p}(u)\,du \biggr) ^{q/p}\,ds \biggr) ^{1/q} \biggr) ^{{\prime }} \\ &\quad =\frac{1}{q} \biggl( \frac{1}{\Upsilon (t)} \int _{0}^{t}\lambda (s) \biggl( \frac{1}{\Upsilon (s)} \int _{0}^{s}\lambda (u)g^{p}(u)\,du \biggr) ^{q/p}\,ds \biggr) ^{(1/q)-1} \\ &\qquad {}\times \frac{\Upsilon (t)\lambda (t) ( \frac{1}{\Upsilon (t)}\int _{0}^{t}\lambda (u)g^{p}(u)\,du ) ^{q/p}-\lambda (t)\int _{0}^{t}\lambda (s) ( \frac{1}{\Upsilon (s)}\int _{0}^{s}\lambda (u)g^{p}(u)\,du ) ^{q/p}\,ds}{\Upsilon ^{2}(t)} \\ &\quad =\frac{\lambda (t)}{q\Upsilon (t)} \bigl[ \bigl( \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \bigr) ^{1-q} \bigl( \mathcal{M}_{p}g(t) \bigr) ^{q}-\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \bigr] . \end{aligned}$$

This and (44) imply that

$$\begin{aligned} & \bigl( \bigl( \Upsilon (t) \bigr) ^{1/\eta ^{\pm }}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \bigr) ^{{\prime }}=\frac{1}{\eta ^{\pm }}\bigl(\Upsilon (t)\bigr)^{(1/\eta ^{\pm })-1}\lambda (t)\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \\ &\qquad {}+\bigl(\Upsilon (t)\bigr)^{(1/\eta ^{\pm })-1}\frac{1}{q} \bigl( \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \bigr) ^{1-q}\lambda (t) \bigl( \mathcal{M}_{p}g(t) \bigr) ^{q} \\ &\qquad {}-\frac{1}{q}\bigl(\Upsilon (t)\bigr)^{(1/\eta ^{\pm })-1}\lambda (t) \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \\ &\quad =\bigl(\Upsilon (t)\bigr)^{(1/\eta ^{\pm })-1}\lambda (t)\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \biggl[ \frac{1}{\eta ^{\pm }}+ \biggl( \frac{\mathcal{M}_{p}g(t)}{\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t)} \biggr) ^{q}-\frac{1}{q} \biggr] . \end{aligned}$$

That is

$$\begin{aligned} \bigl( \bigl( \Upsilon (t) \bigr) ^{1/\eta ^{\pm }}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \bigr) ^{{\prime }} =&\bigl( \Upsilon (t) \bigr)^{(1/\eta ^{\pm })-1}\lambda (t)\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \\ &{}\times \biggl[ \frac{1}{\eta ^{\pm }}+\frac{1}{q} \biggl( \frac{\mathcal{M}_{p}g(t)}{\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t)} \biggr) ^{q}-\frac{1}{q} \biggr] . \end{aligned}$$

(45)

We note that the same equality remains valid if p and q change places, that is

$$\begin{aligned} \bigl( \bigl( \Upsilon (t) \bigr) ^{1/\eta ^{\pm }}\mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) \bigr) ^{{\prime }} =&\bigl( \Upsilon (t) \bigr)^{(1/\eta ^{\pm })-1}\lambda (t)\mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) \\ &{}\times \biggl[ \frac{1}{\eta ^{\pm }}+\frac{1}{p} \biggl( \frac{\mathcal{M}_{q}g(t)}{\mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t)} \biggr) ^{p}-\frac{1}{p} \biggr] . \end{aligned}$$

(46)

It is clear that the signs of the derivatives of the left-hand side of (45) and (46) are determined by the signs of the terms in the square brackets on the right-hand side. In turn, the signs of the square brackets are determined by inequalities (23) and (34). For example, the left-hand side in (23) means that the derivative

$$\begin{aligned} &\bigl( \bigl( \Upsilon (t) \bigr) ^{1/\eta ^{+}}\mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) \bigr) ^{{\prime }} \\ &\quad \geq \bigl( \Upsilon (t) \bigr)^{(1/\eta ^{+})-1}\lambda (t)\mathcal{M}_{p} ( \mathcal{M}_{q}g)(t)\times \biggl[ \frac{1}{\eta ^{+}}+\frac{1}{p} \biggl( \biggl( 1- \frac{p}{\eta ^{+}} \biggr) ^{1/p} \biggr) ^{p}- \frac{1}{p} \biggr] =0, \end{aligned}$$

is nonnegative. Hence, the function $( \Upsilon (t) ) ^{1/\eta ^{+}}\mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t)$ is nondecreasing. Analogously, we can prove the monotonicity of the remaining functions mentioned in the theorem. This completes the proof. □

3 Main results

In this section, first, we prove that the power mean operators $\mathcal{M}_{p}g$ and $\mathcal{M}_{q}g$ of the weight $g\in \mathcal{U}_{p}^{q}$ satisfy the the reverse Hölder inequality with some better exponents.

Theorem 6

Let $p< q$, $p.q\neq 0$, and g be any nonnegative weight, and $\eta ^{+}$ and $\eta ^{-}$ are the roots of equation (22).

$(i)$. If $g\in \mathcal{U}_{p}^{q}(B)$ for $B>1$ and $\eta <\eta ^{+}$ and $\eta \neq 0$, then

$$ \mathcal{M}_{p}g\in \mathcal{U}_{q}^{\eta } \biggl( \frac{\rho _{q} ( \eta ^{-} ) }{\rho _{\eta } ( \eta ^{+} ) } \biggr) ,\quad\textit{and}\quad \mathcal{M}_{q}g\in \mathcal{U}_{p}^{\eta } \biggl( \frac{\rho _{p} ( \eta ^{-} ) }{\rho _{\eta } ( \eta ^{+} ) } \biggr) . $$

(47)

$(\mathit{ii})$. If $g\in \mathcal{U}_{p}^{q}(B)$ for $B>1$ and $\eta >\eta ^{-}$, and $\eta \neq 0$, then

$$ \mathcal{M}_{p}g\in \mathcal{U}_{\eta }^{q} \biggl( \frac{\rho _{\eta } ( \eta ^{-} ) }{\rho _{q} ( \eta ^{+} ) } \biggr) ,\quad\textit{and}\quad \mathcal{M}_{q}g\in \mathcal{U}_{\eta }^{p} \biggl( \frac{\rho _{\eta } ( \eta ^{-} ) }{\rho _{p} ( \eta ^{+} ) } \biggr) . $$

(48)

Proof

$(i)$. Since η is either positive or negative, we will discuss the two cases:

1). Assume that $\eta >0$. By raising (34) to the power η, we obtain for $s< t$ that

$$\begin{aligned} & \bigl( \Upsilon (s) \bigr) ^{-\eta /\eta ^{-}}\lambda (s)\rho _{q}^{ \eta } \bigl(\eta ^{+}\bigr) \bigl[ \bigl( \Upsilon (s) \bigr) ^{1/\eta ^{-}} \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (s) \bigr] ^{\eta } \\ &\quad \leq \lambda (s) \bigl( \mathcal{M}_{p}g(s) \bigr) ^{\eta } \\ &\quad \leq \lambda (s) \bigl( \Upsilon (s) \bigr) ^{-\eta /\eta ^{+}} \rho _{q}^{\eta }\bigl(\eta ^{-}\bigr) \bigl[ \bigl( \Upsilon (s) \bigr) ^{1/ \eta ^{+}}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (s) \bigr] ^{\eta }. \end{aligned}$$

(49)

Using the monotonicity of

$$ \bigl(\Upsilon (t)\bigr)^{1/\eta ^{-}}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t),\quad\text{and}\quad \bigl( \Upsilon (t) \bigr) ^{1/\eta ^{+}} \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t), $$

we have that

$$\begin{aligned} & \bigl( \Upsilon (s) \bigr) ^{-\eta /\eta ^{-}}\lambda (s)\rho _{q}^{ \eta } \bigl(\eta ^{+}\bigr) \bigl[ \bigl( \Upsilon (t) \bigr) ^{1/\eta ^{-}} \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \bigr] ^{\eta } \\ &\quad \leq \bigl( \mathcal{M}_{p}g(s) \bigr) ^{\eta }\lambda (s) \\ &\quad \leq \lambda (s) \bigl( \Upsilon (s) \bigr) ^{-\eta /\eta ^{+}} \rho _{q}^{\eta }\bigl(\eta ^{-}\bigr) \bigl[ \bigl( \Upsilon (t) \bigr) ^{1/ \eta ^{+}}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \bigr] ^{\eta }. \end{aligned}$$

(50)

Let $\eta <\eta ^{+}$. By integrating from 0 to t and dividing by $\Upsilon (t)$, and raising it to the power $1/\eta >0$, we get that

$$\begin{aligned} & \biggl( \frac{\rho _{q}^{\eta }(\eta ^{+}) [ ( \Upsilon (t) ) ^{1/\eta ^{-}}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{\eta }}{\Upsilon (t)} \int _{0}^{t}\lambda (s) \bigl( \Upsilon (s) \bigr) ^{-\eta /\eta ^{-}}\,ds \biggr) ^{1/\eta } \\ &\quad \leq \biggl( \frac{1}{\Upsilon (t)} \int _{0}^{t}\lambda (s) \bigl( \mathcal{M}_{p}g(s) \bigr) ^{\eta }\,ds \biggr) ^{1/\eta } \\ &\quad \leq \biggl( \frac{\rho _{q}^{\eta }(\eta ^{-}) [ ( \Upsilon (t) ) ^{1/\eta ^{+}}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{\eta }}{\Upsilon (t)} \int _{0}^{t}\lambda (s) \bigl( \Upsilon (s) \bigr) ^{-\eta /\eta ^{+}}\,ds \biggr) ^{1/\eta }. \end{aligned}$$

(51)

Since

$$ \int _{0}^{t} \bigl( \Upsilon (s) \bigr) ^{-\eta /\eta ^{+}}\lambda (s)\,ds=\frac{ ( \Upsilon (t) ) ^{-\eta /\eta ^{+}+1}}{ ( -\eta /\eta ^{+} ) +1}, $$

we have

$$\begin{aligned} & \biggl( \frac{\rho _{q}^{\eta }(\eta ^{-}) [ ( \Upsilon (t) ) ^{1/\eta ^{+}}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{\eta }}{\Upsilon (t)} \int _{0}^{t}\lambda (s) \bigl( \Upsilon (s) \bigr) ^{-\eta /\eta ^{+}}\,ds \biggr) ^{1/\eta } \\ &\quad = \biggl( \frac{\rho _{q}^{\eta }(\eta ^{-}) [ ( \Upsilon (t) ) ^{1/\eta ^{+}}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{\eta }}{\Upsilon (t)} \frac{ ( \Upsilon (t) ) ^{-\eta /\eta ^{+}+1}}{ ( -\eta /\eta ^{+} ) +1} \biggr) ^{1/\eta } \\ &\quad = \biggl( \rho _{q}^{\eta }\bigl(\eta ^{-} \bigr) \bigl[ \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \bigr] ^{\eta } \frac{1}{ ( 1-\frac{\eta }{\eta ^{+}} ) } \biggr) ^{1/\eta } \\ &\quad =\frac{\rho _{q}(\eta ^{-})}{\rho _{\eta }(\eta ^{+})}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t). \end{aligned}$$

(52)

Similarly, since $\eta ^{-}<0$, then $-\eta /\eta ^{-}>0$ and hence $-\eta /\eta ^{-}+1>1$, we have that

$$ \int _{0}^{t} \bigl( \Upsilon (s) \bigr) ^{-\eta /\eta ^{-}}\lambda (s)\,ds=\frac{1}{-\eta /\eta ^{-}+1} \int _{0}^{t}\Delta \bigl( \Upsilon (s) \bigr) ^{-\eta /\eta ^{-}+1}= \frac{(\Upsilon (t))^{-\eta /\eta ^{-}+1}}{-\eta /\eta ^{-}+1}. $$

In this case, we have

$$\begin{aligned} & \biggl( \frac{\rho _{q}^{\eta }(\eta ^{+}) [ ( \Upsilon (t) ) ^{1/\eta ^{-}}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{\eta }}{\Upsilon (t)} \int _{0}^{t}\lambda (s) \bigl( \Upsilon (s) \bigr) ^{-\eta /\eta ^{-}} \biggr) ^{1/\eta } \\ &\quad \geq \biggl( \frac{\rho _{q}^{\eta }(\eta ^{+}) [ ( \Upsilon (t) ) ^{1/\eta ^{-}}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{\eta }}{\Upsilon (t)} \frac{ ( \Upsilon (t) ) ^{-\eta /\eta ^{-}+1}}{-\eta /\eta ^{-}+1} \biggr) ^{1/\eta } \\ &\quad =\frac{\rho _{q}(\eta ^{+})}{\rho _{\eta }(\eta ^{-})}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t). \end{aligned}$$

(53)

By substituting (52) and (53) into (51), we obtain

$$ \frac{\rho _{q}(\eta ^{+})}{\rho _{\eta }(\eta ^{-})}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \leq \mathcal{M}_{\eta } ( \mathcal{M}_{p}g ) ( t ) \leq \frac{\rho _{q}(\eta ^{-})}{\rho _{\eta }(\eta ^{+})}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t), $$

which implies that

$$ \mathcal{M}_{p}g\in \mathcal{U}_{q}^{\eta } \biggl( \frac{\rho _{q} ( \eta ^{-} ) }{\rho _{\eta } ( \eta ^{+} ) } \biggr) , $$

that is the second relation in (47) in the case $\eta >0$.

2). Assume that $\eta <0$. By raising (34) to the power η, we obtain for $s< t$ that

$$\begin{aligned} &\lambda (s) \bigl( \Upsilon (s) \bigr) ^{-\eta /\eta ^{-}}\rho _{q}^{ \eta } \bigl(\eta ^{+}\bigr) \bigl[ \bigl( \Upsilon (s) \bigr) ^{1/\eta ^{-}} \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (s) \bigr] ^{\eta } \\ &\quad \geq \lambda (s) \bigl( \mathcal{M}_{p}g(s) \bigr) ^{\eta } \\ &\quad \geq \lambda (s) \bigl( \Upsilon (s) \bigr) ^{-\eta /\eta ^{+}} \rho _{q}^{\eta }\bigl(\eta ^{-}\bigr) \bigl[ \bigl( \Upsilon (s) \bigr) ^{1/ \eta ^{+}}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (s) \bigr] ^{\eta }. \end{aligned}$$

(54)

Using the monotonicity of

$$ \bigl( \Upsilon (t) \bigr) ^{1/\eta ^{-}}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t),\quad\text{and}\quad \bigl( \Upsilon (t) \bigr) ^{1/\eta ^{+}}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t), $$

we have that

$$\begin{aligned} &\lambda (s) \bigl( \Upsilon (s) \bigr) ^{-\eta /\eta ^{-}}\rho _{q}^{ \eta } \bigl(\eta ^{+}\bigr) \bigl[ \bigl( \Upsilon (t) \bigr) ^{1/\eta ^{-}} \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \bigr] ^{\eta } \\ &\quad \geq \lambda (s) \bigl( \mathcal{M}_{p}g(s) \bigr) ^{\eta } \\ &\quad \geq \lambda (s) \bigl( \Upsilon (s) \bigr) ^{-\eta /\eta ^{+}} \rho _{q}^{\eta }\bigl(\eta ^{-}\bigr) \bigl[ \bigl( \Upsilon (t) \bigr) ^{1/ \eta ^{+}}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \bigr] ^{\eta }. \end{aligned}$$

(55)

By integrating from 0 to t and dividing by $\Upsilon (t)$, and raising it to the power $1/\eta <0$, we get that

$$\begin{aligned} &\frac{ [ ( \Upsilon (t) ) ^{1/\eta ^{-}}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{\eta }}{\Upsilon (t)} \rho _{q}^{\eta }\bigl(\eta ^{+} \bigr) \int _{0}^{t}\lambda (s) \bigl( \Upsilon (s) \bigr) ^{-\eta /\eta ^{-}}\,ds \\ &\quad \leq \biggl( \frac{1}{\Upsilon (t)} \int _{0}^{t}\lambda (s) \bigl( \mathcal{M}_{p}g(s) \bigr) ^{\eta }\,ds \biggr) ^{1/\eta } \\ &\quad \leq \frac{ [ ( \Upsilon (t) ) ^{1/\eta ^{+}}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) ] ^{\eta }}{\Upsilon (t)} \rho _{q}^{\eta }\bigl(\eta ^{-}\bigr) \int _{0}^{t}\lambda (s) \bigl( \Upsilon (s) \bigr) ^{-\eta /\eta ^{+}}\,ds. \end{aligned}$$

(56)

Proceeding as in the proof of the first case, we then obtain that

$$ \frac{\rho _{q}(\eta ^{+})}{\rho _{\eta }(\eta ^{-})}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t) \leq \mathcal{M}_{\eta } ( \mathcal{M}_{p}g ) ( t ) \leq \frac{\rho _{q}(\eta ^{-})}{\rho _{\eta }(\eta ^{+})}\mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t). $$

This gives us gain that

$$ \mathcal{M}_{p}g\in \mathcal{U}_{q}^{\eta } \biggl( \frac{\rho _{q} ( \eta ^{-} ) }{\rho _{\eta } ( \eta ^{+} ) } \biggr) , $$

which is the first relation in (47) in the case $\eta <0$. Similarly, we can prove the first relation in (47) using the relation (23). Analogously, we prove the two relations in (48) using the same technique and inequalities (23) and (34). The proof is complete. □

In Theorem 6, we proved that the power mean operators $\mathcal{M}_{p}g$ and $\mathcal{M}_{q}g$ of the weight $g\in \mathcal{U}_{p}^{q}$ satisfy the reverse Hölder inequality with some better exponents. However, the fact that the mean $\mathcal{M}_{p}g$ or $\mathcal{M}_{q}g$ belongs to some class $\mathcal{U}_{p}^{q}$ does not imply that the weight g itself belongs to $\mathcal{U}_{p}^{q}$. Thus, Theorem 6 does not guarantee the self-improvement of the summability exponents of the weight $g\in \mathcal{U}_{p}^{q}$. But, if we additionally assume the condition of the monotonicity of the weight g, then we can obtain the following results for self-improving of exponents.

Theorem 7

Let $p< q$, $p.q\neq 0$, and g be any nonnegative weight belongs to $\mathcal{U}_{p}^{q}(B)$ for $B>1$, and $\eta ^{+}$ and $\eta ^{-}$ are the roots of the equation (22).

$(1)$. If g is nonincreasing, and $\eta <\eta ^{+}$, then

$$ g\in \mathcal{U}_{q}^{\eta } \biggl( \frac{\rho _{p} ( \eta ^{-} ) }{\rho _{\eta } ( \eta ^{+} ) \rho _{p}(\eta ^{+})} \biggr) , \qquad g\in \mathcal{U}_{p}^{\eta } \biggl( \frac{\rho _{q}(\eta ^{-})}{\rho _{q}(\eta ^{+})\rho _{\eta }(\eta ^{+})} \biggr) . $$

(57)

$(2)$. If g is nondecreasing, and $\eta >\eta ^{-}$, then

$$ g\in \mathcal{U}_{\eta }^{q} \biggl( \frac{\rho _{p}(\eta ^{-})\rho _{\eta }(\eta ^{-})}{\rho _{p}(\eta ^{+})} \biggr) , \qquad g\in \mathcal{U}_{\eta }^{p} \biggl( \frac{\rho _{q}(\eta ^{-})\rho _{\eta }(\eta ^{-})}{\rho _{q}(\eta ^{+})} \biggr) . $$

(58)

Proof

$(1)$. Since g is nonincreasing, and since

$$ \mathcal{M}_{p}g(t)= \biggl( \frac{1}{\Upsilon (t)} \int _{0}^{t} \lambda (s)g^{p}(s)\,ds \biggr) ^{1/p},\quad\text{for all }t\in \mathbb{I}, $$

we have that $\mathcal{M}_{q}g(t)\geq g(t)$, and so

$$ \mathcal{M}_{\eta } ( \mathcal{M}_{q}g ) (t)\geq \mathcal{M}_{\eta }g(t). $$

(59)

By applying the second relation in (47), we obtain that

$$ \mathcal{M}_{\eta } ( \mathcal{M}_{q}g ) (t)\leq \frac{\rho _{p} ( \eta ^{-} ) }{\rho _{\eta } ( \eta ^{+} ) } \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t). $$

(60)

By applying the left-hand side of the inequality (23), and since $\mathcal{M}_{q}g(t)$ is nonincreasing (see Lemma 1), we from have (59) and (60) that

$$\begin{aligned} \mathcal{M}_{\eta }g(t) \leq &\mathcal{M}_{\eta } ( \mathcal{M}_{q}g ) (t)\leq \frac{\rho _{p} ( \eta ^{-} ) }{\rho _{\eta } ( \eta ^{+} ) } \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) \\ \leq & \frac{\rho _{p} ( \eta ^{-} ) }{\rho _{\eta } ( \eta ^{+} ) \rho _{p}(\eta ^{+})} \mathcal{M}_{q}g(t). \end{aligned}$$

That is

$$ g\in \mathcal{U}_{q}^{\eta } \biggl( \frac{\rho _{p} ( \eta ^{-} ) }{\rho _{\eta } ( \eta ^{+} ) \rho _{p}(\eta ^{+})} \biggr) , $$

which is the first relation in (57). Similarly, since g is nonincreasing, we have $\mathcal{M}_{p}g(t)\geq g(t)$, and so

$$ \mathcal{M}_{\eta } ( \mathcal{M}_{p}g ) (t)\geq \mathcal{M}_{\eta }g(t). $$

(61)

By applying the first relation in (47), we obtain that

$$ \mathcal{M}_{\eta }g(t)\leq \mathcal{M}_{\eta } \bigl( \mathcal{M}_{p}g(t) \bigr) \leq \frac{\rho _{q} ( \eta ^{-} ) }{\rho _{\eta } ( \eta ^{+} ) } \mathcal{M}_{q} \bigl( \mathcal{M}_{p}g(t) \bigr) . $$

(62)

By applying the left hand side of the inequality (34), and using (61), (62) and the fact that $\mathcal{M}_{p}g(t)$ is nonincreasing (see Lemma 1), we have that

$$\begin{aligned} \mathcal{M}_{\eta } \bigl( g(t) \bigr) \leq &\mathcal{M}_{\eta } \bigl( \mathcal{M}_{p}g(t) \bigr) \leq \frac{\rho _{q} ( \eta ^{-} ) }{\rho _{\eta } ( \eta ^{+} ) } \mathcal{M}_{q} \bigl( \mathcal{M}_{p}g(t) \bigr) \\ \leq & \frac{\rho _{q} ( \eta ^{-} ) }{\rho _{\eta } ( \eta ^{+} ) \rho _{q}(\eta ^{+})} \mathcal{M}_{p}g(t). \end{aligned}$$

That is

$$ g\in \mathcal{U}_{p}^{\eta } \biggl( \frac{\rho _{q} ( \eta ^{-} ) }{\rho _{\eta } ( \eta ^{+} ) \rho _{q}(\eta ^{+})} \biggr) , $$

which is the second relation in (57).

$(2)$. Since g is nondecreasing, then by Lemma 1, the fact that $\mathcal{M}_{p}g(t)$ is nondecreasing and $\mathcal{M}_{p}g(t)\leq g(t)$, we have that

$$ \mathcal{M}_{\eta } ( \mathcal{M}_{p}g ) (t)\leq \mathcal{M}_{\eta }g(t). $$

(63)

By applying the first relation in (48), we obtain that

$$ \mathcal{M}_{\eta } ( \mathcal{M}_{p}g ) (t)\geq \frac{\rho _{q} ( \eta ^{+} ) }{\rho _{\eta } ( \eta ^{-} ) } \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t). $$

(64)

By applying the right-hand side of the inequality (34), we have that

$$ \mathcal{M}_{\eta } ( \mathcal{M}_{p}g ) (t)\geq \frac{\rho _{q} ( \eta ^{+} ) }{\rho _{\eta } ( \eta ^{-} ) } \mathcal{M}_{q} ( \mathcal{M}_{p}g ) (t)\geq \frac{\rho _{q} ( \eta ^{+} ) \mathcal{M}_{p}g(t)}{\rho _{q}(\eta ^{-})\rho _{\eta } ( \eta ^{-} ) }. $$

(65)

By combining (63) and (65), we have that

$$ \mathcal{M}_{p}g(t)\leq \frac{\rho _{q}(\eta ^{-})\rho _{\eta } ( \eta ^{-} ) }{\rho _{q} ( \eta ^{+} ) } \mathcal{M}_{\eta }g(t), $$

that is

$$ g\in \mathcal{U}_{\eta }^{p} \biggl( \frac{\rho _{q}(\eta ^{-})\rho _{\eta } ( \eta ^{-} ) }{\rho _{q} ( \eta ^{+} ) } \biggr) , $$

which is the second relation in (58). Again, since g is nondecreasing, Lemma 2 implies that $\mathcal{M}_{q}g(t)$ is nondecreasing and $\mathcal{M}_{q}g(t)\leq g(t)$, and so

$$ \mathcal{M}_{\eta } ( \mathcal{M}_{q}g ) (t)\leq \mathcal{M}_{\eta }g(t). $$

(66)

By applying the second relation in (48), we obtain that

$$ \mathcal{M}_{\eta } ( \mathcal{M}_{q}g ) (t)\geq \frac{\rho _{p} ( \eta ^{+} ) }{\rho _{\eta } ( \eta ^{-} ) } \mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t). $$

By applying the right-inequality in (23), we have that

$$\begin{aligned} \mathcal{M}_{\eta } ( g ) (t) \geq &\mathcal{M}_{\eta } ( \mathcal{M}_{q}g ) (t)\geq \frac{\rho _{p} ( \eta ^{+} ) }{\rho _{\eta } ( \eta ^{-} ) }\mathcal{M}_{p} ( \mathcal{M}_{q}g ) (t) \\ \geq & \frac{\rho _{p} ( \eta ^{+} ) }{\rho _{p}(\eta ^{-})\rho _{\eta } ( \eta ^{-} ) } \mathcal{M}_{q}g(t). \end{aligned}$$

(67)

By combining (66) and (67), we have that

$$ \mathcal{M}_{q}g(t)\leq \frac{\rho _{p}(\eta ^{-})\rho _{\eta } ( \eta ^{-} ) }{\rho _{p} ( \eta ^{+} ) } \mathcal{M}_{\eta }g(t). $$

That is

$$ g\in \mathcal{U}_{\eta }^{q} \biggl( \frac{\rho _{p}(\eta ^{-})\rho _{\eta } ( \eta ^{-} ) }{\rho _{p} ( \eta ^{+} ) } \biggr) , $$

which is the first relation in (58). The proof is complete. □

In the following, we will apply the above results in deriving the self-improving properties of the two Muckenhoupt and Gehring classes

$$ A_{\lambda }^{p}:=\mathcal{U}_{\frac{1}{1-p}}^{1},\quad \text{and}\quad G_{ \lambda }^{q}:=\mathcal{U}_{1}^{q}. $$

Theorem 8

Let $p>1$ and g be any nonnegative and nondecreasing weight belonging to $A_{\lambda }^{p}(B)$ for $B>1$. Then $g\in A_{\lambda }^{\eta }(B_{2}^{{\prime \prime }})$ for $\eta \in (\eta ^{-}, p]$ where $\eta ^{-}$ is the root of the equation

$$ \frac{p-\eta }{p-1} ( B\eta ) ^{\frac{1}{p-1}}=1, $$

(68)

and

$$ B_{2}^{{\prime \prime }}= \frac{\rho _{1}(\eta ^{-})\rho _{\eta }(\eta ^{-})}{\rho _{1}(\eta ^{+})}. $$

Proof

Since $A_{\lambda }^{p}:=\mathcal{U}_{\frac{1}{1-p}}^{1}$, then equation (22) becomes $C_{p,q}(\eta )=B$, which is written by

$$ \biggl( \frac{x}{x-1} \biggr) \biggl( \frac{(p-1)x}{(p-1)x+1} \biggr) ^{p-1}=B. $$

By applying the transform $\eta \rightarrow 1/(1-x)$, we see that $\eta ^{-}$ is determined from the equation

$$ \frac{p-\eta }{p-1} ( B\eta ) ^{\frac{1}{p-1}}=1, $$

(69)

which is the desired equation (68) and the constant $B_{2}^{{\prime \prime }}$ is obtained from (58) and given by

$$ B_{2}^{{\prime \prime }}= \frac{\rho _{1}(\eta ^{-})\rho _{\eta }(\eta ^{-})}{\rho _{1}(\eta ^{+})}. $$

The proof is complete. □

Theorem 9

Let $q>1$ and g be any nonnegative and nondecreasing weight belonging to $G_{\lambda }^{q}(B)$ for $B>1$. Then $g\in G_{\lambda }^{\eta }(B_{1}^{{\prime \prime }})$ for $\eta \in {}[ q, \eta ^{+})$ where $\eta ^{+}$ is the root of the equation

$$ \biggl( \frac{x-1}{x} \biggr) \biggl( \frac{x}{x-q} \biggr) ^{ \frac{1}{q}}=B, $$

(70)

and

$$ B_{1}^{{\prime \prime }}= \frac{\rho _{1}(\eta ^{-})\rho _{\eta }(\eta ^{-})}{\rho _{1}(\eta ^{+})}. $$

Proof

Since $G_{\lambda }^{q}:=\mathcal{U}_{1}^{q}$, then equation (22) becomes $C_{p,q}(\eta )=B$, which is written by

$$ \biggl( \frac{x}{x-1} \biggr) ^{-1} \biggl( \frac{x}{x-q} \biggr) ^{ \frac{1}{q}}=B, $$

which is the desired equation (70), and the constant $B_{1}^{{\prime \prime }}$ is obtained from (57) and given by

$$ B_{1}^{{\prime \prime }}= \frac{\rho _{1}(\eta ^{-})\rho _{\eta }(\eta ^{-})}{\rho _{1}(\eta ^{+})}. $$

The proof is complete. □

4 Conclusion

In this paper, we have considered a class of generalized Hölder inequalities and proved the self-improving properties of the weights in this class. The main results are proved by employing some properties of a mean operator and additional properties of the composition of different operators with different powers. By employing the self-improving properties of the general class, we have derived the self-improving properties of the Muckenhoupt weights and the Gehring weights, which are compatible with the results obtained by some authors in the literature.