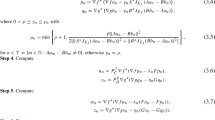Refinement multidimensional dynamic inequalities with general kernels and measures

Abstract

Using the properties of superquadratic and subquadratic functions, we establish some new refinement multidimensional dynamic inequalities of Hardy’s type on time scales. Our results contain some of the recent results related to classical multidimensional Hardy’s and Pólya–Knopp’s inequalities on time scales. To show motivation of the paper, we apply our results to obtain some particular multidimensional cases and provide refinements of some Hardy-type inequalities known in the literature.

1 Introduction

Hardy [13] proved the integral inequality

$$ \int _{0}^{\infty } \biggl( \frac{1}{t} \int _{0}^{t}g(s)\,ds \biggr) ^{p}\,dt \leq \biggl( \frac{p}{p-1} \biggr) ^{p} \int _{0}^{\infty }g^{p}(t)\,dt $$

(1)

for a nonnegative integrable function g in the space $L^{p}({R}_{+})$, $1< p<\infty$, where the constant $( p/(p-1) ) ^{p}$ is the best possible. Rewriting (1) with the function $g^{1/p}$ instead of g and taking the limit as $p\rightarrow \infty$, we get the limiting case of the Hardy inequality, known as the Pólya–Knopp inequality (see [15]),

$$ \int _{0}^{\infty }\exp \biggl( \frac{1}{t} \int _{0}^{t}\ln g(s)\,ds \biggr) \,dt\leq e \int _{0}^{\infty }g(t)\,dt $$

(2)

for positive functions $g\in L^{1}({R}_{+})$, where the constant e is the best possible. Recently, Kaijser et al. [14] have pointed out that both (1) and (2) are just particular cases of the much more general Hardy–Knopp’s inequality

$$ \int _{0}^{\infty }\varPsi \biggl( \frac{1}{t} \int _{0}^{t}g(s)\,ds \biggr) \frac{dt}{t}\leq \int _{0}^{\infty }\varPsi \bigl(g(t)\bigr) \frac{dt}{t} $$

(3)

for convex functions Ψ on ${R}_{+}$ and locally integrable positive functions $g:{R}_{+}\rightarrow {R}_{+}$. The Hardy-type inequalities and their general forms have been studied in the literature in various modifications both in the continuous and discrete settings. They have extensive applications to partial differential and difference equations, harmonic analysis, approximations, number theory, optimization, convex geometry, spectral theory of differential and difference operators, and others (see [24,25,26,27,28, 30]). One such approach involves superquadratic functions, which is a class of functions closely connected to convex functions, and various inequalities with different kernels and extensions to multidimensional cases have been obtained. For example, in 1967, Godunova [10] proved the inequality

$$ \int _{\mathbf{{R}_{+}^{n}}}\varPsi \biggl( \frac{1}{t_{1}\dots t_{n}} \int _{\mathbf{{R}_{+}^{n}}}l \biggl( \frac{s_{1}}{t_{1}},\frac{s_{2}}{t _{2}},\ldots, \frac{s_{n}}{t_{n}} \biggr) g(\mathbf{s})\mathbf{ds} \biggr) \frac{ \mathbf{{dt}}}{t_{1}\dots t_{n}} \leq \int _{\mathbf{{R}_{+}^{n}}}\frac{ \varPsi (g(\mathbf{t}))\mathbf{dt}}{t_{1}\dots t_{n}} $$

(4)

for nonnegative functions $l:{R}_{+}^{n}\rightarrow {R}_{+}$ such that $\int _{{R}_{+}^{n}}l(\mathbf{t})\mathbf{d}\mathbf{t}=1$, convex functions $\varPsi :[0,\infty )\rightarrow {[} 0,\infty )$, and nonnegative functions g on ${R}_{+}^{n}$ such that the function $\varPsi (g(\mathbf{t}))/ [4](t_{1}\dots t_{n})$ is integrable on ${R}_{+}^{n}$.

In 2003, Čižmešija et al. [8] proved a generalization of the Hardy–Knopp inequality (3) with two weighted functions. In particular, they proved that if $0< b\leq \infty$, $\lambda :(0,b)\rightarrow {R}$ is a nonnegative function such that the function $t\rightarrow \lambda (t)/t^{2}$ is locally integrable in $(0, b)$, and Ψ is a convex function on $(a,c)$, where $-\infty \leq a\leq c\leq \infty$, then

$$ \int _{0}^{b}\lambda (t)\varPsi \biggl( \frac{1}{t} \int _{0}^{t}g(s)\,ds \biggr) \frac{dt}{t}\leq \int _{0}^{b} \eta (t)\varPsi \bigl(g(t)\bigr) \frac{dt}{t} $$

(5)

for all integrable functions $g:(0,b)\rightarrow {R}$ such that $g(t)\in (a,c)$ for all $t\in (0,b)$, where $\eta (s):=s\int _{s}^{b}\frac{\lambda (t)}{t^{2}}\,dt$ for $s\in (0,b)$. In 2008, Oguntuase and Persson [17] used the notion of superquadratic and subquadratic functions to obtain a new Hardy-type inequality for $p\geq 2$, which holds in the reverse order for $1< p<2$.

In [18] the authors obtained some new Hardy-type inequalities on time scales by using the notion of superquadratic functions. In particular, they proved that if $( \varOmega _{1}, \varSigma _{1},\mu _{1} )$ and $( \varOmega _{2},\varSigma _{2},{ }\mu _{2} )$ are two time scale measure spaces with positive σ-finite measures, $\lambda :\varOmega _{1}\rightarrow {R}$ and $k:\varOmega _{1}\times \varOmega _{2}\rightarrow {R}$ are nonnegative functions such that $k(t,\cdot )$ is a $\Delta \mu _{2}$-integrable function for $t\in \varOmega _{2}$, $K:\varOmega _{1}\rightarrow {R}$ is defined by $K(t):= \int _{\varOmega _{2}}k(t,s)\Delta \mu _{2}(s)<\infty$, $t\in \varOmega _{1}$, and $\eta (s):=\int _{\varOmega _{1}}\lambda (t) \frac{k(t,s)}{K(t)}\Delta \mu _{1}(t)<\infty$, $s\in \varOmega _{2}$, then

$$\begin{aligned} & \int _{\varOmega _{1}}\lambda (t)\varPsi \bigl(A_{k}g(t)\bigr) \Delta \mu _{1}(t) \\ &\qquad {}+ \int _{\varOmega _{1}} \int _{\varOmega _{2}}\lambda (t)\frac{k(t,s)}{K(t)} \varPsi \bigl( \bigl\vert g(s)-A_{k}g(t) \bigr\vert \bigr)\Delta \mu _{1}(t) \Delta \mu _{2}(s) \\ &\quad \leq \int _{\varOmega _{2}}\eta (t)\varPsi \bigl(g(t)\bigr)\Delta \mu _{2}(t), \end{aligned}$$

(6)

for nonnegative $\Delta \mu _{2}$-integrable functions $g:\varOmega _{2} \rightarrow {R}$ and nonnegative superquadratic functions $\varPsi :[a,\infty )\rightarrow {R}$ ($a\geq 0$), where $A_{k}g:\varOmega _{1}\rightarrow {R}$ is defined by $A_{k}g(t):=\frac{1}{K(t)}\int _{\varOmega _{2}}k(t, s)g(s) \Delta \mu _{2}(s)$, $t\in \varOmega _{1}$. The general idea in this direction is proving a result for a dynamic inequality, where the domain of the unknown function is a so-called time scale T, which may be an arbitrary nonempty closed subset of the real numbers R. Fore more details of calculus on time scales, we refer to the books [3, 6, 7]. Three most popular examples of calculus on time scales are differential calculus, difference calculus, and quantum calculus, that is, when ${T}={R}$, ${T}={N}$, and ${T}=q^{ {N}_{0}}=\{q^{t}:t\in {N}_{0}\}$ with $q>1$, respectively. A time scale T is an arbitrary nonempty closed subset of the real numbers R. We define the time scale interval $[a,b]_{{T}}$ by $[a,b]_{{T}}:=[a,b]\cap {T}$. A function $g:{T}\rightarrow {R}$ is said to be right-dense continuous (rd-continuous) if it is continuous at all right-dense points in T and its left-sided finite limits exist at all left-dense points in T. The set of all such rd-continuous functions is denoted by $\mathrm{C}_{rd}({{T}}):=\mathrm{C}_{rd}( {{T}},{{R)}}$. The graininess μ on time scale T is defined by $\mu (t):=\sigma (t)-t$, and for a function $g:{T}\rightarrow {R}$, $g^{\sigma }(t)$ denotes $g(\sigma (t))$, where $\sigma :{T\rightarrow T}$ is the forward jump operator given by $\sigma (t):= \inf \{s\in {T}:s>t\}$. The basic formulas involving delta derivatives are the following: $g^{\sigma }:=g+\mu g^{\Delta }$, $(gg)^{\Delta }:=f ^{\Delta }g+f^{\sigma }g^{\Delta }:=fg^{\Delta }+f^{\Delta }g^{\sigma }$, and $( \frac{f}{g} ) ^{\Delta }:=\frac{f^{\Delta }g-fg ^{\Delta }}{gg^{\sigma }}$, where g, g are delta differentiable, and $gg^{\sigma }\neq 0$ in the last formula. Let T be a time scale, and let $[a,b)\subset {{T}}$. The Lebesgue integral associated with the measure μ on $[a,b)$ is called the Lebesgue Δ-integral. If $g:[a,b)\rightarrow {R}$, then we denote the corresponding Δ-integral of g over $[a,b)$ by $\int _{a}^{b}g(t)\Delta t$. In particular, if T is an arbitrary time scale and the interval $[a,b)\subset {{T}}$ contains only isolated points, then $\int _{a}^{b}g(t)\Delta t:=\sum_{t\in {[} a,b)}(\sigma (t)-t)g(t)$.

In [21] the authors proved the time scale version of (5) given by

$$ \int _{a}^{b}\lambda (t)\varPsi \biggl( \frac{1}{\sigma (t)-a} \int _{a} ^{\sigma (t)}g(t)\Delta t \biggr) \frac{\Delta t}{t-a}\leq \int _{a} ^{b}\eta (t)\varPsi \bigl(g(t)\bigr) \frac{\Delta t}{t-a}, $$

(7)

where $\lambda \in \mathrm{C}_{rd}({[}a,b{]},{{R)}}$ is a nonnegative function, and the weight function η is defined by $\eta (t):=(t-a)\int _{t}^{b}\frac{\lambda (t)}{(t-a)(\sigma (t)-a)} \Delta t$ for $t\in (a,b)$, $\varPsi :(c,d)\rightarrow {{R}}$ is a continuous convex function, where c, $d\in {{R}}$, and $g\in \mathrm{C}_{rd}({[}a,b{]},{{R)}}$ is a delta-integrable function such that $g(t)\in (c,d)$ for all $t\in [a,b]$. In [5] (see also [22]) the authors proved that if $( \varOmega ,\mathcal{M},\mu _{\Delta } )$ and $( \varLambda ,\mathcal{L},\lambda _{\Delta } )$ are two time scale measure spaces, $k:\varOmega \times \varLambda \rightarrow {R}_{+}$ is such that $K(t):=\int _{\varLambda }k(t,s)\Delta s<\infty$, $t\in \varOmega$, and $\zeta :\varOmega \rightarrow {R}_{+}$ is such that $\eta (s):= \int _{\varOmega }\frac{k(t,s)\zeta (t)}{K(t)}\Delta t<\infty$, $s \in \varLambda$, then

$$ \int _{\varOmega }\zeta (t)\varPsi \biggl( \frac{1}{K(t)} \int _{\varLambda }k(t,s)g(s) \Delta s \biggr) \Delta t\leq \int _{\varLambda }\eta (s)\varPsi \bigl(g(s)\bigr) \Delta s $$

(8)

for $\lambda _{\Delta }$-integrable functions $g:\varLambda \rightarrow {R}$ such that $g(\varLambda )\subset I$ and convex functions $\varPsi \in \mathrm{C}(I,{{R)}}$, where $I\subset {{R}}$.

In recent years, some authors studied the fractional inequalities using the fractional Caputo and Riemann–Liouville derivatives. Note that our results can be extended to different types of fractional operators based on fractional calculus [31]. For the advanced development of the fractional calculus without singular kernel of exponential function, we refer the reader to [28]. For the general fractional derivative, we refer the reader to [9, 32]. We also refer the reader to [11, 12, 23], which give a unification of calculus of the functions on totally disconnected and continuous real line.

In this paper, in the next section, we prove some new refined multidimensional dynamic inequalities of Hardy type with weighted functions and nonnegative kernel using the properties of superquadratic (or subquadratic) functions. Our results contain some recent results related to classical multidimensional Hardy’s and Pólya–Knopp’s inequalities on time scales. To show motivation of the paper, we will apply our results to obtain some particular multidimensional cases and provide refinements of some Hardy-type inequalities known in the literature. We also discuss some particular cases of the obtained inequalities, related to power and exponential functions, and to the most simplest forms of kernels for illustration.

2 Main results

In this section, we obtain the multidimensional time scale for Hardy-type inequality with general kernel and also with several functions. First, we recall the definition and some basic properties of superquadratic functions, introduced by Abramovich et al. [1] (for more information, see also [2]).

Definition 2.1

A function $\varPsi :[0,\infty )\rightarrow {R}$ is called superquadratic if for all $t\geq 0$, there exists a constant $C_{t} \in {R}$ such that

$$ \varPsi (s)-\varPsi (t)-\varPsi \bigl( \vert s-t \vert \bigr)\geq C_{t}(s-t) \quad \text{for all } s\geq 0. $$

(9)

Superquadratic functions are closely related to convex functions. In particular, at the first sight, condition (9) appears to be stronger than convexity. We say that Ψ is subquadratic if −Ψ is superquadratic and the reverse inequality of (9) holds.

Definition 2.2

A function $g:[0,\infty )\rightarrow {R}$ is superadditive if $g(t+s)\geq g(t)+g(s)$ for all t, $s\geq 0$. If the reverse inequality holds, then g is said to be subadditive.

Lemma 2.1

Suppose $\varPsi :[0,\infty )\rightarrow {R}$is continuously differentiable and such that $\varPsi (0)\leq 0$. If $\varPsi ^{\prime }$is superadditive, that is, $\varPsi ^{\prime }(t+s)\geq \varPsi ^{\prime }(t)+\varPsi ^{\prime }(s)$for allt, $s\geq 0$, or the function $t\mapsto \frac{\varPsi ^{\prime }(t)}{t}$is nondecreasing on ${R}_{+}$, thenΨis superquadratic.

As a consequence, the power function $\varPsi :[0,\infty )\rightarrow {R}$, $\varPsi (t)=t^{p}$, is superquadratic for all $p\in {R}_{+}$, $p\geq 2$, and subquadratic for $1< p\leq 2$. Next, we recall a refined Jensen’s inequality for superquadratic functions and Minkowski’s inequality on time scales, which are used in the proof of the main results.

Lemma 2.2

Let $( \varOmega ,\mathcal{M},\mu _{\Delta } )$and $(\varLambda ,\mathcal{L},\lambda _{\Delta })$be two finite-dimensional time scale measures spaces. and letλ, η, andgbe nonnegative functions onΩ, Λ, and $\varOmega \times \varLambda$, respectively. If $p\geq 1$, then

$$\begin{aligned} & \biggl[ \int _{\varOmega } \biggl( \int _{\varLambda }g(t,s)\eta (s)\,d \eta _{\Delta }(s) \biggr) ^{p}\lambda (t)\,d\mu _{\Delta }(t) \biggr] ^{\frac{1}{p}} \\ &\quad \leq \int _{\varLambda } \biggl( \int _{\varOmega }g^{p}(t,s)\lambda (t)\,d \mu _{\Delta }(t) \biggr) \eta (s)\,d\eta _{\Delta }(s), \end{aligned}$$

(10)

provided that all integrals in (10) exist. If $0< p<1$and

$$ \int _{\varOmega } \biggl( \int _{\varLambda }g\eta \,d\eta _{\Delta } \biggr) ^{p} \lambda \,d\mu _{\Delta }>0\quad \textit{and} \quad \int _{\varLambda }g\eta \,d \eta _{\Delta }>0, $$

(11)

then (10) is reversed. For $p<0$, if in addition to (11), $\int _{\varOmega }g^{p} \lambda \,d\mu _{\Delta }>0$, then (10) is also reversed.

In addition, another important characterization of superquadratic functions is the following version of the refined Jensen inequality which is adapted from [4, Theorem 2.5].

Lemma 2.3

Let $a,b\in {T}$and suppose that $g:[a,b]_{{T}^{k}}\rightarrow {[} 0,\infty )$is rd-continuous and $\varPsi :[0,\infty )\rightarrow {R}$is continuous and superquadratic. Then

$$ \varPsi \biggl( \frac{1}{b-a} \int _{a}^{b}g(t)\Delta t \biggr) \leq \frac{1}{b-a} \int _{a}^{b} \biggl[ \varPsi \bigl(g(s)\bigr)- \varPsi \biggl( \biggl\vert g(s)- \frac{1}{b-a} \int _{a}^{b}g(t)\Delta t \biggr\vert \biggr) \biggr] \Delta s. $$

(12)

For the case $\varPsi (t)=t^{p}$, (12) gives the inequality

$$ \biggl( \frac{1}{b-a} \int _{a}^{b}g(t)\Delta t \biggr) ^{p}\leq \frac{1}{b-a} \int _{a}^{b} \biggl[ g^{p}(s)- \biggl( \biggl\vert g(s)- \frac{1}{b-a} \int _{a}^{b}g(t)\Delta t \biggr\vert \biggr) ^{p} \biggr] \Delta s. $$

(13)

We will further assume (usually without mentioning) that all measures are positive, all functions in the statements of the theorems are nonnegative and measurable, and the integrals considered exist. Before presenting the main results for multidimensional inequalities, it is necessary to introduce some further notations. First, let $n\in {Z} _{+}$ and set $0=(0,0,\ldots,0)$, $1=(1,1,\ldots,1)\in {R}^{n}$, and for $\boldsymbol{\lambda }=(\lambda _{1},\ldots,\lambda _{n})$, $\boldsymbol{\eta }=(\eta _{1},\ldots,\eta _{n}) \in {R}^{n}$, denote $\frac{\boldsymbol{\lambda }}{\boldsymbol{\eta }}= ( \frac{\lambda _{1}}{\eta _{1}},\frac{\lambda _{2}}{\eta _{2}},\ldots,\frac{ \lambda _{n}}{\eta _{n}} )$ and $\boldsymbol{\lambda }^{ \boldsymbol{\eta }}=\lambda _{1}^{\eta _{1}}\lambda _{2}^{\eta _{2}}\dots \lambda _{n}^{\eta _{n}}$, and let $\varOmega _{1},\varOmega _{2}\subset {R}^{n}$ be time scale measure spaces. In particular,

$$ \boldsymbol{\lambda }^{\mathbf{{1}}}=\prod_{i=1}^{n} \lambda _{i}, \qquad \boldsymbol{\lambda }^{\mathbf{{2}}}= \Biggl( \prod _{i=1}^{n}\lambda _{i} \Biggr) ^{2}\quad \text{and} \quad {\boldsymbol{\lambda }} ^{\mathbf{{-1}}}= \Biggl( \prod_{i=1}^{n}\lambda _{i} \Biggr) ^{-1}, $$

(14)

where $\mathbf{n}=(n_{1},\ldots,n_{n})$. Correspondingly, $[\mathbf{a},\mathbf{b})$ means the set $[a_{1}, b_{1})\times [a_{2}, b_{2})\times \cdots\times [a_{n},b_{n})$, $\Delta \boldsymbol{\lambda }=(\Delta \lambda _{1}\dots \Delta \lambda _{n})$, and $\boldsymbol{\lambda }^{p}=(\lambda _{1}\dots \lambda _{n})^{p}$. Furthermore, for λ, $\boldsymbol{\eta }\in {R}^{n}$, we write $\boldsymbol{\lambda }< \boldsymbol{\eta }$ if componentwise $\lambda _{i}<\eta _{i}$, $i=1,2,\dots ,n$, and the relations ≤, ≥, and < are defined analogously. Also, for $\mathbf{a},\mathbf{b}\in {R}^{n}$, $\mathbf{a}<\mathbf{b}$, we define $(\mathbf{a},\mathbf{b})=\{\mathbf{t}\in {R}^{n}:\mathbf{a}< \mathbf{t}<\mathbf{b}\}$. Moreover, $(\mathbf{a},\boldsymbol{\infty })=\{ \mathbf{t}\in {R}^{n}:\mathbf{a}<\mathbf{t}<\boldsymbol{\infty }\}$, and the n-cells $[\mathbf{a},\mathbf{b})$, $(\mathbf{a},\mathbf{b}]$, and $[\mathbf{a},\mathbf{b}]$ are defined similarly. Finally, the integral $\int _{[{\mathbf{a}}, \mathbf{b})}g(\mathbf{t})\Delta \mathbf{t}$ is interpreted as

$$ \int _{{[} \mathbf{a},\mathbf{b})}g(\mathbf{t})\Delta {\mathbf{t:=}} \int _{a_{1}}^{b_{1}} \int _{a_{2}}^{b_{2}}\dots \int _{a_{n}}^{b_{n}}g(t _{1},{ }t_{2},\ldots,t_{n})\Delta t_{1}\dots \Delta t_{n}. $$

(15)

In this setting, we can easily prove the following multidimensional time scale Hardy-type inequality with general kernel. We further assume that $( \varOmega _{1},\varSigma _{1},{ }\mu _{1} )$ and $( \varOmega _{2},\varSigma _{2},\mu _{2} )$ are two time scale measure spaces with positive σ-finite measures.

Theorem 2.1

Let $\lambda :\varOmega _{1}\rightarrow {R}$and $k:\varOmega _{1}\times \varOmega _{2}\rightarrow {R}$be nonnegative functions such that $k(t,\cdot )$is a $\Delta \mu _{2}$-integrable function for $t\in \varOmega _{2}$. Suppose that $\mathcal{K}:\varOmega _{1}\rightarrow {R}$is defined by

$$ \mathbf{0}< {K}(\mathbf{t}):= \int _{\varOmega _{2}}k(\mathbf{t},\mathbf{s})\Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s_{n})< \boldsymbol{\infty }, \quad \mathbf{t} \in \varOmega _{1}, $$

(16)

and the functionηbe defined by

$$ \eta (\mathbf{s}):= \biggl( \int _{\varOmega _{1}}\lambda (\mathbf{t}) \biggl( \frac{k( \mathbf{t},\mathbf{s})}{{K}(\mathbf{t})} \biggr) ^{r}\Delta \mu _{1}(t_{1})\dots \Delta \mu _{1}(t_{n}) \biggr) ^{\frac{1}{r}}< \boldsymbol{\infty }, \quad \mathbf{s}\in \varOmega _{2}, $$

(17)

where $r\geq 1$. Furthermore, assume that $g:\varOmega _{2}\rightarrow {R}$is a nonnegative $\Delta \mu _{2}$-integrable function and define $A_{k}g:\varOmega _{1}\rightarrow {R}$by

$$ A_{k}g(\mathbf{t}):=\frac{1}{{K}(\mathbf{t})} \int _{\varOmega _{2}}k(\mathbf{t}, \mathbf{s})g(\mathbf{s})\Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s_{n}), \quad \mathbf{t}\in \varOmega _{1}. $$

(18)

If $\varPsi :[\mathbf{a},\boldsymbol{\infty })_{{T}}\rightarrow {R}$ ($a_{i}\geq 0$, $i=1,2, \dots ,n$) is a nonnegative superquadratic function, then

$$\begin{aligned} & \int _{\varOmega _{1}}\lambda (\mathbf{t})\varPsi ^{r} \bigl(A_{k}g(\mathbf{t})\bigr)\Delta \mu _{1}(t_{1})\dots \Delta \mu _{1}(t_{n}) \\ &\qquad {}+r \int _{\varOmega _{1}} \int _{\varOmega _{2}}\lambda (\mathbf{t})\frac{k(\mathbf{t},\mathbf{s})}{{K}(\mathbf{t})}\varPsi ^{r-1}\bigl(A_{k}g(\mathbf{t})\bigr)\varPsi \bigl( \bigl\vert g( \mathbf{s})-A_{k}g(\mathbf{t}) \bigr\vert \bigr) \\ &\qquad {}\times \Delta \mu _{1}(t_{1})\dots \Delta \mu _{1}(t_{n})\Delta \mu _{2}(s _{1})\dots \Delta \mu _{2}(s_{n}) \\ &\quad \leq \biggl( \int _{\varOmega _{2}}\eta (\mathbf{s})\varPsi \bigl(g(\mathbf{s})\bigr) \Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s_{n}) \biggr) ^{r}. \end{aligned}$$

(19)

IfΨis subquadratic, then the inequality sign in (19) is reversed.

Proof

We start with the identity

$$ \varPsi \bigl(A_{k}g(\mathbf{t})\bigr)=\varPsi \biggl( \frac{1}{{K}(\mathbf{t})} \int _{\varOmega _{2}}k(\mathbf{t},\mathbf{s})g(\mathbf{s})\Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s_{n}) \biggr) . $$

(20)

By applying the refined Jensen inequality to (20), we find that

$$\begin{aligned} &\varPsi \bigl(A_{k}g(\mathbf{t})\bigr)+\frac{1}{{K}(\mathbf{t})} \int _{\varOmega _{2}}k( \mathbf{t},\mathbf{s})\varPsi \bigl( \bigl\vert g(\mathbf{s})-A_{k}g(\mathbf{t}) \bigr\vert \bigr) \Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s_{n}) \\ &\quad \leq \frac{1}{{K}(\mathbf{t})} \int _{\varOmega _{2}}k(\mathbf{t},{ }\mathbf{s}) \varPsi \bigl(g( \mathbf{s})\bigr)\Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s_{n}). \end{aligned}$$

Then, since Ψ is nonnegative and $r\geq 1$, we have that

$$\begin{aligned} & \biggl( \varPsi \bigl(A_{k}g(\mathbf{t})\bigr)+\frac{1}{{K}(\mathbf{t})} \int _{\varOmega _{2}}k(\mathbf{t},\mathbf{s})\varPsi \bigl( \bigl\vert g(\mathbf{s})-A_{k}g(\mathbf{t}) \bigr\vert \bigr) \Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s_{n}) \biggr) ^{r} \\ &\quad \leq \biggl( \frac{1}{{K}(\mathbf{t})} \int _{\varOmega _{2}}k(\mathbf{t}, \mathbf{s})\varPsi \bigl(g(\mathbf{s}) \bigr)\Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s_{n}) \biggr) ^{r}. \end{aligned}$$

(21)

Further, by the well-known Bernoulli inequality it follows that the left-hand side of inequality (21) is not less than

$$ \varPsi ^{r}\bigl(A_{k}g(\mathbf{t})\bigr)+r \frac{\varPsi ^{r-1}(A_{k}g(\mathbf{t}))}{{K}( \mathbf{t})} \int _{\varOmega _{2}}k(\mathbf{t},\mathbf{s})\varPsi \bigl( \bigl\vert g( \mathbf{s})-A_{k}g(\mathbf{t}) \bigr\vert \bigr)\Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s_{n}), $$

(22)

that is,

$$\begin{aligned} &\varPsi ^{r}\bigl(A_{k}g(\mathbf{t})\bigr)+r \frac{\varPsi ^{r-1}(A_{k}g(\mathbf{t}))}{ \mathcal{K}(\mathbf{t})} \int _{\varOmega _{2}}k(\mathbf{t},\mathbf{s})\varPsi \bigl( \bigl\vert g( \mathbf{s})-A_{k}g(\mathbf{t}) \bigr\vert \bigr)\Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s_{n}) \\ &\quad \leq \biggl( \frac{1}{\mathcal{K}(\mathbf{t})} \int _{\varOmega _{2}}k( \mathbf{t},\mathbf{s})\varPsi \bigl(g(\mathbf{s}) \bigr)\Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s _{n}) \biggr) ^{r}. \end{aligned}$$

(23)

Multiplying (23) by $\lambda (\mathbf{t})$ and integrating it over $\varOmega _{1}$ with respect to $\Delta \mu _{1}(t_{1})\dots \Delta \mu _{1}(t _{n})$, we have

$$\begin{aligned} & \int _{\varOmega _{1}}\lambda (\mathbf{t})\varPsi ^{r} \bigl(A_{k}g(\mathbf{t})\bigr)\Delta \mu _{1}(t_{1})\dots \Delta \mu _{1}(t_{n}) \\ &\qquad {}+r \int _{\varOmega _{1}}\frac{\lambda (\mathbf{t})\varPsi ^{r-1}(A_{k}g(\mathbf{t}))}{\mathcal{K}(\mathbf{t})} \biggl( \int _{\varOmega _{2}}k(\mathbf{t},\mathbf{s})\varPsi \bigl( \bigl\vert g(\mathbf{s})-A_{k}g(\mathbf{t}) \bigr\vert \bigr)\Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s_{n}) \biggr) \\ &\qquad {}\times \Delta \mu _{1}(t_{1})\dots \Delta \mu _{1}(t_{n}) \\ &\quad \leq \int _{\varOmega _{1}}\lambda (\mathbf{t}) \biggl( \frac{1}{\mathcal{K}( \mathbf{t})} \int _{\varOmega _{2}}k(\mathbf{t},\mathbf{s})\varPsi \bigl(g(\mathbf{s}) \bigr)\Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s_{n}) \biggr) ^{r} \\ &\qquad {}\times \Delta \mu _{1}(t_{1})\dots \Delta \mu _{1}(t_{n}). \end{aligned}$$

(24)

Applying the Minkowski inequality (10) to the right-hand side of (24), we have

$$\begin{aligned} & \int _{\varOmega _{1}}\lambda (\mathbf{t}) \biggl( \frac{1}{\mathcal{K}( \mathbf{t})} \int _{\varOmega _{2}}k(\mathbf{t},\mathbf{s})\varPsi \bigl(g(\mathbf{s}) \bigr)\Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s_{n}) \biggr) ^{r}\Delta \mu _{1}(t _{1})\dots \Delta \mu _{1}(t_{n}) \\ &\quad \leq \biggl[ \int _{\varOmega _{2}}\varPsi \bigl(g(\mathbf{s})\bigr) \biggl( \int _{\varOmega _{1}}\lambda (\mathbf{t}) \biggl( \frac{k(\mathbf{t},\mathbf{s})}{ \mathcal{K}(\mathbf{t})} \biggr) ^{r}\Delta \mu _{1}(t_{1})\dots \Delta \mu _{1}(t _{n}) \biggr) ^{\frac{1}{r}} \\ &\qquad {}\times\Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s _{n}) \biggr] ^{r}. \end{aligned}$$

(25)

Finally, substituting (25) into (24) and taking into account definition (17) of the weight function η, we obtain that

$$\begin{aligned} & \int _{\varOmega _{1}}\lambda (\mathbf{t})\varPsi ^{r} \bigl(A_{k}g(\mathbf{t})\bigr)\Delta \mu _{1}(t_{1})\dots \Delta \mu _{1}(t_{n}) \\ &\qquad {}+r \int _{\varOmega _{1}} \int _{\varOmega _{2}}\lambda (\mathbf{t})\frac{k(\mathbf{t},\mathbf{s})}{\mathcal{K}(\mathbf{t})}\varPsi ^{r-1}\bigl(A_{k}g(\mathbf{t})\bigr)\varPsi \bigl( \bigl\vert g(\mathbf{s})-A_{k}g(\mathbf{t}) \bigr\vert \bigr) \\ &\qquad {}\times \Delta \mu _{1}(t_{1})\dots \Delta \mu _{1}(t_{n})\Delta \mu _{2}(s _{1})\dots \Delta \mu _{2}(s_{n}) \\ &\quad \leq \biggl( \int _{\varOmega _{2}}\eta (\mathbf{s})\varPsi \bigl(g(\mathbf{s})\bigr) \Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s_{n}) \biggr) ^{r}. \end{aligned}$$

This gives us the desired inequality (19). Similarly to the proof of (19), by the same calculations with Ψ subquadratic, we see that only the inequality sign will be reversed. The proof is complete. □

As a particular case of Theorem 2.1, when $\varPsi (\boldsymbol{\lambda })= \boldsymbol{\lambda }^{p}$ for $p\geq 2$, we have the following result.

Corollary 2.1

Let the assumptions of Theorem 2.1be satisfied, and let $p\geq 2$. Then

$$\begin{aligned} & \int _{\varOmega _{1}}\lambda (\mathbf{t}) \bigl(A_{k}g( \mathbf{t})\bigr)^{pr}\Delta \mu _{1}(t _{1})\dots \Delta \mu _{1}(t_{n}) \\ &\qquad {}+r \int _{\varOmega _{1}} \int _{\varOmega _{2}}\lambda (\mathbf{t})\frac{k(\mathbf{t},\mathbf{s})}{\mathcal{K}(\mathbf{t})} \bigl(A_{k}g(\mathbf{t})\bigr)^{p(r-1)} \bigl\vert g( \mathbf{s})-A_{k}g(\mathbf{t}) \bigr\vert ^{p} \\ &\qquad {}\times \Delta \mu _{1}(t_{1})\dots \Delta \mu _{1}(t_{n})\Delta \mu _{2}(s _{1})\dots \Delta \mu _{2}(s_{n}) \\ &\quad \leq \biggl( \int _{\varOmega _{2}}\eta (\mathbf{s})g^{p}(\mathbf{s})\Delta \mu _{2}(s _{1})\dots \Delta \mu _{2}(s_{n}) \biggr) ^{r}. \end{aligned}$$

(26)

The inequality sign in (26) is reversed if $1< p\leq 2$.

Also, by choosing $\varPsi :[{\mathbf{a}},\boldsymbol{\infty })_{{T}} \rightarrow {R}$ ($a_{i}\geq 0$, $i=1,2,\dots ,n$) and $\varPsi ( \mathbf{t})=e ^{\mathbf{t}}-\mathbf{t}-1$ and replacing $g(\mathbf{t })$ by $\ln g(\mathbf{t})$ in Theorem 2.1, we obtain the following multidimensional version of refined weighted Pólya–Knopp-type inequality with a kernel on time scale.

Corollary 2.2

Assume that the claims in Theorem 2.1are satisfied, and let

$$ A_{k}g(\mathbf{t}):=\frac{1}{\mathcal{K}(\mathbf{t})} \int _{\varOmega _{2}}k( \mathbf{t},\mathbf{s})\ln g(\mathbf{s})\Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s _{n}), \quad \mathbf{t}\in \varOmega _{1}. $$

(27)

Then

$$\begin{aligned} & \int _{\varOmega _{1}}\lambda (t) \bigl[ \exp A_{k}g( \mathbf{t})-A_{k}g( \mathbf{t})-1 \bigr] ^{r}\Delta \mu _{1}(t_{1})\dots \Delta \mu _{1}(t_{n})+I \\ &\quad \leq \biggl( \int _{\varOmega _{2}}\eta (\mathbf{s}) \bigl[ g(\mathbf{s})- \ln g( \mathbf{s})-1 \bigr] \Delta \mu _{2}(s_{1})\dots \Delta \mu _{2}(s_{n}) \biggr) ^{r}, \end{aligned}$$

(28)

where

$$\begin{aligned} I&:=r \int _{\varOmega _{1}} \int _{\varOmega _{2}}\lambda (\mathbf{t})\frac{k( \mathbf{t},\mathbf{s})}{\mathcal{K}(\mathbf{t})} \bigl[ \exp A_{k}g(\mathbf{t})-A _{k}g(\mathbf{t})-1 \bigr] ^{r-1} \\ &\quad {}\times \bigl[ \exp \bigl\vert \ln g(\mathbf{s})-A_{k}g( \mathbf{t}) \bigr\vert - \bigl\vert \ln g(\mathbf{s})-A_{k}g( \mathbf{t}) \bigr\vert -1 \bigr] \\ &\quad {}\times \Delta \mu _{1}(t_{1})\dots \Delta \mu _{1}(t_{n})\Delta \mu _{2}(s _{1})\dots \Delta \mu _{2}(s_{n}). \end{aligned}$$

(29)

Remark 2.1

In Theorem 2.1, if $r=1$, then we see that the result coincides with Theorem 3.4 in [18].

In the following, we will establish some particular cases of inequalities (19) and (26) by applying Theorem 2.1 with

$$ \varOmega =\varOmega _{1}=\varOmega _{2}=[a_{1},b_{1})_{{T}} \times {[} a_{2},b _{2})_{{T}}\times \cdots\times {[} a_{n},b_{n})_{{T}}\subset {R}^{n},\quad 0 \leq a_{i}< b_{i}\leq \infty , $$

(30)

for all $i=1,2,\ldots,n$, where T is an arbitrary time scale, and the Lebesgue scale measures $\Delta \mu _{1}(\mathbf{t})= \Delta {\mathbf{t}}$ and $\Delta \mu _{2}(\mathbf{s})=\Delta {\mathbf{s}}$, and replacing $\lambda (\mathbf{t})$ by $\lambda (\mathbf{t})/\prod_{i=1} ^{n}\sigma (t_{i})$ and $\eta (\mathbf{s})$ by $\omega (\mathbf{s})/ \prod_{i=1}^{n}s_{i}$. Then we have the following corollary.

Corollary 2.3

Let $\lambda :\varOmega \rightarrow {R}$be a nonnegative function, and let $k:\varOmega \times \varOmega \rightarrow {R}$be nonnegative such that $k({\mathbf{t}})$is a Δ-integrable function. Suppose that $K:\varOmega \rightarrow {R}$is defined by

$$ 0< K(\mathbf{t}):= \int _{\varOmega }k(t,s)\Delta s< \infty , \quad t\in \varOmega , $$

(31)

and the functionηis defined by

$$ \omega (\mathbf{s}):= \Biggl( \prod_{i=1}^{n}s_{i} \Biggr) \biggl( \int _{\varOmega } \biggl( \frac{k(\mathbf{t},\mathbf{s})}{\mathcal{K}(\mathbf{t})} \biggr) ^{r} \frac{ \lambda (\mathbf{t})}{\prod_{i=1}^{n}\sigma (t_{i})}\Delta \mathbf{t} \biggr) ^{\frac{1}{r}}< \boldsymbol{\infty }, \quad \mathbf{s}\in \varOmega , $$

(32)

where $r\geq 1$. Furthermore, assume that $g:\varOmega \rightarrow {R} ^{n}$be Δ-integrable function such that $g(\varOmega )\subset {R}$and define $A_{k}g:\varOmega \rightarrow {R}$by

$$ A_{k}g(\mathbf{t}):=\frac{1}{\mathcal{K}(\mathbf{t})} \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}}k(\mathbf{t},\mathbf{s})g(\mathbf{s}) \Delta \mathbf{s}. $$

(33)

If $\varPsi :\varOmega \rightarrow {R}$is a nonnegative superquadratic function, then

$$\begin{aligned} & \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}}\lambda (\mathbf{t})\varPsi ^{r}\bigl(A _{k}g(\mathbf{t})\bigr)\frac{\Delta \mathbf{t}}{\prod_{i=1}^{n}\sigma (t_{i})} \\ &\qquad {}+r \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}} \int _{s_{1}}^{b_{1}}\dots \int _{s_{n}}^{b_{n}}\lambda (\mathbf{t})\varPsi ^{r-1}\bigl(A_{k}g(\mathbf{t})\bigr) \varPsi \bigl( \bigl\vert g(\mathbf{s})-A_{k}g(\mathbf{t}) \bigr\vert \bigr) \frac{ \Delta \mathbf{t}\Delta \mathbf{s}}{\prod_{i=1}^{n}\sigma (t_{i})} \\ &\quad \leq \biggl( \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}}\omega ( \mathbf{s})\varPsi \bigl(g( \mathbf{s})\bigr)\frac{\Delta \mathbf{s}}{\prod_{i=1}^{n}s_{i}} \biggr) ^{r}. \end{aligned}$$

(34)

IfΨis subquadratic, then the inequality sign in (34) is reversed.

As a particular case of Corollary 2.3 when $\varPsi (\boldsymbol{\lambda })=\boldsymbol{\lambda }^{p}$ for $p\geq 2$, we have the following result.

Corollary 2.4

Let the assumptions of Corollary 2.3be satisfied. Then

$$\begin{aligned} & \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}}\lambda (\mathbf{t}) \bigl(A_{k}g( \mathbf{t})\bigr)^{pr}\frac{\Delta \mathbf{t}}{\prod_{i=1}^{n}\sigma (t_{i})} \\ &\qquad {}+r \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}} \int _{s_{1}}^{b_{1}}\dots \int _{s_{n}}^{b_{n}}\lambda (\mathbf{t}) \bigl(A_{k}g(\mathbf{t})\bigr)^{p(r-1)} \bigl\vert g( \mathbf{s})-A_{k}g(\mathbf{t}) \bigr\vert ^{p} \frac{\Delta \mathbf{t}\Delta \mathbf{s}}{\prod_{i=1}^{n}\sigma (t_{i})} \\ &\quad \leq \biggl( \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}}\omega ( \mathbf{s})g^{p}( \mathbf{s})\frac{\Delta \mathbf{s}}{\prod_{i=1}^{n}s_{i}} \biggr) ^{r}. \end{aligned}$$

(35)

The inequality sign in (35) is reversed if $1< p\leq 2$.

Remark 2.2

For $r=1$, Corollaries 2.3 and 2.4 provide refinements of Theorem 3.6 and Corollary 3.7 in [5], respectively.

In the following, we present some particular inequalities with special kernels. Namely, we have the following result.

Corollary 2.5

Suppose the assumptions of Corollary 2.3are satisfied with the kernelksuch that

$$ k(t_{1},\ldots,t_{n},s_{1},\ldots,s_{n}):= \mathbf{0} \quad \textit{if } a _{i}\leq s_{i}\leq \sigma (t_{i})\leq b_{i},1\leq i\leq n. $$

(36)

Let $g:\varOmega \rightarrow {R}^{n}$be a Δ-integrable function such that $g(\varOmega )\subset {R}$, and define

$$\begin{aligned}& \mathcal{K}(\mathbf{t}):= \int _{\sigma (t_{1})}^{b_{1}}\dots \int _{\sigma (t_{n})}^{b_{n}}k(t_{1},\ldots,t_{n},s_{1},\ldots,s_{n}) \Delta \mathbf{s}>\mathbf{0}, \quad \mathbf{t}\in \varOmega , \end{aligned}$$

(37)

$$\begin{aligned}& \omega (\mathbf{s}):= \Biggl( \prod_{i=1}^{n}s_{i} \Biggr) \biggl( \int _{a_{1}}^{s_{1}}\dots \int _{a_{n}}^{s_{n}} \biggl( \frac{k(\mathbf{t}, \mathbf{s})}{\mathcal{K}(\mathbf{t})} \biggr) ^{r}\frac{\lambda (\mathbf{t})}{ \prod_{i=1}^{n}\sigma (t_{i})}\Delta \mathbf{t} \biggr) ^{\frac{1}{r}} < \boldsymbol{\infty }, \quad \mathbf{s}\in \varOmega , \end{aligned}$$

(38)

and

$$ A_{k}g(\mathbf{t}):=\frac{1}{\mathcal{K}(\mathbf{t})} \int _{\sigma (t_{1})} ^{b_{1}}\dots \int _{\sigma (t_{n})}^{b_{n}}k(t_{1},\ldots,t_{n},s_{1},\ldots,s _{n})g(s_{1},{ }\dots ,s_{n})\Delta \mathbf{s}. $$

(39)

If $\varPsi :\varOmega \rightarrow {R}$is a nonnegative superquadratic function, then inequality (34) holds. IfΨis subquadratic, then the inequality sign in (34) is reversed.

Remark 2.3

If in Corollary 2.5, we take ${T=R}$, $r=1$, and $b_{i}= \infty$ for $1\leq i\leq n$, then we see that $\sigma (t_{i})=t_{i}$ for $1\leq i\leq n$, and then (34) takes the form

$$\begin{aligned} & \int _{a_{1}}^{\infty }\dots \int _{a_{n}}^{\infty }\lambda (t_{1},\ldots,t _{n})\varPsi \bigl(A_{k}g(t_{1},\ldots,t_{n}) \bigr)\frac{d\mathbf{t}}{\mathbf{{t}}} \\ &\qquad {}+ \int _{a_{1}}^{\infty }\dots \int _{a_{n}}^{\infty } \biggl( \int _{s_{1}} ^{\infty }\dots \int _{s_{n}}^{\infty }\lambda (\mathbf{t})\varPsi \bigl( \bigl\vert g( \mathbf{s})-A_{k}g(\mathbf{t}) \bigr\vert \bigr) \frac{d\mathbf{t}}{\mathbf{{t}}} \biggr) \,d\mathbf{s} \\ &\quad \leq \int _{a_{1}}^{\infty }\dots \int _{a_{n}}^{\infty }\omega (s_{1},\ldots,s _{n})\varPsi \bigl(g(s_{1},\ldots,s_{n})\bigr) \frac{d\mathbf{s}}{\mathbf{{s}}}, \end{aligned}$$

(40)

where

$$\begin{aligned}& \mathcal{K}(\mathbf{t}):= \int _{t_{1}}^{\infty }\dots \int _{t_{n}}^{\infty }k(t _{1},\ldots,t_{n},s_{1},\ldots,s_{n})\,d \mathbf{s}>\mathbf{0}, \end{aligned}$$

(41)

$$\begin{aligned}& \omega (\mathbf{s}):=s_{1}\dots s_{n} \int _{a_{1}}^{s_{1}}\dots \int _{a_{n}} ^{s_{n}}\frac{\lambda (t_{1},\ldots,t_{n})k(t_{1},\ldots,t_{n},s_{1},\ldots,s _{n})}{K(t_{1},\ldots,t_{n})}\frac{d\mathbf{t}}{\mathbf{{t}}}< \infty , \end{aligned}$$

(42)

and

$$ A_{k}g(\mathbf{t}):=\frac{1}{\mathcal{K}(\mathbf{t})} \int _{t_{1}}^{\infty }\dots \int _{t_{n}}^{\infty }k(t_{1},\ldots,t_{n},s_{1},\ldots,s_{n})g(s_{1},\ldots,s _{n})\,d\mathbf{s}. $$

(43)

If Ψ is subquadratic, then the inequality sign in (40) is reversed. This result provides a refinement of inequality (2.5) in [19, Proposition 2.2].

Corollary 2.6

Assume that the assumptions of Corollary 2.3are satisfied with the kernelksuch that

$$ k(t_{1},\ldots,t_{n},s_{1},\ldots,s_{n}):= \mathbf{0} \quad \textit{if }a_{i} \leq \sigma (t_{i})\leq s_{i}\leq b_{i},1\leq i\leq n. $$

(44)

If $\varPsi :\varOmega \rightarrow {R}$is a nonnegative superquadratic function, then inequality (34) holds for all Δ-integrable functions $g:\varOmega \rightarrow {R}^{n}$such that $g(\varOmega )\subset {R}$, and

$$ A_{k}g(\mathbf{t}):=\frac{1}{\mathcal{K}(\mathbf{t})} \int _{a_{1}}^{\sigma (t _{1})}\dots \int _{a_{n}}^{\sigma (t_{n})}k(t_{1},\ldots,t_{n},s_{1},\ldots,s _{n})g(s_{1},\ldots,s_{n})\Delta \mathbf{s}, $$

(45)

where

$$\begin{aligned}& \mathcal{K}(\mathbf{t}):= \int _{a_{1}}^{\sigma (t_{1})}\dots \int _{a_{n}} ^{\sigma (t_{n})}k(t_{1},\ldots,t_{n},s_{1},\ldots,s_{n}) \Delta \mathbf{s}< \boldsymbol{\infty }, \quad \mathbf{t}\in \varOmega , \end{aligned}$$

(46)

$$\begin{aligned}& \omega (\mathbf{s}):= \Biggl( \prod_{i=1}^{n}s_{i} \Biggr) \biggl( \int _{s_{1}}^{b_{1}}\dots \int _{s_{n}}^{b_{n}} \biggl( \frac{k(\mathbf{t}, \mathbf{s})}{\mathcal{K}(\mathbf{t})} \biggr) ^{r}\frac{\lambda (\mathbf{t}) \Delta \mathbf{t}}{\prod_{i=1}^{n}\sigma (t_{i})} \biggr) ^{\frac{1}{r}}< \infty , \quad \mathbf{s}\in \varOmega . \end{aligned}$$

(47)

IfΨis subquadratic, then the inequality sign in (34) is reversed.

Remark 2.4

If in Corollary 2.6, we take ${T=R}$, $r=1$, and $a_{i}=0$ for $1\leq i\leq n$, then we see that $\sigma (t_{i})=t_{i}$ for $1 \leq i\leq n$, and then (34) takes the form

$$\begin{aligned} & \int _{0}^{b_{1}}\dots \int _{0}^{b_{n}}\lambda (t_{1},\ldots,t_{n}) \varPsi \bigl(A _{k}g(t_{1},\ldots,t_{n})\bigr) \frac{d\mathbf{t}}{\mathbf{{t}}} \\ &\qquad {}+ \int _{0}^{b_{1}}\dots \int _{0}^{b_{n}} \biggl( \int _{0}^{s_{1}}\dots \int _{0}^{s_{n}}\lambda (\mathbf{t})\varPsi \bigl( \bigl\vert g(\mathbf{s})-A_{k}g( \mathbf{t}) \bigr\vert \bigr) \frac{d\mathbf{t}}{\mathbf{{t}}} \biggr) \,d\mathbf{s} \\ &\quad \leq \int _{0}^{b_{1}}\dots \int _{0}^{b_{n}}\omega (s_{1},\ldots,s_{n}) \varPsi \bigl(g(s_{1},\ldots,s_{n})\bigr)\frac{d\mathbf{s}}{\mathbf{{s}}}, \end{aligned}$$

(48)

where

$$\begin{aligned}& \mathcal{K}(\mathbf{t}):= \int _{0}^{t_{1}}\dots \int _{0}^{t_{n}}k(t_{1},\ldots,t _{n},s_{1},\ldots,s_{n})\,d\mathbf{s}>\mathbf{0}, \end{aligned}$$

(49)

$$\begin{aligned}& \omega (\mathbf{s}):=s_{1}\dots s_{n} \int _{s_{1}}^{b_{1}}\dots \int _{s_{n}} ^{b_{n}}\frac{k(t_{1},\ldots,t_{n},s_{1},\ldots,s_{n})\lambda (t_{1},\ldots,t _{n})}{K(t_{1},\ldots,t_{n})}\frac{\mathbf{{t}}}{\mathbf{t}}< \infty , \end{aligned}$$

(50)

and

$$ A_{k}g(\mathbf{t}):=\frac{1}{\mathcal{K}(\mathbf{t})} \int _{0}^{t_{1}}\dots \int _{0}^{t_{n}}k(t_{1},\ldots,t_{n},s_{1},\ldots,s_{n})g(s_{1},\ldots,s_{n})\,d \mathbf{s}. $$

(51)

If Ψ is subquadratic, then the inequality sign in (48) is reversed. This result provides a refinement of inequality (2.2) in [19, Proposition 2.1].

Remark 2.5

For $r=1$, Corollaries 2.5 and 2.6 provide refinements of Corollaries 4.1 and 4.3 in [5], respectively.

We further present some examples. Let K and $A_{k}g$ be defined as in the statements of Corollary 2.5 and use

$$ k(\mathbf{t},\mathbf{s}):= \textstyle\begin{cases} {\mathbf{1}},& \text{if }a_{i}\leq s_{i}\leq \sigma (t_{i}) \leq b_{i},1\leq i\leq n, \\ \mathbf{0},&s_{i}>\sigma (t_{i}). \end{cases} $$

(52)

Then we have the following corollary.

Corollary 2.7

Let $\lambda :\varOmega \rightarrow {R}$be a nonnegative function, and let $k:\varOmega \times \varOmega \rightarrow {R}$be nonnegative such that $k({\mathbf{t}})$is a Δ-integrable function. Suppose that $\mathcal{K}:\varOmega \rightarrow {R}$is defined by

$$ \mathcal{K}(\mathbf{t}):= \int _{a_{1}}^{\sigma (t_{1})}\dots \int _{a_{n}} ^{\sigma (t_{n})}\Delta s_{1}\dots \Delta s_{n}=\prod_{i=1}^{n}\bigl(\sigma (t _{i})-a_{i}\bigr), \quad \mathbf{t}\in {[} {\mathbf{a}}, \mathbf{b})_{ {T}}, $$

(53)

and let

$$ \eta (\mathbf{s}):= \biggl( \int _{s_{1}}^{b_{1}}\dots \int _{s_{n}}^{b_{n}} \lambda (\mathbf{t}) \biggl( \frac{\mathbf{1}}{\prod_{i=1}^{n}(\sigma (t_{i})-a_{i})} \biggr) ^{r}\Delta {\mathbf{t}} \biggr) ^{\frac{1}{r}}< \infty , \quad \mathbf{s}\in {[} {\mathbf{a}}, \mathbf{b})_{{T}}, $$

(54)

where $r\geq 1$. Furthermore, assume that $g:\varOmega \rightarrow {R} ^{n}$is a Δ-integrable function such that $g(\varOmega )\subset {R}^{n}$and $A_{k}g:\varOmega \rightarrow {R}$is defined by

$$ A_{k}g(\mathbf{t}):=\frac{1}{\prod_{i=1}^{n}(\sigma (t_{i})-a_{i})} \int _{a_{1}}^{\sigma (t_{1})}\dots \int _{a_{n}}^{\sigma (t_{n})}g(\mathbf{s})\Delta \mathbf{s}. $$

(55)

If $\varPsi :\varOmega \rightarrow {R}$is a nonnegative superquadratic function, then

$$\begin{aligned} & \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}}\lambda (\mathbf{t})\varPsi ^{r}\bigl(A _{k}g(\mathbf{t})\bigr)\Delta \mathbf{t} \end{aligned}$$

(56)

$$\begin{aligned} &\quad {}+r \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}} \int _{s_{1}}^{b_{1}}\dots \int _{s_{n}}^{b_{n}}\lambda (\mathbf{t})\varPsi ^{r-1}\bigl(A_{k}g(\mathbf{t})\bigr) \varPsi \bigl( \bigl\vert g(\mathbf{s})-A_{k}g(\mathbf{t}) \bigr\vert \bigr) \\ &\quad {}\times \frac{\Delta \mathbf{t}\Delta \mathbf{s}}{\prod_{i=1}^{n}(\sigma (t _{i})-a_{i})}\leq \biggl( \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}} \eta (\mathbf{s})\varPsi \bigl(g( \mathbf{s})\bigr)\Delta \mathbf{s} \biggr) ^{r}. \end{aligned}$$

(57)

IfΨinstead is subquadratic, then (56) holds in the reversed direction.

Remark 2.6

For $r=1$, inequality (56) provides a refinement of inequality (5.2) in [5, Theorem 5.1] and coincides with inequality (3.7) in [18, Corollary 3.8].

Corollary 2.8

Let the assumptions of Corollary 2.7be satisfied, let $\lambda ({\mathbf{t}})$be replaced by $\lambda ({\mathbf{t}})/( \prod_{i=1}^{n}(t_{i}-a_{i}))$, and let $\eta ({\mathbf{s}})$be replaced by $\omega ({\mathbf{s}})/(\prod_{i=1}^{n}(s_{i}-a _{i}))$. Then inequality (56) reads as

$$\begin{aligned} & \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}}\lambda (\mathbf{t})\varPsi ^{r}\bigl(A _{k}g(\mathbf{t})\bigr)\frac{\Delta {\mathbf{t}}}{\prod_{i=1}^{n}(t_{i}-a _{i})} \\ &\quad {}+r \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}} \int _{s_{1}}^{b_{1}}\dots \int _{s_{n}}^{b_{n}}\lambda (\mathbf{t})\varPsi ^{r-1}\bigl(A_{k}g(\mathbf{t})\bigr) \varPsi \bigl( \bigl\vert g(\mathbf{s})-A_{k}g(\mathbf{t}) \bigr\vert \bigr) \\ &\quad {}\times \frac{\Delta {\mathbf{t}}\Delta {\mathbf{s}}}{\prod_{i=1} ^{n}(t_{i}-a_{i})(\sigma (t_{i})-a_{i})}\leq \biggl( \int _{a_{1}}^{b _{1}}\dots \int _{a_{n}}^{b_{n}}\omega (\mathbf{s})\varPsi \bigl(g( \mathbf{s})\bigr)\frac{ \Delta {\mathbf{s}}}{\prod_{i=1}^{n}(s_{i}-a_{i})} \biggr) ^{r}, \end{aligned}$$

(58)

where $r\geq 1$,

$$ \omega (\mathbf{s}):= \Biggl( \prod_{i=1}^{n}(s_{i}-a_{i}) \Biggr) \biggl( \int _{[{\mathbf{s}},\mathbf{b})} \biggl( \frac{\mathbf{1}}{\prod_{i=1} ^{n}(\sigma (t_{i})-a_{i})} \biggr) ^{r} \frac{\lambda (\mathbf{t})}{ \prod_{i=1}^{n}(t_{i}-a_{i})}\Delta {\mathbf{t}} \biggr) ^{\frac{1}{r}} $$

(59)

for ${\mathbf{s}}\in {[} {\mathbf{a}},\mathbf{b})_{ {T}}$, and the operator $A_{k}g$is defined by (55). IfΨinstead is subquadratic, then (58) holds in the reversed direction.

Remark 2.7

For $r=1$, Corollary 2.8 provides a refinement of Theorem 3.1 and Remark 3.1 in [16, Theorem 3.1].

Remark 2.8

As a particular case of Corollary 2.8, when ${T=R}$, $r=1$, and $a_{i}=0$ for $1\leq i\leq n$, we see that $\sigma (t_{i})=t_{i}$ for $1\leq i\leq n$, and inequality (58) reads as

$$\begin{aligned} & \int _{0}^{b_{1}}\dots \int _{0}^{b_{n}}\lambda (\mathbf{t})\varPsi \biggl( \frac{1}{ \mathbf{{t}}} \int _{0}^{t_{1}}\dots \int _{0}^{t_{n}}g(\mathbf{s})\,d\mathbf{s} \biggr) \frac{d\mathbf{t}}{\mathbf{{t}}} \\ &\qquad {}+ \int _{0}^{b_{1}}\dots \int _{0}^{b_{n}} \int _{s_{1}}^{b_{1}}\dots \int _{s _{n}}^{b_{n}}\lambda (\mathbf{t})\varPsi \biggl( \biggl\vert g(\mathbf{s})-\frac{1}{ \mathbf{{t}}} \int _{0}^{t_{1}}\dots \int _{0}^{t_{n}}g(\mathbf{s})\mathbf{ds} \biggr\vert \biggr) \frac{d\mathbf{t}\,d\mathbf{s}}{t_{1}^{2}\dots t_{n}^{2}} \\ &\quad \leq \int _{0}^{b_{1}}\dots \int _{0}^{b_{n}}\omega (\mathbf{s})\varPsi \bigl(g( \mathbf{s})\bigr)\frac{d\mathbf{s}}{\mathbf{{s}}}, \end{aligned}$$

(60)

where

$$ \omega (\mathbf{s}):=s_{1}\dots s_{n} \int _{s_{1}}^{b_{1}}\dots \int _{s_{n}} ^{b_{n}}\frac{\lambda (\mathbf{t})}{t_{1}^{2}\dots t_{n}^{2}}\,d\mathbf{t}< \boldsymbol{\infty }, \quad \mathbf{s}\in {[} \mathbf{0},\mathbf{b}). $$

(61)

If Ψ is subquadratic, then the inequality sing in (60) is reversed, which coincides with inequality (2.2) in [20, Proposition 2.5].

Example 2.1

If we set the weight function $\lambda ({\mathbf{t}})= \mathbf{1}$ and $r=1$ in Corollary 2.8, then the weight function (59) yields

$$\begin{aligned} \omega (\mathbf{s}) &:= \Biggl( \prod_{i=1}^{n}(s_{i}-a_{i}) \Biggr) \biggl( \int _{s_{1}}^{b_{1}}\dots \int _{s_{n}}^{b_{n}}\frac{\Delta {\mathbf{t}}}{ \prod_{i=1}^{n}(t_{i}-a_{i})(\sigma (t_{i})-a_{i})} \biggr) \\ &=- \Biggl( \prod_{i=1}^{n}(s_{i}-a_{i}) \Biggr) \biggl( \int _{s_{1}} ^{b_{1}}\dots \int _{s_{n}}^{b_{n}} \biggl( \frac{1}{\prod_{i=1}^{n}(t_{i}-a _{i})} \biggr) ^{\Delta }\Delta \mathbf{t} \biggr) \\ &=- \Biggl( \prod_{i=1}^{n}(s_{i}-a_{i}) \Biggr) \Biggl( \prod_{i=1}^{n} \biggl( \frac{1}{b_{i}-a_{i}}-\frac{1}{s_{i}-a_{i}} \biggr) \Biggr) \\ &= \textstyle\begin{cases} \prod_{i=1}^{n} ( 1-\frac{s_{i}-a_{i}}{b_{i}-a_{i}} ) & \text{if } b_{i}< \infty ,1\leq i\leq n, \\ \mathbf{1}& \text{if }b _{i}=\infty ,1\leq i\leq n. \end{cases}\displaystyle \end{aligned}$$

Hence inequality (58) in this setting for the case $b_{i}< \infty$ reads

$$\begin{aligned} & \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}}\varPsi \bigl(A_{k}g( \mathbf{t})\bigr)\frac{ \Delta {\mathbf{t}}}{\prod_{i=1}^{n}(t_{i}-a_{i})} \\ &\qquad {}+ \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}} \int _{s_{1}}^{b_{1}}\dots \int _{s_{n}}^{b_{n}}\varPsi \bigl( \bigl\vert g( \mathbf{s})-A_{k}g(\mathbf{t}) \bigr\vert \bigr)\frac{ \Delta {\mathbf{t}}\Delta {\mathbf{s}}}{\prod_{i=1}^{n}(t_{i}-a_{i})( \sigma (t_{i})-a_{i})} \\ &\quad \leq \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}}\prod_{i=1}^{n} \biggl( 1-\frac{s_{i}-a_{i}}{b_{i}-a_{i}} \biggr) \varPsi \bigl(g(\mathbf{s})\bigr) \frac{ \Delta {\mathbf{s}}}{(s_{i}-a_{i})}, \end{aligned}$$

(62)

whereas the case $b_{i}=\infty$ yields

$$\begin{aligned} & \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}}\varPsi \bigl(A_{k}g( \mathbf{t})\bigr)\frac{ \Delta {\mathbf{t}}}{\prod_{i=1}^{n}(t_{i}-a_{i})} \\ &\qquad {}+ \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}} \int _{s_{1}}^{b_{1}}\dots \int _{s_{n}}^{b_{n}}\varPsi \bigl( \bigl\vert g( \mathbf{s})-A_{k}g(\mathbf{t}) \bigr\vert \bigr)\frac{ \Delta {\mathbf{t}}\Delta {\mathbf{s}}}{\prod_{i=1}^{n}(t_{i}-a_{i})( \sigma (t_{i})-a_{i})} \\ &\quad \leq \int _{a_{1}}^{b_{1}}\dots \int _{a_{n}}^{b_{n}}\prod_{i=1}^{n} \varPsi \bigl(g( \mathbf{s})\bigr)\frac{\Delta {\mathbf{s}}}{(s_{i}-a_{i})}, \end{aligned}$$

(63)

where the operator $A_{k}g$ is defined by (55). If Ψ instead is subquadratic, then the inequality sign in (62) and (63) is reversed.

Remark 2.9

Inequalities (62) and (63) provide a refinement of the results in [16, Example 3.1]. For $a_{i}=0$ for $1\leq i\leq n$, they provide a refinement of the results in [5, Corollary 5.3, Example 5.4].

Remark 2.10

If we set $n=1$, then Example 2.1 provides a refinement of Corollary 2.1 in [21, Corollary 2.1]. Also, in the particular case $n=2$, inequality (62) provides a refinement of Theorem 3.2 in [21, Corollary 2.1].

Remark 2.11

As a particular case of Example 2.1, when ${T=R}$ and $a_{i}=0$ for $1\leq i\leq n$, we see that $\sigma (t_{i})=t_{i}$ for $1\leq i\leq n$, and so (62) reads as

$$\begin{aligned} & \int _{0}^{b_{1}}\dots \int _{0}^{b_{n}}\varPsi \biggl( \frac{1}{t_{1}\dots t _{n}} \int _{0}^{t_{1}}\dots \int _{0}^{t_{n}}g(\mathbf{s})\,d\mathbf{s} \biggr) \frac{d \mathbf{t}}{t_{1}\dots t_{n}} \\ &\qquad {}+ \int _{0}^{b_{1}}\dots \int _{0}^{b_{n}} \int _{s_{1}}^{b_{1}}\dots \int _{s _{n}}^{b_{n}}\varPsi \biggl( \biggl\vert g( \mathbf{s})-\frac{1}{t_{1}\dots t _{n}} \int _{0}^{t_{1}}\dots \int _{0}^{t_{n}}g(\mathbf{s})\,d\mathbf{s} \biggr\vert \biggr) \frac{d\mathbf{t}\,d\mathbf{s}}{t_{1}^{2}\dots t_{n}^{2}} \\ &\quad \leq \int _{0}^{b_{1}}\dots \int _{0}^{b_{n}}\prod_{i=1}^{n} \biggl( 1-\frac{s _{i}}{b_{i}} \biggr) \varPsi \bigl(g(\mathbf{s})\bigr) \frac{d\mathbf{s}}{s_{1}\dots s_{n}}, \end{aligned}$$

(64)

which coincides with inequality (2.3) in [20, Remark 2.6]. In the one-dimensional case ($n=1$), this reduces to Example 4.1 in [17]. Inequality (62) yields

$$\begin{aligned} & \int _{0}^{b_{1}}\dots \int _{0}^{b_{n}}\varPsi \biggl( \frac{1}{t_{1}\dots t _{n}} \int _{0}^{t_{1}}\dots \int _{0}^{t_{n}}g(\mathbf{s})\,d\mathbf{s} \biggr) \frac{d \mathbf{t}}{t_{1}\dots t_{n}} \\ &\qquad {}+ \int _{0}^{b_{1}}\dots \int _{0}^{b_{n}} \int _{s_{1}}^{b_{1}}\dots \int _{s _{n}}^{b_{n}}\varPsi \biggl( \biggl\vert g( \mathbf{s})-\frac{1}{t_{1}\dots t _{n}} \int _{0}^{t_{1}}\dots \int _{0}^{t_{n}}g(\mathbf{s})\,d\mathbf{s} \biggr\vert \biggr) \frac{d\mathbf{t}}{t_{1}^{2}\dots t_{n}^{2}}\,d\mathbf{s} \\ &\quad \leq \int _{0}^{b_{1}}\dots \int _{0}^{b_{n}}\varPsi \bigl(g(\mathbf{s})\bigr) \frac{ds _{1}\dots ds_{n}}{s_{1}\dots s_{n}}. \end{aligned}$$

(65)

Now we further consider some generalizations of Pólya–Knopp-type inequalities.

Corollary 2.9

Assume that the assumptions of Corollary 2.7be satisfied with $n=1$, $a_{1}=a\geq 0$, $r\geq 1$, and $b_{1}=\infty$. If $\varPsi :I \rightarrow {R}$is a nonnegative superquadratic function, where $I\subset {R}$is an interval, then

$$\begin{aligned} & \int _{a}^{\infty }\lambda (t)\varPsi ^{r} \biggl( \frac{1}{\sigma (t)-a} \int _{a}^{\sigma (t)}g(s)\Delta s \biggr) \Delta t \\ &\qquad {}+r \int _{a}^{\infty } \int _{s}^{\infty }\lambda (t)\varPsi ^{r-1} \biggl( \frac{1}{ \sigma (t)-a} \int _{a}^{\sigma (t)}g(s)\Delta s \biggr) \\ &\qquad {}\times \varPsi \biggl( \biggl\vert g(\mathbf{s})- \biggl( \frac{1}{\sigma (t)-a} \int _{a}^{\sigma (t)}g(s)\Delta s \biggr) \biggr\vert \biggr) \frac{\Delta t}{\sigma (t)-a}\Delta s \\ &\quad \leq \biggl( \int _{a}^{\infty } \biggl( \int _{s}^{\infty }\lambda (t) \biggl( \frac{1}{\sigma (t)-a} \biggr) ^{r}\Delta t \biggr) ^{ \frac{1}{r}}\varPsi \bigl(g(s)\bigr) \Delta s \biggr) ^{r} \end{aligned}$$

(66)

for all Δ-integrable functions $g:\varOmega \rightarrow {R}$such that $g(\varOmega )\subset I$. IfΨinstead is subquadratic, then (66) holds in the reversed direction.

Example 2.2

In addition to the assumptions of Corollary 2.9, if T consists of only isolated points, then (66) takes the form

$$\begin{aligned} &\sum_{t\in {[} a,\infty )_{{T}}}\lambda (t)\varPsi ^{r} \biggl( \frac{1}{ \sigma (t)-a}\sum_{s\in {[} a,\sigma (t))_{{T}}}g(s) \bigl(\sigma (s)-s\bigr) \biggr) \bigl(\sigma (t)-t\bigr) \\ &\qquad {}+r\sum_{s\in {[} a,\infty )_{{T}}} \biggl( \sum _{t\in {[} s,\infty )_{{T}}}\lambda (t)\varPsi ^{r-1} \biggl( \frac{1}{ \sigma (t)-a}\sum_{s\in {[} a,\sigma (t))_{{T}}}g(s) \bigl(\sigma (s)-s \bigr) \biggr) \\ &\qquad {}\times \varPsi \biggl( \biggl\vert g({s})-\frac{1}{\sigma (t)-a} \sum_{s\in {[} a,\sigma (t))_{{T}}}g(s) \bigl(\sigma (s)-s\bigr) \biggr\vert \biggr) \frac{\sigma (t)-t}{\sigma (t)-a} \biggr) \bigl(\sigma (s)-s\bigr) \\ &\quad \leq \biggl( \sum_{s\in {[} a,\infty )_{{T}}} \biggl( \sum _{t\in {[} s,\infty )_{{T}}}\lambda (t) \biggl( \frac{1}{ \sigma (t)-a} \biggr) ^{r}\bigl(\sigma (t)-t\bigr) \biggr) ^{\frac{1}{r}}\varPsi \bigl(g(s) \bigr) \bigl( \sigma (s)-s\bigr) \biggr) ^{r}. \end{aligned}$$

(67)

Remark 2.12

For $r=1$, Corollary 2.7 and Example 2.2 provide refinements of Corollary 5.7 and Example 5.8 in [5], respectively. They also are a refinement of Theorem 1.1 in [29], but here we use time scales notation instead of the notation given in [29].

Remark 2.13

As in Example 2.2, we can write a discrete version of (56) and (58).