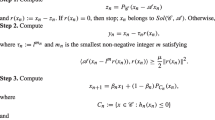Weak and strong convergence of inertial algorithms for solving split common fixed point problems

Abstract

In this paper, we propose two iterative schemes for approximating solutions of split common fixed point problems in multiple linear operators case. The first algorithm implements the Krasnosel’skiĭ–Mann iteration with an inertial effect for which the weak convergence is established under mild assumptions. With the tool of nearly contractive mappings, we introduce a viscosity-type iteration which ensures strong convergence. We apply our results to solve a multiple split monotone variational inclusion problem. A numerical example is given to demonstrate the efficiency of the proposed algorithms.

1 Introduction

Throughout this paper, let $\mathcal{H},\mathcal{K}_{1},\mathcal{K}_{2},\ldots ,\mathcal{K}_{ r}$ be real Hilbert spaces. Given a not necessarily linear operator T from $\mathcal{H}$ into $\mathcal{H}$, we denote by ${\mathrm{Fix}}(T):=\{x\in \mathcal{H}\mid x=Tx\}$ the set of all fixed points of T. We are interested in the following problem [13].

General Split Common Fixed Point Problem (GSCFPP)

$$ \text{Find a point } x\in \bigcap_{i=1}^{p} \operatorname{Fix}(U_{i}) \text{ such that } A_{j}x\in \operatorname{Fix}(T_{j}), \quad \forall j=1, 2, \ldots ,r, $$

where $U_{i}:\mathcal{H}\to \mathcal{H}$, $T_{j}:\mathcal{K}_{j}\to \mathcal{K}_{j}$ are operators, and $A_{j}:\mathcal{H}\to \mathcal{K}_{j}$ is a bounded linear operator for all $i=1, 2,\ldots ,p$ and $j=1, 2,\ldots ,r$.

If $p=r=1$ then the GSCFPP is reduced to the split common fixed point problem.

Split Common Fixed Point Problem (SCFPP)

$$ \text{Find a point } x\in \operatorname{Fix}(U) \text{ such that } Ax\in \operatorname{Fix}(T), $$

which was first introduced by Censor and Segal [12]. They considered the case of directed operators U and T. In [23], Moudafi solved the case of demicontractive mappings, and proposed the following algorithm:

$$ \textstyle\begin{cases} u_{n}=x_{n}-\gamma A^{*}(I-T)Ax_{n}, \\ x_{n+1}=(1-\alpha _{n})u_{n}+\alpha _{n}U(u_{n})\quad \text{for } n\in \mathbb{N}, \end{cases} $$

under suitable conditions of parameters, weak convergence is guaranteed.

Several important inverse problems [5–12, 23], can be rewritten to the description of the GSCFPP. In order to solve the GSCFPP, Chen, Sahu, and Wong [13] proposed several weakly and strongly convergent schemes. In this paper, we study the convergence of the Krasnosel’skiĭ–Mann iteration and the nearly contractive viscosity-type iteration, both involving the inertial effect. The inertial terminology greatly improves the performance of the algorithm (see, e.g. [2, 16, 19, 24]). The inertial method was developed by Polyak [26] firstly. Álvarez and Attouch [1] employed Polyak’s idea, they constructed an algorithm, combined with the proximal point algorithm, named inertial proximal point algorithm as the following form:

$$ \textstyle\begin{cases} z_{n}=x_{n}+\vartheta _{n}(x_{n}-x_{n-1}), \\ x_{n+1}=(I+\lambda _{n} B)^{-1}z_{n}, \quad \text{for } n\in \mathbb{N}, \end{cases} $$

(1.1)

where B is a maximal monotone operator (Sect. 4). Here, $\vartheta _{n}(x_{n}-x_{n-1})$ is named the inertial term. It was proved that the inertial proximal point algorithm (1.1) converges weakly to a zero point of B if $\{\lambda _{n}\}$ is non-decreasing and $\{\vartheta _{n}\}\subset [0,1)$ satisfies

$$ \sum_{n=1}^{\infty }\vartheta _{n} \Vert x_{n}-x_{n-1} \Vert ^{2}< \infty . $$

(1.2)

As in the common case that incorporating the inertial method in an algorithm greatly improves the performance numerically. We refer the related research [4, 14, 15, 20, 29–32] to readers.

In Sect. 2, we review some fundamental tools and results from the convex analysis. In Sect. 3, we construct algorithms for solving the GSCFPP and study their weak and strong convergence. In Sect. 4, we study the multiple split monotone variational inclusion problem. In Sect. 5, we provide a numerical example to demonstrate the performance of our algorithms.

2 Preliminaries

Let I be the identity operator on $\mathcal{H}$. Given a sequence $\{x_{n}\}_{n\in \mathbb{N}}$ in $\mathcal{H}$ and $x\in \mathcal{H}$. The notations “$x_{n}\to x$” and “$x_{n}\rightharpoonup x$” indicate the strong convergence to x and weak convergence of $\{x_{n}\}$ to x, respectively. We denote by $\omega _{w}(x_{n})$ the collection of all points x̄ such that there is a subsequence of $\{x_{n}\}$ converges weakly to x̄.

Definition 2.1

A (not necessarily linear) operator $T:\mathcal{H}\to \mathcal{H}$ is said to be

• quasi-nonexpansive if $\operatorname{Fix}(T)\neq \emptyset$ and $\| Tx-z \|\leq \| x-z \|$, $\forall x\in \mathcal{H}$, $z \in \operatorname{Fix}(T)$;

• firmly nonexpansive if $\|Tx-Ty\|^{2} \leq \langle Tx-Ty,x-y \rangle$, $\forall x,y\in \mathcal{H}$, or equivalently,

  $$ \Vert Tx-Ty \Vert ^{2}\leq \Vert x-y \Vert ^{2}- \bigl\Vert (I-T)x-(I-T)y \bigr\Vert ^{2},\quad \forall x,y\in \mathcal{H}; $$

• α-strongly quasi-nonexpansive with $\alpha >0$ if $\operatorname{Fix}(T)\neq \emptyset$ and

  $$ \langle x-Tx,z-x \rangle \leq \frac{-1-\alpha }{2} \Vert x-Tx \Vert ^{2}, \quad \forall x\in \mathcal{H}, z\in \operatorname{Fix}(T), $$

  or equivalently,

  $$ \Vert Tx-z \Vert ^{2}\leq \Vert x-z \Vert ^{2}- \alpha \Vert x-Tx \Vert ^{2}, \quad \forall x\in \mathcal{H}, z\in \operatorname{Fix}(T); $$

• β-demicontractive with $\beta <1$ if $\operatorname{Fix}(T)\neq \emptyset$ and

  $$ \langle x-Tx,z-x \rangle \leq \frac{\beta -1}{2} \Vert x-Tx \Vert ^{2}, \quad \forall x\in \mathcal{H}, z\in \operatorname{Fix}(T), $$

  or equivalently,

  $$ \Vert Tx-z \Vert ^{2}\leq \Vert x-z \Vert ^{2}+\beta \Vert x-Tx \Vert ^{2}, \quad \forall x\in \mathcal{H}, z\in \operatorname{Fix}(T). $$

Recall the metric projection $P_{C}$ onto a nonempty, closed and convex subset C of $\mathcal{H}$ is defined with that $P_{C}(x)$ is the unique point in C such that $\|x-P_{C}(x)\|=\inf_{w\in C}\|x-w\|$, or equivalently

$$ \bigl\langle x-P_{C}(x), z-P_{C}(x) \bigr\rangle \leq 0,\quad \forall z\in C. $$

(2.1)

It is well known that $P_{C}$ is firmly nonexpansive, 1-strongly quasi-nonexpansive and also $(-1)$-demicontractive.

Lemma 2.2

([21])

If $T:\mathcal{H}\to \mathcal{H}$ is β-demicontractive, then the fixed point set Fix(T) of T is closed and convex.

Definition 2.3

Let $T:\mathcal{H}\to \mathcal{H}$. We say that $I-T$ is demiclosed at zero if for any sequence $\{x_{n}\}$ in $\mathcal{H}$ converging weakly to x and $\{x_{n}-Tx_{n}\}$ converging strongly to 0, we have $(I-T)x=0$.

For example, when T is nonexpansive, $I-T$ is demiclosed at zero.

Lemma 2.4

([25])

Let $\mathcal{H}$ be a Hilbert space and $\{x_{n}\}$ a sequence in $\mathcal{H}$ such that there exists a nonempty set D of $\mathcal{H}$ satisfying:

• (a) For every $z\in D$, $\lim_{n\to \infty }\|x_{n}-z\|$ exists.

• (b) $\omega _{w}(x_{n})\subset D$.

Then there exists $\bar{x}\in D$ such that $x_{n}\rightharpoonup \bar{x}$

Lemma 2.5

([1, 20])

Let $\{\varphi _{n}\}$, $\{\delta _{n}\}$ be two nonnegative sequences, and $\{\vartheta _{n}\}$ be a sequence in $[0,\vartheta ]$ where $\vartheta \in [0,1)$. Assume

• (a) $\varphi _{n+1}-\varphi _{n}\leq \vartheta _{n}(\varphi _{n}-\varphi _{n-1})+ \delta _{n}$, $n\geq 1$,

• (b) $\sum_{n=1}^{\infty }\delta _{n}<\infty$.

Then the sequence $\{\varphi _{n}\}$ is convergent and $\sum_{n=1}^{\infty }[\varphi _{n+1}-\varphi _{n}]_{+}< \infty$, where $[t]_{+}:=\max \{t,0\}$.

Lemma 2.6

([15, 17])

Assume $\{w_{n}\}$ is a sequence of nonnegative real numbers such that

$$\begin{aligned} &w_{n+1}\leq (1-\nu _{n})w_{n}+\nu _{n}u_{n}, \quad n\geq 1, \\ &w_{n+1}\leq w_{n}-\eta _{n}+\sigma _{n}, \quad n\geq 1, \end{aligned}$$

where $\{\nu _{n}\}$, $\{u_{n}\}$ and $\{\sigma _{n}\}$ are sequences of real numbers such that

• (a) $\{\nu _{n}\}\subset (0,1)$ and $\sum_{n=1}^{\infty }\nu _{n}=\infty$,

• (b) $\lim_{n\to \infty }\sigma _{n}=0$,

• (c) $\limsup_{k\to \infty }u_{n_{k}}\leq 0$ whenever $\limsup_{k\to \infty }\eta _{n_{k}}= 0$ for any subsequence of $\{n_{k}\}$ of $\{n\}$.

Then $\lim_{n\to \infty }w_{n}=0$.

3 Iterative algorithms for GSCFPP

We consider the following GSCFPP:

$$ \text{Find a point } x\in \bigcap_{i=1}^{p} \operatorname{Fix}(U_{i}) \text{ such that } A_{j}x\in \operatorname{Fix}(T_{j}),\quad \forall j=1, 2, \ldots ,r, $$

(3.1)

where $U_{i}:\mathcal{H}\to \mathcal{H}$ an $\alpha _{i}$-strongly quasi-nonexpansive operator for $i=1, 2,\ldots ,p$, and $T_{j}:\mathcal{K}_{j}\to \mathcal{K}_{j}$ a $\beta _{i}$-demicontractive operator for $j=1, 2,\ldots ,r$.

In this section, we develop two iterative algorithms for solving GSCFPP (3.1) when $p=r$. For the case $p\neq r$, Wang and Xu [33] set $U_{p+1},U_{p+2},\ldots ,U_{r}$ to be the identity mapping when $p< r$, and set $T_{p+1},T_{p+2},\ldots ,T_{r}$ to be the identity mappings when $p>r$. There is another option: if $p< r$, we define $U_{p+1}:=U_{1}$, $U_{p+2}:=U_{2},\ldots$ , so on; while if $p>r$, we repeat members of $\{A_{j}\}_{j=1}^{r}$ and $\{T_{j}\}_{j=1}^{r}$ in a similar way. In either way, (3.1) is in the case $p=r$. Let Γ be the solution set of GSCFPP (3.1) and suppose $\Gamma \neq \emptyset$ throughout this paper.

Lemma 3.1

([13])

The solution set of GSCFPP (3.1)

$$ \Gamma =\Biggl\{ x\in \bigcap_{i=1}^{p}{ \mathrm{Fix}}(U_{i})\Bigm| A_{j}x\in {\mathrm{Fix}}(T_{j}), \forall j=1, 2,\ldots ,r\Biggr\} $$

is closed and convex.

Definition 3.2

([13])

Let $U_{i}:\mathcal{H}\to \mathcal{H}$ be an $\alpha _{i}$-strongly quasi-nonexpansive operator, $T_{i}:\mathcal{K}_{i}\to \mathcal{K}_{i}$ be a $\beta _{i}$-demicontractive operator, $A_{i}:\mathcal{H}\to \mathcal{K}_{i}$ be a bounded linear operator, $A_{i}^{*}$ be the adjoint operator of $A_{i}$, and $I_{i}$ be the identity operator on $\mathcal{K}_{i}$ for $i=1, 2,\ldots ,p$. We define an operator $S:\mathcal{H}\to \mathcal{H}$ as follows:

$$ Sx=\sum_{i=1}^{p}\omega _{i}U_{i}\bigl(I-\gamma _{i}A_{i}^{*}(I_{i}-T_{i})A_{i} \bigr)x, \quad \text{for } x\in \mathcal{H}, $$

where $\omega _{i}\in (0,1)$ with $\sum_{i=1}^{p}\omega _{i}=1$.

Lemma 3.3

([13])

Let $U_{i}:\mathcal{H}\to \mathcal{H}$ be an $\alpha _{i}$-strongly quasi-nonexpansive operator, $T_{i}:\mathcal{K}_{i}\to \mathcal{K}_{i}$ be a $\beta _{i}$-demicontractive operator, $A_{i}:\mathcal{H}\to \mathcal{K}_{i}$ be a bounded linear operator, and $0<\gamma _{i}<\frac{1-\beta _{i}}{\|A_{i}\|^{2}}$ for $i=1, 2,\ldots ,p$. Define a functional $r:\mathcal{H}\to \mathbb{R}$ by

$$ r(x)=\sum_{i=1}^{p}\omega _{i} \bigl[\gamma _{i}\bigl(1-\beta _{i}-\gamma _{i} \Vert A_{i} \Vert ^{2}\bigr) \bigl\Vert (I_{i}-T_{i})A_{i}x \bigr\Vert ^{2}+\alpha _{i} \Vert V_{i}x-U_{i}V_{i}x \Vert ^{2} \bigr],\quad \textit{for } x\in H, $$

(3.2)

where $V_{i}=I-\gamma _{i}A_{i}^{*}(I_{i}-T_{i})A_{i}$ for $i=1, 2,\ldots ,p$. Then, for $x\in \mathcal{H}$ and $z\in \Gamma$, we have

$$ \Vert Sx-z \Vert ^{2} \leq \Vert x-z \Vert ^{2}-r(x). $$

(3.3)

Remark 3.4

In Lemma 3.3, we observe that $r(x)\geq 0$ for all $x\in \mathcal{H}$. Therefore, the operator S is quasi-nonexpansive.

Lemma 3.5

If $z_{n}:=x_{n}+\vartheta _{n}(x_{n}-x_{n-1})$ where $0\leq \vartheta _{n}<1$ for all $n\in \mathbb{N}$, then, for $z\in \mathcal{H}$,

$$ \Vert z_{n}-z \Vert ^{2}\leq \Vert x_{n}-z \Vert ^{2}+\vartheta _{n} \bigl( \Vert x_{n}-z \Vert ^{2}- \Vert x_{n-1}-z \Vert ^{2} \bigr)+2\vartheta _{n} \Vert x_{n}-x_{n-1} \Vert ^{2}. $$

Proof

Using the identity $2\langle a,b \rangle =\|a\|^{2}+\|b\|^{2}-\|a-b\|^{2}$, we have

$$\begin{aligned} \Vert z_{n}-z \Vert ^{2}&= \bigl\Vert x_{n}-z+\vartheta _{n}(x_{n}-x_{n-1}) \bigr\Vert ^{2} \\ &= \Vert x_{n}-z \Vert ^{2}+2\vartheta _{n} \langle x_{n}-z,x_{n}-x_{n-1} \rangle +\vartheta _{n}^{2} \Vert x_{n}-x_{n-1} \Vert ^{2} \\ &= \Vert x_{n}-z \Vert ^{2}+\vartheta _{n} \bigl( \Vert x_{n}-z \Vert ^{2}+ \Vert x_{n}-x_{n-1} \Vert ^{2}- \Vert x_{n-1}-z \Vert ^{2} \bigr)+\vartheta _{n}^{2} \Vert x_{n}-x_{n-1} \Vert ^{2} \\ &= \Vert x_{n}-z \Vert ^{2}+\vartheta _{n} \bigl( \Vert x_{n}-z \Vert ^{2}- \Vert x_{n-1}-p \Vert ^{2} \bigr)+\vartheta _{n}(1+ \vartheta _{n}) \Vert x_{n}-x_{n-1} \Vert ^{2} \\ &\leq \Vert x_{n}-z \Vert ^{2}+\vartheta _{n} \bigl( \Vert x_{n}-z \Vert ^{2}- \Vert x_{n-1}-z \Vert ^{2} \bigr)+2\vartheta _{n} \Vert x_{n}-x_{n-1} \Vert ^{2}. \end{aligned}$$

Hence, we obtain the desired result. □

3.1 Inertial Krasnosel’skiĭ–Mann algorithm

Algorithm 3.6

(iKMA: Inertial Krasnosel’skiĭ–Mann algorithm)

Let $\vartheta _{n}\in [0,\vartheta ]$ with $\vartheta \in [0,1)$, $\{s_{n}\}$ is a sequence in $(0,1]$, and $\omega _{i}\in (0,1)$ with $\sum_{i=1}^{p}\omega _{i}=1$. Set

$$ \textstyle\begin{cases} x_{0},x_{1}\in \mathcal{H}, \\ z_{n}=x_{n}+\vartheta _{n}(x_{n}-x_{n-1}), \\ x_{n+1}=(1-s_{n})z_{n}+s_{n}\sum_{i=1}^{p}\omega _{i}U_{i}(I- \gamma _{i}A_{i}^{*}(I_{i}-T_{i})A_{i})z_{n}, \quad \text{for } n\in \mathbb{N}. \end{cases} $$

Theorem 3.7

Let $U_{i}:\mathcal{H}\to \mathcal{H}$ be an $\alpha _{i}$-strongly quasi-nonexpansive operator, $T_{i}:\mathcal{K}_{i}\to \mathcal{K}_{i}$ be a $\beta _{i}$-demicontractive operator, $A_{i}:\mathcal{H}\to \mathcal{K}_{i}$ be a bounded linear operator, and $0<\gamma _{i}<\frac{1-\beta _{i}}{\|A_{i}\|^{2}}$ for $i=1, 2,\ldots ,p$. Assume that $I-U_{i}$, $I_{i}-T_{i}$ are demiclosed at 0 for all $i=1, 2,\ldots ,p$, and $\{s_{n}\}$ is a sequence in $[a,1]$ for some $a>0$. Then the sequence $\{x_{n}\}$ generated by Algorithm 3.6converges weakly to a point in Γ, provide that sequence $\{\vartheta _{n}\}$ is chosen in $[0,\vartheta ]$ with $\vartheta \in [0,1)$ such that

$$ \sum_{n=1}^{\infty }\vartheta _{n} \Vert x_{n}-x_{n-1} \Vert ^{2}< \infty . $$

(3.4)

Proof

Let $z\in \Gamma$. Combining Lemma 3.5, we have

$$\begin{aligned} & \Vert x_{n+1}-z \Vert ^{2} \\ &\quad = \bigl\Vert (1-s_{n}) (z_{n}-z)+s_{n}(Sz_{n}-z) \bigr\Vert ^{2} \\ &\quad \leq (1-s_{n}) \Vert z_{n}-z \Vert ^{2}+ s_{n} \Vert Sz_{n}-z \Vert ^{2} \\ &\quad \leq (1-s_{n}) \Vert z_{n}-z \Vert ^{2}+ s_{n}\bigl( \Vert z_{n}-z \Vert ^{2}-r(z_{n})\bigr) \quad \bigl(\text{by (3.3)} \bigr) \\ &\quad = \Vert z_{n}-z \Vert ^{2}- s_{n}r(z_{n}) \\ &\quad \leq \Vert x_{n}-z \Vert ^{2}+ \vartheta _{n} \bigl( \Vert x_{n}-z \Vert ^{2}- \Vert x_{n-1}-z \Vert ^{2} \bigr)+2 \vartheta _{n} \Vert x_{n}-x_{n-1} \Vert ^{2}-s_{n}r(z_{n}) \end{aligned}$$

(3.5)

$$\begin{aligned} &\quad \leq \Vert x_{n}-z \Vert ^{2}+ \vartheta _{n} \bigl( \Vert x_{n}-z \Vert ^{2}- \Vert x_{n-1}-z \Vert ^{2} \bigr)+2 \vartheta _{n} \Vert x_{n}-x_{n-1} \Vert ^{2}. \end{aligned}$$

(3.6)

Applying Lemma 2.5 to (3.6), we conclude that the sequence $\{\|x_{n}-z\|\}$ is convergent. The condition (3.4) implies

$$ \Vert z_{n}-x_{n} \Vert ^{2}= \vartheta _{n}^{2} \Vert x_{n}-x_{n-1} \Vert ^{2}\leq \vartheta _{n} \Vert x_{n}-x_{n-1} \Vert ^{2}\to 0,\quad \text{as } n\to \infty . $$

(3.7)

It follows from the assumption on parameters and (3.5) that

$$\begin{aligned} 0&\leq s_{n}r(z_{n}) \\ &\leq \Vert x_{n}-z \Vert ^{2}- \Vert x_{n+1}-z \Vert ^{2}+ \vartheta _{n} \bigl( \Vert x_{n}-z \Vert ^{2}- \Vert x_{n-1}-z \Vert ^{2} \bigr) \\ &\quad{}+2\vartheta _{n} \Vert x_{n}-x_{n-1} \Vert ^{2},\quad \text{for all } n\in \mathbb{N}. \end{aligned}$$

(3.8)

Letting $n\to \infty$ in (3.8), and observing the assumption $s_{n}\geq a$ for all $n\in \mathbb{N}$, we have $r(z_{n})\to 0$. Since the coefficients in the finite sum (3.2) are all positive, we obtain

$$ \lim_{n\to \infty } \bigl\Vert (I_{i}-T_{i})A_{i}z_{n} \bigr\Vert =\lim_{n\to \infty } \bigl\Vert (I-U_{i})V_{i}z_{n} \bigr\Vert =0, \quad \forall i=1, 2,\ldots ,p. $$

(3.9)

For any subsequence $\{x_{n_{k}}\}$ of $\{x_{n}\}$ which converges weakly to x̃. By (3.7), the subsequence $\{z_{n_{k}}\}$ of $\{z_{n}\}$ also converges weakly to x̃. Then $A_{i}z_{n_{k}}\rightharpoonup A_{i}\tilde{x}$ for all $i=1, 2,\ldots ,p$. Hence, using the demiclosedness of $I-U_{i}$ and $I_{i}-T_{i}$ for all $i=1, 2,\ldots ,p$ in (3.9), we conclude that $\omega _{w}(x_{n})\subset \Gamma$. It follows that $\{x_{n}\}$ converges weakly to a point in Γ by Lemma 2.4. □

Remark 3.8

(a) Given $\vartheta \in [0,1)$, and $\{\varepsilon _{n}\}$ is any positive sequence such that $\sum_{n=1}^{\infty }\varepsilon _{n}<+\infty$. The value of $\vartheta _{n}$ can be chosen from $[0,\bar{\vartheta _{n}}]$ where

$$ \bar{\vartheta _{n}}= \textstyle\begin{cases} \min \{\frac{\varepsilon _{n}}{ \Vert x_{n}-x_{n-1} \Vert ^{2}},\vartheta \},&\text{if } x_{n}\neq x_{n-1}; \\ \vartheta ,&\text{otherwise}. \end{cases} $$

(b) In Theorem 3.7, the parameter $s_{n}$ is a relax condition to the classical Krasnosel’skiĭ–Mann algorithm (see, e.g. [3, Theorem 5.15]). When $s_{n}\equiv 1$, the Algorithm 3.6 turns to the Picard iteration.

3.1.1 Strong convergence: inertial NC-viscosity-type algorithm

Let f be a contraction on $\mathcal{H}$. The viscosity approximation method proposed by Moudafi [22] generates a strongly convergent sequence:

$$ \textstyle\begin{cases} x_{0}\in \mathcal{H}, \\ x_{n+1}=t_{n}f(x_{n})+(1-t_{n})Tx_{n} \quad \text{for } n\in \mathbb{N}, \end{cases} $$

which converges strongly to a fixed point $x^{*}$ of T. In [34], Xu further proved that the above $x^{*}$ also satisfies the following variational inequality:

$$ \bigl\langle f\bigl(x^{*}\bigr)-x^{*}, x-x^{*} \bigr\rangle \leq 0,\quad \forall x\in \operatorname{Fix}(T), $$

provided that $\{t_{n}\}$ fulfills certain conditions.

Recall that a sequence of mappings $\{f_{n}\}$ from $\mathcal{H}$ into $\mathcal{H}$ is called a nearly contractive mappings with sequence $\{(\kappa _{n}, a_{n})\}$ in $[0,1)\times [0,\infty )$ [18, 27, 28] if $a_{n}\to 0$, and for any $x,y\in \mathcal{H}$ and $n\in \mathbb{N}$, we have

$$ \bigl\Vert f_{n}(x)-f_{n}(y) \bigr\Vert \leq \kappa _{n} \Vert x-y \Vert +a_{n}. $$

Here, we give two examples of nearly contractive mappings. Let $\mathcal{H}=\mathbb{R}$, a sequence of mappings $\{f_{n}\}$ defined by

$$ f_{n}(x)= \textstyle\begin{cases} \frac{\sin x}{n+1},&x\leq 0, \\ \frac{2}{n+1}, &x> 0. \end{cases} $$

Then it can be verified that $|f_{n}(x)-f_{n}(y)|\leq \frac{1}{n+1}|x-y|+ \frac{3}{n+1}$, for all $x,y\in \mathcal{H}$, $n\in \mathbb{N}$. Also, if $f_{n}\equiv f$ for all n, where f is a contraction on $\mathcal{H}$, then $f_{n}$ is a nearly contractive mappings with sequences $\kappa _{n}\equiv \kappa$, $a_{n}\equiv 0$.

Algorithm 3.9

(iNCVA: Inertial NC-Viscosity-type algorithm)

Let $\{t_{n}\}$, $\{s_{n}\}$ be two sequences in $(0,1)$, $\vartheta _{n}\in [0,\vartheta ]$ with $\vartheta \in [0,1)$, and $\{f_{n}\}$ be a nearly contractive mappings with $\{(\kappa _{n}, a_{n})\}$. Set

$$ \textstyle\begin{cases} x_{0},x_{1}\in \mathcal{H}, \\ z_{n}=x_{n}+\vartheta _{n}(x_{n}-x_{n-1}), \\ x_{n+1}=(1-s_{n})z_{n}+s_{n} (t_{n}f_{n}(z_{n})\\ \hphantom{x_{n+1}=}{}+(1-t_{n})\sum_{i=1}^{p} \omega _{i}U_{i}(I-\gamma _{i}A_{i}^{*}(I_{i}-T_{i})A_{i})z_{n} ), \quad \text{for all } n\in \mathbb{N}. \end{cases} $$

Lemma 3.10

Let $U_{i}:\mathcal{H}\to \mathcal{H}$ be an $\alpha _{i}$-strongly quasi-nonexpansive operator, $T_{i}:\mathcal{K}_{i}\to \mathcal{K}_{i}$ be a $\beta _{i}$-demicontractive operator, $A_{i}:\mathcal{H}\to \mathcal{K}_{i}$ be a bounded linear operator, and $0<\gamma _{i}<\frac{1-\beta _{i}}{\|A_{i}\|^{2}}$ for $i=1, 2,\ldots ,p$. Given a contraction f with $\kappa \in (0,1)$ and $x^{*}=P_{\Gamma }f(x^{*})$. Assume that $I-U_{i}$ and $I_{i}-T_{i}$ are demiclosed at 0 for all i, and $\{f_{n}\}$ is a nearly contractive mappings with $\{(\kappa _{n}, a_{n})\}$ such that $\kappa _{n}\to \kappa$. Assume that the following conditions are satisfied:

• (C1) $t_{n}\in (0,1)$ such that $\lim_{n\to \infty } t_{n}=0$ and $\sum_{n=1}^{\infty } t_{n}=\infty$;

• (C2) $0<\eta \leq s_{n}\leq \xi <1$ for all $n\in \mathbb{N}$;

• (C3) $\lim_{n\to \infty } f_{n}(x^{*})=f(x^{*})$;

• (C4) $\lim_{n\to \infty }\frac{\vartheta _{n}}{t_{n}}\|x_{n}-x_{n-1} \|=0$.

Then the sequence $\{x_{n}\}$ generated by Algorithm 3.9converges strongly to $x^{*}=P_{\Gamma }f(x^{*})$.

Proof

Let $y_{n}=t_{n}f_{n}(z_{n})+(1-t_{n})Sz_{n}$, we have

$$\begin{aligned} & \bigl\Vert y_{n}-x^{*} \bigr\Vert \\ &\quad \leq t_{n} \bigl\Vert f_{n}(z_{n})-x^{*} \bigr\Vert +(1-t_{n}) \bigl\Vert Sz_{n}-x^{*} \bigr\Vert \\ &\quad \leq t_{n} \bigl( \bigl\Vert f_{n}(z_{n})-f_{n} \bigl(x^{*}\bigr) \bigr\Vert + \bigl\Vert f_{n} \bigl(x^{*}\bigr)-x^{*} \bigr\Vert \bigr)+(1-t_{n}) \bigl\Vert z_{n}-x^{*} \bigr\Vert \\ &\quad \leq t_{n}\bigl(\kappa _{n} \bigl\Vert z_{n}-x^{*} \bigr\Vert +a_{n} \bigr)+t_{n} \bigl\Vert f_{n}\bigl(x^{*} \bigr)-x^{*} \bigr\Vert +(1-t_{n}) \bigl\Vert z_{n}-x^{*} \bigr\Vert \\ &\quad \leq \bigl(1-(1-\kappa _{n})t_{n}\bigr) \bigl\Vert z_{n}-x^{*} \bigr\Vert +t_{n}\bigl( \bigl\Vert f_{n}\bigl(x^{*}\bigr)-x^{*} \bigr\Vert +a_{n}\bigr). \end{aligned}$$

Therefore,

$$\begin{aligned} & \bigl\Vert x_{n+1}-x^{*} \bigr\Vert \\ &\quad = \bigl\Vert (1-s_{n}) \bigl(z_{n}-x^{*} \bigr)+s_{n}\bigl(y_{n}-x^{*}\bigr) \bigr\Vert \\ &\quad \leq (1-s_{n}) \bigl\Vert z_{n}-x^{*} \bigr\Vert +s_{n} \bigl\Vert y_{n}-x^{*} \bigr\Vert \\ &\quad \leq (1-s_{n}) \bigl\Vert z_{n}-x^{*} \bigr\Vert +s_{n}\bigl(1-(1-\kappa _{n})t_{n} \bigr) \bigl\Vert z_{n}-x^{*} \bigr\Vert +s_{n}t_{n}\bigl( \bigl\Vert f_{n} \bigl(x^{*}\bigr)-x^{*} \bigr\Vert +a_{n}\bigr) \\ &\quad = \bigl(1-(1-\kappa _{n})s_{n}t_{n} \bigr) \bigl\Vert z_{n}-x^{*} \bigr\Vert +s_{n}t_{n}\bigl( \bigl\Vert f_{n} \bigl(x^{*}\bigr)-x^{*} \bigr\Vert +a_{n}\bigr) \\ &\quad = \bigl(1-(1-\kappa _{n})s_{n}t_{n} \bigr) \bigl\Vert z_{n}-x^{*} \bigr\Vert +(1-\kappa _{n})s_{n}t_{n} \biggl(\frac{ \Vert f_{n}(x^{*})-x^{*} \Vert +a_{n}}{1-\kappa _{n}} \biggr) \\ &\quad = \bigl(1-(1-\kappa _{n})s_{n}t_{n} \bigr) \bigl\Vert x_{n}-x^{*}+\vartheta _{n}(x_{n}-x_{n-1}) \bigr\Vert +(1-\kappa _{n})s_{n}t_{n} \biggl( \frac{ \Vert f_{n}(x^{*})-x^{*} \Vert +a_{n}}{1-\kappa _{n}} \biggr) \\ &\quad \leq \bigl(1-(1-\kappa _{n})s_{n}t_{n} \bigr) \bigl\Vert x_{n}-x^{*} \bigr\Vert +\vartheta _{n} \Vert x_{n}-x_{n-1} \Vert +(1-\kappa _{n})s_{n}t_{n} \biggl( \frac{ \Vert f_{n}(x^{*})-x^{*} \Vert +a_{n}}{1-\kappa _{n}} \biggr) \\ &\quad \leq \bigl(1-(1-\kappa _{n})s_{n}t_{n} \bigr) \bigl\Vert x_{n}-x^{*} \bigr\Vert +(1-\kappa _{n})s_{n}t_{n} \biggl(\frac{ \Vert f_{n}(x^{*})-x^{*} \Vert +a_{n}}{1-\kappa _{n}} \\ & \qquad {}+\frac{\vartheta _{n}}{(1-\kappa _{n})s_{n}t_{n}} \Vert x_{n}-x_{n-1} \Vert \biggr). \end{aligned}$$

(3.10)

Since $\lim_{n\to \infty } f_{n}(x^{*})=f(x^{*})$, $\lim_{n\to \infty }\kappa _{n}=\kappa$ and $\lim_{n\to \infty }a_{n}=0$, we conclude that the sequence $\{ \frac{\|f_{n}(x^{*})-x^{*}\|+a_{n}}{1-\kappa _{n}} \}$ is bounded. On the other hand, the conditions $(C2)$ and $(C4)$ imply the sequence $\{ \frac{\vartheta _{n}}{(1-\kappa _{n})s_{n}t_{n}}\|x_{n}-x_{n-1}\| \}$ is also bounded. Let an upper bound of

$$ \biggl\{ \frac{ \Vert f_{n}(x^{*})-x^{*} \Vert +a_{n}}{1-\kappa _{n}}+ \frac{\vartheta _{n}}{(1-\kappa _{n})s_{n}t_{n}} \Vert x_{n}-x_{n-1} \Vert \biggr\} $$

be M. Then we write (3.10) as

$$ \bigl\Vert x_{n+1}-x^{*} \bigr\Vert \leq \max \bigl\{ \bigl\Vert x_{n}-x^{*} \bigr\Vert ,M\bigr\} , $$

by induction, we have

$$ \bigl\Vert x_{n+1}-x^{*} \bigr\Vert \leq \max \bigl\{ \bigl\Vert x_{1}-x^{*} \bigr\Vert ,M\bigr\} . $$

Hence, $\{\|x_{n}-x^{*}\|\}$ is bounded, so is $\{\|z_{n}-x^{*}\|\}$ and $\{\|y_{n}-x^{*}\|\}$. Also,

$$\begin{aligned} \bigl\Vert f_{n}(z_{n}) \bigr\Vert &\leq \bigl\Vert f_{n}(z_{n})-f_{n}\bigl(x^{*}\bigr) \bigr\Vert + \bigl\Vert f_{n}\bigl(x^{*}\bigr) \bigr\Vert \\ &\leq \kappa _{n} \bigl\Vert z_{n}-x^{*} \bigr\Vert +a_{n}+ \bigl\Vert f_{n}\bigl(x^{*} \bigr) \bigr\Vert . \end{aligned}$$

It follows that $\{f_{n}(z_{n})\}$ is bounded. From the inequality

$$ \langle u,v \rangle \leq \Vert u \Vert \Vert v \Vert \leq 1/2\bigl( \Vert u \Vert ^{2}+ \Vert v \Vert ^{2}\bigr), $$

we have

$$\begin{aligned} \bigl\Vert y_{n}-x^{*} \bigr\Vert ^{2}&= \bigl\Vert t_{n}\bigl(f_{n}(z_{n})-x^{*} \bigr)+(1-t_{n}) \bigl(Sz_{n}-x^{*}\bigr) \bigr\Vert ^{2} \\ & = t_{n} \bigl\langle f_{n}(z_{n})-x^{*},y_{n}-x^{*} \bigr\rangle +(1-t_{n}) \bigl\langle Sz_{n}-x^{*},y_{n}-x^{*} \bigr\rangle \\ & = t_{n} \bigl( \bigl\langle f_{n}(z_{n})-f_{n} \bigl(x^{*}\bigr), y_{n}-x^{*} \bigr\rangle + \bigl\langle f_{n}\bigl(x^{*}\bigr)-f\bigl(x^{*}\bigr), y_{n}-x^{*} \bigr\rangle \bigr) \\ &\quad{}+t_{n} \bigl\langle f\bigl(x^{*} \bigr)-x^{*}, y_{n}-x^{*} \bigr\rangle +(1-t_{n}) \bigl\langle Sz_{n}-x^{*},y_{n}-x^{*} \bigr\rangle \\ & \leq t_{n} \bigl( \bigl\Vert f_{n}(z_{n})-f_{n} \bigl(x^{*}\bigr) \bigr\Vert + \bigl\Vert f_{n} \bigl(x^{*}\bigr)-f\bigl(x^{*}\bigr) \bigr\Vert \bigr) \bigl\Vert y_{n}-x^{*} \bigr\Vert \\ &\quad{}+ t_{n} \bigl\langle f\bigl(x^{*} \bigr)-x^{*}, y_{n}-x^{*} \bigr\rangle +(1-t_{n}) \bigl\Vert Sz_{n}-x^{*} \bigr\Vert \cdot \bigl\Vert y_{n}-x^{*} \bigr\Vert \\ & \leq t_{n} \bigl[\bigl(\kappa _{n} \bigl\Vert z_{n}-x^{*} \bigr\Vert +a_{n}\bigr)+ \bigl\Vert f_{n}\bigl(x^{*}\bigr)-f\bigl(x^{*}\bigr) \bigr\Vert \bigr] \bigl\Vert y_{n}-x^{*} \bigr\Vert \\ &\quad{}+ t_{n} \bigl\langle f\bigl(x^{*} \bigr)-x^{*}, y_{n}-x^{*} \bigr\rangle +(1-t_{n}) \bigl\Vert Sz_{n}-x^{*} \bigr\Vert \cdot \bigl\Vert y_{n}-x^{*} \bigr\Vert \\ &\leq \frac{t_{n}\kappa _{n}}{2} \bigl( \bigl\Vert z_{n}-x^{*} \bigr\Vert ^{2}+ \bigl\Vert y_{n}-x^{*} \bigr\Vert ^{2} \bigr)+\frac{1-t_{n}}{2} \bigl( \bigl\Vert Sz_{n}-x^{*} \bigr\Vert ^{2} + \bigl\Vert y_{n}-x^{*} \bigr\Vert ^{2} \bigr) \\ &\quad {} + t_{n} \bigl\langle f\bigl(x^{*} \bigr)-x^{*}, y_{n}-x^{*} \bigr\rangle +t_{n} \bigl(a_{n}+ \bigl\Vert f_{n} \bigl(x^{*}\bigr)-f\bigl(x^{*}\bigr) \bigr\Vert \bigr) \bigl\Vert y_{n}-x^{*} \bigr\Vert \\ & \leq \frac{t_{n}\kappa _{n}}{2} \bigl\Vert z_{n}-x^{*} \bigr\Vert ^{2}+\frac{1}{2} \bigl\Vert y_{n}-x^{*} \bigr\Vert ^{2}+ t_{n} \bigl\langle f\bigl(x^{*} \bigr)-x^{*}, y_{n}-x^{*} \bigr\rangle \\ &\quad{}+t_{n} \bigl(a_{n}+ \bigl\Vert f_{n} \bigl(x^{*}\bigr)-f\bigl(x^{*}\bigr) \bigr\Vert \bigr) \bigl\Vert y_{n}-x^{*} \bigr\Vert + \frac{1-t_{n}}{2} \bigl\Vert Sz_{n}-x^{*} \bigr\Vert ^{2}. \end{aligned}$$

This implies that

$$\begin{aligned} \bigl\Vert y_{n}-x^{*} \bigr\Vert ^{2} &\leq t_{n}\kappa _{n} \bigl\Vert z_{n}-x^{*} \bigr\Vert ^{2}+2t_{n} \bigl(a_{n}+ \bigl\Vert f_{n}\bigl(x^{*}\bigr)-f\bigl(x^{*}\bigr) \bigr\Vert \bigr) \bigl\Vert y_{n}-x^{*} \bigr\Vert \\ &\quad{}+2t_{n} \bigl\langle f\bigl(x^{*} \bigr)-x^{*}, y_{n}-x^{*} \bigr\rangle +(1-t_{n}) \bigl\Vert Sz_{n}-x^{*} \bigr\Vert ^{2}. \end{aligned}$$

Then, together with the inequality

$$ \bigl\Vert Sz_{n}-x^{*} \bigr\Vert ^{2}\leq \bigl\Vert z_{n}-x^{*} \bigr\Vert ^{2}-r(z_{n}), $$

we have

$$\begin{aligned} \bigl\Vert y_{n}-x^{*} \bigr\Vert ^{2} &\leq t_{n}\kappa _{n} \bigl\Vert z_{n}-x^{*} \bigr\Vert ^{2}+2t_{n} \bigl(a_{n}+ \bigl\Vert f_{n}\bigl(x^{*}\bigr)-f\bigl(x^{*}\bigr) \bigr\Vert \bigr) \bigl\Vert y_{n}-x^{*} \bigr\Vert \\ &\quad{}+ 2t_{n} \bigl\langle f\bigl(x^{*} \bigr)-x^{*}, y_{n}-x^{*} \bigr\rangle +(1-t_{n}) \bigl\Vert z_{n}-x^{*} \bigr\Vert ^{2}- (1-t_{n})r(z_{n}) \\ &\leq \bigl[1-(1-\kappa _{n})t_{n} \bigr] \bigl\Vert z_{n}-x^{*} \bigr\Vert ^{2}+2t_{n} \bigl(a_{n}+ \bigl\Vert f_{n}\bigl(x^{*}\bigr)-f \bigl(x^{*}\bigr) \bigr\Vert \bigr) \bigl\Vert y_{n}-x^{*} \bigr\Vert \\ &\quad{}+ 2t_{n} \bigl\langle f\bigl(x^{*} \bigr)-x^{*}, y_{n}-x^{*} \bigr\rangle -(1-t_{n})r(z_{n}). \end{aligned}$$

Hence,

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2}&= \bigl\Vert (1-s_{n}) \bigl(z_{n}-x^{*} \bigr)+s_{n}\bigl(y_{n}-x^{*}\bigr) \bigr\Vert ^{2} \\ &= (1-s_{n}) \bigl\Vert z_{n}-x^{*} \bigr\Vert ^{2}+s_{n} \bigl\Vert y_{n}-x^{*} \bigr\Vert ^{2}-s_{n}(1-s_{n}) \Vert z_{n}-y_{n} \Vert ^{2} \\ &\leq (1-s_{n}) \bigl\Vert z_{n}-x^{*} \bigr\Vert ^{2}-s_{n}(1-s_{n}) \Vert z_{n}-y_{n} \Vert ^{2} \\ &\quad{}+s_{n} \bigl[1-(1-\kappa _{n})t_{n} \bigr] \bigl\Vert z_{n}-x^{*} \bigr\Vert ^{2}+2s_{n}t_{n} \bigl\langle f \bigl(x^{*}\bigr)-x^{*}, y_{n}-x^{*} \bigr\rangle \\ &\quad{}+2s_{n}t_{n} \bigl(a_{n}+ \bigl\Vert f_{n}\bigl(x^{*}\bigr)-f\bigl(x^{*}\bigr) \bigr\Vert \bigr) \bigl\Vert y_{n}-x^{*} \bigr\Vert -s_{n}(1-t_{n})r(z_{n}) \\ &= \bigl[1-(1-\kappa _{n})s_{n}t_{n} \bigr] \bigl\Vert z_{n}-x^{*} \bigr\Vert ^{2}+ 2s_{n}t_{n} \bigl\langle f\bigl(x^{*} \bigr)-x^{*}, y_{n}-x^{*} \bigr\rangle \\ &\quad{}+2s_{n}t_{n} \bigl(a_{n}+ \bigl\Vert f_{n}\bigl(x^{*}\bigr)-f\bigl(x^{*}\bigr) \bigr\Vert \bigr) \bigl\Vert y_{n}-x^{*} \bigr\Vert -s_{n}(1-s_{n}) \Vert z_{n}-y_{n} \Vert ^{2} \\ &\quad{}-s_{n}(1-t_{n})r(z_{n}). \end{aligned}$$

(3.11)

Using the inequality $\|u+v\|^{2}\leq \|u\|^{2}+2\langle v,u+v\rangle$, we get

$$\begin{aligned} \bigl\Vert z_{n}-x^{*} \bigr\Vert ^{2}&= \bigl\Vert x_{n}-x^{*}+\vartheta _{n}(x_{n}-x_{n-1}) \bigr\Vert ^{2} \\ &\leq \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}+2\vartheta _{n}\bigl\langle x_{n}-x_{n-1},z_{n}-x^{*} \bigr\rangle \\ &\leq \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}+2\vartheta _{n} \Vert x_{n}-x_{n-1} \Vert \bigl\Vert z_{n}-x^{*} \bigr\Vert . \end{aligned}$$

(3.12)

Combining (3.11) and (3.12), we have

$$\begin{aligned} & \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} \\ &\quad \leq \bigl[1-(1-\kappa _{n})s_{n}t_{n} \bigr] \bigl( \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}+2 \vartheta _{n} \Vert x_{n}-x_{n-1} \Vert \bigl\Vert z_{n}-x^{*} \bigr\Vert \bigr) \\ &\qquad{}+2s_{n}t_{n} \bigl\langle f\bigl(x^{*} \bigr)-x^{*}, y_{n}-x^{*} \bigr\rangle +2s_{n}t_{n} \bigl(a_{n}+ \bigl\Vert f_{n}\bigl(x^{*}\bigr)-f\bigl(x^{*}\bigr) \bigr\Vert \bigr) \bigl\Vert y_{n}-x^{*} \bigr\Vert \\ &\qquad{}-s_{n}(1-s_{n}) \Vert z_{n}-y_{n} \Vert ^{2}-s_{n}(1-t_{n})r(z_{n}) \\ &\quad \leq \bigl[1-(1-\kappa _{n})s_{n}t_{n} \bigr] \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}+2s_{n}t_{n} \bigl\langle f \bigl(x^{*}\bigr)-x^{*}, y_{n}-x^{*} \bigr\rangle \\ &\qquad{}+2\vartheta _{n} \Vert x_{n}-x_{n-1} \Vert \bigl\Vert z_{n}-x^{*} \bigr\Vert +2s_{n}t_{n} \bigl(a_{n}+ \bigl\Vert f_{n}\bigl(x^{*}\bigr)-f\bigl(x^{*}\bigr) \bigr\Vert \bigr) \bigl\Vert y_{n}-x^{*} \bigr\Vert \\ &\qquad{}-s_{n}(1-s_{n}) \Vert z_{n}-y_{n} \Vert ^{2}-s_{n}(1-t_{n})r(z_{n}). \end{aligned}$$

(3.13)

Set $w_{n}=\|x_{n}-x^{*}\|^{2}$, $\tau _{n}=s_{n}(1-s_{n})\|z_{n}-y_{n}\|^{2}+s_{n}(1-t_{n})r(z_{n})$, and

$$\begin{aligned} u_{n}&= \frac{2}{(1-\kappa _{n})} \biggl( \bigl(a_{n}+ \bigl\Vert f_{n}\bigl(x^{*}\bigr)-f\bigl(x^{*}\bigr) \bigr\Vert \bigr) \bigl\Vert y_{n}-x^{*} \bigr\Vert + \bigl\langle f\bigl(x^{*}\bigr)-x^{*}, y_{n}-x^{*} \bigr\rangle \\ &\quad{}+ \frac{\vartheta _{n}}{s_{n}t_{n}} \Vert x_{n}-x_{n-1} \Vert \bigl\Vert z_{n}-x^{*} \bigr\Vert \biggr). \end{aligned}$$

Then we rewrite (3.13) as

$$\begin{aligned} &w_{n+1}\leq \bigl[1-(1-\kappa _{n})s_{n}t_{n} \bigr]w_{n}+(1-\kappa _{n})s_{n}t_{n}u_{n}, \end{aligned}$$

(3.14)

$$\begin{aligned} &w_{n+1}\leq w_{n}-\tau _{n}+ \sigma _{n}, \end{aligned}$$

(3.15)

where

$$\begin{aligned} \sigma _{n}&= 2s_{n}t_{n} \bigl\langle f \bigl(x^{*}\bigr)-x^{*}, y_{n}-x^{*} \bigr\rangle +2\vartheta _{n} \Vert x_{n}-x_{n-1} \Vert \bigl\Vert z_{n}-x^{*} \bigr\Vert \\ &\quad{}+2s_{n}t_{n} \bigl(a_{n}+ \bigl\Vert f_{n}\bigl(x^{*}\bigr)-f\bigl(x^{*}\bigr) \bigr\Vert \bigr) \bigl\Vert y_{n}-x^{*} \bigr\Vert . \end{aligned}$$

Since $\sum_{n=1}^{\infty }t_{n}=\infty$ and $(C2)$ holds, $\lim_{n\to \infty }\kappa _{n}=\kappa$. It follows that

$$ \sum_{n=1}^{\infty }(1-\kappa _{n})s_{n}t_{n}=\infty . $$

Because $t_{n}\in (0,1)$ and $(C4)$, we see that $\lim_{n\to \infty }\vartheta _{n}\|x_{n}-x_{n-1}\|=0$. Together with the boundedness of $\{\|z_{n}-x^{*}\|\}$, $\{\|y_{n}-x^{*}\|\}$ and $\lim_{n\to \infty }t_{n}=0$, we have $\lim_{n\to \infty }\sigma _{n}=0$.

In order to prove $\lim_{n\to \infty }w_{n}=0$, with Lemma 2.6, it remains to show that $\lim_{k\to \infty }\tau _{n_{k}}= 0$ implies $\limsup_{k\to \infty }u_{n_{k}}\leq 0$ for any subsequence of $\{n_{k}\}$ of $\{n\}$. Let $\{\tau _{n_{k}}\}$ be a subsequence of $\{\tau _{n}\}$ such that $\lim_{k\to \infty }\tau _{n_{k}}= 0$. Since $\lim_{k\to \infty } t_{n_{k}}=0$, $0<\eta \leq s_{n_{k}}\leq \xi <1$, we have

$$ \lim_{k\to \infty } \Vert z_{n_{k}}-y_{n_{k}} \Vert ^{2}=0, $$

(3.16)

and $\lim_{k\to \infty }r(z_{n_{k}})=0$, that is,

$$ \lim_{k\to \infty } \bigl\Vert (I_{i}-T_{i})A_{i}z_{n_{k}} \bigr\Vert ^{2}=\lim_{k\to \infty } \bigl\Vert (I-U_{i})V_{i}z_{n_{k}} \bigr\Vert ^{2}=0, \quad \forall i=1, 2,\ldots ,p. $$

(3.17)

Taking a subsequence $\{y_{n_{k_{j}}}\}$ of $\{y_{n_{k}}\}$ such that

$$ \limsup_{k\to \infty } \bigl\langle f\bigl(x^{*} \bigr)-x^{*}, y_{n_{k}}-x^{*} \bigr\rangle =\lim _{j\to \infty } \bigl\langle f\bigl(x^{*}\bigr)-x^{*}, y_{n_{k_{j}}}-x^{*} \bigr\rangle . $$

Since $\{y_{n}\}$ is bounded, we further assume that $\{y_{n_{k_{j}}}\}$ converges weakly to a point ỹ. It follows from (3.16) that $\{z_{n_{k_{j}}}\}$ also converges weakly to the same point ỹ. Due to (3.17), we get $\tilde{y}=U_{i}\tilde{y}$ and $A_{i}\tilde{y}=T_{i}A_{i}\tilde{y}$ for all $i=1, 2,\ldots ,p$ by the demiclosedness of $\{I-U_{i}\}$ and $\{I_{i}-T_{i}\}$. Then ỹ is a point in Γ. It follows, from equation (2.1), that

$$\begin{aligned} \limsup_{k\to \infty } \bigl\langle f\bigl(x^{*} \bigr)-x^{*}, y_{n_{k}}-x^{*} \bigr\rangle &=\lim _{j\to \infty } \bigl\langle f\bigl(x^{*}\bigr)-x^{*}, y_{n_{k_{j}}}-x^{*} \bigr\rangle \\ &= \bigl\langle f\bigl(x^{*}\bigr)-P_{\Gamma }f \bigl(x^{*}\bigr), \tilde{y}-P_{\Gamma }f\bigl(x^{*} \bigr) \bigr\rangle \leq 0. \end{aligned}$$

(3.18)

Together with $\lim_{n\to \infty }a_{n}=0$, $\lim_{n\to \infty }f_{n}(x^{*})=f(x^{*})$ and $\lim_{n\to \infty }\frac{\vartheta _{n}}{t_{n}}\|x_{n}-x_{n-1} \|=0$, we conclude that

$$\begin{aligned} \limsup_{k\to \infty }u_{n_{k}}=\limsup_{k\to \infty } \frac{2}{(1-\kappa _{n_{k}})} \bigl\langle f\bigl(x^{*}\bigr)-x^{*}, y_{n_{k}}-x^{*} \bigr\rangle \leq 0. \end{aligned}$$

Hence, $x_{n}\to x^{*}$ as $n\to \infty$. □

Remark 3.11

The value of $\vartheta _{n}$ can be chosen from $[0,\bar{\vartheta _{n}}]$, where

$$ \bar{\vartheta _{n}}= \textstyle\begin{cases} \min \{\frac{t_{n}\varepsilon _{n}}{ \Vert x_{n}-x_{n-1} \Vert }, \vartheta \},&\text{if } x_{n}\neq x_{n-1}; \\ \vartheta ,&\text{otherwise}, \end{cases} $$

and $\{\varepsilon _{n}\}$ is a positive sequence such that $\lim_{n\to \infty }\varepsilon _{n}=0$.

Theorem 3.12

Let $U_{i}:\mathcal{H}\to \mathcal{H}$ be an $\alpha _{i}$-strongly quasi-nonexpansive operator, $T_{i}:\mathcal{K}_{i}\to \mathcal{K}_{i}$ be a $\beta _{i}$-demicontractive operator, $A_{i}:\mathcal{H}\to \mathcal{K}_{i}$ be a bounded linear operator, and $0<\gamma _{i}<\frac{1-\beta _{i}}{\|A_{i}\|^{2}}$ for $i=1, 2,\ldots ,p$. Given a sequence $\{v_{n}\}$ in $\mathcal{H}$ strongly converges to some vector v. Assume that $I-U_{i}$ and $I_{i}-T_{i}$ are demiclosed at 0 for all i, and the following conditions are satisfied:

• (C1) $t_{n}\in (0,1)$ such that $\lim_{n\to \infty } t_{n}=0$ and $\sum_{n=1}^{\infty } t_{n}=\infty$,

• (C2) $0<\eta \leq s_{n}\leq \xi <1$ for all $n\in \mathbb{N}$,

• (C3’) $\lim_{n\to \infty }\frac{\vartheta _{n}}{t_{n}}\|x_{n}-x_{n-1} \|=0$.

Then the sequence $\{x_{n}\}$ generated by the following:

$$ \textstyle\begin{cases} x_{0}, x_{1}\in \mathcal{H}, \\ z_{n}=x_{n}+\vartheta _{n}(x_{n}-x_{n-1}), \\ x_{n+1}=(1-s_{n})z_{n}+s_{n}(t_{n}v_{n}+(1-t_{n})Sz_{n}) \quad \textit{for all } n\in \mathbb{N}, \end{cases} $$

converges strongly to $P_{\Gamma }v$. In particularly, if $v_{n}\to 0$, then the sequence $\{x_{n}\}$ converges strongly to the solution $x_{\min}$ which satisfies $\|x_{\min }\|=\min \{\|x\|:x\in \Gamma \}$.

Proof

Define contraction mappings $f(x):=v$, and $f_{n}(x):=v_{n}$. Then $\{f_{n}(x)\}$ satisfies the conditions in Lemma 3.10. Hence, the proof is done. □

Remark 3.13

When we set $f_{n}\equiv f$ for some contraction mapping, the Algorithm 3.9 becomes the viscosity algorithm. The condition $(C3)$ in Lemma 3.10 is satisfied automatically.

4 Applications

Definition 4.1

A set-valued operator $B:\mathcal{H}\to 2^{\mathcal{H}}$ is said to be

• monotone if for all $(x,u),(y,v)\in \text{graph }B$, i.e., $u\in Bx$ and $v\in By$, we have

  $$ \langle x-y, u-v \rangle \geq 0; $$

• maximal monotone if it is monotone and its graph is not properly contained in another the graph of monotone operator;

• η-strongly monotone if there exists $\eta >0$ such that for all $(x,u),(y,v)\in \text{graph }B$, we have $\langle x-y, u-v \rangle \geq \eta \|x-y\|^{2}$;

• ν-inverse strongly monotone (or ν-cocoercive) if there exists $\nu >0$ such that

  $$ \langle x-y, u-v \rangle \geq \nu \Vert u-v \Vert ^{2}, $$

  for all $(x,u),(y,v)\in \text{graph }B$.

We denote $\operatorname{zero}(B)=\{x\in \mathcal{H}\mid 0\in Bx\}$.

Definition 4.2

Let $B:\mathcal{H}\to 2^{\mathcal{H}}$ be a set-valued operator and $\lambda >0$. The resolvent of B is defined as follows:

$$ J_{\lambda B}:=(I+\lambda B)^{-1}. $$

Proposition 4.3

([3])

Let $B_{1}:\mathcal{H}\to 2^{\mathcal{H}}$ be maximal monotone and $B_{2}: \mathcal{H}\to \mathcal{H}$ is ν-inverse strongly monotone. Then, for $\lambda \in (0,2\nu )$, the forward–backward operator $J_{\lambda B_{1}}(I-\lambda B_{2})$ is $\frac{2\nu }{4\nu -\lambda }$-averaged, or equivalently,

$$\begin{aligned} & \bigl\Vert J_{\lambda B_{1}}(I-\lambda B_{2})x-J_{\lambda B_{1}}(I- \lambda B_{2})y \bigr\Vert ^{2} \\ &\quad \leq \Vert x-y \Vert ^{2}-\frac{2\nu -\lambda }{2\nu } \bigl\Vert \bigl(I-J_{\lambda B_{1}}(I- \lambda B_{2})\bigr)x-\bigl(I-J_{\lambda B_{1}}(I- \lambda B_{2})\bigr)y \bigr\Vert ^{2}, \end{aligned}$$

(4.1)

for all $x,y\in \mathcal{H}$.

Remark 4.4

As a consequence of Proposition 4.3, if the set $\operatorname{zero}(B_{1}+B_{2})$ is non-empty, then $\operatorname{zero}(B_{1}+B_{2})={\mathrm{Fix}}(J_{\lambda B_{1}}(I- \lambda B_{2}))$ and $J_{\lambda B_{1}}(I-\lambda B_{2})$ is $\frac{2\nu -\lambda }{2\nu }$-strongly quasi-nonexpansive ($-(\frac{2\nu _{2}-\lambda }{2\nu _{2}})$-demicontractive) for $\lambda \in (0,2\nu )$. Also, the forward–backward operator $U=J_{\lambda B_{1}}(I-\lambda B_{2})$ is nonexpansive, thus $I-U$ is demiclosed at zero.

We propose the multiple-set split monotone variational inclusion problem (MSSMVIP) as follows:

$$ \text{Find a point } x\in \mathcal{H}\text{ such that } 0\in \bigcap_{i=1}^{p} \bigl(f_{i}(x)+F_{i}(x) \bigr) \text{ and } 0\in \bigcap_{j=1}^{r} \bigl(g_{j}(Ax)+G_{j}(Ax) \bigr) , $$

(4.2)

where $F_{i}:\mathcal{H}\to 2^{\mathcal{H}}$, $G_{j}:\mathcal{K}\to 2^{\mathcal{K}}$ are set-valued maximal monotone operators, $f_{i} : \mathcal{H}\to \mathcal{H}$, $g_{j} : \mathcal{K}\to \mathcal{K}$ are inverse strongly monotone operators for $i=1,2,\ldots ,p$, $j=1,2,\ldots ,r$, and $A:\mathcal{H}\to \mathcal{K}$ is a bounded linear operator.

We remark that there are some cases, $f_{i}(x)+F_{i}$ may not be a maximal monotone operator, even if it is so, the resolvent $J_{\lambda (f_{i}(x)+F_{i})}$ might not be able to carry an analytic form easily.

Set $U_{i}=J_{\lambda F_{i}}(I-\lambda f_{i})$ for all $i=1,2,\ldots ,p$ and $T_{j}=J_{\lambda G_{j}}(I-\lambda g_{j})$ for all $j=1,2,\ldots ,r$, respectively. Hence, according Remark 4.4, the operator $U_{i}$ is a strongly quasi-nonexpansive and the operator $T_{j}$ is a demicontractive operator for all i, j. Also, $I-U_{i}$ and $I-T_{j}$ are demiclosed at zero. Then MSSMVIP (4.2) becomes to GSCFPP (3.1) where $\mathcal{K}_{1}=\mathcal{K}_{2}=\cdots =\mathcal{K}_{r}= \mathcal{K}$ and $A_{1}=A_{2}=\cdots =A_{r}=A$. Assume that $p=r$ and the solution set of MSSMVIP (4.2) (denoted $\Gamma _{\mathrm{M}}$) is not empty. The associated operator is

$$ S=\sum_{i=1}^{p}\omega _{i}J_{\lambda F_{i}}(I- \lambda f_{i}) \bigl(I- \gamma _{i} A^{*} \bigl(I-J_{\lambda G_{i}}(I-\lambda g_{i})\bigr)A\bigr), $$

where $\omega _{i}\in (0,1)$ with $\sum_{i=1}^{p}\omega _{i}=1$.

Theorem 4.5

Let $\mathcal{H}$ and $\mathcal{K}$ be two real Hilbert spaces and $A :\mathcal{H}\to \mathcal{K}$ be a bounded linear operator. Let $f_{i} : \mathcal{H}\to \mathcal{H}$ and $g_{j} : \mathcal{K}\to \mathcal{K}$ be $\nu _{i}$-inverse strongly monotone for all $i=1,2,\ldots ,p$ and $\mu _{j}$-inverse strongly monotone for all $j=1,2,\ldots ,p$ on $\mathcal{H}$ and $\mathcal{K}$, respectively. Let $\{F_{i}\}$, $\{G_{j}\}$ be two families of maximal monotone operators. Set $\mu :=\min \{\nu _{1},\nu _{2},\ldots ,\nu _{p},\mu _{1},\mu _{2}, \ldots ,\mu _{p}\}$, $\lambda \in [0,2\mu ]$, and $\gamma _{j}\in (0,\frac{2-\lambda /2\mu _{j}}{\|A\|^{2}})$ for $j=1,2,\ldots ,p$.

• (iKMA) If $\{s_{n}\}$ is a sequence in $(a,1]$ for some $a>0$, then the sequence $\{x_{n}\}$ generated by

  $$ \textstyle\begin{cases} x_{0},x_{1}\in \mathcal{H}, \\ z_{n}=x_{n}+\vartheta _{n}(x_{n}-x_{n-1}), \\ x_{n+1}=(1-s_{n})z_{n}+s_{n}Sz_{n},\quad n\in \mathbb{N}, \end{cases} $$

  converges weakly to a point in $\Gamma _{\mathrm{M}}$ provided that the sequence $\{\vartheta _{n}\}\subset [0,\vartheta ]$ with $\vartheta \in [0,1)$ satisfies the following condition:

  $$ \sum_{n=1}^{\infty }\vartheta _{n} \Vert x_{n}-x_{n-1} \Vert ^{2}< \infty . $$

• (iNCVA) Given a contraction h with $\kappa \in (0,1)$ and $x^{*}=P_{\Gamma _{\mathrm{M}}}h(x^{*})$. Suppose that $\{h_{n}\}$ is a sequence of nearly contractive mappings with $\{(\kappa _{n}, a_{n})\}$ such that $\kappa _{n}\to \kappa$, and the following conditions are satisfied:

  • (C1) $t_{n}\in (0,1)$ such that $\lim_{n\to \infty } t_{n}=0$ and $\sum_{n=1}^{\infty } t_{n}=\infty$,

  • (C2) $0<\eta \leq s_{n}\leq \xi <1$ for all $n\in \mathbb{N}$,

  • (C3) $\lim_{n\to \infty } h_{n}(x^{*})=h(x^{*})$,

  • (C4) $\lim_{n\to \infty }\frac{\vartheta _{n}}{t_{n}}\|x_{n}-x_{n-1} \|=0$.

  Then the sequence $\{x_{n}\}$ generated by

  $$ \textstyle\begin{cases} x_{0},x_{1}\in \mathcal{H}, \\ z_{n}=x_{n}+\vartheta _{n}(x_{n}-x_{n-1}), \\ x_{n+1}=(1-s_{n})z_{n}+s_{n}(t_{n}h_{n}(z_{n})+(1-t_{n})Sz_{n}), \quad \textit{for all } n\in \mathbb{N}, \end{cases} $$

  converges strongly to $x^{*}$.

5 Numerical experience

In this section, we utilize those results to demonstrate convergence of our algorithms for solving GSCFPP in finite dimensional Hilbert spaces. We present the behavior of these inertial-iterations in a synthetic experiment. The codes were written by MATLAB (R20013b) and run on a ASUS laptop with RAM 8 GB and Intel(R) Core(TM) i5-4200H CPU @ 2.80 GHz. We consider the following GSCFPP.

Example 5.1

Let $p=r=3$, $\mathcal{H}=\mathbb{R}^{2}$, $\mathcal{K}_{1}=\mathcal{K}_{2}=\mathbb{R}^{2}$, and $\mathcal{K}_{3}=\mathbb{R}^{3}$. The three closed balls in $\mathcal{H}$ are as follows:

$$\begin{aligned}& C_{1}=\bigl\{ \bigl(x^{1},x^{2} \bigr)^{T}\in \mathcal{H}\mid \sqrt{\bigl(x^{1}-2 \bigr)^{2}+\bigl(x^{2}-2\bigr)^{2}} \leq 5\bigr\} , \\& C_{2}=\bigl\{ \bigl(x^{1},x^{2} \bigr)^{T}\in \mathcal{H}\mid \sqrt{\bigl(x^{1}-1 \bigr)^{2}+\bigl(x^{2}-3\bigr)^{2}} \leq 4\bigr\} , \\& C_{3}=\bigl\{ \bigl(x^{1},x^{2} \bigr)^{T}\in \mathcal{H}\mid \sqrt{\bigl(x^{1}-3 \bigr)^{2}+\bigl(x^{2}-2\bigr)^{2}} \leq 4\bigr\} . \end{aligned}$$

The three sets $Q_{1}$, $Q_{2}$, $Q_{3}$ are setting as

$$\begin{aligned}& Q_{1}=\bigl\{ \bigl(y^{1},y^{2} \bigr)^{T}\in \mathcal{K}_{1}\mid -8\leq y^{1} \leq -5 \text{ and } 4\leq y^{2}\leq 7\bigr\} , \\& Q_{2}=\bigl\{ \bigl(y^{1},y^{2} \bigr)^{T}\in \mathcal{K}_{2}\mid 12\leq y^{1}\leq 15 \text{ and } -6\leq y^{2}\leq -2\bigr\} , \\& Q_{3}=\bigl\{ \bigl(y^{1},y^{2},y^{3} \bigr)^{T}\in \mathcal{K}_{3}\mid -7\leq y^{1} \leq -5,-2\leq y^{2}\leq 2 ,\text{ and } 9\leq y^{3}\leq 11 \bigr\} . \end{aligned}$$

The three matrices are

$$ A_{1}= \begin{pmatrix} 2 & -5 \\ 0 & 3 \end{pmatrix} ,\qquad A_{2}= \begin{pmatrix} 5 & 2 \\ 0 & -2 \end{pmatrix} , \quad \text{and}\quad A_{3}= \begin{pmatrix} -3 & 0 \\ 3 & -3 \\ 3 & 2 \end{pmatrix} . $$

Checking the point $(2,2)^{T}$ is in the solution set

$$ \Gamma =\Biggl\{ x=\bigl(x^{1},x^{2}\bigr)^{T}\in \mathcal{H}\Bigm| x\in \bigcap_{i=1}^{3}C_{i} \text{ and } A_{j}x\in Q_{j}\text{ for } j=1,2,3\Biggr\} . $$

The iKMA is set as

$$ \textstyle\begin{cases} x_{0},x_{1}\in \mathcal{H}, \\ z_{n}=x_{n}+\vartheta _{n}(x_{n}-x_{n-1}), \\ x_{n+1}=0.2z_{n}+0.8\sum_{i=1}^{3}\frac{1}{3}P_{C_{i}}(z_{n}- \gamma _{i}A_{i}^{T}(I-P_{Q_{i}})A_{i}z_{n}), \quad \text{for } n\in \mathbb{N}. \end{cases} $$

The iNCVA is set as

$$ \textstyle\begin{cases} x_{0},x_{1}\in \mathcal{H}, \\ z_{n}=x_{n}+\vartheta _{n}(x_{n}-x_{n-1}), \\ x_{n+1}=0.2z_{n}+0.8 [\frac{1}{n}v_{0}+(1-\frac{1}{n})\sum_{i=1}^{3} \frac{1}{3}P_{C_{i}}(z_{n}-\gamma _{i}A_{i}^{T}(I-P_{Q_{i}})A_{i}z_{n}) ], \quad \text{for all } n\in \mathbb{N}, \end{cases} $$

where $\vartheta _{n}\in [0,\vartheta ]$ with $\vartheta \in [0,1)$, and the parameters $\gamma _{j}=0.9\times 1/\|A_{j}\|^{2}$ for all $j=1, 2,3$. The initial points are chosen by $x_{0}=(0,3)^{T}$, $x_{1}=(3,2)^{T}$ and $v_{0}=(2,2)^{T}$. We present the behavior of the value of the function ϕ at each iteration, where ϕ is defined by

$$ \phi (x)=\frac{1}{2}\sum_{i=1}^{p} \frac{1}{p} \Vert x-P_{C_{i}}x \Vert ^{2}+ \frac{1}{2}\sum_{j=1}^{r} \frac{1}{r} \Vert A_{j}x-P_{Q_{j}}A_{j}x \Vert ^{2},\quad x \in \mathcal{H}. $$

The Remark 3.8 illustrates whereby to choose the parameter sequence $\{\vartheta _{n}\}$. For the Example 5.1, the parameter sequence $\{\vartheta _{n}\}$ is chosen as follows:

$$ \vartheta _{n}= \textstyle\begin{cases} \min \{\frac{1}{n^{2} \Vert x_{n}-x_{n-1} \Vert ^{2}},\vartheta \}, &\text{if } x_{n}\neq x_{n-1}; \\ \vartheta ,&\text{otherwise}, \end{cases} $$

where ϑ is a real number in $[0,1)$.

Figure 1 (a), (b) show that the performance of iKMA and iNCVA with $\vartheta =0.8$ and $\vartheta =0$ (i.e., without the inertial terms), respectively. To be properly presented, we use the semilog plotting. Figure 1 (c) demonstrates the inertial action of iKMA of each even terms.

Figure 1

(a) Behavior of $\phi (x_{n})$ $(n=1,2,\ldots ,20)$ of KMA and iKMA for Example 5.1. (b) Behavior of $\phi (x_{n})$ $(n=1,2,\ldots ,5)$ of NCVA and iNCVA for Example 5.1. (c) The graph of level curve of ϕ in Example 5.1 with sequence $\{x_{2k}\mid k=1,2,\ldots ,9\}$ which is generated by iKMA

6 Conclusion

We present weak convergence and strong convergence results with inertial method for the split common fixed point problem with multiple-sets, multiple-operators and the wide class of quasi-nonexpansive type operators. Numerical simulations show that the algorithms involving the inertial effect converge more quickly than without inertial terms.