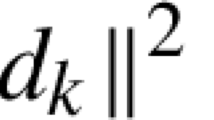1 Introduction

The absolute value equation of the type

$$ Ax+B \vert x \vert =b $$
(1.1)

was investigated in [14, 22, 25,26,27,28]. If \(\det (B)\neq 0\), then (1.1) can be reduced to the form

$$ Ax- \vert x \vert =b. $$
(1.2)

The absolute value Eq. (1.2) has also been intensively studied, e.g., see [9, 12, 13, 15,16,17, 19, 30, 33, 34]. In this paper, we propose a new generalized absolute value equation (GAVE) problem of the form

$$ \vert A \vert x- \vert B \vert \vert x \vert =b, $$
(1.3)

where \(A=(a_{ij})\in R^{n\times n}\) is a symmetric matrix, \(B=(b_{ij})\in R^{n\times n}\) is a diagonal matrix, the absolute values of matrices are defined as \(|A|=(|a_{ij}|)\), \(|B|=(|b_{ij}|)\), \(i, j=1,2,\ldots,n\), \(b\in R^{n}\) and \(|x|=(|x_{1}|,|x_{2}|,\ldots,|x_{n}|)^{T}\). As we all know, the study of absolute value equations comes from linear complementarity problem. The general linear complementarity problem [5], which subsumes many mathematical programming problems, bimatrix games, and equilibrium programming problems, can be formulated as the absolute value equations of the forms such as (1.1)–(1.3). Mangasarian [14] showed that (1.1) is NP-hard. Prolopyev [22] stated the relations of (1.1) with linear complementarity problem and mixed integer programming problem. Rohn et al. [30] gave the sufficient conditions for unique solvability of AVE (1.2) and an iterative method to solve it. Mangasarian et al. [17] gave the existence and nonexistence results of (1.2) and proved the equivalence relations between (1.2) and the generalized linear complementarity problem. Hu et al. [9] proved that (1.2) can be equivalently reformulated as a standard linear complementarity problem without any assumption. In [16] and [15], Mangasarian proposed a concave minimization optimization method and a generalized Newton method, respectively. Zhang et al. [34] presented a generalized Newton method. Noor et al. [19] gave an iterative algorithm for solving (1.2). Yong [33] proposed a smoothing Newton algorithm to solve (1.2). Saheya et al. [31] focused on numerical comparisons based on four smoothing functions for (1.2). Bello Cruz et al. [2] showed the global Q-linear convergence of the inexact semi-smooth Newton method for solving (1.2). Ke et al. [10] studied a SOR-like iteration method for solving system of (1.2). Abdallah et al. [1] reformulated (1.2) as a sequence of concave minimization problems and gave a smoothing method to solve it. Cacceta et al. [4] proposed a smoothing Newton method with global and quadratic convergence for solving (1.2). Rohn [29] proved a theorem of alternatives for equation \(|Ax|-|B||x|=b\) and gave some sufficient conditions for solvability of the equation. The current research on the methods for solving (1.1) and (1.2) is based mostly on nonlinear optimization techniques. Little attention, however, has been paid so far to the nonlinear conjugate gradient method with smaller storage capacity and faster convergence speed for solving GAVE (1.3). In this paper, we propose a modified HS conjugate gradient method to compute the solution of GAVE (1.3).

This paper is organized as follows. In Sect. 2, we provide a sufficient condition for the solution of GAVE (1.3). In Sect. 3, a modified HS conjugate gradient method for solving GAVE (1.3) is given. Under mild conditions, we prove the global convergence theorem of the given method. In Sect. 4, we present numerical results of the relevant numerical experiments to show the effectiveness and the efficiency of the proposed method.

Throughout the paper, lowercase \(x, y, \ldots \) denote vectors, \(\beta ,\varepsilon ,\ldots \) denote parameters, uppercase letters \(A, B, \ldots \) denote matrices.

2 General absolute value equation and unconstrained optimization problem

We will start by showing that (1.3) is equivalent to an unconstrained optimization problem with an objective function that is continuously differentiable. Firstly, we introduce the relevant definition from [24, 25].

Definition 2.1

Given two matrices \(E, F \in R^{n \times n}\) and \(F \geq 0\), the set of matrices

$$ \varSigma =\bigl\{ \widetilde{A} | \vert E \vert -F \leq \widetilde{A}\leq \vert E \vert +F \bigr\} $$

is called an interval matrix. Σ is called regular if ∀Ã is nonsingular.

Theorem 2.1

Suppose that \(\widetilde{\varSigma }=\{\tilde{A}||A|-F \leq \widetilde{A}\leq |A|+F \}\) is regular and \(|B| \leq F\), then (1.3) has a unique solution.

Proof

By \(x^{+} = \max \{x,0\} = \frac{|x|+x}{2}\), \(x^{-} =\min \{x,0\} = \frac{|x|-x}{2}\), we get

$$ \vert x \vert = x^{+} + x^{-},\qquad x=x^{+} - x^{-}. $$

Then (1.3) can be rewritten as

$$ x^{+}=\bigl( \vert A \vert - \vert B \vert \bigr)^{-1}\bigl( \vert A \vert + \vert B \vert \bigr)x^{-}+\bigl( \vert A \vert - \vert B \vert \bigr)^{-1}b. $$
(2.1)

From \(|B| \leq F\), we know that \(|A|-|B|, |A|+|B| \in \widetilde{\varSigma }\) and \((|A|-|B|)^{-1}\) exists. Similar to Theorem 1 in [25], by [18, 23], we know that (2.1) has a unique solution. Hence (1.3) has a unique solution. We finish the proof. □

In the remaining part of this section, we transform (1.3) to an unconstraint optimization problem. Denote

$$ f(x)=\bigl\langle { \vert A \vert x,x}\bigr\rangle -\bigl\langle { \vert B \vert \vert x \vert ,x}\bigr\rangle -2 \langle {b,x}\rangle , $$
(2.2)

where A, B are defined similarly as (1.3). \(\langle {\cdot } \rangle \) denotes the inner product of vectors, namely \(\forall x, y \in R ^{n}\)

$$ \langle {x,y} \rangle =\sum_{i=1}^{n} x_{i}y_{i}. $$

Now, we give the related notation and lemmas.

Definition 2.2

Suppose that matrix \(A \in R^{n \times n}\) is symmetric, then A is a positive definite matrix if and only if \(\langle x,Ax \rangle >0\) is set up for arbitrarily nonzero vector \(x \in R^{n}\).

In the remainder of this paper, we consider the matrices A and B such that \(|A|-|B|D\) is positive definite for any arbitrary matrix D. If A is symmetric and B, D are both diagonal matrices, then \(|A|-|B|D\) is symmetric. The diagonal matrix D is defined as \(D=\partial |x|=\operatorname{diag}(\operatorname{sign}(x))\), where \(\operatorname{diag}(x)\) denote a vector with components equal to 1, 0, −1 depending on whether the corresponding component of x is positive, zero, or negative.

Theorem 2.2

If matrix \(|A|-|B|D\) is a positive definite matrix, then x is a solution of (1.3) ⇔x is a minimum of the function \(f(x)\), where \(f(x)\) is defined as (2.2).

Proof

Case I. For arbitrary \(\alpha \in R \) and \(\nu \in R^{n}\), by Taylor’s series, we get

$$ f(x+\alpha \nu )=f(x)+\alpha \bigl\langle \nabla f(x),\nu \bigr\rangle + \frac{ \alpha ^{2}}{2} \bigl\langle \nabla ^{2} f(x)\nu ,\nu \bigr\rangle , $$

where \(\nabla f(x)=2(|A|x-|B||x|-b)\), \(\nabla ^{2}f(x)=2(|A|-|B|D)\). Let \(C=|A|-|B|D\), then C is a positive definite matrix and

$$ f(x+\alpha \nu )=f(x)+2\alpha \bigl\langle \vert A \vert x- \vert B \vert \vert x \vert -b,\nu \bigr\rangle + \alpha ^{2} \langle C \nu ,\nu \rangle . $$

Let \(g:R^{n} \rightarrow R\) be a function about α, we get

$$ g(\alpha )=f(x)+2\alpha \bigl\langle \vert A \vert x- \vert B \vert \vert x \vert -b,\nu \bigr\rangle +\alpha ^{2} \langle C \nu ,\nu \rangle , $$

then g has the minimum point with \(\langle C\nu , \nu \rangle >0\),

$$ \alpha =-\frac{ \langle \vert A \vert x- \vert B \vert \vert x \vert -b,\nu \rangle }{\langle C \nu , \nu \rangle }, $$

and

$$ g(\alpha )=f(x)-\frac{ \langle \vert A \vert x- \vert B \vert \vert x \vert -b,\nu \rangle ^{2}}{\langle C \nu ,\nu \rangle }. $$

So, we have

$$ f(x+\alpha \nu ) \leq f(x),\quad \forall \nu \neq 0. $$

The above strict inequality is impossible. Then we have

$$ \bigl\langle \vert A \vert x- \vert B \vert \vert x \vert -b,\nu \bigr\rangle =0. $$

And it follows that

$$ f(x)=f(x+\alpha \nu ). $$

If \(x^{*}\) satisfies \(|A|x^{*}-|B||x^{*}|=b\), then \(\langle |A|x^{*}-|B||x ^{*}|-b,\nu \rangle =0\) for arbitrary ν and \(f(x)\) cannot be made any smaller than \(f(x^{*})\). Then \(x^{*}\) minimizes f.

Case II. Suppose that \(x^{*}\) is the minimum point of \(f(x)\), then \(\forall \nu \in R^{n}\), \(\alpha \in R\), it follows that

$$ f\bigl(x^{*}+\alpha \nu \bigr) \geq f\bigl(x^{*}\bigr). $$

So,

$$ \bigl\langle \vert A \vert x^{*}- \vert B \vert \bigl\vert x^{*} \bigr\vert -b,\nu \bigr\rangle =0. $$

Then the above equation implies that

$$ \vert A \vert x^{*}- \vert B \vert \bigl\vert x^{*} \bigr\vert -b=0, $$

that is,

$$ \vert A \vert x^{*}- \vert B \vert \bigl\vert x^{*} \bigr\vert =b. $$

This shows that \(x^{*}\) is a solution of (1.3). Hence, this completes the proof. □

Therefore, GAVE (1.3) can be transformed into the following unconstrained optimization problem:

$$ \min_{x \in R} f(x), $$

where f is defined by formula (2.2). It is well known that nonlinear conjugate gradient methods such as Hestenes–Stiefel (HS) method [8], Fletcher–Reeves (FR) method [7], Polak–Ribiere–Polyak (PRP) method [20, 21], Dai–Yuan (DY) method [6], and other methods [3, 11, 32, 35, 36] are very efficient for large-scale smooth optimization problems due to their simplicity and low storage. Moreover, we notice that some modified HS conjugate gradient methods are more efficient to solve the unconstrained optimization problem than classical methods, see [11, 32]. In the next section, we give a modified HS conjugate gradient method for (1.3). To develop an efficient optimization method for (1.3), we also use the Armijo-type line search globalization technique [36].

3 Modified HS conjugate gradient method

In this section, we firstly propose the modified HS conjugate gradient method based on [11] with Armijo-type line search based on [36]. Then we present the global convergence of the given method under mild conditions.

Algorithm 3.1

(Modified HS Conjugate Gradient Method)

Step 0. Choose initial point \(x_{0}\in R^{n}\) and constants \(\delta _{1}, \delta _{2}, \rho \in (0,1)\), \(\varepsilon >0\). Let \(k:=0\).

Step 1. Denote \(g_{k}=\nabla f(x_{k})\). If \(\|g_{k}\| \leq \varepsilon \), stop. Otherwise, compute \(d_{k}\) by

$$ d_{k}= \textstyle\begin{cases} -g_{k},& \mbox{if }k=0, \\ - g_{k}+ \beta ^{\operatorname{NHS}}_{k} d_{k-1}-\beta ^{\operatorname{NHS}}_{k}\frac{g^{T}_{k}d_{k-1}}{ \Vert g_{k} \Vert ^{2}}g_{k}, & \mbox{if } k>0, \end{cases} $$
(3.1)

where

$$ \beta _{k}^{\operatorname{NHS}}=\frac{g_{k}^{T}(g_{k}-g_{k-1})}{ z_{k} }, \quad z_{k}=\max \bigl\{ t \Vert d_{k-1} \Vert ,d_{k-1}^{T}(g_{k}-g_{k-1}) \bigr\} . $$

Step 2. Determine \(\alpha _{k}\) by the Armijo-type line search, that is, \(\alpha _{k}=\max \{ \rho ^{j},j=0,1,2,\ldots\}\) satisfying

$$ f(x_{k}+\alpha _{k}d_{k})\leq f(x_{k})+\delta _{1} \alpha _{k} g_{k}^{T}d _{k}-\delta _{2} \alpha _{k}^{2} \Vert d_{k} \Vert ^{2}. $$
(3.2)

Step 3. Set \(x_{k+1}=x_{k}+\alpha _{k}d_{k}\), \(k:=k+1\). Go to Step 1.

To get the convergence of Algorithm 3.1, we only need the following mild assumption.

Assumption 3.1

The level set \(\varOmega =\{x|f(x)\leq f(x _{0})\}\) is bounded.

Lemma 3.1

Let Assumption 3.1 hold, \(g(x)=2(|A|x-|B||x|-b)\), then \(g(x)\) satisfies the Lipschitz condition, that is,

$$ \bigl\Vert g(x)-g(y) \bigr\Vert \leq L \Vert x-y \Vert , $$

where \(\forall x,y\in N\), N is a neighborhood of Ω and \(L>0\) is a constant.

Proof

By \(g(x)=2(|A|x-|B||x|-b)\), we get

$$\begin{aligned} \bigl\Vert g(x)-g(y) \bigr\Vert &=2 \bigl\Vert \vert A \vert x- \vert B \vert \vert x \vert -b- \vert A \vert y+ \vert B \vert \vert y \vert +b \bigr\Vert \\ & =2 \bigl\Vert \vert A \vert x- \vert B \vert \vert x \vert - \vert A \vert y+ \vert B \vert \vert y \vert \bigr\Vert \\ & =2 \bigl\Vert \vert A \vert (x-y)- \vert B \vert \bigl( \vert x \vert - \vert y \vert \bigr) \bigr\Vert \\ & \leq 2 \bigl\Vert \vert A \vert (x-y) \bigr\Vert +2 \bigl\Vert \vert B \vert \bigl( \vert x \vert - \vert y \vert \bigr) \bigr\Vert \\ &\leq 2\bigl(\vert \!\Vert A\vert \!\Vert + \vert \!\Vert B\vert \!\Vert \bigr) \bigl( \Vert x-y \Vert \bigr)=L \Vert x-y \Vert . \end{aligned}$$

Denote \(L=2(|\!|\!|A|\!|\!|+|\!|\!|B|\!|\!|)\), we get this lemma. □

Remark 3.1

On account of the descent property of \(\{f(x_{k})\}\), the sequence \(\{x_{k}\}\) generated by Algorithm 3.1 is contained in Ω. Besides, it follows from Assumption 3.1 that there exists a constant \(\eta >0\) such that

$$ \bigl\Vert g(x) \bigr\Vert \leq \eta ,\quad \forall x \in \varOmega . $$

Lemma 3.2

([11])

Let \(\{d_{k}\}\) be computed by Algorithm 3.1, then

$$ g_{k}^{T}d_{k}=- \Vert g_{k} \Vert ^{2} $$
(3.3)

holds for arbitrary \(k>0\).

From Assumption 3.1, Lemma 3.1, and Lemma 3.2, we can get the following lemma.

Lemma 3.3

([11])

Suppose that Assumption 3.1 holds. Let \(\{d_{k}\}\) and \(\{x_{k}\}\) be generated by Algorithm 3.1, then there exists a positive constant c such that

$$ \Vert d_{k} \Vert \leq c,\quad \forall k>0. $$
(3.4)

Based on the above assumptions and lemmas, we now give the global convergence theorem of Algorithm 3.1.

Theorem 3.1

Suppose that Assumption 3.1 holds. If \(\{x_{k}\}\) is generated by Algorithm 3.1, then

$$ \liminf_{k\rightarrow \infty } \Vert g_{k} \Vert =0. $$
(3.5)

Proof

Now, assume that this theorem is not true, namely (3.5) does not hold, then there exists a positive constant \(\tau >0\) such that

$$ \Vert g_{k} \Vert \geq \tau ,\quad \forall k\geq 0. $$
(3.6)

From Assumption 3.1 and (3.2), it follows

$$ \sum_{k\geq 0}\bigl(-\delta _{1} \alpha _{k} g_{k}^{T}d_{k}+\delta _{2} \alpha _{k}^{2} \Vert d_{k} \Vert ^{2}\bigr)< \infty , $$

this with (3.3) indicates

$$ \sum_{k\geq 0} \alpha _{k}^{2} \Vert d_{k} \Vert ^{2}< \infty , $$

and

$$ -\sum_{k\geq 0}\alpha _{k} g_{k}^{T}d_{k}= \sum _{k\geq 0} \alpha _{k} \Vert g_{k} \Vert ^{2} < \infty , $$

then we obtain

$$ \lim_{k\rightarrow \infty }\alpha _{k} \Vert g_{k} \Vert ^{2}=0. $$
(3.7)

If \(\liminf_{k \to \infty } {\alpha }_{k} > 0\), then we have \(\liminf_{k\rightarrow \infty } \| g_{k}\|=0\) by (3.7), which contradicts (3.6).

If \(\liminf_{k\rightarrow \infty } \alpha _{k}=0\), then there exists a set \(K\in N\) such that

$$ \lim_{k\in K, k\rightarrow \infty }\alpha _{k}=0. $$
(3.8)

The Armijo-type line search rule suggests that \(\rho ^{-1}\alpha _{k}\) does not satisfy line search condition (3.2) for k sufficiently enough, namely

$$\begin{aligned} f\bigl(x_{k}+\rho ^{-1} \alpha _{k}d_{k} \bigr)-f(x_{k}) >& \delta _{1}\rho ^{-1} \alpha _{k} g_{k}^{T}d_{k}-\delta _{2} \rho ^{-2}\alpha _{k}^{2} \Vert d_{k} \Vert ^{2} \\ =& -\delta _{1}\rho ^{-1} \alpha _{k} \Vert g_{k} \Vert ^{2}-\delta _{2} \rho ^{-2}\alpha _{k}^{2} \Vert d_{k} \Vert ^{2}. \end{aligned}$$
(3.9)

By the mean value theorem and Lemma 3.1, there exists \(\xi _{k} \in (0,1)\) such that

$$\begin{aligned} f\bigl(x_{k}+\rho ^{-1} \alpha _{k}d_{k} \bigr)-f(x_{k}) &=\rho ^{-1} \alpha _{k} g\bigl(x _{k}+\xi _{k}\rho ^{-1} \alpha _{k}d_{k}\bigr)^{T}d_{k} \\ &=\rho ^{-1} \alpha _{k} g_{k}^{T}d_{k}+ \rho ^{-1} \alpha _{k} \bigl[g\bigl(x_{k}+ \xi _{k}\rho ^{-1} \alpha _{k}d_{k} \bigr)-g(x_{k})\bigr]^{T}d_{k} \\ &\leq \rho ^{-1} \alpha _{k} g_{k}^{T}d_{k} + L\rho ^{-2}\alpha _{k}^{2} \Vert d_{k} \Vert ^{2} \\ &=-\rho ^{-1} \alpha _{k} \Vert g_{k} \Vert ^{2}+L\rho ^{-2}\alpha _{k}^{2} \Vert d _{k} \Vert ^{2}. \end{aligned}$$

This together with Lemma 3.3 and (3.9) implies

$$ \Vert g_{k} \Vert ^{2} < \frac{L+\delta _{2}}{(1-\delta _{1})\rho }c^{2} \alpha _{k}. $$

Then we obtain \(\liminf_{k\in K, k\rightarrow \infty } \|g_{k}\|=0\) from (3.8), which also contradicts (3.6). The proof is completed. □

Remark 3.2

In Step 2 of Algorithm 3.1, we adopt the Armijo-type line search [36]. The following line searches are also well defined in Algorithm 3.1 since the search directions are descent. The Wolfe line search [6]

$$ f(x_{k}+\alpha _{k}d_{k})\leq f(x_{k})+\rho \alpha _{k} g_{k}^{T}d_{k} $$

and

$$ g_{k+1}^{T}d_{k}\geq \sigma g_{k}^{T}d_{k},\quad \rho \in \biggl(0,\frac{1}{2}\biggr), \sigma \in (\rho ,1), $$

and the standard Armijo line search [35]

$$ f(x_{k}+\alpha _{k}d_{k})\leq f(x_{k})+\rho _{1} \alpha _{k} g_{k}^{T}d _{k},\quad \rho _{1} \in (0,1). $$
(3.10)

4 Numerical experiments

In this section, we present numerical results to show the efficiency of the modified HS conjugate gradient method (Algorithm 3.1). The numerical testing was carried out on a Lenovo PC with the use of Matlab. The following tables and figures list the numerical results for the given GAVE problems, where we set \(\varepsilon =10^{-6}\), \(\rho =0.6\), \(\rho _{1}=0.4\), \(\delta _{1}=0.4\), \(\delta _{2}=0.4\), \(t=2\).

Example 4.1

Consider GAVE (1.1), where

$$ A= \begin{pmatrix} 7&2&2 \\ 2&7&2 \\ 2&2&7 \end{pmatrix}, \qquad B= \begin{pmatrix} 3&0&0 \\ 0&-3&0 \\ 0&0&-3 \end{pmatrix},\qquad b= \begin{pmatrix} 8 \\ 8 \\ 8 \end{pmatrix}. $$

The exact solution of Example 4.1 is \((1,1,1)^{T}\). The initial points in Algorithm 3.1 are taken randomly five times. The detailed numerical results are showed in Table 1 and Fig. 1. \(x^{*}\) denotes the numerical solution, k denotes the number of iterations, and Val denotes \(\||A|x_{k}-|B||x_{k}|-b\|_{\infty }\). From Table 1 and Fig. 1, we can see that Algorithm 3.1 is promising.

Figure 1
figure 1

Numerical results for Example 4.1

Full size image
Table 1 Numerical results for Example 4.1
Full size table

Example 4.2

Consider GAVE (1.1), where

$$\begin{aligned} &A= \begin{pmatrix} 6&-3&-3&-3&-3&-3 \\ -3&6&-3&-3&-3&-3 \\ -3&-3&6&-3&-3&-3 \\ -3&-3&-3&6&-3&-3 \\ -3&-3&-3&-3&6&-3 \\ -3&-3&-3&-3&-3&6 \end{pmatrix},\\ & B= \begin{pmatrix} 2&0&0&0&0&0 \\ 0&-1&0&0&0&0 \\ 0&0&2&0&0&0 \\ 0&0&0&-1&0&0 \\ 0&0&0&0&2&0 \\ 0&0&0&0&0&-1 \end{pmatrix},\qquad b= \begin{pmatrix} 19 \\ 20 \\ 19 \\ 20 \\ 19 \\ 20 \end{pmatrix}. \end{aligned}$$

The exact solution of this example is \((1,1,1,1,1,1)^{T}\). Compute this example by Algorithm 3.1 with random initial points uniformly distributed in \((0,1)\). The results of the numerical experiments are showed in Table 2, where \(x^{*}\) denotes the numerical solution, k denotes the number of iterations, and Val denotes \(\||A|x_{k}-|B||x _{k}|-b\|_{\infty }\). From Table 2 and Fig. 2, we can see that Algorithm 3.1 is also efficient to get the solution of this kind of GAVE.

Figure 2
figure 2

Numerical results for Example 4.2

Full size image
Table 2 Numerical results for Example 4.2
Full size table

Example 4.3

Consider GAVE (1.1), where \(A \in R^{n\times n}\) whose diagonal elements are 2n and other elements are 1, \(B \in R^{n\times n}\) whose diagonal elements are n and other elements are 0, and \(b=(2n-1)e\). The exact solution of this example is \((1,1,\ldots,1)^{T}\). We use random initial points uniformly distributed in \((0,1)\) to compute this example by Algorithm 3.1 with Armijo line search (3.10) and Algorithm 3.1 stops at iteration \(x_{k}\) if \(\||A|x_{k}-|B||x_{k}|-b\|<10^{-3}\). The results of the numerical experiments are showed in Table 3, where n denotes the dimension of the vector, \(x^{*}\) denotes the numerical solution, k denotes the number of iterations, and Val denotes \(\||A|x_{k}-|B||x _{k}|-b\|_{\infty }\). Figure 3 represents the number of iterations with \(n=300\). From Table 3 and Fig. 3, we can see that Algorithm 3.1 can also efficiently get the solution of this kind of GAVE.

Figure 3
figure 3

Numerical results for Example 4.3 with \(n=300\)

Full size image
Table 3 Numerical results for Example 4.3
Full size table

5 Conclusions

Absolute value equation problem has been widely used in mathematical programming and other related areas of science and engineering. However, little attention has been paid to solving general absolute value equation problems by the nonlinear conjugate gradient method. In this paper, we provide a sufficient condition for the unique solution of general absolute value equation of the form as (1.3) and propose a modified HS conjugate gradient method to solve it. The global convergence of the nonlinear conjugate gradient method is proved under only one mild assumption. This method is also very easy to implement and is also very promising.