1 Introduction

The regular heterogeneous networks consisting of macro base stations and several small base stations (SBSs) are incapable of meeting of imminent tele-traffic demands. As one of the key technologies of 5G networks, UDNs can greatly increase user communication rates [1,2,3,4]. However, a large number of deployed SBSs bring serious inter-cell interference. To reduce interference, a user-centric virtual cell clustering method is proposed [5], in which each UE is cooperatively served by a few of SBSs. By using this method, the interference signal is converted into the useful signal. Thus, the purpose of utilizing joint transmission technology [6] to reduce interference and enhance useful signals can be achieved, thereby greatly increasing the user rates. However, under the virtual cell architecture, inter-cell interference still exists within a certain range. Due to the irregular network topology and randomly distributed UEs, the cell load may be imbalance, which will cause the degradation of the system performance. Therefore, it is necessary to seek a joint user association and resource allocation scheme under the virtual cell architecture. It is worth noting that the process of user association is equivalent to the process of virtual cell clustering in this paper.

There have been quite a few studies on coordinated multiple points (CoMP) transmission, which can effectively suppress inter-cell interference, improve system capacity and meet QoS of edge users. In [7], authors propose a two-step joint clustering and scheduling scheme. A load-aware clustering scheme is designed and solved by game theory in the first step. Based on clustering results, a fair graph-coloring based inter-cell resource scheduling can be employed at the second step to maximize the resource utilization. [8, 9] present load-aware user-centric CoMP clustering algorithms which consider trade-off between load balance and spectrum efficiency. In addition, some other studies focus on user-centric virtual cell, where each UE has some base stations associated with it to avoid low signal to interference plus noise ratio (SINR) [10, 11] propose load-aware virtual cell schemes, which can meet the user QoS requirements. Firstly, the authors find the optimal radius of the virtual cell. Then they select the appropriate activation radius based on the cell load. In [12], the authors propose a beamforming problem to maximize the sum-rate in a virtual cell network [13] formulate an energy efficiency maximization problem in the user-centric virtual cell networks by optimizing beamforming vectors and access points cluster, and considering both rate requirements and power budgets.

In recent years, some significant efforts are devoted to reducing the computational complexity of user association and resource allocation. In [14], the authors propose a cluster-based energy-saving resource allocation method in UDNs. Firstly, a modified K-means method is proposed in the clustering stage, which can reduce complexity and inter-cluster interference. And then in resource allocation stage, a two-step PRB allocation algorithm is performed and an iterative power allocation scheme is designed and solved by a non-cooperative game [15] presents the joint optimization scheme of capacity maximization and power minimization for user association and resource allocation. To reduce the complexity, the clustering scheme is adopted in the solution of the optimization problem. As an effective method to reduce the computational complexity, graph theory has been widely used in resource allocation [16,17,18,19]. [20] formulates a graph-based joint user-centric overlapped clustering and resource allocation problem, in which traffic-load and the limited number of PRBs are considered. In order to improve system throughput and reduce computational complexity, [21,22,23,24,25] utilize the DC programming technology, which can be used to convert a non-convex function into the difference of two convex functions, and to obtain an approximately optimal solution through an iterative method. However, the joint user association and resource allocation scheme under the virtual cell architecture, considering the use of multiple PRBs for each user to reduce interference, cell load balance, guarantee QoS requirements and improve system throughput, has not been studied in previous work.

In this paper, under the virtual cell architecture, a QoS-based joint user association and resource allocation scheme is proposed to mitigate the interference, balance cell load and improve the system throughput. It is worth mentioning that the joint problem is a non-convex NP-hard problem. To solve this problem, we propose a three-step scheme. In the first step, we design a user association scheme, in which QoS requirements and cell load is considered. In the second step, we use the modified graph theory for PRB allocation to achieve the purpose of reducing inter-cell interference. In the third step, we apply the DC programming technology to power allocation, and perform an iterative update algorithm to obtain an approximate optimal solution for convergence. Finally, simulations indicate that our scheme is proved to be better than the other schemes.

The main contributions of this paper can be summarized as follows:

  1. 1.

    A novel framework is proposed for jointly designing QoS-based user association and resource allocation under the virtual cell architecture. This is the first attempt to consider the use of multiple PRBs for each user to reduce interference, balance cell load, guarantee QoS requirements of UE and improve system throughput.

  2. 2.

    To solve the non-convex NP-hard joint user association and resource allocation problem, three independent sub-problems are formulated.

    1. a.

      A new user-centric overlapped virtual cell clustering scheme is proposed to solve the user association problem of load imbalance with considering the QoS requirements.

    2. b.

      A low-complexity PRB allocation scheme is constructed by using modified graph-based method to further mitigate virtual inter-cell interference.

    3. c.

      The DC programing method is used to power allocation and an iterative update algorithm is performed to obtain an approximate optimal solution for convergence.

  3. 3.

    Simulations verify that the performance of our proposed scheme is better than that of other schemes in terms of user rates, cell load and system throughput.

The rest of the paper is organized as follows. We give the system model and formulate the joint optimization problem in Sect. 2. Section 3 describes our three-step joint scheme and discuss its implementation process. We analyze the complexity of our scheme in Section IV. Section V evaluates the proposed methods and compares the performance with the other method. Finally, conclusions are drawn in the last section.

2 System model and problem formulation

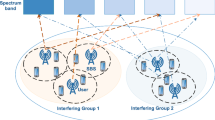
The two-tier heterogeneous UDNs scenario [8] is one of the main scenarios of 5G. We consider a downlink two-tier heterogeneous UDNs that consists of a macro base station (MBS), \(N\) SBSs and \(K\) UEs, as is shown Fig. 1. In order to harvest densification gains and avoid cross-tier interference, the control plane (C-plane) and user plane (U-plane) split architecture in [26] is adopted in our system, where a network controller unit (NCU) is installed in MBS. The NCU takes charge of virtual cell formation, wireless radio resources allocation, and mobility management. SBSs only undertake the task of data transmission. The SBS index set is \({\mathcal{N}} = \left\{ {1,...,N} \right\}\), the UE index set is \({\mathcal{K}} = \left\{ {1,...,K} \right\}\). We make three assumptions: (1) SBSs and UEs are randomly distributed following Poisson point process (PPP) distribution within coverage area of MBS; (2) backhaul is ideal and channel state information (CSI) knowledge is perfect; (3) with zero-forcing (ZF) precoding, intra-cluster interference is completely eliminated.

Fig. 1
figure 1

The user-centric virtual cells system model of the ultra-dense network

Full size image

The matrix \(X\) is defined as a user association matrix, in which the elements are \(x_{k,n}\), where \(\, x_{k,n} \in \left\{ {0,1} \right\}, \, \forall k \in {\mathcal{K}}, \, \forall n \in {\mathcal{N}}\). \(\, x_{k,n} = 0\) means that SBS \(n\) is not accessed by UE \(k\), and \(\, x_{k,n} = 1\) means that SBS \(n\) is accessed by UE \(k\). \(L\) represents the total number of PRBs per cell, and the PRB index set is \({\mathcal{L}} = \left\{ {1,...,L} \right\}\). The matrix \(Y\) is defined as a PRB allocation matrix, in which the elements are \(y_{k,l}\), where \(\, y_{k,l} \in \left\{ {0,1} \right\}, \, \forall k \in {\mathcal{K}}, \, \forall l \in {\mathcal{L}}\). \(\, y_{k,l} = 0\) indicates that PRB \(l\) is not allocated to UE \(k\), \(\, y_{k,l} = 1\) indicates that PRB \(l\) is allocated to UE \(k\). \(p_{n,l}\) represents the power allocated by SBS \(n\) to PRB \(l\), and \(h_{k,n,l}\) represents the channel gain between SBS \(n\) and UE \(k\) on PRB \(l\). \(\sigma^{2}\) indicates the additive white Gaussian noise (AWGN). Each PRB is assumed to have a bandwidth of \(B\). The SINR of UE \(k\) on PRB \(l\) can be written as

$${\text{SINR}}_{k,l} = \frac{{\sum\limits_{{n \in {\mathcal{C}}_{k} }} {p_{n,l} h_{k,n,l} } }}{{\sum\limits_{{k^{\prime} = 1,k^{\prime} \ne k}}^{K} {\sum\limits_{{n^{\prime} \in {\mathcal{C}}_{{k^{\prime}}} }} { p_{{n^{\prime},l}} h_{{k,n^{\prime},l}} } } + \sigma^{2} }}$$
(1)

where \({\mathcal{C}}_{k}\) represents the serving virtual cell cluster of UE \(k\).

According to the Shannon formula, the rate of UE \(k\) on PRB \(l\) can be expressed as

$$R_{k,l} = y_{k,l} B\log_{2} \left( {1 + \frac{{\sum\limits_{n = 1}^{N} {x_{k,n} p_{n,l} h_{k,n,l} } }}{{\sum\limits_{{k^{\prime} = 1,k^{\prime} \ne k}}^{K} {\sum\limits_{n = 1}^{N} {x_{{k^{\prime},n}} p_{n,l} h_{k,n,l} } } + \sigma^{2} }}} \right)$$
(2)

The rate of UE \(k\) can be written as

$$r_{k} = \sum\limits_{l = 1}^{L} {R_{k,l} }$$
(3)

The total system throughput is

$$R_{\text{total}} = \sum\limits_{k = 1}^{K} {r_{k} }$$
(4)

The joint optimization problem is formulated as

$$\begin{gathered} \, \mathop {\max }\limits_{{x_{k,n} ,y_{k,l} ,p_{n,l} }} R_{total} \hfill \\ s.t. \hfill \\ \, C1: \, 0 \le \sum\limits_{k = 1}^{K} {\sum\limits_{l = 1}^{L} {x_{k,n} y_{k,l} p_{n,l} \le p_{n}^{\max } } } ,\forall n \hfill \\ \, C2: \, 1 \le \sum\limits_{l = 1}^{L} {y_{k,l} \le L} ,\forall k \hfill \\ \, C3: \, 0 \le \sum\limits_{k = 1}^{K} {\sum\limits_{l = 1}^{L} {x_{k,n} y_{k,l} \le L} } ,\forall n \hfill \\ \, C4: \, 1 \le \sum\limits_{n = 1}^{N} {x_{k,n} \le N_{\max } } ,\forall k \hfill \\ \, C5: \, \sum\limits_{l = 1}^{L} {y_{k,l} B} \log_{2} \left( {1 + SINR_{k,l} } \right) \ge R_{k,\min } ,\forall k \hfill \\ \, C6: \, x_{k,n} \in \left\{ {0,1} \right\},\forall k,n \hfill \\ \, C7: \, y_{k,l} \in \left\{ {0,1} \right\},\forall k,l \hfill \\ \end{gathered}$$
(5)

where \(p_{n}^{\max }\) is the maximum transmission power of SBS \(n\). \(N_{{{\text{max}}}}\) is the maximum number of SBSs in the virtual cell cluster. \(R_{k,\min }\) is the minimum required rate of UE \(k\). \(C1\) indicates that the total allocated power of UEs cannot be larger than the maximum transmission power limit for each SBS. \(C2\) implies that at least one PRB is allocated to each UE. \(C3\) means that the number of PRBs used by users cannot be more than the maximum number of PRBs in each small cell (SC). \(C4\) expresses that the number of each UE accessed SBSs cannot be larger than the maximum number of SBSs in the virtual cell cluster. \(C5\) explains that the UE rate should be greater than the minimum required rate.

3 QoS-based joint user association and resource allocation scheme in UDNs

It can be observed that the objective function (5) is a non-convex NP-hard problem. Since the problem of user association and resource allocation are coupled, joint optimization problem (5) will result in extremely high computational complexity, especially in UDN scenarios. So, a novel framework is proposed for jointly designing QoS-based user association and resource allocation under the virtual cell architecture. The flowchart of the proposed user-centric overlapped clusters framework is described in Fig. 2. We divide the problem (5) into three sub-problems: user association, PRB allocation and power allocation. The user association sub-problem is to determine the serving virtual cell cluster for each UE based on PRB estimation. A two-step graph-based approach is applied to the PRB allocation sub-problem. The DC programing method is used to power allocation sub-problem. Both of the PRB allocation and the power allocation sub-problem are to reduce virtual inter-cell interference and improve the system throughput. In this section, we will describe the three parts of the proposed scheme, and discuss implementation process for the scheme in practical systems.

Fig. 2
figure 2

Flowchart of the proposed user-centric overlapped clusters framework

Full size image

3.1 User association

Our proposed user association scheme is divided into two stages: the estimation stage and the allocation stage. In the estimation stage, in order to estimate the number of PRBs required by each UE and cell load of each SC, we make two assumptions: 1) the transmit power of each SBS is equally allocated to all PRBs; 2) for each UE, the interference on each PRB comes from all SBSs except cooperative SBSs. The SINR of UE \(k\) can be written as

$${\text{SINR}}_{k} { = }\frac{{\sum\limits_{{n \in {\mathcal{C}}_{k} }} {p_{n}^{\max } h_{k,n} } }}{{\sum\limits_{{n^{\prime} \in {\mathcal{N}}\backslash {\mathcal{C}}_{k} }} {p_{{n^{\prime}}}^{\max } h_{{k,n^{\prime}}} } + L\sigma^{2} }}$$
(6)

where \(h_{k,n}\) is the channel gain between SBS \(n\) and UE \(k\). The number of PRBs required by UE \(k\) can be estimated by

$$N_{k} = \left\lceil {\frac{{R_{k,\min } }}{{R_{k} }}} \right\rceil ,\forall k \in {\mathcal{K}}$$
(7)

where \(\left\lceil \cdot \right\rceil\) denotes the ceiling function that rounds up to the nearest integer. \(R_{k}\) is the maximum achievable throughput from one PRB, it can be estimated as:

$$R_{k} = B\log_{2} \left( {1 + {\text{SINR}}_{k} } \right)$$
(8)

The estimated load of SC \(n\) is

$$\eta_{n} = \frac{{\sum\nolimits_{{k \in {\mathcal{N}}_{n} }} {N_{k} } }}{L},\forall n \in {\mathcal{N}}$$
(9)

where \({\mathcal{N}}_{n}\) is the set of UEs associated to SC \(n\).

We define the Max Reference Signal Receiving Power (RSRP) rule: each UE associates SBSs with the first a few maximum RSRP values as its virtual cell cluster.

Here we introduce our proposed user association scheme in detail from the perspectives of UE and SBS. In the initial state, the candidate SBSs list for each UE consists of all SBSs. In the estimation stage, from the perspective of UE, \(N_{\text{max}}\) SBSs are selected by each UE as its virtual cell cluster based on Max RSRP rule. From the perspective of SBS, we estimate the load and get the UEs list for each SC. In the allocation stage, from the perspective of SBS, the SCs is sorted in descending order according to the SC load. If the first SC is overloaded, we will sort the UEs of this SC in descending order based on SINR values. And the UE with the largest SINR is preferentially accepted and allocated PRBs. For other UEs we sequentially judge whether the remaining PRBs in this SC are sufficient or not. If the remaining PRBs are sufficient, the user association request is accepted, otherwise the request is rejected and UE is removed from the UE list of this SC. From the perspective of UE, the SBS of the first overloaded SC is removed from the candidate SBSs list for the UEs that are not associated to this SBS. Those UEs will reselect the cooperative SBSs according to the Max RSRP rule, and associate in turn until all the SCs are not overloaded. The specific algorithm is given in Algorithm 1.

As an example in Fig. 3, we assume that the maximum number of SBSs in the virtual cell cluster is 2, the number of PRBs for all SBSs is 16, and the number of PRBs required by each UE is 4. As shown in Fig. 3a, UE1, …, UE6 select cooperative SBSs based on the Max RSRP rule respectively. In Fig. 3b, according to the Max SINR rule, UE1, …, UE4 is preferentially accepted, and the UE5 is rejected by the SBS1. At this time, the cooperative SBSs cluster of UE1 and UE2 are {SBS1, SBS2}, and the cooperative SBSs cluster of UE3 and UE4 are {SBS3, SBS4}. SBS1 is removed in candidate SBSs list of UE5 and UE6. UE5 and UE6 re-associate the SBSs according to the Max RSRP rule, thereby obtaining Fig. 3c. So far, the user-centric virtual cells are formed for each UE.

figure a
Fig. 3
figure 3

User association based on PRB estimation

Full size image

Now we can obtain the user association matrix \(X\) based on Algorithm 1. And the clustering result of virtual cells is \(\left\{ {{\mathcal{C}}_{1} ,{\mathcal{C}}_{2} ,...,{\mathcal{C}}_{K} } \right\}\).

3.2 PRB allocation

After the UEs are associated to the SBSs, the next step is to solve the user-centric PRB allocation problem. Let \(F = XX^{T} - N_{\max } I_{K}\), then the matrix \(F\) is the overlapped indicator matrix of the virtual cell cluster \({\mathcal{C}}_{i}\) and \({\mathcal{C}}_{j}\) (where \(i,j \in \left\{ {1,...,K} \right\}\)). The element \(f_{i,j}\) represents the number of overlapped SBSs in the virtual cell cluster \({\mathcal{C}}_{i}\) and \({\mathcal{C}}_{j}\).

The graph coloring method has been widely used in resource allocation for decades to reduce the computational complexity. In the graph theory, each UE represents a vertex and the edge between the two vertices indicates interference between the two UEs. It can be easily seen that the underlying PRB allocation sub-problem can be converted into a graph coloring problem, but this graph coloring problem cannot be directly solved by existing graph-based method. In [20], each UE is only allocated to one PRB, but in our proposed scheme each UE can be allocated to multiple PRBs. Thus, the previous graph coloring method cannot be used in our proposed scheme directly. In order to use the graph coloring theory, we extend the graph coloring scheme in [20] for PRB allocation. The specific process is as follows.

3.2.1 Graph construction

The graph is constructed as \(G = \left( {V,E} \right)\), where \(V\) is the set of vertices \(\left\{ {C_{1} ,C_{2} ,...,C_{K} } \right\}\) corresponding to the virtual cell clusters \(\left\{ {{\mathcal{C}}_{1} ,{\mathcal{C}}_{2} ,...,{\mathcal{C}}_{K} } \right\}\), and \(E\) is the edge connecting any two vertices. \(d\left( {C_{k} } \right)\) represents the degree of the vertex \(C_{k}\), which is equal to the number of all edges associated with the vertex \(C_{k}\). We construct edges based on matrix \(F\). If \(f_{i,j} > 1\), an edge between the cluster \({\mathcal{C}}_{i}\) and the cluster \({\mathcal{C}}_{j}\) is formed.

We can get the number of PRBs used by each SC \(N_{n}^{{{\text{use}}d}} ,\forall n \in {\mathcal{N}}\) by Algorithm 1. We assume that the total transmitted power of each SBS is allocated equally to the PRBs used by each SC, ie. \({{P_{n}^{\max } } \mathord{\left/ {\vphantom {{P_{n}^{\max } } {N_{n}^{{{\text{use}}d}} }}} \right. \kern-\nulldelimiterspace} {N_{n}^{{{\text{use}}d}} }},\forall n \in {\mathcal{N}}\). The interference of UE \(k\) on PRB \(l\) can be written as

$$I_{k,l} = \sum\limits_{{k^{\prime} = 1,k^{\prime} \ne k}}^{K} {\sum\limits_{{n^{\prime} \in {\mathcal{C}}_{{k^{\prime}}} }} {y_{{k^{\prime},l}} \frac{{p_{{n^{\prime}}}^{\max } }}{{N_{{n^{\prime}}}^{{{\text{used}}}} }}h_{{k,n^{\prime},l}} } }$$
(10)

3.2.2 Graph coloring

The vertex with the maximum degree should be colored preferentially. The reasons are as follows: (1) the higher the vertex degree is, the larger the number of vertices adjacent to the vertex are. This means that the number of clusters overlapped SBSs is larger; (2) the orthogonal PRBs need to be allocated among the clusters with the same serving SBS; (3) since the number of PRBs are insufficient, PRBs need to be reused. If the vertex with the maximum degree is colored, we can choose more PRBs to other vertices with lower degrees. To solve this problem conveniently, our method is divided into two stages: the sorting stage and coloring stage.

In the sorting stage, we search for the vertex \(C_{1}^{*}\) with the highest degree in the \(V\) firstly. We define the set \(D_{{C_{k} }}\) as the set of the vertices adjacent to the vertex \(C_{k}\),where \(C_{k} \in V,\forall k \in {\mathcal{K}}\). Then, we find the set \(D_{{C_{1}^{*} }}\) based on matrix \(F\). The degree of all vertices in \(D_{{C_{1}^{*} }}\) is reduced by one. This operation is performed on the remaining vertices in the \(V\) to obtain vertices \(C_{2}^{*}\), \(C_{3}^{*}\), …, until all vertices are sequentially placed into empty set \(S\).

$$S = \left\{ {C_{1}^{*} ,,...,C_{K}^{*} } \right\}$$
(11)

In the coloring stage, we sequentially label the PRBs required by each vertex in the set \(S\), and get the set \({\mathcal{L}}_{S}\)

$${\mathcal{L}}_{S} { = }\left\{ {L_{1}^{{C_{1}^{*} }} ,...,L_{{N_{1}^{*} }}^{{C_{1}^{*} }} ,L_{1}^{{C_{2}^{*} }} ,...,L_{{N_{2}^{*} }}^{{C_{2}^{*} }} , \ldots ,L_{1}^{{C_{K}^{*} }} ,...,L_{{N_{K}^{*} }}^{{C_{K}^{*} }} } \right\}$$
(12)

The corresponding natural number set is \(L_{S} = \left\{ {1,...,\sum\limits_{k = 1}^{K} {N_{k}^{*} } } \right\}\).The subset \(\left\{ {L_{1}^{{C_{k}^{*} }} ,...,L_{{N_{k}^{*} }}^{{C_{k}^{*} }} } \right\}\) of \({\mathcal{L}}_{S}\) represents the set of \(N_{k}^{*}\) PRBs required by vertex \(C_{k}^{*}\). Each PRB is assumed have a specific color in the \(G\).

We assign the colors to the elements in the set \({\mathcal{L}}_{S}\) in turn. For the first \(L\) elements of the set \({\mathcal{L}}_{S}\), we randomly assign \(L\) different colors to them and update matrix \(Y\). For other elements of the set \({\mathcal{L}}_{S}\), we firstly find the vertex \(C_{k}^{*}\) corresponding to the element. Then, we find the set \(D_{{C_{k}^{*} }}\) based on matrix \(F\). Thirdly, we choose the PRB with the minimum interference that is not used by the vertices of the set \(D_{{C_{k}^{*} }}\), and assign the color to vertex \(C_{k}^{*}\). Finally, we update the interference on this PRB and matrix \(Y\).

figure b

Now we can obtain the PRB allocation matrix \(Y\) based on Algorithm 2.

3.2.3 Power allocation

After forming the user-centric overlapped virtual cell cluster and allocating PRB to each UE, we will solve the user-centric power allocation problem. Relying on the user association matrix \(X\) and the PRB allocation matrix \(Y\), the problem (5) is converted into the problem (13)

$$\begin{gathered} \mathop {\max }\limits_{{p_{n,l} }} \, R_{{{\text{total}}}} \hfill \\ s.t. \hfill \\ C1: \, 0 \le \sum\limits_{k = 1}^{K} {\sum\limits_{l = 1}^{L} {x_{k,n} y_{k,l} p_{n,l} \le p_{n}^{\max } } } ,\forall n \hfill \\ C5: \, \sum\limits_{l = 1}^{L} {y_{k,l} B} \log_{2} \left( {1 + SINR_{k,l} } \right) \ge R_{k,\min } ,\forall k \hfill \\ \end{gathered}$$
(13)

where

$$R_{{{\text{total}}}} = \sum\limits_{k = 1}^{K} {\sum\limits_{l = 1}^{L} {y_{k,l} B} \log_{2} \left( {1 + \frac{{\sum\limits_{n = 1}^{N} {x_{k,n} p_{n,l} h_{k,n,l} } }}{{\sum\limits_{{k^{\prime} = 1,k^{\prime} \ne k}}^{K} {\sum\limits_{n = 1}^{N} {x_{{k^{\prime},n}} p_{n,l} h_{k,n,l} } } + \sigma^{2} }}} \right)}$$

We can observe that the objective function of (13) is not concave [23]. However, it has a special structure that we can utilize. The specific utilization process is as follows.

We define \(f\left( {\varvec{p}} \right) = \sum\limits_{k = 1}^{K} {\sum\limits_{l = 1}^{L} {f_{k,l} } } \left( {\varvec{p}} \right)\), and \(g\left( {\varvec{p}} \right) = \sum\limits_{k = 1}^{K} {\sum\limits_{l = 1}^{L} {g_{k,l} } } \left( {\varvec{p}} \right)\), where

$$f_{k,l} \left( {\varvec{p}} \right) = y_{k,l} B\log_{2} \left( {\sum\limits_{n = 1}^{N} {x_{k,n} p_{k,n,l} } h_{k,n,l} + \sum\limits_{{k^{\prime} = 1,k^{\prime} \ne k}}^{K} {\sum\limits_{n = 1}^{N} {x_{{k^{\prime},n}} p_{n,l} h_{k,n,l} } } + \sigma^{2} } \right)$$
(14)
$$g_{k,l} \left( {\varvec{p}} \right) = y_{k,l} B\log_{2} \left( {\sum\limits_{{k^{\prime} = 1,k^{\prime} \ne k}}^{K} {\sum\limits_{n = 1}^{N} {x_{{k^{\prime},n}} p_{n,l} h_{k,n,l} } } + \sigma^{2} } \right)$$
(15)

and \({\varvec{p}} \in P\), \(P\) denotes the feasible set spanned by constraints \(C1\) and \(C5\). Then,

$$f\left( {\varvec{p}} \right) = \sum\limits_{k = 1}^{K} {\sum\limits_{l = 1}^{L} {y_{k,l} B\log_{2} \left( {\sum\limits_{n = 1}^{N} {x_{k,n} p_{k,n,l} } h_{k,n,l} + \sum\limits_{{k^{\prime} = 1,k^{\prime} \ne k}}^{K} {\sum\limits_{n = 1}^{N} {x_{{k^{\prime},n}} p_{n,l} h_{k,n,l} } } + \sigma^{2} } \right)} }$$
(16)
$$g\left( {\varvec{p}} \right) = \sum\limits_{k = 1}^{K} {\sum\limits_{l = 1}^{L} {y_{k,l} B} } \log_{2} \left( {\sum\limits_{{k^{\prime} = 1,k^{\prime} \ne k}}^{K} {\sum\limits_{n = 1}^{N} {x_{{k^{\prime},n}} p_{n,l} h_{k,n,l} } } + \sigma^{2} } \right)$$
(17)

\(f\left( {\varvec{p}} \right)\) and \(g\left( {\varvec{p}} \right)\) are obviously two concave functions. Thus, utilizing the structure of objective function, the DC programming method [21,22,23,24,25] can be applied to convert the objective function of (13) into \(f\left( {\varvec{p}} \right) - g\left( {\varvec{p}} \right)\). In the similar manner, \(C5\) can be written as

$$\sum\limits_{l = 1}^{L} {\left( {f_{k,l} \left( {\varvec{p}} \right) - g_{k,l} \left( {\varvec{p}} \right)} \right)} \ge R_{k,\min } ,\forall k$$
(18)

In DC programming, we can start from a feasible initial point and solve the optimization problem iteratively. In order to solve the convex problem, let \(\tau\) denote the iteration number. At the \(\tau\)-th iteration, we employ the first-order Taylor approximation for \(g\left( {\varvec{p}} \right)\) and \(g_{k,l} \left( {\varvec{p}} \right)\), then

$$g\left( {\varvec{p}} \right) \approx g\left( {{\varvec{p}}^{\left( \tau \right)} } \right) + {\nabla }g^{T} \left( {{\varvec{p}}^{\left( \tau \right)} } \right)\left( {{\varvec{p}} - {\varvec{p}}^{\left( \tau \right)} } \right)$$
(19)
$$g_{k,l} \left( {\varvec{p}} \right) \approx g_{k,l} \left( {{\varvec{p}}^{\left( \tau \right)} } \right) + {\nabla }g_{k,l}^{T} \left( {{\varvec{p}}^{\left( \tau \right)} } \right)\left( {{\varvec{p}} - {\varvec{p}}^{\left( \tau \right)} } \right)$$
(20)

where \({\varvec{p}}^{\left( \tau \right)}\) is the solutions of the problem at \(\tau\)-th iteration, \({\nabla }\) denote the gradient operation, and \(\nabla g\left( {{\varvec{p}}^{\left( \tau \right)} } \right)\) is a column vector with \(NL\) elements. Each element of \(\nabla g\left( {{\varvec{p}}^{\left( \tau \right)} } \right)\) can be computed as

$$\frac{{\partial g({\varvec{p}}^{(\tau )} )}}{\partial p} = \frac{B}{\ln 2} \cdot \sum\limits_{k = 1}^{K} {\sum\limits_{l = 1}^{L} {\frac{{y_{k,l} x_{k\prime ,n} h_{k,n,l} }}{{\sum\nolimits_{{k = 1,k^{\prime } \ne k}}^{K} {\sum\nolimits_{n = 1}^{N} {x_{{k^{\prime } ,n}} p_{n,l} h_{k,n,l} + \sigma^{2} } } }}} }$$
(21)

Hence, by substituting \(g({\varvec{p}}^{(\tau )} )\) and \(\nabla g({\varvec{p}}^{(\tau )} )\) into the optimization problem (13), the problem (13) can be written as

$$\begin{array}{*{20}l} {\mathop {\max }\limits_{p} f({\varvec{p}}) - g({\varvec{p}}^{(\tau )} ) + \nabla g({\varvec{p}}^{(\tau )} )({\varvec{p}} - {\varvec{p}}^{(\tau )} )} \hfill \\ {s.t} \hfill \\ {C1:\;0 \le \sum\limits_{k = 1}^{K} {\sum\limits_{l = 1}^{L} {x_{k,n} y_{k,l} p_{n,l} \le p_{n}^{\max } , + \forall n} } } \hfill \\ {C^{\prime } 5:\;\sum\limits_{l = 1}^{L} {(f_{k,l} ({\varvec{p}}) - \nabla g_{k,l}^{T} ({\varvec{p}}^{(\tau )} )(\user2{p - p}^{(\tau )} )) \ge R_{k,\min } ,\forall k} } \hfill \\ \end{array}$$
(22)

In order to use the DC programming method to solve the power allocation sub-problem, we need to prove the following three propositions.

Proposition 1

The approximation of (19) gives a tight lower bound for the objective function of (13).

Proof

Since \(g\left( {{\varvec{p}}^{\left( \tau \right)} } \right)\) is a concave function, due to the first-order condition of the concave functions [27], we have.

$$g\left( {\varvec{p}} \right) \le g\left( {{\varvec{p}}^{\left( \tau \right)} } \right) + {\nabla }g\left( {{\varvec{p}}^{\left( \tau \right)} } \right)\left( {{\varvec{p}} - {\varvec{p}}^{\left( \tau \right)} } \right)$$
(23)

From (23), we can conclude that \(f\left( {\varvec{p}} \right) - g\left( {\varvec{p}} \right) \ge f\left( {\varvec{p}} \right) - g\left( {{\varvec{p}}^{\left( \tau \right)} } \right) - {\nabla }g\left( {{\varvec{p}}^{\left( \tau \right)} } \right)\left( {{\varvec{p}} - {\varvec{p}}^{\left( \tau \right)} } \right)\). When \({\varvec{p}} = {\varvec{p}}^{\tau }\), the equality holds which shows the tightness of the lower bound.

Proposition 2

The approximation of. (19) results in a sequence of improved solutions for the problem of (13).

Proof:

The objective function of (13) in the \(\tau\)-th iteration is \(f\left( {{\varvec{p}}^{\left( \tau \right)} } \right) - g\left( {{\varvec{p}}^{\left( \tau \right)} } \right)\). We have.

$$\begin{gathered} \, f\left( {{\varvec{p}}^{{\left( {\tau + 1} \right)}} } \right) - g\left( {{\varvec{p}}^{{\left( {\tau + 1} \right)}} } \right) \hfill \\ \mathop \ge \limits^{\left( a \right)} f\left( {{\varvec{p}}^{{\left( {\tau + 1} \right)}} } \right) - g\left( {{\varvec{p}}^{\left( \tau \right)} } \right) - {\nabla }g\left( {{\varvec{p}}^{\left( \tau \right)} } \right)\left( {{\varvec{p}}^{{\left( {\tau + 1} \right)}} - {\varvec{p}}^{\left( \tau \right)} } \right) \hfill \\ \mathop \ge \limits^{\left( b \right)} f\left( {{\varvec{p}}^{\left( \tau \right)} } \right) - g\left( {{\varvec{p}}^{\left( \tau \right)} } \right) - {\nabla }g\left( {{\varvec{p}}^{\left( \tau \right)} } \right)\left( {{\varvec{p}}^{\left( \tau \right)} - {\varvec{p}}^{\left( \tau \right)} } \right) \hfill \\ = f\left( {{\varvec{p}}^{\left( \tau \right)} } \right) - g\left( {{\varvec{p}}^{\left( \tau \right)} } \right) \hfill \\ \end{gathered}$$
(24)

where the inequality \(\left( a \right)\) follows from the convexity of \(g\left( {\varvec{p}} \right)\), and the inequality \(\left( b \right)\) follows from the fact that \({\varvec{p}}^{{\left( {\tau + 1} \right)}}\) is the optimal solution of problem (22) at the \(\tau + 1\)-th iteration.

Thus, the objective function of (13) takes larger values as iterations continue.

Proposition 3

Proposition 3: The approximation of (19) has a tight bound for the objective problem of (13).

Proof

The objective function of (13) in the \(\tau\)-th iteration is \(f\left( {{\varvec{p}}^{\left( \tau \right)} } \right) - g\left( {{\varvec{p}}^{\left( \tau \right)} } \right)\). Obviously, \(f\left( {{\varvec{p}}^{\left( \tau \right)} } \right) - g\left( {{\varvec{p}}^{\left( \tau \right)} } \right)\) is a continuous function, and the interval formed by \(C^{\prime}1\) and \(C^{\prime}2\) is a closed interval. Using the closed interval set theorem (theorem 4.15 in [28]), proposition 3 is proved.

Hence, the objective value of \(f\left( {{\varvec{p}}^{\left( \tau \right)} } \right) - g\left( {{\varvec{p}}^{\left( \tau \right)} } \right)\) is finite and monotonically increasing sequences with upper bounds. According to the nature of theorem 3.14 in [28], the DC approximation always converges.

Notice that function (22) is a concave function since it is the addition of a line and a concave function, and at the same time \(C1\) and \(C^{\prime}5\) are also convex. The proposed iterative DC algorithm for solving the problem in (22) is presented in Algorithm 3. We initialize \({\varvec{p}}^{{0}}\) to a column vector with \(NL\) elements, where the fix power allocation of each PRB in our algorithm 2 is used as the initial power \({\varvec{p}}^{0}\).

figure c

4 Computational complexity

Here, we evaluate the complexity of our proposed scheme. The complexity of Algorithm 1 is \({\mathcal{O}} (KN^2N_{\max} +NK^2N_{\max})\). For comparison, the complexity of exhaustive search for the optimal solution of user association is \({\mathcal{O}} \left(\prod\limits_{k=1}^{K} \sum\limits_{n=0}^{N_{\max}} C_{N}^{n}\right)\). The complexity of Algorithm 2(PRB allocation algorithm) is \({\mathcal{O}} (NKL^2N_{\max}^{2} + L^2),\) where the complexity of graph construction algorithm is \({\mathcal{O}} (NKL^2N_{\max}^{2}),\) and the complexity of PRB allocation algorithm is \({\mathcal{O}} (L^2)\). As a comparison, the complexity of exhaustive search algorithm for the optimal solution is \({\mathcal{O}} (K^L)\) and the complexity of SA algorithm or RA algorithm is \({\mathcal{O}} (L)\). The complexity of the optimal exhaustive search increases exponentially as the number of UEs increases. Hence, compared with the optimal exhaustive search solution, our proposed solution efficiently reduces the complexity in UDNs.

5 Simulation results and discussion

5.1 System simulation

In this section, we aim to characterize the performance of the proposed framework under different conditions via numerical simulations. We consider one MBS coverage with a circle of 300 m radius. SBSs and UEs are randomly distributed following PPP distribution with density \(\lambda_{M}\) and \(\lambda_{K}\). By default, we set \(\lambda_{M} { = 50}\;{\text{SBS}}/{\text{km}}^{2}\), \(\lambda_{K} { = 350}\;{\text{UE}}/{\text{km}}^{2}\) and \(N_{\max } { = 3}\). We consider three different rate requirements of UEs: 256kbps, 512kbps and 1024kbps, where each user rate requirement is randomly simulated. The other simulation parameters are listed in Table 1. We consider Reyleigh fading to models the channels and assume that the path loss model of each SBS is given by [29]

$$PL \, = \, 36.7\log_{{{10}}} \left( d \right){ + 22}{\text{.7 + 26}}\log_{{{10}}} \left( {f_{c} } \right)$$
(25)

5.2 Analysis of the simulation results

Figures 4 and 5 show the changes of the load of each SC caused by different the size of virtual cell cluster based on the two different user association schemes under the conditions of 350 UE/km3 and 50 SBS/km2. It can be seen that as the cluster size increases, the load of the SC increases under the two different user association schemes. The reasons are as follows: as the size of the SBS cluster increases, from the perspective of the UE, more SBSs become the cooperative SBSs of UE, from the perspective of SBS, more UEs are associated to SBS. Figure 4 shows the user association results based on the Max RSRP rule. Larger cluster size may improve RSRP but may also reduce total throughput. When \(N_{\max }\) is not less than 4, the SCs are overloaded because of insufficient PRBs. However, due to interference issue, the maximum cluster size of SBSs or CoMP will restrict to 3 in most cellular system. Thus, we set \(N_{\max } { = 3}\) by default. Figure 5 gives us the results of user association rule based on Algorithm 1. Compared with the Max RSRP rule, Algorithm 1 eliminates the overloaded SC within a certain range.

Fig. 4
figure 4

SC load of Max RSRP user association with 350 UE/km3 and 50 SBS/km2

Full size image
Fig. 5
figure 5

SC load of algorithm 1 user association with 350 UE/km3 and 50 SBS/km2

Full size image

Figures 6 and 7 depict the SC load versus the different density of SBSs under user association rule based on Max RSRP and algorithm 1 respectively. Figures 8 and 9 show the SC load versus the different density of UEs under user association rule based on Max RSRP and algorithm 1 respectively. It is clearly observed that the SC load is balanced by Algorithm1, and SBSs are reselected as cooperative SBSs cluster for UEs that cannot associate to the overload SBSs.

Fig. 6
figure 6

SC load of Max RSRP user association versus the different density of SBSs

Full size image
Fig. 7
figure 7

SC load of algorithm 1 user association versus the different density of SBSs

Full size image
Fig. 8
figure 8

SC load of Max RSRP user association versus the different density of UEs

Full size image
Fig. 9
figure 9

SC load of algorithm 1 user association versus the different density of UEs

Full size image

Figures 10 show that the system throughput of the proposed user association based on Algorithm1 is higher than that of the user association based on Max RSRP rule. This is because that the SC load is considered by Algorithm 1. The UEs of overloaded SC are transferred to the non-overloaded SC, which effectively guarantees user QoS requirements. Through Figs. 4, 5 and 10, we have a conclusion that the optimal number of \(N_{\max }\) is 3 considering the trade-off between load balance and system throughput.

Fig. 10
figure 10

Comparison of the system throughput for Max RSRP and Algorithm 1 user association with 350 UE/km2 and 50 SBS/km2

Full size image

In Figs. 11 and 12, we compare Algorithm 2 with other algorithm such as random allocation (RA) [30], sequential allocation (SA) [30] and uniform frequency reuse (UFR) [31] on user-centric clusters by Algorithm1. Figure 11 depicts the system throughput versus the different density of UEs under 50 SBS/km2. We observe in Fig. 11 that the system throughput is increased for all the solutions when the UEs become denser. However, the performance of our proposed Algorithm 2 outperforms that of other algorithms in mitigating the virtual inter-cell interference and improving system throughput.

Fig. 11
figure 11

The system throughput versus the density of UEs

Full size image
Fig. 12
figure 12

The system throughput versus the density of SBSs

Full size image

Next, Fig. 12 describes system throughput versus the different density of UEs under 350 UE/km2. We can observe that when the density of SBSs is less than 50 the system throughput increases. And then the system throughput becomes stable. This is because when the density of the SBCs is small, only a few UEs can be served by the SBSs due to the limited number of PRBs. As SBSs become denser, the UEs can be served by more cooperative SBSs and the system throughput also increases. From Figs. 11 and 12, we can conclude that our proposed algorithm 2 performance is superior to that of other algorithms.

We validate the convergence of our power allocation scheme by examining the evolution of system throughput in iterations. Figure 13 describes the system throughput of different the density of UEs when the density of SBSs is 50 SBS/km2. And Fig. 14 shows the system throughput of different the density of SBSs when the density of UEs is 350 UE/km2. We can see that the throughput can reach stable state in less than 12 iterations. In Figs. 11 and 12, due to the density and the locations of UEs (or SBSs) are different, the final convergent values of system throughput in different density of UEs (or SBSs) are unequal. This shows that the performance of power allocation scheme using the DC programing method is better than that of the original fixed power allocation scheme in terms of system throughput.

Fig. 13
figure 13

The system throughput evolution in different density of UEs

Full size image
Fig. 14
figure 14

The system throughput evolution in different density of SBSs

Full size image

6 Conclusion

In this paper, we propose a novel QoS-based joint user association and resource allocation scheme under the virtual cell architecture in a downlink two-tier heterogeneous UDNs. To mitigate interference, balance cell load, guarantee QoS requirements of UE and improve system throughput, a non-convex NP-hard problem is formulated, and this joint problem is decoupled into the three independent sub-problems. To effectively solve these sub-problems, we propose three schemes: a new user-centric overlapped virtual cell clustering scheme, a low-complexity PRB allocation scheme and a power allocation scheme using the DC programing method. Simulation results confirm that our proposed schemes are better than existing schemes in terms of user rates, cell load and system throughput.

Table 1 Simulation parameters
Full size table