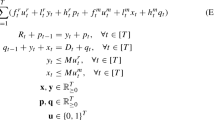Background

In the economic lot-sizing problem with product returns and remanufacturing (ELSR) the objective is to determine the quantities to produce and remanufacture at each period in order to meet the demand requirements of a single product on time, minimizing all the costs involved. Eventually, disposal option for returns is considered. This kind of problem has attracted growing attention over the last years from both the academic as well as the industry side [1–5]. Governmental, social pressures and economic opportunities have motivated many firms to become involved with the return of used products for recovery. Among the industrial options for recovering, the remanufacturing activity can be defined as the recovery process of returned products after which it is warranted that the remanufactured products offer the same quality and functionality that those newly manufactured [6, 7]. Products that are remanufactured include automotive parts, engines, tires, aviation equipment, cameras, medical instruments, furniture, toner cartridges, copiers, computers, and telecommunications equipment. Remanufacturing offers benefits for all of the parties involved. From the consumer’s point-of-view, remanufactured products assume the same quality of new products and are sometimes offered at an inferior market price. For the manufacturer, remanufacturing provides cost savings in energy consumption, raw materials, and labour. Finally, the environment benefits from the more efficient use of raw materials and energy employed during the production phase. In addition, remanufacturing tends to reduce the total number of products put in the market and later disposed, i.e. long-life products. For overviews about remanufacturing, the reader is referred to Ijomah [6], Hormozi [8], Sundin [9] and Gutowski et al. [10].

Richter and Sombrutzki [11] and Richter and Weber [12] consider the ELSR for the particular case in which the number of returns in the first period is sufficient to satisfy the total demand over the planning horizon. Golany et al. [13] provide a Network Flow formulation for the ELSR and an exact algorithm of O(T 3) time for the case of linear cost functions. They also show that the ELSR is NP-hard for the case of general concave cost functions. Yang et al. [14] show the same result of complexity for the case of stationary concave cost functions and suggest a heuristic procedure of O(T 4) time for the ELSR. van den Heuvel [15] shows that ELSR is NP-hard for the case of set-up and unit costs for the activities and unit costs for holding inventory, even in the time-invariant case, i.e., the same values for every period. Teunter et al. [16] consider two ELSR variants with joint and separate set-up costs for the production and remanufacturing, respectively. For the case of joint set-up costs they provide an exact algorithm of O(T 4). For the case of separate set-up costs, they adapt and compare three well-known heuristics, including the Silver-Meal based heuristic. Later, Schulz [17] extends and improves the work of Teunter et al. [16] about the Silver-Meal based heuristic for the ELSR, and Retel-Helmrich et al. [18] provide and compare different mathematical formulations for the ELSR with both separate and joint set-up costs. They also show that both ELSR variants are NP-hard in general. In Piñeyro and Viera [19] we suggest and compare several inventory policies for the ELSR using a divide-and-conquer approach, including a Tabu Search-based on procedure. Piñeyro and Viera [20] consider the problem of determining the remanufacturing quantities of an optimal solution of the ELSR assuming that the periods where the remanufacturing is allowed are known in advance. Li et al. [21] suggest and evaluate a more sophisticated Tabu Search based on procedure for the ELSR. They propose a block-chain method to produce high-quality initial solutions and a new LP formulation for determining the minimum cost of each block. Baki et al. [22] also exploit the block-chain structure of the ELSR solutions in order to provide a dynamic programming based procedure of polynomial time. In Sifaleras et al. [23] Variable Neighborhood Search (VNS) based on procedures are suggested and compared with others solving methods in the literature. The authors also present a benchmark set of problem instances with a large number of periods. Several authors have considered extensions of the ELSR. Pan et al. [24] address a dynamic lot-sizing problem with returns recovery and capacity constraints. Mitra [25] analyzes a two-echelon inventory system with returns. Piñeyro and Viera [26] consider the ELSR with substitution of remanufactured products by new ones but not viceversa.

In this paper we consider the ELSR formulation introduced by Teunter et al. [16] for the separate set-up scheme, i.e., separate set-up costs for producing and remanufacturing. We note that this ELSR formulation is also considered in Schulz [17], Li et al. [21], Baki et al. [22] and Sifaleras et al. [23]. Our contributions for this formulation of the ELSR are threefold. First we provide a new theoretical result about the form of the optimal solutions of the ELSR, which can be considered an extension of the well-known zero-inventory property for the classic economic lot-sizing problem without returns options (ELSP). We also note that this result is also valid for the case of time-variant costs with non-speculative motives. Secondly, we use this theoretical result for improving the Tabu Search based on procedure suggested in Piñeyro and Viera [19] for the ELSR. Finally, we evaluate the original as well as the optimized version of the procedure in a benchmark set of large instances (52 periods) introduced by Sifaleras et al. [23]. The numerical experiment carried out shows that both the original and the optimized version of the Tabu Search procedure outperform the VNS based procedure suggested in Sifaleras et al. [23] in over 90 % of the tested cases and in about tenth of computation time in the worst case.

The rest of the paper is organized as follows. Methods section provides the problem formulation and a theoretical result about the optimal solutions of the ELSR. Then we describe the improvement performed on the Tabu Search based on procedure of Piñeyro and Viera [19]. In Results and discussion section we report the numerical experiment carried out for the set of large instances introduced by Sifaleras et al. [23]. The paper ends with the Conclusions section with some guidelines for future research.

Methods

Problem formulation and analysis

We address a dynamic lot-sizing problem of a single product for which the demand requirements of each period over a finite planning horizon must be satisfied on time either by producing new items or by remanufacturing used items returned to the origin. Figure 1 shows a picture of the flows of items for the inventory system that represents the lot-sizing problem under consideration.

Fig. 1
figure 1

Flow of items in the ELSR

Full size image

There are set-up costs for producing and remanufacturing, and unit costs for carrying ending positive inventory from one period to the next. As in Teunter et al. [16], we consider the following assumptions. Unit costs are assumed zero for both production and remanufacturing. Inventory costs for used items are at most equal to the inventory costs for serviceable items, i.e. low-cost returns. Cost values are time-invariant, i.e. stationary costs pattern. The objective is to determine the quantities to produce and remanufacture for each one of the periods in the planning horizon in order to meet the demand requirements on time and minimizing the sum of the involved costs. This problem can be formulated as the following Mixed Integer Linear Programming (MILP) [16, 17, 21–23]:

$$ \min {\displaystyle \sum_{t=1}^T\left\{{K}^p{\delta}_t^p+{K}^r{\delta}_t^r+{h}^s{y}_t^s+{h}^u{y}_t^u\right\}} $$
(1)

subject to:

$$ {y}_t^s={y}_{t-1}^s+{p}_t+{r}_t-{D}_t\kern1em \forall t=1,2,\dots, T $$
(2)
$$ {y}_t^u={y}_{t-1}^u-{r}_t+{R}_t\kern1em \forall t=1,2,\dots, T $$
(3)
$$ M{\delta}_t^p\ge {p}_t\kern1em \forall t=1,2,\dots, T $$
(4)
$$ M{\delta}_t^r\ge {r}_t\kern1em \forall t=1,2,\dots, T $$
(5)
$$ {y}_0^s={y}_0^u=0 $$
(6)
$$ {\delta}_t^p,{\delta}_t^r\in \left\{0,1\right\}\kern0.5em {p}_t,{r}_t,{y}_t^s,{y}_t^u\ge 0\kern1em \forall t=1,2,\dots, T $$
(7)

In model (1) – (7) the parameters T, D t and R t denote the length of the planning horizon, demand and returns values in periods t = 1, …, T, respectively; K p (K r), is the set-up cost for production (remanufacturing); h s (h u) is the unit cost of holding inventory for serviceable (used) products; M is a number at least as large as max{D 1T , R 1T }, where D ij and R ij are the accumulative demand and returns between periods i and j, with 1 ≤ i ≤ j ≤ T. The decision variables p t and r t denote the number of units produced and remanufactured in periods t = 1, …, T, respectively; \( {\delta}_t^p \) (\( {\delta}_t^r \)) is a binary variable equal to 1 if production (remanufacturing) is carried out in periods t = 1, …, T, or 0 otherwise; \( {y}_t^s \) ( \( {y}_t^u \)) is the inventory level of serviceable (used) items for periods t = 1, …, T.

A result about the optimal solutions form

In this section we present a property about the form of optimal solutions of the ELSR. It can be considered a generalization of the well-known zero-inventory property for the ELSP introduced by Wagner and Whitin [27]. Also Teunter et al. [16] generalize this property for the case of joint set-up scheme of the ELSR and Richter and Sombrutzki [11] and Richter and Weber [12] for the case of sufficiently large number of returned products in the first period. Here we demonstrate that there is an optimal solution for which it holds that for any couple of periods i and j of either positive production or positive remanufacturing, there must be at least one period with zero-inventory level of serviceable items. Note that if it not the case, we can obtain a new feasible solution by transferring at least one unit of the production (remanufacturing) quantity from period i to the next period j, thus reducing the inventory level of serviceable items and with at most the same cost.

Proposition 1. There is an optimal solution for which it holds that for any pair of periods i and j, i < j, there is at least one period t such that \( {p}_i{y}_t^s{p}_j=0 \) and \( {r}_i{y}_t^s{r}_j=0 \), with i ≤ t < j.

Proof. Consider an ELSR feasible solution s = (p, r) with a production plan p and a remanufacturing plan r, respectively. Without loss of generality, suppose first that there is only one pair of successive periods i and j for which \( {p}_i{y}_t^s{p}_j>0 \) for all period t in 1 ≤ i ≤ t < j ≤ T. Then, define \( \varepsilon = \min \left\{{p}_i,{y}_i^s,{y}_{i+1}^s,\dots, {y}_{j-2}^s,{y}_{j-1}^s\right\}>0 \) and determine a new solution s 1 = (p 1, r 1) with r 1 = r and p 1 = p except by \( {p}_i^1=\left({p}_i-\varepsilon \right) \) and \( {p}_j^1=\left({p}_j+\varepsilon \right) \). This new solution s 1 is feasible since it satisfies that \( {y}_t^{1s}\ge 0 \) for all t in 1 ≤ t ≤ T. For s 1 we have that \( {p}_i^1{y}_t^{1s}{p}_j^1=0 \) for some period t in 1 ≤ i ≤ t < j ≤ T, since at least one of the following two equations is fulfilled: \( {p}_i^1=0 \) and/or \( {y}_t^{1s}=0,\kern0.5em t:1\le i\le t<j\le T \). Note that the cost of s 1 is lower than the cost of the original solution s at least by a term equal to h s(j − i). The same reasoning is valid for the remanufacturing plan r. In this case, the new solution is less costly than the original at least by a term equal to (h s − h u)(j − i). Note that (h s − h u) ≥ 0 since we are assuming low-cost returns. Therefore, given any feasible solution s = (p, r), even optimal, we can determine a new feasible solution with at most the same cost and fulfilling the property of Proposition 1.

From Proposition 1 we can establish that in order to determine an optimal solution of the ELSR we may avoid those solutions in which the serviceable-inventory level is positive between any pair of successive periods of either positive production or positive remanufacturing. We also note that the zero-serviceable-inventory property as stated in Proposition 1 is valid in the case of time-variant costs with non-speculative motives, even with positive unit costs. Non-speculative motives on the costs mean that it is profitable to produce or remanufacture as late as possible, i.e., \( {c}_i^p+{\displaystyle \sum_{t=i}^{\left(j-1\right)}{h}_t^s}\ge {c}_j^p \) and \( {c}_i^r+{\displaystyle \sum_{t=i}^{\left(j-1\right)}\left({h}_t^s-{h}_t^u\right)}\ge {c}_j^r \) with 1 ≤ i ≤ j ≤ T. The proof for this case is straightforward and follows from the proof of above, since we are transferring forward either newly manufactured o remanufactured items. We state this generalization of Proposition 1 in the next corollary.

Corollary 1. Proposition 1 is also valid in the case of time-variant costs with non-speculative motives, even with positive unit costs.

The Tabu Search based on procedure

The ELSR as formulated in (1) – (7) is a NP-hard problem [18, 22]. Therefore, it is unlikely that we can develop any efficient time procedure for determining an optimal solution of the problem. Considering this complexity result, many authors have proposed heuristic methods for obtaining high quality solutions [14, 16, 17, 21–23]. In Piñeyro and Viera [19] we suggest a Tabu Search based on procedure in order to obtain a near optimal solution to the ELSR, even with a more general cost structure and disposal option for returns. The procedure is referred in that paper as Basic Tabu Search procedure (BTS) because it uses only the rudiments of the Tabu Search metaheuristic [28]. In addition, a simple notion of neighbourhood is used and only one move is defined to explore it. Despite this fact, the numerical experiment carried out in Piñeyro and Viera [19] show the effectiveness of the BTS procedure in a wide range of demand-returns-cost patterns. In Piñeyro and Viera [20] we present a thorough analysis about the problem of determining the remanufacturing quantities of an optimal solution that can be considered a theoretical support for the good behaviour of the BTS procedure reported in Piñeyro and Viera [19].

The original BTS procedure description

The BTS procedure begins by determining an initial ELSR solution from the set of periods fixed as positive-remanufacturing periods received as input. For each period i fixed as positive-remanufacturing period, the remanufacturing quantity is determined by means of the following remanufacturing rule:

$$ {r}_i= \min \left({y}_{i-1}^u+{R}_i,{D}_{i\left(j-1\right)}\right),\kern1em 1\le i<j\le T+1 $$
(8)

In (8) the period j is the next positive-remanufacturing period if it exists, or (T + 1) in the case that period i is the last one. Then, the corresponding optimal production plan (periods and quantities) is determined by means of a W-W algorithm type. The initial solution is marked as current solution and the exploration phase of the process begins. The set of neighbouring solutions is obtained from the current one by swapping the periods where remanufacturing occurs. For each one of the neighbouring solution, the remanufacturing quantities are determined by means of equation (8) and the corresponding optimal production plan by applying the W-W algorithm. The neighbouring solution with smaller cost is marked as the current solution for the next step. The exploration phase continues until either the number of iterations is greater than the total number of iterations allowed or the number of iterations without improvement is greater than the maximum allowed. The procedure returns the best global solution evaluated. For more details about the procedure we refer to Piñeyro and Viera [19].

An optimization process for the BTS procedure

Given the solution returned by the BTS procedure, we can check whether that solution satisfy the zero-serviceable-inventory property of Proposition 1. First we note that for any solution considered by the BTS procedure, the production plan satisfies the property stated in Proposition 1, since it is determined using a W-W algorithm [27]. Therefore, we must check the property only for the remanufacturing plan. We proceed as follows. For each period i of the remanufacturing plan with a strictly positive remanufacturing quantity consider the immediately next period j for which \( {r}_i{y}_t^s{r}_j>0 \) for all period t in 1 ≤ i ≤ t < j ≤ T. Define q > 0 as the minimum quantity between the remanufacturing level of period i and the serviceable-inventory level for all periods t in 1 ≤ i ≤ t < j ≤ T, i.e. \( q= \min \left\{{r}_i,{y}_i^s,{y}_{i+1}^s,\dots, {y}_{j-2}^s,{y}_{j-1}^s\right\}>0 \). Then, determine a new feasible remanufacturing plan by subtracting the quantity q to the remanufacturing level of period i, and adding q to the remanufacturing level of period j. The new remanufacturing plan satisfies the zero-serviceable-inventory property of Proposition 1 since either the remanufacturing level of period i or the serviceable-inventory level is zero for some period t in 1 ≤ i ≤ t < j ≤ T. In Fig. 2 we provide the pseudocode of the optimization stage added to the end of the BTS procedure according to the description above.

Fig. 2
figure 2

Pseudocode of the optimization suggested for the BTS procedure

Full size image

We note that the optimization process of Fig. 2 is O(T 2) time, thus keeping the running time of the original BTS procedure. This fact can be appreciated in the time consumption of CPU reported for both BTS variants in the next section about the numerical experiment.

Results and discussion

In this section we report the results of the numerical experiment carried out for the original BTS procedure of Piñeyro and Viera [19] and the optimized version according to the improvement suggested above. For the experiment we resort to the benchmark set of 108 different large instances of 52 periods developed by Sifaleras et al. [23] and downloadable from the authors web site http://users.uom.gr/~sifalera/benchmarks.html (last access: 24/07/2015). The benchmark set was designed with the aim to evaluate the robustness of the RGVNS procedure suggested in that paper. It is based on the Schulz [17] well-known benchmark set, but with instances more than four times larger. As the authors claim “this new benchmark set is more difficult and larger than those that have ever been used in the literature, for the ELSR problem”. For this benchmark set of large instances, the different values for both setup costs are 200, 500 and 2000; the values for the holding cost of used items are 0.2, 0.5 and 0.8. The holding cost for serviceable items is equal to 1. Demand values follow a normal distribution of mean 100 per period. Returns values also follow a normal distribution but three different means of 30, 50 and 70 are considered. The coefficient of variation of the normal distributions can be of 10 % and 20 % (small and large variance respectively). A total of 108 different instances of 52 periods were generated.

For both BTS procedure variants we use the following configuration values. The size of the tabu list is fixed at 1,000,000. The total number of iterations is 10,000 and the maximum without improvement is 50. The size of the tabu list and the total number of iterations are greater than those considered in Piñeyro and Viera [19] since the ELSR instances considered here are four times longer. However, we set the maximum number of iterations without improvement in 50 rather than 500 in order to maintain low computation times. The zero-remanufacturing plan is used as initial solution for all the instances, as in Piñeyro and Viera [19] and later in Sifaleras et al. [23].

The BTS procedure was coded in Java and the experiment was carried out in a Java Runtime Environment 1.8.0_25 on HP laptop with Intel(R) Core(TM) i5-42010 CPU, 8.00 GB of RAM, and operating system Windows 8.1 of 64 bits. We note that this computing environment is less powerful of that used in Sifaleras et al. [23].

In Table 1, Table 2, Table 3 and Table 4 we report the results for Gurobi optimizer, the VNS procedure from Sifaleras et al. [23] and for both BTS variants from our numerical experiment. As in Sifaleras et al. [23], in the 2nd column we mark in bold those instances for which Gurobi reaches the optimal solution. In the 3rd column we mark in bold those instances for which the VNS procedure achieves a minor cost solution than both BTS variants and with italic for only the original BTS procedure. Finally, in the 5th column we mark in bold those instances for which both BTS variants obtain the same solution, i.e. the optimization performed is not able to improve the solution of the original BTS. In order to compare the results obtained, the error is defined as in Sifaleras et al. [23], that is the percentage gap between the objective value of Gurobi (g) and the objective value of the solution determined by the procedure under consideration (p): 100 × (p − g)/g.

Table 1 Results on benchmark set of Sifaleras et al. [23]. Instances 1–27.
Full size table
Table 2 Results on benchmark set of Sifaleras et al. [23]. Instances 28–54
Full size table
Table 3 Results on benchmark set of Sifaleras et al. [23]. Instances 55–81
Full size table
Table 4 Results on benchmark set of Sifaleras et al. [23]. Instances 82–108
Full size table

From Tables 1 to 4 we note that both BTS procedure variants outperform the RGVNS procedure of Sifaleras et al. [23] in most cases. The original BTS achieves better solutions in 100 of 108 instances, and the optimized version in 102 instances, that is 92.59 % and 94.44 % of the total number of instances respectively. In addition, the optimized BTS achieves better solutions than the original version in 70 instances, which results in 64.81 % of the total number of instances. The original BTS procedure is able to achieve the same objective value as Gurobi in 5 instances, all them optimal values, and the optimized variant in 2 instances more, one of them optimal. In Fig. 3 you can clearly see the good performance of both BTS procedures.

Fig. 3
figure 3

Error values of the RGVNS and BTS procedures for the 108 instances

Full size image

Tables 5 and 6 provide the statistics of percentage errors and computation times respectively. As stated in Sifaleras et al. [23] the Gurobi optimizer is set to 3600 s of maximum time of running and 10−4 of tolerance. The RGVNS ran for 30s for all instances.

Table 5 Percentage cost errors
Full size table
Table 6 CPU times in seconds
Full size table

In average, solutions achieved by the optimized BTS procedure are nearly three times more cost-effective than those of the VNS procedure with a running time of 1.31 seconds and in less than tenth computation time in the worst case. In addition, the extra running time required for the optimization phase is almost negligible. Although the solutions provided by Gurobi are more cost-effective in most cases, the BTS procedure variants may also offer high quality solutions and with 1870 times less computational effort on average.

Conclusions

In this paper we have tackled the economic lot-sizing problem with remanufacturing under the assumptions of time-invariant costs and low-costs for the returns. We present a new theoretical result about the form of optimal solutions that can be considered a generalization of the well-known zero-inventory property of the classic economic lot-sizing problem, i.e. without returns options. Based on this extended property we develop an improvement to the Basic Tabu Search procedure of Piñeyro and Viera [19] for the ELSR. The original and the optimized version of the BTS procedure are compared against the VNS procedure of Sifaleras et al. [23] on a benchmark set of large instances (108 instances of 52 periods). The numerical experiment performed reveals that the original BTS procedure outperforms the VNS procedure in 92.59 % and the optimized version in 94.44 % of the total number of instances, respectively. The running time required to obtain the solution by both BTS procedures is about twenty times less on average and ten in the worst case. In addition, the optimized version outperforms the original BTS procedure in 64.81 % of the total number of instances in the benchmark set. We also note that both the original and the optimized BTS are able to reach an optimal solution for some of the instances.

In future works it would be interesting to see what the consequences are on the production plan of the optimization process on the remanufacturing plan presented here. Since the remanufacturing quantities may be changed during the optimization process, this can lead in a different optimal production plan [19]. We also note that the numerical experiment carried out in this paper is for a planning horizon of 52 periods which seems to be unrealistic in practice under deterministic assumptions. Therefore, it would be interesting to evaluate the optimized BTS procedure in a benchmark set of instances with smaller number of periods, in which the parameter values of the problem can be estimated more accurately. The cases of multi-item [29] or heterogeneous quality for the returns [30] are also interesting extensions for future works about the ELSR.