1 Introduction

Vehicle collision is a major cause that can lead to more severe spinning and drifting and even out of control of vehicle [1]. Vehicle dynamics control after a collision is of great importance to enhance vehicle dynamics safety and reduce casualties [2, 3]. Statistics from the National Highway Traffic Safety Administration (NHTSA) showed that 6.45 million vehicle crashes were reported in 2017 in the United States, resulting in 34560 fatalities [4]. Similarly, there were 247646 traffic accidents in 2019 in China, resulting in 62763 fatalities and 256101 injuries [5]. In particular, multi-impact crashes account for more than 30% of all the fatal accidents [6]. Due to the panic after an initial vehicle impact, the driver may fail to make appropriate response within a limited timeline [7]. A secondary impact may happen and bring about more serious consequence to the vehicle and its occupants. Thus, it is essential to effectually address vehicle stability control after an initial impact.

A vehicle collision model is first needed to analyze the impact process and to evaluate the impact impulse. Two types of collision modelling methods have been developed in the literature, including the structural analysis and the momentum conservation method. The structural analysis method usually constructs a numerical model in a finite element analysis software such as LS-DYNA [8] and PAM-CRASH [9]. To improve modelling accuracy, Calspan Corporation developed a dedicated program for NHTSA [10]. The structural analysis method can provide deeper insights into the collision process; however, it relies heavily on large sets of component and materials property configurations. In contrast, the momentum conservation method puts more emphasis on vehicle kinematic state change due to vehicle collisions, which makes it easier to implement. On this regard, Brach et al. treated vehicle as a rigid body with three degrees of freedom and defined the recovery and the friction coefficient [11]. Zhou et al. further took vehicle roll motion and tire forces into consideration and verified its superiority [12]. These studies cast new light on impact impulse magnitude calculation and motion prediction under different driving conditions and lay the foundation for designing collision mitigation controllers [13].

Early efforts towards secondary collision damage reduction has been directed to improving occupants protection using passive safety systems such as air bag [14] and safety belt [15]. In order to restore vehicle stability after an initial impact, researchers also resorted to active safety systems, and these can be divided into single actuator control and multiple actuators coordination control.

Single actuator control can further be classified into post-impact braking control (PIBC) and post-impact steering control (PISC). PIBC can reduce the harm of secondary collisions through dissipating vehicle kinetic energy. For instance, a PIBC modified from autonomous emergency braking is proved to be effective in 21% of post-impact cases [16], while BOSCH Co. Ltd. coordinated the airbag and electronic stability program (ESP) to achieve secondary collision mitigation [17]. Furthermore, Shotaro et al. [18] established an adaptive braking intensity control strategy for PIBC and improved its adaptiveness to different scenarios. Different from PIBC, PISC can improve post-impact stability in a more direct manner by adjusting lateral tire forces. Chan et al. developed a look-ahead controller for front steering angle adjustment to narrow lateral deviation [19]. Similarly, Cao et al. utilized model predictive control (MPC) to construct a PISC scheme [20]. Both PIBC and PISC controllers are proved to be effective in light collision cases. However, the efficacy may be largely compromised under severe drifting and large side slip angle after high-intensity impacts [21].

Multiple actuators coordination control has been proposed to better regulate vehicle motion after initial collisions. Benefiting from more control freedoms, better control performance can be achieved. According to different control objectives, the existing coordination control can be divided into system stability control and trajectory optimization. System stability control focuses on simultaneously regulating undesired post-impact motions including drifting, over-spinning and rollover. For example, Zhou et al. presented a sliding mode controller and an optimal allocator to coordinate the front steering and the differential braking to regulate sideslip angle and yaw rate [22]. Another MPC controller is also developed to mitigate the rollover risk [23]. Although the undesired motions were suppressed, the trajectory safety during stabilization control is not explicitly addressed. Trajectory optimization has also been studied to navigate second collision hazards. For instance, a trajectory optimization scheme was developed to minimize the maximum lateral path deviation using differential braking based on a quasi-linear optimal controller [24]. Furthermore, Kim et al. combined the desired final yaw angle with the lateral path deviation minimization based on linear time-varying MPC to avoid secondary collisions [25]. To avoid complex modeling, Yin et al. trained a multi-layer perception as a deterministic control policy to achieve self-learning drifting motion control for post-impact automated vehicles [26].

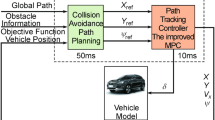
Previous studies have described various methods for post-impact stability control. However, challenges still remain in motion planning and stability control while achieving obstacle avoidance to prevent secondary collisions. In this study, a post-impact motion planning method combining the polynomial curve and artificial potential field (APF) is developed to restore vehicle stability when the vehicle falls into over-spinning and drifting. Different from traditional polynomial curve methods, three polynomial curves are respectively adopted to represent the longitudinal, lateral and yaw movements in the ground coordinate system. As such, the vehicle motion can be fully described without nonholonomic constraints. In addition, a time-varying linear quadratic regulator (TVLQR) is proposed to calculate the desired generalized forces based on the error dynamics model. By making full use of the instinct multi-objective optimization associated with LQR, the planned multi-dimensional motions can be simultaneously tracked. Furthermore, a nonlinear-optimization allocation (NOA) algorithm is designed to realize the desired generalized forces when tire forces are saturated. The schematic of the proposed scheme is illustrated as shown in Figure 1.

Figure 1
figure 1

The schematic of the proposed control scheme

Full size image

The remainder of this paper is organized as follows: Section 2 introduces the motion planning method by combining the polynomial curve and post-impact APF. Section 3 elaborates on the TVLQR controller to track the planned motion. Section 4 introduces the NOA algorithm to realize the desired generalized force/moment. Section 5 offers verification based on comprehensive hardware-in-loop (HIL) tests, followed by the key conclusions summarized in Section 6.

2 Post-impact Motion Planning By Combining the Polynomial Curve and APF

Previous vehicle path and trajectory planning schemes focus on the topology and the velocity planning [27]. These are achieved by assuming that the vehicle is driving stably without severe sideslip or over-spinning. Thus, the desired vehicle yaw motion can be determined by the velocity and the route curvature through nonholonomic constraints formulation [28]. However, the vehicle may tend to become unstable with significant drifting and over-spinning due to large collision impulse, and the stable driving assumption becomes invalid. This study aims to provide a motion planning method to simultaneously regulate the vehicle trajectory and yaw motion. Traditional planning methods mainly include the A* heuristic search, visibility graph method, generalized Voronoi diagram and artificial potential field, etc [29, 30]. Considering the continuity and smoothness of vehicle motion under extreme conditions, the combination of the quintic polynomial and artificial potential field is utilized to solve the motion optimization problem.

In order to fully depict vehicle motions, multiple coordinate systems are established as shown in Figure 2. The inertial ground coordinate system X-Y, the chassis coordinate system x-y and the tire coordinate system are appropriately defined. The X-axis is parallel to the road with the x-axis pointing to the vehicle-forward direction. Three different coordinate systems are associated through the yaw angle ψ and the front steering angle δ. It should be noted that the single-track vehicle dynamics model is utilized during motion planning, as the desired tire lateral forces can be directly deduced from parameterized vehicle motion through the single-track model, so that the dynamics constraints can be easily imposed on the polynomial curve.

Figure 2
figure 2

The single-track vehicle dynamics model in multiple coordinate systems

Full size image

The motion to be planned after impacts can be described with the coordinate in the inertial ground coordinate system (X, Y) and the yaw angle ψ, which are represented by a group of polynomial functions of the planning time τ as indicated in Eq. (1). It is worth noted that both the cubic and quartic curves can satisfy the smoothness requirement, but their corresponding third-derivative functions are constant and linear, respectively. It means that the inherent implicit boundary constrains would be applied to the corresponding jerks that are equivalent to control output gradients. To balance the planning freedom and problem formulation complexity, the quintic curve is adopted as a compromise. By taking the first and the second derivative of the quintic polynomial curves with respect to τ, the velocity (\(\dot{X,} \, \dot{Y,}\dot{\psi}\)) and the acceleration state (\(\ddot{X,} \ddot{Y,} \ddot{\psi}\)) can be obtained in the planned time interval as

$$\left\{ \begin{gathered} X(\tau ) = \sum\limits_{k = 0}^{5} {a_{k} (\tau - \tau_{0} )^{k} ,} \hfill \\ Y(\tau ) = \sum\limits_{k = 0}^{5} {b_{k} (\tau - \tau_{0} )^{k} ,} \hfill \\ \psi (\tau ) = \sum\limits_{k = 0}^{5} {c_{k} (\tau - \tau_{0} )^{k} ,} \hfill \\ \end{gathered} \right.$$
(1)

where τ0 is the starting time of motion planning, and k is the order of the corresponding items in the quintic curves varying from 0 to 5. Then, the problem can be transformed to derive the quintic polynomial curve parameters ak, bk and ck. With known vehicle states, the parameters a0, b0, c0, a1, b1 and c1 can be directly obtained according to initial vehicle states while the motion planning begins with [31, 32]

$$\left\{ \begin{gathered} a_{0} = X(\tau_{0} ),\;b_{0} = Y(\tau_{0} ),\;c_{0} = \psi (\tau_{0} ), \hfill \\ a_{1} = \dot{X}(\tau_{0} ),\;b_{1} = \dot{Y}(\tau_{0} ),\;\;c_{1} = \dot{\psi }(\tau_{0} ). \hfill \\ \end{gathered} \right.$$
(2)

There are twelve parameters to be determined, which are capsulated in a vector p as

$${\varvec{p}}(1:12) = [a_{2} ,a_{3} ,a_{4} ,a_{5} ,b_{2} ,b_{3} ,b_{4} ,b_{5} ,c_{2} ,c_{3} ,c_{4} ,c_{5} ].$$
(3)

Then the optimal solution is pursued to design the motion for obstacle avoidance and stability restoration considering vehicle dynamics constraints.

The obstacle locations can be obtained via environmental perception [33, 34]. In order to describe the safety of the post-impact obstacle avoidance trajectory, the artificial potential field method is utilized to construct the objective function. For describing the impact of the obstacles ahead with the coordinate (Xb, Yb), the exponential potential function is employed with a safety radius Dr given as

$$U_{1} = e^{{ - (\sqrt {(X(\tau ) - X_{b} )^{2} + (Y(\tau ) - Y_{b} )^{2} } - D_{r} )}} .$$
(4)

Based on the exponential function characteristics, it can be deduced that the punishment effect would be amplified exponentially once the relative distance is smaller than Dr so as to force the vehicle away from the obstacles. Thus, the determination of Dr should cover both the vehicle and obstacle contours and the safety margin. The exponential potential function for the road boundaries is defined as U2, in which Ds, Ymax and Ymin are the safety distance and the upper and lower road boundaries, respectively. Similarly, the choice of Ds should cover the vehicle contour and the safety margin.

$$U_{2} = e^{{ - (\left| {Y(\tau ) - Y_{\max } } \right| - D_{s} )}} { + }e^{{ - (\left| {Y(\tau ) - Y_{\min } } \right| - D_{s} )}} .$$
(5)

A 3-D map of the potential field that displays the threats around the vehicle at a particular instant is illustrated in Figure 3. The final field function for a specified trajectory U is set to maximize the weighted sum of U1 and U2 within the planning time interval as shown in Eq. (6), where τf and k1 and k2 are the ending time and the weighting factors, respectively. Since the collisions with obstacles or road boundaries should be treated equally, k1 and k2 are set to be the same. It should be noted that it is expected to punish the most dangerous position of a trajectory. Thus, the maximum of the combined function within the planning time interval [τ0, τf] is adopted as the final field function given as

$$U = \mathop {\max }\limits_{{\tau \in [\tau_{0} ,\tau_{f} ]}} (k_{1} U_{1} + k_{2} U_{2} ).$$
(6)
Figure 3
figure 3

The potential field of the surrounding obstacles

Full size image

Considering that the vehicle may endure over-spinning and drifting after light impacts and that one primary goal is to restore vehicle stability, another objective function V for the approaching stability is designed based on the average vehicle sideslip angle. The vehicle sideslip angle is calculated as the difference between the heading angle and the yaw angle in the ground coordinate system. The objective function V can be given by

$$V = \frac{1}{{\tau_{f} - \tau_{0} }}\int {\left( {\left| {\arctan (\frac{{\dot{Y}(\tau )}}{{\dot{X}(\tau )}}) - \psi (\tau )} \right|} \right)} \rm{d}\tau .$$
(7)

The final objective function S is composed of the final field function U and the stability approaching function V through the weighting factors k3 and k4, which is given by

$$S = k_{3} U + k_{4} V.$$
(8)

There is no uniform rule for choosing k3 and k4, which need to be calibrated through massive tests. Based on our calibration experience, it is recommended to keep them approximately the same.

Some linear and nonlinear constraints need to be given to rationalize the optimization problem. The linear constraints are constructed according to the requirements on the terminal vehicle states. It would be ideal that the final lateral velocity \(\dot{Y}(\tau_{f})\) and yaw rate \(\dot{\psi}(\tau_{f})\) can drop to zero. Also, the lateral displacement \(Y(\tau_{f})\) and yaw angle \({\psi}(\tau_{f})\) of the vehicle should satisfy the road conditions. After substituting the parameters in Eq. (2), the known terminal states above and the ending time τf into Eq. (1), Eq. (9) can be derived. The polynomial equation of the left side can be seen as a linear combination of the optimization variables given in Eq. (3). The items in the right side are all known. Thus, Eq. (9) constitutes the linear constraints on the motion planning problem, which is given by

$$\left\{ \begin{aligned} \sum\limits_{k = 2}^{5} {b_{k} } (\tau_{f} - \tau_{0} )^{k} & = Y(\tau_{f} ) - Y(\tau_{0} ) - \dot{Y}(\tau_{0} )(\tau_{f} - \tau_{0} ), \\ \sum\limits_{k = 2}^{5} {c_{k} } (\tau_{f} - \tau_{0} )^{k} & = \psi (\tau_{f} ) - \psi (\tau_{0} ) - \dot{\psi }(\tau_{0} )(\tau_{f} - \tau_{0} ), \\ \sum\limits_{k = 2}^{5} {kb_{k} } (\tau_{f} - \tau_{0} )^{k - 1} & = \dot{Y}(\tau_{f} ) - \dot{Y}(\tau_{0} ), \\ \sum\limits_{k = 2}^{5} {kc_{k} } (\tau_{f} - \tau_{0} )^{k - 1} & = \dot{\psi }(\tau_{f} ) - \dot{\psi }(\tau_{0} ). \\ \end{aligned} \right.$$
(9)

The nonlinear constraint is constructed according to vehicle dynamics. First, the maximum acceleration is confined by road adhesion. The resultant acceleration a(τ) at the planning time τ for a specified trajectory can be calculated by

$$a(\tau ) = \sqrt {\ddot{X}(\tau )^{2} + \ddot{Y}(\tau )^{2} },$$
(10)

where \(\ddot{X}(\tau) \, \text{and} \, \ddot{Y}(\tau)\) are the longitudinal and lateral accelerations in the ground coordinate system determined by the polynomial curves. Then, the maximum acceleration can be given by

$$\mathop {\max }\limits_{{\tau \in [\tau_{0} ,\tau_{f} ]}} (a(\tau )) \le g\mu ,$$
(11)

where μ and g are the road friction coefficient and the gravitational acceleration, respectively.

The vehicle dynamics restrictions on the coordination of the vehicle lateral force and yaw moment are also considered. According to the D'Alembert principle, every acceleration movement can be equivalent to a D'Alembert inertia force or moment. Thus, the vehicle dynamics problem can be reformulated into a pseudo-static one. The D'Alembert lateral force \(F_{y}^{\prime}(\tau)\) and yaw moment \(M_{z}^{\prime}(\tau)\) determined by the polynomial at time step τ can be given as

$$F_{y}^{^{\prime}} (\tau ) = m( - \ddot{X}(\tau ) \times \sin (\psi (\tau )) + \ddot{Y}(\tau ) \times \cos (\psi (\tau ))),$$
(12)
$$M_{z}^{^{\prime}} (\tau ) = I_{z} \times \ddot{\psi }(\tau ),$$
(13)

where m and Iz are the vehicle mass and yaw moment of inertia. The static moment equilibrium about the front tire can be calculated as

$$F_{y}^{^{\prime}} (\tau )L_{f} - F_{yr} (\tau )(L_{f} + L_{r} ) - M_{z}^{^{\prime}} (\tau ) = 0,$$
(14)

where Lf and Lr are the distances from the center of gravity (CG) to the front and the rear axle, respectively; Fyr(τ) is the lateral force at the rear tires required by a specified trajectory. It can be regrouped as

$$F_{yr} (\tau ) = \frac{{L_{f} \times F_{y}^{^{\prime}} (\tau ) - M_{z}^{^{\prime}} (\tau )}}{{L_{f} + L_{r} }}.$$
(15)

The absolute value of Fyr should be well below the rear-axis adhesion limitation, and then the second nonlinear constraint is constructed as

$$\mathop {\max }\limits_{{\tau \in [\tau_{0} ,\tau_{f} ]}} (\left| {F_{yr} (\tau )} \right|) \le \frac{{mgL_{f} }}{{L_{f} + L_{r} }} \times \mu .$$
(16)

The optimization-based motion planning can be summarized into finding the polynomial parameter p with the lowest value of the combined index S, while satisfying the linear and the nonlinear constraints, which is given by

$$\begin{gathered} {\varvec{p}} = \arg \min S, \\ s.t.\;\;{\text{Eqs}}.\;(9)\;(11)\;(16). \\ \end{gathered}$$
(17)

It should be noted that a numerical solution instead of the analytical solution is computed. The optimization problem is solved using the fmincon toolbox in MATLAB. Once the parameters p is derived, the motion planning is completed.

3 Motion Tracking Control Based on the TVLQR

The reference coordinates (Xd, Yd) and the yaw angle ψd at time step t can be obtained by calculating the polynomial values. In order to achieve the desired motions and positions derived from Section 2 against unknown disturbances, a motion tracking controller is designed based on the TVLQR approach.

High-order continuity and differentiability are achieved by using the quintic polynomial curves in motion planning. Thus, the desired motion (\(\dot{X}_{d}\), \(\dot{Y}_{d}\), \({\dot{\psi}}_{d}\)) and acceleration (\(\ddot{X}_{d}\), \(\ddot{Y}_{d}\), \({\ddot{\psi}}_{d}\)) in the ground coordinate system at time step t can be attained by calculating the first and the second derivative, respectively. The desired motion in the vehicle coordinate system including the longitudinal velocity \(U_{xd}\), lateral velocity \(U_{yd}\) and yaw rate \(r_{d}\) can be given by

$$(U_{xd} ,U_{yd} ,r_{d} )^{\prime} = {\varvec{T}}_{{{{co}}}} (\dot{X}_{d} ,\dot{Y}_{d} ,\dot{\psi }_{d} )^{\prime},$$
(18)

where Tco is the coordinate transformation matrix from the ground to the vehicle coordinate, which is given by

$${\varvec{T}}_{co} = \left[ {\begin{array}{*{20}ll} {\cos (\psi_{d} )} & {\sin (\psi_{d} )} & 0 \\ { - \sin (\psi_{d} )} & {\cos (\psi_{d} )} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right].$$
(19)

Similarly, the open-loop reference control inputs including the longitudinal force \(F_{xr}\), lateral force \(F_{yr}\) and yaw moment \(M_{r}\) can be reformulated in the same way, which is given by

$$(F_{xr} ,F_{yr} ,M_{r} )^{\prime} = {\varvec{T}}_{co} (m\ddot{X}_{d} ,m\ddot{Y}_{d} ,I_{z} \ddot{Z}_{d} )^{\prime}.$$
(20)

The open-loop control can be deduced in an ideal case, but the actual implementation performance is subject to undesired disturbances such as error accumulation and parameter uncertainties. Thus, a closed-loop correction based on the TVLQR method is introduced.

The vehicle dynamics equations are introduced as

$$\left\{ \begin{aligned} F_{xo} &= m \times (\dot{U}_{x} - r \times U_{y} ), \\ F_{yo} &= m \times (\dot{U}_{y} + r \times U_{x} ), \\ M_{zo} & = I_{z} \times \dot{r}, \\ \end{aligned} \right.$$
(21)

where Ux, Uy and r are the longitudinal velocity, lateral velocity and yaw rate; Fxo, Fyo and Mzo are the objective longitudinal force, lateral force and yaw moment. And the vehicle kinematic equations are given as

$$\left\{ \begin{aligned} \dot{X} & = U_{x} \times \cos (\psi ) - U_{y} \times \sin (\psi ), \\ \dot{Y}& = U_{x} \times \sin (\psi ) + U_{y} \times \cos (\psi ), \\ \dot{\psi } &= r. \\ \end{aligned} \right.$$
(22)

Obviously, the dynamics and kinematic equations constitute a nonlinear system, which is modified by local linearization. Then, its linear state-space form with the system state vector x and the system input vector u can be given as

$$\left\{ \begin{aligned} {\dot{\varvec{x}}} &= {\varvec{Ax}} + {\varvec{Bu}}, \\ {\varvec{x}} & = (U_{x} ,U_{y} ,r,X,Y,\psi )^{\prime}, \\ {\varvec{u}}& = (F_{xo} ,F_{yo} ,M_{zo} )^{\prime}, \\ \end{aligned} \right.$$
(23)

where A is the Jacobian matrix for local linearization and B is the input matrix, and they are given as

$${\varvec{A}} = \left[ {\begin{array}{*{20}c} 0 & r & {U_{y} } & 0 & 0 & 0 \\ { - r} & 0 & { - U_{x} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ {\cos (\varphi )} & { - \sin (\varphi )} & 0 & 0 & 0 & { - U_{x} \sin (\varphi ) - U_{y} \cos (\varphi )} \\ {\sin (\varphi )} & {\cos (\varphi )} & 0 & 0 & 0 & {U_{x} \cos (\varphi ) - U_{y} \sin (\varphi )} \\ 0 & 0 & 1 & 0 & 0 & 0 \\ \end{array} } \right],$$
(24)
$${\varvec{B}} = \left[ {\begin{array}{*{20}l} \frac{1}{m} & 0 & 0 & 0 & 0 & 0 \\ 0 & \frac{1}{m} & 0 & 0 & 0 & 0 \\ 0 & 0 & {\frac{1}{{I_{z} }}} & 0 & 0 & 0 \\ \end{array} } \right]^{\prime } .$$
(25)

The continuous system in Eq. (23) is discretized with the sampling time of T by

$${\dot{\varvec{x}}} = \frac{{{\varvec{x}}_{k + 1} - {\varvec{x}}_{k} }}{T},$$
(26)
$${\varvec{x}}_{k + 1} = {\varvec{A}}_{dk} {\varvec{x}}_{k} + {\varvec{B}}_{d} {\varvec{u}}_{k} ,$$
(27)

where Adk and Bd are the time-varying state transition and input matrices with

$$\left\{ \begin{gathered} {\varvec{A}}_{dk} = \left. {\varvec{A}} \right|_{{x = x_{dk} }} \times T + {\varvec{I}}, \hfill \\ {\varvec{B}}_{d} = {\varvec{B}} \times T. \hfill \\ \end{gathered} \right.$$
(28)

The error dynamics of the vehicle is constructed by

$${{\varvec{\xi}}}_{k + 1} = {\varvec{A}}_{dk} {{\varvec{\xi}}}_{k} + {\varvec{B}}_{d} {\varvec{\Delta u}}_{k} ,$$
(29)

where ξk and Δuk are the state error vector and the control input correction, which are expressed as

$$\left\{ \begin{gathered} {{\varvec{\xi}}}_{k} = {\varvec{x}}_{k} - {\varvec{x}}_{dk} , \hfill \\{\varvec{\varDelta}}{\varvec{u}}_{k} = {\varvec{u}}_{k} - {\varvec{u}}_{rk} , \hfill \\ \end{gathered} \right.$$
(30)

where xdk is the desired vehicle motion and position deduced from the planned polynomial while urk is the reference open-loop control input from Eq. (20) at time step k, which are

$${\varvec{x}}_{dk} = \left. {[\begin{array}{*{20}c} {U_{xd} } & {U_{yd} } & {r_{d} } & {X_{d} } & {Y_{d} } & {Z_{d} } \\ \end{array} ]^{\prime}} \right|_{t = kT} ,$$
(31)
$${\varvec{u}}_{rk} = \left. {\left[ {\begin{array}{*{20}c} {F_{xr} } & {F_{yr} } & {M_{r} } \\ \end{array} } \right]^{\prime } } \right|_{t = kT} .$$
(32)

Linear quadratic regulator (LQR) is a kind of closed-loop optimal control method for linear systems to achieve quadratic minimization of the objective function [35]. Considering computational efficiency and multi-objective optimization, the LQR controller is adopted to achieve closed-loop motion tracking. The discrete linear model for LQR has been established in Eq. (29). The assumption of full state accessibility makes the application of LQR possible. Time-varying state transition matrix Adk would replace the traditional constant state transition matrix at each time step, thus forming the TVLQR control problem. The quadratic cost function is given by

$$J = \sum\limits_{k = 0}^{\infty } {\left( {{{\varvec{\xi}}}_{k}^{\rm{T}} {\varvec{Q\xi }}_{k} + {\varvec{\Delta u}}_{k}^{\rm{T}} {\varvec{R\Delta u}}_{k} } \right)} ,$$
(33)

where Q=QT and R=RT are the positive definite weighting coefficient matrices that are used to penalize the states error and control input correction, respectively. Then, the control correction Δuk to minimize the cost function is given by

$${\varvec{\Delta u}}_{k} = - {\varvec{K}}_{k} {{\varvec{\xi}}}_{k} ,$$
(34)

where Kk is the gain matrix given by

$${\varvec{K}}_{k} = ({\varvec{B}}_{d}^{\rm{T}} {\varvec{XB}}_{d} + {\varvec{R}})^{ - 1} {\varvec{B}}_{d}^{\rm{T}} {\varvec{XA}}_{dk} ,$$
(35)

where X is the solution to the Riccati equation, which is expressed as

$${\varvec{A}}_{dk}^{\rm{T}} {\varvec{XA}}_{dk} - {\varvec{X}} - {\varvec{A}}_{dk}^{\rm{T}} {\varvec{XB}}_{d} ({\varvec{B}}_{d}^{\rm{T}} {\varvec{XB}}_{d} + {\varvec{R}})^{ - 1} {\varvec{B}}_{d}^{\rm{T}} {\varvec{XA}}_{dk} + {\varvec{Q}} = 0.$$
(36)

Finally, solving the Riccati equation is accomplished with the MATLAB function dare. The solving process is executed at each time step to account for the time-varying system model. After obtaining the control correction, the overall control input can be derived as

$${\varvec{u}}_{k} = {\varvec{\Delta u}}_{k} + {\varvec{u}}_{rk} .$$
(37)

The derived outcome is used in the allocation algorithm presented in the following section.

4 Nonlinear-Optimization-Based Allocation Algorithm under Extreme Conditions

The objective resultant forces (Fxo, Fyo) and yaw moment Mzo are derived in the previous section. It is essential to coordinate multiple chassis actuators including the propulsion, braking and steering actuators to achieve the desired resultant forces and moment. Active safety control systems such as ESP and direct yaw-moment control (DYC) often adopt direct control allocation [36], quadratic programming allocation [37] and daisy chain allocation [38] to achieve coordination control. To simplify the allocation problem, these traditional allocation methods often impose constraints on the longitudinal tire forces to keep the tires working in the linear region to neglect the coupling relationship between the longitudinal and the lateral tire forces [39]. Nevertheless, this limits the control performance and may introduce large deviations especially in extreme conditions where the vehicle may endure severe spinning and/or drifting due to external impacts. In this study, a nonlinear-optimization allocation algorithm that is competent under tire force saturation in extreme conditions is developed.

Different from the single-track dynamics model used in motion planning, a four-wheel vehicle dynamics model is developed to determine each actuator’s output as shown in Figure 4. To fully verify the effectiveness of the proposed control scheme, a four-wheel-independent-drive electric vehicle (FWID EV) is used as the research object. It should be noted that the proposed scheme is also suitable for conventional vehicles equipped with ESP by modifying the constrains. In fact, combining 4-wheel-drive (4WD) and ESP can achieve similar effects.

Figure 4
figure 4

The four-wheel  vehicle dynamics model for FWIA EVs

Full size image

The primary goal of the allocation algorithm is to obtain proper control commands for the steering, propulsion and braking chassis subsystems, which is given by

$${\varvec{x}}_{c} = [\delta \;F_{x1} \;F_{x2} \;F_{x3} \;F_{x4} \;F_{y1} \;F_{y2} \;F_{y3} \;F_{y4} ],$$
(38)

where Fxi and Fyi are the longitudinal and lateral forces of each tire with the subscript i= (1, 2, 3, 4) representing the front-left, front-right, rear-left and rear-right tires, respectively. According to the force analysis, the resultant forces (Fx, Fy) and yaw moment Mz produced by the steering angle and tire forces can be calculated as

$$\left\{ \begin{gathered} F_{x} = F_{x1} \cos (\delta ) - F_{y1} \sin (\delta ) + F_{x2} \cos (\delta ) - F_{y2} \sin (\delta ) + F_{x3} + F_{x4} , \hfill \\ F_{y} = F_{x1} \sin (\delta ) + F_{y1} \cos (\delta ) + F_{x2} \sin (\delta ) + F_{y2} \cos (\delta ) + F_{y3} + F_{y4} , \hfill \\ M_{z} = - (F_{x1} \cos (\delta ) - F_{y1} \sin (\delta ))\frac{{D_{b} }}{2} + (F_{x1} \sin (\delta ) + F_{y1} \cos (\delta ))L_{f} \hfill \\ \;\;\;\;\;\;\;\;\;\; + (F_{x2} \cos (\delta ) - F_{y2} \sin (\delta ))\frac{{D_{b} }}{2} + (F_{x2} \sin (\delta ) + F_{y2} \cos (\delta ))L_{f} \hfill \\ \;\;\;\;\;\;\;\;\;\; - F_{x3} \frac{{D_{b} }}{2} - F_{y3} L_{r} + F_{x4} \frac{{D_{b} }}{2} - F_{y4} L_{r} , \hfill \\ \end{gathered} \right.$$
(39)

where Db is the track width. In order to make the resultant forces and yaw moment approach their target values, an objective function Vo is set as

$$V_{o} = \varepsilon_{1} \left( {F_{xo} - F_{x} } \right)^{2} + \varepsilon_{2} (F_{yo} - F_{y} )^{2} + \varepsilon_{3} (M_{zo} - M_{z} )^{2} ,$$
(40)

ε1, ε2 and ε3 are the weighting coefficients for adjusting tracking priorities among the longitudinal force, lateral force and yaw moment of the vehicle. Considering that obstacle avoidance is feasible only when the violent over-spinning motion is suppressed in the early stage to a certain extent, the yaw moment bears more importance and should be given higher priority. Thus, ε3 is recommended to be slightly larger than the other two.

To ensure that the optimization problem can be solved within a feasible timeline, the constraints are analyzed. The tire forces are strongly associated with the cornering velocities, vertical forces at each tire and road friction coefficient. Assuming that the vehicle velocities (Ux, Uy) and yaw rate r can be attained in real-time, the vehicle longitudinal and lateral velocities (vxi, vyi) at the i-th tire center can be calculated as

$$v_{xi} = U_{x} \pm D_{b} r/2,$$
(41)
$$v_{yi} = U_{y} \pm L_{(f,\;r)} r.$$
(42)

The sign in Eq. (41) is set to be positive for the right wheels while negative for the left. The sign in Eq. (42) is set to be positive for the front wheels while negative for the rear. Then, the side-slip angle of the i-th tire can be calculated by

$$\left\{ \begin{gathered} \alpha_{i(i = 1,2)} = \delta - \arctan \left(\frac{{v_{yi} }}{{v_{xi} }}\right), \hfill \\ \alpha_{i(i = 3,4)} = - \arctan \left(\frac{{v_{yi} }}{{v_{xi} }}\right). \hfill \\ \end{gathered} \right.$$
(43)

It should be noted that the roll dynamics of the sprung mass can influence the vertical tire forces. The vehicle roll dynamics and state estimation have been investigated in our previous studies [31], which can provide precise vertical forces. In this study, a simplified quasi-static calculation method is utilized for simplification. The vertical forces at different corners Fzi can be approximatively calculated according to the longitudinal acceleration ax and the lateral acceleration ay by

$$\left\{ \begin{gathered} F_{z1} = \frac{{mgL_{r} }}{2L} - \frac{{mha_{x} }}{2L} - \frac{{ma_{y} hL_{r} }}{{D_{b} L}}, \hfill \\ F_{z2} = \frac{{mgL_{r} }}{2L} - \frac{{mha_{x} }}{2L} + \frac{{ma_{y} hL_{r} }}{{D_{b} L}}, \hfill \\ F_{z3} = \frac{{mgL_{f} }}{2L} + \frac{{mha_{x} }}{2L} - \frac{{ma_{y} hL_{f} }}{{D_{b} L}}, \hfill \\ F_{z4} = \frac{{mgL_{f} }}{2L} + \frac{{mha_{x} }}{2L} + \frac{{ma_{y} hL_{f} }}{{D_{b} L}}, \hfill \\ \end{gathered} \right.$$
(44)

where h is the height of CG and L is the wheelbase given by

$$L = L_{f} + L_{r} .$$
(45)

It is difficult to precisely capture the tires forces due to its nonlinear characteristics and the coupling relationship between the longitudinal and the lateral force [40]. In order to simplify the tire force constraints, a combination of the lateral force Magic Formula and the elliptical formula is utilized to represent the nonlinear characteristics and coupling relationship in this study.

The lateral Magic Formula under pure sideslip conditions can be expressed as

$$F_{ymf} = D_{y} \sin (C_{y} \arctan (B_{y} \alpha - E_{y} (B_{y} \alpha - \arctan (B_{y} \alpha )))),$$
(46)

where By, Cy, Dy and Ey are the stiffness, shape, peak and curvature coefficients, which can be calculated by

$$\left\{ \begin{gathered} B_{y} = b_{3} \sin (b_{4} \arctan (b_{5} F_{z} )/C_{y} D_{y} , \hfill \\ D_{y} = b_{1} F_{z}^{2} + b_{2} F_{z} , \hfill \\ E_{y} = b_{6} F_{z}^{2} + b_{7} F_{z} + b_{8} , \hfill \\ \end{gathered} \right.$$
(47)

where b1–b8 in the Magic Formula are identified by fitting the bench test data obtained from CARSIM. The road friction coefficient corresponding to the test data is set to be 1. The fitting is conducted offline through the Curve Fitting Tool in MATLAB and the results are listed in Table 1.

Table 1 The offline fitted lateral Magic Formula parameters
Full size table
Table 2 The detailed vehicle specifications
Full size table

The Magic Formula model only avails for a certain road friction condition. In order to extend its feasibility on various road surfaces, a method called friction similarity is used [41]. It predicts the change in the limit shear force while maintaining the linear behavior for light slip. Given the road friction coefficient μ0 for tire measurements and the road friction coefficient μ for simulation, the modified lateral force with no longitudinal tire force is given by

$$F_{y0i} = \frac{\mu }{{\mu_{0} }}F_{ymfi} (F_{zi} ,\frac{{\mu_{0} }}{\mu }\alpha_{i} ).$$
(48)

The lateral force would decline as the longitudinal tire force increases. Instead of adjusting the tire force based on the slip rate and sideslip angle in the traditional Magic Formula, the ellipse formula is utilized to depict the coupling relationship as shown in Eq. (49). The correction coefficient ξ is utilized to adapt to the longitudinal tire force attenuation due to the transition from rolling to sliding while the slip rate is approaching its limit, and it is set to be 0.95. The comparison between the combination tire model and the test data from CARSIM Tire Tester is shown in Fig. 5. Different from the adhesion ellipse formula induced by anisotropy, the ellipse formula used here can depict the working point of tire force under a specified sideslip condition. The error is small when α is 8° and is relatively larger when α is 3°. Considering the extreme conditions after collisions, the tire sideslip is severe in most of the time and the error is within an acceptable range. Also, it should be noted that the lateral force and sideslip angle should always be at the same side, which is given by

$$\left( {\frac{{F_{xi} }}{{\mu \xi F_{zi} }}} \right)^{2} { + }\left( {\frac{{F_{yi} }}{{F_{y0i} }}} \right)^{2} = 1,\;\;{\text{sign}}\left( {F_{yi} \alpha_{yi} } \right) > 0.$$
(49)
Figure 5
figure 5

Tire forces from the proposed tire model and the CARSIM Tire Tester

Full size image

Also, the magnitude and changing rate boundaries of the front steering wheel angle and each driving/braking torque are formulated into the constraints as

$$\left\{ {\begin{array}{*{20}l} {\delta _{{\min }} \le \delta \le \delta _{{\max }} ,} \\ {T_{{w\min }} \le F_{x} r_{w} \le T_{{w\max }} ,} \\ {\left| {\delta _{k} - \delta _{{k - 1}} } \right|\Delta \delta _{{\max }} ,} \\ {\left| {F_{{xk}} - F_{{x(k - 1)}} } \right|r_{w} \le \Delta T_{{w\max }} ,} \\ \end{array} } \right.$$
(50)

where δmin and δmax are the lower and upper boundaries for the steering wheel angle; Twmin and Twmax are the lower and upper torque limits for each wheel; \(\Delta \delta_{\text{max}}\) and \(\Delta T_{w{\text{max}}}\) are their respective maximum changing-rates; rw is the effective rolling radius with its variation neglected.

The optimal allocation problem can be summarized into finding the optimum control input xc to minimize the objective function Vo while satisfying the tire force and actuator output constraints. It can be expressed as

$$\begin{gathered} {\varvec{x}}_{c} = \arg \min V_{o} , \\ s.t.\;\;{\text{Eqs}}.\;(49)\;(50). \\ \end{gathered}$$
(51)

The nonlinear optimization problem is then solved using the fmincon toolbox in MATLAB. In order to improve the computing efficiency, the warm booting technique is utilized, which adopts the solution of the previous time step as the initial value at the current time step. After obtaining the optimal longitudinal tire forces, the single wheel dynamics model is established to calculate the wheel torque Twi by

$$T_{wi} - F_{xi} r_{w} - T_{fi} = J_{w} \dot{\omega }_{i} ,$$
(52)

where Jw, Tfi and ωi are the rotational inertia, rolling resistance and angular velocity of the i-th wheel, respectively. A positive value for Twi represents a drive torque while a negative one corresponds to a brake torque. With the rolling resistance and rotational inertia ignored, the propulsion or braking torque can be calculated as

$$T_{wi} = F_{xi} r_{w} .$$
(53)

5 HIL Test Results and Discussions

The proposed scheme is examined based on the HIL tests against the disturbances of signal delays, computing power limitation and communication errors. The control area network (CAN) is used to connect different subsystems. The HIL test rig mainly includes the Simulink Real-time system, ZLG CAN bus monitor system and ETAS LABCAR system. The Simulink Real-Time is an embedded kernel that helps create real-time applications from Simulink models and serves as the rapid control prototyping (RCP) in this study. After configuring the drivers and Vector CAN Interface Support from the Vehicle Network Toolbox, the Simulink Real-Time can receive and transmit CAN signals through a specified CAN card. In this study, the RCP of the Simulink Real-Time runs on a computer with a CPU of AMD 3700 and a RAM of 32 GB.

The ETAS LABCAR can carry the predefined vehicle model in CARSIM and serves as the controlled plant. The vehicle model together with the input and output ports is compiled first and then downloaded to LABCAR through RJ45. The LABCAR system receives control commands from the Simulink Real-time and broadcasts vehicle states through the CAN network. In addition, another ZLG CAN card with an upper computer is connected to the CAN network for signals monitoring. The overall HIL system is shown in Figure 6.

Figure 6
figure 6

The overall HIL system

Full size image

A medium SUV from the CARSIM database is used to verify the effectiveness of the proposed scheme with its detailed specifications listed in Table 2. The original drive system is replaced with an independent in-wheel drive system at each wheel to simulate the characteristic of an FWIA EV [42]. The torque commands are directly applied to four wheels.

The actual collision scenarios could be complicated since the impact directions and strengths can be diverse. The theorem of momentum is used to depict an impact process, and the impact on vehicle is simplified to an impulse (Px, Py, Pz) on a reference point (Xp, Yp, Zp) in the vehicle coordinate. Although CARSIM cannot deal with the impact process, it can provide a user-defined external force acting on a specified point of the vehicle, which is utilized to load the impact impulse. The phase plane analysis in Ref. [43] showed that the post-impact instability mainly results from the large yaw rate followed by the sharply increased vehicle sideslip angle. Thus, the lateral-rear offset impact is adopted to examine the performance of the proposed control scheme in such an extreme condition and the lateral impulse Py is imposed as shown in Figure 7. According to the crash test data, the impact impulse can be represented by the haversine, sine, square and triangular pulses with a duration of 0.1–0.15 s [44]. In this study, a triangular pulse of 0.1 s is adopted.

Figure 7
figure 7

The lateral-rear offset impact scenario

Full size image

The overall control scheme is constructed in the Simulink Real-time. The motion planning module is activated once the impact impulse ends, followed by the tracking and the allocation controller working with a sampling time of 0.02 s. It should be noted that solving the nonlinear optimization problem using the fmincon toolbox is time-consuming. In order to improve computing efficiency, some modifications are made to the fmincon toolbox configuration. The sqp optimization algorithm is chosen and the maximum iteration is set to be 40. The overall controller parameters are well calibrated through massive tests and are given as

$$\left\{ \begin{gathered} k_{1} = k_{2} = \;k_{3} = 1\;\;k_{4} = 0.9, \hfill \\ {\varvec{Q}} = \rm{diag}([5\;\;5\;\;90\;\;6 \times 10^{5} \;\;5 \times 10^{5} \;\;1 \times 10^{6} ]), \hfill \\ {\varvec{R}} = \rm{diag}([1 \times 10^{ - 4} \;\;1 \times 10^{ - 4} \;\;1 \times 10^{ - 4} ]), \hfill \\ \varepsilon_{1} { = 9}\;\;\varepsilon_{2} { = }1\;\;\varepsilon_{3} { = }10. \hfill \\ \end{gathered} \right.$$
(54)

Considering the capabilities of different actuators, the actuator control outputs are constrained by

$$\left\{ \begin{gathered} \delta_{\min } = - 0.24\uppi \;, \hfill \\ \delta_{\max } = 0.24{\uppi ,}\;\;\;\;\;\; \hfill \\ \Delta \delta_{\max } = 0.02{\uppi ,} \hfill \\ T_{w\min } = - 1561\;{\text{N}} \cdot {\text{m,}} \hfill \\ \;T_{w\max } = 1561\;{\text{N}} \cdot {\text{m,}}\;\; \hfill \\ \Delta T_{w\max } = 278\;{\text{N}} \cdot {\text{m}}{.} \hfill \\ \end{gathered} \right.$$
(55)

5.1 Motion Planning Test in Complicated Environments

In this section, the proposed scheme is examined under the scenario, in which the vehicle is forced to execute a leftward lane change to avoid the obstacles ahead while suppressing the instability after an initial impact. A road with two lanes of 4 m width is established and a normal road surface with the road friction coefficient of 0.9 is adopted. The vehicle is driving straightly at an initial speed of 108 km/h and the lateral-rear offset impact impulse is set to be 2400 N∙s, referring to the collision scene configuration in Ref. [22]. The reference impact point is set to (−3.7, −0.9, 0.65). Also, two obstacles are assigned on two lanes, which are 30 and 40 m ahead of the collision location as shown in Figure 8. The safety distances for the road boundaries and obstacles are set to be 1 and 1.7 m. The terminal constraints for motion planning are chosen as \(Y(\tau_{f})=4\), \(\dot{Y}(\tau_{f})=0\), \(\psi(\tau_{f})=0\) and \(\dot{\psi}(\tau_{f})=0\) while the terminal time τf is set to be 3.6 s.

Figure 8
figure 8

The planned motion and trajectory in the lateral-rear offset impact scenario

Full size image

Figure 8 shows the planned vehicle motion and trajectory at different time and the contour map of the potential function. It can be seen that the planned motion can lead the vehicle back to stability while avoiding a second collision with the obstacles and road boundaries after the initial impact. A similar leftward lane change trajectory is successfully given, and the vehicle would safely drive onto the other lane with an attitude similar to drifting.

Figure 9(a) and (b) show the evolutions of the planned acceleration and of the rear tire lateral forces, both of which are within their respective limits as described in Equations (11) and (16). It means that the motion planning results are reasonable while satisfying the vehicle dynamics constraints. It should be noted that the result is a locally optimal solution due to the nonconvexity of the optimization problem and the adopted gradient-based method. In most cases, the locally optimal solution is effective and sufficient.

Figure 9
figure 9

The constraint satisfaction analysis in motion planning

Full size image

5.2 Control Performance Comparison and Analysis

In order to prove the superiority of the NOA algorithm under extreme conditions over the existing allocation methods, the quadratic programming allocation (QPA) method is used as the baseline for comparison [45, 46]. It simplified the tire force coupling relationship to form a quadratic programming problem and considered the tire workload usage as the optimization objective. It optimizes the four longitudinal tire forces to realize the desired vehicle longitudinal force and direct yaw moment, while the four lateral tire forces are left as the constraints. For simplicity, the quadratic programming problem is formulated into Eq. (56), where ρ=0.1, ξ1=1 and ξ2=1 are the weighting coefficients for adjusting the priorities among the tire workload usage and the vehicle longitudinal force and direct yaw moment. The direct yaw moment \(M_{zo}^{*}\) is calculated by removing the yaw moment produced by lateral tire forces from the desired overall yaw moment. The steering angle is set to zero. Then the QPA problem can be solved by the quadprog toolbox. For fare comparison, the same desired resultant vehicle forces and yaw moment from the TVLQR and vehicle states are provided for the NOA and QPA in the following analysis.

$$\left\{ \begin{aligned} &J_{qpa} = \arg \min \left[ {({\varvec{Bu}} - {\varvec{v}})^{\prime}{\varvec{W}}_{{\varvec{v}}} ({\varvec{Bu}} - {\varvec{v}}) + \rho {\varvec{u^{\prime}W}}_{{\varvec{u}}} {\varvec{u}})} \right], \hfill \\ &{\varvec{B}}= \frac{1}{{r_{w} }}\left[ {\begin{array}{*{20}ll} {\cos (\delta )} & {\cos (\delta )} & 1 & 1 \\ { - \frac{{D_{b} }}{2}\cos (\delta ) + L_{f} \sin (\delta )} & {\frac{{D_{b} }}{2}\cos (\delta ) + L_{f} \sin (\delta )} & { - \frac{{D_{b} }}{2}} & {\frac{{D_{b} }}{2}} \\ \end{array} } \right], \hfill \\ &{\varvec{u}} = (T_{w1} ,T_{w2} ,T_{w3} ,T_{w4} )^{\prime}, \hfill \\ & {\varvec{v}} = (F_{xo} ,M_{zo}^{ * } )^{\prime}, \hfill \\ &{\varvec{W}}_{{\varvec{u}}} = (r_{w} \mu )^{ - 2} diag(F_{z1}^{ - 2} ,F_{z2}^{ - 2} ,F_{z3}^{ - 2} ,F_{z4}^{ - 2} )\;\;\;{\varvec{W}}_{{\varvec{v}}} = diag(\xi_{1} ,\xi_{2} ), \hfill \\ &{\text{s}}.t.\;\max \left( - r_{w} \sqrt {\mu^{2} F_{zi}^{2} - F_{y0i}^{2} } ,T_{w\min } ) \le T_{wi} \le \min (r_{w} \sqrt {\mu^{2} F_{zi}^{2} - F_{y0i}^{2} } ,T_{w\max } \right). \hfill \\ \end{aligned} \right.$$
(56)

First, the motion tracking performance is analyzed. Figure 10(a)–(c) demonstrate the motions and trajectories after a left-rear impact under the proposed control scheme, AFS control and no control. Partial ghosts trail from CARSIM VS Visualizer is also used, where two traffic barrels are configured on the road to represent obstacles. It can be seen that the post-impact vehicles under the proposed and the AFS controller can both return back to stability, but their trajectories exhibit considerable deviations. The vehicle under the proposed scheme can closely track the planned motion while avoiding the barriers and road boundaries. The vehicle with the AFS controller is closer to the road boundaries due to larger tracking errors. The vehicle no control falls into rapid spinning and drifting, resulting in a secondary collision.

Figure 10
figure 10

Vehicle motion and partial ghosts trail after the initial left-rear impact

Full size image

To be more specific, the trajectories under the TVLQR and the AFS are compared quantitatively as shown in Figure 11(a) together with the trajectory planned in Section 5.1. It can be seen that the TVLQR can closely follow the planned trajectory throughout the maneuver with a maximum error of about 0.2 m. However, a large deviation of up to 0.8 m can be observed for that under the AFS controller, which results from the system inertia and oscillation after the initial impact.

Figure 11
figure 11

Performance comparison of different control schemes

Full size image

The \(\beta-\dot{\beta}\) phase plane analysis is also provided in Figure 11(b), which is widely used as a stability assessment criterion. Three phase paths corresponding to the TVLQR, AFS and without control are compared. It can be seen that all the three phase paths are compelled to the point A from the initial stable point O with the sideslip angular rates increasing sharply. This results from the large, sudden yaw rate change due to the lateral-rear offset impact, which indicates that the point A is also the impact ending time. The phase path of the vehicle without control moves in the direction of increasing sideslip angle while both the TVLQR and AFS can control the vehicle back to the initial stable point O. Also, it can be seen that the AFS controller can more efficiently suppress the sideslip motion before the intersection point B, with a maximum sideslip angle of 45° compared with 60° under the TVLQR. Since the TVLQR has to produce large longitudinal force to achieve obstacle avoidance during the drifting process as shown in Figure 13(a), the stabilizing effect is partially sacrificed. After the intersection point B, the TVLQR stabilizes the vehicle quickly while the AFS experiences sustained oscillations.

The simulation results in the time domain are also provided to verify the TVLQR’s superior tracking performance. In particular, Figure 12(a) shows the vehicle longitudinal and lateral velocities with the planned motion extracted from the polynomial curve as the reference. It can be seen that both the vehicle longitudinal and lateral velocities can closely track their references. Similarly, the vehicle yaw angle and yaw rate can also accurately follow the planned motion throughout the maneuver as shown in Figure 12(b). The excellent motion tracking the foundation for obstacle-avoidance and stability control.

Figure 12
figure 12

Velocities and yaw motion tracking results of TVLQR

Full size image

Second, the control allocation performance of the NOA and QPA are compared as shown in Figure 13. Figure 13(a)–(c) depicts the comparison results of the longitudinal forces, lateral forces and yaw moment of the vehicle, respectively. The NOA algorithm tracks the desired resultant forces and yaw moment from the TVLQR better than the QPA does. The failure of the QPA can be mainly ascribed to the optimization boundary simplification and model linearization. The lateral tire force has nearly exhausted the tire adhesion force for a drifting or spinning vehicle, and there is no room to adjust the longitudinal tire force. It can be seen in Figure 13(e) that the tire workload usages under the QPA and NOA are both close to 1, meaning saturated tire forces. Thus, the QPA only avails with unsaturated tire forces while the NOA can extend the optimization boundary to tire force saturation scenarios to obtain superior performance.

Figure 13
figure 13

Performance comparison of different control allocation methods

Full size image

Moreover, no active steering angle adjustment fails to fully capitalize on the potential of chassis coordinated control and only makes the lateral force a passive variable. On top of this, the QPA exhibits considerable lateral force allocation error as shown in Figure 13(b). Instead, the steering angle is well optimized by the NOA algorithm as shown in Figure 13(d) and is restricted between \({\delta}_{\text{min}}\) and \({\delta}_{\text{max}}\). For example, the counter-steering process is observed at the initial stage to restrain over-spinning similar to vehicle drifting maneuver.

The optimization derivation time can be controlled within the HIL sampling time of 20 ms despite of the existence of packet loss as shown in Figure 13(f).

As shown in Figure 14, the desired tire forces from the presented NOA allocator and from the actual ones exported from the Labcar model are consistent in most of the time albeit there are slight delays and lateral force deviation. The delays may result from ignoring the rotational inertia of wheel in the wheel dynamics model, while the lateral force deviation can be ascribed to the errors of the proposed combined tire force model. But the delays and deviation are still within acceptable ranges and have little influence on the overall control performance.

Figure 14
figure 14

Tire forces comparison

Full size image

In a nutshell, the traditional path planning and steering control cannot deal with the complicated scenarios of obstacle avoidance after an initial external impact. The impact breaks the nonholonomic constraints of vehicle dynamics and thus cause the AFS lose trajectory tracking ability. Simultaneously, large overshoot and oscillations exist in the approaching process to the stability point. Moreover, the existing QPA algorithm cannot efficiently allocate the desired control commands in drifting or over-spinning conditions. In contrast, the proposed scheme can effectively restrain the post-impact over-spinning and restore vehicle stability while keeping high-accuracy tracking of the planned trajectory for obstacle avoidance.

6 Conclusions

Traditional path planning and motion control need be executed under normal conditions with the assumption of a quasi-steady state, in which the vehicle sideslip angle and tire lateral forces are small. However, the assumption may become invalid under extreme conditions especially after an external impact. This paper presents an enabling scheme for automated vehicles to achieve obstacle avoidance and stability restoration after initial impacts. First, a motion planning method based on the polynomial is developed to regulate the vehicle trajectory and yaw motion at the same time. Then, a discrete time-varying vehicle dynamics model is established and a time-varying linear quadratic regulator is proposed to track the desired motions. Finally, a nonlinear-optimization allocation algorithm based on a combined tire model is designed to coordinate multiple chassis actuators to achieve the desired resultant forces and yaw moment. The complete scheme is examined under critical driving conditions based on the HIL tests. The results verify the feasibility and effectiveness of the proposed control scheme to restore vehicle stability while realizing obstacle avoidance after initial collisions under extreme scenarios.