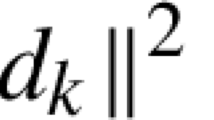On a general filter regularization method for the 2D and 3D Poisson equation in physical geodesy

Abstract

In this paper, we consider a Cauchy problem for the Poisson equation with nonhomogeneous source. The problem is shown to be ill-posed as the solution exhibits unstable dependence on the given data function. Using a new method, we regularize the given problem and obtain some new results. Two numerical examples are given to illustrate the effectiveness of our method.

MSC:35K05, 35K99, 47J06, 47H10.

1 Introduction

The Poisson equation is

$$\mathrm{\Delta }u=f,$$

(1)

where Δ is the Laplace operator, f and u are real or complex-valued functions on a manifold.

In case of $f=0$, equation (1) is called Laplace’s equation which arises naturally in many areas of engineering and science, especially in wave propagation and vibration phenomena such as the vibration of a structure [1], the acoustic cavity problem [2], the radiation wave [3] and the scattering of a wave [4]. For example, certain problems related to the search for mineral resources, which involve interpretation of the earth’s gravitational and magnetic fields, are equivalent to the Cauchy problem for Laplace’s equation. In another application of geophysical underground prospection, the geoelectrical method has been initiated in recent years (see the historical account in Zhdanov and Keller [5]). In fact, by now the geoelectrical method involves, even in its most basic formulation, the solution of the Cauchy problem for Laplace’s equation.

Nowadays, the Cauchy problem for Laplace’s equation, and more generally for elliptic equations, has a central position in all inverse boundary value problems which represent electrical impedance tomography, optical tomography and transient phenomenon in a time-like variable, while elliptic equations describe steady-state processes in physical fields.

In physics, a gravitational field is a model used to explain the influence that a massive body extends into the space around itself, producing a force on another massive body. Therefore, a gravitational field characterizes gravitational phenomena and is measured in Newtons per kilogram (N/kg). In its original concept, gravity was a force between point masses. Following Newton, Laplace attempted to model gravity as some kind of radiation field or fluid, although the 19th century explanations of gravity have usually been sought in terms of a field model rather than a point attraction. A gravitational field is the force field created around massive bodies that causes attraction of other massive bodies. A distribution of matter of density $\rho =\rho (x,y,z)$ gives rise to a gravitational potential ϕ which satisfies the three-dimensional (3D) Poisson equation

$$\mathrm{\Delta }\varphi =-4\pi G\rho$$

(2)

at the points inside the distribution, where G is the universal gravitational constant.

Motivated by important applications of the Poisson equation, in this paper we are interested in considering the Cauchy problem of identification of the gravitational field ϕ which satisfies a Poisson equation (two-dimensional case or three-dimensional case). As first pointed out by Hadamard, the Cauchy problem for Laplace’s equation is an ill-posed problem. It means the problem’s solutions do not always exist and, whenever they do exist, there is no continuous dependence on the given data. A small perturbation in the Cauchy data therefore can affect the solution significantly. Readers are referred to [1–4, 6–13] for earlier materials on the Cauchy problem for Laplace’s equation. For the homogeneous case of source term, the elliptic problem was considered in a series of articles analyzing the stability and convergence (see, e.g., [6–8, 10, 11, 14]). A similar version of Laplace’s equation with homogeneous case was considered by Regińska et al. [15, 16], Lesnic et al. [17], Tautenhahn [18] and Wei et al. [19–21].

Although we have many works on the homogeneous case of the elliptic problem, the literature on the inhomogeneous case, for example, the Poisson equation, is quite scarce. The earlier work on the abstract elliptic second order equation with inhomogeneous source was introduced in [22] by Showalter (see p.469). The main aim of this paper is to present a general regularization method and investigate the error estimate between the regularized solution and the exact solution.

Our paper is organized as follows. In Sections 2 and 3, we construct stable approximate solutions of the equation and give the convergence estimates for 2D and 3D cases, respectively. Finally, in Section 4, two numerical examples for each 2D and 3D case are devised to test the effectiveness of proposed methods.

2 The 2D case of the Poisson equation

2.1 Mathematical model

We consider the problem of finding $\varphi (x,y)$ such that

$$\mathrm{\Delta }\varphi ={\varphi }_{xx}+{\varphi }_{yy}=f(x,y),(x,y)\in \mathrm{\Omega }\times (0,1)$$

(3)

subject to the boundary condition $\varphi (x,y)=0$, $x\in \partial \mathrm{\Omega }$. Here $\mathrm{\Omega }=(0,\pi )$ and $\phi ,g\in L^2(0,\pi )$ are given functions. We will derive the solution of Problem (3) for source term $f(x,y)\in L^2(0,1;L^2(0,\pi ))$. Let $\{u_p(x)\}$ be an orthogonal system of $L^2(0,\pi )$. Then

$$\varphi (x,y)=\sum _{p=1}^{\mathrm{\infty }}〈\varphi (x,y),u_p(x)〉u_p(x),$$

and we have

$$〈{\varphi }_{xx}+{\varphi }_{yy},u_p(x)〉=〈f(x,y),u_p(x)〉.$$

(4)

Set ${\varphi }_p(y)=〈\varphi (x,y),u_p(x)〉={\int }_0^{\pi }\varphi (x,y)u_p(x)dx$. By transformation of (4), we have

$$\begin{array}{c}{\varphi }_p^{″}(y)+{\varphi }_x(\pi ,y)u_p(\pi )-{\varphi }_x(0,y)u_p(0)-\varphi (\pi ,y)u_p^{\prime }(\pi )\hfill \\ +\varphi (0,y)u_p^{\prime }(0)-{\int }_0^{\pi }\varphi (x,y)u_p^{″}(x)dx\hfill \\ =〈f(x,y),u_p(x)〉.\hfill \end{array}$$

By choosing $u_p$ and ${\lambda }_p$ such that

$$u_p^{″}(x)={\lambda }_p{u}_p(x),u_p(0)=u_p(\pi )=0,$$

(5)

we have the following system:

$$\begin{array}{c}{\varphi }_p^{″}(y)+{\lambda }_p{\varphi }_p(y)=f_p(y),\hfill \\ {\varphi }_p(0)={\phi }_p,\hfill \\ {\varphi }_p^{\prime }(0)=g_p,\hfill \end{array}$$

(6)

where $f_p(y)=〈f(x,y),u_p(x)〉$, ${\phi }_p=〈\phi (x),u_p(x)〉$, $g_p=〈g(x),u_p(x)〉$. By solving (5), we obtain ${\lambda }_p=-p^2$ and $u_p(x)=sinpx$. This leads to

$${\varphi }_p(y)=cosh(py){\phi }_p+\frac{sinh(py)}{p}{g}_p+{\int }_0^y\frac{sinh(p(y-s))}{p}{f}_p(s)ds.$$

(7)

Hence, we obtain the solution of Problem (3) as follows:

$$\varphi (x,y)=\sum _{p=1}^{\mathrm{\infty }}[cosh(py){\phi }_p+\frac{sinh(py)}{p}{g}_p+{\int }_0^y\frac{sinh(p(y-s))}{p}{f}_p(s)ds]sinpx.$$

(8)

From (8), we see that the data error can be arbitrarily amplified by the ‘kernel’ function $cosh(py)$. That is the reason why equation (3) is ill-posed in the sense of Hadamard. In the paper of Hadamard, he provided a fundamental example which shows that a solution of a Cauchy problem for Laplace’s equation does not depend continuously on the data. The example is as follows:

$$\mathrm{\Delta }u=0,(x,y)\in R^2,y>0,$$

(9)

$$u(x,0)=0,$$

(10)

$$u_y(x,0)=A_{n}sinnx,x\in R.$$

(11)

We have

$$u_n(x,y)=\frac{A_n}{n}sinnxsinhny.$$

(12)

If we choose $A_n=\frac{1}{n^p}$ for some $p>0$, then $u_{n,y}(x,0)\to 0$ uniformly as $n\to \mathrm{\infty }$; whereas, for any $y>0$, the function $u_n(x,y)$ containing factor $sinhny$ blows up as $n\to \mathrm{\infty }$.

2.2 A general filter regularization method

To find some regularized solutions, we should replace ‘instability’ kernels $cosh(py)$, $sinh(py)$, $sinh(p(y-s))$ by the ‘stability’ kernels $A(\beta ,p,y)$, $B(\beta ,p,y)$, $C(\beta ,p,y)$ that satisfy the following properties:

$$\begin{array}{r}\underset{\beta \to 0}{lim}A(\beta ,p,y)=cosh(py),\\ ({\mathrm{P}}_1)& \underset{\beta \to 0}{lim}B(\beta ,p,y)=sinh(py),\\ \underset{\beta \to 0}{lim}C(\beta ,p,y,s)=sinh(p(y-s))\end{array}$$

(13)

and some suitable conditions which are given later. Following property (P₁), one can construct other kernels. Furthermore, the idea of the above property can be applied to other ill-posed problems such as, e.g., the backward heat conduction problem [23].

Throughout this section, we assume that the functions $\phi ,g\in L^2(0,\pi )$ and $f\in L^2(0,1;L^2(0,\pi ))$. In reality, they can only be measured with some measurement errors, and we would actually have noisy data:

$${\phi }^{ϵ}(x)=\sum _{p=1}^{\mathrm{\infty }}{\phi }_p^{ϵ}sinpx,g^{ϵ}(x)=\sum _{p=1}^{\mathrm{\infty }}{g}_p^{ϵ}sinpx$$

for which

$$\parallel {\phi }^{ϵ}-\phi \parallel \le ϵ,\parallel g^{ϵ}-g\parallel \le ϵ.$$

Here the constant $ϵ>0$ represents a bound on the measurement error and $\parallel \cdot \parallel$ denotes the norm in $L^2(\mathrm{\Omega })$. As noted above, we present the following general regularized solution:

$${\varphi }^{ϵ}(x,y)=\sum _{p=1}^{\mathrm{\infty }}[A(\beta ,p,y){\phi }_p^{ϵ}+\frac{B(\beta ,p,y)}{p}{g}_p^{ϵ}+{\int }_0^y\frac{C(\beta ,p,y,s)}{p}{f}_p(s)ds]sinp,$$

(14)

where

$$\begin{array}{c}A(\beta ,p,y)=\frac{P(\beta ,p,y)e^{py}+e^{-py}}{2},\hfill \\ B(\beta ,p,y)=\frac{P(\beta ,p,y)e^{py}-e^{-py}}{2},\hfill \\ C(\beta ,p,y,s)=\frac{P(\beta ,p,y)e^{p(y-s)}-e^{p(s-y)}}{2},\hfill \end{array}$$

(15)

and $P(\beta ,p,y)$ is chosen suitably.

Theorem 1 (A general regularization method)

Assume that $\varphi (x,y)$ is the exact solution of Problem (3) and $M_2$ is a real-valued function such that

$$\sum _{p=1}^{\mathrm{\infty }}(M_2^2(p)|〈\varphi (x,y),sinpx〉{|}^2+\frac{M_2^2(p)}{p^2}\left|〈{\varphi }_y(x,y),sinpx〉{|}^2\right)\le 2E^2,$$

(16)

where E is a positive number. Let $P(\beta ,p,y)$ be a function in such a way that, for any $\beta >0$, there exist $M_1(\beta )$ and $M_3(\beta )$ satisfying

$$(\mathrm{a})1-P(\beta ,p,y)\le M_1(\beta )M_2(p),$$

(17)

$$(\mathrm{b})P(\beta ,p,y)\le M_3(\beta )e^{-py}.$$

(18)

Then ${\varphi }^{ϵ}(x,y)$ defined by equation (14) fulfills the following estimate:

$$\parallel {\varphi }^{ϵ}-\varphi \parallel \le ϵ\sqrt{2M_3^2(\beta )+2}+M_1(\beta )E.$$

(19)

A choice $\beta =\beta (ϵ)$ is admissible if

$$\underset{ϵ\to 0}{lim}\beta (ϵ)=\underset{ϵ\to 0}{lim}{M}_1(\beta )=\underset{ϵ\to 0}{lim}ϵM_3(\beta )=0.$$

(20)

Proof The proof will be split into two parts as follows.

Part 1. We estimate $\parallel {\varphi }^{ϵ}-v^{ϵ}\parallel$, where $v^{ϵ}$ is defined as

$$v^{ϵ}(x,y)=\sum _{p=1}^{\mathrm{\infty }}[A(\beta ,p,y){\phi }_p+\frac{B(\beta ,p,y)}{p}{g}_p+{\int }_0^y\frac{C(\beta ,p,y,s)}{p}{f}_p(s)ds]sinpx.$$

(21)

By a simple calculation, we get

$$\begin{array}{rcl}{\parallel {\varphi }^{ϵ}(\cdot ,y)-v^{ϵ}(\cdot ,y)\parallel }^2& =& \sum _{p=1}^{\mathrm{\infty }}{[A(\beta ,p,y)({\phi }_p^{ϵ}-{\phi }_p)+\frac{B(\beta ,p,y)}{p}(g_p^{ϵ}-g_p)]}^2\\ \le & 2\sum _{p=1}^{\mathrm{\infty }}{A}^2(\beta ,p,y){({\phi }_p^{ϵ}-{\phi }_p)}^2+2\sum _{p=1}^{\mathrm{\infty }}{B}^2(\beta ,p,y){(g_p^{ϵ}-g_p)}^2\\ \le & \frac{M_3^2(\beta )+1}{2}(2{\parallel {\phi }^{ϵ}-\phi \parallel }^2+2{\parallel g^{ϵ}-g\parallel }^2)\\ \le & 2{ϵ}^2(M_3^2(\beta )+1).\end{array}$$

(22)

Hence

$$\parallel {\varphi }^{ϵ}(\cdot ,y)-v^{ϵ}(\cdot ,y)\parallel \le ϵ\sqrt{2M_3^2(\beta )+2}.$$

(23)

Part 2. We estimate $\parallel v^{ϵ}-\varphi \parallel$. In fact, we have

$$\begin{array}{c}〈\varphi (x,y)-v^{ϵ}(x,y),sinpx〉\hfill \\ =(A(\beta ,p,y)-cosh(py)){\phi }_p+\frac{B(\beta ,p,y)-sinh(py)}{p}{g}_p\hfill \\ +{\int }_0^y\frac{C(\beta ,p,y,s)-sinh(py-ps)}{p}{f}_p(s)ds\hfill \\ =\frac{e^{py}-P(\beta ,p,y)e^{py}}{2}({\phi }_p+\frac{g_p}{p}+{\int }_0^y{e}^{-ps}{f}_p(s)ds).\hfill \end{array}$$

(24)

From (8), the partial derivative of ϕ with respect to y is

$${\varphi }_y(x,y)=\sum _{p=1}^{\mathrm{\infty }}[sinh(py){\phi }_p+\frac{cosh(py)}{p}{g}_p+{\int }_0^y\frac{cosh(p(y-s))}{p}{f}_p(s)ds]sinpx.$$

This implies that

$$〈\varphi (x,y),sinpx〉+\frac{1}{p}〈{\varphi }_y(x,y),sinpx〉=e^{py}({\phi }_p+\frac{g_p}{p}+{\int }_0^y{e}^{-ps}{f}_p(s)ds).$$

(25)

Combining (24) and (25), we obtain

$$〈\varphi (x,y)-v^{ϵ}(x,y),sinpx〉=\frac{1-P(\beta ,p,y)}{2}(〈\varphi (x,y),sinpx〉+\frac{1}{p}〈{\varphi }_y(x,y),sinpx〉).$$

(26)

Hence

$$\begin{array}{rcl}{\parallel \varphi (\cdot ,y)-v^{ϵ}(\cdot ,y)\parallel }^2& =& \sum _{p=1}^{\mathrm{\infty }}|〈\varphi (x,y)-v^{ϵ}(x,y),sinpx〉{|}^2\\ \le & \sum _{p=1}^{\mathrm{\infty }}\frac{{(1-P(\beta ,p,y))}^2}{4}{(〈\varphi (x,y),sinpx〉+\frac{1}{p}〈{\varphi }_y(x,y),sinpx〉)}^2\\ \le & \sum _{p=1}^{\mathrm{\infty }}\frac{M_1^2(\beta )M_2^2(p)}{2}\left(\right|〈\varphi (x,y),sinpx〉{|}^2+\frac{1}{p^2}\left|〈{\varphi }_y(x,y),sinpx〉{|}^2\right)\\ \le & \frac{M_1^2(\beta )}{2}\sum _{p=1}^{\mathrm{\infty }}(M_2^2(p)|〈\varphi (x,y),sinpx〉{|}^2+\frac{M_2^2(p)}{p^2}\left|〈{\varphi }_y(x,y),sinpx〉{|}^2\right)\\ \le & M_1^2(\beta )E^2.\end{array}$$

(27)

Combining (23) and (27), we have

$$\begin{array}{rcl}\parallel \varphi (\cdot ,y)-{\varphi }^{ϵ}(\cdot ,y)\parallel & \le & \parallel \varphi (\cdot ,y)-v^{ϵ}(\cdot ,y)\parallel +\parallel {\varphi }^{ϵ}(\cdot ,y)-v^{ϵ}(\cdot ,y)\parallel \\ \le & ϵ\sqrt{2M_3^2(\beta )+2}+M_1(\beta )E.\end{array}$$

(28)

This completes the proof. □

Theorem 2 (The first regularized solution)

Let $P(\beta ,p,y)=e^{-\beta p^{2}y}$. Assume that ϕ is the exact solution of Problem (3) such that ${\parallel {\varphi }_{xx}(\cdot ,y)\parallel }^2+{\parallel {\varphi }_{xy}(\cdot ,y)\parallel }^2\le 2E^2$ for $y\in [0,1]$. If we select $\beta =\frac{1}{4kln(\frac{1}{ϵ})}$ ($0<k<1$), then

$$\parallel {\varphi }^{ϵ}-\varphi \parallel \le \frac{E}{4kln(\frac{1}{ϵ})}+\sqrt{2{ϵ}^2+2{ϵ}^{2-2k}}.$$

(29)

Proof First, we find the functions $M_1$, $M_2$, $M_3$ such that $P(\beta ,p,y)$ holds (17), (18). Using the inequality $1-e^{-m}\le m$, we have

$$1-P(\beta ,p,y)=1-e^{-\beta p^{2}y}\le \beta p^{2}y\le \beta p^2.$$

Since (17), we can choose $M_1(\beta )=\beta$ and $M_2(p)=p^2$. The condition

$$\sum _{p=1}^{\mathrm{\infty }}(M_2^2(p)|〈\varphi (x,y),sinpx〉{|}^2+\frac{M_2^2(p)}{p^2}\left|〈{\varphi }_y(x,y),sinpx〉{|}^2\right)\le 2E^2$$

(30)

is equivalent to

$$\begin{array}{c}\sum _{p=1}^{\mathrm{\infty }}\left(p^4\right|〈\varphi (x,y),sinpx〉{|}^2+p^2\left|〈{\varphi }_y(x,y),sinpx〉{|}^2\right)\hfill \\ ={\parallel {\varphi }_{xx}(\cdot ,y)\parallel }^2+{\parallel {\varphi }_{xy}(\cdot ,y)\parallel }^2\le 2E^2.\hfill \end{array}$$

(31)

Using the inequality $p-\beta p^2\le \frac{1}{4\beta }$, we get

$$e^{py}P(\beta ,p,y)=e^{(p-\beta p^2)y}\le e^{\frac{y}{4\beta }}\le e^{\frac{1}{4\beta }}.$$

Since (18), we can choose $M_3(\beta )=e^{\frac{1}{4\beta }}$. The admissible regularization parameter is $\beta =\frac{1}{4kln(\frac{1}{ϵ})}$ ($0<k<1$). In fact, it is easy to check that

$$\underset{ϵ\to 0}{lim}\beta (ϵ)=\underset{ϵ\to 0}{lim}{M}_1(\beta )=\underset{ϵ\to 0}{lim}\frac{1}{4kln(\frac{1}{ϵ})}=0$$

and

$$\underset{ϵ\to 0}{lim}ϵM_3(\beta )=\underset{ϵ\to 0}{lim}ϵe^{\frac{1}{4\beta }}=\underset{ϵ\to 0}{lim}{ϵ}^{1-k}=0.$$

Applying Theorem 1, we obtain

$$\parallel {\varphi }^{ϵ}-\varphi \parallel \le ϵ\sqrt{2M_3^2(\beta )+2}+M_1(\beta )E\le \frac{E}{4kln(\frac{1}{ϵ})}+\sqrt{2{ϵ}^2+2{ϵ}^{2-2k}}.$$

(32)

 □

Theorem 3 (The second regularized solution)

Let $P(\beta ,p,y)=\frac{e^{-py}}{\beta p+e^{-py}}$. Assume that ϕ is the exact solution of Problem (3) such that ${\parallel {\varphi }_{xx}(\cdot ,y)\parallel }^2+{\parallel {\varphi }_{yy}(\cdot ,y)\parallel }^2\le 2E^2$ for $y\in [0,1]$. If we select $\beta ={ϵ}^k$ ($0<k<1$), then

$$\parallel {\varphi }^{ϵ}-\varphi \parallel \le \frac{E}{4kln(\frac{1}{ϵ})}+\sqrt{2{ϵ}^2+2{ϵ}^{2-2k}}.$$

(33)

Proof First, we find the functions $M_1$, $M_2$, $M_3$ such that $P(\beta ,p,y)$ holds (17), (18). We have

$$1-P(\beta ,p,y)=1-\frac{e^{-py}}{\beta p+e^{-py}}=\frac{\beta p}{\beta p+e^{-py}}.$$

On the other hand, for $0\le y\le 1$, we have

$$\frac{1}{\beta p+e^{-py}}\le \frac{1}{\beta p+e^{-p}}\le \frac{1}{\beta ln(\frac{1}{\beta })},\beta \in (0,e).$$

Hence

$$1-P(\beta ,p,y)\le \frac{p}{ln(\frac{1}{\beta })}.$$

(34)

Since (17), we can choose $M_1(\beta )=\frac{1}{ln(\frac{1}{\beta })}$, $M_2(p)=p$. The condition

$$\sum _{p=1}^{\mathrm{\infty }}(M_2^2(p)|〈\varphi (x,y),sinpx〉{|}^2+\frac{M_2^2(p)}{p^2}\left|〈{\varphi }_y(x,y),sinpx〉{|}^2\right)\le 2E^2$$

(35)

is equivalent to

$$\begin{array}{c}\sum _{p=1}^{\mathrm{\infty }}\left(p^2\right|〈\varphi (x,y),sinpx〉{|}^2+\left|〈{\varphi }_y(x,y),sinpx〉{|}^2\right)\hfill \\ ={\parallel {\varphi }_x(\cdot ,y)\parallel }^2+{\parallel {\varphi }_y(\cdot ,y)\parallel }^2\le 2E^2.\hfill \end{array}$$

(36)

Since (18), we can choose $M_3(\beta )=\frac{1}{\beta ln(\frac{1}{\beta })}$. Next, we prove that this regularization parameter $\beta ={ϵ}^k$ ($0<k<1$) is admissible by checking condition (20). In fact,

$$\underset{ϵ\to 0}{lim}\beta (ϵ)=\underset{ϵ\to 0}{lim}{M}_1(\beta )=\underset{ϵ\to 0}{lim}\frac{1}{ln(\frac{1}{{ϵ}^k})}=0$$

and

$$\underset{ϵ\to 0}{lim}ϵM_3(\beta )=\underset{ϵ\to 0}{lim}ϵe^{\frac{1}{4\beta }}=\underset{ϵ\to 0}{lim}{ϵ}^{1-k}\frac{1}{ln(\frac{1}{{ϵ}^k})}=0.$$

Applying Theorem 1, we obtain

$$\parallel {\varphi }^{ϵ}-\varphi \parallel \le ϵ\sqrt{2M_3^2(\beta )+2}+M_1(\beta )E\le \frac{E}{ln(\frac{1}{{ϵ}^k})}+\sqrt{2{ϵ}^2+\frac{{ϵ}^{2-2k}}{{ln}^2(\frac{1}{{ϵ}^k})}}.$$

(37)

 □

3 The 3D Poisson equation

Let ρ be the given mass density. For simplification, we consider the problem: determine the gravitational potential ϕ such that the Poisson equation

$$\mathrm{\Delta }\varphi (x,y,z)=-4\pi G\rho (x,y,z)$$

(38)

subject to the homogeneous Dirichlet boundary condition $\varphi (x,y,z)=0$, $(x,y)\in \partial \mathrm{\Omega }$, $z\in (0,1)$, where $\mathrm{\Omega }=(0,\pi )\times (0,\pi )$. The data of ϕ at $z=0$: $\varphi (x,y,0)=\phi (x,y)$ and ${\varphi }_z(x,y,0)=g(x,y)$, where φ, g are known.

By a similar way as in (8), we find the solution of (38) that

$$\begin{array}{rcl}\varphi (x,y,z)& =& \sum _{p,q=1}^{\mathrm{\infty }}[cosh\left(z\sqrt{p^2+q^2}\right){\phi }_{pq}+\frac{sinh(z\sqrt{p^2+q^2})}{\sqrt{p^2+q^2}}{g}_{pq}\\ +4\pi G{\int }_0^y\frac{sinh((z-s)\sqrt{p^2+q^2})}{\sqrt{p^2+q^2}}{\rho }_{pq}(s)ds]sinpxsinqy.\end{array}$$

(39)

Physically, φ can only be measured with some measurement errors, and we would actually have a disturbed data function

$$\begin{array}{c}{\phi }^{ϵ}(x,y)=\sum _{p,q=1}^{\mathrm{\infty }}{\phi }_{pq}^{ϵ}sinpxsinqy\in L^2(\mathrm{\Omega }),\hfill \\ g^{ϵ}(x,y)=\sum _{p,q=1}^{\mathrm{\infty }}{g}_{pq}^{ϵ}sinpxsinqy\in L^2(\mathrm{\Omega })\hfill \end{array}$$

for which

$$\parallel {\phi }^{ϵ}-\phi \parallel \le ϵ,\parallel g^{ϵ}-g\parallel \le ϵ,$$

where the constant $ϵ>0$ represents a bound on the measurement error, $\parallel \cdot \parallel$ denotes the $L^2$-norm.

By a similar method as in Section 4, we present the following general regularized solution:

$$\begin{array}{rcl}{\varphi }^{ϵ}(x,y,z)& =& \sum _{p,q=1}^{\mathrm{\infty }}[A(\beta ,p,q,z){\phi }_{pq}^{ϵ}+\frac{B(\beta ,p,q,z)}{\sqrt{p^2+q^2}}{g}_{pq}^{ϵ}\\ +4\pi G{\int }_0^y\frac{C(\beta ,p,q,z,s)}{\sqrt{p^2+q^2}}{\rho }_{pq}(s)ds]sinpxsinqy,\end{array}$$

(40)

where

$$\begin{array}{c}A(\beta ,p,q,z)=\frac{P(\beta ,p,q,z)e^{z\sqrt{p^2+q^2}}+e^{-z\sqrt{p^2+q^2}}}{2},\hfill \\ B(\beta ,p,q,z)=\frac{P(\beta ,p,q,z)e^{z\sqrt{p^2+q^2}}-e^{-z\sqrt{p^2+q^2}}}{2},\hfill \\ C(\beta ,p,q,z,s)=\frac{P(\beta ,p,q,z)e^{(z-s)\sqrt{p^2+q^2}}-e^{(s-z)\sqrt{p^2+q^2}}}{2},\hfill \end{array}$$

(41)

and $P(\beta ,p,y)$ is chosen suitably.

Theorem 4 Assume that $\varphi (x,y,z)$ is the exact solution of Problem (38) and $N_2(p,q)$ is a real-valued function such that

$$\begin{array}{r}\sum _{p=1}^{\mathrm{\infty }}(N_2^2(p,q)|〈\varphi (x,y,z),sinpxsinqy〉{|}^2+\frac{N_2^2(p,q)}{p^2+q^2}\left|〈{\varphi }_z(x,y,z),sinpxsinqy〉{|}^2\right)\\ \le 2E^2,\end{array}$$

(42)

where E is a positive number. Let $P(\beta ,p,q,z)$ be a function such that for any $\beta >0$, there exist functions $N_1(\beta )$ and $N_3(\beta )$ satisfying

$$(\mathrm{a})1-P(\beta ,p,q,z)\le N_1(\beta )N_2(p,q),$$

(43)

$$(\mathrm{b})P(\beta ,p,q,z)\le N_3(\beta )e^{-z\sqrt{p^2+q^2}},$$

(44)

then ${\varphi }^{ϵ}(x,y,z)$ defined by equation (40) fulfills the following estimate:

$$\parallel {\varphi }^{ϵ}-\varphi \parallel \le ϵ\sqrt{2N_3^2(\beta )+2}+N_1(\beta )E.$$

(45)

A choice $\beta =\beta (ϵ)$ is admissible if

$$\underset{ϵ\to 0}{lim}\beta (ϵ)=\underset{ϵ\to 0}{lim}{N}_1(\beta )=\underset{ϵ\to 0}{lim}ϵN_3(\beta )=0.$$

(46)

Theorem 5 Let $P(\beta ,p,q,z)=\frac{e^{-z\sqrt{p^2+q^2}}}{\beta {(\sqrt{p^2+q^2})}^m+e^{-z\sqrt{p^2+q^2}}}$ for $m\ge 1$. Assume that ϕ is the exact solution of Problem (3) such that

$$\begin{array}{c}\sum _{p=1}^{\mathrm{\infty }}\left({(p^2+q^2)}^{m/2}\right|〈\varphi (x,y,z),sinpxsinqy〉{|}^2+{(p^2+q^2)}^{m-1}\left|〈{\varphi }_z(x,y,z),sinpxsinqy〉{|}^2\right)\hfill \\ \le 2E^2\hfill \end{array}$$

(47)

for $z\in [0,1]$. If we select $\beta ={ϵ}^k$ ($0<k<1$), then

$$\parallel {\varphi }^{ϵ}-\varphi \parallel \le \frac{E}{4kln(\frac{1}{ϵ})}+\sqrt{2{ϵ}^2+2{ϵ}^{2-2k}}.$$

(48)

Proof First, we find the functions $N_1$, $N_2$, $N_3$ such that $P(\beta ,p,q,z)$ holds (43), (44). We have

$$1-P(\beta ,p,q,z)=1-\frac{e^{-z\sqrt{p^2+q^2}}}{\beta {(\sqrt{p^2+q^2})}^m+e^{-z\sqrt{p^2+q^2}}}=\frac{\beta {(\sqrt{p^2+q^2})}^m}{\beta {(\sqrt{p^2+q^2})}^m+e^{-\sqrt{p^2+q^2}z}}.$$

On the other hand, for $0\le z\le 1$, we have

$$\frac{1}{\beta {(\sqrt{p^2+q^2})}^m+e^{-\sqrt{p^2+q^2}z}}\le \frac{1}{\beta {(\sqrt{p^2+q^2})}^m+e^{-\sqrt{p^2+q^2}}}.$$

Now, we prove that

$$\frac{1}{\beta {(\sqrt{p^2+q^2})}^m+e^{-\sqrt{p^2+q^2}}}\le \frac{m^m}{\beta {ln}^m(\frac{1}{m\beta })}.$$

In fact, let the function h be defined by $h(x)=\frac{1}{\beta x^m+e^{-Mx}}$. By taking the derivative of h, one has

$$h^{\prime }(x)=\frac{\beta m{x}^{m-1}-M{e}^{-Mx}}{-{(\beta x^m+e^{-Mx})}^2}.$$

(49)

The equation $h^{\prime }(x)=0$ gives a unique solution $x_0$ such that $\beta m{x}_0^{m-1}-M{e}^{-M{x}_0}=0$. It means that $x_0^{m-1}{e}^{M{x}_0}=\frac{M}{m\beta }$. Thus the function h achieves its maximum at a unique point $x=x_0$. Thus

$$h(x)\le \frac{1}{ϵx_0^m+e^{-M{x}_0}}.$$

(50)

Since $e^{-M{x}_0}=\frac{k\beta }{M}{x}_0^{k-1}$, one has

$$h(x)\le \frac{1}{ϵx_0^m+e^{-M{x}_0}}\le \frac{1}{\beta x_0^m+\frac{m\beta }{M}{x}_0^{m-1}}.$$

(51)

By using the inequality $e^{M{x}_0}\ge M{x}_0$, we get

$$\begin{array}{rcl}\frac{M}{mϵ}& =& x_0^{m-1}{e}^{M{x}_0}\\ \le & \frac{1}{M^{m-1}}{e}^{(m-1)M{x}_0}{e}^{M{x}_0}\\ =& \frac{1}{M^{m-1}}{e}^{mM{x}_0}.\end{array}$$

This gives $e^{mM{x}_0}\ge \frac{M^m}{m\beta }$ or $mM{x}_0\ge ln(\frac{M^m}{m\beta })$. Therefore

$$x_0\ge \frac{1}{mM}ln\left(\frac{M^m}{m\beta }\right).$$

Hence, we obtain

$$h(x)\le \frac{1}{\beta x_0^m}\le \frac{{(mM)}^m}{\beta {ln}^m(\frac{M^m}{m\beta })}.$$

(52)

Using this inequality for $M=1$, we have

$$1-P(\beta ,p,q,z)\le \frac{m^m}{{ln}^m(\frac{1}{m\beta })}{\left(\sqrt{p^2+q^2}\right)}^m$$

(53)

and

$$P(\beta ,p,q,z)\le \frac{m^m}{\beta {ln}^m(\frac{1}{m\beta })}{e}^{-z\sqrt{p^2+q^2}}.$$

(54)

By choosing $N_1(\beta )=\frac{m^m}{{ln}^m(\frac{1}{m\beta })}$, $N_2(p,q)={(\sqrt{p^2+q^2})}^m$ and $N_3(\beta )=\frac{m^m}{\beta {ln}^m(\frac{1}{m\beta })}$, the conditions (43), (44) hold. It is easy to check that (46) holds.

Applying Theorem 5, we obtain

$$\parallel {\varphi }^{ϵ}-\varphi \parallel \le ϵ\sqrt{2M_3^2(\beta )+2}+M_1(\beta )E\le \frac{E}{ln(\frac{1}{{ϵ}^k})}+\sqrt{2{ϵ}^2+\frac{{ϵ}^{2-2k}}{{ln}^2(\frac{1}{{ϵ}^k})}}.$$

(55)

 □

4 Numerical experiment

In this section, simple examples for the 2D and 3D Poisson equations are devised for verifying the validity of our proposed methods.

4.1 Example 1

Consider the 2D Poisson equation as follows:

$$\{\begin{array}{l}{\varphi }_{xx}+{\varphi }_{yy}=f(x,y),(x,y)\in (0,\pi )\times (0,1),\\ \varphi (x,0)=\phi (x),x\in (0,\pi ),\\ {\varphi }_y(x,0)=g(x),x\in (0,\pi ),\end{array}$$

(56)

where

$$\begin{array}{c}\phi (x)=0,\hfill \\ f(x,y)=(4x^2+4y^2-{\pi }^5-5)e^{-x^2+y^2}sin(x)sin(\pi y)\hfill \\ \phantom{f(x,y)=}-(2\pi y+{\pi }^2)e^{-(x^2+y^2)}sin(x)cos(\pi y)\hfill \\ \phantom{f(x,y)=}-4x{e}^{-(x^2+y^2)}cos(x)sin(\pi y)\hfill \\ \phantom{f(x,y)=}+e^{-2(x^2+y^2)}sin(2x)sin(2\pi y)(16y^2-4x^2-4{\pi }^2-8)\hfill \\ \phantom{f(x,y)=}-e^{-2(x^2+y^2)}sin(2x)cos(2\pi y)(8y\pi +4{\pi }^2)\hfill \\ \phantom{f(x,y)=}-12x{e}^{-2(x^2+y^2)}cos(2x)sin(2\pi y),\hfill \\ g(x)=\pi e^{(-x^2)}sin(x)+2\pi e^{-2x^2}sin(2x).\hfill \end{array}$$

Problem (56) has a unique solution as follows:

$$\varphi (x,y)=e^{x^2+y^2}sin(x)sin(\pi y)+e^{-2(x^2+y^2)}sin(2x)sin(2\pi y).$$

Now we are seeking a solution of the following problem:

$$\{\begin{array}{l}{\varphi }_{xx}^{ϵ}+{\varphi }_{yy}^{ϵ}=f^{ϵ}(x,y),(x,y)\in (0,\pi )\times (0,1),\\ {\varphi }^{ϵ}(x,0)={\phi }^{ϵ}(x),x\in (0,\pi ),\\ {\varphi }_y^{ϵ}(x,0)=g^{ϵ}(x),x\in (0,\pi ).\end{array}$$

(57)

We assume $h^{ϵ}$ to be a measured data as follows:

$$h^{ϵ}(x)=\sum _{p=1}^{p_0}(h_p+ϵrand(p))sin(px),$$

where $p_0\le p_{\mathrm{\infty }}$ and $\{rand(\cdot )\}$ is an array of pseudo-random numbers satisfying

$$\sum _{p=1}^{p_0}|rand(p){|}^2\le 1.$$

Let $(p_0,p_{\mathrm{\infty }})$ satisfy

$$O(\parallel h\parallel ):=\sqrt{\sum _{p=p_0+1}^{p_{\mathrm{\infty }}}{|f_p|}^2}\le ϵ.$$

(58)

In this paper, we choose $p_0=30$, $p_{\mathrm{\infty }}=100$, then (58) is satisfied.

Step 1. Choose L and K to generate the temporal and spatial discretization in such a manner that

$$\begin{array}{c}{x}_i=i\mathrm{\Delta }x,\mathrm{\Delta }x=\frac{\pi }{K},i=0,\dots ,K,\hfill \\ y_j=j\mathrm{\Delta }y,\mathrm{\Delta }y=\frac{1}{L},j=0,\dots ,L.\hfill \end{array}$$

Of course, the higher value of K and L will provide more accurate and stable numerical results; however, in the following numerical examples $K=L=101$ are satisfied.

Step 2. We choose the following functions:

$$\begin{array}{c}{\phi }^{ϵ}=\phi +ϵ\ast rand(),\hfill \\ g^{ϵ}=g+ϵ\ast rand(),\hfill \\ f^{ϵ}=f+ϵ\ast rand(,).\hfill \end{array}$$

Step 3. Set ${\varphi }_{\beta }^{ϵ}(x_i)={\varphi }_{\beta ,j}^{ϵ}$ and $\varphi (x_j)={\varphi }_j$, construct two vectors containing all discrete values of ${\varphi }_{\beta }^{ϵ}$ and f denoted by ${\mathrm{\Lambda }}_{\beta }^{ϵ}$ and Ψ, respectively,

$$\begin{array}{c}{\mathrm{\Lambda }}_{\beta }^{ϵ}=\left[\begin{array}{cccc}{\varphi }_{\beta ,0}^{ϵ}& {\varphi }_{\beta ,1}^{ϵ}& \cdots & {\varphi }_{\beta ,K}^{ϵ}\end{array}\right]\in {\mathbb{R}}^{K+1},\hfill \\ \mathrm{\Psi }=[\begin{array}{ccccc}{\varphi }_0& {\varphi }_1& \cdots & {\varphi }_{K-1}& {\varphi }_K\end{array}]\in {\mathbb{R}}^{K+1}.\hfill \end{array}$$

Step 4. Error estimate between the exact solutions and regularized solutions. At a fixed point $y^{\ast }$, the error estimation ${\delta }^{i,ϵ}$ in $L_2$ between the exact solution ϕ and the regularized solutions ${\varphi }^{i,ϵ}$ is given by the following formula. Relative error estimation:

$${\delta }^{ϵ}=\frac{\sqrt{{\sum }_{i=0}^K{|{\varphi }_{\beta }^{ϵ}(x_i)-\varphi (x_i)|}_{L^2(0,\pi )}^2}}{\sqrt{{\sum }_{i=0}^K{|\varphi (x_i)|}_{L^2(0,\pi )}^2}}.$$

In one example, we have the first regularized solution (defined in Theorem 2). In method two, we have the second regularized solution (defined in Theorem 3). With parameter $k=1/2$, in the first method we choose $\beta =\frac{-1}{2lnϵ}$, and in the second method we choose $\beta ={ϵ}^{1/2}$.

Tables 1 and 2 show the computed error estimations ${\delta }^{ϵ}$ at each fixed value $y=j/10$, $j=0,\dots ,10$. The errors are significantly small when $ϵ\le {10}^{-3}$. Comparing the errors of two regularized solutions in the table, we can see that the second one is better. We show the error between the exact solution and the regularized solution at $\beta =\frac{-1}{2lnϵ}$. For the purpose of better illustration, we also present some graphical figures. Figure 1 is the 3D representation of the exact solution and regularized solutions when $ϵ={10}^{-1}$, $ϵ={10}^{-2}$ and $ϵ={10}^{-3}$. Figure 2 shows graphs of section cut of these solutions at value $y=0.5$ when $ϵ={10}^{-1}$, $ϵ={10}^{-2}$ and $ϵ={10}^{-3}$. It is easy to see that our methods are stably convergent.

Figure 1

3D graphs of the exact solution $\mathit{\varphi }\mathbf{(}\mathit{x}\mathbf{,}\mathit{y}\mathbf{)}$ and three regularized solutions ${\mathit{\varphi }}^{\mathit{i}\mathbf{,}\mathit{ϵ}}\mathbf{(}\mathit{x}\mathbf{,}\mathit{y}\mathbf{)}$ at $\mathit{i}\mathbf{=}\mathbf{1}\mathbf{,}\mathbf{2}$ .

Figure 2

Section cut of the exact solution and regularized solutions at $\mathit{y}\mathbf{=}\mathbf{0.5}$ , $\mathit{ϵ}\mathbf{=}{\mathbf{10}}^{\mathbf{-}\mathbf{1}}$ , $\mathit{ϵ}\mathbf{=}{\mathbf{10}}^{\mathbf{-}\mathbf{2}}$ , $\mathit{ϵ}\mathbf{=}{\mathbf{10}}^{\mathbf{-}\mathbf{3}}$ .

Table 1 Discrete relative error estimations for the regularized solution at fixed values from $\mathit{y}\mathbf{=}\mathbf{0.0}$ to $\mathit{y}\mathbf{=}\mathbf{0.5}$

Table 2 Discrete relative error estimations for the regularized solution at fixed values from $\mathit{y}\mathbf{=}\mathbf{0.6}$ to $\mathit{y}\mathbf{=}\mathbf{1.0}$

4.2 Example 2

We consider the following 3D problem:

$$\{\begin{array}{l}{\varphi }_{xx}+{\varphi }_{yy}+{\varphi }_{zz}=f(x,y,z),(x,y,z)\in \mathrm{\Omega }\times (0,2),\\ \varphi (x,y,z)=0,(x,y)\in \partial \mathrm{\Omega },\\ \varphi (x,y,0)=\phi (x,y),\\ {\varphi }_z(x,y,0)=g(x,y),\end{array}$$

(59)

where $\mathrm{\Omega }=(0,\pi )\times (0,\pi )$.

Step 1. Choose Q and K (in our computations, $Q=K=101$ are chosen) to have

$$\begin{array}{c}{x}_i=i\mathrm{\Delta }x,\mathrm{\Delta }x=\frac{\pi }{Q},j=\overline{0,Q},\hfill \\ y_j=j\mathrm{\Delta }y,\mathrm{\Delta }y=\frac{\pi }{K},i=\overline{0,K},\hfill \\ z_k=k\mathrm{\Delta }z,\mathrm{\Delta }z=\frac{2}{L},z=\overline{0,L}.\hfill \end{array}$$

Step 2. We choose the following functions and fix z,

$$\begin{array}{c}{\phi }^{ϵ}=\phi +ϵrand(\cdot ,\cdot ),\hfill \\ g^{ϵ}=g+ϵrand(\cdot ,\cdot ),\hfill \\ f^{ϵ}(\cdot ,\cdot ,z)=f(\cdot ,\cdot ,z)+ϵrand(\cdot ,\cdot ).\hfill \end{array}$$

Step 3. In this example, we fix z. We put $\varphi {(\cdot ,\cdot ,z^{\ast })}_{\beta (ϵ)}^{ϵ}(x_i,y_j)=\varphi {(\cdot ,\cdot )}_{\beta (ϵ),i,j}^{ϵ}$ and $\varphi (\cdot ,\cdot ,z^{\ast })(x_i,y_j)=u_{i,j}$, construct two vectors containing all discrete values of $\varphi {(\cdot ,\cdot )}_{\beta }^{ϵ}$ and $\varphi (\cdot ,\cdot )$ denoted by ${\mathrm{\Lambda }}_{\beta }^{ϵ}$ and Ξ, respectively,

$$\begin{array}{c}{\mathrm{\Lambda }}_{\beta (ϵ)}^{ϵ}=\left[\begin{array}{ccccc}{\varphi }_{(0,0,0)}^{\beta (ϵ),ϵ}& {\varphi }_{(0,0,1)}^{\beta (ϵ),ϵ}& \cdots & {\varphi }_{(0,0,K-1)}^{\beta (ϵ),ϵ}& {\varphi }_{(0,0,K)}^{\beta (ϵ),ϵ}\\ {\varphi }_{(0,1,0)}^{\beta (ϵ),ϵ}& {\varphi }_{(0,1,1)}^{\beta (ϵ),ϵ}& \cdots & {\varphi }_{(0,1,K-1)}^{\beta (ϵ),ϵ}& {\varphi }_{(0,1,K)}^{\beta (ϵ),ϵ}\\ {\varphi }_{(0,2,0)}^{\beta (ϵ),ϵ}& {\varphi }_{(0,2,1)}^{\beta (ϵ),ϵ}& \cdots & {\varphi }_{(0,2,K-1)}^{\beta (ϵ),ϵ}& {\varphi }_{(0,2,K)}^{\beta (ϵ),ϵ}\\ \cdots & \cdots & \ddots & \cdots & \cdots \\ {\varphi }_{(0,Q,0)}^{\beta (ϵ),ϵ}& {\varphi }_{(0,Q,1)}^{\beta (ϵ),ϵ}& \cdots & {\varphi }_{(0,Q,K-1)}^{\beta (ϵ),ϵ}& {\varphi }_{(0,Q,K)}^{\beta (ϵ),ϵ}\end{array}\right]\in {\mathbb{R}}^{K+1}\times {\mathbb{R}}^{Q+1},\hfill \\ \mathrm{\Xi }=\left[\begin{array}{ccccc}{\varphi }_{(0,0)}& {\varphi }_{(0,1)}& \cdots & {\varphi }_{(0,K-1)}& {\varphi }_{(0,K)}\\ {\varphi }_{(1,0)}& {\varphi }_{(1,1)}& \cdots & {\varphi }_{(1,K-1)}& {\varphi }_{(1,K)}\\ {\varphi }_{(2,0)}& {\varphi }_{(2,1)}& \cdots & {\varphi }_{(2,K-1)}& {\varphi }_{(2,K)}\\ \cdots & \cdots & \ddots & \cdots & \cdots \\ {\varphi }_{(Q,0)}& {\varphi }_{(Q,1)}& \cdots & {\varphi }_{(Q,K-1)}& {\varphi }_{(Q,K)}\end{array}\right]\in {\mathbb{R}}^{K+1}\times {\mathbb{R}}^{Q+1}.\hfill \end{array}$$

Step 4. The error estimation.

Relative error estimation:

$${\delta }_2=\frac{\sqrt{{\sum }_{i=1}^Q{\sum }_{j=1}^K{|{\varphi }^{ϵ}(x_i,y_j,z^{\ast })-\varphi (x_i,y_j,z^{\ast })|}_{L^2(\mathrm{\Omega })}^2}}{\sqrt{{\sum }_{i=1}^Q{\sum }_{j=1}^K{|\varphi (x_i,y_j,z^{\ast })|}_{L^2(\mathrm{\Omega })}^2}},$$

(60)

where

$$\begin{array}{c}\mathrm{\Omega }=(0,\pi )\times (0,\pi ),\hfill \\ f(x,y,z)=(-{\pi }^2-{\left(\frac{\pi }{5}\right)}^2)sin(\pi (x-\pi ))sin(\frac{\pi }{5}(y-\pi ))\hfill \\ \phantom{f(x,y,z)=}\times [1-z{\left(\frac{\pi }{3}\right)}^{2}cos(\frac{\pi }{3}(x-\pi ))cos(\frac{\pi }{3}(y-\pi ))],\hfill \\ \varphi (x,y)=sin(\pi (x-\pi ))sin(\frac{\pi }{5}(y-\pi )),\hfill \\ g(x,y)=sin(\pi (x-\pi ))sin(\frac{\pi }{5}(y-\pi ))cos(\frac{\pi }{3}(x-\pi ))cos(\frac{\pi }{3}(y-\pi )).\hfill \end{array}$$

From (59) and (60), we get

$$\varphi (x,y,z)=sin(\pi (x-\pi ))sin(\frac{\pi }{5}(y-\pi ))[1+zcos(\frac{\pi }{3}(x-\pi ))cos(\frac{\pi }{3}(y-\pi ))].$$

Now we are seeking a solution of the following problem:

$$\{\begin{array}{l}{\varphi }_{xx}^{ϵ}+{\varphi }_{yy}^{ϵ}+{\varphi }_{zz}^{ϵ}=f^{ϵ}(x,y,z),(x,y)\in (0,\pi )\times (0,2),\\ {\varphi }^{ϵ}(x,y,0)={\phi }^{ϵ}(x,y),x\in (0,\pi ),\\ {\varphi }_y^{ϵ}(x,y,0)=g^{ϵ}(x,y),x\in (0,\pi ).\end{array}$$

(61)

Due to the computational cost, we only computed the value of regularized solution ${\varphi }^{ϵ}(x,y,z)$ at the fixed values $y^{\ast }=\pi /12$ and $z^{\ast }=1.5$. The discrete relative error estimation in one dimension is defined as follows:

$${\delta }^{ϵ}(y^{\ast },z^{\ast })=\frac{{\sum }_{i=1}^{p_0}|\varphi (x_i,y^{\ast },z^{\ast })-{\varphi }^{ϵ}(x_i,y^{\ast },z^{\ast }){|}^2}{{\sum }_{i=1}^{p_0}|\varphi (x_i,y^{\ast },z^{\ast }){|}^2}$$

(62)

with $N=30$ being the grid size along x axis. The regularized solution is calculated by formula (40) and Theorem 5 with parameter $\beta ={ϵ}^{\frac{1}{2}}$. Computational results are shown in Tables 3 and 4 (the relative error) and in Figure 3 (section cut graphs). In this problem, the regularized solution is very accurate just with $ϵ={10}^{-1}$, $ϵ={10}^{-2}$ and $ϵ={10}^{-3}$, respectively. In Figures 4 and 5, we show the 3D representation of the exact ϕ and the regularized ϕ and 3D representation of the exact $g(x,y)$ and the regularized $g^{ϵ}(x,y)$ at $ϵ={10}^{-1}$, $ϵ={10}^{-2}$ and $ϵ={10}^{-3}$. In Figure 6, we show the 3D representation of the exact solution and the regularized solution when $ϵ={10}^{-1}$, $ϵ={10}^{-2}$, $ϵ={10}^{-3}$.

Figure 3

Section cut of the exact solution and regularized solutions at $\mathit{y}\mathbf{=}\frac{\mathit{\pi }}{\mathbf{12}}$ and $\mathit{z}\mathbf{=}\mathbf{1.5}$ .

Figure 4

3D graphs of $\mathit{\phi }\mathbf{(}\mathit{x}\mathbf{,}\mathit{y}\mathbf{)}$ and three regularized solutions ${\mathit{\phi }}^{\mathit{i}\mathbf{,}\mathit{ϵ}}\mathbf{(}\mathit{x}\mathbf{,}\mathit{y}\mathbf{)}$ .

Figure 5

3D graphs of $\mathit{g}\mathbf{(}\mathit{x}\mathbf{,}\mathit{y}\mathbf{)}$ and three regularized solutions ${\mathit{g}}^{\mathit{i}\mathbf{,}\mathit{ϵ}}\mathbf{(}\mathit{x}\mathbf{,}\mathit{y}\mathbf{)}$ .

Figure 6

3D graphs of $\mathit{\varphi }\mathbf{(}\mathit{x}\mathbf{,}\mathit{y}\mathbf{)}$ and two regularized solutions ${\mathit{\varphi }}^{\mathit{i}\mathbf{,}\mathit{ϵ}}\mathbf{(}\mathit{x}\mathbf{,}\mathit{y}\mathbf{)}$ .

Table 3 Discrete relative error estimations for the regularized solution at fixed values $\mathit{y}\mathbf{=}\mathit{\pi }\mathbf{/}\mathbf{12}$ and $\mathit{z}\mathbf{=}\mathbf{1.5}$ from $\mathit{y}\mathbf{=}\mathbf{0.0}$ to $\mathit{y}\mathbf{=}\mathbf{0.5}$

Table 4 Discrete relative error estimations for the regularized solution at fixed values $\mathit{y}\mathbf{=}\mathit{\pi }\mathbf{/}\mathbf{12}$ and $\mathit{z}\mathbf{=}\mathbf{1.5}$ from $\mathit{y}\mathbf{=}\mathbf{0.6}$ to $\mathit{y}\mathbf{=}\mathbf{1.0}$

5 Conclusion

The study on the inverse Poisson-type problem with inhomogeneous source in 2D and 3D is still limited. This work is a continuous development of our previous study.

In theoretical results, we have suggested a general filter regularization method of regularized solution (Section 2.2). Subsequently, we have shown which sets are fundamental to solving problem (3) numerically and obtained the error estimation of logarithm type. We deduced two regularized solutions. In Section 2.2, we have shown the regularized solution for this case, method one. In Section 2.2, we have shown the regularized solution for the second method. The numerical results prove the efficiency of the theoretical suggestion, i.e., regularized solutions stably converge to the exact solution.