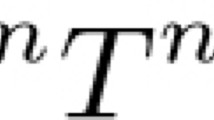The k-quasi-∗-class contractions have property PF

Abstract

First, we will see that if T is a contraction of the k-quasi-∗-class operator, then the nonnegative operator $D=T^{\ast k}(|T^2|-{|T^{\ast }|}^2)T^k$ is a contraction whose power sequence ${\{D^n\}}_{n=1}^{\mathrm{\infty }}$ converges strongly to a projection P and $T{T}^{\ast k}P=0$. Second, it will be proved that if T is a contraction of the k-quasi-∗-class operator, then either T has a non-trivial invariant subspace or T is a proper contraction. Finally it will be proved that if T belongs to the k-quasi-∗-class and is a contraction, then T has a Wold-type decomposition and T has the PF property.

MSC:47A10, 47B37, 15A18.

1 Introduction

Throughout this paper, let H and K be infinite dimensional separable complex Hilbert spaces with inner product $〈\cdot ,\cdot 〉$. We denote by $L(H,K)$ the set of all bounded operators from H into K. To simplify, we put $L(H):=L(H,H)$. For $T\in L(H)$, we denote by kerT the null space and by $T(H)$ the range of T. The closure of a set M will be denoted by $\overline{M}$. We shall denote the set of all complex numbers by ℂ and the set of all nonnegative integers by ℕ.

For an operator $T\in L(H)$, as usual, by $T^{\ast }$ we mean the adjoint of T and $|T|={(T^{\ast }T)}^{\frac{1}{2}}$. An operator T is said to be hyponormal, if ${|T|}^2\ge {|T^{\ast }|}^2$. An operator T is said to be paranormal, if

$$\parallel T^{2}x\parallel \ge {\parallel Tx\parallel }^2$$

for any unit vector x in H [1]. Further, T is said to be ∗-paranormal, if

$$\parallel T^{2}x\parallel \ge {\parallel T^{\ast }x\parallel }^2$$

for any unit vector x in H [2]. T is said to be a k-paranormal operator if ${\parallel Tx\parallel }^{k+1}\le \parallel T^{k+1}x\parallel {\parallel x\parallel }^k$ for all $x\in H$, and T is said to be a k-∗-paranormal operator if ${\parallel T^{\ast }x\parallel }^{k+1}\le \parallel T^{k+1}x\parallel {\parallel x\parallel }^k$, for all $x\in H$.

Furuta et al. [3] introduced a very interesting class of bounded linear Hilbert space operators: class defined by

$$\left|T^2\right|\ge {|T|}^2,$$

and they showed that the class is a subclass of paranormal operators and contains hyponormal operators. Jeon and Kim [4] introduced the quasi-class . An operator T is said to be a quasi-class , if

$$T^{\ast }\left|T^2\right|T\ge T^{\ast }{|T|}^{2}T.$$

We denote the set of quasi-class by $\mathcal{Q}\mathcal{A}$. An operator T is said to be a k-quasi-class , if

$$T^{\ast k}\left|T^2\right|T^k\ge T^{\ast k}{|T|}^2{T}^k.$$

We denote the set of quasi-class by $\mathcal{Q}\mathcal{A}(k)$.

Duggal et al. [5], introduced ∗-class operator. An operator T is said to be a ∗-class operator, if

$$\left|T^2\right|\ge |T^{\ast }{|}^2.$$

A ∗-class is a generalization of a hyponormal operator [[5], Theorem 1.2], and ∗-class is a subclass of the class of ∗-paranormal operators [[5], Theorem 1.3]. We denote the set of ∗-class by ${\mathcal{A}}^{\ast }$. Shen et al. in [6] introduced the quasi-∗-class operator: an operator T is said to be a quasi-∗-class operator, if

$$T^{\ast }\left|T^2\right|T\ge T^{\ast }|T^{\ast }{|}^{2}T.$$

We denote the set of quasi-∗-class by $\mathcal{Q}{\mathcal{A}}^{\ast }$. Mecheri [7] introduced the k-quasi-∗-class operator.

Definition 1.1 An operator $T\in L(H)$ is said to be a k-quasi-∗-class operator, if

$$T^{\ast k}\left(\right|T^2|-|T^{\ast }{|}^2)T^k\ge O$$

for a nonnegative integer k.

We denote the set of the k-quasi-∗-class by $\mathcal{Q}{\mathcal{A}}^{\ast }(k)$.

Example 1.2 Let T be an operator defined by

$$T=\left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 0\\ 0& 1& 0\end{array}\right).$$

Then $|T^2|-{|T^{\ast }|}^2\ngeqq O$ and so T is not a class ${\mathcal{A}}^{\ast }$. However, $T^{\ast k}(|T^2|-{|T^{\ast }|}^2)T^k=O$ for every positive number k, which implies that T is a k-quasi-class ${\mathcal{A}}^{\ast }$ operator.

A contraction is an operator T such that $\parallel Tx\parallel \le \parallel x\parallel$ for all $x\in H$. A proper contraction is an operator T such that $\parallel Tx\parallel <\parallel x\parallel$ for every nonzero $x\in H$ [8]. A strict contraction is an operator such that $\parallel T\parallel <1$ (i.e., ${sup}_{x\ne 0}\frac{\parallel Tx\parallel }{\parallel x\parallel }<1$). Obviously, every strict contraction is a proper contraction and every proper contraction is a contraction. An operator T is said to be completely non-unitary (c.n.u.) if T restricted to every reducing subspace of H is non-unitary.

An operator T on H is uniformly stable, if the power sequence ${\{T^n\}}_{n=1}^{\mathrm{\infty }}$ converges uniformly to the null operator (i.e., $\parallel T^n\parallel \to O$). An operator T on H is strongly stable, if the power sequence ${\{T^n\}}_{n=1}^{\mathrm{\infty }}$ converges strongly to the null operator (i.e., $\parallel T^{n}x\parallel \to 0$, for every $x\in H$).

A contraction T is of class $C_{0\cdot }$ if T is strongly stable (i.e., $\parallel T^{n}x\parallel \to 0$ and $\parallel Tx\parallel \le \parallel x\parallel$ for every $x\in H$). If $T^{\ast }$ is a strongly stable contraction, then T is of class $C_{\cdot 0}$. T is said to be of class $C_{1\cdot }$ if ${lim}_{n\to \mathrm{\infty }}\parallel T^{n}x\parallel >0$ (equivalently, if $T^{n}x\nrightarrow 0$ for every nonzero x in H). T is said to be of class $C_{\cdot 1}$ if ${lim}_{n\to \mathrm{\infty }}\parallel T^{\ast n}x\parallel >0$ (equivalently, if $T^{\ast n}x\nrightarrow 0$ for every nonzero x in H). We define the class $C_{\alpha \beta }$ for $\alpha ,\beta =0,1$ by $C_{\alpha \beta }=C_{\alpha \cdot }\cap C_{\cdot \beta }$. These are the Nagy-Foiaş classes of contractions [[9], p.72]. All combinations are possible leading to classes $C_{00}$, $C_{01}$, $C_{10}$, and $C_{11}$. In particular, T and $T^{\ast }$ are both strongly stable contractions if and only if T is a $C_{00}$ contraction. Uniformly stable contractions are of class $C_{00}$.

Lemma 1.3 [[10], Holder-McCarthy inequality]

Let T be a positive operator. Then the following inequalities hold for all $x\in H$:

• (1) $〈T^{r}x,x〉\le {〈Tx,x〉}^r{\parallel x\parallel }^{2(1-r)}$ for $0<r<1$;

• (2) $〈T^{r}x,x〉\ge {〈Tx,x〉}^r{\parallel x\parallel }^{2(1-r)}$ for $r\ge 1$.

Lemma 1.4 [[7], Lemma 2.1]

Let T be a k-quasi-∗-class operator, where $T^k$ does not have a dense range, and let T have the following representation:

$$T=\left(\begin{array}{cc}A& B\\ O& C\end{array}\right)\mathit{\text{on }}H=\overline{T^k(H)}\oplus ker{T}^{\ast k}.$$

Then A is class ${\mathcal{A}}^{\ast }$ on $\overline{T^k(H)}$, $C^k=O$, and $\sigma (T)=\sigma (A)\cup \{0\}$.

2 Main results

Theorem 2.1 If T is a contraction of the k-quasi-∗-class operator, then the nonnegative operator

$$D=T^{\ast k}\left(\right|T^2|-|T^{\ast }{|}^2)T^k$$

is a contraction whose power sequence ${\{D^n\}}_{n=1}^{\mathrm{\infty }}$ converges strongly to a projection P and $T^{\ast }{T}^{k}P=O$.

Proof Suppose that T is a contraction of the k-quasi-∗-class operator. Then

$$D=T^{\ast k}\left(\right|T^2|-|T^{\ast }{|}^2)T^k\ge O.$$

Let $R=D^{\frac{1}{2}}$ be the unique nonnegative square root of D, then for every x in H and any nonnegative integer n, we have

$$\begin{array}{rcl}〈D^{n+1}x,x〉& =& {\parallel R^{n+1}x\parallel }^2\\ =& 〈D{R}^{n}x,R^{n}x〉\\ =& 〈T^{\ast k}\left|T^2\right|T^k{R}^{n}x,R^{n}x〉-〈T^{\ast k}|T^{\ast }{|}^2{T}^k{R}^{n}x,R^{n}x〉\\ \le & {\parallel |T^2{|}^{\frac{1}{2}}{T}^k{R}^{n}x\parallel }^2-{\parallel T^{\ast }{T}^k{R}^{n}x\parallel }^2\\ \le & {\parallel R^{n}x\parallel }^2-{\parallel T^{\ast }{T}^k{R}^{n}x\parallel }^2\\ \le & {\parallel R^{n}x\parallel }^2\\ =& 〈D^{n}x,x〉.\end{array}$$

Thus R (and so D) is a contraction (set $n=0$), and ${\{D^n\}}_{n=1}^{\mathrm{\infty }}$ is a decreasing sequence of nonnegative contractions. Then ${\{D^n\}}_{n=1}^{\mathrm{\infty }}$ converges strongly to a projection P. Moreover,

$$\sum _{n=0}^m{\parallel T^{\ast }{T}^k{R}^{n}x\parallel }^2\le \sum _{n=0}^m({\parallel R^{n}x\parallel }^2-{\parallel R^{n+1}x\parallel }^2)={\parallel x\parallel }^2-{\parallel R^{m+1}x\parallel }^2\le {\parallel x\parallel }^2$$

for all nonnegative integers m and for every $x\in H$. Therefore $\parallel T^{\ast }{T}^k{R}^{n}x\parallel \to 0$ as $n\to \mathrm{\infty }$. Then we have

$$T^{\ast }{T}^{k}Px=T^{\ast }{T}^k\underset{n\to \mathrm{\infty }}{lim}{D}^{n}x=\underset{n\to \mathrm{\infty }}{lim}{T}^{\ast }{T}^k{R}^{2n}x=0$$

for every $x\in H$. So that $T^{\ast }{T}^{k}P=O$. □

A subspace M of space H is said to be non-trivial invariant (alternatively, T-invariant) under T if $\{0\}\ne M\ne H$ and $T(M)\subseteq M$. A closed subspace $M\subseteq H$ is said to be a non-trivial hyperinvariant subspace for T if $\{0\}\ne M\ne H$ and is invariant under every operator $S\in L(H)$, which fulfills $TS=ST$.

Recently Duggal et al. [11] showed that if T is a class contraction, then either T has a non-trivial invariant subspace or T is a proper contraction and the nonnegative operator $D=|T^2|-{|T|}^2$ is strongly stable. Duggal et al. [12] extended these results to contractions in $\mathcal{Q}\mathcal{A}$. Jeon and Kim [13] extended these results to contractions $\mathcal{Q}\mathcal{A}(k)$. Gao and Li [14] have proved that if a contraction $T\in {\mathcal{A}}^{\ast }$ has a no non-trivial invariant subspace, then (a) T is a proper contraction and (b) the nonnegative operator $D=|T^2|-{|T^{\ast }|}^2$ is a strongly stable contraction. In this paper we extend these results to contractions in the k-quasi-∗-class for $k>0$.

Theorem 2.2 Let T be a contraction of the k-quasi-∗-class for $k>0$. If T has a no non-trivial invariant subspace, then:

• (1) T is a proper contraction;

• (2) the nonnegative operator

  $$D=T^{\ast k}\left(\right|T^2|-|T^{\ast }{|}^2)T^k$$

is a strongly stable contraction.

Proof We may assume that T is a nonzero operator.

• (1) If either kerT or $\overline{T^k(H)}$ is a non-trivial subspace (i.e., $kerT\ne \{0\}$ or $\overline{T^k(H)}\ne H$), then T has a non-trivial invariant subspace. Hence, if T has no non-trivial invariant subspace, then T is injective and $\overline{T^k(H)}=H$. Furthermore, T is a class ${\mathcal{A}}^{\ast }$ operator. The proof now follows from [[14], Theorem 2.2].

• (2) Let T be a contraction of the k-quasi-∗-class . By the above theorem, we see that D is a contraction, ${\{D^n\}}_{n=1}^{\mathrm{\infty }}$ converges strongly to a projection P, and $T^{\ast }{T}^{k}P=O$. So, $P{T}^{\ast k}T=O$. Suppose T has no non-trivial invariant subspaces. Since kerP is a nonzero invariant subspace for T whenever $P{T}^{\ast k}T=O$ and $T\ne O$, it follows that $kerP=H$. Hence $P=O$, and we see that ${\{D^n\}}_{n=1}^{\mathrm{\infty }}$ converges strongly to the null operator O, so D is a strongly stable contraction. Since D is self-adjoint, $D\in C_{00}$. □

Corollary 2.3 Let T be a contraction of the k-quasi-∗-class . If T has no non-trivial invariant subspace, then both T and the nonnegative operators

$$D=T^{\ast k}\left(\right|T^2|-|T^{\ast }{|}^2)T^k$$

are proper contractions.

Proof A self-adjoint operator T is a proper contraction if and only if T is a $C_{00}$ contraction. □

Definition 2.4 If the contraction T is a direct sum of the unitary and $C_{\cdot 0}$ (c.n.u.) contractions, then we say that T has a Wold-type decomposition.

Definition 2.5 [15]

An operator $T\in L(H)$ is said to have the Fuglede-Putnam commutativity property (PF property for short) if $T^{\ast }X=XJ$ for any $X\in L(K,H)$ and any isometry $J\in L(K)$ such that $TX=X{J}^{\ast }$.

Lemma 2.6 [16, 17]

Let T be a contraction. The following conditions are equivalent:

• (1) For any bounded sequence ${\{x_n\}}_{n\in \mathbb{N}\cup \{0\}}\subset H$ such that $T{x}_{n+1}=x_n$ the sequence ${\{\parallel x_n\parallel \}}_{n\in \mathbb{N}\cup \{0\}}$ is constant;

• (2) T has a Wold-type decomposition;

• (3) T has the PF property.

Duggal and Cubrusly in [16] have proved: Each k-paranormal contraction operator has a Wold-type decomposition. Pagacz in [17] has proved the same and also proved that each k-∗-paranormal operator has a Wold-type decomposition. In this paper, we extend to contractions in $\mathcal{Q}{\mathcal{A}}^{\ast }(k)$.

Theorem 2.7 Let T be a contraction of the k-quasi-∗-class . Then T has a Wold-type decomposition.

Proof Since T is a contraction operator, the decreasing sequence ${\{T^n{T}^{\ast n}\}}_{n=1}^{\mathrm{\infty }}$ converges strongly to a nonnegative contraction. We denote by

$$S={\left(\underset{n\to \mathrm{\infty }}{lim}{T}^n{T}^{\ast n}\right)}^{\frac{1}{2}}.$$

The operators T and S are related by $T^{\ast }{S}^{2}T=S^2$, $O\le S\le I$ and S is self-adjoint operator. By [18] there exists an isometry $V:\overline{S(H)}\to \overline{S(H)}$ such that $VS=S{T}^{\ast }$, and thus $S{V}^{\ast }=TS$, and $\parallel S{V}^{m}x\parallel \to \parallel x\parallel$ for every $x\in \overline{S(H)}$. The isometry V can be extended to an isometry on H, which we still denote by V.

For an $x\in \overline{S(H)}$, we can define $x_n=S{V}^{n}x$ for $n\in \mathbb{N}\cup \{0\}$. Then for all nonnegative integers m we have

$$T^m{x}_{n+m}=T^{m}S{V}^{m+n}x=S{V}^{\ast m}{V}^{m+n}x=S{V}^{n}x=x_n,$$

and for all $m\le n$ we have

$$T^m{x}_n=x_{n-m}.$$

Since T is a k-quasi-∗-class operator and the non-trivial $x\in \overline{S(H)}$ we have

$$\begin{array}{rcl}{\parallel x_n\parallel }^4& =& {\parallel T^k{x}_{n+k}\parallel }^4\\ =& {〈T^{\ast }T{T}^{k-1}{x}_{n+k},T^{k-1}{x}_{n+k}〉}^2\\ \le & {\parallel T^{\ast }{T}^k{x}_{n+k}\parallel }^2{\parallel T^{k-1}{x}_{n+k}\parallel }^2\\ =& {〈T^{\ast k}|T^{\ast }{|}^2{T}^k{x}_{n+k},x_{n+k}〉}^2{\parallel x_{n+1}\parallel }^2\\ \le & {〈T^{\ast k}\left|T^2\right|T^k{x}_{n+k},x_{n+k}〉}^2{\parallel x_{n+1}\parallel }^2\\ \le & {〈|T^2{|}^2{T}^k{x}_{n+k},T^k{x}_{n+k}〉}^{\frac{1}{2}}{\parallel T^k{x}_{n+k}\parallel }^{2(1-\frac{1}{2})}{\parallel x_{n+1}\parallel }^2\\ =& \parallel T^{k+2}{x}_{n+k}\parallel \parallel T^k{x}_{n+k}\parallel {\parallel x_{n+1}\parallel }^2\\ =& \parallel x_{n-2}\parallel \parallel x_n\parallel {\parallel x_{n+1}\parallel }^2.\end{array}$$

Then

$${\parallel x_n\parallel }^3\le \parallel x_{n-2}\parallel {\parallel x_{n+1}\parallel }^2;$$

hence

$$\parallel x_n\parallel \le {\parallel x_{n-2}\parallel }^{\frac{1}{3}}{\parallel x_{n+1}\parallel }^{\frac{2}{3}}\le \frac{1}{3}(\parallel x_{n-2}\parallel +2\parallel x_{n+1}\parallel ).$$

Thus

$$2(\parallel x_{n+1}\parallel -\parallel x_n\parallel )\ge \parallel x_n\parallel -\parallel x_{n-2}\parallel =(\parallel x_n\parallel -\parallel x_{n-1}\parallel )+(\parallel x_{n-1}\parallel -\parallel x_{n-2}\parallel ).$$

Put

$$b_n=\parallel x_n\parallel -\parallel x_{n-1}\parallel ,$$

and we have

$$2b_{n+1}\ge b_n+b_{n-1}.$$

(1)

Since $x_n=T{x}_{n+1}$, we have

$$\parallel x_n\parallel =\parallel T{x}_{n+1}\parallel \le \parallel x_{n+1}\parallel \text{for every }n\in \mathbb{N},$$

then the sequence ${\{\parallel x_n\parallel \}}_{n\in \mathbb{N}\cup \{0\}}$ is increasing. From

$$S{V}^n=S{V}^{\ast }{V}^{n+1}=TS{V}^{n+1}$$

we have

$$\parallel x_n\parallel =\parallel S{V}^{n}x\parallel =\parallel TS{V}^{n+1}x\parallel \le \parallel S{V}^{n+1}x\parallel \le \parallel x\parallel$$

for every $x\in \overline{S(H)}$ and $n\in \mathbb{N}\cup \{0\}$. Then ${\{\parallel x_n\parallel \}}_{n\in \mathbb{N}\cup \{0\}}$ is bounded. From this we have $b_n\ge 0$ and $b_n\to 0$ as $n\to \mathrm{\infty }$.

It remains to check that all $b_n$ equal zero. Suppose that there exists an integer $i\ge 1$ such that $b_i>0$. Using the inequality (1) we get $b_{i+1}>0$ and $b_{i+2}>0$, so there exists $ϵ>0$ such that $b_{i+1}>ϵ$ and $b_{i+2}>ϵ$. From that, and using again the inequality (1), we can show by induction that $b_n>ϵ$ for all $n>i$, thus arriving at a contradiction. So $b_n=0$ for all $n\in \mathbb{N}$ and thus $\parallel x_{n-1}\parallel =\parallel x_n\parallel$ for all $n\ge 1$. Thus the sequence ${\{\parallel x_n\parallel \}}_{n\in \mathbb{N}\cup \{0\}}$ is constant.

From Lemma 2.6, T has a Wold-type decomposition. □

For $T\in L(H)$ and $x\in H$, ${\{T^{n}x\}}_{n=0}^{\mathrm{\infty }}$ is called the orbit of x under T, and is denoted by $\mathcal{O}(x,T)$. When the linear span of the orbit $\mathcal{O}(x,T)$ is norm dense in H, x is called a cyclic vector for T and T is said to be a cyclic operator. If $\mathcal{O}(x,T)$ is norm dense in H, then x is called a hypercyclic vector for T. An operator $T\in L(H)$ is called hypercyclic if there is at least one hypercyclic vector for T. We say that an operator $T\in L(H)$ is supercyclic if there exists a vector $x\in H$ such that $\mathbb{C}\mathcal{O}(x,T)=\{\lambda T^{n}x:\lambda \in \mathbb{C},n=0,1,2,\dots \}$ is norm dense in H.

Theorem 2.8 Let $T\in L(H)$ be a quasi-∗-class such that $\sigma (T)\subseteq \{\lambda \in \mathbb{C}:|\lambda |=1\}$. If the inverse of T is a quasi-∗-class , then T is not a supercyclic operator.

Proof Let $T\in L(H)$ be a quasi-∗-class . Since $\sigma (T)\subseteq \{\lambda \in \mathbb{C}:|\lambda |=1\}$, T is an invertible operator. From [7]T is normaloid, thus $\parallel T\parallel =r(T)=1$. Since $T^{-1}\in \mathcal{Q}({\mathcal{A}}^{\ast })$, $\parallel T^{-1}\parallel =1$. Consequently, T is unitary. Since no unitary operator on an infinite dimensional Hilbert space can be supercyclic, we see that T is not a supercyclic operator. □

Remark 2.9 The condition that the inverse of the operator T belongs to quasi-∗-class cannot be removed from Theorem 2.8, because there are invertible operators from the quasi-∗-class , such that their inverse does not belong to the quasi-∗-class . This is shown in the following example.

Given a bounded sequence of complex numbers $\{{\alpha }_n:n\in \mathbb{Z}\}$ (called weights), let T be the bilateral weighted shift on an infinite dimensional Hilbert space operator $H=l_2$, with the canonical orthonormal basis $\{e_n:n\in \mathbb{Z}\}$, defined by $T{e}_n={\alpha }_n{e}_{n+1}$ for all $n\in \mathbb{Z}$.

Lemma 2.10 Let T be a bilateral weighted shift operator with weights $\{{\alpha }_n:n\in \mathbb{Z}\}$. Then T is a quasi-∗-class operator if and only if

$${|{\alpha }_n|}^2\le |{\alpha }_{n+1}||{\alpha }_{n+2}|$$

for all $n\in \mathbb{Z}$.

Lemma 2.11 Let T be a non-singular bilateral weighted shift operator with weights $\{{\alpha }_n:n\in \mathbb{Z}\}$. Then $T^{-1}$ is a quasi-∗-class operator if and only if

$${|{\alpha }_{n-1}|}^2\ge |{\alpha }_{n-2}||{\alpha }_{n-3}|$$

for all $n\in \mathbb{Z}$.

Example 2.12 Let us denote by T the bilateral weighted shift operator, with weighted sequence $\{{\alpha }_n:n\in \mathbb{Z}\}$, given by the relation

$${\alpha }_n=\{\begin{array}{ll}1& \text{if }n\le 1,\\ 2& \text{if }n=2,\\ 1& \text{if }n=3,\\ 4& \text{if }n=4,\\ 1& \text{if }n=5,\\ 16& \text{if }n\ge 6.\end{array}$$

From Lemma 2.10 it follows that T is a quasi-∗-class operator. Since $\{{\alpha }_n:n\in \mathbb{Z}\}$ is a bounded sequence of positive numbers with $inf\{{\alpha }_n:n\in \mathbb{Z}\}>0$, T is an invertible operator [[19], Proposition II.6.8]. But $T^{-1}$ is not a quasi-∗-class operator, which follows from Lemma 2.11, for $n=4$.

Theorem 2.13 Let $T\in L(H)$ be a quasi-∗-class operator and $\mathbb{D}=\{z:|z|<1\}$. If $T^{\ast }$ is a hypercyclic operator and for every hyperinvariant $M\subseteq H$ of T, the inverse of $T{|}_M$, whenever it exists, is a normaloid operator, then $\sigma (T{|}_M)\cap \mathbb{D}\ne \mathrm{\varnothing }$ and $\sigma (T{|}_M)\cap (\mathbb{C}\setminus \overline{\mathbb{D}})\ne \mathrm{\varnothing }$.

Proof Assume that $T^{\ast }$ is a hypercyclic operator. Then there exists a vector $x\in H$ such that $\overline{{\{{(T^{\ast })}^{n}x\}}_{n=0}^{\mathrm{\infty }}}=H$. Let $S=T{|}_M$ for some closed T-invariant subspace and let P be the orthogonal projection of H onto M. Since ${(S^{\ast })}^{n}Px=P{(T^{\ast })}^{n}x$ for each $n\in \mathbb{N}\cup \{0\}$ we have

$$\overline{{\{{\left(S^{\ast }\right)}^n(Px)\}}_{n=0}^{\mathrm{\infty }}}=P\overline{{\left\{{\left(T^{\ast }\right)}^{n}x\right\}}_{n=0}^{\mathrm{\infty }}}=P(H)=M,$$

thus $S^{\ast }$ is hypercyclic.

From [[20], Corollary 3] we have $\parallel S^{\ast }\parallel >1$. Since S is a quasi-∗-class , S is normaloid, thus $r(T{|}_M)=\parallel S\parallel =\parallel S^{\ast }\parallel >1$. Therefore $\sigma (T{|}_M)\cap (\mathbb{C}\setminus \overline{\mathbb{D}})\ne \mathrm{\varnothing }$.

Suppose that $\sigma (T{|}_M)\subset (\mathbb{C}\setminus \overline{\mathbb{D}})$. Then $\sigma (S^{-1})\subset \overline{\mathbb{D}}$, and since $S^{-1}$ is normaloid, $\parallel S^{-1}\parallel =r(S^{-1})\le 1$. Since $S^{\ast }$ is hypercyclic, from [[20], Theorem 6] ${(S^{\ast })}^{-1}$ is hypercyclic, so $\parallel {(S^{\ast })}^{-1}\parallel >1$. Thus $\parallel S^{-1}\parallel =\parallel {(S^{\ast })}^{-1}\parallel >1$. This is a contradiction, therefore $\sigma (T{|}_M)\cap \mathbb{D}\ne \mathrm{\varnothing }$. □