A class of generalized pseudo-splines

Abstract

In this paper, a class of refinable functions is given by smoothening pseudo-splines in order to get divergence free and curl free wavelets. The regularity and stability of them are discussed. Based on that, the corresponding Riesz wavelets are constructed.

1 Introduction

We denote by ℤ and ℝ the set of integers and real numbers, respectively. Let $L_p(\mathbb{R})$ stand for the classical Lebesgue space

$$L_p(\mathbb{R}):=\{f,{\int }_{\mathbb{R}}|f(t){|}^{p}dt<+\mathrm{\infty }\}$$

with the norm ${\parallel f\parallel }_p={({\int }_{\mathbb{R}}{|f(t)|}^{p}dt)}^{\frac{1}{p}}$ and $L_{\mathrm{\infty }}(\mathbb{R})$ consisting of all Lebesgue measurable and bounded functions on ℝ. Similarly, the discrete space ${\ell }_p(\mathbb{Z}):=\{\{a_n\},{\sum }_n{|a_n|}^p<+\mathrm{\infty },n\in \mathbb{Z}\}$ with ${\parallel \{a_n\}\parallel }_p={({\sum }_n{|a_n|}^p)}^{\frac{1}{p}}$. As usual, given $f\in L_1(\mathbb{R})\cap L_2(\mathbb{R})$, its Fourier transform is defined by

$$\hat{f}(\omega ):={\int }_{\mathbb{R}}f(x)e^{-ix\omega }dx$$

on ℝ. The Fourier transform of a function in $L_2(\mathbb{R})$ is understood as the unitary extension. We write $h=f\ast g$ for the convolution $h(x)={\int }_{\mathbb{R}}f(x-t)g(t)dt$, defined for any pair of functions f and g such that the integral exists almost everywhere. Clearly, $\hat{h}(\omega )=\hat{f}(\omega )\hat{g}(\omega )$ in the frequency domain, when all the Fourier transforms exist in that formula. Given $g\in L_2(\mathbb{R})$, $\{g(x-k),k\in \mathbb{Z}\}$ is called a Riesz basis of its linearly generating space, if for each $\{{\lambda }_k\}\in {\ell }_2(\mathbb{Z})$ there exist two positive constants A and B such that

$$A\sum _{k\in \mathbb{Z}}{\lambda }_k^2\le {\parallel \sum _{k\in \mathbb{Z}}{\lambda }_{k}g(x-k)\parallel }_2^2\le B\sum _{k\in \mathbb{Z}}{\lambda }_k^2.$$

(1.1)

The numbers A, B are called lower Riesz bound and upper Riesz bound, respectively.

Multiresolution analysis provides a classical method to construct wavelets.

Definition 1 A multiresolution analysis of $L_2(\mathbb{R})$ means a sequence of closed linear subspaces $V_j$ of $L_2(\mathbb{R})$ which satisfies

• (i) $V_j\subset V_{j+1}$, $j\in \mathbb{Z}$,

• (ii) $f(x)\in V_j$ if and only if $f(2x)\in V_{j+1}$,

• (iii) $\overline{{\bigcup }_{j\in \mathbb{Z}}{V}_j}=L_2(\mathbb{R})$ and ${\bigcap }_{j\in \mathbb{Z}}{V}_j=\{0\}$,

• (iv) there exists a function $\varphi \in L_2(\mathbb{R})$ such that $\{\varphi (x-k),k\in \mathbb{Z}\}$ forms a Riesz basis of $V_0$.

The function ϕ in Definition 1 is said to be a scaling function, if it satisfies

$$\varphi (x)=\sum _k{a}_k\varphi (2x-k)$$

(1.2)

for some sequence $\{a_k\}\in {\ell }_2(\mathbb{Z})$. Define the Fourier series $\hat{c}$ of a sequence $\{c_k\}\in {\ell }_2(\mathbb{Z})$ by

$$\hat{c}(\xi ):=\sum _{k\in \mathbb{Z}}{c}_k{e}^{-ik\xi },\xi \in \mathbb{R}.$$

Then the refinement equation (1.2) becomes

$$\hat{\varphi }(\xi )=\hat{a}(\xi /2)\hat{\varphi }(\xi /2),\xi \in \mathbb{R}.$$

The function $\hat{a}$ is called the refinement mask of ϕ. The pseudo-spline of Type I was first introduced in [1] to construct tight framelets. The pseudo-spline of Type II was first studied by Dong and Shen in [2]. There have been many developments in the theory of pseudo-splines over the past ten years [3, 4]. Its applications in image denoising and image in-painting are also very extensive [5, 6]. The pseudo-spline is defined by its refinement mask. The refinement mask of a pseudo-spline of Type I with order $(m,\ell )$ is given by

$$|{}_1\hat{a}(\xi ){|}^2:=|{}_1{\hat{a}}_{m,\ell }(\xi ){|}^2:={cos}^{2m}(\xi /2)\sum _{j=0}^{\ell }\left(\begin{array}{c}m+\ell \\ j\end{array}\right){sin}^{2j}(\xi /2){cos}^{2(\ell -j)}(\xi /2)$$

(1.3)

and the refinement of a pseudo-spline of Type II with order $(m,\ell )$ is given by

$${}_2\hat{a}(\xi ):={}_2{\hat{a}}_{m,\ell }(\xi ):={cos}^{2m}(\xi /2)\sum _{j=0}^{\ell }\left(\begin{array}{c}m+\ell \\ j\end{array}\right){sin}^{2j}(\xi /2){cos}^{2(\ell -j)}(\xi /2).$$

(1.4)

The mask of Type I is obtained by taking the square root of the mask of Type II using the Fejér-Riesz lemma [7], i.e. ${}_2\hat{a}(\xi )={|{}_1\hat{a}(\xi )|}^2$. The corresponding pseudo-spline can be defined in terms of their Fourier transform, i.e.

$${}_k\hat{\varphi }_{m,\ell }(\xi ):=\prod _{j=1}^{\mathrm{\infty }}{}_k{\hat{a}}_{m,\ell }\left(2^{-j}\xi \right),k=1,2.$$

In order to smoothen the pseudo-spline, one can use the convolution method. Take the smoothed pseudo-spline

where ${\chi }_{[-\frac{1}{2},\frac{1}{2}]}$ denotes the characteristic function of interval $[-\frac{1}{2},\frac{1}{2}]$ and $n⩾m$. This is equivalent to

$${\hat{\varphi }}_{n,m,\ell }(\xi )={\hat{\varphi }}_{m,\ell }(\xi ){\left(\frac{sin(\xi /2)}{\xi /2}\right)}^{n-m}.$$

Thus the symbol of ${\varphi }_{n,m,\ell }$ becomes

$${\hat{a}}_{n,m,\ell }(\xi )={\hat{\varphi }}_{n,m,\ell }(2\xi )/{\hat{\varphi }}_{n,m,\ell }(\xi )={\hat{a}}_{m,\ell }(\xi ){(cos(\xi /2))}^{n-m}.$$

Therefore, we define the smoothed pseudo-spline by its refinement mask for Type I:

$$|{}_1{\hat{a}}_{n,m,\ell }{|}^2:={cos}^{2n}(\xi /2)\sum _{j=0}^{\ell }\left(\begin{array}{c}m+\ell \\ j\end{array}\right){sin}^{2j}(\xi /2){cos}^{2(\ell -j)}(\xi /2)$$

(1.5)

and for Type II:

$${}_2\hat{\varphi }_{r,m,\ell }:={cos}^r(\xi /2)\sum _{j=0}^{\ell }\left(\begin{array}{c}m+\ell \\ j\end{array}\right){sin}^{2j}(\xi /2){cos}^{2(\ell -j)}(\xi /2),$$

where $r⩾2m$. When $r=2m$, it is the pseudo-spline. When $r\ne 2m$, it can be considered as an extension of pseudo-spline. Define the translated form of the Type II by

$${}_T\hat{\varphi }_{r,m,\ell }(\xi ):={e^{-ir\frac{\xi }{2}}}_2{\hat{\varphi }}_{r,m,\ell }(\xi ).$$

Then we get the differential relation

$${}_T\varphi _{r+1,m,\ell }^{\prime }(x)={}_T{\varphi }_{r,m,\ell }(x){-}_T{\varphi }_{r,m,\ell }(x-1).$$

(1.6)

This inherits the property of a B-spline.

Remark 1 One may think that smoothing the pseudo-splines by convolving them with B-splines seems unnecessary since one can simply increase m of the original pseudo-splines. However, by increasing m, we cannot get the differential relation (1.6), which is important for the construction of divergence free wavelets and curl free wavelets in the analysis of incompressible turbulent flows [8, 9].

Remark 2 Similar to the definition of (1.5), we can define a smoothed dual pseudo-spline by its refinement mask,

$${\hat{b}}_{n,m,\ell }(\xi )=e^{i\xi /2}{cos}^{2n+1}(\xi /2)\sum _{j=0}^{\ell }\left(\begin{array}{c}m+1/2+\ell \\ j\end{array}\right){sin}^{2j}(\xi /2){cos}^{2(\ell -j)}(\xi /2),$$

(1.7)

as an extension of dual pseudo-splines in [3] and get the corresponding wavelets.

Remark 3 In addition, one can assume $n\in \mathbb{R}$ in (1.5) and (1.7), as a generalization of fractional splines in [10].

2 Some lemmas

This section gives some lemmas that will be used to prove several results of this paper. We start with some results from [2].

Lemma 1 [2]

For given nonnegative integers m, j, ℓ,

$$2^{\ell }{\left(\begin{array}{c}m+\ell \\ \ell \end{array}\right)}^{\frac{1}{2}}⩽\sum _{j=0}^{\ell }\left(\begin{array}{c}m+\ell \\ j\end{array}\right)\mathit{\text{for all }}m⩾1\mathit{\text{ and }}0⩽\ell ⩽m-1.$$

This lemma will be used in Section 4 in order to prove the Riesz basis property of wavelets. Define $P_{m,\ell }(y):={\sum }_{j=0}^{\ell }\left(\begin{array}{c}m+\ell \\ j\end{array}\right)y^j{(1-y)}^{\ell -j}$, $R_{m,\ell }(y):={(1-y)}^m{P}_{m,\ell }(y)$ and $R_{r,m,\ell }={(1-y)}^{\frac{r}{2}}{P}_{m,\ell }(y)$ where $y={sin}^2(\xi /2)$, r, m, ℓ are nonnegative integers and $r⩾2m$. Then one can find that

$$R_{m,\ell }({sin}^2(\xi /2)){=}_2{\hat{a}}_{m,\ell }(\xi )\text{and}{R}_{r,m,\ell }({sin}^2(\xi /2)){=}_2{\hat{a}}_{r,m,\ell }(\xi )$$

and the following lemma holds.

Lemma 2 [2]

For nonnegative integers m and ℓ with $\ell ⩽m-1$, let $P_{m,\ell }$ and $R_{m,\ell }$ be the polynomials defined above. Then

• (1) $P_{m,\ell }(y)={\sum }_{j=0}^{\ell }\left(\begin{array}{c}m-1+j\\ j\end{array}\right)y^j$;

• (2) $R_{m,\ell }^{\prime }(y)=-(m+\ell )\left(\begin{array}{c}m+\ell -1\\ \ell \end{array}\right)y^{\ell }{(1-y)}^{m-1}$.

With the two lemmas in hand, the basic property of the polynomial $R_{r,m,\ell }$, which will be used in Section 4, is given.

Lemma 3 For nonnegative integers r, m and ℓ,

• (1) define $Q(y):=R_{r,m,\ell }(y)+R_{r,m,\ell }(1-y)$; then

  $$\underset{y\in [0,1]}{min}Q(y)=Q\left(\frac{1}{2}\right)=2^{1-\frac{r}{2}-\ell }\sum _{j=0}^{\ell }\left(\begin{array}{c}m+\ell \\ j\end{array}\right);$$

• (2) define $S(y):=R_{r,m,\ell }^2(y)+R_{r,m,\ell }^2(1-y)$; then

  $$\underset{y\in [0,1]}{min}S(y)=S\left(\frac{1}{2}\right)=2^{1-r-2\ell }{\left(\sum _{j=0}^{\ell }\left(\begin{array}{c}m+\ell \\ j\end{array}\right)\right)}^2.$$

Proof Since $R_{r,m,\ell }(y)={(1-y)}^{\frac{r}{2}-m}{R}_{m,\ell }(y)$, its derivative is

$$R_{r,m,\ell }^{\prime }(y)=-(\frac{r}{2}-m){(1-y)}^{\frac{r}{2}-m-1}{R}_{m,\ell }(y)+{(1-y)}^{\frac{r}{2}-m}{R}_{m,\ell }^{\prime }(y).$$

So the derivative is $Q^{\prime }(y)=R_{r,m,\ell }^{\prime }(y)+R_{r,m,\ell }^{\prime }(1-y)=I+\mathit{II}$, where

$$I=(\frac{r}{2}-m)y^{\frac{r}{2}-m-1}{R}_{m,\ell }(1-y)-(\frac{r}{2}-m){(1-y)}^{\frac{r}{2}-m-1}{R}_{m,\ell }(y)$$

and

$$\mathit{II}={(1-y)}^{\frac{r}{2}-m}{R}_{m,\ell }^{\prime }(y)-y^{\frac{r}{2}-m}{R}_{m,\ell }^{\prime }(1-y).$$

Now, we compute them, respectively. For I, by using (1) of Lemma 2, one has

$$I=(\frac{r}{2}-m)\sum _{j=0}^{\ell }\left(\begin{array}{c}m-1+j\\ j\end{array}\right)[y^{\frac{r}{2}-1}{(1-y)}^j-y^j{(1-y)}^{\frac{r}{2}-1}].$$

For II, by using (2) of Lemma 2, one has

$$\mathit{II}=(m+\ell )\left(\begin{array}{c}m+\ell -1\\ \ell \end{array}\right)[y^{\frac{r}{2}-1}{(1-y)}^{\ell }-{(1-y)}^{\frac{r}{2}-1}{y}^{\ell }].$$

For $j=0,\dots ,\ell$, since $y^{\frac{r}{2}-1}{(1-y)}^j⩽{(1-y)}^{\frac{r}{2}-1}{y}^j$ for all $y\in [0,\frac{1}{2}]$ and $y^{\frac{r}{2}-1}{(1-y)}^j⩾{(1-y)}^{\frac{r}{2}-1}{y}^j$ for all $y\in [\frac{1}{2},1]$, one has

$$Q^{\prime }(y)=I+\mathit{II}\{\begin{array}{ll}⩽0,& y\in [0,\frac{1}{2}];\\ ⩾0,& y\in [\frac{1}{2},1].\end{array}$$

This means $Q(y)$ reaches its minimum value at the point $y=1/2$. Furthermore,

$$Q(1/2)=2R_{r,m,\ell }(1/2)=2^{1-\frac{r}{2}}{P}_{m,\ell }(1/2)=2^{1-\frac{r}{2}-\ell }\sum _{j=0}^{\ell }\left(\begin{array}{c}m+\ell \\ j\end{array}\right).$$

This completes the proof of (1). For (2) of this lemma, since

$$S(y)=R_{r,m,\ell }^2(y)+R_{r,m,\ell }^2(1-y)={(1-y)}^{r-2m}{R}_{m,\ell }^2(y)+y^{r-2m}{R}_{m,\ell }^2(1-y),$$

we have $S^{\prime }(y)=\mathit{III}+\mathit{IV}$, where

$$\mathit{III}=(r-2m)[y^{r-2m-1}{R}_{m,\ell }^2(1-y)-{(1-y)}^{r-2m-1}{R}_{m,\ell }^2(y)]$$

and

$$\mathit{IV}=2{(1-y)}^{r-2m}{R}_{m,\ell }(y)R_{m,\ell }^{\prime }(y)-2y^{r-2m}{R}_{m,\ell }(1-y)R_{m,\ell }^{\prime }(1-y).$$

For III, by (1) of Lemma 2, we have

$$\begin{array}{rcl}\mathit{III}& =& (r-2m)[y^{r-1}{P}_{m,\ell }^2(1-y)-{(1-y)}^{r-1}{P}_{m,\ell }^2(y)]\\ =& (r-2m)({\left(\sum _{j=0}^{\ell }\left(\begin{array}{c}m-1+j\\ j\end{array}\right)y^{\frac{1}{2}(r-1)}{(1-y)}^j\right)}^2\\ -{\left(\sum _{j=0}^{\ell }\left(\begin{array}{c}m-1+j\\ j\end{array}\right){(1-y)}^{\frac{1}{2}(r-1)}{y}^j\right)}^2)\\ =& (r-2m)\left(\sum _{j=0}^{\ell }\left(\begin{array}{c}m-1+j\\ j\end{array}\right)(y^{\frac{1}{2}(r-1)}{(1-y)}^j+{(1-y)}^{\frac{1}{2}(r-1)}{y}^j)\right)\\ \times \left(\sum _{j=0}^{\ell }\left(\begin{array}{c}m-1+j\\ j\end{array}\right)(y^{\frac{1}{2}(r-1)}{(1-y)}^j-{(1-y)}^{\frac{1}{2}(r-1)}{y}^j)\right).\end{array}$$

For IV, by (2) of Lemma 2, we have

$$\begin{array}{rcl}\frac{\mathit{IV}}{2}& =& {(1-y)}^{r-2m}{P}_{m,\ell }(y)R_{m,\ell }^{\prime }(y)-y^{r-2m}{P}_{m,\ell }(1-y)R_{m,\ell }^{\prime }(1-y)\\ =& R_{m,\ell }^{\prime }(y)\sum _{j=0}^{\ell }\left(\begin{array}{c}m-1+j\\ j\end{array}\right)y^j{(1-y)}^{r-2m}-R_{m,\ell }^{\prime }(1-y)\sum _{j=0}^{\ell }\left(\begin{array}{c}m-1+j\\ j\end{array}\right){(1-y)}^j{y}^{r-2m}\\ =& (m+\ell )\left(\begin{array}{c}m-1+j\\ j\end{array}\right)\left(\sum _{j=0}^{\ell }\left(\begin{array}{c}m-1+j\\ j\end{array}\right)(y^{r-1}{(1-y)}^{\ell +j}-y^{\ell +j}{(1-y)}^{r-1})\right).\end{array}$$

Since

$$y^{\frac{1}{2}(r-1)}{(1-y)}^j-{(1-y)}^{\frac{1}{2}(r-1)}{y}^j\{\begin{array}{ll}⩽0,& y\in [0,\frac{1}{2}];\\ ⩾0,& y\in [\frac{1}{2},1],\end{array}$$

and for every j,

$$y^{r-1}{(1-y)}^{\ell +j}-y^{\ell +j}{(1-y)}^{r-1}\{\begin{array}{ll}⩽0,& y\in [0,\frac{1}{2}];\\ ⩾0,& y\in [\frac{1}{2},1],\end{array}$$

we have

$$S^{\prime }(y)=\mathit{III}+\mathit{IV}\{\begin{array}{ll}⩽0,& y\in [0,\frac{1}{2}];\\ ⩾0,& y\in [\frac{1}{2},1].\end{array}$$

This means $S(y)$ reaches its minimum at point $y=1/2$. Furthermore, we have

$$S(1/2)=2{(2^{-\frac{r}{2}}{P}_{m,\ell }(y))}^2=2^{1-r-2\ell }{\left(\sum _{j=0}^{\ell }\left(\begin{array}{c}m-1+j\\ j\end{array}\right)\right)}^2.$$

This completes the lemma. □

3 Regularity and stability of scaling function

In this section, we discuss the regularity and stability of a scaling function generated by the refinement mask of a smoothed pseudo-spline. Let

$$\hat{\varphi }(\xi ):=\prod _{j=1}^{\mathrm{\infty }}\hat{a}\left(2^{-j}\xi \right).$$

Then the decay of $|\hat{\varphi }|$ can be characterized by $|\hat{a}|$ as stated in the following theorem.

Theorem 1 [2]

Let $\hat{a}(\xi )$ be a refinement mask of the refinable function ϕ of the form

$$|\hat{a}(\xi )|={cos}^n(\xi /2)|\mathcal{L}(\xi )|,\xi \in [-\pi ,\pi ].$$

Suppose that

$$\begin{array}{c}|\mathcal{L}(\xi )|⩽\left|\mathcal{L}\left(\frac{2\pi }{3}\right)\right|\mathit{\text{for }}|\xi |⩽\frac{2\pi }{3},\hfill \\ |\mathcal{L}(\xi )\mathcal{L}(2\xi )|⩽|\mathcal{L}\left(\frac{2\pi }{3}\right){|}^2\mathit{\text{for }}\frac{2\pi }{3}⩽|\xi |⩽\pi .\hfill \end{array}$$

Then $|\hat{\varphi }(\xi )|⩽C{(1+|\xi |)}^{-n+\kappa }$, with $\kappa =log(\mathcal{L}(|\frac{2\pi }{3})|)/log2$, and this decay is optimal.

In order to use this lemma, one needs to consider the polynomial corresponding to $\mathcal{L}(\xi )$. In fact, Dong and Shen give an important proposition to estimate it in the following proposition.

Proposition 1 [2]

Let $P_{m,\ell }(y)$ be defined as in Section  2, where m, ℓ are nonnegative integers with $\ell ⩽m-1$. Then

$$\begin{array}{c}{P}_{m,\ell }(y)⩽P_{m,\ell }\left(\frac{3}{4}\right)\mathit{\text{for }}y\in [0,\frac{3}{4}],\hfill \\ P_{m,\ell }(y)P_{m,\ell }(4y(1-y))⩽{\left(P_{m,\ell }\left(\frac{3}{4}\right)\right)}^2\mathit{\text{for }}y\in [\frac{3}{4},1].\hfill \end{array}$$

Combing Theorem 1 and Proposition 1, we have the following theorem, which characterizes the regularity of a smoothed pseudo-spline.

Theorem 2 Let ₂ϕ be the smoothed pseudo-spline of Type II with order r, m, ℓ, then

$$|{}_2\hat{\varphi }(\xi )|⩽C{(1+|\xi |)}^{-r+\kappa },$$

where $\kappa =log(P_{m,\ell }(\frac{3}{4}))/log2$. Consequently, ${}_2\varphi \in C^{{\alpha }_2-ϵ}$ where ${\alpha }_2=r-\kappa -1$. Furthermore, let ₁ϕ be the smoothed pseudo-spline of Type I with order n, m, ℓ. Then

$$|{}_1\hat{\varphi }(\xi )|⩽C{(1+|\xi |)}^{-n+\frac{\kappa }{2}}.$$

Consequently, ${}_1\varphi \in C^{{\alpha }_1-ϵ}$ with ${\alpha }_1=n-\frac{\kappa }{2}-1$.

Proof Notice that $|\mathcal{L}(\xi )|$ in Theorem 1 is exactly $P_{m,\ell }({sin}^2(\frac{\xi }{2}))$ and $4y(1-y)={sin}^2(\xi )$; one can easily prove this theorem by Theorem 1 and Proposition 1. □

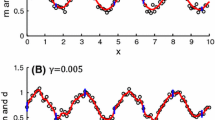
This theorem shows ${}_k\varphi \in L_2(\mathbb{R})$ for $k=1,2$. Since $r⩾2m$, the regularity of ϕ is better than a pseudo-spline but the support is longer. For $r=6$, $m=2$, $\ell =1$ the smoothed pseudo-spline ${}_2\varphi _{r,m,\ell }$ is shown in Figure 1.

Figure 1

The scaling function ${}_{\mathbf{2}}\mathit{\varphi }_{\mathbf{3}\mathbf{,}\mathbf{2}\mathbf{,}\mathbf{1}}$ .

Now, we consider the stability of the smoothed pseudo-spline. When ϕ is compactly supported in $L_2(\mathbb{R})$, it was shown by Jia and Micchelli [11] that the upper Riesz bound in (1.1) always exists. Furthermore, they assert that the existence of a lower Riesz bound is equivalent to

$${(\hat{\varphi }(\xi +2k\pi ))}_{k\in \mathbb{Z}}\ne \mathbf{0}\text{for all }\xi \in \mathbb{R},$$

(3.1)

where 0 denotes the zero sequence in ${\ell }_2(\mathbb{Z})$. Since a smoothed pseudo-spline is compactly supported and belongs to $L_2(\mathbb{R})$ for $k=1,2$, the stability is equivalent to (3.1).

Theorem 3 Smoothed pseudo-splines are stable.

Proof By the definition of refinement mask, for each fixed $\frac{r}{2}⩾m⩾1$ and for any $0⩽\ell ⩽m-1$, ${cos}^{2m}(\xi /2)⩽{}_2{\hat{a}}_{r,m,\ell }(\xi )$ holds for all $\xi \in \mathbb{R}$. Therefore, we have

$$|{\hat{B}}_r(\xi )|⩽|{\hat{\varphi }}_{r,m,\ell }(\xi )|,$$

where $B_r$ stands for the B-spline with order r. Since $B_r$ is stable, the vector ${({\hat{B}}_r(\xi +2k\pi ))}_{k\in \mathbb{Z}}\ne \mathbf{0}$. Hence ${({\hat{\varphi }}_{r,m,\ell }(\xi +2k\pi ))}_{k\in \mathbb{Z}}\ne \mathbf{0}$.

For a smoothed pseudo-spline of Type I, since ${}_2\hat{a}_{2n,m,\ell }(\xi )={|{}_1{\hat{a}}_{n,m,\ell }|}^2={}_1{\hat{a}}_{n,m,\ell }(\xi ){\cdot }_1{\hat{a}}_{n,m,\ell }(-\xi )$, one has

$${}_2\hat{\varphi }_{2n,m,\ell }(\xi )={}_1{\hat{\varphi }}_{n,m,\ell }(\xi )\cdot {}_1{\hat{\varphi }}_{n,m,\ell }(-\xi ).$$

Therefore, the set of zeros of ${}_1\hat{\varphi }_{n,m,\ell }(\xi )$ is contained in that of ${}_2\hat{\varphi }_{2n,m,\ell }(\xi )$ and this guarantees the stability of ${}_1\varphi (\xi )$. □

This theorem shows the stability of a smoothed pseudo-spline. From the definition of a Riesz basis, one can find that the translate of a smoothed pseudo-spline is also linearly independent.

4 Riesz wavelets

Since all smoothed pseudo-splines are compactly supported, refinable, stable in $L_2(\mathbb{R})$, the sequence of spaces ${(V_n)}_{n\in \mathbb{Z}}$ defined via Definition 1 forms an MRA. The corresponding wavelets can be constructed by the classical method. Define

$$\hat{\psi }(\xi )=\hat{b}\left(\frac{\xi }{2}\right)\hat{\varphi }\left(\frac{\xi }{2}\right),\text{where }\hat{b}(\xi )=e^{-i\xi }\overline{\hat{a}(\xi +\pi )}$$

and $X(\psi ):=\{{\psi }_{n,k}=2^{n/2}\psi (2^n-k),n,k\in \mathbb{Z}\}$. Then $X(\psi )$ is a Riesz basis. To prove this, the following theorem is needed.

Theorem 4 [2]

Let $\hat{a}(\xi )$ be a finitely supported refinement mask of a refinable function $\varphi \in L_2(\mathbb{R})$ with $\hat{a}(0)=1$ and $\hat{a}(\pi )=0$, such that $\hat{a}$ can be factorized into the form

$$|\hat{a}(\xi )|={cos}^n(\xi /2)|\mathcal{L}(\xi )|,\xi \in [-\pi ,\pi ],$$

where ℒ is the Fourier series of a finitely supported sequence with $\mathcal{L}(\pi )\ne 0$. Suppose that

$$|\hat{a}(\xi ){|}^2+|\hat{a}(\xi +\pi ){|}^2\ne 0,\xi \in [-\pi ,\pi ].$$

Define $\hat{\psi }(2\xi ):=e^{-i\xi }\overline{\hat{a}(\xi +\pi )}\hat{\varphi }(\xi )$ and $\tilde{\mathcal{L}}:=\frac{\mathcal{L}(\xi )}{{|\hat{a}(\xi )|}^2+{|\hat{a}(\xi +\pi )|}^2}$. Assume that ${\parallel \mathcal{L}(\xi )\parallel }_{L_{\mathrm{\infty }}(\mathbb{R})}<2^{n-1}$ and ${\parallel \tilde{\mathcal{L}}(\xi )\parallel }_{L_{\mathrm{\infty }}(\mathbb{R})}<2^{n-1}$. Then $X(\psi )$ is a Riesz basis for $L_2(\mathbb{R})$.

From the above theorem, the key step is to estimate the upper Riesz bound of $|\mathcal{L}(\xi )|$ and $|\tilde{\mathcal{L}}(\xi )|$. Notice that

$$|{}_1{\hat{a}}_{n,m,\ell }(\xi ){|}^2={}_2{\hat{a}}_{2n,m,\ell }(\xi )={cos}^{2n}(\xi /2)P_{m,\ell }({sin}^2(\xi /2)).$$

One has $|{}_1\mathcal{L}(\xi )|={(P_{m,\ell }({sin}^2(\xi /2)))}^{\frac{1}{2}}$, $|{\mathcal{L}}_2(\xi )|=P_{m,\ell }({sin}^2(\xi /2))$ and

$$|{\tilde{\mathcal{L}}}_1|=\frac{{(P_{m,\ell }(y))}^{\frac{1}{2}}}{R_{2n,m,\ell }(y)+R_{2n,m,\ell }(1-y)},|{\tilde{\mathcal{L}}}_2|=\frac{P_{m,\ell }(y)}{R_{r,m,\ell }^2(y)+R_{r,m,\ell }^2(1-y)}.$$

Thus, we have the following theorem.

Theorem 5 Let _k ϕ, $k=1,2$ be the smoothed pseudo-spline of Types I and II with order $(r,n,m,\ell )$. The refinement masks _k a are given in (1.3) and (1.4). Define

$${}_k\hat{\psi }(2\xi ):=e^{-i\xi }{\overline{{}_k\hat{a}(\xi +\pi )}}_k\hat{\varphi }(\xi ).$$

Then $X(\psi )$ forms a Riesz basis for $L_2(\mathbb{R})$.

Proof By (1) of Lemma 3, one obtains

$$\begin{array}{rcl}{\parallel {}_1\tilde{\mathcal{L}}\parallel }_{L_{\mathrm{\infty }}(\mathbb{R})}& =& \underset{y\in [0,1]}{sup}\frac{{(P_{m,\ell }(y))}^{\frac{1}{2}}}{R_{2n,m,\ell }(y)+R_{2n,m,\ell }(1-y)}\\ ⩽& \frac{{\left(\begin{array}{c}m+\ell \\ \ell \end{array}\right)}^{\frac{1}{2}}}{{min}_{y\in [0,1]}(R_{2n,m,\ell }(y)+R_{2n,m,\ell }(1-y))}\\ ⩽& \frac{2^{n+\ell -1}{\left(\begin{array}{c}m+\ell \\ \ell \end{array}\right)}^{\frac{1}{2}}}{{\sum }_{j=0}^{\ell }\left(\begin{array}{c}m+\ell \\ j\end{array}\right)}.\end{array}$$

Applying Lemma 1, one obtains $\parallel {}_1{\tilde{\mathcal{L}}}_{\mathrm{\infty }}\parallel ⩽2^{n-1}<2^{n-\frac{1}{2}}$. Similarly, one can get

$${\parallel {}_2\tilde{\mathcal{L}}\parallel }_{L_{\mathrm{\infty }}(\mathbb{R})}⩽2^{r-1}<2^{r-\frac{1}{2}}.$$

Notice that

$${|{}_k\hat{a}(\xi )|}^2+{|{}_k\hat{a}(\xi +\pi )|}^2⩽1\text{for all }\xi \in \mathbb{R}.$$

Hence, $|{}_k\mathcal{L}(\xi )|⩽|{}_k\tilde{\mathcal{L}}(\xi )|$ for $k=1,2$. By using Theorem 4, one gets the desired result. □

By definition, the wavelets are also in $L_2(\mathbb{R})$ and have the same regularity as the scaling function. Still, the support is longer than for pseudo-spline wavelets. For $r=6$, $m=2$, $\ell =1$, the smoothed pseudo-spline ${}_2\psi _{6,2,1}$ is shown in Figure 2.

Figure 2

The corresponding wavelets.